-
The ultra-relativistic heavy-ion experimental programs at the Relativistic Heavy Ion Collider (RHIC) and the Large Hadron Collider (LHC) have created a new type of matter, namely the quark gluon plasma (QGP) [1–3]. One of the interesting features of QGP is jet quenching (parton energy loss): high energy partons propagate through the hot and dense medium, and lose their energy by interacting with the medium. Usually, the jet quenching phenomenon can be characterized by the jet quenching parameter, defined by the average transverse momentum square transferred from the traversing parton per unit mean free path [4]. Alternately, this phenomenon could be studied from the drag force: heavy quarks move through the QGP and experience a drag force, loosing energy as a consequence. In weakly coupling theories, this jet quenching has already been investigated in many studies [5–11]. However, a lot of experiments find strong evidence that QGP does not behave as a weakly coupled gas, but rather as a strongly coupled fluid. Consequently, computational techniques for strongly coupled, real-time QCD dynamics are required. Such techniques are now available via the gauge/gravity duality or AdS/CFT correspondence [12–14].
AdS/CFT, a conjectured duality between a string theory in the AdS space and a conformal field theory on the AdS space boundary, has provided many important insights for exploring various aspects of QGP [15]. In the framework of AdS/CFT, the drag force of a heavy quark moving in
$ {\cal N} = 4 $ SYM plasma was proposed in [16, 17]. Therein, this force could be related to the damping rate u (or referred to as the friction coefficient), defined by the Langevin equation,$ {\rm d}p/{\rm d}t = -u p+f $ , subject to a driving force f. For$ {\rm d}p/{\rm d}t = 0 $ , i.e., constant speed trajectory, f equals to the drag force. It was found that [16, 17]$ f_{\rm SYM} = -\frac{\pi\sqrt{\lambda}T^2}{2}\frac{v}{\sqrt{1-v^2}}, $

(1) where v, T,
$ \lambda $ are the quark velocity, plasma temperature and 't Hooft coupling, respectively. Subsequently, this has been generalized to various cases, such as chemical potential [18–20], finite coupling [21], non-commutativity plasma [22] and AdS/QCD models [23–25]. Other studies in this direction can be found in [26–34].In this study, we investigate the drag force in a soft wall-like model, i.e., the SW
$ _{T,\mu} $ model, which is motivated by the soft wall model of [35]. The SW$_{T,\mu} $ model was proposed in [36] to investigate the heavy quark free energy and the QCD phase diagram. It was shown that such a model provides a good phenomenological description of the quark-antiquark interaction as well as some hadronic properties. Recently, the authors of Ref. [37] investigated the imaginary potential in this model and found that the presence of the confining scale tends to reduce the quarkonia dissociation, and hence reverse the effect of the chemical potential. Moreover, there are other investigations of models of this type [38–43]. Motivated by this fact, we consider the drag force in this model to understand the possible physical implications of our results in this dual plasma. Another motivation for this study is that previous works either discuss the drag force in some strongly coupled thermal gauge theories (not holographic QCD) with chemical potential [18–20] or holographic QCD without chemical potential [23–25]. Here, we provide such analysis in holographic QCD with chemical potential.The structure of this paper is as follows. In the next section, we introduce the geometry of the SW
$ _{T,\mu} $ model given in Ref. [36]. In Section 3 and Section 4, we analyze the behavior of the drag force and the diffusion coefficient for the SW$ _{T,\mu} $ model. Summary and discussions are given in the final section. -
To begin with, we introduce the holographic models in terms of the action [44]
$\begin{split} S = &\frac{1}{16\pi G_5}\int {\rm d}^5x\sqrt{-g}\bigg({\cal R}-\frac{1}{2}\partial_M\phi\partial^M\phi\\&-V(\phi)-\frac{f(\phi)}{4}F_{MN}F^{MN}\bigg), \end{split}$

(2) where
$ G_5 $ is the five-dimensional (5D) Newton constant. g denotes the determinant of the metric$ g_{MN} $ .$ {\cal R} $ represents the Ricci scalar.$ \phi $ denotes the scalar that induces the deformation away from conformality.$ V(\phi) $ refers to the potential, which contains the cosmological constant and some other terms.$ F_{MN} $ and$ f(\phi) $ are the field strength tensor and gauge kinetic function, respectively.For Eq. (2), the equations of motion are
$ {\cal R}_{MN}-\frac{1}{2}{\cal R}g_{MN} = T_{MN}, $

(3) $ \nabla_M(f(\phi)F^{MN}) = 0, $

(4) $ \nabla^M\nabla_M\phi = V^\prime(\phi)+\frac{f^\prime(\phi)}{4}F_{MN}F^{MN}, $

(5) with
$\begin{split} T_{MN} =& \frac{1}{2}\left[f(\phi)\left(F_{MA}F_N^A-\frac{1}{4}g_{MN}F_{AB}F^{AB}\right)\right.\\&+\left.\left(\partial_M\phi\partial_N\phi-\frac{1}{2}g_{MN}\partial_A\phi\partial^A\phi\right)-g_{MN}V(\phi)\right], \end{split}$

(6) where
$ \nabla_M $ represents the Levi-Civita covariant derivative related to$ g_{MN} $ .With
$ \phi = 0 $ , the AdS black hole arises as a solution of Eq. (3)–(6). Subsequently, by considering a non-vanishing gauge-field component$ A_0 $ with the conditions$ A_0(z = 0) = \mu R,\qquad A_0(z_0 = z_h) = 0, $

(7) and solving Eq. (3)–(6), one can obtain the AdS-RN spacetime, whose metric is given by
$ {\rm d}s^2 = \frac{R^2}{z^2}\left(-f(z){\rm d}t^2+{\rm d}\vec{x}^2+\frac{{\rm d}z^2}{f(z)}\right), $

(8) with
$ f(z) = 1-(1+Q^2)\frac{z^4}{z_h^4}+Q^2\frac{z^6}{z_h^6}, \quad Q = \mu z_h/\sqrt{3} $

(9) where R is the AdS radius. Q denotes the black hole charge, constrained in
$ 0\leqslant Q\leqslant \sqrt{2} $ . z stands for the fifth coordinate with$ z = z_h $ as the horizon and$ z = 0 $ as the boundary.$ \mu $ represents the chemical potential. The chemical potential implemented here is not the quark (or baryon) chemical potential of QCD, but a chemical potential corresponding to the R-charge of$ {\cal N} = 4 $ SYM. Nevertheless, it could serve as a simple way of introducing finite density effects into the system.Moreover, the temperature of the black hole is
$ T = \frac{1}{\pi z_h}\left(1-\frac{Q^2}{2}\right). $

(10) Explicitly, for given
$ (T,\mu) $ in the boundary theory,$ (z_h,Q) $ of the bulk theory can be expressed as$ z_h(T,\mu) = \frac{3\pi T}{\mu^2}\left[\sqrt{1+\frac{2}{3\pi^2}(\frac{\mu}{T})^2}-1\right], $

(11) $ Q(T,\mu) = \frac{\sqrt{3}\pi T}{\mu}\left[\sqrt{1+\frac{2}{3\pi^2}(\frac{\mu}{T})^2}-1\right]. $

(12) To emulate confinement in the boundary theory at vanishing temperature, one can introduce a warp factor to the background, similar to [38, 45]. Then the metric of the SW
$ _{T,\mu} $ model is given by [36]$ {\rm d}s^2 = \frac{R^2}{z^2}h(z)\left(-f(z){\rm d}t^2+{\rm d}\vec{x}^2+\frac{{\rm d}z^2}{f(z)}\right), \quad h(z) = {\rm e}^{{c^2z^2}}, $

(13) where c is the deformation parameter (related to the confining scale) with the dimension of energy. Here, we will not focus on a specific model, but rather study the behavior of the drag force in a class of models parametrized by c. Thus, we make c dimensionless by normalizing it to fixed temperatures and express other quantities in units of c. In Ref. [46], it was shown that the range of
$ 0\leqslant c/T\leqslant 2.5 $ may be most relevant for a comparison with QCD. We employ this range in the current study.To proceed, if one uses
$ r = R^2/z $ is used as the radial coordinate, then metric Eq. (13) turns into$ {\rm d}s^2 = \frac{r^2h(r)}{R^2}(-f(r){\rm d}t^2+{\rm d}\vec{x}^2)+\frac{R^2h(r)}{r^2f(r)}{\rm d}r^2, $

(14) with
$ f(r) = 1-(1+Q^2)\left(\frac{r_h}{r}\right)^4+Q^2\left(\frac{r_h}{r}\right)^6,\quad h(r) = {\rm e}^{\textstyle\frac{c^2R^4}{r^2}}, $

(15) now
$ T = \dfrac{r_h}{\pi R^2}\left(1-\dfrac{Q^2}{2}\right) $ ,$ \mu = \dfrac{\sqrt{3}Qr_h}{R^2} $ . The horizon and boundary are$ r = r_h $ and$ r = \infty $ , respectively. Metric Eq. (13) and metric Eq. (14) are equivalent, but they have different coordinate systems. -
In this section, we will follow the argument in Refs. [16, 17] to analyze the drag force in the SW
$ _{T,\mu} $ model. The string dynamic is described by the Nambu-Goto action, given by$ S = -\frac{1}{2\pi\alpha^\prime}\int {\rm d}\tau {\rm d}\sigma\sqrt{-g}, $

(16) with g the determinant of the induced metric and
$ g_{\alpha\beta} = g_{\mu\nu}\frac{\partial X^\mu}{\partial\sigma^\alpha} \frac{\partial X^\nu}{\partial\sigma^\beta}, $

(17) with
$ g_{\mu\nu} $ the brane metric and$ X^\mu $ the target space coordinates.One considers a heavy quark moving with constant speed v in one direction, (e.g., the
$ x_1 $ direction) and takes the gauge$ t = \tau, \quad x_1 = vt+\xi(r),\quad x_2 = 0,\quad x_3 = 0,\quad r = \sigma, $

(18) then, the induced metric can be obtained by plugging Eq. (18) into Eq. (14),
$ g_{tt} = -\frac{r^2f(r)h(r)}{R^2}, \quad g_{xx} = \frac{r^2h(r)}{R^2},\quad g_{rr} = \frac{R^2h(r)}{r^2f(r)}. $

(19) Given that, the Lagrangian density reads
$\begin{split} \mathcal L =& \sqrt{-g_{rr}g_{tt}-g_{rr}g_{xx}v^2-g_{xx}g_{tt}{\xi^\prime}^2} \\=& h(r)\sqrt{\left[1-\frac{v^2}{f(r)}+\frac{r^4f(r)}{R^4}{\xi^\prime}^2\right]}, \end{split} $

(20) with
$ \xi^\prime = {\rm d}\xi/{\rm d}\sigma $ . As the action does not explicity depend on$ \xi $ , the energy-momentum current$ \Pi_\xi $ is a constant,$ \Pi_\xi = \frac{\partial\mathcal L }{\partial \xi^\prime} = \xi^\prime\frac{h(r)r^4f(r)/R^4}{\sqrt{1-\displaystyle\frac{v^2}{f(r)}+\displaystyle\frac{r^4f(r)}{R^4}{\xi^\prime}^2}} ={\rm constant} , $

(21) yielding
$ \xi^\prime = \frac{\Pi_\xi R^2}{r^2f(r)}\sqrt{\frac{f(r)-v^2}{r^4h^2(r)f(r)/R^4-{\Pi_\xi}^2}}, $

(22) where
$ \xi^\prime $ can be regarded as the configuration of the string tail.Near the horizon
$ r_h $ , the denominator and numerator (inside the square root of Eq. (22)) are negative for small r and positive for large r. Moreover, the ratio should be positive. Under these conditions, one obtains that the numerator and denominator should change sign at the same point (namely$ r_c $ ). For the numerator, one obtains$ f(r_c) = v^2, $

(23) resulting in
$ Q^2\left(\frac{r_h}{r_c}\right)^6-(1+Q^2)\left(\frac{r_h}{r_c}\right)^4+1-v^2 = 0, $

(24) For given values of Q and v, the analytic expressions of
$ r_h/r_c $ can be determined from Eq. (24), however these are cumbersome and not very illuminating. Here, we mainly focus on the numerical results.The denominator also changes sign at
$ r_c $ , yielding$ {\Pi_\xi} = \frac{r_c^2h(r_c)\sqrt{f(r_c)}}{R^2}, $

(25) with
$ h(r_c) = {\rm e}^{\textstyle\frac{c^2R^4}{r_c^2}}. $

(26) In contrast, the current density reads
$ \pi_x^r = -\frac{1}{2\pi\alpha^\prime}\xi^\prime\frac{g_{tt}g_{xx}}{-g}, $

(27) and the drag force reads
$ f = \frac{{\rm d}p_1}{{\rm d}t} = \sqrt{-g}\pi_x^r, $

(28) where the minus indicates that the drag force is against the direction of motion, as expected.
Next, applying the relations
$ \lambda = g_{YM}^2N_c = \frac{R^4}{{\alpha^\prime}^2},\qquad T = \frac{r_h}{\pi R^2}\left(1-\frac{Q^2}{2}\right), $

(29) one arrives at the drag force in the SW
$ _{T,\mu} $ model$ f = -\frac{\pi T^2\sqrt{\lambda}}{2}\frac{vh(r_c)}{\left(1-\dfrac{Q^2}{2}\right)^2\left(\dfrac{r_h}{r_c}\right)^2}. $

(30) By taking
$ Q = 0 $ (or$ \mu = 0 $ , which gives$\left (\dfrac{r_h}{r_c}\right)^2 = $ $ \sqrt{1-v^2} $ ) and$ c = 0 $ (corresponding to$ h(r_c) = 1 $ ) in Eq.(30), the results of$ {\cal N} = 4 $ SYM [16, 17] are recovered.To proceed, we compare the drag force in the SW
$ _{T,\mu} $ model with its counterpart of the$ {\cal N} = 4 $ SYM as the following$ \frac{f}{f_{\rm SYM}} = \frac{h(r_c)\sqrt{1-v^2}}{\left(1-\dfrac{Q^2}{2}\right)^2\left(\dfrac{r_h}{r_c}\right)^2}. $

(31) In Fig. 1, we plot
$ f/f_{\rm SYM} $ against$ \mu/T $ for two fixed values of$ c/T $ . The left panel is for$ c/T = 0.1 $ and the right one is for$ c/T = 2.5 $ . From these figures, one sees that the drag force in the SW$ _{T,\mu} $ model is larger than that of$ {\cal N} = 4 $ SYM plasma. Furthermore, increasing$ \mu/T $ leads to an enhanced drag force. Namely, the chemical potential enhances the drag force, consistently with [18–20]. Comparing the two panels, one finds that increasing$ c/T $ enhances the drag force as well. Thus, we can conclude that the confining scale also enhances the drag force, in accordance with Ref. [24].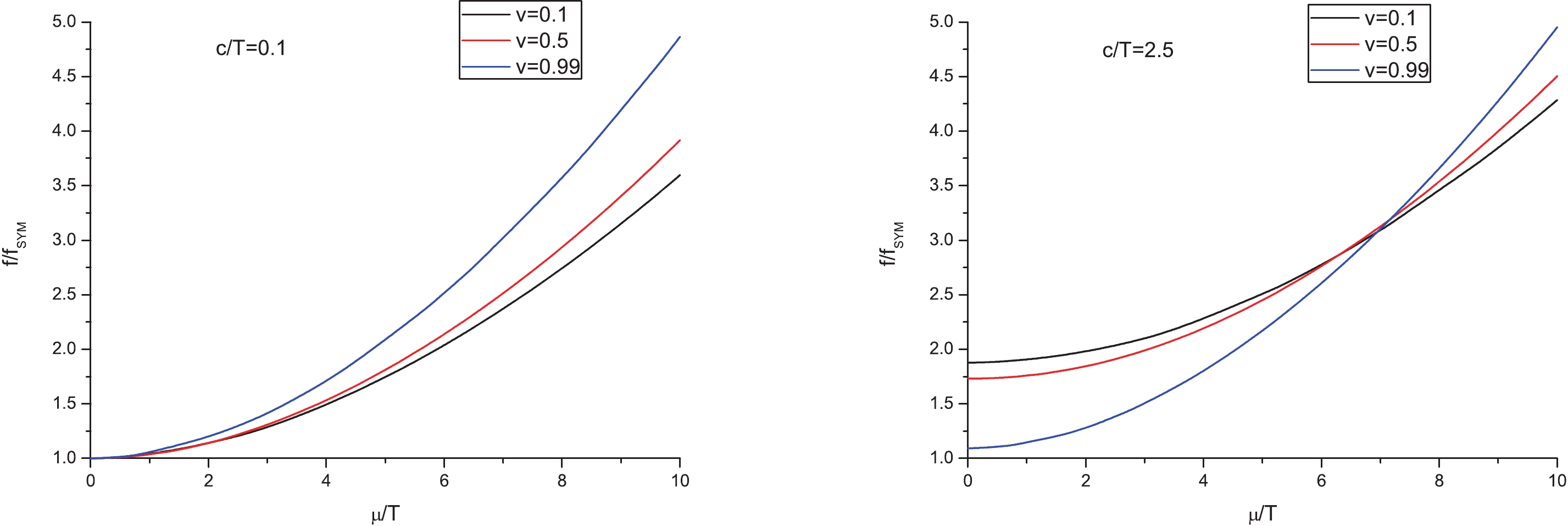
Figure 1. (color online)
$ f/f_{\rm SYM} $ versus$ \mu/T $ . The speed of light is assumed as a unit.In Fig. 2, we plot
$ f/f_{\rm SYM} $ versus v for various cases. From the left panel (small$ c/T $ case), one finds that increasing v enhances f, and this effect is especially more pronounced for large$ \mu/T $ . However, the right panel (large$ c/T $ case) is different: for small$ \mu/T $ ,$ f/f_{\rm SYM} $ decreases with v, whereas for large$ \mu/T $ the situation is reversed. Interestingly, a similar non-monotone behavior appears in the studies of the drag force with curvature-squared corrections [21].The effect of c and
$ \mu $ on the viscosity can be analyzed. A stronger force implies a more strongly coupled medium, closer to an ideal liquid. As the drag force in the SW$ _{T,\mu} $ model is larger than that of$ {\cal N} = 4 $ SYM, one could infer that the plasma is less viscous in the SW$ _{T,\mu} $ model than in$ {\cal N} = 4 $ SYM plasma.Recently, Ref. [26] has addressed the drag force in the soft wall model and estimated the spatial string tension at finite T and
$ \mu $ . -
In this section, we investigate the behavior of the diffusion coefficient in the SW
$ _{T,\mu} $ model. First, we remember the results of$ {\cal N} = 4 $ SYM. The drag force is given by$ f_{\rm SYM} = \frac{{\rm d}p_1}{{\rm d}t} = -\frac{\pi T^2\sqrt{\lambda}}{2}\frac{v}{\sqrt{1-v^2}}. $

(32) Assuming
$ p_1 = mv/\sqrt{1-v^2} $ , Eq. (37) becomes$ \frac{{\rm d}p_1}{{\rm d}t} = -\frac{\pi T^2\sqrt{\lambda}}{2}\frac{p_1}{m}. $

(33) Integrating Eq. (33), one obtains
$ p_1(t) = p_1(0){\rm e}^{-t/t_{\rm SYM}},\qquad t_{\rm SYM} = \frac{2m}{\pi T^2\sqrt{\lambda}}, $

(34) where
$ t_{\rm SYM} $ is the relaxation time of$ {\cal N} = 4 $ SYM.In contrast, the diffusion coefficient is related to the temperature, the heavy quark mass and the relaxation time as [16, 17]
$ D = \frac{T}{m}t_D. $

(35) Using the above approach, one readily gets
$ D_{\rm SYM} = \frac{2}{\pi T\sqrt{\lambda}}. $

(36) Likewise, from Eq. (30) one can rewrite the drag force in the SW
$ _{T,\mu} $ as$ f = -\frac{\pi p_1 T^2\sqrt{\lambda}}{2m}\frac{\sqrt{(1-v^2)}h(r_c)}{\left(1-\dfrac{Q^2}{2}\right)^2\left(\dfrac{r_h}{r_c}\right)^2}. $

(37) In a similar manner, one arrives at the diffusion coefficient in the SW
$ _{T,\mu} $ model$ D = \frac{T}{m}t_D = -\frac{T}{m}\frac{p_1}{f} = \frac{\left(1-\dfrac{Q^2}{2}\right)^2\left(\dfrac{r_h}{r_c}\right)^2}{h(r_c)\sqrt{1-v^2}}\frac{2}{\pi T\sqrt{\lambda}}. $

(38) In Fig. 3, we plot
$ D/D_{\rm SYM} $ as a function of$ \mu/T $ . One can see that$ \mu $ and c both reduce the diffusion coefficient.
Figure 3. (color online)
$ D/D_{\rm SYM} $ versus$ \mu/T $ . The speed of light is assumed as a unit.The inclusion of
$ \mu $ and c may influence the heavy quark mass. As discussed in Ref. [47], the relaxation time$ t_D = \dfrac{m}{T}D $ should be larger than the inverse temperature$ t_D>>\frac{1}{T}, $

(39) yielding
$ m>>\frac{h(r_c)\sqrt{1-v^2}}{\left(1-\dfrac{Q^2}{2}\right)^2\left(\dfrac{r_h}{r_c}\right)^2}\frac{\pi T\sqrt{\lambda}}{2}, $

(40) one can see that
$ \mu $ and c may enhance the heavy quark mass. -
We studied the drag force and diffusion coefficient in a soft wall model with finite temperature and chemical potential. Our aim is to understand the interplay between the presence of confining scale (such that the plasma is not conformal) and the chemical potential (the QGP is assumed to carry a finite, albeit small, baryon number density) when estimating the drag force of a heavy quark in strongly coupled plasma. It is shown that with fixed c, the presence of
$ \mu $ increases the drag force and decreases the diffusion coefficient, in agreement with the findings of [18–20]. Moreover, with fixed$ \mu $ the inclusion of c increases the drag force as well, in accordance with Ref. [24]. Therefore, our results ($ \mu $ and c exist at the same time) confirm the results of$ \mu $ , or c stands alone. In contrast, the results show that the plasma is less viscous in the SW$ _{T,\mu} $ model than in$ {\cal N} = 4 $ SYM.Nevertheless, the SW
$ _{T,\mu} $ model considered here has several drawbacks. First, it is not a consistent model, since it does not solve the Einstein equations. It would be interesting to provide such analysis in some consistent models, e.g., [48–52] (generally, the metrics of those models are only known numerically, such that the calculations are quite challenging. Further, in these models the dilaton field would be non-trivial, such that the coupling of the dilaton to the word-sheet should be taken into account [53–55]). Moreover, the SW$ _{T,\mu} $ model may omit one part in the phase transition, since Refs. [56–59] argued that there may be a first order phase transition if one sets the warp factor to be$ c z^2 $ and solves the equation of motion self-consistently. Consider these effects would be significant.Finally, it is also of interest to study the jet quenching parameter [60] and stopping distance [61–63] in the SW
$ _{T,\mu} $ model and compare it with the results of this work. We leave this as a further study.We would like to extend our gratitude to Dr. Zi-qiang Zhang for helpful and encouraging discussions.
Drag force on heavy quarks from holographic QCD
- Received Date: 2019-06-28
- Available Online: 2019-11-01
Abstract: We study the drag force of a relativistic heavy quark using a holographic QCD model with conformal invariance broken by a background dilaton. The effects of the chemical potential and the confining scale on this quantity are analyzed. The drag force in this model is shown to be larger than that of






 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF















 DownLoad:
DownLoad: