-
Phase transitions are an interesting and challenging experimental and theoretical topic, appearing in both biological [1] and physical systems [2]. In terms of physical systems, phase transitions play an important role in elementary particle physics [3], condensed matter [4-6], standard thermodynamics [7], cosmology [8], black holes [9] and other branches of physics. In general, there are at least three well-known approaches to discussing phase transitions inside a black hole. Two of these approaches are based on a macroscopic point of view (methods by Davies and Landau-Lifshitz discuss the behavior of heat capacity and thermodynamic fluctuations, respectively), and one of them is based on a microscopic viewpoint (thermodynamic geometry or Ruppeiner geometry). In this regard, we focus on the thermodynamic phase transition of black holes. There are several well-known approaches to studying the critical behavior of black holes. One of them uses heat capacity in the context of a canonical ensemble. The discontinuity of heat capacity is where the phase transition takes place. Another method is based on studying the van der Waals-like behavior of black holes in the extended phase space by considering the proportionality between the cosmological constant and dynamical pressure. This method is based on an equation of state, which originates from temperature. For more details, please refer to earlier reviews on phase transitions of black holes, black rings, black Saturns, and black membranes [10-13], where classical instability and horizon topology-changing transitions are also discussed.
In this paper, we consider a method for extracting the critical values and van der Waals phase transition based on the divergence of heat capacity (Davies' method). We should note that our method is applicable in the extended phase space thermodynamics of a black hole, in which the cosmological constant is considered as dynamic pressure. Because our approach uses the behavior of heat capacity, it is not a novel approach but an alternative way to obtain the properties of heat capacity based on the canonical ensemble. In other words, this method is the same as Davies' method but with a different point of view. We introduce an alternative approach for obtaining the critical values of the van der Waals-like behavior by using the slope of T versus S, and give two relevant examples. In other words, in the usual extended phase space, one calculates
$ T = \left( \displaystyle\frac{\partial M}{\partial S} \right) $ to obtain an equation of state. Other calculations and interpretations are based on such an equation of state. In our approach, we use$ \left( \displaystyle\frac{\partial T}{\partial S}\right) = \left( \displaystyle\frac{\partial ^{2}M}{\partial S^{2}}\right)=0 $ to obtain a new relation for pressure. This relation is free of temperature and is therefore not the usual equation of state. One can find that this relation and other related quantities and phase diagrams are different from those obtained in the usual extended phase space. Our method provides the possibility of mapping all phase transition points in a system. In addition, it can pin point the non-physical range of horizon radii, where the black hole solutions do not exist. Furthermore, the rate of increase of non-physical range of horizon radii for different critical values can be obtained. As a final point, we should note that our approach is quite different from Poincare's turning point method [14-17], which is a powerful tool for investigating turning point and stability. Unlike this method, our approach is based on the extended phase space thermodynamics and the slope of T versus S as a primitive equation for obtaining the dynamical pressure, where its maximum is related to a critical point and possible phase transition.The remainder of this paper is organized as follows: In Sec. 2, we give a brief review of the canonical ensemble and van der Waals approaches to black hole phase transitions. In Sec. 3, we introduce an alternative method for calculating the phase transition parameters, and we apply this method to the usual van der Waals system. In Sec. 4, we perform a case study on the Reissner-Nordström AdS black hole to demonstrate the proposed method in more detail. Finally, we provide several concluding remarks.
-
In the canonical ensemble, discontinuities of the heat capacity indicate the phase transition points. The heat capacity in the context of the canonical ensemble is given by
${C_Q} = \frac{T}{{{{\left( {\displaystyle\frac{{{\partial ^2}M}}{{\partial {S^2}}}} \right)}_Q}}} = T{\left( {\frac{{\partial S}}{{\partial T}}} \right)_Q}.$

(1) The main application of heat capacity is for studying thermal stability. Positivity of
$ C_{Q} $ can guarantee the thermal stability of a system, while its negativity is regarded as an instability.On the other hand, to study the critical behavior of a thermodynamical system, one is required to obtain an equation of state,
$P = P(T,V)$ . In the context of black hole thermodynamics, one may find the temperature of a typical black hole in the presence of the cosmological constant$ T = T(m,r_{+},\Lambda ,Q, {\rm other\;hairs}) $ . We can consider the cosmological constant as a dynamical pressure and take into account the relation between the event horizon radius ($ r_{+} $ ) and the volume to find an equation of state,$ P = P(T,V) $ . Applying the properties of a critical point in an isothermal$ P-V $ diagram (inflection point), one may obtain${\left( {\displaystyle\frac{{\partial P}}{{\partial V}}} \right)_T} = {\left( {\displaystyle\frac{{{\partial ^2}P}}{{\partial {V^2}}}} \right)_T} = 0$ . This relation helps us to find the critical points and possible phase transitions. This method very much depends on the temperature value. It is worth noting that this method is not practical for black holes with non-spherical horizons in most gravitational theories. To avoid such a restriction, we should use an alternative method for obtaining the critical values in the extended phase space. -
The van der Waals system is one of the important models for describing a real liquid–gas system and its critical behavior. The equation of state of this model is a modification of the ideal gas equation and considers the non-zero sizes of molecules and the attraction between molecules. The van der Waals equation of state is given by [18]
$\left( {P + \frac{a}{{{v^2}}}} \right)\left( {v - b} \right) = kT(P,v),$

(2) where P and T are the pressure and temperature, respectively. Also, v is the specific volume
$ v = \displaystyle\frac{V}{N} $ , b is a free parameter related to the non-zero size of the molecules of a fluid, and a represents the strength of attraction between the molecules. Here, k is a constant that can be set to unity without loss of generality. Note that setting$ a = b = 0 $ yields the familiar ideal gas law. Due to the van der Waals-black hole correspondence, one can use the analogy between the temperature (and hence equation of state) of the fluid and the temperature of the black hole. The existence of critical behavior can be determined by examining the properties of the inflection point, which satisfy$ {\left( {\frac{{\partial P}}{{\partial v}}} \right)_T} = {\left( {\frac{{{\partial ^2}P}}{{\partial v^2}}} \right)_T} = 0. $

(3) Using the inflection point of the equation of state of the van der Waals system in Eq. (2), it is straightforward to find the following critical values:
${v_c} = 3b,\quad {P_c} = \frac{a}{{27{b^2}}},\quad {T_c} = \frac{{8a}}{{27bk}}.$

(4) Inserting
$ T = T_{c} $ into the equation of state, we find two inseparable liquid-gas phases with a possible phase transition between them. For the case of$ T<T_{c} $ , we have a phase transition between two phases of liquid and gas. However, there exists a region of specific volume in which no physical system exists and the phase transition takes place over it. In other words, for this case, two specific volumes with the same pressure exist, and the phase transition takes place between them. In order to obtain all of these critical behaviors and their specific critical values, all temperatures smaller than$ T_{c} $ must be considered, which is practically impossible. The method proposed introduced in this paper provides the possibility of obtaining all of these critical points analytically. We will demonstrate this possibility in the remainder of this paper.The Gibbs free energy of this system can be expressed in the following form:
$G = - kT\left( {1 + \ln \left[ {\frac{{v - b}}{\Phi }{T^{\textstyle\frac{3}{2}}}} \right]} \right) - \frac{a}{v} + Pv,$

(5) where
$ \Phi $ is a constant characterizing the gas. The entropy of the system can be obtained from the differential equation$ {\rm d}G = -S{\rm d}T+v{\rm d}P $ , which leads to$S = k\left( {\frac{5}{2} + \ln \left[ {\frac{{v - b}}{\Phi }{T^{\textstyle\frac{3}{2}}}} \right]} \right).$

(6) Using the equation of state and inserting the temperature into Eq. (6), one can obtain the following
$ S(v,P) $ $S(v,P) = k\left( {\frac{5}{2} + \ln \left[ {\frac{{{{\left( {v - b} \right)}^{\textstyle\frac{5}{2}}}{{\left( {P + \displaystyle\frac{a}{{{v^2}}}} \right)}^{\textstyle\frac{3}{2}}}}}{{{k^{\textstyle\frac{3}{2}}}\Phi }}} \right]} \right).$

(7) To use the proposed method, one must determine the enthalpy of the system. This quantity can be calculated using different methods, and the following relation is one of them:
$H = G + TS = \frac{3}{2}kT - \frac{a}{v} + Pv,$

(8) The above is known as the enthalpy of the van der Waals system. Using the equation of state, it is easy to find the following relation for
$ H(v,P) $ :$H(v,P) = \left( {\frac{{5v - 3b}}{2}} \right)P + \frac{{a\left( {v - 3b} \right)}}{{2{v^2}}},$

(9) where, in principle, one may remove
$ v $ from Eqs. (7) and (9) to obtain$ H = H(S,P) $ . -
Taking into account the postulates of the usual thermodynamics, it appears that all complete differentiations can be written as functions of three thermodynamic variables. It is known that these three variables are not independent, for instance, an equation of state can reduce the number of degrees of freedom to two. On the other hand, the equations for the thermodynamical properties of the system are combinations of different variables. For example, in most cases, pressure and temperature, Gibbs free energy and internal energy, etc., of a thermodynamical system are not independent of each other. Pressure and temperature are related by the equation of state, and the Gibbs free energy may be derived by the Legendre transform of the internal energy. Hence, internal and Gibbs free energies are also dependent on each other.
In practice, obtaining all possible critical points of a system as well as the ranges in which phase transitions take place is not possible with the usual methods. The main reason for this is that one must take the value of a particular thermodynamical quantity as smaller than its critical value to obtain the critical points and their corresponding range of phase transitions. Mathematically, it is not possible to solve such a problem analytically using the usual methods. Here, we introduce an alternative method that provides such a possibility and uncovers new relations between thermodynamical quantities. These relations provide information about the phase transitions of a system and their corresponding ranges.
Since divergence points of the heat capacity
$\left(\left(\displaystyle\frac{\partial W}{\partial T}\right)_P=\displaystyle\frac{1}{\left(\displaystyle\frac{\partial T}{\partial S}\right)_P} \to \infty \right) $ hint at possible phase transition (see Eq. (1)), the equation of vanishing slope of T versus S helps us to obtain a new relation for pressure, which can be maximized to look for phase transitions. We should note that in order to find the critical behavior of a system, the vanishing slope of T versus S is necessary but not sufficient in our approach.The proposed method is as follows: instead of considering the usual equation of state, we use the equation of vanishing slope of T versus S,
${\left( {\displaystyle\frac{{\partial T}}{{\partial S}}} \right)_P}=0$ . This equation is solved with respect to pressure in the extended phase space. This leads to a new relation for pressure that is completely volume dependent. This relation differs from other relations obtained using the usual equation of state. The existence of a maximum of pressure from this relation must be examined. The maximum (maxima) of this relation is (are) the critical point(s) where the phase transition takes place. In other words, the maximum of this relation is where the system undergoes a phase transition.It is evident that by finding a maximum, one is able to extract the critical pressure and the horizon radius (volume) at the same time. It is worth mentioning that to obtain the relation for pressure one can use
${\left( {\displaystyle\frac{{{\partial ^2}H}}{{\partial {S^2}}}} \right)_P}$ instead of$ \left( \displaystyle\frac{\partial T}{\partial S}\right) _{P} $ , where H is the enthalpy of the system. The maximum is where the system acquires a phase transition (the maximum indicates the critical values for a system). On the other hand, thermodynamical concepts indicate that for pressures smaller than the critical one, two critical volumes exist between which a phase transition takes place. For pressures larger than the critical pressure, no phase transition exists. We see that due to the existence of critical pressure at the maximum of this relation, such a property is preserved in our method, and all possible critical points and their corresponding ranges are obtained. Furthermore, using the new relation for pressure, and replacing it in the usual equation of state, one can obtain a new relation for temperature that is free of pressure. The same can be done for enthalpy, internal energy, or Gibbs free energy, which leads to new relations that are completely volume dependent. To demonstrate the efficiency of the presented method in more detail, we will give two typical but general examples in the contexts of both the usual thermodynamics and black hole thermodynamics. -
We are now in a position to use our method for the case of a van der Waals system. Because both the entropy
$ S(v) $ and enthalpy$ H(v) $ are volume dependent at constant pressure (see Eqs. (7) and (9)), we can use the following relation:${\left( {\frac{{{\partial ^2}H}}{{\partial {S^2}}}} \right)_P} = \left( {\frac{{\partial S}}{{\partial v}}} \right)_P^{ - 1}\frac{\partial }{{\partial v}}{\left[ {{{\left( {\frac{{\partial H}}{{\partial v}}} \right)}_P}\left( {\frac{{\partial S}}{{\partial v}}} \right)_P^{ - 1}} \right]_P},$

(10) which leads to the following relation for a van der Waals liquid/gas system
${\left( {\frac{{{\partial ^2}H}}{{\partial {S^2}}}} \right)_P} = \frac{{2\left( {v - b} \right)\left( {P + \frac{a}{{{v^2}}}} \right)\left( {P{v^3} - av + 2ab} \right)}}{{{k^2}\left( {5P{v^3} - av + 6ab} \right)}}.$

(11) From the above relation, one can find that enthalpy changes during a phase transition. In other words, the increasing/decreasing behavior of enthalpy is different before and after a phase transition as well as and after a critical point. By solving
$ {\left( {\displaystyle\frac{{{\partial ^2}H}}{{\partial {S^2}}}} \right)_P}=0$ with respect to P, one can obtain the following new relation for pressure, which differs from the usual equation of state:${P_{\rm new}} = \left\{ {\begin{array}{*{20}{l}} {\displaystyle\frac{{v - 2b}}{{{v^3}}}a,}&({{\rm{allowed}}})\\ { - \displaystyle\frac{a}{{{v^2}}},}&({{\rm{unallowed, due}}\;{\rm{to}}\;{\rm{the}}\;{\rm{equation}}\;{\rm{of}}\;{\rm{state}}}) \end{array}} \right.$

(12) Using the concept of the extremum of this (allowed) relation, i.e., the critical point, one can obtain the following critical volume and pressure:
${v_c} = 3b,\;\;\;\& \;\;{P_c} = \frac{a}{{27{b^2}}},$

(13) which are identical to those obtained previously in Eq. (4). By replacing the new pressure in the equation of state, Gibbs free energy, and enthalpy, one can obtain new relations for these thermodynamical quantities (as well as for other), which are pressure independent:
$\begin{split} {T_{\rm new}} =& \frac{{2a{{\left( {b - v} \right)}^2}}}{{k{v^3}}},\\ {G_{\rm new}} =& - kT\left( {1 + 2\ln \left[ {\frac{{v - b}}{\Phi }{T^{\frac{3}{2}}}} \right]} \right) - \frac{{2ab}}{v},\\ {H_{\rm new}} =& \frac{3}{2}kT - \frac{{2ab}}{{{v^2}}}. \end{split}$

These new relations enable us to extract all possible critical temperatures, Gibbs free energies and enthalpies that a system can have. To highlight this aspect of our method, we refer you to the plot in Fig. 1.

Figure 1. (color online) Application of the proposed method to the case of a van der Waals system. Top panel:
$P_{\rm new}$ (dash-dotted line) and P versus v for$T = 0.9T_{c}$ (continuous line),$T = T_{c}$ (dotted line) and$T = 1.1T_{c}$ (dashed line). Bottom panel:$T_{\rm new}$ (dash-dotted line) and T versus v for$P = 0.9P_{c}$ (continuous line),$P = P_{c}$ (dotted line) and$P = 1.1P_{c} $ (dashed line). In both diagrams, we chose b = 1, a = 4 and k = 1.It is evident that the maxima of the new relations for the temperature
$ T_{\rm new} $ and pressure$ P_{\rm new} $ are where the system undergoes a phase transition. Note that in the$ P-v $ picture, the temperature is kept constant, while in the$ T-v $ picture, the pressure is kept constant. In addition, for pressures (temperatures) smaller than the critical one, the new relation gives a single pressure (temperature) with two related volumes. The phase transition takes place between these two volumes at a specific pressure. As one can see, all possible critical points and the corresponding ranges of phase transitions are included in this method. This is one of the important features of our method that was not possible with previous methods. It is interesting to note that the minima of T (P) coincide with the maxima of$ T_{\rm new} $ ($ P_{\rm new} $ ). We continue with another example in the context of black holes. -
The main motivation to study asymptotically AdS black holes stems from the hypothesis of AdS/CFT correspondence. Using the thermal field theoretic approaches, it has been deduced that AdS black holes undergo certain phase transitions. The first sign of such phase transitions was observed by Page and Hawking for the Schwarzschild AdS black hole [19]. With the addition of parameters, such as electric charge and spin, the phase transition process is more elaborate and enhanced. It is quite interesting to note that the pressure-volume picture of the ideal gas for constant temperature is also mimicked by AdS black holes (see top panel of Fig. 1). This analogy between a gravitational system (AdS black hole) and a non-gravitational thermal system (such as an ideal gas or a van der Waals fluid) is established by identifying a correspondence between their parameters, i.e., mass with enthalpy, temperature with surface gravity, entropy with area, and cosmological constant with pressure. Thus, in the first law of thermodynamics, the cosmological constant appears as pressure, which is conjugate to the volume of a black hole [20]. Besides, using the reverse isoperimetric inequality, it has been deduced that entropy inside the horizon of a given volume is maximized for the Schwarzschild AdS black hole [21].
In black hole systems, it has been shown that one can take the negative cosmological constant as thermodynamical pressure [22] with the following relation:
$P = - \frac{\Lambda }{{8\pi }}.$

(14) On a complimentary note, we should mention that for specific black holes in modified general relativity, such as dilatonic gravity and gravity rainbow, one has to use a modified proportionality relation instead of Eq. (14) [23, 24]. Although in this paper we consider a well-known Reissner-Nordström AdS black hole, our technique is consistent with the other black holes in modified theories of gravity. Replacing the cosmological constant with thermodynamical pressure (working in the extended phase space thermodynamics) leads to the following important results:
I) The resulting temperature for the black hole is the equation of state.
II) The total mass of the black hole is no longer the internal energy. In fact, it is replaced by the enthalpy in such a scenario, which results in the following relation for the Gibbs free energy:
$G = M - TS.$

(15) We now demonstrate the validity of our approach and its consistency with previous methods in the context of black hole systems. For this purpose, we study the critical behavior of the
$ d- $ dimensional Reissner-Nordström AdS black hole. Previously, the results for this specific black hole were derived using the usual method in Ref. [18]. The metric of this black hole in spherically symmetric spacetime is given as${\rm d}{s^2} = - \psi (r){\rm d}{t^2} + \frac{{{\rm d}{r^2}}}{{\psi (r)}} + {r^2}{\rm d}\Omega _{{d_2}}^2,$

(16) where we use the notation
$ d_{i} = d-i $ . In Eq. (16),$ {\rm d} \Omega _{d_{2}}^2 $ denotes the metric of a$ d_{2}- $ dimensional unit sphere, and$\psi (r) = 1 - \frac{m}{{{r^{{d_3}}}}} - \frac{{2\Lambda }}{{{d_1}{d_2}}}{r^2} + \frac{{2{d_3}{q^2}}}{{{d_2}{r^{2{d_3}}}}}.$

(17) The temperature, entropy, and total finite mass of this black hole are calculated using the surface gravity, area law, and ADM approach, respectively, which lead to
$T = \frac{{{d_3}}}{{4\pi {r_ + }}} - \frac{{\Lambda {r_ + }}}{{2\pi {d_2}}} - \frac{{d_3^2{q^2}}}{{2\pi {d_2}r_ + ^{2{d_{5/2}}}}},$

(18) $S = \frac{{r_ + ^{{d_2}}}}{4},$

(19) $M = \frac{{{d_2}}}{{16\pi }}m,$

(20) where
$ r_{+} $ is the outer horizon of the black hole. By evaluating the metric function on the outer horizon ($ \psi \left( r = r_{+}\right) = 0 $ ), we obtain$M = \frac{{{d_2}}}{{16\pi }}\left( {r_ + ^{{d_3}} - \frac{{2r_ + ^{{d_1}}}}{{{d_1}{d_2}}}\Lambda + \frac{{2{d_3}{q^2}}}{{{d_2}r_ + ^{{d_3}}}}} \right),$

(21) with the following relation for Gibbs free energy:
$G = \frac{{r_ + ^{{d_3}}}}{{16\pi }} + \frac{{{d_3}\left( {2d - 5} \right){q^2}}}{{8\pi {d_2}r_ + ^{{d_3}}}} - \frac{{r_ + ^{{d_1}}}}{{{d_1}{d_2}}}P.$

(22) Another interesting method for calculating the thermodynamic potentials (such as Gibbs free energy) in a gravitational system is based on the Euclidean on-shell action. Because bulk action of the theory diverges, we use the counter-term action to remove the divergency. In addition, we should add the Gibbons-Hawking and electromagnetic boundary terms to the bulk action to obtain a well-defined action. The well-behaved finite action can be written as (see [25])
$\begin{split} I =& {I_b} + {I_{ct}} - \frac{1}{{8\pi }}\int_{\partial M} {{{\rm d}^n}} x\;\sqrt \gamma \;K \\&- \frac{1}{{4\pi }}\int_{\partial M} {{{\rm d}^n}} x\;\sqrt \gamma {n_\mu }{F^{\mu \nu }}{A_\nu },\end{split}$

(23) where
$ I_{b} $ and$ I_{ct} $ are the bulk and counter-term actions of the Einstein-Maxwell gravity, respectively. Also,$ \gamma _{ij} $ and$ K $ are the induced metric and extrinsic curvature of the boundary, respectively. Using Eq. (23), it is straightforward to calculate the total on-shell action with respect to the volume of the unit$ d_{2}$ sphere$I = \frac{\beta }{{16\pi }}\left( {r_ + ^{{d_3}} + \frac{{2\Lambda r_ + ^{{d_1}}}}{{{d_1}{d_2}}} + \frac{{2{d_3}(2d - 5){q^2}}}{{{d_2}r_ + ^{{d_3}}}}} \right),$

(24) where
$ \beta $ is the inverse of the Hawking temperature. Using the fact that$ G = I/\beta $ along with Eq. (14), we get$G = \frac{1}{{16\pi }}\left( {r_ + ^{{d_3}} - \frac{{16\pi Pr_ + ^{{d_1}}}}{{{d_1}{d_2}}} + \frac{{2{d_3}(2d - 5){q^2}}}{{{d_2}r_ + ^{{d_3}}}}} \right),$

(25) which is the same as Eq. (22), as expected.
We are now in a position to calculate the critical values with the usual method. First, we calculate the volume conjugate to the pressure as
$V = {\left( {\frac{{\partial H}}{{\partial P}}} \right)_{S,Q}} = {\left( {\frac{{\partial M}}{{\partial P}}} \right)_{S,Q}} = \frac{{r_ + ^{{d_1}}}}{{{d_1}}}.$

(26) Because the volume depends on the horizon radius, one can use the horizon radius to investigate the thermodynamic behavior of the black hole proportionally (linearly) to its specific volume [18]. Using Eqs. (14) and (18), one can obtain the equation of state as
$P = \frac{{{d_2}\left( {4\pi Tr_ + ^3 - {d_3}r_ + ^2} \right)}}{{16\pi r_ + ^4}} + \frac{{2d_3^2{q^2}r_ + ^{ - 2{d_4}}}}{{16\pi r_ + ^4}}.$

(27) We now employ the proprieties of the inflection point,
${\left( {\displaystyle\frac{{\partial P}}{{\partial {r_ + }}}} \right)_T} = {\left( {\displaystyle\frac{{{\partial ^2}P}}{{\partial r_ + ^2}}} \right)_T} = 0$ , to obtain the critical horizon radius (volume)$ r_{c} $ , which leads to$r_c^2 - 4{d_3}{d_{5/2}}{q^2}r_c^{ - 2{d_4}} = 0$

(28) with the following solution [18]:
${r_c} = {\left( {4{q^2}{d_3}{d_{5/2}}} \right)^{\textstyle\frac{1}{{2{d_3}}}}}.$

(29) The critical temperature and pressure can then be obtained as
${T_c} = \frac{{{d_3}}}{{2\pi {{\left( {4{q^2}{d_3}{d_{5/2}}} \right)}^{\textstyle\frac{1}{{2{d_3}}}}}}} - \frac{{{{\left( {4{q^2}{d_3}{d_{5/2}}} \right)}^{\textstyle\frac{{{d_{5/2}}}}{{{d_3}}}}}d_3^2{q^2}}}{\pi },$

(30) ${P_c} = \frac{{{d_2}{d_3}}}{{16\pi {{\left( {4{q^2}{d_3}{d_{5/2}}} \right)}^{\textstyle\frac{1}{{{d_3}}}}}}} - \frac{{{d_{5/2}}d_3^2{q^2}}}{{4\pi {{\left( {4{q^2}{d_3}{d_{5/2}}} \right)}^{\textstyle\frac{{{d_2}}}{{{d_3}}}}}}}.$

(31) Let us now determine the critical values using our approach. Using Eqs. (19) and (21) and replacing the cosmological constant with the pressure in Eq. (14), one can obtain (because at constant pressure both
$ S = S(r_{+}) $ and$ M = M(r_{+}) $ are independent of temperature, the equation of state for removing T, which was used is not required as it was before in the van der Waals liquid/gas system)${\left( {\frac{{{\partial ^2}M}}{{\partial {S^2}}}} \right)_{q,P}} = \frac{{16P}}{{d_2^2r_ + ^{{d_3}}}} - \frac{{{d_3}}}{{\pi {d_2}r_ + ^{{d_1}}}} + \frac{{4{d_{5/2}}d_3^2{q^2}}}{{\pi d_2^2r_ + ^{3{d_{7/3}}}}}.$

(32) Solving
$ {\left( {\displaystyle\frac{{{\partial ^2}M}}{{\partial {S^2}}}} \right)_{q,P}} =0 $ with respect to P, we obtain a new relation for the pressure:${P_{\rm new}} = \frac{{{d_2}{d_3}}}{{16\pi r_ + ^2}} - {\kern 1pt} \frac{{{d_{5/2}}d_3^2{q^2}}}{{4\pi r_ + ^{2{d_2}}}}.$

(33) Replacing the pressure in the relations for temperature in Eq. (18), mass in Eq. (21), and Gibbs free energy in Eq. (22) with the new pressure relation in Eq. (33), one can obtain new relations for these thermodynamical quantities in the following form:
${T_{\rm new}} = \frac{{{d_3}}}{{2\pi {r_ + }}} - \frac{{d_3^2r_ + ^{5 - 2d}{q^2}}}{\pi },$

(34) ${M_{\rm new}} = \frac{{d_2^2r_ + ^{{d_3}}}}{{8\pi {d_1}}} - \frac{{{d_2}{d_3}{d_4}{q^2}}}{{4\pi {d_1}r_ + ^{{d_3}}}},$

(35) ${G_{\rm new}} = \frac{{r_ + ^{{d_3}}}}{{8\pi {d_1}}} + \frac{{{d_{5/2}}{d_3}{q^2}}}{{2\pi {d_1}r_ + ^{{d_3}}}}.$

(36) It is evident that the relation for pressure in Eq. (33) is different from the usual equation of state in Eq. (27). To obtain the maximum of this relation, we use the mathematical nature of the extremum,
${\left. {\left( {\frac{{{\rm d}{P_{\rm new}}}}{{{\rm d}{r_ + }}}} \right)} \right|_{{r_ + } = {r_{\rm NC}}}} = \frac{{{d_2}d_3^2{d_{5/2}}{q^2}}}{{2\pi r_{\rm NC}^{2{d_{3/2}}}}} - \frac{{{d_2}{d_3}}}{{8\pi r_{\rm NC}^3}} = 0$

(37) with the following solution for the new critical (NC) horizon radius,
$ r_{\rm {NC}} :$ ${r_{\rm NC}} = {\left( {4{d_3}{d_{5/2}}{q^2}} \right)^{\textstyle\frac{1}{{2{d_3}}}}},$

(38) which is exactly the same as that obtained in Eq. (29). Replacing this horizon radius in Eqs. (34) and (33), we can derive the following:
${T_{\rm NC}} = \frac{{{d_3}}}{{2\pi {{\left( {4{q^2}{d_3}{d_{5/2}}} \right)}^{\textstyle\frac{1}{{2{d_3}}}}}}} - \frac{{{{\left( {4{q^2}{d_3}{d_{5/2}}} \right)}^{\textstyle\frac{{{d_{5/2}}}}{{{d_3}}}}}d_3^2{q^2}}}{\pi },$

(39) ${P_{\rm NC}} = \frac{{{d_2}{d_3}}}{{16\pi {{\left( {4{q^2}{d_3}{d_{5/2}}} \right)}^{\textstyle\frac{1}{{{d_3}}}}}}} - \frac{{{d_{5/2}}d_3^2{q^2}}}{{4\pi {{\left( {4{q^2}{d_3}{d_{5/2}}} \right)}^{\textstyle\frac{{{d_2}}}{{{d_3}}}}}}},$

(40) which are exactly the same as the previously calculated critical temperature in Eq. (30) and pressure in Eq. (31), respectively. These results show that the critical values calculated in our approach are consistent with those calculated with the usual method in extended phase space.
Using the critical radius in Eq. (38) with the new relations for mass (Eq. (35)) and Gibbs free energy (Eq. (36)), we can also obtain the critical mass (enthalpy) and critical Gibbs free energy:
$\begin{split} {M_{\rm NC}} =& \frac{{{d_2}{d_3}\left( {{d^2} - 5d + 7} \right)q}}{{4\pi {d_1}\sqrt {{d_3}{d_{5/2}}} }},\\{G_{\rm NC}} =& \frac{{\sqrt {{d_3}{d_{5/2}}} q}}{{2\pi {d_1}}}.\end{split}$

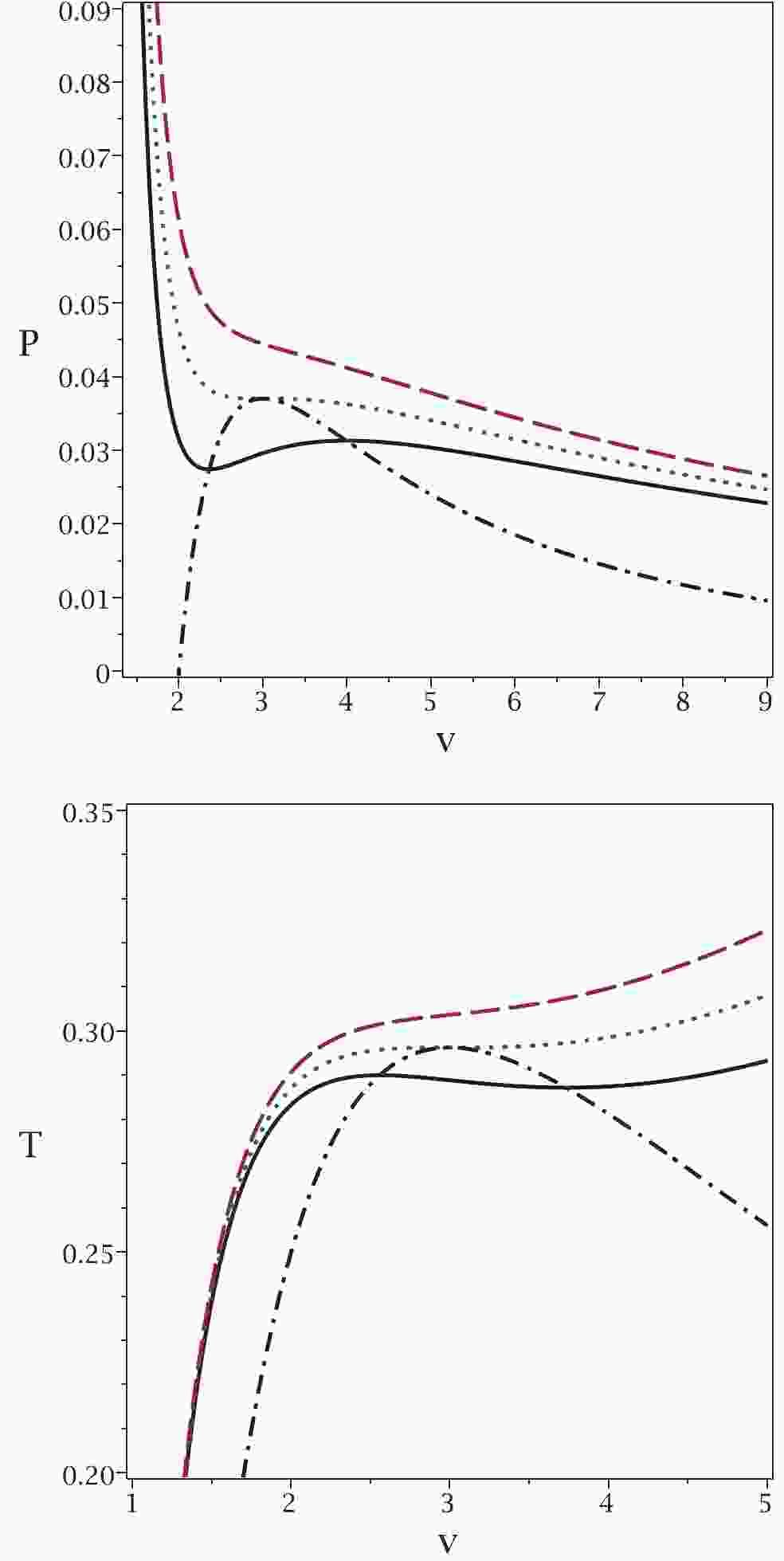
To illustrate the results of our approach in more detail, Fig. 2 shows plots of the obtained relations for temperature and pressure. It is clear that for pressures (temperatures) larger than the critical one, no phase transition is observed for the van der Waals-like diagram (dashed lines in top and middle panels of Fig. 2). If no phase transition occurs in a black hole, this implies that the black hole remains physically intact, i.e., its mass and other physical parameters remain the same. The black hole remains stable and does not radiate thermally. This may correspond to a state of thermal equilibrium. If the equilibrium becomes unstable, the heat capacity of the black hole become negative, causing the black hole to radiate. In this case, a phase transition does take place. Similarly, under the same conditions, no critical pressure is observed in our approach. On the contrary, for pressures (temperatures) smaller than the critical value, two critical horizons are observed for any pressure (temperature), which is in agreement with the results of our approach (continuous lines in top and middle panels of Fig. 2). Finally, we observe that the critical pressure (critical temperature) and the critical horizon radius calculated by the usual method, coincide with the maximum of the new relation for pressure and its related horizon radius. This also indicates that the results of our method are completely in agreement with those of the previous method.

Figure 2. (color online) Top panel:
$P_{\rm new}$ (dash-dotted line) and P versus$r_{+}$ , for sub-critical case$T=0.9T_{c}$ (continuous line), critical case$T=T_{c}$ (dotted line) and super-critical case$T=1.1T_{c}$ (dashed line). Middle panel:$T_{\rm new}$ (dash-dotted line) and T versus$r_{+}$ , for sub-critical$P=0.9P_{c}$ (continuous line), critical$P=P_{c}$ (dotted line) and super-critical$P=1.1P_{c}$ (dashed line). Bottom panel:$P_{\rm new}$ (dash-dotted line) and$C_{Q}$ versus$r_{+}$ , for sub-critical$P=0.9P_{c}$ (continuous line), critical$P=P_{c}$ (dotted line) and super-critical$P=1.1P_{c}$ (dashed line). In all three panels, q = 1 and d = 4.Finally, we plot the heat capacity (bottom panel in Fig. 2) to demonstrate the consistency of the new pressure. It is evident that for
$ P<P_{c} $ , two points of discontinuity exist for the heat capacity, which are coincident with the phase transition points observed in the other methods. If the pressure is equal to the critical pressure, only one discontinuity is observed in the heat capacity, as in the other methods. For$ P>P_{c} $ , no discontinuity is observed for the heat capacity. This behavior indicates that all methods give consistent results.In the top panel of Fig. 2, one can see the so-called saturation curve (dash-dotted line). Taking into account the
$ P-V $ isothermal diagram with$ T<T_{c} $ (continuous line), we can decrease the horizon radius to find two points of intersection with the saturation curve ($ r_{+1} $ and$ r_{+2} $ with$ r_{+1}<r_{+2} $ ). The black hole system is unstable for$ r_{+1}<r_{+}<r_{+2} $ . In other words, there is a phase transition between a small and a large black hole (between$ r_{+1} $ and$ r_{+2} $ ). This phase transition may occur with a sudden burst of thermal Hawking radiation, i.e., the size of the black hole suddenly shrinks from$ r_{+2} $ to$ r_{+1} $ without changing the black hole temperature. Black hole solutions are not physical between these two points. This can be explained by the fact that the heat capacity is negative (see bottom panel of Fig. 2) and also by the fact that the speed of sound is higher than the speed of light [26]. Note that similar discontinuities in specific heat capacity occur in Born-Infeld black holes [11]. It is worth noting that for$ T = T_{c} $ , the intersection points meet and are equal to the critical horizon radius$ r_{+1} = r_{+2} = r_{c} $ . The same statement could be made for the temperature in the middle panel of Fig. 2 .Before finishing the paper, it is worth pointing out the significance of our approach.
First, our method provides the possibility of obtaining different thermodynamical quantities that are independent of each other. In other words, as one can see from Eqs. (34)-(36), they only depend properties such as dimension, electric charge, and horizon radius. If we generalize the action to other gravitational theories or include other matter fields, the resultant new temperature, pressure, mass, and Gibbs free energy obtained using our method will have the same properties (they are only a function of black hole properties).
Secondly, the new relations include only critical points that a black hole could acquire in different conditions. In the usual methods, to obtain all points between which phase transitions take place, one must consider all pressures equal to or smaller than the critical pressure. Technically, such a task is impossible. Using our method, one can find all possible phase transitions, horizon radii, and corresponding pressures that a system could acquire. The same could be said for the new relations for temperature, mass, and Gibbs free energy. In other words, by using our approach, one can obtain all phase transition points and the corresponding critical temperature, pressure, mass, and Gibbs free energy that system can acquire in analytical form.
Thirdly, using our method, one can determine the range of horizon radii that depend on the critical values in which the black hole solutions do not exist. For clarification, refer to the diagram of new pressure in the top panel of Fig. 2 (dashed-dotted line). Clearly, the phase transition takes place between two points with the same pressures. The prohibited range of horizon radii for the black hole is between these points. Taking a closer look, one can see that by using our approach, the maximum range of horizon radii in which the black hole solutions do not exist can be found. Such a maximum could not be obtained easily with the usual methods. In addition, by using our approach, one can determine the rate of increase of the prohibited range of horizon radii by studying the behavior of its diagram. Such a procedure may encounter significant problems for the usual method. Finally, we should point out that these three features are also valid for usual thermodynamical systems.
-
Motivated by interest in van der Waals-like behavior and recent progress in the thermodynamic phase transitions of black holes, we introduced an alternative approach for studying the phase transition points in both usual thermodynamical systems and black holes.
Although the usual method of studying a phase transition originates from temperature in the equation of state, our method is based on the slope of temperature versus entropy and is a powerful method for addressing the critical behavior of a thermodynamical system.
The results of our method are in agreement with those of other methods. However, it also provides further information regarding the critical behavior of thermodynamical systems, which could not be derived with the other methods. The main highlights of our method are as follow: I) obtaining new relations for different thermodynamical quantities that are independent of each other and II) mapping all possible critical points and regions in which phase transitions take place.
Because it is known that the four-dimensional Reissner-Nordström black hole has the reentrant phase transition, it would be interesting to examine whether our method confirms (or not) the existence of the reentrant phase transition. The method introduced here is applicable to both usual thermodynamical systems and black holes. This shows that one can also employ the general structure of this method in the context of other physical systems, such as superconductors, condensed matter systems, gauge/gravity duality, and even quantum systems. It is also interesting to build a geometrical theory based on the Legendre invariance, such as the known theory of geometro-thermodynamics, or on other types of symmetries. As a future task, it would be interesting to extend the present study of phase transitions and critical phenomenon to AdS/CFT [27]. Furthermore, how phase transitions alter the geometry and topology of black holes is a separate investigation. We also plan to investigate the relationship between the cosmic censorship hypothesis and the various phase transitions of black holes and to work on the phase transitions and critical behavior of black rings, black Saturns, and black membranes.
We would like to thank our anonymous referee for their useful comments, the editor of Chinese Physics C for improving the language and presentation of this paper, and Shiraz University Research Council. This work was supported financially by the Research Institute for Astronomy and Astrophysics of Maragha, Iran.
Alternative approach to thermodynamic phase transitions
- Received Date: 2018-08-28
- Accepted Date: 2019-03-15
- Available Online: 2019-11-01
Abstract: One of the major open problems in theoretical physics is the lack of a consistent quantum gravity theory. Recent developments in our knowledge on thermodynamic phase transitions of black holes and their van der Waals-like behavior may provide an interesting quantum interpretation of classical gravity. Studying different methods of investigating phase transitions can extend our understanding of the nature of quantum gravity. In this paper, we present an alternative theoretical approach for finding thermodynamic phase transitions in the extended phase space. Unlike the standard methods based on the usual equation of state involving temperature, our approach uses a new quasi-equation constructed from the slope of temperature versus entropy. This approach addresses some of the shortcomings of the other methods and provides a simple and powerful way of studying the critical behavior of a thermodynamical system. Among the applications of this approach, we emphasize the analytical demonstration of possible phase transition points and the identification of the non-physical range of horizon radii for black holes.





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF













 DownLoad:
DownLoad: