-
Nuclear energy levels are one of the most featured topics in nuclear physics [1, 2]. Statistical analysis of nuclear energy levels in many-nucleon systems provides useful information on the nuclear structure and forces [3, 4]. Moreover, it is possible to use fractal analysis to describe the nuclear structure properties [5, 6]. In many systems, the fractal analysis is not sufficient to characterize nuclear dynamics. The mathematical analysis of multifractals provides invaluable information on dynamic phenomena, as they occur at varying degrees of complexity [7]. Hence, the multifractal spectrum of the nuclei as a many-body system can provide accurate information about the degree of chaotic behavior of wave functions [8, 9]. Many of the spectral properties in the low-energy regime can be explained with the nuclear shell model. This model is based on the mean-field potential and two-body residual interactions [10]. Knowledge about the physics of many-body complex systems as nuclei is provided by quantum chaos theory [11, 12]. The statistical analysis for the sd-shell (
$ 0d_{\frac{5}{2}}, 0d_{\frac{3}{2}}, 1s_{\frac{1}{2}} $ ) nuclei exhibits strongly chaotic behavior [13]. In the pf-shell ($ 1f_{\frac{7}{2}} $ ,$ 2p_{\frac{3}{2}} $ ,$ 1f_{\frac{5}{2}} $ ,$ 2p_{\frac{1}{2}} $ ) nuclei, the situation becomes more interesting. The nearest neighbor spacing (NNS) distribution$ P(S) $ is the simplest prediction of random matrix theory. The RMT predicts the Gaussian orthogonal ensemble (GOE) for non-integrable physical systems and the Poisson ensemble for integrable ones [14–16]. However, in many systems, intermediate behavior between the two cases are observed. This type of situation can often be described by the Brody distribution [17]. This has been used by many authors as a simple way to quantify the shape of the$ P(s) $ , especially for the nuclear structure [18, 19].Our aim in this study is to investigate the influence of the single-particle energy spacing and the residual interaction of valence nucleons on the behavior of the nuclear structure. The residual interaction between neutron-neutron and neutron-proton can have a different influence on the behavior of the multifractal and statistical spectrums. In previous studies, calcium isotopes are selected for the shell model research. Calcium isotopes are neutron-rich, and this chain has doubly magic isotopes [20–23], hence they represent a good choice for our studies. To investigate the influence of neutron-proton interaction on the behavior of the spectral statistics, we choose
$ ^{46}{\rm{Ti}} $ in the neighbor of$ ^{46}{\rm{Ca}} $ . We perform our analyses in two situations: (1) Multifractal analysis of$ ^{46}{\rm{Ca}} $ ,$ ^{48}{\rm{Ca}} $ , and$ ^{46}{\rm{Ti}} $ , (2) Statistical analysis for$ ^{46}{\rm{Ca}} $ and$ ^{48}{\rm{Ca}} $ as neutron-rich isotopes and$ ^{46}{\rm{Ti}} $ with proton and neutron in its valence space.In the first part of this paper, the theoretical status of the nuclear shell model is summarized. The second part presents the multifractal analysis, and the third part consists of quantum chaos theory and spectral statistics. The last section contains the results of multifractal analysis and the spectral statistics in the selected isotopes, as well as a brief discussion.
-
The second quantization form of the nuclear shell model Hamiltonian is written as
$ H = {\Sigma_{i}\varepsilon_{i}a_{i}^{\dagger}a_{i}}+\dfrac{1}{4}{\Sigma_{i,j,k,l}<ij|V|kl>a_{i}^{\dagger}a_{j}^{\dagger}a_{l}a_{k}}, $

(1) where
$ \varepsilon_{i} $ is the single-particle energy and$ <ij|V|kl> $ s are the two-body matrix elements [24, 25]. The construction and diagonalization of the Hamiltonian is performed with the NuShellX computer program [26].The wave functions of the system are represented as a linear combination of configuration state functions with the same symmetry as
$ |\alpha> = \sum_i\psi_{i}|\phi>. $

(2) The amplitudes
$ \psi_{i} $ are expansion coefficients obtained through diagonalization of the Hamiltonian [27]. Dimensional analysis can be executed based on the eigenvectors. Moreover, eigenvalues can provide a statistical analysis of the system. -
The multifractal analysis is a powerful tool for the characterization of nonlinear dynamical systems [28, 29]. The multifractality of the critical eigenstate is characterized by its associated singularity spectrum
$ f(\alpha) $ . To calculate$ f(\alpha) $ , wave functions of the nuclear shell model Hamiltonian Eq. (1) are required. For this purpose, we solve the time-independent Schrödinger equation, and we achieve the wave functions Eq. (2). Let$ |\psi_i|^2 $ be the value at the ith site of a normalized wave function in our discretized d-dimensional system with volume$ L^d $ . If we cover the system with$ N_l $ boxes of linear size l, the probability of finding a nucleon in the kth box is simply given by,$ \mu_{k}(l) = \Sigma_{i}|\psi_{i}|^{2}, \,\,\,\,\,\, k = 1,...,N_{l}, $

(3) $ \mu_{k}(l) $ constitutes a normalized measure for which we can define the qth moment as Eq. (4),$ P_{q}(l) = \Sigma_{k = 1}^{N_{l}}\mu^{q}_{k}(l). $

(4) The general assumption underlying multifractality is that within a certain range of values for the ratio
$ \lambda\equiv{l/L} $ , the moments$ P_q $ exhibit power-law behavior, indicating the absence of length scales in the system. In the scaling law of Eq. (4), we considered$ 350 $ eigenfunctions, each with size$ N = L^2 = 32^2 $ , partitioned into smaller boxes with linear size l, such that condition$ 0<l<L $ is fulfilled. This ensures that multifractal fluctuations of$ |\alpha|^2 $ are properly measured. We found that the scaling property of multifractality is properly recovered when values of the box size are assumed to be in the range$ l\in[1,10] $ . The ensemble average of$ P_q $ exhibits power-law behavior, as written in Eq. (5),$ <P_{q}> = L^{d}<|\psi(r)|^{2q}> \sim L^{-\tau(q)}. $

(5) Hence, one can obtain mass exponents
$ \tau(q) $ , which according to Eq. (6) conduces to the determination of fractal dimension D,$ \tau(q) = D_{q}(q-1), $

(6) where
$ D_{q} $ is the generalized dimension. For delocalized systems$ D_{q} = d $ and for localized ones$ D_{q} = 0 $ . In this regard, the singularity spectrum$ f(\alpha) $ is defined as follows,$ f(\alpha) = q\alpha(q)-(q-1)D_{q}, $

(7) $ \alpha_{q} = \frac{\rm d}{{\rm d}q}[(q-1)D_{q}]. $

(8) $ f(\alpha) $ is a convex function of$ \alpha $ . It reaches to a maximum value ($ f(\alpha_{0}) = d_{0} $ ) at$ \alpha_{0} $ .$ f(\alpha) $ will be concentrated in a single point$ \alpha = d $ , with$ f(d_{0}) = d_{0} $ for delocalized systems. In contrast, when the system becomes localized, the singularity spectrum broadens. Hence, to characterize the behavior of different systems, one can compare the width of their singularity spectrums [30]. -
Random matrix theory is a suitable method for the study of the fluctuation properties of nuclear energy levels [19]. We consider
$ {E_i} $ as the set of eigenvalues of the system. Thus,$ E_{n}-E_{n-1} = S_{n} $ is defined as the nearest-neighbor level spacing (NNS). To quantify the degree of chaoticity in the systems with intermediate behavior, the Brody distribution is used as follows,$ P_{\beta}(s) = \alpha\left( \beta+1\right) s^{\beta} \exp \left( -\alpha s^{\beta+1}\right), $

(9) where
$ \alpha = \left(\Gamma\left[ \dfrac{\beta+2}{\beta+1}\right]\right)^{\beta+1} $ and β is the Brody parameter. In the limit of$ \beta = 0 $ , the distribution is Poissonian (localized systems), and it is proportional to$ e^{-s} $ . For delocalized systems ($ \beta = 1 $ ) the distribution is well-described by the Wigner distribution, and it is proportional to$ e^{-\pi s^2/4} $ [31, 32].The Brody parameter is obtained by fitting the numerical distribution with
$ P_\beta(s) $ , and this evaluates quantitatively the degree of level repulsion [33]. -
We use
$ ^{40}{\rm{Ca}} $ as an inert core and the KB3 Hamiltonian for a total angular momentum J and total isospin T [34, 35]. Energy levels and wave functions are provided by the NuShellX calculation for an analysis of the multifractal spectrum and NNS distribution of$ ^{46,48}{\rm{Ca}} $ and$ ^{46}{\rm{Ti}} $ . -
A nuclear system is a fractal object. Its topological dimension approaches three for stable systems, and the values of the fractal dimension decrease because of the increase in the nuclear mass number. For this reason, in the multifractal analysis of the nuclear system, we choose
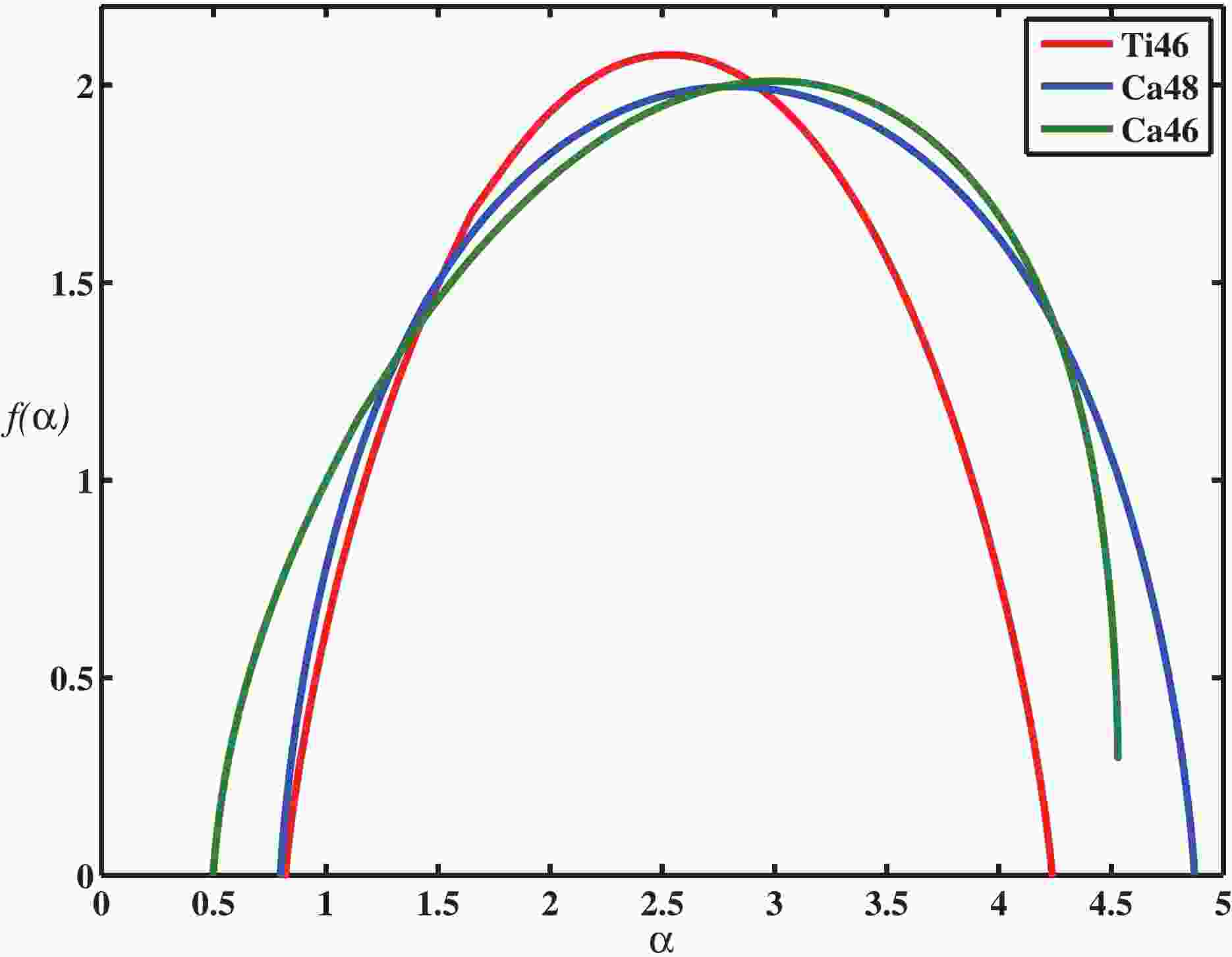
$ d_{0}\approx2 $ [5]. The multifractal formalism has been applied to a sequence of wave functions for$ ^{46,48}{\rm{Ca}} $ and$ ^{46}{\rm{Ti}} $ . Numerical results of the singularity spectrum for$ ^{46}{\rm{Ca}} $ ,$ ^{48}{\rm{Ca}} $ , and$ ^{46}{\rm{Ti}} $ are presented in Fig. 1. This demonstrates that the domain of$ f(\alpha) $ decreases for$ ^{48}{\rm{Ca}} $ in comparison with$ ^{46}{\rm{Ca}} $ , indicating that the transition to delocalization is increased with increasing neutron numbers. Moreover, this represents that the domain of the multifractal spectrum of$ ^{46}{\rm{Ti}} $ becomes narrower than$ ^{46}{\rm{Ca}} $ , and it tends to a delocalized phase. Hence, one can claim that the proton-neutron interaction has a stronger effect on the nuclear structure in comparison to the neutron-neutron interaction.
Figure 1. (color online) Multifractal spectrum of calcium isotopes and titanium for
$J=0^{+}$ . The green line corresponds to the singularity spectrum of$^{46}{\rm{Ca}}$ . The blue line displays$f(\alpha)$ for$^{48}{\rm{Ca}}$ . The red line corresponds to the singularity spectrum of$^{46}{\rm{Ti}}.$ The generalized dimension for these isotopes is shown in Fig. 2. Meanwhile, for
$ ^{46}{\rm{Ca}} $ , a wider multifractal characteristic is observed. For a complete characterization of the nuclear shell model Hamiltonian, and particularly to determine its chaoticity, we require the analysis of the nuclear energy levels. In the next section, we quantify the transition from Poisson to the Wigner-Dyson distribution by employing the Brody distribution. We fit our numerical calculation with$ P_{\beta} $ , using β as a fitting parameter.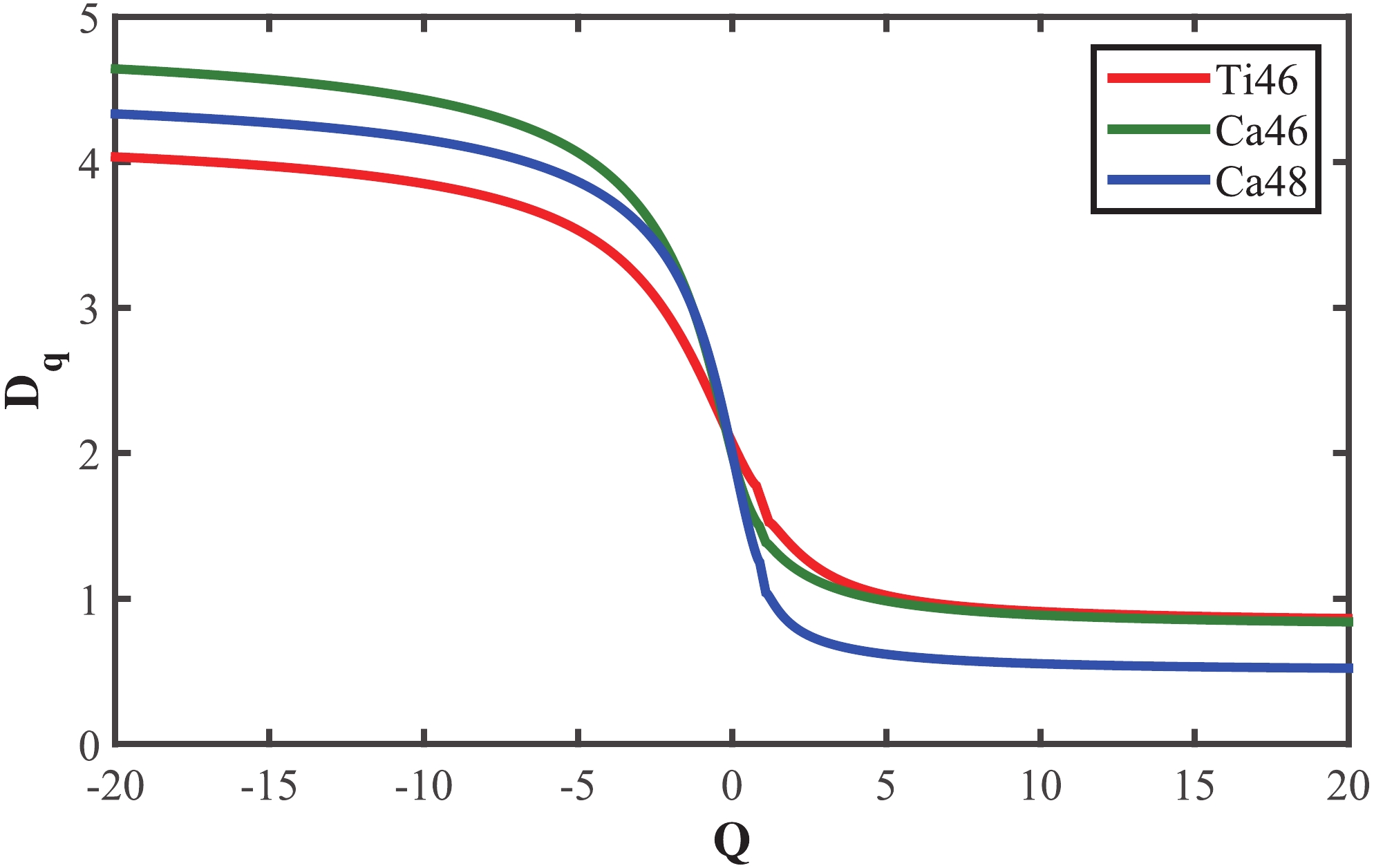
Figure 2. (color online) Generalized dimension of calcium isotopes and titanium for
$J=0^{+}$ . The green line corresponds to the singularity spectrum of$^{46}{\rm{Ca}}$ . The blue line displays$f(\alpha)$ for$^{48}{\rm{Ca}}$ . The red line corresponds to the singularity spectrum of$^{46}{\rm{Ti}}.$ -
The level spectrum is performed, and the Brody parameter is calculated for each isotope (Table 1).
Ca isotopes $ ^{46}{\rm Ca}$ 

$ ^{48}{\rm Ca}$ 

$ ^{46}{\rm Ti}$ 

Brody parameter 0.65 0.81 0.91 Table 1. Brody parameters of
$J=0^{+}$ states for$^{46,48}{\rm{Ca}} $ and$^{46}{\rm{Ti}}$ .NNS is illustrated in Fig. 3 for the spectrum of
$ J = 0^{+} $ for$ ^{46,48}{\rm{Ca}} $ (blue line). This tends to the Poisson curve for$ ^{46}{\rm{Ca}} $ (see Fig. 3(a)). Fig. 3(b) represents the transition toward GOE limit for$ ^{48}{\rm{Ca}} $ .
Figure 3. (color online) Nearest neighbor level distribution for
$J=0^{+}$ states (a)$^{46}{\rm{Ca}} $ ,(b)$^{48}{\rm{Ca}} $ , (c)$^{46}{\rm{Ti}} $ . GOE distribution (green curve), Poissonian distribution (red curve), Brody distribution (black curve), Calculation results (blue histogram).These results state that chaoticity increases from
$ ^{46}{\rm{Ca}} $ to$ ^{48}{\rm{Ca}} $ with the increase in the number of valence neutrons. Our results are in good agreement with the previous studies [24, 36].Titanium is one of the neighboring nuclei of calcium, and it has protons in its valance space. Fig. 3(c) shows the spectrum analysis of
$ ^{46}{\rm{Ti}} $ with$ 2 $ protons in pf valence space. Titanium exhibits highly chaotic behavior compared to$ ^{46}{\rm{Ca}} $ . The proton-neutron interaction is stronger than the neutron-neutron interaction [37, 38]. The Brody parameter (Table 1) reached up to 0.91 for this isotope. -
The spectral statistics of nuclear energy levels based on RMT provide further information on the nuclear structure in different isotopes. The nearest neighbor spacing distribution
$ P(s) $ represents considerable distinction from Poisson behavior in$ ^{48}{\rm{Ca}} $ respect to$ ^{46}{\rm{Ca}} $ . This behavior is the result of increasing the number of valence neutrons in$ ^{48}{\rm{Ca}} $ , such that the shell structure changes as a function of the neutron numbers. The multifractal analysis moreover confirms the same behavior for these isotopes.A strong tendency to the GOE curve for
$ ^{46}{\rm{Ti}} $ with both proton and neutron in its valence space was also observed. This shows that the interaction between neutron-proton is stronger than the neutron-neutron interaction, such that it can impair regular mean-field motion. The two-body residual part of the Hamiltonian is a nonlinear part of the system, and when it becomes stronger, it leads to chaotic behavior for the system. In this situation, particles cannot move independently, hence level repulsion occurs, and spectral statistics follow the Wignarin shape. The multifractal spectrum and generalized dimension also exhibit delocalized wave functions, i.e., chaotic behavior, for$ ^{46}{\rm{Ti}} $ .
Multifractal spectrum and spectral behavior of calcium and titanium isotopes based on nuclear shell model
- Received Date: 2019-06-02
- Accepted Date: 2019-09-14
- Available Online: 2019-11-01
Abstract: We investigate the effect of valence space nucleons on the multifractal analysis (MFA) and spectral analysis of calcium and titanium isotopes. The multifractality of wavefunctions is characterized by its associated singularity spectrum f(α) and generalized dimension Dq. The random matrix theory (RMT) has been employed in the study of properties of the distribution of energy levels. In particular, we find that the number of nucleons and two-body residual interactions particularly affect the singularity and energy level spectra.





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF













 DownLoad:
DownLoad: