-
The production of light nuclei in ultra-relativistic heavy-ion collisions is of importance for many topics in nuclear and particle physics. It does not only help to understand the mechanism of cluster formation in the interior of the fireball in a heavy-ion collision, but can also serve as an effective probe of the fireball freeze-out properties [1-8]. Experimental measurements of light nuclei have been extensively performed at the Relativistic Heavy Ion Collider (RHIC) [9-13], at relatively low-energy collisions by the NA49 Collaboration at the Super Proton Synchrotron (SPS) [14-18], and more recently in very high energy reactions at the Large Hadron Collider (LHC) [19-22]. An interesting phenomenon observed at the LHC is that the yield ratio
$d/p$ in Pb-Pb collisions is larger by a factor of about two than in pp collisions, while the ratios of hadrons such as$p/\pi$ and$\Lambda/K_S^0$ , etc., do not show significant differences between Pb-Pb and pp collisions [19, 23]. Up to now, there is no satisfactory explanations for such phenomena.There are two popular production mechanisms used to describe light nucleus formation. One is the thermal model [24-26], and the other is the recombination/coalescence model [27-35]. The mechanism of the recombination/coalescence production for light nuclei was studied already in 1960s and is now rather well understood [27-35]. In the recombination/coalescence models, the light nuclei can be formed by coalescence of nucleons produced just after hadronization and/or those from resonance decays. Since the binding energies of light nuclei are very small (~a few MeV), final-state coalescence, i.e., nucleons that recombining into light nuclei at the final stage of the hadronic phase evolution (at the final kinetic freeze-out), is commonly adopted in different recombination/coalescence models [32-35]. In fact, light nuclei can be formed during the entire dynamical process of hadronic phase evolution. In the beginning of hadronic evolution, when the temperature is high, light nuclei may be formed and then destroyed immediately due to disruptive collisions in the environment. As the temperature decreases, they may be created again during final-state coalescence. An important question is whether light nuclei are mainly produced just after hadronization, i.e., in a relatively high temperature environment, or at a later stage of hadronic evolution via final-state coalescence [36].
In this paper, we make an estimate of how many light nuclei can be formed just after hadronization, and with what probability the formed light nuclei can coming from until the final kinetic freeze-out. Also, we determine the proportion of the finally observed light nuclei that survive the early formation, and those that are regenerated in the hadronic evolution stage. We employ a hadron recombination model to make a systematic study of the production of light nuclei just after hadronization and at the final kinetic freeze-out, based on an exclusive description of the directly-produced and final-state hadrons using the quark combination model SDQCM developed by the ShanDong group [37-39].
The paper is organized as follows. In Section 2, we introduce the hadron recombination model which describes the light nucleus formation. In Section 3, we calculate the rapidity densities
${\rm d}N/{\rm d}y$ , yield ratios and$p_T$ spectra of$d$ and 3He just after hadronization and at the final kinetic freeze-out in Pb-Pb collisions at$\sqrt{s_{NN}}=$ 2.76 TeV. We present the results and discussions in this section. Section 4 summarizes our findings. -
After hadronization of the partonic system produced early in high energy heavy-ion collisions, various kinds of hadrons are produced, and light nuclei can then be formed through the recombination of protons and neutrons. The hadron recombination model deals with how nucleons recombine into different light nuclei. In this model, the momentum distributions of
$d$ and 3He can be expressed as follows$\begin{split} {f_d}({p_d}) =& \int {\rm d} {x_1}{\rm d}{x_2}{\rm d}{p_1}{\rm d}{p_2}{f_{pn}}({x_1}, {x_2};{p_1}, {p_2})\\ & \times {{\cal R}_d}({x_1}, {x_2};{p_1}, {p_2}, {p_d}), \end{split}$

(1) $ \begin{split} {f_{^3{\rm{He}}}}({p_{^{\rm{3}}{\rm{He}}}}){\rm{ = }}&\int {\rm d} {x_{\rm{1}}}{\rm d}{x_{\rm{2}}}{\rm d}{x_{\rm{3}}}{\rm d}{p_{\rm{1}}}{\rm d}{p_{\rm{2}}}{\rm d}{p_{\rm{3}}}{f_{ppn}}({x_{\rm{1}}}, {x_{\rm{2}}}, {x_{\rm{3}}};{p_{\rm{1}}}, {p_{\rm{2}}}, {p_{\rm{3}}})\\ &\times{{\cal R}_{^{\rm{3}}{\rm{He}}}}({x_{\rm{1}}}, {x_{\rm{2}}}, {x_{\rm{3}}};{p_{\rm{1}}}, {p_{\rm{2}}}, {p_{\rm{3}}}, {p_{^{\rm{3}}{\rm{He}}}}). \quad\quad\quad\quad\quad\;\;(2) \end{split}$

$f_{pn}(x_1, x_2;p_1, p_2)$ is the two-nucleon joint coordinate-momentum distribution for the$(pn)$ cluster, and$f_{ppn}(x_1, x_2, x_3;p_1, p_2, $ $p_3)$ is the three-nucleon joint coordinate-momentum distribution for the$(ppn)$ cluster. Kernel functions$\mathcal {R}_{d}(x_1, x_2;p_1, p_2, p_d)$ and$\mathcal {R}_{^3\rm{He}}(x_1, x_2, x_3;$ $p_1, p_2, p_3, p_{^3\rm{He}}) $ denote the probability densities for$p$ and$n$ , with momenta$p_1$ and$p_2$ at$x_1$ and$x_2$ , to recombine into a$d$ of momentum$p_d$ , and for$p$ ,$p$ and$n$ , with momenta$p_1$ ,$p_2$ and$p_3$ at$x_1$ ,$x_2$ and$x_3$ , to recombine into a 3He of momentum$p_{^3\rm{He}}$ , respectively. Eqs. (1) and (2) are the starting point for describing the production of light nuclei in high energy reactions based on the basic recombination/coalescence idea. All coordinate and momentum variables in Eqs. (1) and (2) are three-dimensional and the integration refers to the whole coordinate and momentum space.Joint distributions
$f_{pn}$ and$f_{ppn}$ are the number densities that satisfy$\int f_{pn}(x_1, x_2;p_1, p_2) {\rm d}x_1{\rm d}x_2 {\rm d}p_1{\rm d}p_2 = N_{pn}$ and$\int f_{ppn}(x_1, x_2, x_3;p_1, p_2, p_3) {\rm d}x_1{\rm d}x_2{\rm d}x_3 {\rm d}p_1{\rm d}p_2{\rm d}p_3=N_{ppn}.$ Here,$N_{pn}=N_pN_n$ is the number of all possible$(pn)$ clusters and$N_{ppn}=N_p(N_p-1)N_n$ is the number of all the possible$(ppn)$ clusters in the bulk hadronic system that we consider.$N_p$ and$N_n$ are the number of protons and of neutrons in the corresponding hadronic system. We rewrite$f_{pn}(x_1, x_2;p_1, p_2) = N_{pn} f^{(n)}_{pn}(x_1, x_2;p_1, p_2)$ and$f_{ppn}(x_1, x_2, x_3; $ $p_1, p_2, p_3) = N_{ppn} f^{(n)}_{ppn}(x_1, x_2, x_3;p_1, p_2, p_3)$ , so that the coordinate-momentum distributions are normalized to unity, which we denote by the superscript ($n$ ). In terms of these normalized joint distributions, we have$\begin{split} {f_d}({p_d}) =& {N_{pn}}\int {\rm d} {x_1}{\rm d}{x_2}{\rm d}{p_1}{\rm d}{p_2}f_{pn}^{(n)}({x_1}, {x_2};{p_1}, {p_2})\\ & \times {{\cal R}_d}({x_1}, {x_2};{p_1}, {p_2}, {p_d}), \end{split}$

(3) $\begin{split} {f_{^3{\rm{He}}}}({p_{^{\rm{3}}{\rm{He}}}}){\rm{ = }}&{N_{ppn}}\int {\rm d} {x_{\rm{1}}}{\rm d}{x_{\rm{2}}}{\rm d}{x_{\rm{3}}}{\rm d}{p_{\rm{1}}}{\rm d}{p_{\rm{2}}}{\rm d}{p_{\rm{3}}}f_{ppn}^{(n)}({x_{\rm{1}}}, {x_{\rm{2}}}, {x_{\rm{3}}};\\ & {p_{\rm{1}}}, {p_{\rm{2}}}, {p_{\rm{3}}}){{\cal R}_{^{\rm{3}}{\rm{He}}}}({x_{\rm{1}}}, {x_{\rm{2}}}, {x_{\rm{3}}};{p_{\rm{1}}}, {p_{\rm{2}}}, {p_{\rm{3}}}, {p_{^{\rm{3}}{\rm{He}}}}). \end{split}$

(4) Kernel functions
$\mathcal {R}_{d}$ and$\mathcal {R}_{^3\rm{He}}$ carry the kinematical and dynamical information of the nucleons recombining into light nuclei, but their precise forms are ambiguous due to their complicated non-perturbative properties. Despite this, we know that the kernel functions should have the following three properties. The first is that they must satisfy momentum conservation, so they should contain the term$\delta\left(\displaystyle{\sum^2_{i=1}} p_i-p_d\right)$ or$\delta\left(\displaystyle{\sum^3_{i=1}} p_i-p_{^3\rm{He}}\right)$ . The energy conservation in the classical recombination process of two/three on-shell nucleons is broken. However, considering the nucleon interaction dynamics, the nucleons entering light nuclei are intermediate scattering states which are not on the mass-shell, so that the exact energy-momentum conservation can also be satisfied. In practice, since the momentum interval between two/three nucleons in recombination is usually very small$\Delta p\leqslant $ 0.2 GeV/c, the relative magnitude to which energy conservation is broken$\Delta p/m$ is only a few percent even for on-shell nucleon recombination. The second property is that the kernel functions should depend on the intrinsic quantum numbers of the formed light nuclei, which are denoted by$C_d$ and$C_{^3\rm{He}}$ . Considering the simple spin counting, we have$C_d=3/4$ and$C_{^3\rm{He}}=1/2$ . The last and the most important property is the coordinate and momentum dependence of the kernel functions. Even though they can not be solved explicitly from first principles, we know that they should increase as the relative space positions and relative momenta of the recombined nucleons decrease. In general, the coordinate and momentum dependence of the kernel functions may be coupled to each other. In this paper, we do not study such coupling effects and in the following, we consider only the simple case where the coordinate and momentum dependence of the kernel functions are decoupled from each other, i.e. they are factorized. Based on the above three properties, we can write the kernel functions as follows.$\begin{split} {{\cal R}_d}({x_1}, {x_2};{p_1}, {p_2}, {p_d}) =& {C_d}{\cal R}_d^{(x)}({x_1}, {x_2}){\cal R}_d^{(p)}({p_1}, {p_2})\\ & \times \delta \left(\displaystyle\mathop \sum \limits_{i = 1}^2 {p_i} - {p_d}\right), \end{split}$

(5) $\begin{split} &{{\cal R}_{^3{\rm{He}}}}({x_{\rm{1}}}, {x_{\rm{2}}}, {x_{\rm{3}}};{p_{\rm{1}}}, {p_{\rm{2}}}, {p_{\rm{3}}}, {p_{^{\rm{3}}{\rm{He}}}}){\rm{ = }}{C_{^{\rm{3}}{\rm{He}}}}{{\cal R}_{^{\rm{3}}{\rm{He}}}^{(x)}}({x_{\rm{1}}}, {x_{\rm{2}}}, {x_{\rm{3}}})\\ &\quad \times {{\cal R}_{^{\rm{3}}{\rm{He}}}^{(p)}}({p_{\rm{1}}}, {p_{\rm{2}}}, {p_{\rm{3}}})\delta \left(\displaystyle\mathop \sum \limits_{{{i = 1}}}^{\rm{3}} {p_i}{\rm{ - }}{p_{^{\rm{3}}{\rm{He}}}}\right). \end{split}$

(6) The coordinate and momentum parts are given from the Wigner function method as Gaussians
$\mathcal {R}^{(x)}_{d}(x_1, x_2)=$ $ 8e^{-\frac{\left(x'_1-x'_2\right)^2}{2R_d^2}}$ ,$\mathcal {R}^{(p)}_{d}(p_{1}, p_{2})=e^{-\frac{\left(p'_{1}-p'_{2}\right)^2}{2\sigma_d^2}}$ ,$\mathcal {R}^{(x)}_{^3\rm{He}}(x_1, x_2, x_3)=8^2e^{-\frac{\left(x'_1-x'_2\right)^2}{2R_{^3\rm{He}}^2}}$ $ e^{-\frac{\left(x'_1+x'_2-2x'_3\right)^2}{6R_{^3\rm{He}}^2}}$ , and$\mathcal {R}^{(p)}_{^3\rm{He}}(p_1, p_2, p_3)= $ $e^{-\frac{\left(p'_1-p'_2\right)^2}{2\sigma_{^3\rm{He}}^2}} e^{-\frac{\left(p'_1+p'_2-2p'_3\right)^2}{6\sigma_{^3\rm{He}}^2}}$ . The superscript ‘$'$ ’ in the coordinate and momentum variables denotes the coordinates and momenta of the nucleons in the rest frame of the forming light nuclei. The widths of the Gaussian distributions are:$R_d=\sqrt{\displaystyle\frac{4}{3} RMS_d^2}=2.26$ fm,$\sigma_d=1/\sqrt{\displaystyle\frac{4}{3} RMS_d^2}=0.087$ GeV,$R_{^3\rm{He}}=RMS_{^3\rm{He}}=1.76$ fm, and$\sigma_{^3\rm{He}}=1/\sqrt{RMS_{^3\rm{He}}^2}=0.112$ GeV [34].$RMS_d$ and$RMS_{^3\rm{He}}$ are the root-mean-square radii for$d$ and 3He, and are$RMS_d=1.96$ fm and$RMS_{^3\rm{He}}=1.76$ fm [40], respectively.We further assume that the normalized joint distributions of the nucleons are coordinate and momentum factorized as follows
$f_{pn}^{(n)}({x_1}, {x_2};{p_1}, {p_2}) = f_{pn}^{(n)}({x_1}, {x_2})f_{pn}^{(n)}({p_1}, {p_2}), $

(7) $f_{ppn}^{(n)}({x_1}, {x_2}, {x_3};{p_1}, {p_2}, {p_3}) = f_{ppn}^{(n)}({x_1}, {x_2}, {x_3})f_{ppn}^{(n)}({p_1}, {p_2}, {p_3}).$

(8) Substituting Eqs. (5-8) into Eqs. (3) and (4), we have
$\begin{split} {f_d}({p_d}) =& {N_{pn}}{C_d}\int {\rm d} {x_1}{\rm d}{x_2}f_{pn}^{(n)}({x_1}, {x_2}){\cal R}_d^{(x)}({x_1}, {x_2})\\ & \times \int {\rm d} {p_1}{\rm d}{p_2}f_{pn}^{(n)}({p_1}, {p_2}){\cal R}_d^{(p)}({p_1}, {p_2})\delta \left(\displaystyle\mathop \sum \limits_{i = 1}^2 {p_i} - {p_d}\right), \end{split}$

(9) $\begin{split} {f_{^3{\rm{He}}}}({p_{^{\rm{3}}{\rm{He}}}}){\rm{ = }}&{N_{ppn}}{C_{^{\rm{3}}{\rm{He}}}}\\ & \times \int {\rm d} {x_{\rm{1}}}{\rm d}{x_{\rm{2}}}{\rm d}{x_{\rm{3}}}f_{ppn}^{(n)}({x_{\rm{1}}}, {x_{\rm{2}}}, {x_{\rm{3}}}){\cal R}_{^{\rm{3}}{\rm{He}}}^{(x)}({x_{\rm{1}}}, {x_{\rm{2}}}, {x_{\rm{3}}})\\ & \times \int {\rm d} {p_{\rm{1}}}{\rm d}{p_{\rm{2}}}{\rm d}{p_{\rm{3}}}f_{ppn}^{(n)}({p_{\rm{1}}}, {p_{\rm{2}}}, {p_{\rm{3}}}){\cal R}_{^{\rm{3}}{\rm{He}}}^{(p)}({p_{\rm{1}}}, {p_{\rm{2}}}, {p_{\rm{3}}}) \\ & \times \delta \left(\displaystyle\mathop \sum \limits_{i{\rm{ = 1}}}^{\rm{3}} {p_i}{\rm{ - }}{p_{^{\rm{3}}{\rm{He}}}}\right). \end{split}$

(10) We denote the coordinate integrals in Eqs. (9) and (10) as
$\mathcal {A}_d$ and$\mathcal {A}_{^3\rm{He}}$ to get$\begin{split} {f_d}({p_d}) =& {N_{pn}}{C_d}{{\cal A}_d}\int {\rm d} {p_1}{\rm d}{p_2}f_{pn}^{(n)}({p_1}, {p_2}){\cal R}_d^{(p)}({p_1}, {p_2})\\ & \times \delta \left(\displaystyle\mathop \sum \limits_{i = 1}^2 {p_i} - {p_d}\right), \end{split}$

(11) $\begin{split} {f_{^3{\rm{He}}}}({p_{^{\rm{3}}{\rm{He}}}}){\rm{ = }}&{N_{ppn}}{C_{^{\rm{3}}{\rm{He}}}}{{\cal A}_{^{\rm{3}}{\rm{He}}}}\int {\rm d} {p_{\rm{1}}}{\rm d}{p_{\rm{2}}}{\rm d}{p_{\rm{3}}}f_{ppn}^{(n)}({p_{\rm{1}}}, {p_{\rm{2}}}, {p_{\rm{3}}})\\ & \times {\cal R}_{^{\rm{3}}{\rm{He}}}^{(p)}({p_{\rm{1}}}, {p_{\rm{2}}}, {p_{\rm{3}}})\delta \left(\displaystyle\mathop \sum \limits_{i{\rm{ = 1}}}^{\rm{3}} {p_i}{\rm{ - }}{p_{^{\rm{3}}{\rm{He}}}}\right), \end{split}$

(12) where
${{\cal A}_d} = 8\int {\rm d} {x_1}{\rm d}{x_2}f_{pn}^{(n)}({x_1}, {x_2}){e^{ - \frac{{{{\left({{x'}_1} - {{x'}_2}\right)}^2}}}{{2R_d^2}}}}, $

(13) $\begin{split} {{\cal A}_{^3{\rm{He}}}}{\rm{ = }}&{{\rm{8}}^{\rm{2}}}\int {\rm d} {x_{\rm{1}}}{\rm d}{x_{\rm{2}}}{\rm d}{x_{\rm{3}}}f_{ppn}^{(n)}({x_{\rm{1}}}, {x_{\rm{2}}}, {x_{\rm{3}}}){e^{{\rm{ - }}\frac{{{{\left(x_1'{\rm{ - }}x_2'\right)}^{\rm{2}}}}}{{{\rm{2}}R_{^{\rm{3}}{\rm{He}}}^2}}}}\\ & \times e^{{\rm{ - }}\frac{{{{\left(x_1'{\rm{ + }}x_2'{\rm{ - 2}}x_3'\right)}^{\rm{2}}}}}{{{\rm{6}}R_{^{\rm{3}}{\rm{He}}}^2}}}. \end{split}$

(14) From Eqs. (13) and (14), one can easily see that the
$\mathcal {A}$ coefficients originate from the overlap integral between the nuclear spatial wave function and the spatial distribution of nucleons which form the light nuclei.We change the two integral variables in Eq. (13) to
$r_1= \displaystyle\frac{x_1-x_2}{\sqrt{2}}$ and$r_2= \displaystyle\frac{x_1+x_2}{\sqrt{2}}$ and those in Eq. (14) to$r_1= \displaystyle\frac{x_1-x_2}{\sqrt{2}}$ ,$r_2= \displaystyle\frac{x_1+x_2-2x_3}{\sqrt{2}}$ , and$r_3= \displaystyle\frac{x_1+x_2+x_3}{3}$ . Then we can write${{\cal A}_d} = 8\int {\rm d} {r_1}{\rm d}{r_2}f_{pn}^{(n)}({r_1}, {r_2}){e^{ - \frac{{r_{1'}^2}}{{R_d^2}}}}, $

(15) ${{\cal A}_{^3{\rm{He}}}}{\rm{ = }}{{\rm{8}}^{\rm{2}}}\int {\rm d} {r_{\rm{1}}}{\rm d}{r_{\rm{2}}}{\rm d}{r_{\rm{3}}}f_{ppn}^{(n)}({r_{\rm{1}}}, {r_{\rm{2}}}, {r_{\rm{3}}}){e^{{\rm{ - }}\frac{{r_1^{'2}}}{{R_{^{\rm{3}}{\rm{He}}}^2}}}}{e^{{\rm{ - }}\frac{{r_2^{'2}}}{{{\rm{3}}R_{^{\rm{3}}{\rm{He}}}^2}}}}, $

(16) and the normalization constraints
$\int {f_{pn}^{(n)}} ({r_1}, {r_2}){\rm d}{r_1}{\rm d}{r_2} = 1, $

(17) $\int {f_{ppn}^{(n)}} ({r_1}, {r_2}, {r_3}){\rm d}{r_1}{\rm d}{r_2}{\rm d}{r_3} = 1.$

(18) To evaluate
$\mathcal {A}_d$ and$\mathcal {A}_{^3\rm{He}}$ , we assume that the coordinate variables are decoupled in the coordinate distributions as$f_{pn}^{(n)}({r_1}, {r_2}) = f_{pn}^{(n)}({r_1})f_{pn}^{(n)}({r_2}), $

(19) $f_{ppn}^{(n)}({r_1}, {r_2}, {r_3}) = f_{ppn}^{(n)}({r_1})f_{ppn}^{(n)}({r_2})f_{ppn}^{(n)}({r_3}).$

(20) The normalized distributions of the relative space positions of the nucleons are
$f^{(n)}_{pn}(r_1) = \frac{1}{\left(2\pi R_f^2\right)^{1.5}} e^{-\frac{r_1^2}{2R_f^2}}$ ,$f^{(n)}_{ppn}(r_1) = $ $ \frac{1}{\left(2\pi R_f^2\right)^{1.5}} e^{-\frac{r_1^2}{2R_f^2}}$ and$f^{(n)}_{ppn}(r_2) = \frac{1}{\left(4\pi R_f^2\right)^{1.5}} e^{-\frac{r_2^2}{4R_f^2}}$ [41].$R_f$ is the Gaussian width of the relative space positions of the nucleons, and is about 6.1 fm just after hadronization, and 7.0 fm at the final kinetic freeze-out [41, 42]. Note that$R_f$ used here is the effective radius of the fireball as it evolves till the freeze-out of light nuclei in the static picture, and is not equivalent to the geometrical radius of the fireball [43].$R_f$ is linked to the effective correlation length of nucleons in the fireball in the static picture. That is why we adopt the value of this radius as obtained from experiential measurements of the femtoscopic radii [42], rather than that extracted from hydrodynamic or transport models at the final kinetic freeze-out [43, 44]. Substituting Eqs. (19) and (20) into Eqs. (15) and (16), we have$\mathcal {A}_d = \frac{8}{\left(2\pi R_f^2\right)^{1.5}} \int {\rm d}r_1 e^{-\frac{r_1^2}{2R_f^2}} e^{-\frac{r_1'^2}{R_d^2}}, $

(21) $\begin{split} {{\cal A}_{^3{\rm{He}}}}{\rm{ = }}&\frac{{{\rm{64}}}}{{{{\left({\rm{2}}\pi R_f^{\rm{2}}\right)}^{{\rm{1}}.{\rm{5}}}}{{\left({\rm{4}}\pi R_f^{\rm{2}}\right)}^{{\rm{1}}.{\rm{5}}}}}}\int {\rm d} {r_{\rm{1}}}{e^{{\rm{ - }}\frac{{r_{\rm{1}}^{\rm{2}}}}{{{\rm{2}}R_f^{\rm{2}}}}}}{e^{{\rm{ - }}\frac{{r_1^{{\rm{'2}}}}}{{R_{^{\rm{3}}{\rm{He}}}^2}}}} \\ &\times \int {\rm d} {r_{\rm{2}}}{e^{{\rm{ - }}\frac{{r_{\rm{2}}^{\rm{2}}}}{{{\rm{4}}R_f^{\rm{2}}}}}}{e^{{\rm{ - }}\frac{{r_2^{{\rm{'2}}}}}{{{\rm{3}}R_{^{\rm{3}}{\rm{He}}}^2}}}}, \end{split}$

(22) Assuming the instantaneous recombination in the rest frame of the formed
$(pn)$ or$ (ppn) $ cluster, we can easily get the numerical results for$\mathcal {A}_d$ and$\mathcal {A}_{^3\rm{He}}$ .The production of light nuclei just after hadronization and at the final kinetic freeze-out can be computed using Eqs. (11) and (12), as the joint-momentum distributions
$f_{pn}(p_1, p_2)$ and$f_{ppn}(p_1, p_2, p_3)$ are known. Ignoring the nucleon correlations, we have$f_{pn}(p_1, p_2)=f_{p}(p_1)f_{n}(p_2)$ and$f_{ppn}(p_1, p_2, p_3)= f_{p}(p_1)f_{p}(p_2)$ $f_{n}(p_3)$ , where the single nucleon momentum distributions$f_p$ and$f_n$ just after hadronization can be easily computed by SDQCM. When resonance decays and hadronic scattering effects are included, we get$f_p$ and$f_n$ at the final kinetic freeze-out.As a brief summary of this section, we would like to emphasize that with the exclusive quark combination model SDQCM, used to obtain momentum distributions of different light, strange and heavy flavor hadrons, we can apply the hadron recombination model to investigate the production of light nuclei, hypernuclei and other molecular states. There are no extra free parameters in this method apart from the assumptions and/or approximations explicitly stated above, such as the coordinate and momentum factorization of the kernel and joint distribution functions, and decoupling of different coordinate variables in the coordinate distributions. This newly proposed method, an exclusive quark combination model + an inclusive hadron recombination model, is an attempt to mimic the quantum mechanical process of recombination/coalescence. It is very convenient for studying different production sources of light nuclei, hypernuclei and other molecular states.
-
In this section, we present a systematic study of the production of light nuclei at midrapidity in central Pb-Pb collisions at
$\sqrt{s_{NN}}= 2.76$ TeV. First, we employ SDQCM to compute rapidity density${\rm d}N/{\rm d}y$ and$p_T$ distribution of various hadrons.$ $ SDQCM is unique for its ability to provide yields, rapidity distributions and$p_T$ spectra of different hadrons, and has been successfully applied in studies of$e^+e^-$ annihilation, p-p reactions and relativistic heavy-ion collisions [23, 37-39, 45-47]. The starting point of SDQCM is a system consisting of different flavors of constituent quarks and antiquarks, whose phase space distributions are given as input. The quarks and antiquarks combine into different species of directly-produced hadrons according to a sophisticated combination rule [37-39]. After hadronization, directly-produced hadrons undergo a hadronic evolution stage during which short lifetime resonances decay and scattering among different hadrons occurs. Hadronic evolution involves many effects and is very complicated. We do not investigate all effects here, but only focus on those that influence hadron yields and shapes of hadron$p_T$ spectra. For hadron yields, we only consider resonance decay contributions and neglect scattering effects, which are comparatively small [48, 49]. We directly use the UrQMD results at the LHC energies for hadrons before and after hadronic evolution [50, 51] to correct the shape of hadron$p_T$ distributions. We calculate the production of relatively stable hadrons, such as$\pi$ ,$K$ ,$\phi$ mesons and$p$ ,$\Lambda$ ,$\Xi$ ,$\Omega$ baryons etc., so that the above approximation for handling the effects of the hadronic evolution is sufficient.To compute momentum distributions of directly-produced hadrons with SDQCM, we need the momentum distributions of constituent quarks just before hadronization. As we focus on the midrapidity region at the LHC energy, the influence of net quarks from incident nuclei is ignored. Also, the isospin symmetry for
$u$ and$d$ quarks is assumed. The input values for the rapidity densities of$u$ ,$d$ and$s$ quarks are${\rm d}N_u/{\rm d}y={\rm d}N_d/{\rm d}y=679$ and${\rm d}N_s/{\rm d}y=272$ , respectively. The longitudinal rapidity distributions for$u$ ,$d$ and$s$ quarks are chosen to be uniform since we focus on hadron production in the rapidity window$|y|<0.5$ . For the transverse momentum distributions of light and strange quarks, we use an exponential parametrization${\rm d}N/(p_T{\rm d}p_T) \propto \exp\left(-\sqrt{p_T^2+m^2}/T\right)$ as we focus on thermal hadron production. The slope parameter$T$ for$u$ ,$d$ quarks is 0.27 GeV, and 0.33 GeV for the$s$ quark. These values are slightly smaller than those obtained in our previous work [52], where the production of various light, strange and charm hadrons was studied and the corresponding constituent quark distributions included in the collective radial flows generated during the partonic evolution stage and the hadronic evolution stage. In this study, constituent quark distributions carry only the radial flows created during partonic evolution. The radial flows generated during the hadronic evolution stage are added to hadrons produced after hadronization.With the above inputs, the rapidity densities
${\rm d}N/{\rm d}y$ and$p_T$ distributions for directly-produced hadrons, i.e., those hadrons produced just after hadronization, can be calculated with SDQCM. Including very short lifetime$\rho$ ,$K^*$ ,$\Delta$ and$\Sigma^*$ decays and considering hadronic scattering, we obtain${\rm d}N/{\rm d}y$ and$p_T$ distributions of hadrons at the final kinetic freeze-out. We want to point out that some processes, for example strong decays of some hadrons such as$\Xi^*$ , electromagnetic decays and weak decays, are not included because their lifetimes are relatively long and they decay after the kinetic freeze-out. After considering all strong and electromagnetic decays, we have${\rm d}N/{\rm d}y$ and$p_T$ distributions for the total final state hadrons, which can be compared to the LHC experimental data. For more information on how SDQCM models hadronization, see Refs. [38, 39, 52, 53].Rapidity densities
${\rm d}N/{\rm d}y$ of hadrons in central Pb-Pb collisions at$\sqrt{s_{NN}}=2.76$ TeV are listed in Table 1. The experimental data in the second column are from Refs. [54-57]. The third column presents the results for directly-produced hadrons. The fourth column gives the results for hadrons at the final kinetic freeze-out. The last column are the results for the total final state hadrons, which agree with the experimental data, and are comparable to our previous results calculated by analytical formulas [52] and the results given in [58]. The results for directly produced$\phi$ and$\Omega$ , those created at the final kinetic freeze-out and the total final state ones are the same, since there are no other decay contributions. The directly-produced$K/\pi$ ratio is about 0.4, which reveals the strangeness in heavy-ion collisions and is comparable to our previous studies [39]. Directly-produced protons are about half of the total final state protons, while the other half come from$\Delta$ decays. The lifetime of$\Delta$ is so short that they decay before the final kinetic freeze-out occurs. As a result, protons at kinetic freeze-out are identical to the total final state protons. This is the reason why some coalescence models use the momentum distribution of protons measured experimentally as input when studying the production of light nuclei [34].$\Lambda$ baryons are directly produced or come from$\Sigma^*$ and$\Sigma^0$ decays, so that there are more of them in the total final state than after the kinetic freeze-out, and both are more numerous than directly-produced ones.$\Xi^*$ can decay to$\Xi$ , and the decay takes place after kinetic freeze-out. The directly-produced$\Xi$ and those after the kinetic freeze-out are the same, and both are less in number than the total final state ones. For more information of hadron decays, see Ref. [59].hadron experimental data SDQCM DI KI TFS ${\pi^+}$ 

${733\pm54}$ 

55 501 737 ${\pi^-}$ 

${732\pm52}$ 

55 501 737 ${K^+}$ 

${109\pm9}$ 

22 88 111 ${K^-}$ 

${109\pm9}$ 

22 88 111 ${K_S^{0}}$ 

${110\pm10}$ 

0 0 106 ${\phi}$ 

${13.8\pm0.5\pm1.7}$ 

13.2 13.2 13.2 ${p}$ 

${34\pm3}$ 

16 33 33 ${\bar p}$ 

${33\pm3}$ 

16 33 33 ${\Lambda}$ 

${26\pm3}$ 

7.8 17 25 ${\bar\Lambda}$ 

− 7.8 17 25 ${\Xi^-}$ 

${3.34\pm0.06\pm0.24}$ 

2.60 2.60 3.90 ${\bar\Xi^+}$ 

${3.28\pm0.06\pm0.23}$ 

2.60 2.60 3.90 ${\Omega^-}$ 

${0.58\pm0.04\pm0.09}$ 

0.52 0.52 0.52 ${\bar\Omega^+}$ 

${0.60\pm0.05\pm0.09}$ 

0.52 0.52 0.52 Table 1. Rapidity densities dN/dy of identified hadrons in central Pb-Pb collisions at
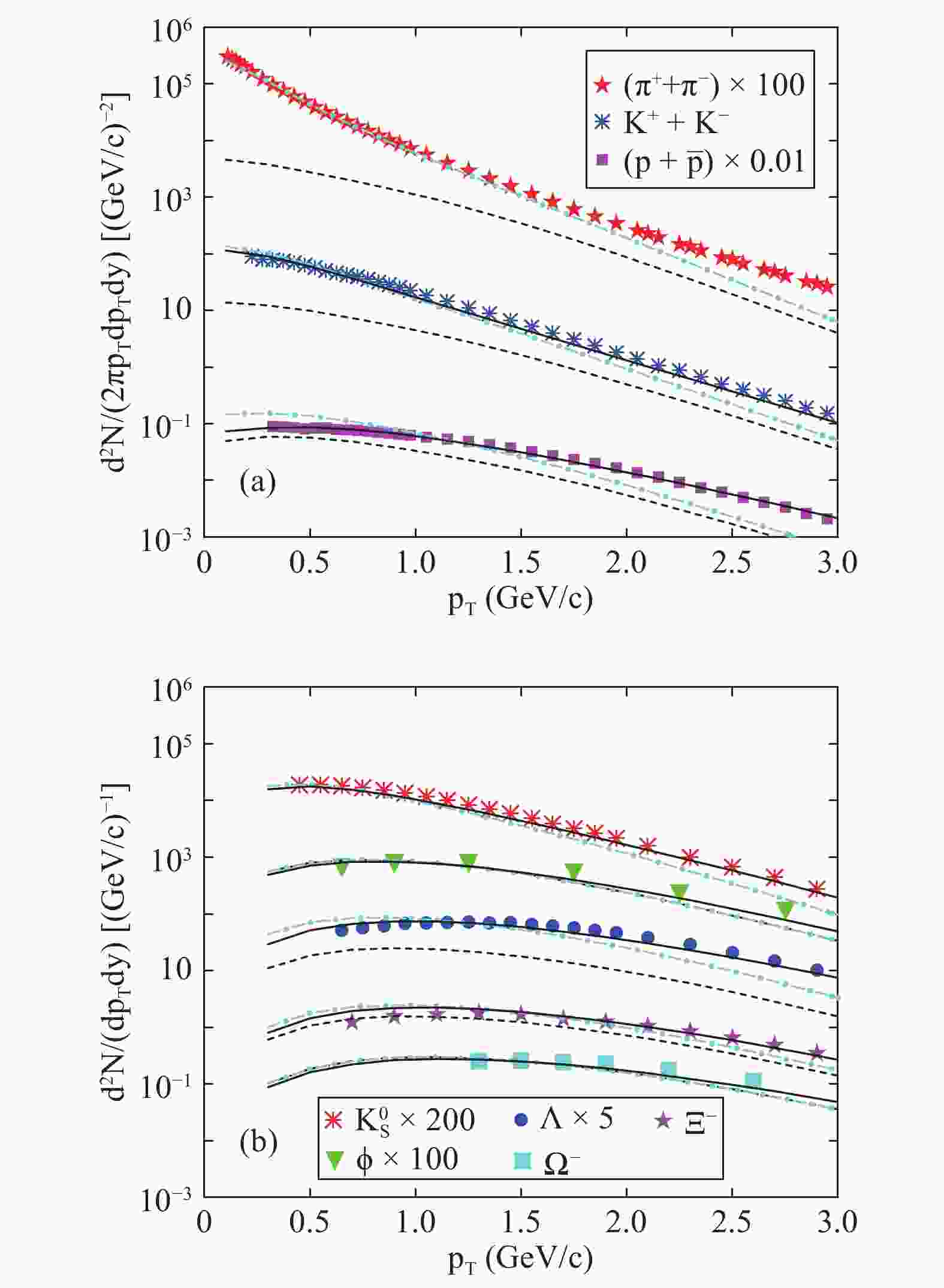
${\sqrt{s_{N\!N}}=2.76}$ TeV. The experimental data are from Refs. [54-57]. The last three columns are the results calculated with SDQCM for DIrectly-produced hadrons, hadrons at KInetic freeze-out and Total Final State hadrons.$ p_T $ distributions for hadrons are also computed with SDQCM and the results are shown in Fig. 1. The filled symbols are the experimental data from Refs. [54-57]. Dashed lines are the results for directly-produced hadrons just after hadronization. Solid lines and dot-dashed lines are for the total final state hadrons, including strong and electromagnetic decays in cases when hadronic interactions are turned on and off, respectively. The three lines for$\Omega^-$ baryons are almost the same as there are no resonance decay contributions to$\Omega^-$ and hadronic interactions of multistrange hadrons are very small. The same holds for$\phi$ mesons. Distributions for directly-produced$\pi^{\pm}$ ,$K^{\pm}$ ,$p \bar p$ ,$\Lambda$ and$\Xi^{-}$ (dashed lines) are harder than those for the final state with decay contributions only (dot-dashed lines), especially for$\pi^{\pm}$ and$K^{\pm}$ mesons. Hadronic interactions after hadronization push$p_T$ spectra of hadrons, especially for$p \bar p$ and$\Lambda$ , to higher values since more collective radial flows are created at this stage. The effects of hadronic interactions on$\pi^{\pm}$ $p_T$ distribution are very complicated since many mesons and baryons decay to$\pi^{\pm}$ , and we do not plot it in Fig.1. Solid lines for total final state hadrons$K^{\pm}$ ,$K_S^{0}$ ,$\phi$ ,$p \bar p$ ,$\Lambda$ ,$\Xi^{-}$ and$\Omega^-$ agree very well with the experimental data. A good reproduction of the measurements for the total final state, kinetic freeze-out and directly-produced protons is necessary for the study of light nuclei.
Figure 1. (color online) pT distributions of hadrons at midrapidity in central Pb-Pb collisions at
${\sqrt{s_{N\!N}}=2.76}$ TeV. The filled symbols are the experimental data from Refs. [54-57]. Dashed lines are the results for directly-produced hadrons just after hadronization. Solid lines and dot-dashed lines are for the total final state hadrons including strong and electromagnetic decays in cases when the hadronic interactions are turned on and off.In view of the good performance of SDQCM for hadrons①), we turn to the study of light nuclei at midrapidity in central Pb-Pb collisions at
$\sqrt{s_{NN}}= 2.76$ TeV. We perform the calculations using the hadron recombination model introduced in Sec. 2, for the stages just after hadronization and at the final kinetic freeze-out. We take into account the destructive and regenerative collisions during the production of light nuclei in the intervening time based on an effective method, rather than using the conventional transport and/or kinetic models such as in Refs. [60, 61]. We compute the production of light nuclei just after hadronization and before hadronic evolution using the distributions of directly-produced nucleons. These light nuclei are formed immediately and are denoted by JAH (Just After Hadronization). The JAH light nuclei undergo hadronic scatterings with hadrons. The influence of hadronic scattering on JAH light nuclei are taken into account by modifying the coordinates and momenta of the constituent-nucleons affected by the scattering. After hadronic evolution, i.e., at the final kinetic freeze-out, we check to see if the constituent-nucleons still meet the requirements of binding together into light nuclei. If that is the case, the JAH light nuclei are kept, otherwise they are discarded and the corresponding constituent-nucleons are promoted as real nucleons.Recalling Eqs. (11) and (12), we calculate rapidity densities
${\rm d}N/{\rm d}y$ and$p_T$ spectra of$d$ and 3He just after hadronization as well as at the final kinetic freeze-out as we know$f_{pn}(p_1, p_2)$ and$f_{ppn}(p_1, p_2, p_3)$ . We count the initially produced light nuclei just after hadronization by evaluating the probability for recombination of every possible directly-produced$(pn)$ pair or$(ppn)$ cluster to recombine into a$d$ or 3He. If an initially produced light nucleus is destroyed during hadronic evolution, the constituent nucleons are separated in phase space. Otherwise, they are still close enough. Taking into account this feature, we re-calculate the number of light nuclei at the final kinetic freeze-out using the evolved distributions of these directly-produced nucleons (after accounting for the volume expansion of the hadronic system and the flow generation during the hadronic evolution stage). We treat these light nuclei as a part of the initially produced light nuclei. We also calculate the number of light nuclei at the final kinetic freeze-out formed from nucleons from$\Delta$ resonance decays and denote these light nuclei as regenerated during the hadronic evolution stage. The input nucleon momentum distributions just after hadronization are$f_{pn}(p_1, p_2)=f_p^{(di)}(p_1)f_n^{(di)}(p_2)$ and$f_{ppn}(p_1, p_2, p_3)=$ $f_p^{(di)}(p_1)f_p^{(di)}(p_2)f_n^{(di)}(p_3) $ , where the superscript$(di)$ denotes directly-produced nucleons. The input momentum distributions at the final kinetic freeze-out are as follows.$f_{pn}(p_1, p_2)=f_p^{(ki)}(p_1)f_n^{(ki)}(p_2), $

(23) $f_{ppn}(p_1, p_2, p_3)=f_p^{(ki)}(p_1)f_p^{(ki)}(p_2)f_n^{(ki)}(p_3).$

(24) The superscript
$(ki)$ denotes nucleons at the final kinetic freeze-out, which are composed of two parts. One is from the directly-produced nucleons denoted by the superscript$(ki-di)$ , and the other is from$\Delta$ resonance decays denoted by the superscript$(de)$ , i.e.,$\begin{split} &{f_{pn}}({p_1}, {p_2})\\ & \quad=\left[f_p^{(ki-di)}({p_1}) + f_p^{(de)}({p_1})\right]\left[f_n^{(ki-di)}({p_2}) + f_n^{(de)}({p_2})\right]\\ & \quad=f_p^{(ki - di)}({p_1})f_n^{(ki - di)}({p_2}) + f_p^{(ki - di)}({p_1})f_n^{(de)}({p_2})\\ &\quad\quad + f_p^{(de)}({p_1})f_n^{(ki - di)}({p_2}) + f_p^{(de)}({p_1})f_n^{(de)}({p_2}), \end{split}$

(25) $\begin{split} &{f_{ppn}}({p_1}, {p_2}, {p_3})\\ &\quad = \left[f_p^{(ki-di)}({p_1}) + f_p^{(de)}({p_1})\right]\left[f_p^{(ki-di)}({p_2}) + f_p^{(de)}({p_2})\right]\\ &\quad\quad \times \left[f_n^{(ki-di)}({p_3}) + f_n^{(de)}({p_3})\right]\\ &\quad = f_p^{(ki - di)}({p_1})f_p^{(ki - di)}({p_2})f_n^{(ki - di)}({p_3})\\ &\quad\quad + f_p^{(ki - di)}({p_1})f_p^{(ki - di)}({p_2})f_n^{(de)}({p_3})\\ &\quad\quad + f_p^{(ki - di)}({p_1})f_p^{(de)}({p_2})f_n^{(ki - di)}({p_3})\\ &\quad\quad + f_p^{(de)}({p_1})f_p^{(ki - di)}({p_2})f_n^{(ki - di)}({p_3})\\ &\quad\quad + f_p^{(ki - di)}({p_1})f_p^{(de)}({p_2})f_n^{(de)}({p_3})\\ &\quad\quad + f_p^{(de)}({p_1})f_p^{(ki - di)}({p_2})f_n^{(de)}({p_3})\\ &\quad\quad + f_p^{(de)}({p_1})f_p^{(de)}({p_2})f_n^{(ki - di)}({p_3})\\ &\quad\quad + f_p^{(de)}({p_1})f_p^{(de)}({p_2})f_n^{(de)}({p_3}). \end{split}$

(26) Note that
$f_p^{(ki-di)}$ and$f_n^{(ki-di)}$ are momentum distributions for nucleons produced just after hadronization that have survived till kinetic freeze-out. They carry the radial flows generated during the hadronic evolution stage besides those from the partonic stage. The first terms in Eqs. (25) and (26) contribute to the surviving light nuclei, while all the other terms contribute to regenerated light nuclei.With the momentum distributions of directly-produced protons and those at final kinetic freeze-out (i.e., total final state ones) shown in Fig. 1, we can compute rapidity densities
${\rm d}N/{\rm d}y$ and$p_T$ spectra of$d$ and 3He. Momentum distributions of neutrons are the same as those of protons due to isospin symmetry. The third and fourth columns in Table 2 are the${\rm d}N/{\rm d}y$ results for just after hadronization and at the final kinetic freeze-out, respectively. The experimental data in the second column are from Ref. [19]. From Table 2, one can see that the results computed for just after hadronization are much lower than the experimental data. The result for$d$ calculated at the final kinetic freeze-out agree well with the data, while that of 3He is smaller than the lower limit of the data. The reason for underestimating of 3He is that we only include the dominant production contribution for 3He, while the other contributions such as$d+p\rightarrow ^3$ He and decay contributions from$^3_\Lambda$ H are not included. The number of surviving$d$ and 3He formed just after hadronization and including the regenerated ones at the final kinetic freeze-out are shown in the last two columns inTable 2. About half of$d$ produced just after hadronization survive hadronic evolution, but only about one fourth of 3He do so. This is because we treat$d$ as a cluster of two quasi-free constituent nucleons and 3He as a cluster of three quasi-free constituent nucleons when considering hadronic scattering effects. The dissociation probability for$d$ is proportional to 2 times the nucleon-hadron rescattering cross section, while that for 3He is proportional to three times the same cross section. It is therefore much easier for 3He to be destroyed compared to$d$ . The fraction of disassociated JAH deuterons is about 1/2, and that of JAH 3He is about 3/4, instead of 1. This is because the rate of inter-particle interactions/scatterings in the hadronic phase decreases quickly as the hadronic system expands. From this point, it ismeaningful to discuss JAH light nuclei production. For the total light nuclei at the final kinetic freeze-out, about 77% of$d$ and 90% of 3He are regenerated. These numerical results explicitly illustrate the different production sources of$d$ and 3He.experimental data just after hadronization kinetic surviving at kinetic regenerated at kinetic d (9.82±0.04±1.58)×10−2 4.18×10−2 9.05×10−2 2.11×10−2 6.94×10−2 3He (2.76±0.09±0.62)×10−4 0.68×10−4 1.62×10−4 0.17×10−4 1.45×10−4 Table 2. Rapidity densities dN/dy of d and 3He in central Pb-Pb collisions at
${\sqrt{s_{NN}}=2.76}$ TeV. The experimental data are from Ref. [19]. The third and fourth columns are the results for just after hadronization and at the final kinetic freeze-out. The surviving light nuclei and the regenerated nuclei at final kinetic freeze-out are given in the last two columns.A series of interesting observables are yield ratios for light nuclei, such as
$d/p$ , 3He$/p$ and 3He$/d$ . Recalling Eqs. (11) and (12), we have$\frac{d}{p}{\rm{ = }}{N_p}{C_d}{{\cal A}_d}\int {\rm d} {p_1}{\rm d}{p_2}f_{pn}^{(n)}({p_1}, {p_2}){\cal R}_d^{(p)}({p_1}, {p_2}), $

(27) $\begin{split} &\displaystyle\frac{{^{\rm{3}}{\rm{He}}}}{p}{\rm{ = }}N_p^{\rm{2}}{C_{^{\rm{3}}{\rm{He}}}}{{\cal A}_{^{\rm{3}}{\rm{He}}}}\\ &\quad\quad \times \int {\rm d} {p_{\rm{1}}}{\rm d}{p_{\rm{2}}}{\rm d}{p_{\rm{3}}}f_{ppn}^{(n)}({p_{\rm{1}}}, {p_{\rm{2}}}, {p_{\rm{3}}}){\cal R}_{^{\rm{3}}{\rm{He}}}^{(p)}({p_{\rm{1}}}, {p_{\rm{2}}}, {p_{\rm{3}}}), \end{split}$

(28) $\begin{split} &\displaystyle\frac{{^3{\rm{He}}}}{d}{\rm{ = }}{N_p}\displaystyle\frac{{{C_{^3{\rm{He}}}}}}{{{C_d}}}\displaystyle\frac{{{{\cal A}_{^{\rm{3}}{\rm{He}}}}}}{{{{\cal A}_d}}}\\ &\quad\quad \times \displaystyle\frac{{\int {\rm d} {p_{\rm{1}}}{\rm d}{p_{\rm{2}}}{\rm d}{p_{\rm{3}}}f_{ppn}^{(n)}({p_{\rm{1}}}, {p_{\rm{2}}}, {p_{\rm{3}}}){\cal R}_{^{\rm{3}}{\rm{He}}}^{(p)}({p_{\rm{1}}}, {p_{\rm{2}}}, {p_{\rm{3}}})}}{{\int {\rm d} {p_{\rm{1}}}{\rm d}{p_{\rm{2}}}f_{pn}^{(n)}({p_{\rm{1}}}, {p_{\rm{2}}}){\cal R}_d^{(p)}({p_{\rm{1}}}, {p_{\rm{2}}})}}. \end{split}$

(29) To analyze the behavior of the yield ratios, analytical expressions for
${A}_d$ and${A}_{^3\rm{He}}$ are required. We consider the Lorentz contraction effect, and replace$r_1'$ and$r_2'$ with$r_1/\widetilde{\gamma}$ and$r_2/\widetilde{\gamma}$ , respectively, where$\widetilde{\gamma}$ is the effective Lorentz contraction factor related to the coordinate transformation from the laboratory frame to the center-of mass frame. In this case, we have${{\cal A}_d} = 8{\left(1 + \frac{{3R_f^2}}{{2{{\tilde \gamma }^2}R_d^2}}\right)^{ - 3/2}}, $

(30) ${{\cal A}_{^3{\rm{He}}}}{\rm{ = 64}}{\left({\rm{1 + }}\frac{{{\rm{3}}R_f^{\rm{2}}}}{{{\rm{2}}{{\tilde \gamma }^{\rm{2}}}R_{^{\rm{3}}{\rm{He}}}^2}}\right)^{{\rm{ - 3/2}}}}{\left({\rm{1 + }}\frac{{R_f^{\rm{2}}}}{{{{\tilde \gamma }^{\rm{2}}}R_{^{\rm{3}}{\rm{He}}}^2}}\right)^{{\rm{ - 3/2}}}}.$

(31) One can easily see from Eqs. (30) and (31) that the
$\mathcal {A}$ factors for$d$ and 3He decrease with increasing fireball radius at freeze-out. This means that it becomes more difficult for a certain$(pn)$ or$(ppn)$ cluster to form a light nucleus when the freeze-out fireball becomes larger. Considering that$R_f$ is about 6~7 fm in heavy-ion collisions at the LHC energies [41, 42], and that$R_d=2.26$ fm and$R_{^3\rm{He}}=1.76$ fm, both$R_f/R_d$ and$R_f/R_{^3\rm{He}}$ are much larger than 1. As$\widetilde{\gamma}$ is slightly larger than 1, we get that$\mathcal {A}_d \propto 1/ $ $R_f^3$ and$\mathcal {A}_{^3\rm{He}} \propto 1/R_f^6$ . Momentum integrals in Eqs. (27-29) are very weakly dependent on the collision centrality as the normalized nucleon momentum distributions do not show significant differences in different centrality collisions.$C_{d}$ and$C_{^3\rm{He}}$ depend only on the intrinsic quantum numbers of light nuclei and are independent of the collision energy and centrality. Therefore, one can see that the ratios in Eqs. (27-29) are approximately proportional to nucleon densities instead of nucleon numbers, and this can well explain the constant behavior of$d/p$ and 3He$/p$ as function of the average charge multiplicity observed by the ALICE Collaboration [19]. The calculated values of$d/p$ , 3He$/p$ and 3He$/d$ for just after hadronization and at the final kinetic freeze-out are given in the third and fourth columns in Table 3. The experimental data in the second column in Table 3 are from Ref. [19].ratio data just after hadronization kinetic kinetic (noHI) data for pp 7 TeV d/p (3.2188±0.0142±0.6067)×10−3 2.61×10−3 2.74×10−3 1.31×10−3 (1.63±0.20)×10−3 3He/p (1.0611±0.0359±0.2570)×10−5 0.43×10−5 0.49×10−5 0.22×10−5 − 3He/d (2.81±0.86)×10−3 1.63×10−3 1.79×10−3 1.63×10−3 − Table 3. Yield ratios d/p, 3He/p and 3He/d in central Pb-Pb collisions at
${\sqrt{s_{N\!N}}=2.76}$ TeV. The experimental data in the second column are from Ref. [19]. The third and fourth columns are the results for just after hadronization and at the final kinetic freeze-out. The fifth column is the result at the final kinetic freeze-out when hadronic interactions are turned off. The last column are the experimental data for pp collisions at${\sqrt{s}=7}$ TeV.In order to better understand the effects of hadronic interactions during the hadronic evolution stage on the production of light nuclei, we also calculate these yield ratios at the final kinetic freeze-out in the case when hadronic interactions are turned off after hadronization. In that case, there is no formation nor destruction of light nuclei during the hadronic system evolution, and the number of light nuclei is just that after hadronization. The number of protons includes those from resonance decays, apart the directly-produced ones, i.e.,
$(d/p)_{\rm noHI} = \frac { (d)_{\rm JAH} } {(p)_{\rm KI}}, $

(32) ${{(^3}{\rm{He/}}p)_{\rm noHI}}{\rm{ = }}\frac{{{{{(^{\rm{3}}}{\rm{He}})}_{\rm JAH}}}}{{{{(p)}_{\rm KI}}}}, $

(33) ${{(^3}{\rm{He/}}d)_{\rm noHI}}{\rm{ = }}\frac{{{{{(^{\rm{3}}}{\rm{He}})}_{\rm HAH}}}}{{{{(d)}_{\rm JAH}}}}.$

(34) The numerical results for this case are given in the fifth column in Table 3, which shows that d/p,3He/p and 3He/d ratios decrease by about 48%, 45% and 91% , respectively, when hadronic interactions are turned off compared to those including hadronic interactions. This decrease can be also seen in pp collisions, where hadronic interactions after hadronization disappear. In column six of Table 3, the experimental result for d/p in pp collisions at
$\sqrt{s}=7$ TeV [19] is given, and is seen to be comparable with the numerical result for d/pin Pb-Pb collisions without hadronic interaction effects. Additional measurements of 3He/p and 3He/d in pp collisions could help to confirm the effect of negligable hadronic interactions in the hadronic system evolution.$p_T$ distributions for$d$ and 3He are shown in Fig. 2. The open circles and diamonds are the experimental data for$d$ and 3He, respectively, measured by the ALICE Collaboration in Ref. [19]. In Fig. 2(a), the calculated results for just after hadronization are shown by a dashed line, and those at the final kinetic freeze-out by a solid line. For both$d$ and 3He,$p_T$ spectra calculated just after hadronization are softer than at the final kinetic freeze-out. This is because the$p_T$ distribution of directly-produced protons is softer than that at the kinetic freeze-out, as it acquires more radial flows during hadronic evolution. In Fig. 2(b),$p_T$ distributions of the surviving and regenerated$d$ and 3He at the final kinetic freeze-out are represented with a dotted line and dot-dashed line, respectively. The solid lines denoting the total$d$ and 3He at the kinetic freeze-out are shown for guidence.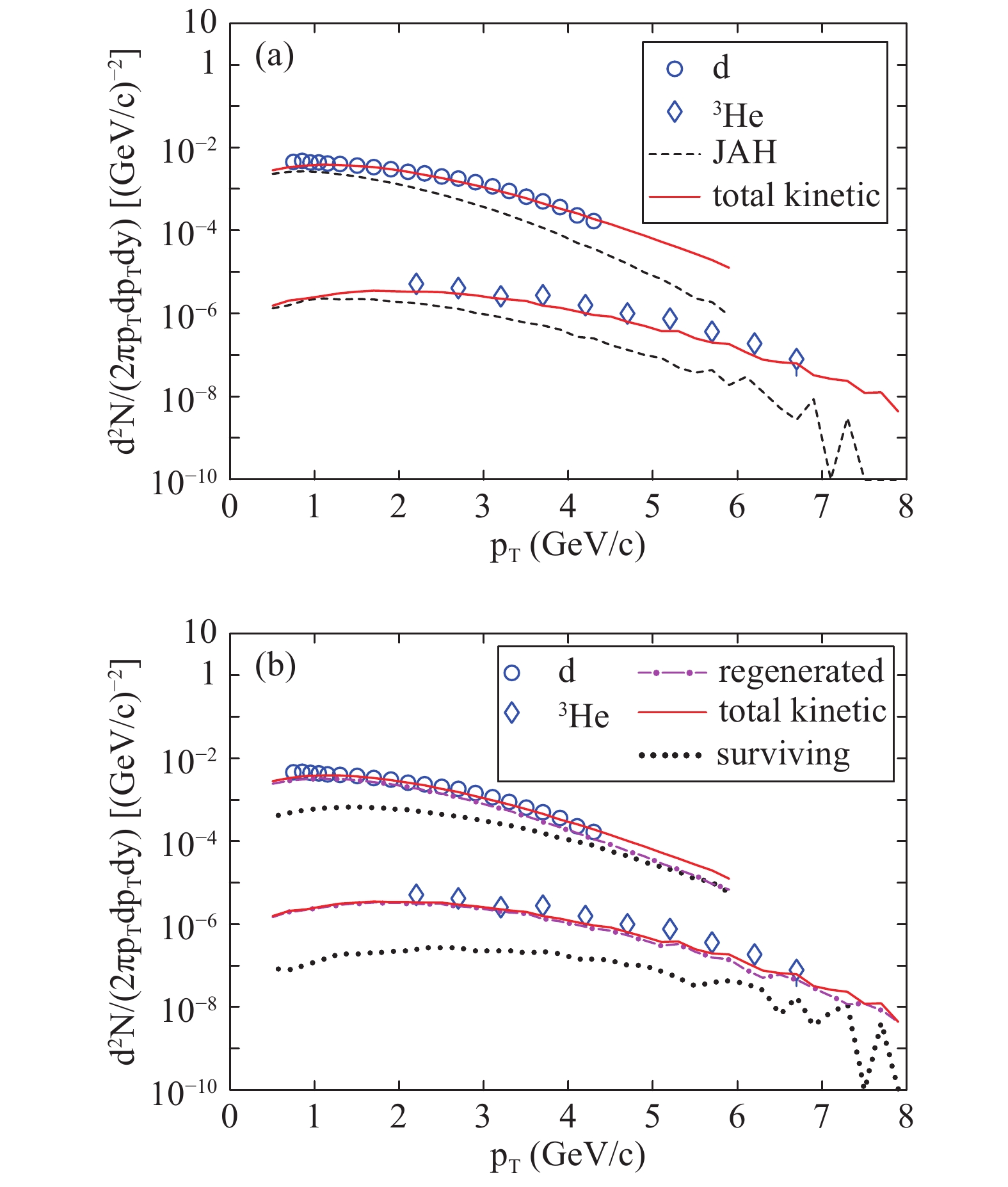
Figure 2. (color online) pT distributions of d and 3He at midrapidity in central Pb-Pb collisions at
${\sqrt{s_{N\!N}}=2.76}$ TeV. The open circles and diamonds are the experimental data for d and 3He from [19]. (a) The solid lines are the results at the final kinetic freeze-out, and the dashed lines are for just after hadronization. (b) The solid, dotted and dash-dotted lines are the results for the total, surviving and regenerated light nuclei at the final kinetic freeze-out. -
We have proposed in this paper a new method, an exclusive quark combination model + an inclusive hadron recombination model, for a systematic study of different production sources of light nuclei in ultra-relativistic heavy-ion collisions. Using the exclusive quark combination model SDQCM, we obtained momentum distributions for directly-produced hadrons and those at the final kinetic freeze-out, including the hadronic scattering and resonance decays. These momentum distributions were taken as input for the inclusive hadron recombination model to calculate the production of light nuclei. In the hadron recombination model, we analytically deduced the formulas for formation of d and 3He, and explicitly stated the assumptions used, such as coordinate and momentum factorization for kernel functions and nucleon joint distributions, and the decoupling of different coordinate variables in the coordinate distributions. We computed
${\rm d}N/{\rm d}y$ and$p_T$ spectra of$d$ and 3He as well as their ratios just after hadronization and at the final kinetic freeze-out in Pb-Pb collisions at$\sqrt{s_{NN}}=2.76$ TeV. Light nuclei produced by the directly-produced nucleon combination and those combined from nucleons from$\Delta$ resonance decays (or those obtained by recombination of nucleons from decays with directly-produced ones) are clearly distinguished in our method.The results of our calculations showed that about a half of d and a fourth of 3He created just after hadronization cansurvive after the hadronic evolution process. Nucleons from
$\Delta$ resonance decays contribute considerably to the regeneration of light nuclei, and their proportion at the final kinetic freeze-out is about 77% and 90% for$d$ and 3He, respectively. Ratios such as$d/p$ , 3He$/p$ and 3He$/d$ were found to be effective observables to probe different production sources of light nuclei. Values of$d/p$ , 3He$/p$ and 3He$/d$ just after hadronization are all smaller than those at the final kinetic freeze-out.$d/p$ , 3He$/p$ and 3He$/d$ were also found to be effective probes of hadronic interaction effects on light nucleus formation after hadronization. Values of$d/p$ 3He$/p$ and 3He$/d$ when the hadronic interactions are turned off reduce to about 48%, 45% and 91% of those with hadronic interactions. The constant behavior of$d/p$ and 3He$/p$ as function of the average charge multiplicity in Pb-Pb collisions was explained. A possible explanation of the observed difference in$d/p$ data in Pb-Pb collisions and in pp collisions at the LHC was also provided. All these results open new insights for understanding of the production of light nuclei in ultra-relativistic heavy-ion collisions.The authors thank Qiang Zhao, Lie-Wen Chen and Kai-Jia Sun for helpful discussions.
Different production sources of light nuclei inultra-relativistic heavy-ion collisions
- Received Date: 2018-05-10
- Accepted Date: 2018-11-13
- Available Online: 2019-02-01
Abstract: We systematically study different production sources of light nuclei in ultra-relativistic heavy-ion collisions with a new method, an exclusive quark combination model + an inclusive hadron recombination model. We take deuterons and 3He produced in Pb-Pb collisions at






 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF





















 DownLoad:
DownLoad: