-
Heavy nuclei when bombarded by nucleons or light nuclei at relativistic energies, or the inverse reaction, produce a large number of neutrons and isotopes, from protons to the reacting heavy nuclei. This kind of nuclear reaction was described by Serber several decades ago and called spallation [1]. The spallation reaction plays an important role in a wide domain of applications, such as neutron sources, production of rare isotopes, transmutation of nuclear waste and astrophysics. Neutrons can be produced in a spallation process of the steel target bombarded by short proton pulses [2]. In radioactive ion beam facilities, the rare isotopes generated by spallation are separated and focussed as secondary beams [3, 4]. Moreover, spallation reactions induced by either protons or neutrons are considered as a cornerstone for accelerator-driven subcritical reactors [5-7]. In astrophysics, cross-sections of proton induced spallation are used to evaluate the propagation of cosmic rays in the interstellar medium [8].
A decade ago, the International Atomic Energy Agency (IAEA) promoted a benchmark in an effort to collect data and assess the prediction capabilities of the spallation models [9]. In the IAEA benchmark, the codes contain descriptions of the fast excitation stage by dynamical models and the slow decay processes by statistical-decay models. These two-step models were successful in extracting valuable information about the influence of de-excitation. Recently, an effort has been made to clarify the emission mechanism of the intermediate-mass fragments (IMF). The production of IMF in spallation was already studied in the pioneering experiments [10-13]. With the help of high-resolution detector arrays, recent experiments tried to reconstruct the process of the IMF production by their velocity distribution [14-17]. From the theoretical point of view, IMF could originate from multi-fragmentation of the most excited configurations or from asymmetric fission. Comparing the experimental data to predictions of several de-excitation models coupled to intranuclear cascade models, it was found that the multi-fragmentation stage is not crucial for obtaining a good prediction of cross-sections for fragment production [17, 18]. However, investigations with the dynamical models indicate that the unstable modes in spallation should exhibit quite a similar phenomenology as spinodal instability in dissipative central heavy-ion collisions [19-21].
The present study is an attempt to describe the emission mechanism of IMF in the 136Xe + p spallation at 1000 MeV/nucleon. In contrast to the two-step models in the IAEA benchmark, spallation is described dynamically until hot fragments with excitation energy less than a certain value Estop are formed. A statistical code is applied to simulate the light-particle evaporation from hot fragments. The dependence of IMF production on
$E_{\rm stop}$ is studied. The paper is organized as follows: in Section 2, the method is introduced, in Section 3, the results are presented, and the summary is given in Section 4. -
In the IQMD model, the system of nucleons is described by the
$N$ -body wave function, which is a direct product of the Gaussian wave packets for each nucleon.$ \phi({{r}}, t) = \prod\limits_{i=1}^{N} \frac{1}{(2\pi L)^{3/4}} {\rm e}^{-\frac{[{{r}}-{{r}}_{i}(t)]^2}{4L}} {\rm e}^{ \frac{{\rm i}{{r}}\cdot{{p}}_{i}(t)}{\hbar}}, $

(1) where
${{r}}_{i}$ and${{p}}_{i}$ are the central position and momentum of the i-th nucleon. The width of the Gaussian wave packet depends on the parameter$L$ .Using the Wigner transformation, the quantum wave function can be transformed to the one-body phase-space density, which is given by
$ f({{r}}, {{p}}, t) = \sum\limits_{i=1}^{N}\frac{1}{(\pi\hbar)^3} {\rm e}^{{-\frac{[{{r}}-{{r}}_{i}(t)]^2}{2L}}} {\rm e}^{{-\frac{[{{p}}-{{p}}_{i}(t)]^2 \cdot 2L}{\hbar^2}}}. $

(2) The local density is then,
$ \rho({{r}}, t) = \frac{1}{(2\pi L)^{3/2}} \sum\limits_{i=1}^{N} {\rm e}^{{-\frac{[{{r}}-{{r}}_{i}(t)]^2}{2L}}}. $

(3) In this case, the Hamiltonian can be calculated by the integral,
$ H = T + U_{\rm Coul} + \int V [\rho ({r})] {\rm d}{{r}}, $

(4) where,
$T$ is the kinetic energy,$U_{\rm Coul}$ is the Coulomb potential energy, and the third term is the nuclear potential energy, which is given by$ \begin{aligned} V(\rho, \delta) = & \frac{\alpha}{2} \frac{\rho^2}{\rho_0} + \frac{\beta}{\gamma+1} \frac{\rho^{\gamma+1}}{\rho_0^{\gamma}} + \frac{C_{sp}}{2}\left(\frac{\rho}{\rho_{0}}\right)^{\gamma_{i}} \rho \delta ^{2}, \end{aligned} $

(5) where
$\rho_0$ is the normal density, and$\delta$ is asymmetry. The parameters used in this study are$\alpha$ = 356.00 MeV,$\beta$ = 303.00 MeV,$\gamma$ = 7/6,$C_{sp}$ = 38.06 MeV, and$\gamma_{i}$ = 0.75.The time evolution of nucleons in the self-consistently generated mean-field is governed by the Hamiltonian equations of motion,
$ \begin{aligned} &\dot{{{r}}}_{i} = \nabla_{{{p}}_{i}} H , \\ &\dot{{{p}}}_{i} = -\nabla_{{{r}}_{i}} H . \end{aligned} $

(6) Moreover, nucleon-nucleon (NN) collisions are included in order to simulate the short-range residual interactions. In the appropriate energy region, elastic NN scattering and inelastic NN collisions, which produce
$\Delta$ particles, are also considered. NN collisions are described by the differential cross-section, which is a product of the cross-section in free space$\sigma^{\rm free}$ , the angular distribution$f^{\rm angl}$ , and the in-medium factor$f^{\rm med}$ ,$ \left( \frac{{\rm d} \sigma}{{\rm d} \Omega} \right)_{i} = \sigma _{i}^{\rm free} f_{i}^{\rm angl} f _{i}^{\rm med}. $

(7) The subscript
$i$ refers to the channels of NN collisions:$i$ = pp is for elastic proton-proton scattering,$i$ = nn for elastic neutron-neutron scattering,$i$ = np for elastic neutron-proton scattering, and$i$ = in is for inelastic NN collisions. We use the parametrization of the cross-sections, angular distributions and in-medium factors given in Refs. [22, 23].An important feature of the model is that the fermionic nature of nucleons is taken into account by the Pauli blocking and the phase space density constraint (PSDC). The PSDC method was introduced by M. Papa et al. [24], who found that the method affects the dynamics of the nucleus-nucleus collisions by producing on average a nonlocal repulsion effect, and hence reducing the number of low-momentum particles. J. Su et al. suggested that the PSDC method can increase the production of IMF [25]. The phase space occupation probability of each nucleon can be calculated as,
$ \overline{f}_{i} = \sum\limits_{n} \delta _{\tau_{n}, \tau_{i}} \delta _{s_{n}, s_{i}} \int _{h^{3}} \frac{1}{\pi ^{3} \hbar ^{3}} {\rm e}^{ -\frac{({{r}}-{{r}}_{n})^{2}}{2L} -\frac{({{p}}-{{p}}_{n})^{2}L}{\hbar ^{2}} } {\rm d}^{3}r {\rm d}^{3}p. $

(8) The integration is performed on an hypercube of volume h
$^{3}$ in the phase space element centered around the point (${{r}}_{i}$ ,${{p}}_{i}$ ). Pauli blocking is defined by accepting those NN collisions which produce final states with$\overline{f}_{i} <$ 1 and$\overline{f}_{j} <$ 1. Even when Pauli blocking is taken into account, the phase space occupation probabilities of some nucleons may be larger than 1. Therefore, the phase space occupation probabilities need to be checked for each time step. The many-body elastic scattering is performed for those nucleons with$\overline{f}_{i} >$ 1.In the IAEA benchmark, the dynamical model is only applied in the excitation stage, while IMF emission in the decay stage is described statistically. In this study, the dynamical description is used not only for the excitation stage but also for IMF emission. After the excitation stage, the time evolution in the IQMD code continues until the excitation energy of the heaviest hot fragment decreases to a certain value
$E_{\rm stop}$ in each event. If the excitation energy is lower than$E_{\rm stop}$ at t=25 fm/c, IQMD calculation stops and the charge, mass, excitation energy and momentum of each hot fragment are recorded. The value of$E_{\rm stop}$ corresponds to the threshold energy for IMF emission. If the excitation energy of a fragment is smaller than$E_{\rm stop}$ , nucleon evaporation is dominant. The decay time for nucleon evaporation is longer than for IMF emission. The spurious nucleon emission in the IQMD model, meaning that a few nucleons may evaporate even if the excitation energy of the fragment is close to zero, becomes stronger with increasing time and for lighter nuclei. Thus, we choose to describe nucleon evaporation statistically rather than dynamically. -
The output of the IQMD code are the hot fragments. In order to obtain the cold fragments, emission of light-particles (Z < 3) from hot fragments is performed by the statistical code GEMINI [ 26]. A Monte Carlo technique is employed to follow the decay chains until the excitation energy of the product is zero. The partial decay widths are taken from the Hauser-Feshbach formalism,
$\begin{split} & \Gamma_{J_{2}}(Z_{1}, A_{1}, Z_{2}, A_{2}) =\\ &\quad \frac{2J_{1}+1}{2\pi \rho_{0}} \sum\limits_{l = |J_{0}-J_{2}|}^{J_{0}+J_{2}} \int_{0}^{E^{*}-B-E_{\rm rot}} T_{l}(\varepsilon) \rho_{2}(E^{*}-B-E_{\rm rot}-\varepsilon, J_{2}) {\rm d}\varepsilon, \end{split} $

(9) where
$Z_{i}$ is the charge number,$A_{i}$ the mass number,$J_{i}$ the spin, and$\rho_{i}$ is the level density. The subscript$i$ is 0, 1, and 2, which refer to the initial fragment, emitted light particle, and residual fragments. E*, B,$ E_{\rm rot}$ , and$\varepsilon$ are the excitation energy, separation energy, rotation plus deformation energy, and kinetic energy.$T_{l}$ is the transmission coefficient. The separation energy B is calculated from the tabulated masses. -
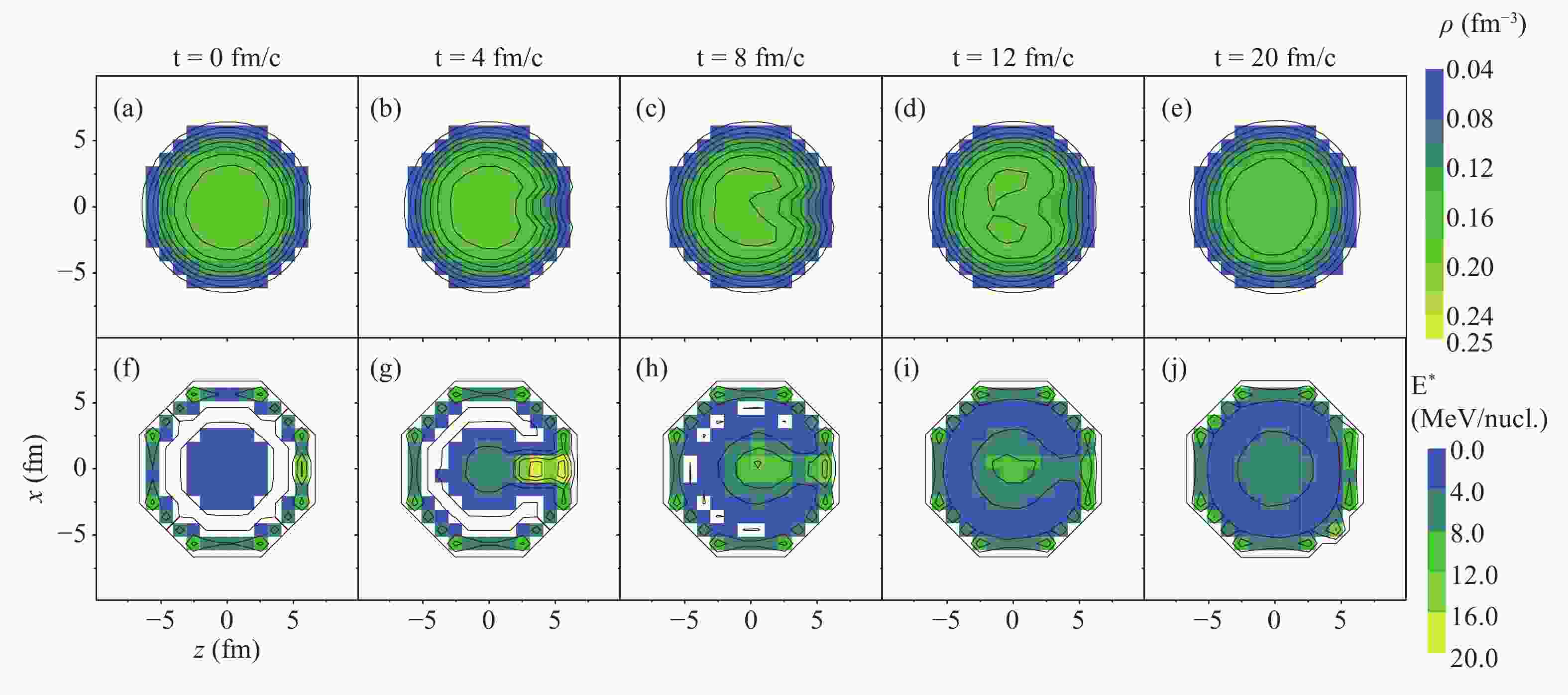
The excitation stage in spallation is depicted by the time evolution of the local density (top panels) and local excitation energy (bottom panels) in the x-z plane in Fig. 1. In order to calculate the distribution of the density and excitation energy, the
${}^{136}{\rm Xe}$ nucleus is divided into subsystems with Cartesian coordinate grids. The average density$\rho$ in each grid is calculated for 10000 events. The energy per nucleon E in the grids is calculated from the density$\rho$ and the transverse kinetic energy$E_{tr}$ .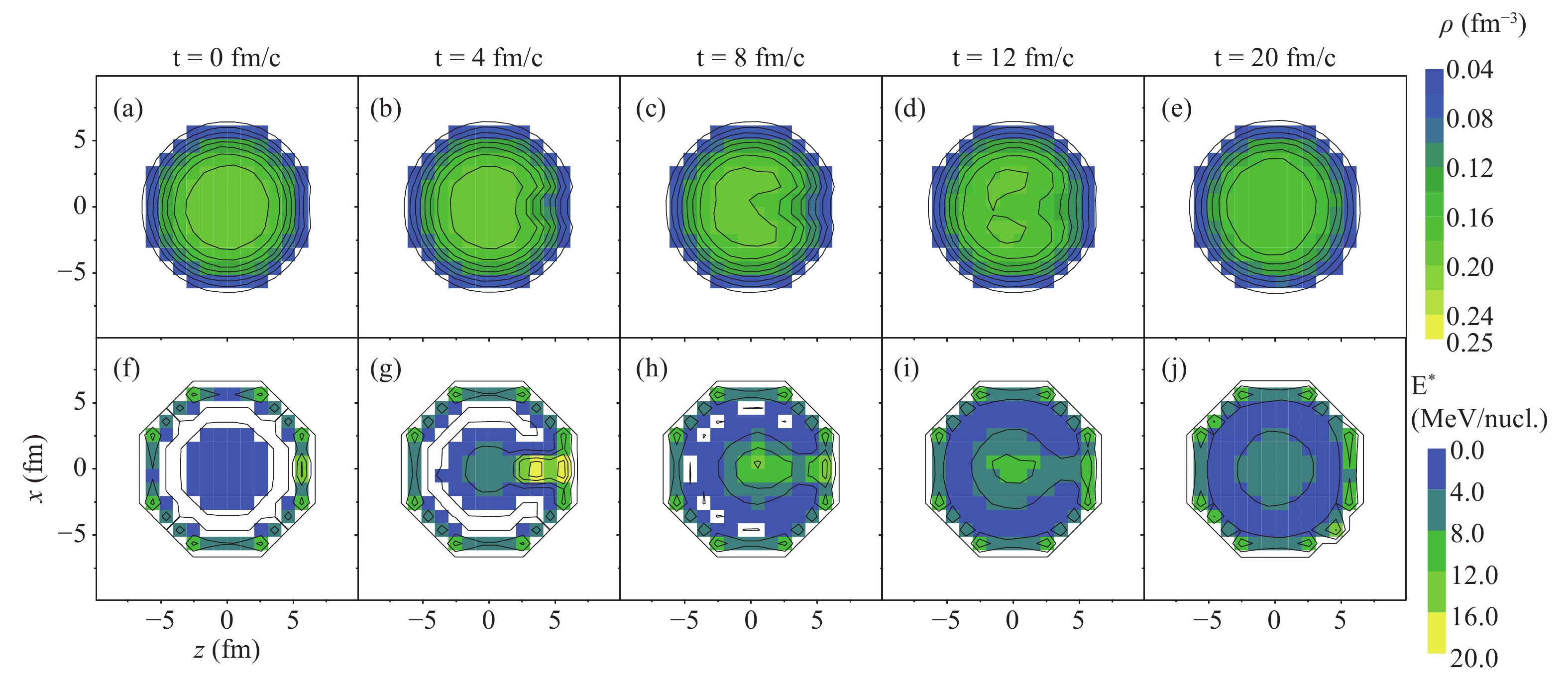
Figure 1. (color online) Time evolution of (a-e) density and (f-j) excitation energy in the x-z plane in the central 136Xe + p collision at 1000 MeV/nucleon.
$ E = \frac{\alpha}{2}\frac{\rho}{\rho_{0}} +\frac{\beta}{\gamma+1}\left( \frac{\rho}{\rho_{0}} \right)^{\gamma} + \frac{3}{2}\overline{E_{tr}}. $

(10) The local excitation energy is obtained by comparing the energy per nucleon of the subsystem to that of nuclear matter at zero temperature.
The initial time t = 0 fm/c is defined as the moment when the proton touches the surface of the 136Xe nucleus. The kinetic energy of the proton gradually dissipates into the thermal energy of the 136Xe nucleus, and the 136Xe nucleus is heated from one side. The local excitation energy on that side reaches a maximum of 20 MeV. Because of high excitation, some nucleons escape from the hot spot, leaving a region with low density. After 20 fm/c, the hot spot moves to the center of the nucleus, and the density distribution returns to spherical symmetry. At the same time, the average excitation energy reaches its maximum, see Fig. 2. In the two-step models, this excitation stage is described dynamically, while the de-excitation stage is described statistically with the equilibrium hypothesis. In this study, we describe the reaction dynamically until IMF are produced. For this purpose, we need to identify the fragments during the evolution, and decide when does the dynamical evolution stop.
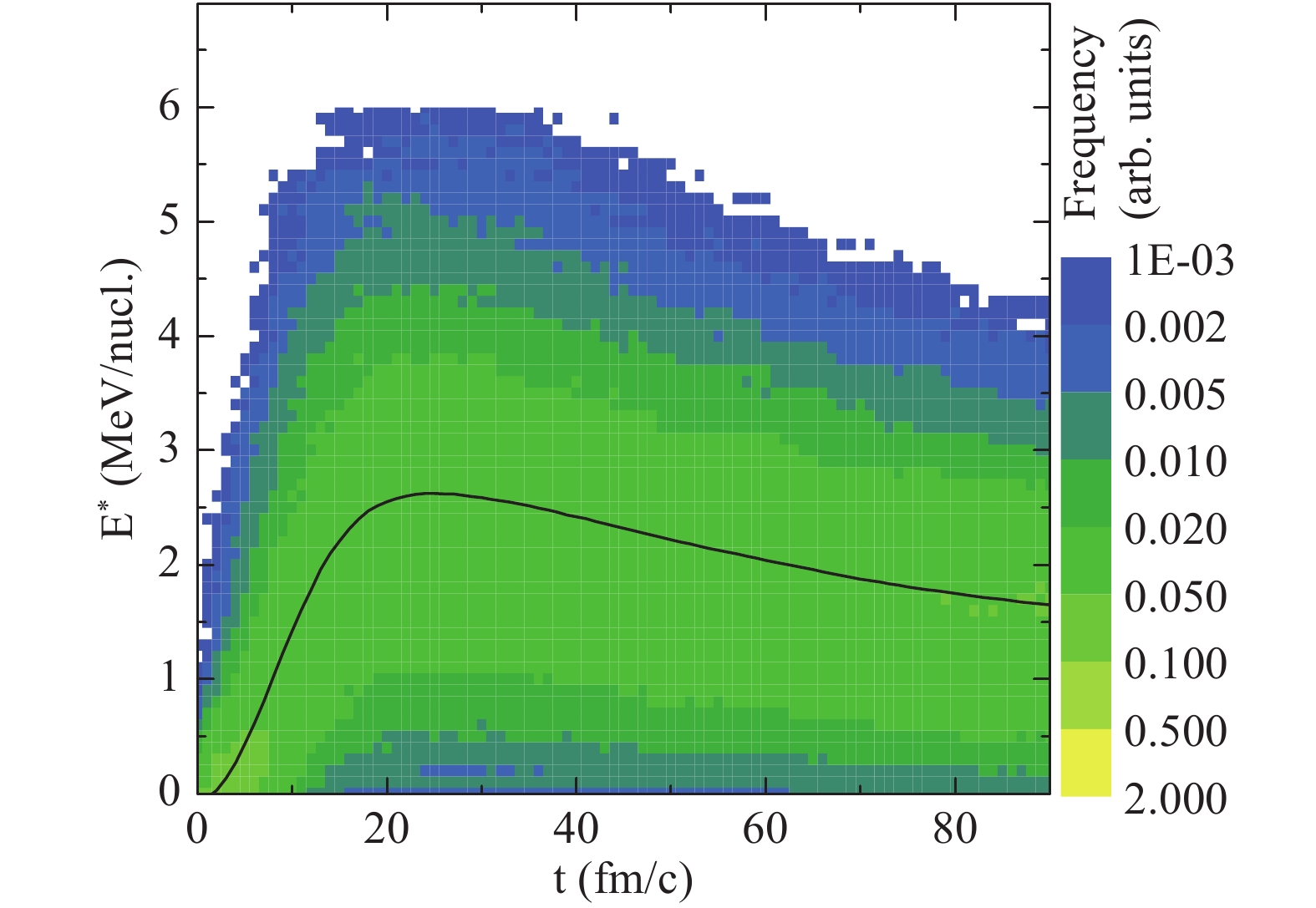
Figure 2. (color online) Time evolution of the excitation energy of the largest fragment in the central 136Xe + p collision at 1000 MeV/nucleon. The solid curve shows the average value. The colors show the distribution of the excitation energy.
The minimum spanning tree (MST) algorithm is applied to identify the fragments at each time step. The nucleons with relative distances of coordinates and momenta of
$|r_{i} - r_{j}| \leqslant R_{0}$ and$|p_{i} - p_{j}| \leqslant P_{0}$ belong to a fragment. The parameters$R_{0}$ = 3.5 fm and$P_{0}$ = 250 MeV/c are chosen. The excitation energy of the fragments can be calculated with$ E^{*} = U + T - B(Z_{f}, A_{f}), $

(11) where U is the potential energy, T the internal kinetic energy, B the binding energy,
$Z_{f}$ the charge number of the fragment, and$A_{f}$ is the mass number of the fragment.The excitation energy of the largest fragment as function of time is shown in Fig. 2. The solid curve shows the average value, and the colors show the event distribution. The average value of the excitation energy rises rapidly in the excitation stage and then falls slowly in the de-excitation stage. As the average value increases, the distribution of the excitation energy becomes wider. This is the dissipation-fluctuation phenomenon, which indicates that the dissipation of the kinetic energy of the incident proton is responsible for the fluctuation of the excitation energy.
The duration of the dynamical evolution in the IQMD model is chosen using the excitation energy of the largest fragment, i.e. the value for each event and not the average. When the excitation energy of the largest fragment is less than a certain value
$E_{\rm stop}$ , the dynamical evolution is stopped and the GEMINI code is switched on. The choice of$E_{\rm stop}$ depends on the threshold energy for IMF emission. It has been proposed that the threshold energy for multi-fragmentation in central heavy ion collisions is close to 3 MeV/nucleon [27]. However, IMF emission in spallation may correspond to a different breakup mechanism. Hance, we don't use the value of$E_{\rm stop}$ = 3 MeV/nucleon straight away, but first study the$E_{\rm stop}$ dependence of IMF production.Figure 3 (a) shows the cross-section
$\sigma$ as function of the charge number Z of the fragments. The solid circles show the experimental data taken from Ref. [16]. The cross-section for 3 < Z < 20 follows a power law, which is considered a characteristic feature of multi-fragmentation. The solid and dashed curves show the calculated values with and without the sequential decays performed with the GEMINI code. In the calculations,$E_{\rm stop}$ = 2 MeV/nucleon is used. Since the fragments from the IQMD model are excited, they are denoted as hot fragments. In contrast, the fragments from the IQMD+GEMINI model are cold fragments. Overall, the calculations reproduce the U-shape of the data. Only the cross-section in the valley (15 < Z < 30) is somewhat underestimated. The main effect of GEMINI, as observed from the difference between the hot and cold fragments, is a small increment of light ( Z = 1 and 2) and heavy fragments ($Z >$ 30), and a reduction of IMF caused by the evaporation of protons and$\alpha$ particles in the final de-excitation stage.Figure 3 (b) shows the cross-section
$\sigma$ as function of the neutron number N of the fragments in${}^{136}$ Xe + p at 1000 MeV/nucleon. The experimental data also follow the U-shape, with a flat section in the region of 60 < N < 80. The I ( Z = 53) and Te (Z = 52) isotopes, which are produced abundantly in peripheral collisions, are responsible for this flat. Without the sequential decays calculated by the GEMINI code, the model reproduces the cross-section for N < 20, but underestimates grossly those in the region of 20 < N < 70. With neutron evaporation, the calculations for the cold fragments reproduce the data rather well. The effect of using the GEMINI code is obvious. However, neutron evaporation is the reason for overestimating the odd-even staggering.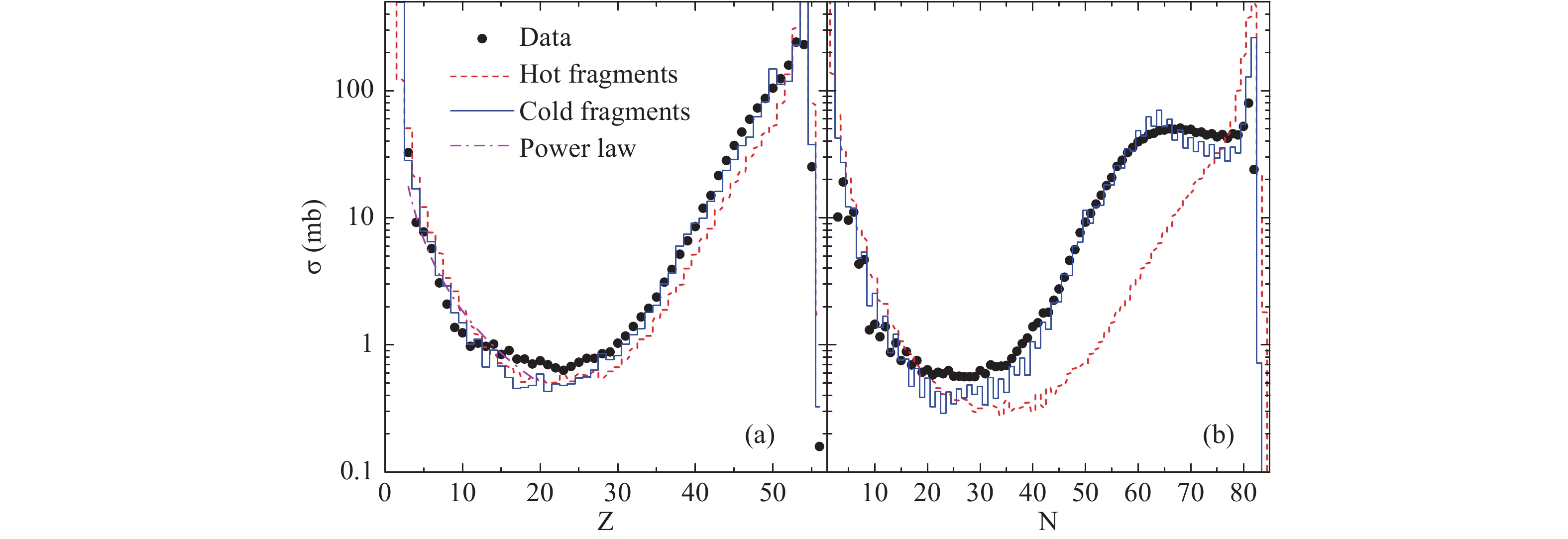
Figure 3. (color online) Cross-section as function of (a) charge number and (b) neutron number of the hot and cold fragments produced in the 136Xe + p spallation at 1000 MeV/nucleon. The calculations are performed with Estop = 2 MeV/nucleon. The experimental data (solid circles) are taken from Ref. [16].
Figure 4 (a) shows the mean neutron-to-proton ratio
$\langle N \rangle/Z$ as function of the charge number of the hot and cold fragments. The calculated$\langle N \rangle/Z$ values for hot fragments show a uniform increase with Z in the region of IMF, and keep the peak value of N/Z = 1.52 for Z > 30. After the decay of the hot fragments,$\langle N \rangle/Z$ decreases, indicating that neutron evaporation dominates. The experimental data are not well described by the model. The data show that Li and Be production is neutron rich, but the calculations underestimate their$\langle N \rangle/Z$ . For IMF, the odd-even staggering is weak in the data but clear in the calculations.Figure 4 (b) shows the
$E_{\rm stop}$ dependence of$\langle N \rangle/Z$ for the fragments. Three values for$E_{\rm stop}$ , i.e. 1, 2, and 3 MeV/nucleon, are proposed. The isospin memory is somewhat kept in the IQMD evolution. After decays,$\langle N \rangle/Z$ values converge towards the valley of stability, because GEMINI uses tabulated masses. When a smaller$E_{\rm stop}$ value is used, more isospin memory is kept due to the longer evolution in IQMD and less evaporated nucleons in GEMINI. We also see larger overall$\langle N \rangle/Z$ values for$E_{\rm stop}$ = 1 MeV/nucleon. Remarkably, the calculations for$E_{\rm stop}$ = 3 MeV/nucleon reproduce the data rather well, except for the region near Z = 45. The calculations without the PSDC method for$E_{\rm stop}$ = 1 MeV/nucleon are also displayed. The effect of PSDC on$\langle N \rangle/Z$ can be seen by comparing the calculations with and without the PSDC method for the same$E_{\rm stop}$ (1 MeV/nucleon). It is found that the PSDC method increases$\langle N \rangle/Z$ values of IMF, but decreases those for heavy fragments.In order to show the isospin effect of the PSDC method, we display the number of free nucleons as function of time in Fig. 5. The shapes of the curves with and without the PSDC method are similar. In the excitation stage (before 20 fm/c), the system mainly loses neutrons rather than protons due to the fact that it is neutron rich, as well as due to the Coulomb barrier for protons. In the decay stage (after 30 fm/c), both neutrons and protons are emitted. Compared to protons, neutrons are emitted earlier. This is why we see smaller
$\langle N \rangle/Z$ values for$E_{\rm stop}$ = 3 MeV/nucleon than for$E_{\rm stop}$ = 1 MeV/nucleon. Comparing the calculations with and without PSDC, it is found that the PSDC method increases the stability of pre-fragments and decreases the number of free nucleons.
Figure 5. (color online) Number of free nucleons as function of time in the central 136Xe + p collision at 1000 MeV/nucleon. The cases with and without the PSDC method are shown. The average excitation energy is also displayed.
Figure 6 shows the
$E_{\rm stop}$ dependence of the cross-sections for the fragments. All calculations, with three values of$E_{\rm stop}$ , reproduce the U-shape of the experimental data and the flat section in the region of 60 < N < 80. The results without the PSDC method for$E_{\rm stop}$ = 1 MeV/nucleon are also displayed. The cross-sections for IMF and heavy fragments without PSDC are much smaller than with the PSDC method. However, these cross-sections depend strongly on the$E_{\rm stop}$ values. During the de-excitation of the hot fragments from 3 to 1 MeV/nucleon, IMF are produced throughout. For$E_{\rm stop}$ = 1 MeV/nucleon, the system is fragmenting too much. Compared to this case, the calculations without PSDC for$E_{\rm stop}$ = 1 MeV/nucleon considerably underestimate the data. This may be related to the fermionic nature of the nucleons introduced by the PSDC method. On the one hand, the PSDC method compensates this effect and hence increases the production of IMF, while on the other hand, it provides more repulsive force between the fragments and causes excessive fragmentation.
Figure 6. (color online) Cross-section as function of (a) charge number and (b) neutron number of the cold fragments produced in 136Xe + p at 1000 MeV/nucleon. The calculations are performed for three values of Estop as indicated. The experimental data (solid circles) are taken from Ref. [16].
More interestingly, only the calculations for
$E_{\rm stop}$ = 2 MeV/nucleon reproduce the data well, implying that the threshold energy of IMF emission in spallation is about 2 MeV/nucleon, which is smaller than the value of 3 MeV/nucleon suggested by B. Borderie et al. for heavy-ion collisions [27]. This may be related to different mechanisms of IMF emission in heavy-ion collisions and in spallation. In heavy-ion collisions, the incident energy dissipates into both the potential energy and thermal energy. The system undergoes the compression-expansion phase, and then splits into fragments. The spinodal decomposition is a major mechanism behind IMF emission in heavy-ion collisions. In spallation, the incident energy mainly dissipates into thermal energy, and the compression-expansion phase is absent. It is still an open question whether the excited system undergoes multi-fragmentation. The model developed in this study can be applied to further study the breakup mechanisms in spallation.In Fig. 7 (a), we show the
$E_{\rm stop}$ dependence of IMF production. The columns correspond to the calculations, and the dashed line to the data. Clearly, the calculated cross-sections decrease with increasing$E_{\rm stop}$ . Figure 7 (b) shows the yield of IMF as function of the excitation energy of the fragmenting source, which is defined as the excitation energy of the largest fragment at 20 fm/c. For all$E_{\rm stop}$ values, the yields of IMF decrease with decreasing excitation energy, and reach zero at the$E_{\rm stop}$ value. This means that the current version of the IQMD model can describe IMF emission dynamically, but we must choose an appropriate threshold energy at which dynamical evolution stops. It is only for$E_{\rm stop}$ = 2 MeV/nucleon that the data for IMF production are well described by the model. On the other hand, the mean neutron-to-proton ratio$\langle N \rangle/Z$ in Fig. 4 indicates that$E_{\rm stop}$ = 3 MeV/nucleon is the best choice for this observable.
Figure 4. (color online) Calculated mean neutron-to-proton ratio
${\langle N \rangle}/Z$ as function of the charge number of fragments produced in 136Xe + p at 1000 MeV/nucleon, in comparison with the experimental data taken from Ref. [16]. Panel (a) shows the ratio for hot and cold fragments calculated with Estop = 2 MeV/nucleon. Panel (b) shows the ratio for cold fragments calculated with three values of Estop as indicated.
Figure 7. (color online)
$E_{\rm stop}$ dependence of IMF production in the 136Xe + p spallation at 1000 MeV/nucleon. In the calculations, Estop = 1, 2 and 3 MeV/nucleon are used. Panel (a) shows the cross-sections for IMF as function of Estop. Panel (b) shows the yield of IMF as function of the excitation energy of the fragmenting source. -
In this study, the 136Xe + p spallation at 1000 MeV/nucleon was investigated with the isospin-dependent quantum molecular dynamics (IQMD) model in conjuction with the statistical code GEMINI. The IQMD model is used to describe not only the excitation stage but also the emission of intermediate-mass fragments (IMF). In the GEMINI code, only the channel for light-particle evaporation is used. The dynamical evolution of the central collisions shows that the 136Xe nucleus is heated from one side. Due to high excitation, some nucleons escape from the hot spot, leaving a region with low density. As the kinetic energy of the incident proton is dissipated, fluctuations of the excitation energy of the largest fragment become stronger. When the average excitation energy reaches its maximum of 2.6 MeV/nucleon, the excitation energies of fragments are distributed from 0 to 6 MeV/nucleon. In order to describe the IMF emission dynamically and to avoid the spurious emissions of nucleons during the dynamical evolution, the evolution time of each event is chosen as the moment when the excitation energy of the largest fragment is less than a certain value
$E_{\rm stop}$ . We find that the experimental data for IMF production are well described by the model when$E_{\rm stop}$ is 2 MeV/nucleon. However, comparison of the experimental data for mean neutron-to-proton ratio with the calculations suggests a value of$E_{\rm stop}$ = 3 MeV/nucleon. It seems that the fermionic nature of nucleons is compensated by the PSDC method, and hence that the production of IMF is larger. Nevertheless, the model still does not describe IMF emission consistently, as different values of$E_{\rm stop}$ are needed to reproduce the cross-sections and the neutron-to-proton ratios of the fragments.
A dynamical description of the 136Xe + p spallation at 1000 MeV/nucleon
- Received Date: 2018-11-24
- Available Online: 2019-02-01
Abstract: We propose a dynamical description of the 136Xe + p spallation at 1000 MeV/nucleon with the aim of probing the mechanism which rules the production of intermediate-mass fragments (IMF). The isospin-dependent quantum molecular dynamics (IQMD) model is used to describe the dynamical process of spallation until hot fragments with excitation energy less than a certain value Estop are formed. The statistical code GEMINI is applied to simulate the light-particle evaporation from hot fragments. It is found that IMF production is well described by the model when Estop = 2 MeV/nucleon is used. Comparison of the calculated mean neutron-to-proton ratio and the experimental data indicates that Estop should be 3 MeV/nucleon.





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF













 DownLoad:
DownLoad: