-
It is well known that symmetric nuclear matter is saturated at nuclear density
$\rho_0$ ($\sim0.16$ ${\rm fm}^{-3}$ ) with the binding energy per nucleon$E_{\rm b}$ ($\sim-16$ MeV/A). However, at$\rho_0$ , the nuclear incompressibility$K$ , the symmetry energy$J$ , and its density slope$L$ are less determined. During the last decade, their magnitudes have been studied extensively, and significant progress has been made both experimentally and theoretically. The incompressibility is extracted by fitting the data on the isoscalar giant monopole resonance. The range for$K=(240\pm20)$ MeV is generally accepted [1]; possible higher values of$K$ (250-315 MeV) are given in Ref. [2] by re-analyzing the experimental data. The nuclear symmetry energy and its density dependence play an important role in understanding the physics of many terrestrial nuclear experiments and astrophysical observations. A recent review article [3] provided the range for$J=(31.7\pm3.2)$ MeV and$L=(58.7\pm28.1)$ MeV by data collective analysis. The nuclear matter parameters mentioned above can provide the constraints on nuclear mean field models.It is known that the knowledge of the properties of nuclear matter at various densities is of critical importance in the study of the formation and structure of neutron stars (NSs). It is difficult to study them directly by calculation within the quantum chromodynamics (QCD). The Nambu-Jona-Lasinio (NJL) model with quark degrees of freedom [4-6] is one of the popular effective field theories, which has in common with QCD important features, e.g., chiral symmetry and Lorentz invariance. However, the NJL model does not consider quark confinement and cannot be used to describe nuclear matter. Thus, the present work uses a so-called extended NJL (eNJL) model that considers nucleons as the degrees of freedom. This model can give a reasonable equation of state and behavior of the nuclear effective mass, and it is successful in describing the properties of nuclear matter, finite nuclei, and NSs including the pasta phase in the inner crust and the hadron-quark phase transition at high densities [7-11]. The main difference between this eNJL model and the commonly used relativistic mean field (RMF) models, in which nucleons interact with each other via the exchange of mesons [12-16] or by zero-range point couplings [17, 18], is that the scalar density in the eNJL model is not zero in vacuum owing to the chiral spontaneous symmetry breaking, and it contributes the most to vacuum nucleon mass. In the common RMF models, the scalar density is zero in vacuum because it represents the scalar mean field in medium, and the vacuum nucleon mass stems from the explicit mass term.
The aim of this work is the detailed investigation of the effects of the eNJL model coefficients, e.g., the bare nucleon mass
$m_0$ in Eq. (1), and some parameters at nuclear saturation density$\rho_0$ , e.g., the slope$L$ of symmetry density, on nuclear matter and NS properties in the RMF approximation, focusing on the appearance of the two$m_0$ values for a unique compressibility.The remainder of this article is organized as follows. In Section 2, the formulae necessary for describing nuclear matter and NSs are described. In Section 3, the calculated results and some discussions are presented. Finally, the study is summarized in Section 4.
-
The eNJL Lagrangian used in this work is given as
$ \begin{split} L=&\bar{\psi}(i\gamma^{\mu}\partial_{\mu}-m_0)\psi+\frac{G_S}{2}\left[(\bar{\psi}\psi)^2-\left(\bar{\psi}\gamma_5\vec{\tau}\psi\right)^2\right]\\ &{}-\frac{G_V}{2}\left[(\bar{\psi}\gamma^{\mu}\psi)^2+(\bar{\psi}\gamma^{\mu}\gamma_5\psi)^2\right]\\ &{}-\frac{G_{\rho}}{2}\left[(\bar{\psi}\gamma^{\mu}\vec{\tau}\psi)^2+(\bar{\psi}\gamma^{\mu}\gamma_5\vec{\tau}\psi)^2\right]\\ &{}+\frac{G_{SV}}{2}\left[(\bar{\psi}\psi)^2-(\bar{\psi}\gamma_5\vec{\tau}\psi)^2\right]\\ &\times\left[(\bar{\psi}\gamma^{\mu}\psi)^2+(\bar{\psi}\gamma^{\mu}\gamma_5\psi)^2\right]\\ &{}-\frac{G_{\rho V}}{2}\left[(\bar{\psi}\gamma^{\mu}\vec{\tau}\psi)^2+(\bar{\psi}\gamma^{\mu}\gamma_5\vec{\tau}\psi)^2\right]\\ &\times\left[(\bar{\psi}\gamma^{\mu}\psi)^2+(\bar{\psi}\gamma^{\mu}\gamma_5\psi)^2\right]\\ &{}-\frac{G_{\rho S}}{2}\left[(\bar{\psi}\gamma^{\mu}\vec{\tau}\psi)^2+(\bar{\psi}\gamma^{\mu}\gamma_5\vec{\tau}\psi)^2\right]\\ &\times\left[(\bar{\psi}\psi)^2-(\bar{\psi}\gamma_5\vec{\tau}\psi)^2\right]\, \, , \end{split} $

(1) where
$\psi$ denotes the Dirac spinor of nucleons,$m_0$ is the bare nucleon mass,$G_S$ ,$G_V$ , and$G_{SV}$ are the scalar, vector, and scalar-vector coupling constants, respectively, which are required to obtain the saturation property in nuclear matter;$G_{\rho}$ ,$G_{\rho V}$ , and$G_{\rho S}$ are the isovector, isovector-vector, and isovector-scalar coupling constants, respectively, which allow the description of isospin asymmetric nuclear matter and can modify the density dependence of the symmetry energy. The relevant expressions used in this work are obtained using the mean field approximation. The nucleon effective mass is defined as$M^*=m_0+\Sigma_S$ , with$ \Sigma_S=-$ $\left(G_S+G_{SV}\rho^2-G_{\rho S}\rho_3^2\right)\rho_S$ , in which$\rho=\rho_p+\rho_n$ ,$\rho_3=\rho_p-\rho_n$ , and$\rho_S=\rho_{Sp}+\rho_{Sn}$ are nuclear, isovector, and scalar densities, respectively, with$ \begin{aligned} \rho_i&=\nu_i\int^{{k_{\rm F}}_i}_0\frac{{\rm d}^3p}{(2\pi)^3}\, \, , \;\;\;\;i=p, n\, \, , \end{aligned} $

(2) $ \begin{aligned} \rho_{Si}&=-\nu_i\int_{{k_{\rm F}}_i}^{\Lambda}\frac{{\rm d}^3p}{(2\pi)^3}\frac{M^*}{\sqrt{p^2+{M^{*}}^2}}\, \, , \;\;\;\;i=p, n\, \, , \end{aligned} $

(3) where
$\nu_i=2$ is the spin degeneracy,$k_{\rm F}$ is the Fermi momentum, and$\Lambda$ is the momentum cutoff for regulating the divergent contribution of the Dirac sea. The energy density is given by$ \begin{split} \epsilon=&-\sum\limits_i\nu_i\int_{{k_{\rm F}}_i}^{\Lambda}\frac{{\rm d}^3p}{(2\pi)^3}\sqrt{p^2+{M^{*}}^2}+\frac{G_S}{2}\rho_S^2+\frac{G_V}{2}\rho^2\\ &{}+\frac{G_{\rho}}{2}\rho_3^2+\frac{G_{SV}}{2}\rho_S^2\rho^2+\frac{G_{{\rho} {V}}}{2}\rho_3^2\rho^2-\frac{G_{{\rho S}}}{2}\rho_3^2\rho_S^2+\epsilon_0\, \, , \end{split} $

(4) where
$\epsilon_0$ ensures that the energy density of the vacuum is zero. It is given by$ \begin{aligned} \epsilon_0=\sum\limits_i\nu_i\int_0^{\Lambda}\frac{{\rm d}^3p}{(2\pi)^3}\sqrt{p^2+M_{\rm N}^2}-\frac{(M_{\rm N}-m_0)^2}{2G_S}\, \, , \end{aligned} $

(5) where
$M_{\rm N}=939$ MeV, which is the nucleon mass in vacuum. The pressure$P$ is given by the thermodynamic relation$\epsilon+P=\sum\mu_i\rho_i$ , and the chemical potential is given by$ \begin{split} \mu_i=&\sqrt{{k_{\rm F}}_i^2+{M^*}^2}+G_V\rho-G_{SV}\rho_S^2\rho+G_{\rho V}\rho_3^2\rho\\ &{}+G_{\rho}\rho_3\tau_i+{G_{\rho V}}\rho_3\rho^2\tau_i+{G_{\rho S}}\rho_3\rho_S^2\tau_i, \quad i=p, n\, \, , \end{split} $

(6) where
$\tau_p=1$ and$\tau_n=-1$ . The expression of pressure is given as$ \begin{split} P=&-\sum\limits_i\frac{\nu_i}{3}\int_{{k_{\rm F}}_i}^{\Lambda}\frac{{\rm d}^3p}{(2\pi)^3}\frac{p^2}{\sqrt{p^2+{M^{*}}^2}}-\frac{G_S}{2}\rho_S^2+\frac{G_V}{2}\rho^2\\ &{}+\frac{G_{\rho}}{2}\rho_3^2-\frac{3G_{SV}}{2}\rho_S^2\rho^2+\frac{3G_{\rho V}}{2}\rho_3^2\rho^2+\frac{3G_{\rho S}}{2}\rho_3^2\rho_S^2\\ &{}+\frac{2\Lambda^3\sqrt{\Lambda^2+{M^{*}}^2}}{3\pi^2}-\epsilon_0\, \, . \end{split} $

(7) The composition of the NS matter with
$npe\mu$ is obtained by the well-known condition of chemical equilibrium and charge neutrality as$ \begin{aligned} &\mu_n-\mu_p=\mu_e=\mu_{\mu}\, \, , \end{aligned} $

(8) $ \begin{aligned} &\rho_p=\rho_e+\rho_{\mu}\, \, . \end{aligned} $

(9) -
The eNJL model has eight parameters:
$\Lambda$ ,$m_0$ ,$G_S$ ,$G_V$ ,$G_{SV}$ ,$G_{\rho}$ ,$G_{\rho V}$ ,$G_{\rho S}$ . The bare nucleon mass$m_0$ can be arbitrarily assigned a few reasonable values as in Ref. [9], or it can be assigned the experimental values about$\pi$ meson [8, 10, 11]. In this work,$m_0$ will be regarded as an adjustable parameter. The incompressibility$K$ is plotted as a function of$m_0$ in Fig. 1. The calculated results for six values of$\Lambda$ , from 300 to 500 MeV, are displayed: three above 400 MeV (red curves) and three below 350 MeV (black curves). The couplings,$G_S$ ,$G_V$ , and$G_{SV}$ , are determined by the nucleon mass in vacuum$M=939$ MeV, the saturation density$\rho_0=0.16$ ${\rm{fm}}^{-3}$ , and the binding energy per nucleon$E_{\rm b}=\epsilon/\rho-M=-16$ MeV. For$\Lambda\gtrsim450$ MeV, it is shown that the incompressibility is significantly greater than the empirical value and is hardly affected by$m_0$ . For$\Lambda\lesssim 400$ MeV, the sensitivity of the incompressibility to$m_0$ gradually becomes clear, and the double-solution phenomenon of$m_0$ can be easily observed for a given value of$K$ with a certain$\Lambda$ . For$\Lambda=300$ MeV, one can see that the maximum value of$K$ is greater than 850 MeV, and the minimum is lesser than 100 MeV for very large or small$m_0$ , which are far from the actual value of$K$ . Note that the results for very small$\Lambda$ s ($\lesssim300$ MeV) and high densities [19] should be obtained carefully because to avoid unrealistic values. In fact, for$\Lambda\lesssim320$ MeV, a very small effective nucleon mass can be obtained ($M^* < 0.4M_{\rm N}$ ) at saturation density, compared with other nuclear models or experiments, which generally lies in$0.55M_{\rm N}\lesssim M^*\lesssim0.75M_{\rm N}$ . In this figure, the four black dots correspond to the double solutions for$\Lambda=350$ MeV with$K=240$ MeV and for$\Lambda=400$ MeV with$K=290$ MeV. According to the black dots, four sets of parameters are obtained and listed in Table 1, labeled by the numerical values of$\Lambda$ with '$S$ ' and '$L$ ' as the subscript, corresponding to small and large$m_0$ , respectively. I will perform numerical calculations based on these four sets of parameters for comparison in the present work.Λ/MeV m0/MeV GS/fm2 GV/fm2 GSV/fm2 K/MeV 350S 27.6845 12.7478 11.6581 18.3975 240 350L 392.211 7.6487 5.9614 18.3961 240 400S 42.3652 8.4985 8.0303 10.3539 290 400L 266.524 6.3739 5.5756 10.4732 290 Table 1. Parameters of the eNJL Lagrangian necessary to calculate the binding energy of symmetric nuclear matter. The subscripts 'S ' and 'L' denote small and large solutions of m0, respectively, for Λ = 350 MeV with incompressibility K= 240 MeV and Λ = 400 MeV with K= 290 MeV.
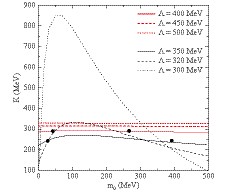
Figure 1. (color online) Incompressibility
\small${K}$ as a function of the bare nucleon mass${m_0}$ for fixed cutoff${\Lambda}$ . Four black dots correspond to double solutions for${\Lambda=350}$ MeV with${K=240}$ MeV and for${\Lambda=400}$ MeV with${K=290}$ MeV.Figure 2 illustrates the behavior of the binding energy per nucleon as a function of the nuclear density
$\rho$ based on the parameter sets in Table 1. It can be seen that small$m_0$ ($m_{0 S}$ ) corresponds to stiff curves compared with larger$m_0$ ($m_{0 L}$ ). Note that small$K$ does not imply a soft curve, and the curve labeled by$m_{0 S}$ with$\Lambda=350$ MeV and$K=240$ MeV is the stiffest curve in Fig. 2. This may mainly be caused by the large coupling$G_V$ , from Table 1, which provides sufficient nuclear repulsive force to support the stiff matter.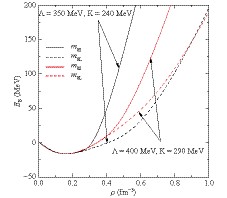
Figure 2. (color online) Binding energy per nucleon in nuclear matter as a function of the density.
${m_{0S}}$ and${m_{0L}}$ correspond to small and large solutions of${m_0}$ , respectively.Three coefficients in the eNJL model, i.e.,
$G_{\rho}$ ,$G_{\rho V}$ ,$G_{\rho S}$ , must be determined. In this work, numerical calculations were conducted for$\alpha=G_{\rho S}/G_{SV} =0, 1, 2$ . The symmetry energy at the saturation density was fixed at$J=32$ MeV. Then,$G_{\rho}$ and$G_{\rho V}$ were varied for three values of the density slope of the symmetry energy at saturation density,$L=40, 80, 120$ MeV, (although the last value is greater than the upper limit of the current constraint of$L=(58.7\pm28.1)$ MeV, it was still considered for the comparison). The obtained$G_{\rho}$ and$G_{\rho V}$ values are shown in Fig. 3. It can be seen that both$G_{\rho}$ and$G_{\rho V}$ vary linearly with$\alpha$ for a given slope$L$ . Further, I plotted a horizontal line for$G_{\rho V}=0$ . One can recognize that most$G_{\rho V}$ values chosen in this work, in particular, all values for$L=120$ MeV, are positive; this can affect the trend of symmetry energy with densities.
Figure 3. (color online) Isovector
${G_{\rho}}$ and isovector-vector${G_{\rho V}}$ coupling constants as functions of the ratio of${G_{\rho S}}$ to${G_{SV}}$ ,${\alpha=G_{\rho S}/G_{SV}}$ , for${L=40, 80, 120}$ MeV, with four parameter sets listed in Table. 1. Horizontal line corresponds to${G_{\rho V}=0}$ .To observe the effects of various model parameters on the symmetry energy more clearly, symmetry energy is plotted against nuclear densities in Figs. 4 and 5, calculated with the parameters present in Table 1 and Fig. 3. Figs. 4 and 5 correspond to
$\Lambda=350$ and 400 MeV, respectively; the subscripts '$S$ ' and '$L$ ' denote different values of$m_0$ . The figures show that the softer curves are accompanied by a smaller slope$L$ s in the presence of identical$\alpha$ . The symmetry energy increases monotonically with the densities for the model parameter sets with$G_{\rho V}>0$ , i.e., those above the horizontal line in Fig. 3. However, it is soft for negative$G_{\rho V}$ , and it decreases at a certain density and becomes negative at high densities. This phenomenon can be attributed to the different contributions from the coupling constants to the symmetry energy. From Eq. (A6), it can be seen that the symmetry energy is increased when$G_{\rho}$ ,$G_{\rho S}$ , and$G_{\rho V}$ are greater than zero.$G_{\rho}$ is proportional to the nuclear density$\rho$ , while the$G_{\rho V}$ is proportional to$\rho^3$ . Moreover, it is shown in Fig. 3 that the values of$G_{\rho V}$ are significantly greater than those of the corresponding$G_{\rho}$ . From Eq. (3), it can be seen that the contribution of$G_{\rho S}$ to the symmetry energy is suppressed at high densities owing to$M^*/E^*$ in$\rho_S$ . Therefore, the isovector-vector interaction significantly contributes to the symmetry energy at high densities, and the sign of$G_{\rho V}$ is critical in the determination of the trend. This can also explain the stiffness of the symmetry energy with increasing densities observed in Figs. 4, 5, when$G_{\rho S}$ increases, because$G_{\rho V}$ increases linearly with$\alpha$ for a given$L$ , as shown in Fig. 3. From, Fig. 3, for the appropriate symmetry energy at saturation density ($J=32$ MeV in the present work), it can be seen that the positive$G_{\rho S}$ is generally accompanied by a positive$G_{\rho V}$ , except for cases with small$L$ . Hence, cases with$G_{\rho S} < 0$ were not considered in this study because they may lead to super-soft symmetry energy and unreasonable EoS for the NS matter. It should be mentioned that this conclusion does not eliminate the possibility of super-soft symmetry energy. For other models, e.g., a non-relativistic method [20] or a non-Newtonian gravity model [21], the feasible EoS of NSs and super-soft symmetry energy may coexist.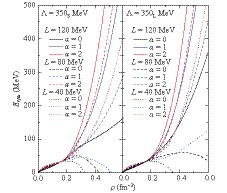
Figure 4. (color online) Symmetry energy versus density for cutoff
${\Lambda=350}$ MeV for various${\alpha=G_{\rho S}/G_{SV}}$ and density slope of symmetry energy${L}$ . Left and right panels correspond to small and large solutions of${m_0}$ for incompressibility${K=240}$ MeV, respectively.
Figure 5. (color online) Same as in Fig. 4 but for
${\Lambda=400}$ MeV and${K=290}$ MeV.From the Appendix, it can be seen that the fourth-order symmetry energy
$E_{{\rm sym}, 4}$ is affected by$G_S$ ,$G_{SV}$ , and$G_{\rho S}$ ; and$G_V$ ,$G_{\rho}$ , and$G_{\rho V}$ have no effect on it. In Table 2, with the four sets of parameters listed in Table 1, the calculated values of$E_{{\rm sym}, 4}$ at nuclear saturation density$J_4$ are compared for different ratios of$G_{\rho S}$ to$G_{SV}$ , and the effect of$G_{\rho S}$ on$J_4$ can be observed clearly. This table shows that the small solutions of$m_0$ correspond to greater$J_4$ . Until now, theoretical calculations using other nuclear models [22-26] predict that$J_4$ is generally less than 2 MeV. For the eNJL model, this work shows that$J_4$ increases with an increase in the value of$\alpha$ . However, it still seems unlikely to exceed 2 MeV, which disagrees with the clearly larger values predicted from the quantum molecular dynamics simulation [27],$J_4=3.27$ MeV for the similar value of symmetry energy$J$ chosen in this work, and an extended nuclear mass formula [28],$J_4=(20.0\pm4.6)$ MeV. Thus, to obtain such large fourth-order symmetry energy by using the existing nuclear models, I believe, new physical factors will have to be considered.$\alpha$ 

350 $_S$ 

350 $_L$ 

400 $_S$ 

400 $_L$ 

0 0.615 0.572 0.593 0.554 1 1.210 0.895 0.932 0.821 2 1.563 1.115 0.962 0.864 Table 2. Calculated fourth-order symmetry energy at saturation density in MeV for four parameter sets listed in Table 1. Three ratios,
${\alpha=G_{\rho S}/G_{SV}}$ , are chosen. -
It is known that the homogeneous
$\beta$ -equilibrium matter in NSs at high densities will be transformed into inhomogeneous matter at low densities. The so-called core-crust transition density$\rho_t$ plays an important role in understanding many properties of NSs.$\rho_t$ can be estimated by some dynamical methods, such as the random phase approximation [29] and relativistic Vlasov equation formalism [30, 31], which consider the occurrence of unstable collective modes of uniform matter as a phase transition to nonuniform matter. In this work, I used a simple method, the thermodynamical method, to obtain the transition density$\rho_t$ , which satisfies the equation [32, 33]$ \begin{split} V_{{\rm thermal}}=&2\rho\frac{{\partial E}_{\rm b}(\rho, x_p)}{\partial\rho}+\rho^2\frac{\partial^2 E_{\rm b}(\rho, x_p)}{\partial\rho^2}\\ &{}\left.-\left(\frac{\partial^2 E_{\rm b}(\rho, x_p)}{\partial\rho{\partial x}_p}\rho\right)^2\right/\frac{\partial^2 E_{\rm b}(\rho, x_p)}{{\partial x}_p^2}=0\, \, , \end{split} $

(10) where
$E_{\rm b}(\rho, x_p)$ is the energy per baryon in the$\beta$ -equilibrium NS matter and$x_p = \rho_p/\rho$ . This method is the long-wavelength limit of the dynamical method and neglects the finite size effects and Coulomb interaction. However, I believe that the conclusions are still instructive for investigating the effects of the various parameters in the eNJL model on the core-crust transition properties. The calculated results of$\rho_t$ are depicted in Fig. 6. It is shown that the different solutions of$m_0$ , with a fixed$\Lambda$ , have a negligible effect on$\rho_t$ . One can also see that the calculated values of$\rho_t$ are$[0.100, 0.106]$ $ \,{\rm fm}^{-3}$ for$L=40$ MeV,$[0.077, 0.092]$ ${\rm fm}^{-3}$ for$L=80$ MeV,$[0.065, 0.083]$ ${\rm fm}^{-3}$ for$L=120$ MeV. It appears that the range of possible$\rho_t$ values becomes larger with an increase in$L$ . The almost linear decrease in$\rho_t$ with the increasing$L$ is evident. This anticorrelation between$L$ and$\rho_t$ has been confirmed by numerous studies with other models, e.g., Refs. [32, 34-39]. Thus, the current constraint on the density slope parameter$L=(58.7\pm28.1)$ MeV from Ref. [3] can give the constraint for the core-crust transition density.
Figure 6. (color online) Core-crust transition density versus density slope of symmetry density at saturation density for four parameter sets listed in Table 1. Three ratios,
${\alpha=G_{\rho S}/G_{SV}}$ , are chosen. Gray region depicts the constraint on the density slope parameter${L=(58.7\pm28.1)}$ MeV from Ref. [3].Figs. 7 and 8 show the EoSs for the NS matter in
$\beta$ -equilibrium; the baryonic part is obtained from Eqs. (4, 7) and the leptonic part is obtained by considering the leptons as free Fermi gas. These figures show that all EoSs for the calculations of heavy NSs satisfy the causality condition${\rm d}P/{\rm d}\epsilon < 1$ . Further, there are two types of EoSs: one that increases monotonically and the other decreases above a certain density. Similar to the explanation for the symmetry energy, the trend of the EoSs is correlated with the sign of$G_{\rho V}$ .$G_{\rho V}>0$ corresponds to the type of EoSs that increases monotonically, while$G_{\rho V} < 0$ to the other. Except the blue curve for$L=40$ MeV in the upper-left panel in Fig. 7, the remaining EoSs for$\alpha=1$ in the two figures increase monotonically. For$\alpha=0$ , the EoSs for$L=120$ MeV increase monotonically, while those for$L=40, 80$ MeV reduce at very low densities that they must not be the reality. When observing the EoSs that increase monotonically with densities, the following can be observed: 1) the interaction between the slope of the symmetry energy and the isovector-scalar has a negligible effect on the EoSs, because the difference between the proton and the neutron fractions at high densities becomes small for monotonically increasing EoSs; 2) the EoSs for greater$\Lambda$ or a larger solution of$m_0$ with a fixed$\Lambda$ are softer.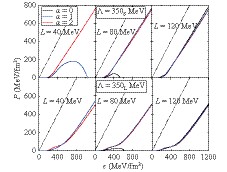
Figure 7. (color online) Calculated equations of state in
${\beta}$ -equilibrium neutron star matter for cutoff${\Lambda=350}$ MeV for various${\alpha=G_{\rho S}/G_{SV}}$ and${L}$ . The top and bottom panels correspond to small and large solutions of${m_0}$ for${K=240}$ MeV, respectively. The slope of dotted lines is 1, which is taken as a reference for the EoSs.
Figure 8. (color online) Same as in Fig. 7 but for
${\Lambda=400}$ MeV and${K=290}$ MeV.By solving the Tolman-Oppenheimer-Vokoff equations with the EoS at low baryonic densities (
$\rho_B < 0.01$ ${\rm{fm}}^{3}$ ) provided by the BPS model [40] and at higher densities constructed with the eNJL model, a given central density or central pressure can provide the unique solution of the structure of a static, spherically symmetric NS. The resulting NS mass-radius relations are plotted in Figs. 9, 10. The two precisely measured highest NS masses so far are$ M=1.97\pm$ $0.04M_{\bigodot}$ [41] or$M=1.928\pm0.017M_{\bigodot}$ [42] for pulsar PSR J1614+2230 and$M=2.01\pm0.04M_{\bigodot}$ for PSR J0348+0432 [43]. It can be seen that the calculations with eNJL model are all above 2$M_{\bigodot}$ , which are consistent with these astronomical observations. Moreover, the present analyses for the information on the binary NS merger GW170817 [44-47] provide the range of upper limits on the NS$M_{{\rm max}}$ as approximately$2.2 M_{\bigodot}$ , which prefer the large-$m_0$ solutions in the eNJL models.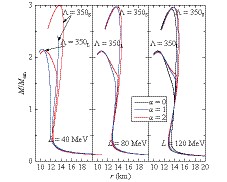
Figure 9. (color online) Calculated mass-radius relations of neutron stars for
${\Lambda=350}$ MeV and${K=240}$ MeV for various${\alpha=G_{\rho S}/G_{SV}}$ and${L}$ . Except for${L=120}$ MeV, the cases with${\alpha=0}$ are not plotted for${L=40, 80}$ MeV because they undoubtedly violate astronomy observations.
Figure 10. (color online) Same as in Fig. 9 but for
${\Lambda=400}$ MeV and${K=290}$ MeV.For the radius of 1.4
$M_{\bigodot}$ canonical NSs, labeled by$R_{1.4}$ , the reported results extracted from the recent analyses and observations still suffer from relatively large uncertainties, most of which are in the range of$10\sim14$ km [48-52]. It is beyond the aim of this work to make any judgment on these analyses and observations. Here,$R=13.6$ km was used as an example; the black solid horizontal line in Fig. 11, as the upper limit of$R_{1.4}$ [48]. Because NS radii depend primarily on the pressure at approximately$2\rho_0$ [53], there are strong correlations between the radii and the slope$L$ of the symmetry energy at nuclear saturation density, which has been pointed out by previous studies, e.g., [9, 54, 55]. In Fig. 11, it can be seen that the lower slopes$L$ are related to the smaller 1.4$M_{\bigodot}$ NS radii, which can be understood qualitatively as being highly effective in pushing against gravity for stiff symmetry energy at approximately$2\rho_0$ , generally accompanied by large$L$ , and thus generating large star radii. One can also see that small isovector-scalar coupling$G_{\rho S}$ leads to a small NS radii. This is owing to the positive linear correlation between$G_{\rho V}$ and$G_{\rho S}$ for a given slope$L$ and soft symmetry energy caused by small$G_{\rho V}$ . Thus, Fig. 11 shows that a 1.4$M_{\bigodot}$ NS requires low$L$ , small high-order isovector couplings, or a suitable combination of both to have a small radius.
Figure 11. Calculated radius of 1.4
${M_{\bigodot}}$ canonical neutron stars versus density slope of symmetry density at saturation density for four parameter sets listed in Table. 1 for various${\alpha=G_{\rho S}/G_{SV}}$ . Left panel corresponds to${\Lambda=350}$ MeV and${K=240}$ MeV, and right panel${\Lambda=400}$ MeV and${K=290}$ MeV. As an example, an upper limit of${R_{1.4}}$ [48] is shown as black solid horizontal line.Recent observations of the gravitational wave event GW170817 has allowed us to put the limits on the dimensionless tidal deformability Λ1.4 of a 1.4
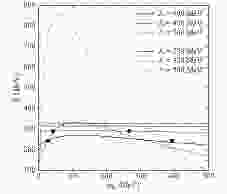
$M_{\bigodot}$ NS [47, 56]. The details to calculate the tidal deformability can be found in Refs. [57, 58]. The calculated results of Λ1.4 for$L=40, 80, 120$ MeV with various eNJL model parameters are depicted in Fig. 12. Considering the magnetic braking during the evolution of the NS binary system, the low spin prior in the binary is a reasonable assumption. For this case, the upper limit is given by Λ1.4 < 800, while Λ 1.4 < 1400 is allowed to be a loosely constrained upper limit for the high spin prior case. Moreover, the latest work in Ref. [ 47] explores a very large range of physically plausible EoSs and suggests a lower limit of Λ1.4 > 375. These limits provide a strong constraint on the model parameters. In Fig. 12, only those for$L=40$ MeV with$\alpha=1$ fulfill$\Lambda_{1.4} < 800$ . However, most calculations still fulfill the looser constraint$\Lambda_{1.4}< 1400$ except for some large$L$ ($L=120$ MeV in this work) results. With regard to the lower limit of$\Lambda_{1.4}>375$ , it indicates for some cases with low$L$ , e.g., the case of the large-solution$m_0$ with$\alpha=1$ and$\Lambda=350$ MeV for$L=40$ MeV, may be ruled out. This figure also shows that lower$L$ and smaller$\alpha$ ($G_{\rho S}$ ), which are accompanied by soft symmetry energy, lead to smaller$\Lambda_{1.4}$ . One can see in Figs. 11 and 12 that the small solutions of$m_0$ correspond to greater radii$R_{1.4}$ and tidal deformability$\Lambda_{1.4}$ , which can be easily recognized for small$\Lambda$ (350 MeV). For large$\Lambda$ (400 MeV), the differences between the double solutions of$m_0$ are very small.
Figure 12. Dimensionless tidal deformability
${\Lambda_{1.4}}$ of a 1.4${M_{\bigodot}}$ neutron star versus${L}$ . Solid and hollow shapes correspond to small (${m_{0S}}$ ) and large (${m_{0L}}$ ) solutions of${m_0}$ , respectively. Left panel corresponds to${\Lambda=350}$ MeV and${K=240}$ MeV, and right panel${\Lambda=400}$ MeV and${K=290}$ MeV. For comparison, the upper limits${\Lambda_{1.4}=800}$ and${\Lambda_{1.4}=1400}$ , and the lower limit${\Lambda_{1.4}=375}$ , are plotted as solid, dashed, and dotted horizontal lines, respectively. -
In summary, the properties of nuclear matter and NSs in the eNJL model, which is an extended Nambu-Jona-Lasinio model with nucleons as the degrees of freedom, were investigated. Two values of cutoff
$\Lambda$ were chosen in this work. Then, when the slope of the symmetry energy and isovector-scalar coupling constant were given, the other model parameters were determined by the nucleon vacuum mass and the bulk properties of the nuclear matter at saturation density. One sees that for$\Lambda\gtrsim450$ MeV, the incompressibility was significantly greater than the empirical value and was hardly affected by$m_0$ , while for$\Lambda\lesssim 400$ MeV, the double-solution phenomenon of$m_0$ was evident for a given$\Lambda$ . The large-$m_0$ solution corresponds to soft EoS, and vice versa. The nuclear fourth-order symmetry energy at the saturation density was studied. Quantitatively, the values were estimated to be approximately$J_4=0.55\sim1.56$ MeV according to different values of$\alpha$ within the selected parameter sets, which is in agreement with other theoretical calculations; however, the values were lesser than the predictions of quantum molecular dynamics simulation and nuclear experimental data analysis. It can be seen that the isovector-vector interaction significantly contributes to the symmetry energy at high densities and the sign of$G_{\rho V}$ is critical for the determination of the trend. With the identical isoscalar couplings,$G_{\rho V} < 0$ corresponds to super-soft symmetry energy that is less than zero above a certain density. When$G_{\rho V}$ increases and becomes greater than zero, accompanied by an increase in$G_{\rho S}$ or greater$L$ , the symmetry energy becomes stiff and increases with densities. Similarly, the super-soft EoS in the$\beta$ -equilibrium NS matter is accompanied by$G_{\rho V} < 0$ . When$G_{\rho V}>0$ , the EoS increases monotonically and is not significantly affected by$G_{\rho S}$ and the slope$L$ owing to the lesser isovector effects at high densities because of the difference between the proton and the neutron fractions. The core-crust transition density$\rho_t$ of NSs is obtained with the thermodynamical method, and the anticorrelation between$L$ and$\rho_t$ can be seen. The NS mass-radius relations using the eNJL EoSs was also studied. It was shown that all the calculated results of the NS maximum mass are greater than$2M_{\bigodot}$ , and the present analyses on the binary NS merger GW170817 prefer the solutions with large$m_0$ the eNJL models. The calculated 1.4$M_{\bigodot}$ star radii lie in approximately$R_{1.4}=11.7\sim14.5$ km. Low$L$ , small high-order isovector couplings, or a suitable combination of them are needed to satisfy the present extraction of upper limits on NS radius and the tidal deformability from recent GW170817 measurements, while some low-$L$ cases may be ruled out by recent suggestions of the lower limit on tidal deformability. The NJL model is used to investigate the properties of isospin asymmetric quark matter [59], quark stars [60], and hybrid stars [61]. Thus, the studies on the isospin effects from the quark phase to the nuclear phase including the eNJL model may be interesting and will be performed in the next step. -
In this appendix, the expressions of the compression modulus of nuclear matter K, the symmetry energy
${E_{sym}}$ and the fourth-order symmetry energy$E_{sym, 4}$ in this study are provided.$ \tag{A1} \begin{split} K=&9\rho\frac{{\rm d}^2\epsilon}{{\rm d}\rho^2} = 9\rho\left[G_V-G_{SV}\rho_s^2+\frac{\pi^2}{2p_{\rm F}E_{\rm F}}+\frac{M^*}{E_{\rm F}}\frac{\partial\Sigma_S}{\partial\rho}\right.\\ &\left.{}-2G_{SV}\rho_S\rho\frac{{\rm d}\rho_S}{{\rm d}\rho}+\frac{M^*}{E_{\rm F}}\frac{\partial\Sigma_S}{\partial\rho_S}\frac{{\rm d}\rho_S}{{\rm d}\rho}\right] , \end{split} $

with
$ \tag{A2} \begin{aligned} \frac{\partial\Sigma_s}{\partial\rho}=-2G_{SV}\rho\rho_S, \;\;\;\;\;\frac{\partial\Sigma_s}{\partial\rho_S}=-(G_S+G_{SV}\rho^2)\, \, , \end{aligned} $

and
$ \tag{A3} \frac{{\rm d}\rho_S}{{\rm d}\rho}=\displaystyle\frac{\displaystyle\frac{M^*}{E_{\rm F}}+\displaystyle\frac{{\rm d}\rho_S}{{\rm d}M^*}\displaystyle\frac{\partial\Sigma_s}{\partial\rho}}{1-\displaystyle\frac{{\rm d}\rho_S}{{\rm d}M^*}\displaystyle\frac{\partial\Sigma_s}{\partial\rho_s}}\, \, , $

and
$ \tag{A4} \frac{{\rm d}\rho_S}{{\rm d}M^*}=\Phi(p_{\rm F}, M^*)-\Phi(\Lambda, M^*)\, \, , $

with
$ \tag{A5} \Phi(x, M^*)\!\!=\!\!\frac{1}{\pi^2}\left[\frac{x^3+3xM^{*2}}{\sqrt{x^2+M^{*2}}}\!\!-\!\!3M^{*2}\ln\left(x\!\!+\!\!\sqrt{x^2\!\!+\!\!M^{*2}}\right)\right]\, \, , $

$ \tag{A6} \begin{split} E_{{\rm sym}}=&\left.\frac{1}{2!}\frac{\partial^2\epsilon(\rho, \delta)}{\rho\partial\delta^2}\right|_{\delta=0} = \frac{p_{\rm F}^2}{6E_{\rm F}}+\frac{1}{2}G_{\rho}\rho+\frac{1}{2}G_{\rho V}\rho^3+\frac{1}{2}G_{\rho S}\rho_S^2\rho\, \, , \end{split} $

$ \tag{A7} \begin{split} E_{{\rm s}ym, 4}=&\left.\frac{1}{4!}\frac{\partial^4\epsilon(\rho, \delta)}{\rho\partial\delta^4}\right|_{\delta=0} =\left.\frac{1}{4}G_{\rho S}\rho\rho_S\frac{\partial^2\rho_S}{\partial\delta^2}\right|_{\delta=0}\\ &{}+\frac{\pi^2\rho}{48}\left[\frac{\pi^4\rho^2}{4p_{\rm F}^4}\frac{\partial^2A(p_{\rm F}, M^*)}{\partial p_{\rm F}^2}-\frac{\pi^4\rho^2}{2p_{\rm F}^5}\frac{\partial A(p_{\rm F}, M^*)}{\partial p_F}\right.\\ &\left.{}+3(2G_{\rho S}\rho^2\rho_S+\frac{\partial\Sigma_s}{\partial\rho_S}\frac{\partial^2\rho_s}{\partial\delta^2})\frac{\partial A(p_{\rm F}, M^*)}{\partial M^*}\right]_{\delta=0}\, \, , \\ \end{split} $

with
$ \tag{A8} A(p_{\rm F}, M^*)=\frac{1}{p_{\rm F}\sqrt{p_{\rm F}^2+M^{*2}}}\, \, , $

and
$ \tag{A9} \begin{aligned} \left.\displaystyle\frac{\partial^2\rho_S}{\partial\delta^2}\right|_{\delta=0}=\frac{\displaystyle\frac{\pi^2\rho^2M^*}{2p_{\rm F}(p_{\rm F}^2+M^{*2})^{3/2}}-2G_{\rho S}\rho^2\rho_S\displaystyle\frac{{\rm d}\rho_S}{{\rm d}M^*}}{\displaystyle\frac{{\rm d}\rho_S}{{\rm d}M^*}\displaystyle\frac{\partial\Sigma_s}{\partial\rho_S}-1}\, \, , \end{aligned} $

where
$\delta=(\rho_n-\rho_p)/(\rho_n+\rho_p)$ and the nuclear matter parameters at saturation density are defined as$ \tag{A10} J=E_{{\rm sym}}(\rho_0)\, \, , \quad J_4=E_{{\rm sym}, 4}(\rho_0)\, \, , L=\left.3\rho_0\frac{{\rm d}E_{{\rm sym}}(\rho)}{{\rm d}\rho}\right|_{\rho=\rho_0}\, \, . $

Nuclear matter and neutron star properties with the extended Nambu-Jona-Lasinio model
- Received Date: 2018-11-08
- Available Online: 2019-03-01
Abstract: An extended Nambu-Jona-Lasinio (eNJL) model with nucleons as the degrees of freedom is used to investigate properties of nuclear matter and neutron stars (NSs), including the binding energy and symmetry energy of the nuclear matter, the core-crust transition density, and mass-radius relation of NSs. The fourth-order symmetry energy at saturation density is also investigated. When the bulk properties of nuclear matter at saturation density are used to determine the model parameters, the double solutions of parameters are obtained for a given nuclear incompressibility. It is shown that the isovector-vector interaction has a significant influence on the nuclear matter and NS properties, and the sign of isovector-vector coupling constant is critical in the determination of the trend of the symmetry energy and equation of state. The effects of the other model parameters and symmetry energy slope at saturation density are discussed.





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF













 DownLoad:
DownLoad: