Possibilities for synthesis of new neutron-deficient isotopes of superheavy nuclei

The production of superheavy nuclei (SHN) in the laboratory has drawn considerable attention, because it is related to the existence of an island stability in SHN [1-5] and depends on its location. Currently, there is a gap between the SHN synthesized by hot fusion and cold fusion reactions [6-11]. To fully understand the shell effects and other properties, and to develop theoretical models that will be able to predict the properties of SHN located beyond this area, expanding the span of known isotopes of SHN is extremely important.

In recent years, many efforts were devoted to the investigation of the synthesis mechanism of SHN [12–26], and many approaches were proposed to calculate the fusion probability [27–34]. To date, however, none of these approaches are predominant [35]. The dinuclear system (DNS) concept represents one of these approaches [16, 17,36-39]. Based on the DNS model, calculated evaporation residue cross-sections (ERCS) for the cold and hot fusion reactions leading to heavy and SHN are in good agreement with available experimental data [40–60].

Selecting the optimal composition of the colliding nuclei is one of the most important factors for the successful synthesis of SHN. In order to fill the gap, several isotopes of actinide nuclei can be used as targets. The use of beams of ³⁶S, ⁴⁰Ar, and ⁴⁴Ca as the projectiles is also interesting. Recently, the first measurement of ERCSs in the complete fusion reaction ³⁶S + ²³⁸U and the observation of ²⁷⁰Hs has already been performed in experimental studies [61].

One of the aims of the present study is to investigate several fusion reactions leading to the formation of the same compound nucleus of unknown isotopes of SHN, and those between already obtained SHN in cold and hot fusion. Usually, fusion hindrance is smaller for the mass-asymmetric reaction system, and hence the corresponding cross-section may be enhanced. Once the best projectile is selected, to find the optimal conditions of synthesis, it is necessary to study the dependence of the ERCS on the isospin composition of colliding nuclei. In the present study, the influence of the target neutron number on the capture cross section, fusion probability, and survival probability for the reactions ³⁶S + ^236−244Pu is investigated in detail. In addition, we systematically study the ERCSs of the ³⁶S bombarding targets of the actinide isotopic chain. The aim of our study is to predict the ERCSs of unknown neutron-deficient isotopes of SHN.

The evaporation residue cross-section (ERCS) in heavy-ion fusion reactions is calculated as the summation over all partial waves $ J $ [16,17],

where $ E_{{\rm c.m.}} $ is the incident energy in the center-of-mass frame. $ T(E_{{\rm c.m.}}, J) $ is the transmission probability of the two colliding nuclei overcoming the Coulomb potential barrier in the entrance channel to form the DNS. The capture cross-section $ \sigma_{{\rm cap}} = \displaystyle\frac{\pi \hbar^{2}}{2\mu E_{{\rm c.m.}}}\sum_{J}(2J+1)T(E_{{\rm c.m.}}, J) $ is calculated with an empirical coupled-channel approach [23, 62]. The $ P_{{\rm CN}} $ is the probability that the system evolves from a touching configuration to the compound nucleus in competition with the quasifission process. The last term $ W_{{\rm sur}} $ is the survival probability of the formed compound nucleus, which can be estimated with a statistic method [63].

The capture cross-section is:

where the transmission probability can be written as

where $ \hbar\omega(J) $ is the width of the parabolic Coulomb barrier at the position $ R_{B}(J) $, and an empirical coupled channel method is used via a barrier distribution function, which is taken as an asymmetric Gaussian form [55]. The nucleus-nucleus interaction potential with quadrupole deformation was used, which is addressed in detail in Ref. [52].

The fusion dynamics are described as a diffusion process by numerically solving a two-variable master equation (ME) in the corresponding potential energy surfaces [23, 53]. The temporal evolution of the probability distribution function $ P(Z_{1}, N_{1}, \varepsilon_{1}, t) $ for fragment 1 with $ Z_{1} $ and $ N_{1} $ with the local excitation energy $ \varepsilon_{1} $ at time $ t $ is described by the following ME:

where $ W_{Z_{1}, N_{1};Z_{1}, N'_{1}} $ is the mean transition probability from channel ($ Z_{1}, N'_{1} $) to ($ Z_{1}, N_{1} $), and $ d_{Z_{1}, N_{1}} $ denotes microscopic dimensions corresponding to the macroscopic state ($ Z_{1}, N_{1} $) [18, 27, 64, 65], which is shown later. $ \varepsilon_{1} $ denotes the local excitation energy and is likewise shown later. The sum is taken over all possible proton and neutron numbers that fragment $ Z'_{1} $, $ N'_{1} $ may assume, but only one nucleon transfer is considered in the model.

The probability $ P(Z_{1}, N_{1}, \varepsilon_{1}, t) $ distributed in the bottom of pocket has the possibility to decay out of the DNS, i.e., the evolution of the DNS along the variable $ R $ leads to the quasifission of the DNS, with the corresponding quasifission rate $ \Lambda_{Z, N}^{{\rm qf}}(\Theta) $. In order to consider the influence of the DNS decay on the probability distribution $ P(Z_{1}, N_{1}, \varepsilon_{1}, t) $, we need to include the effect of the quasifission rate on the ME. The quasifission rate $ \Lambda_{{\rm qf}} $ in Eq. (10) is estimated with the one-dimensional Kramers formula [66, 67].

The quasifission barrier $ B_{{\rm qf}} $ measures the depth of the pocket of the nucleus-nucleus interaction potential. The quasifission barrier $ B_{{\rm qf}} $ decreases with increasing $ Z $, and for near symmetric configurations there is no minimum of the nucleus-nucleus potential [46, 48]. In the present study, in the case where the nucleus-nucleus interaction potential has no minimum, we assumed that the height of the quasifission barrier $ B_{{\rm qf}} $ is 0.5 MeV. The temperature $ \Theta(Z, N) $ of the DNS is calculated with the expression $ \Theta(Z, N) = \sqrt{\varepsilon/a} $ where $ \varepsilon $ depicts the local excitation energy of the DNS. The level density parameter is calculated with the expression $ a = A/12 $ ${\rm MeV}^{-1} $. Here, $ \omega $ is the frequency of the harmonic oscillator approximating the potential along the internuclear distance around the bottom of the pocket. The frequency $ \omega^{B_{\rm{qf}}} $ is the frequency of the inverted harmonic oscillator approximating the interaction potential of two nuclei along the internuclear distance around the top of the quasifission barrier. The quantity $ \Gamma $ denotes the double average width of the contributing single-particle states. In the present study, constant values $ \Gamma = 2.8 $ MeV, $ \hbar\omega^{B_{\rm{qf}}} = 2.0 $ MeV, and $ \hbar\omega = 3.0 $ MeV were employed.

Solving Eq. (4) numerically, the temporal evolution of the probability distribution $ P(Z_{1}, N_{1}, \varepsilon_{1}, t) $ to find fragment 1 ($ Z_{1}+N_{1} $) with excitation energy $ \varepsilon_{1} $ at time $ t $ is obtained. All the components on the left side of the Businaro-Gallone (BG) point contribute to the compound nuclear formation. The fusion probability represents the Z-N configuration at the BG point, beyond which the system falls into the fusion valley in the potential energy surface as a function of the mass-charge asymmetry parameter. Therefore, the fusion probability $ P_{{\rm CN}} $ is the summation of $ P(Z_{1}, N_{1}, \varepsilon_{1}, t) $ from ($ Z_{1} = 1, N_{1} = 1 $) to ($ Z_{{\rm BG}}, N_{{\rm BG}} $) configurations. The compound nucleus formation probability at the minimum of the nucleus-nucleus potential ($ B_{m} $), which corresponds to a certain orientation of the colliding nuclei in the entrance channel, and for the angular momentum $ J $, is given by

The interaction time $ \tau_{{\rm int}} $ (this will be shown later) in the dissipative process of two colliding nuclei is dependent on the incident energy $ E_{{\rm c.m.}} $, $ J $ and $ B_{m} $, and it is determined by using the deflection function method [68]. Finally, we obtain the fusion probability $ P_{{\rm CN}}(E_{{\rm c.m.}}, J) $ as

where the barrier distribution function is provided in an asymmetric Gaussian form [18].

In order to numerically solve Eq. (4), interaction time and local excitation energy are needed as input. The time interval between formation and break of the composite system is defined as the interaction time $ \tau_{{\rm int}} $. As shown in Fig. 1 in Ref. [68], during this process the composite system rotates about its center of mass. On the one hand, for a given value $ J_{i} $ of the incident angular momentum, $ \tau_{{\rm int}}(J_{i}) $ is determined by the rotation of the composite system through the angle

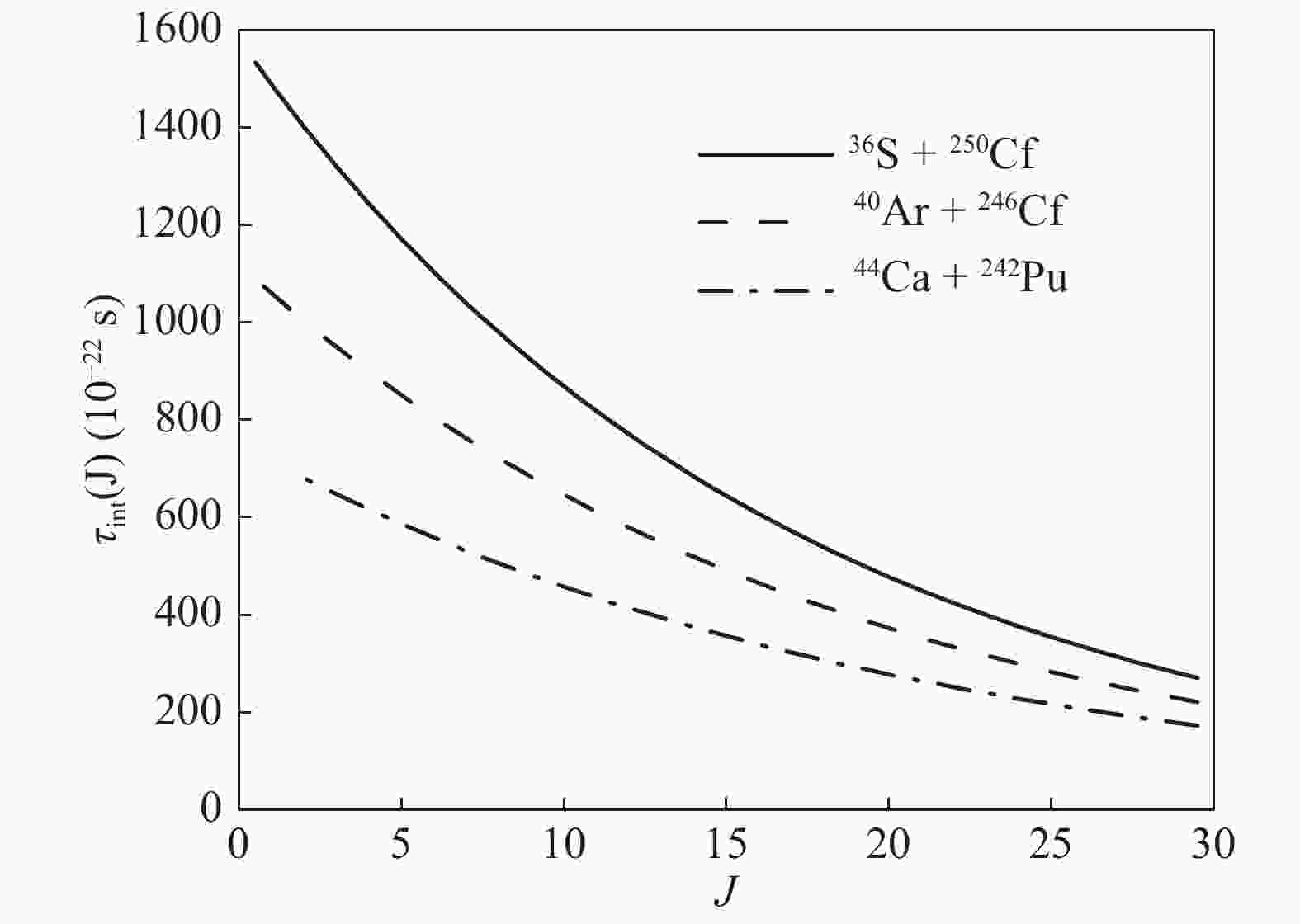
Figure 1.  Mean interaction times are shown as a function of incident angular momentum $J$ for ³⁶S + ²⁵⁰Cf, ⁴⁰Ar + ²⁴⁶Cm, and ⁴⁴Ca + ²⁴²Pu reactions with corresponding excitation energy $E_{{\rm CN}}^{*} = 40$ MeV.

where the Coulomb angles $ \vartheta_{i} $ and $ \vartheta_{f} $ are given by Coulomb trajectories in the entrance and exit channels with the corresponding the energies $ E_{i} $, $ E_{f} $ and the angular momenta $ J_{i} $, $ J_{f} $ values, respectively.

where $ \varepsilon_{i(f)} = \alpha/(E_{{\rm c.m.}}b_{i(f)}) $, $ \alpha = Z_{P}Z_{T}e^{2} $, and $b_{i(f)} =\hbar J_{i(f)}/ $$ \sqrt{2\mu E_{{\rm c.m.}}} $.

The essential ingredient of the model is the determination of the deflection function $ \Theta(J_{i}) $ from the experimental angular distribution. However, this is achieved by introducing the parametrization [69]

The first term on the right-hand side is the Coulomb deflection function. The second term describes the deviation from the Coulomb deflection function due to nuclear interaction between the projectile and target. The parameters $ \delta $ and $ \beta $ are determined by a fit of the differential cross-section obtained from experimental data. The initial angular momentum is assumed as $ J_{i} = J $. The details of $ \delta $ and $ \beta $ are given in Ref. [70]. The grazing angular momentum $ J_{{\rm gr}} $ can be expressed:

where $ V(R_{{\rm int}}) $ denotes the interaction barrier at the interaction radius $ R_{{\rm int}} $. $ A_{{\rm red}} $ is the reduced mass.

During this process, the composite system rotates about its center of mass. The relation between $ \Delta\vartheta $ and $ \tau_{{\rm int}} $ is given by the integral

with the time-dependent angular momentum $ J(t) $ and relative moment of inertia $ \zeta_{{\rm rel}}(t) $. The dissipation of the relative angular momentum $ <J(t)> $ is described by

where the limiting value $ J_{{\rm st}} $ given by the sticking condition is $ J_{{\rm st}} = J_{i}\zeta_{{\rm rel}}^{0}/\zeta_{{\rm tot}}^{0} $. The relaxation time $ \tau_{J} $ is $ 1.5\times 10^{-21} $ s. For the relative and total moments of inertia, we assume the rigid-body values: $ \zeta_{{\rm rel}} = \mu R^{2} $ ($ \zeta_{{\rm rel}}^{0} = \mu R^{2}_{0} $) and $\zeta_{{\rm tot}} = \mu R^{2}+ $$ \displaystyle\frac{2}{5}m_{1}R_{1}^{2}+\displaystyle\frac{2}{5}m_{2}R_{2}^{2} $$ \left(\zeta_{{\rm tot}}^{0} = \mu R^{2}_{0}+\displaystyle\frac{2}{5}m_{1}R_{1}^{2}+\displaystyle\frac{2}{5}m_{2}R_{2}^{2} \right)$; where $ m_{1} $, $ m_{2} $, $ \mu $, $ R_{1} $, $ R_{2} $ are the masses, the reduced mass, and radii of the fragments, respectively. $ R_{0} $ is the radius of the rotating composite system two nuclei form at close contact. The coupled Eqs. (8)–(13) are solved by iteration to obtain the interaction time $ \tau_{{\rm int}} $.

For the subsequent three ³⁶S + ²⁵⁰Cf, ⁴⁰Ar + ²⁴⁶Cm, and ⁴⁴Ca + ²⁴²Pu reactions, the average interaction times are calculated by the deflection function method [68-70]. In Fig. 1, we plot the mean interaction time as a function of the incident angular momentum $ J $ with the corresponding excitation energies $ E_{{\rm CN}}^{*} = 40 $ MeV. Fig. 1 shows that the interaction time of the composite system is long for partial waves with a small incident angular momentum $ J $. Moreover, we found that the interaction time decreases with increasing $ J $. In Fig. 1, we also observe the decrease of interaction time with decreasing mass asymmetry in the entrance channel with the special excitation energy and angular momentum $ J $. This is because the Coulomb repulsion increases gradually with the decrease in mass asymmetry.

The local excitation energy is defined as [18, 71]

where the dissipation energy $ E_{x} $ of the composite system is converted from the relative kinetic energy loss. The dissipation energy $ E_{x} $ is related to the minimum of the nucleus-nucleus potential ($ B_{m} $) and is determined for each initial relative angular momentum $ J $ by the parametrization method of the classical deflection function.

$ \tau_{{\rm rad}} $ denotes the relaxation time of the dissipation of the radial kinetic energy. The quantity $ E_{{\rm rad}}^{i} $ denotes the initial radial kinetic energy at the interaction radius. The radial energy at the initial state is $ E_{{\rm rad}}^{i}(J, 0) =E_{{\rm c.m.}}-B_{m}-EJ_{i} (J_{i} + $ $1)\hbar^{2}/ (2\zeta_{{\rm rel}}) $. The initial angular momentum is assumed to be $ J_{i} = J $. The value of $ \tau_{{\rm rad}} $ is $ 3\times10^{-22} $ s [69]. Fig. 1 shows that the angular momentum is within the range of our research, and that the interaction time $ \tau^{J}_{{\rm int}} $ is much larger than $ \tau_{{\rm rad}} $. Therefore, for the current three reaction systems, the $ <E_{{\rm rad}}(J, t)> $ value at $ E_{{\rm CN}}^{*} = 40 $ MeV is infinitely close to zero.

The second term of Eq. (14) is the driving potential energy [16-18] of the system for the nucleon transfer of the DNS, which is:

where $ Z = Z_{1}+Z_{2} $ and $ N = N_{1}+N_{2} $, and $ \beta_{i} (i = 1, 2) $ and $ \beta $ represent quadrupole deformations of the two fragments and the compound nucleus, respectively. The $ B(Z_{1}, N_{1}, \beta_{1}) $, $ B(Z_{2}, N_{2}, \beta_{2}) $, and $ B(Z, N, \beta) $ are the binding energies of two deformed nuclei and the compound nucleus [72], respectively. The $ Q_{gg} $ ($Q_{gg} = B(Z_{1}, N_{1}, \beta_{1})+B(Z_{2}, N_{2}, \beta_{2})- B(Z, N, \beta) $) denotes the ground state $ Q $ value. In the present study, the deformation parameters and binding energies are taken from Refs. [73, 74]. Wong's formula [75] is adopted to calculate the Coulomb interaction, and the nuclear potential is calculated with Skyrme-type interaction without considering the momentum and spin dependence [76]. Here, the inner fusion barrier appears on the driving potential energy surface during the evolution of the mass (charge) asymmetry axis. The inner fusion barrier is determined by the difference between the maximum value of the driving potential and its value at the point corresponding to the initial charge asymmetry of the considered reaction. To form a compound nucleus, the inner fusion barrier must be overcome.

In Eq. (4), $ W_{Z_{1}, N_{1};Z_{1}, N'_{1}} $, $ d_{Z_{1}, N_{1}} $, $ \Lambda_{{\rm qf}} $, and $ \Lambda_{{\rm fs}} $ are all dependent on the local excitation energy of the DNS. The transition probability is related to the local excitation energy, and the neutron transition probability $ W_{Z_{1}, \;N_{1},\; \beta_{1},\; \beta_{2};\;Z_{1},\;N'_{1},\; \beta_{1},\; \beta_{2}} $ can be written as [64, 65]

where $ i $ denotes all remaining quantum numbers. The memory time $ \tau_{{\rm mem}} $

can be interpreted as the coherence time for the transitions between the subsets ($ Z_{1}, N_{1}, \varepsilon_{1} $) and ($ Z_{1}, N'_{1}, \varepsilon'_{1} $) [64, 65], where $ <V^{2}(t)>_{Z_{1}, N_{1}, \varepsilon_{1}} $ and $ <V^{2}(t)>_{Z_{1}, N'_{1}, \varepsilon'_{1}} $ stand for the average expectation value with $ Z_{1}, N_{1}, \varepsilon_{1} $ and $ Z_{1}, N'_{1}, \varepsilon'_{1} $ being fixed, respectively. Thus, the memory time $ \tau_{{\rm mem}} $ depends on the neutron number $ N_{1} $, proton number $ Z_{1} $ , and the local excitation energy $ \varepsilon_{1} $. For the ³⁶S + ²⁵⁰Cf reaction, the memory time $ \tau_{{\rm mem}} (Z = 16, N = 20;Z = 16, $N = 21) is $ 0.75\times10^{-22} $ s when the excitation energy $ E_{{\rm CN}}^{*} $ = 40 MeV.

The transition probability of Eq.(18) can be written as

where

The averages in Eqs. (18), (19), and (21) are carried out by using the method of spectral distributions [77, 78]. We obtain

which contains some fixed independent parameters $ U_{kk'}(t) $ and $ \Delta_{kk'}(t) $. In the present work, the strength parameters $ U_{kk'}(t) $ are assumed as [64]

In our calculation $ \Delta_{11}(t) $ = $ \Delta_{12}(t) $ = $ \Delta_{22}(t) $ = $ \Delta_{21}(t) $ = 2, and the dimensionless strength parameters $ \gamma_{11} $ = $ \gamma_{12} $ = $ \gamma_{22} $ = $ \gamma_{21} $ = 3 are assumed. Owing to the excitation, a valence space $ \Delta\varepsilon_{k} $ forms symmetrically around the Fermi surface. Only the particles in the states within this valence space are actively involved in the excitation and transfer [64, 65].

Here $ \varepsilon $ deontes the local excitation energy of the DNS. The microscopic dimension is [64, 65]

There are $ N_{k} = g_{k}\Delta\varepsilon_{k} $ valence states and $ m_{k} = N_{k}/2 $ valence nucleons in $ \Delta\varepsilon_{k} $.

The survival probability of the compound nucleus at excitation energies is a probability for the compound system to resist fission decay in the form of emission of light particles and $ \gamma $-decay. For the sake of simplicity, the present work as well as other Refs. [24-26] consistently neglect the $ \gamma $-decay width and other charged particles at high excitation energies of interest in hot fusion reactions, compared with the evaporation of successive emission neutrons. The survival probability of the excited compound nucleus in the de-excitation process, by means of the neutron evaporation in competition with fission, is expressed as follows:

where $ F(E^{*}_{{\rm CN}}, x, J) $ is the realization probability of the $ xn $ channel at the excitation energy $ E^{*}_{{\rm CN}} (E_{{\rm c.m.}}+Q) $ of the compound nucleus with angular momentum $ J $, $ i $ the index of evaporation step, $ \Gamma_{n} $ and $ \Gamma_{f} $ are the partial widths of neutron emission and fission.

The partial width for emission of a neutron from a compound nucleus with the excitation energy $ E_0 $ is given by the Weisskopf formula

where $ m_{n} $ and $ g $ are the mass and spin degeneracy of the emitted neutron, respectively; $ \sigma_{{\rm inv}} $ is the cross section for the formation of the decaying nucleus in the inverse process; $ \rho_{0}(E_{0}-\delta_0) $ is the level density of the parent nucleus at the thermal excitation energy corrected for its pairing energy $ \delta_0 $, and $ \rho_{n}(E_0-B_n-\delta_n-\varepsilon) $ is the corresponding level density of the daughter nucleus after emitting a neutron. $ B_n $ and $ \delta_n $ are the neutron separation energy and the pairing energy of the daughter nucleus, respectively.

The fission width can be expressed in terms of the transition state theory as

where $ \rho_{n}(E_0-B_f-\delta_f-\varepsilon) $ is the level density of the fissile nucleus at the saddle configuration. The calculations of the width of the fission channel are performed, taking into account the effects of nuclear viscosity and the fission delay time,

where the curvatures of the potential at the ground-state ($ \omega_{{\rm gs}} $) and saddle point ($ \omega_{{\rm sd}} $), and the reduced friction parameter $ \beta $ have been fixed with the default values of $ \hbar\omega_{{\rm gs}} = 2.0 $ MeV, $ \hbar\omega_{{\rm sd}} = 2.4 $ MeV and $ \hbar\beta = 3.0 $ MeV, respectively.

The back-shift Fermi-gas model at energies of the hot-fusion reaction of interest is used to determine the level density,

with $ \sigma^2 = \displaystyle\frac{\Theta_{{\rm rigid}}}{\hbar^2}\sqrt{\frac{U}{a}} $, $ \Theta_{{\rm rigid}} = \displaystyle\frac{2}{5}m_{u}AR^2 $, $ U = E-\delta $. The back shifts $ \delta = -\Delta $ (odd-odd), 0 (odd A) and $ \Delta $ (even-even), respectively, are related to the neutron and proton paring gap $ \Delta = 1/2[\Delta_n(Z, N)+\Delta_p(Z, N)] $, which is employed from mass differences of the neighboring nuclei [79]. The dependence of the level density parameter $ a $ on the shell correction and the excitation energy was initially proposed as

with $ \tilde{a}(A) = \alpha A+\beta A^{2/3} $ and $ f(U) = 1-\exp{(-\gamma_{\rm D} U)} $. It is worth noting that the differences between the corresponding level density parameters are mainly related to different shell corrections, and thus one should use these parameters at the same shell correction energies. In the present study, parameters $ \alpha = 0.1337 $, $ \beta = -0.06571 $, and $ \gamma_{\rm D} = 0.04884 $ [79] are determined by fitting to experimental level density data with the help of the microscopic shell correction from FRDM95 [80], which is adopted to calculate the level density using in the evaporation calculations.

We calculated the angular momentum dependence of the transmission, fusion, and survival probabilities as shown in Fig. 2 for the reaction ³⁶S + ²⁵⁰Cf at incident energies 169.64 MeV. The values of the three stages decrease significantly with increasing relative angular momentum. Hence, in the following estimation of the ERCSs, we cut off the maximal angular momentum at $ J_{{\rm max}} $ = 30. A similar result is also illustrated in Ref. [81].

Figure 2.  Calculated transmission, fusion, and survival probabilities as functions of relative angular momenta in the reaction ³⁶S + ²⁵⁰Cf at excitation energies of compound nucleus of 40 MeV.

Very recently, in order to review our calculated abilities on the ERCSs to synthesize superheavy nuclei using DNS model, the hot fusion reactions producing SHN with $ Z\geqslant 104 $ are systematically studied [82]. The results of systematic calculation show that the current theoretical method can describe the ERCS of SHN. In the present work, the calculations for all reactions were performed with the same parameters and assumptions.

In order to predict the most suitable projectile-target combination among the probable candidates, production cross-sections of new neutron-deficient SHN with charged numbers $ Z $ = 108−114 are analyzed systematically with ³⁶S, ⁴⁰Ar, and ⁴⁴Ca projectiles. In the present study, based on the framework of the DNS model, we calculated the ERCSs of the SHN based on the actinide targets ^249−252Cf, ^245−248Cm, and ^241−244Pu with the projectiles ³⁶S, ⁴⁰Ar, and ⁴⁴Ca, as shown in Fig. 3. The ERCSs decreases by about one order of magnitude with increasing charge number of projectile from $ Z = 16 $ to $ Z = 20 $. This is due to the strong decrease in fusion probability $ P_{{\rm CN}} $ and the increase in the quasifission with increasing asymmetry in the entrance channel.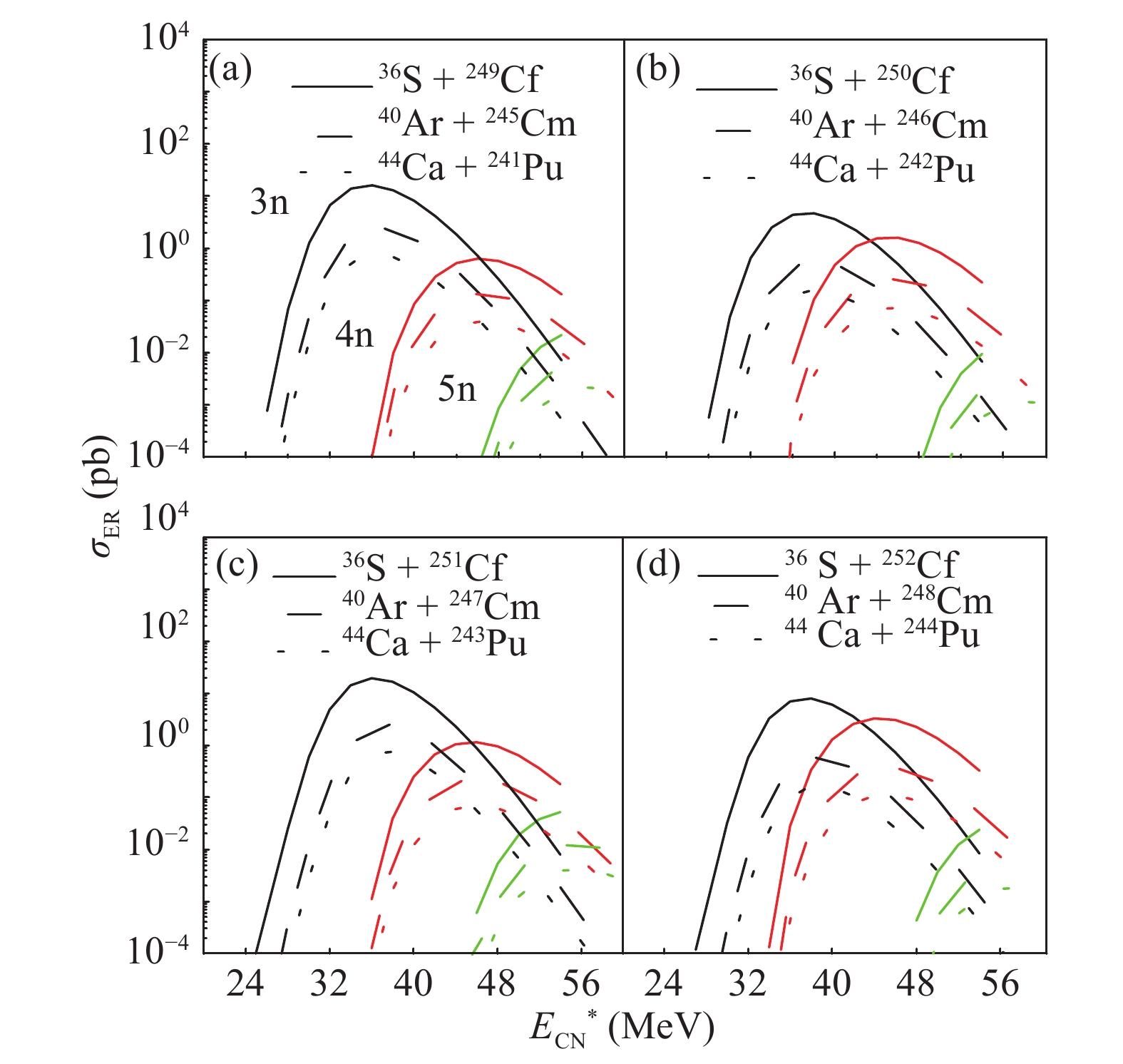

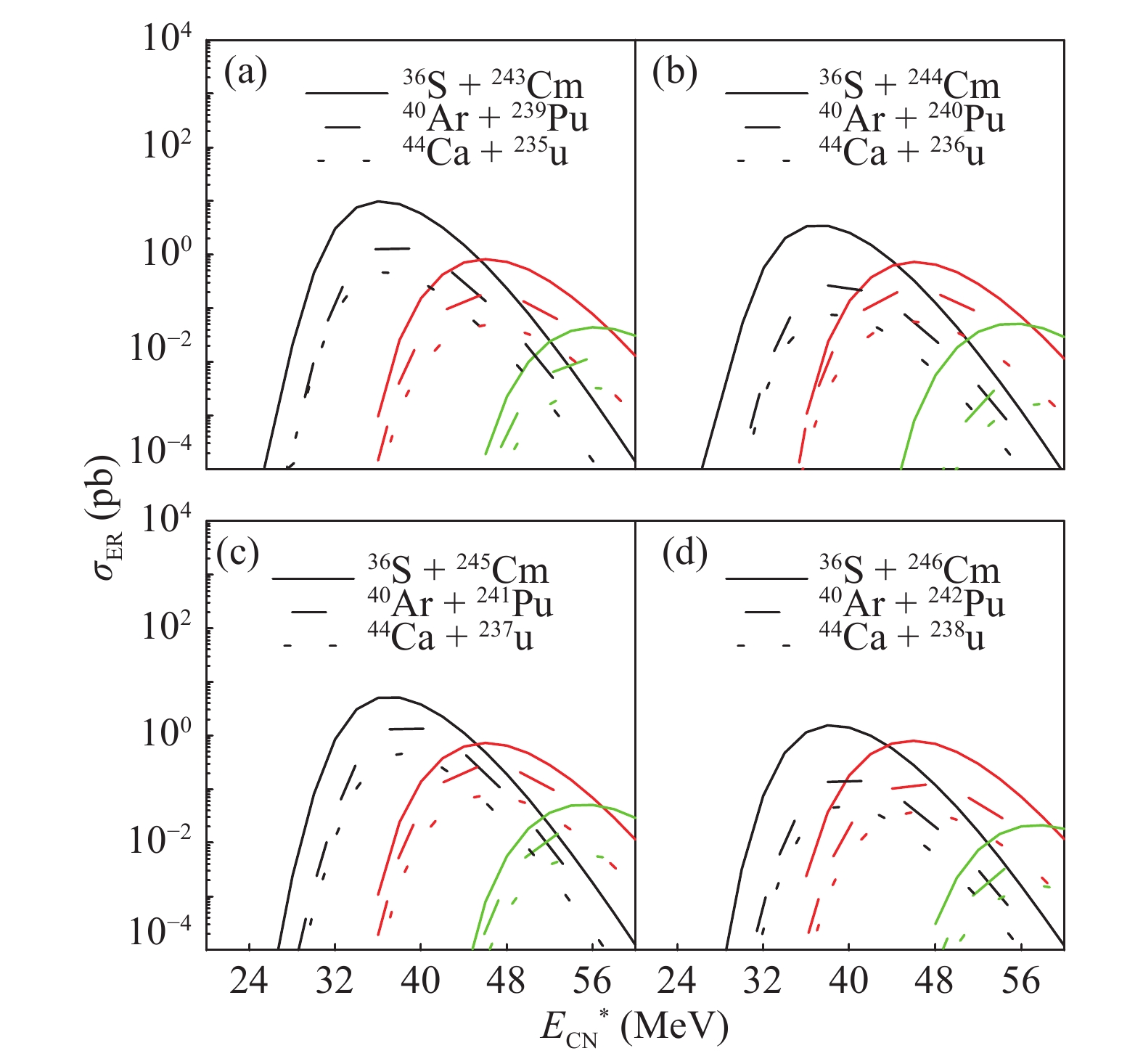
Figure 3.  (color online) Evaporation residue excitation functions in production of isotopes of superheavy nuclei Fl in reactions ³⁶S + ^249−252Cf, ⁴⁰Ar + ^245−248Cm, and ⁴⁴Ca + ^241−244Pu.

In Fig. 3(c), the calculated ERCSs are shown for the production of new neutron deficient isotopes of Fl in the fusion reactions of ³⁶S with ²⁵¹Cf targets and for the ⁴⁰Ar + ²⁴⁷Cm fusion reaction leading to the same compound nucleus as in the ⁴⁴Ca + ²⁴³Pu reaction. The parameters relevant to the exit channels, such as the neutron separation energies and the fission barrier heights, are nearly identical for both reactions at the same excitation energy (neglecting small differences in angular momentum of the compound nucleus after its formation). However, as shown in Fig. 3(c), the use of an ⁴⁰Ar beam is less favorable than ³⁶S. This is attributable to a worse fusion probability of the ⁴⁰Ar + ²⁴⁷Cm fusion reaction, as the dinuclear system becomes more symmetric, and the fusion probability decreases. Our calculations also demonstrated that the use of a ⁴⁴Ca beam instead of ³⁶S decreases the yield of the same SHN, owing to a worse fusion probability. Calculations were performed for the reactions ³⁶S + ^243−246Cm, ⁴⁰Ar + ^239−242Pu, and ⁴⁴Ca + ^235−238U to produce the superheavy nuclei Cn, as shown in Fig. 4. The strong dependence of the calculated ERCSs for the production of SHN on the mass asymmetry in the entrance channel makes the ³⁶S projectile most promising for the further synthesis of SHN.

Figure 4.  (color online) Evaporation residue excitation functions in production of isotopes of superheavy nuclei Cn in reactions ³⁶S + ^243−246Cm, ⁴⁰Ar + ^239−242Pu, and ⁴⁴Ca + ^235−238U.

The calculated maximal ERCSs, 3$ n $and 4$ n $, and the corresponding optimal excitation energies of the compound nuclei in the 3$ n $ and 4$ n $ evaporation channel are presented in Fig. 5 for the reactions ³⁶S + ^APu as functions of the mass number A of the target, respectively. In the 3n and 4n emission channel for the ³⁶S + ^APu reaction, it Fig. 5(b) shows that the maximum ERCSs increases with the increase in neutron number to the maximum value and then decreases with the further increase in the neutron number. The lower part of Fig. 5(c)indicates that the excitation energies of 3 and 4 neutron emission decrease slowly with the increase in neutron number. To analyze the trend of the change above, the whole process of SHN synthesis needs to be investigated in detail. Next, we investigate the influence of the target neutron number on the capture cross-section, fusion probability, and survival probability.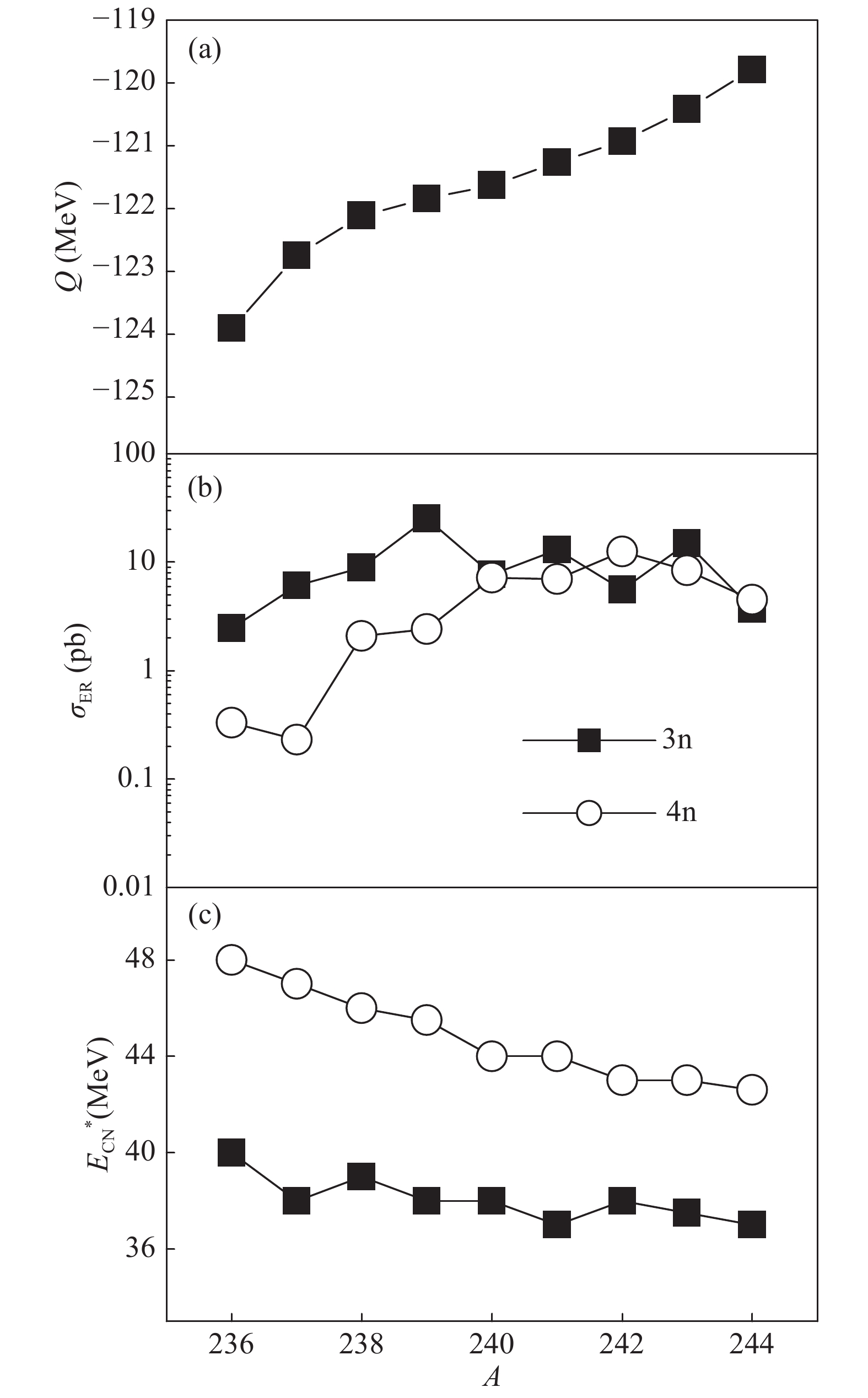

Figure 5.  Isospin dependence from ³⁶S + ^APu hot fusion reactions: (a) Q values for fusion reactions ³⁶S + ^APu; (b) maximal evaporation residue cross sections as functions of target mass number A, for 3n and 4n emission channels; (c) corresponding excitation energies of compound nuclei.

Fig. 6(a) shows that the capture cross-section as a function of the incident energy is quite close for the three above-mentioned reactions owing to a slight difference in Coulomb barriers. Fig. 6(b) shows the capture cross-section $ \sigma_{{\rm cap}} $ as a function of the excitation energy of the compound nucleus. In the lower excitation energy region $ E^{*}_{{\rm CN}}<37 $ MeV, the capture cross-sections for the reactions ³⁶S + ²³⁶Pu are larger than those of the reaction systems ³⁶S + ²⁴⁴Pu, because of the large negative $ Q $ values ($ E_{{\rm CN}}^{*} = E_{{\rm c.m.}}+Q $) of the former reactions. When the excitation energy increases beyond 37 MeV, the differences caused by the Q values become less significant, and the capture cross-sections tend to be almost consistent.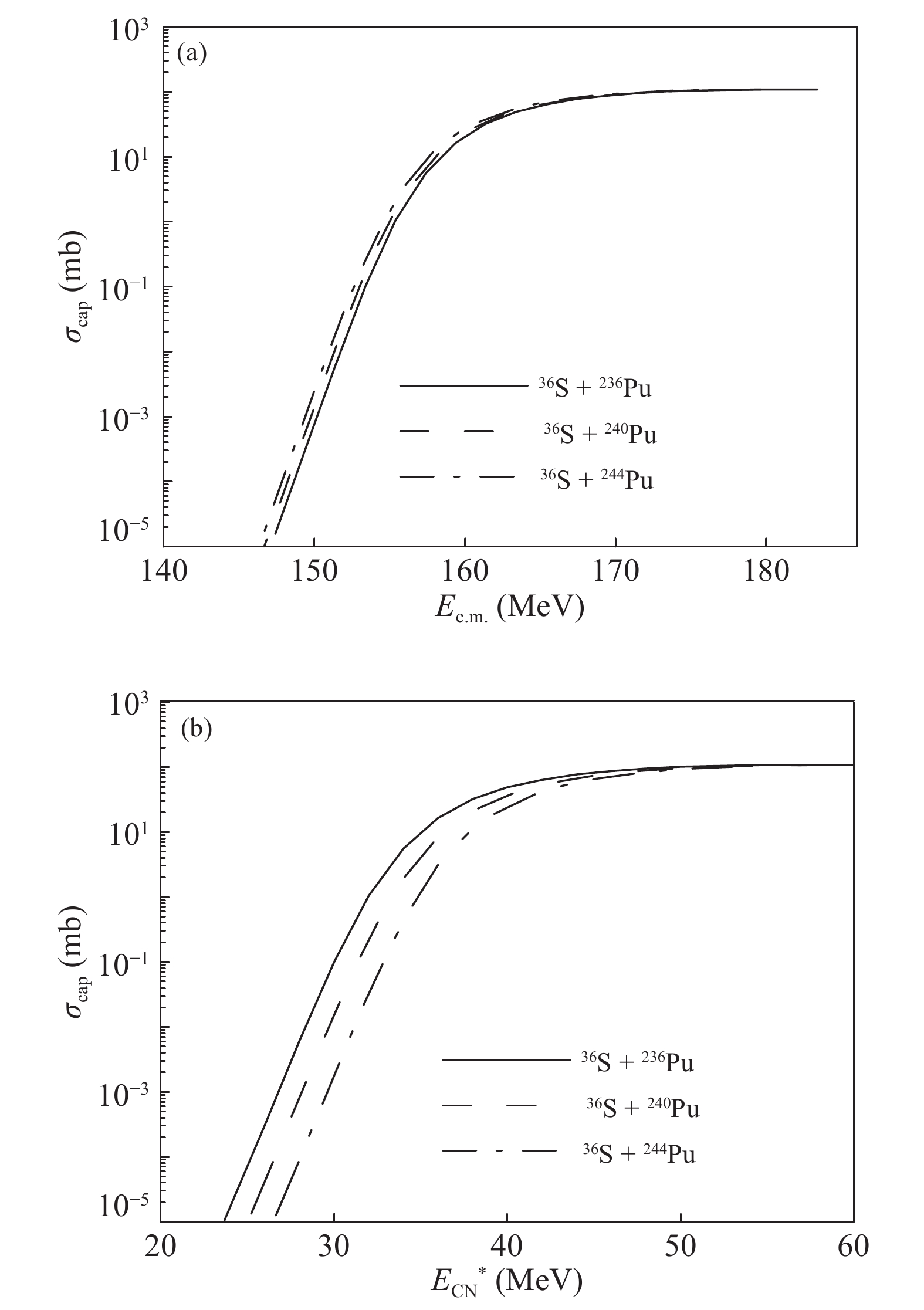

Figure 6.  (a) Calculated capture cross-sections as functions of incident energy in center-of-mass frame for reactions ³⁶S + ^{236, 240, 244}Pu. (b) Calculated capture cross-sections are functions of excitation energy of compound nucleus.

Considering only the effects of mass asymmetry on the fusion probability, when the neutron number in the target nucleus increases, the dinuclear system becomes more asymmetric, and the fusion probability increases [30, 83]. Fig. 7(a) shows that our calculated fusion probability is a function of the excitation energy of the compound nucleus for the reaction ³⁶S + ^{236, 240, 244}Pu. However, we are aware that during the calculation for ³⁶S + ²³⁶Pu and ³⁶S + ²⁴⁰Pu, the fusion probability $ P_{{\rm CN}} $ decreases with increasing neutron number in the lower excitation energy region $ E^{*}_{{\rm CN}}<45 $ MeV. When excitation energy increases beyond 45 MeV, the differences between fusion probabilities among the three reactions become very small, and the results tend to be consistent. The irregular behavior of the fusion probability $ P_{{\rm CN}} $ changes with increasing neutron number of the targets. The fusion probability depends on the details of the driving potential, which is decided by the ground state $ Q_{gg} $ value of the nuclei in each DNS and their interactions [54]. Therefore, our results show that in addition to the mass asymmetry, the reaction $ Q_{gg} $ value plays an important role in the fusion probability.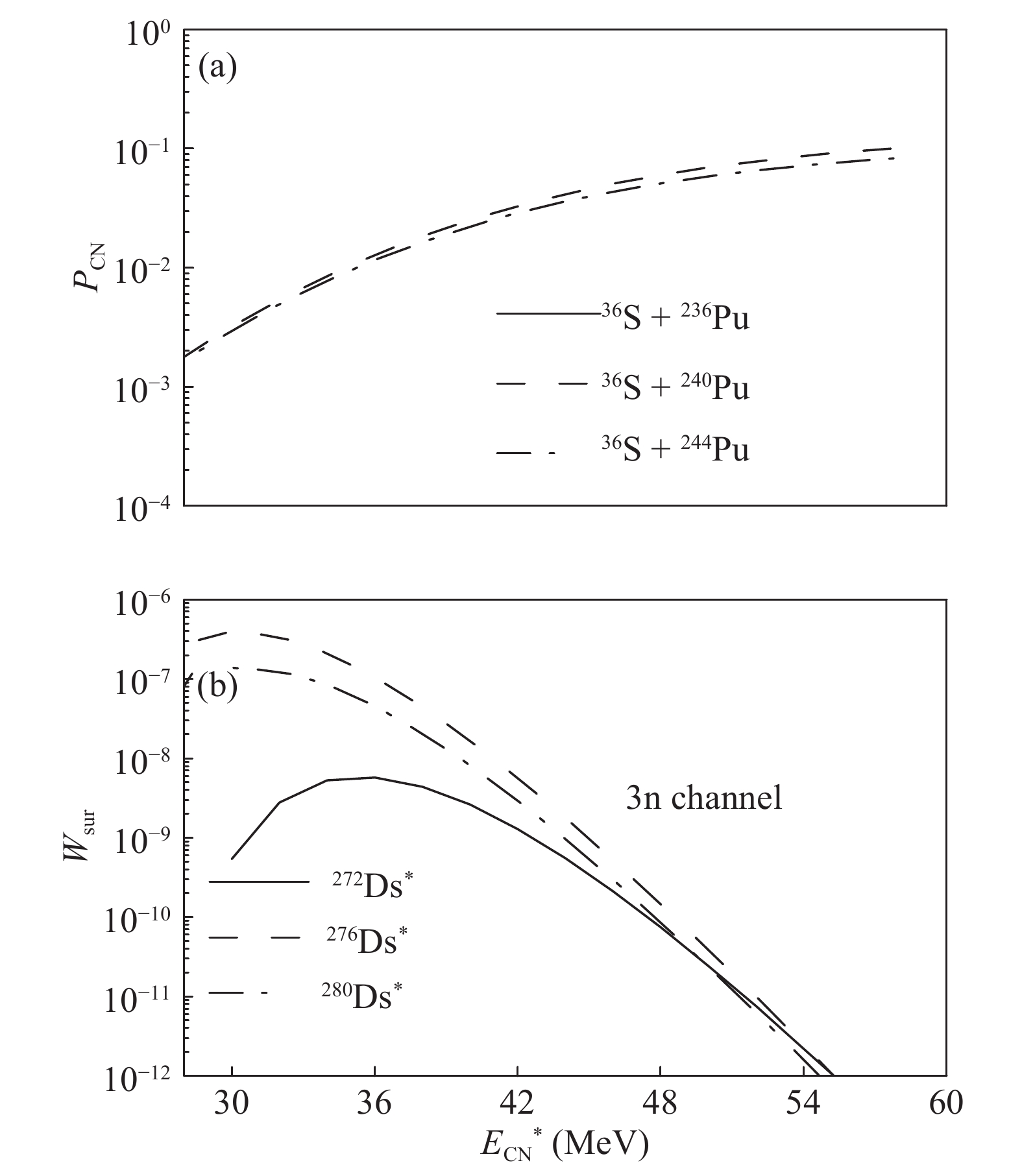

Figure 7.  (a) Calculated fusion probabilities are functions of excitation energy of compound nucleus for reactions ³⁶S + ^{236, 240, 244}Pu. (b) Calculated survival probabilities as functions of compound nucleus excitation energy.

The survival probability of the hot compound nucleus is highly sensitive to the value of the neutron separation energy $ B_{n} $ and fission barrier $ B_{f} $. The fission barriers of the 3$ n $ evaporation channel for compound nuclei ^272−280Ds basically increase with an increase in the neutron number to the maximum value, and subsequently decrease with the further increase in neutron number [80]. The survival probabilities of 3$ n $ evaporation channel are shown in Fig. 7(b) for the compound nuclei ^{272， 276， 280}Ds. The survival probabilities increase with the increase in the neutron number for excitation energies lower than 50 MeV. Therefore, for the 3$ n $ evaporation channel, the increase of survival probability of compound nuclei from ²⁷²Ds to ²⁷⁵Ds is not cancelled by an decreasing capture cross-section and fusion probability. The calculated maximal ERCSs $ \sigma_{3n} $ is larger in the ³⁶S + ²³⁹Pu reaction than in the ³⁶S + ^236−238Pu reactions owing to the larger value of survival probability. For the 4$ n $ evaporation channel, the change of the target neutron number has little influence on the fusion probability and capture cross-section. The variation trend of 4$ n $ ERCS with the neutron number of target nuclei is mainly determined by the survival probability. Therefore, the 4$ n $ evaporation channel corresponding to the ERCS basically increases with the increase in neutron number to the maximum value, and then decreases with the further increase in neutron number.

Figure 8 shows the comparison of the calculated ERCS with the experimental data in the reaction ³⁶S + ²³⁸U. The measured ERCSs of the 3$ n $ and 4$ n $ channels are denoted by solid squares and open circles [61], respectively. For the 3$ n $ channel, calculated results are closer to the experimental data. We also realized that one calculated ERCS of the 4$ n $ channel in the reaction ³⁶S + ²³⁸U peaks at the excitation energy of approximately 44 MeV, which is smaller than the excitation energy used in the experiment for ²³⁸U(³⁶S, 4$ n $)²⁷⁰Hs [61]. However, for the 4$ n $ evaporation channel, the peak position is not clear owing to the lack of experimental data. Taking into account the experimental error bars, we assume that the agreement between our calculated ERCS and the experimental value [61] is sufficient for the ³⁶S + ²³⁸U reaction.

Figure 8.  Excitation functions for ³⁶S + ²³⁸U reaction. Calculated results and experimental data [61] are denoted by lines and symbols, respectively. Measured ERCSs of 3n and 4n channels are denoted by solid squares and open cycles, respectively. Calculated 3n, 4n, and 5n channels are indicated by solid, dashed, and dotted lines, respectively.

The isospin dependence of the ERCS of some SHN is based on the same assumptions with one set of parameters. The maximum ERCS, $ \sigma_{{\rm ER}} $(pb), for 3$ n $ and 4$ n $ emission channels out of ³⁶S bombarding actinide isotopic chains: ^AU, ^ANp, ^AAm, ^ACm, ^ABk, and ^ACf are shown in Fig. 9 as a function of the mass number of the target. From Figure 9 shows that the isotopes of target nucleus with the largest neutron excess are favorable for most cases of hot fusion with the ³⁶S projectile. Except for the 3$ n $ emission channel in the ³⁶S + ^ACm reaction, in all other channels the ERCSs basically increase with increasing neutron numbers, though sometimes not very distinctly.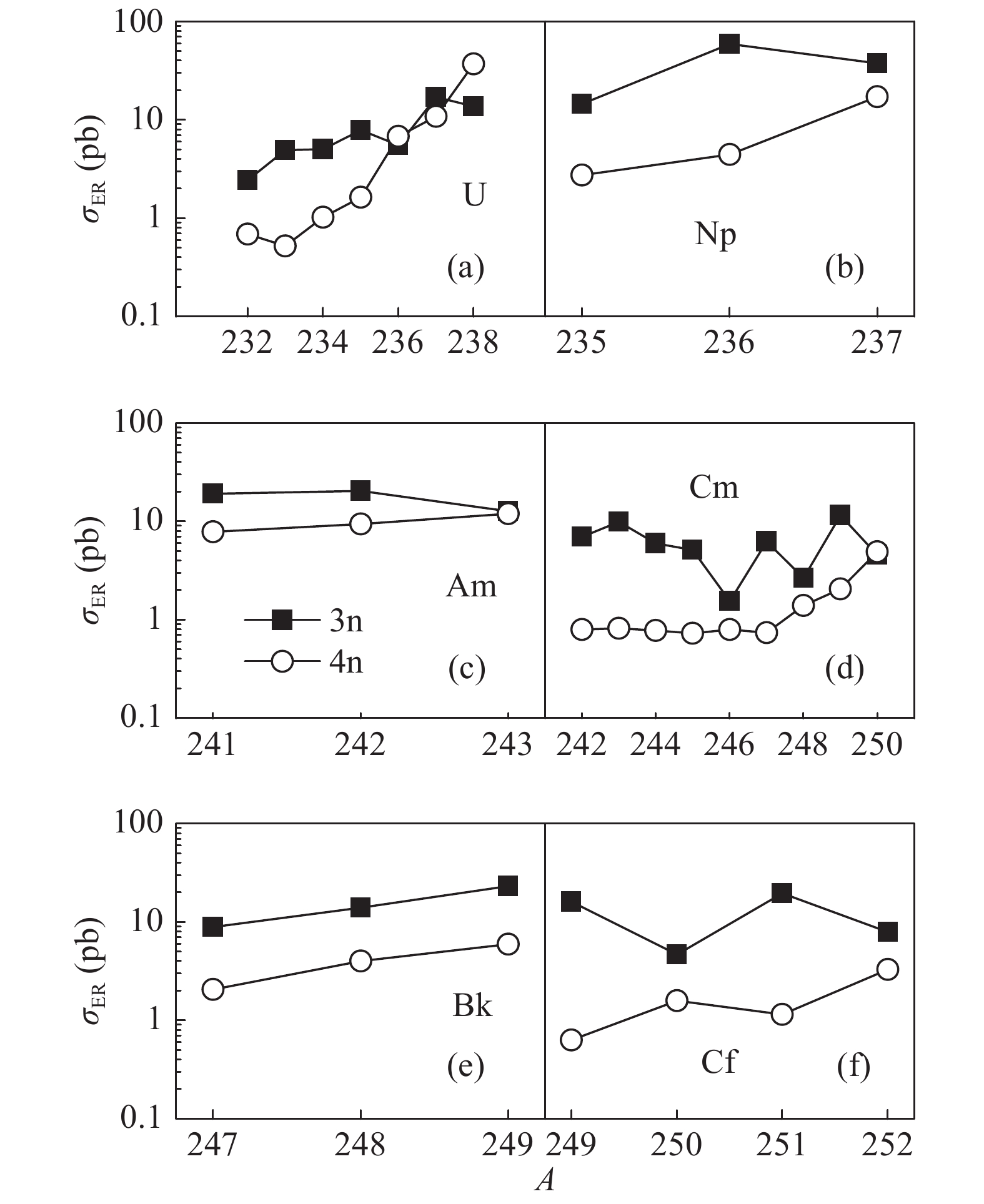

Figure 9.  Isospin dependence of maximal evaporation residue cross-sections from hot fusion reactions: (a) ³⁶S + ^AU, (b) ³⁶S + ^ANp, (c) ³⁶S + ^AAm, (d) ³⁶S + ^ACm, (e) ³⁶S + ^ABk, and (f) ³⁶S + ^ACf as functions of target mass number A, for 3n and 4n emission channels.

Next, we investigate the influence of the target neutron number on ERCS. Similarly to the results of the reactions ³⁶S + ^APu, our calculations show that the capture cross-sections for the neutron-deficient target nucleus are larger than in the neutron-rich target nucleus in the lower excitation energy region for the above projectile target combinations. We are also aware that during the calculation, the fusion probability $ P_{{\rm CN}} $ for ³⁶S + ^AU, ³⁶S + ^ANp, ³⁶S + ^AAm, ³⁶S + ^ACm, ³⁶S + ^ABk, and ³⁶S + ^ACf , the P_CN change with increasing neutron number of the target is not regular. The behavior of the fusion probability $ P_{{\rm CN}} $ with increasing neutron number of the targets depends on the details of the driving potential, which is decided by the properties of nuclei in each DNS and their interactions.

For 3$ n $ emission, in most cases, the increases in $ W_{{\rm sur}} $ are not cancelled by the decreasing $ \sigma_{{\rm cap}} $ and the irregularly changing $ P_{{\rm CN}} $ with increasing neutron number. Therefore, the 3$ n $ evaporation channel corresponding to the ERCS basically increases with the increase in the neutron number. However, for compound nuclei ^278−286Cn, the 3$ n $ evaporation channel ^275−283Cn corresponding to the fission barriers [80] basically decreases to the minimum value with the increase in neutron number, and then increases with a further increase in neutron number. Therefore, the ERCSs of the reactions ³⁶S + ^ACm decrease to the minimum value with the increase in neutron number, and then increase with the further increase in neutron number.

For the 4$ n $ evaporation channel, the change of the target neutron number has little influence on the fusion probability and the capture cross-section. The variation trend of the 4$ n $ ERCS with the neutron number of target nuclei is mainly determined by the survival probability. Therefore, the 4$ n $ evaporation channel corresponding to the ERCS basically increases with the increase in neutron number. Figure 9 shows that the ERCSs of SHN decrease slowly with the charged numbers of compound nuclei from $ Z = 108 $ to $ Z = 114 $ owing to the increase in survival probability $ W_{{\rm sur}} $, which is not canceled by the decreasing $ P_{{\rm CN}} $.

Currently, there is a gap between the SHN synthesized by cold fusion and those by hot fusion [7]. Considerably large cross-sections ($ \sigma_{1n}\geqslant $ 1 pb) for many reaction channels used to fill the gap. For example, as shown in Figs. 9(b), given the predicted excitation function of $ xn $ ERCSs for the reaction ³⁶S + ^ANp. For the ³⁶S+²³⁵Np reaction, the maximal ERCSs of the 4$ n $ channel is 2.74 pb at $ E_{{\rm c.m.}} = 168.39 $ MeV ($ E_{{\rm c.m.}} = E_{{\rm CN}}^{*}+Q $). It is 17.14 pb at $ E_{{\rm c.m.}} = 165.11 $ MeV for the ³⁶S + ²³⁷Np reaction. Through the analysis of Fig. 5(c) and Fig. 9, we found that the nucleus ^{267, 269}Mt, ^{268, 272, 274−276}Ds, ^{273, 275, 276}Rg, ^{274−276, 278−280}Cn, ^279−281Nh, and ^281−283Fl may be produced. Figure 10 shows that at fixed charge asymmetry in the entrance channel, the optimal excitation energy $ E_{{\rm CN}}^{*} $ of compound nucleus decreases with increasing neutron excess in the target. One can expect large ERCSs in the actinide-based reactions with the ³⁶S beam. Moreover, based on the targets ^235−237Np, ^241−243Am, and ^247−249Bk, the production of odd SHN with $ Z = $109, 111, and 113, are promising.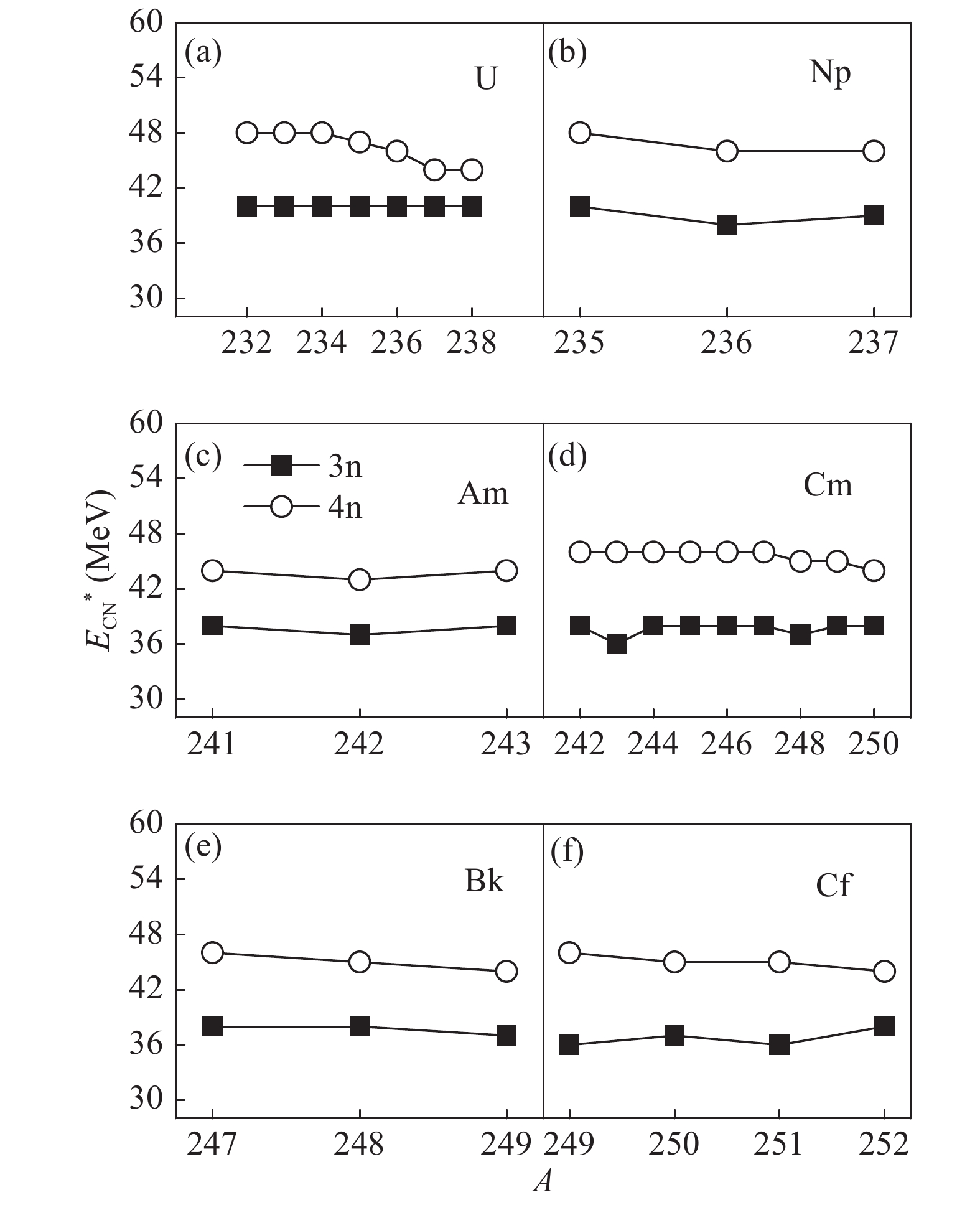

Figure 10.  Isospin dependence of excitation energies of compound nuclei corresponding to maximal evaporation residue cross-sections from hot fusion reactions: (a) ³⁶S + ^AU, (b) ³⁶S + ^ANp, (c) ³⁶S + ^AAm, (d) ³⁶S + ^ACm, (e) ³⁶S + ^ABk, and (f) ³⁶S + ^ACf as functions of target mass number A, for 3n and 4n emission channels.

To investigate the conditions for the synthesis of new neutron-deficient SHN, the projectiles ³⁶S, ⁴⁰Ar, and ⁴⁴Ca bombarding some actinide isotope chains are systematically studied within the DNS model. Our results demonstrate that the strong dependence of the calculated ERCSs for the production of SHN on mass asymmetry in the entrance channel makes the ³⁶S projectile the most promising for further synthesis of new neutron-deficient SHN. The influence of the target neutron number on ERCSs in hot fusion reactions is also investigated. There is a certain probability to produce new neutron-deficient SHN by using ³⁶S to bombard ^232−238U, ^236−244Pu, ^242−250Cm, and ^249−251Cf. Thus, one can expect to produce new neutron-deficient SHN of the Hs, Ds, Cn, and Fl with ERCS ranging from > 1 pb up to 10 pb. Some new nuclides of Mt, Rg, and Nh may be produced by the reaction channels ³⁶S + ^235−237Np, ^241−243Am, ^247−249Bk with ERCS larger than 1 pb. Hopefully, the results will shed light on the experimental synthesis of new nuclides.