-
A strongly interacting hot and dense QCD matter called quark-gluon plasma (QGP) is created in the experiments with high-energy heavy-ion collisions at the Relativistic Heavy Ion Collider (RHIC) and the Large Hadron Collider (LHC) [1-6]. To understand the properties and phase structure of strongly interacting nuclear matter, the Beam Energy Scan (BES) program involving Au+Au collisions has been carried out at RHIC. Various observables have been measured such as the particle production ratios [7, 8], Hanbury-Brown-Twiss (HBT) terferometry [9], moments of the conserved quantities [10] and collective flow [11]. In this paper, we focus on the second harmonic of the collective flow,
$ v_{2} $ . Analyzing the anisotropic flow in nucleus-nucleus collisions is one of the most important directions in studying the properties of created matter [12-14], since it is sensitive to the pressure gradient, degrees of freedom, equation of state (EoS) [15, 16] and degree of thermalization in the early stages of nuclear collisions.Some interesting phenomena have been observed in heavy-ion collisions in the BES program. In particular, smaller
$ v_{2} $ for$ \overline{p} $ ,$ K^{-} $ and$ \pi^{+} $ than for p,$ K^{+} $ and$ \pi^{-} $ were observed, and these$ v_{2} $ differences decrease with increasing collision energy [17-21]. These interesting results were attributed to the different$ v_{2} $ of transported and produced quarks during the initial stage of heavy-ion collisions in Ref. [22]. It is argued that this effect results from quark transport from forward to middle rapidity. The authors assume that$ v_{2} $ of transported quarks is larger than of produced quarks. Thus, the different number of constituent quarks and anti-quarks in the particles and corresponding antiparticles leads to a systematically larger$ v_{2} $ for baryons compared to anti-baryons. The energy dependence is explained by the increase of nuclear stopping in heavy-ion collisions with decreasing collision energy [23]. In Ref. [24], it is suggested that the chiral magnetic effect induced by the strong magnetic field in non-central collisions could be responsible for the observed difference between$ v_{2} $ of$ \pi^{+} $ and$ \pi^{-} $ .A calculation [25, 26] based on the Nambu-Jona-Lasino(NJL) model can also qualitatively explain the differences between
$ p - \overline{p} $ ,$ \Lambda - \overline{\Lambda} $ and$ K^{+} - K^{-} $ by incorporting a repulsive potential for quarks and attractive potential for antiquarks, which results in different flow patterns. Another study [27] , based on the AMPT model including mean-field potential, can also qualitatively explain the difference between the elliptic flow of particles and their corresponding antiparticles. Due to the stronger attractive potential for$ \overline{p} $ compared to p, smaller$ v_{2} $ is obtained for$ \overline{p} $ . With the attractive potential for$ K^{-} $ and repulsive for$ K^{+} $ , and slightly attractive potential for$ \pi^{+} $ and repulsive for$ \pi^{-} $ , smaller$ v_{2} $ is obtained for$ K^{-} $ and$ \pi^{+} $ than for$ K^{+} $ and$ \pi^{-} $ .In this paper, we study the elliptic flow of protons with 3, 2, 1 and 0 initial quarks and anti-protons at BES energies with the ultra relativistic quantum molecular dynamics (UrQMD) model [28, 29]. The paper is organized as follows: in Section 2, the observable is introduced. A brief description of the UrQMD model is given in Section 3. The results and discussion are presented in Section 4. Finally, a summary is given in Section 5.
-
The azimuthal anisotropy is one of the most important observables in heavy-ion collisions. In the non-central heavy-ion collisions, the overlap region is an almond shape with the major axis perpendicular to the reaction plane, which is defined by the impact parameter and the beam direction. As the system evolves, the pressure gradient from the overlapping region of two nuclei in the collision is at the origin of collective motion at mid-rapidity. The anisotropy in the coordinate space is transferred to the anisotropy in the momentum space. The anisotropic parameters are defined by the Fourier coefficients of the expansion of the azimuthal distribution [30, 31] of the produced particles with respect to the reaction plane, which can be written as
$ E\frac{{{{\rm d}^3}N}}{{{\rm d}{p^3}}} = \frac{1}{{2\pi }}\frac{{{{\rm d}^2}N}}{{p_{{\rm T}}{\rm d}{p_{\rm T}}{\rm d}y}}\left(1 + 2\sum {{v_n}\cos [n(\phi-{\Psi _{{\rm{RP}}}})]} \right), $

(1) where
$ \phi $ is the azimuthal angle of the particles.$ \Psi_{\rm{RP}} $ is the reaction plane. The anisotropic parameter is defined as the$ n^{th} $ Fourier coefficient$ v_{n} $ :$ {v_n} = \left\langle {\cos [n(\phi-{\Psi _{{\rm{RP}}}})]} \right\rangle, $

(2) where
$ \left \langle \cdots \right \rangle $ is the average over all the particles in the sample. The second harmonic coefficient is denoted as elliptic flow$ v_{2} $ . In the UrQMD model,$ \Psi_{\rm{RP}} $ is fixed at zero degrees. -
The ultrarelativistic quantum molecular dynamics (UrQMD) model is a microscopic transport model which simulates p + p, p + A, and A + A collisions at relativistic energies, and describes the time-evolution of a many-body system using covariant equations of motion. It includes the string excitation and fragmentation, the formation and decay of hadronic resonances, and rescattering of hadrons. At low and intermediate energies, this microscopic transport model focuses on the interactions between known baryon and meson species and their resonances. The excitation and fragmentation of color strings play important roles in the particle production at high energies in the UrQMD model. The version of the UrQMD model we used in this study is 2.3, and no modification was made to the model itself, except for some additional output for tracing the particle origin as explained in ref. [32]. We marked particles as transported and produced by tracing the number of initial quarks in a particle. In this paper, protons with 3, 2, 1 and 0 initial quarks are marked as p (3 iq), p (2 iq), p (1 iq) and p (0 iq), respectively. There are two special cases. Protons with three initial quarks are treated as transported protons (p (3 iq)). Protons with zero initial quarks are treated as produced protons (p (0 iq)). Produced protons and anti-protons are both made of three produced quarks, thus they are expected to be similar in many aspects.
-
By tracing the number of initial quarks in a proton, p (3 iq) accounts for 17.4% at 7.7 GeV, 8.3% at 11.5 GeV, 1.26% at 39 GeV and 0.36% at 200 GeV of all protons and anti-protons at mid- rapidity (
$ |{Y}| < 1 $ ). p (2 iq) accounts for 80.8% at 7.7 GeV, 84% at 11.5 GeV, 52.83% at 39 GeV and 10.9% at 200 GeV. p (1 iq) accounts for 0.91% at 7.7 GeV, 3% at 11.5 GeV, 12.46% at 39 GeV and 14.4% at 200 GeV. p (0 iq) accounts for 0.45% at 7.7 GeV, 2.4% at 11.5 GeV, 15.4% at 39 GeV and 39.1% at 200 GeV.$ \overline{p} $ accounts for 0.44% at 7.7 GeV, 2.3% at 11.5 GeV, 18.05% at 39 GeV and 35.24% at 200 GeV. The upper panel of Fig. 1 shows the elliptic flow of p (3 iq), p (2 iq), p (1 iq), p (0 iq) and$ \overline{p} $ within$ 0.2 < p_{{\rm T}} < 2.0 $ GeV/c as a function of collision centrality in Au+Au collisions at various collision energies. One finds that$ v_{2} $ shows strong centrality dependence, since it is mainly driven by the initial spatial eccentricity. The lower panel shows the difference of$ v_{2} $ between p (3 iq), p (2 iq), p (1 iq), p (0 iq) and$ \overline{p} $ . The difference of$ v_{2} $ between p (0 iq) (produced) and$ \overline{p} $ does not clearly show the centrality dependence, and is approximately consistent with 0. As we mentioned above, p (0 iq) should be similar to$ \overline{p} $ in many aspects, as they are both made of produced quarks. p (0 iq) and$ \overline{p} $ are produced in the early stage of the system when the energy density is relatively large at low collision energies. Both p (0 iq) and$ \overline{p} $ experience the full evolution of the system, which leads to a similar magnitude of$ v_{2} $ . Larger elliptic flow of p (3 iq) than of p (0 iq) or of$ \overline{p} $ is observed. This suggests that$ v_{2} $ of p (3 iq) derives from the transport from forward rapidity to mid-rapidity due to the nuclear stopping effect. The transported quarks, which are transported over a large rapidity, suffer more scatterings than produced quarks, which results in a larger$ v_{2} $ , and leads to a larger$ v_{2} $ of p (3 iq) than of p (0 iq). The difference of$ v_{2} $ between p (3 iq) and$ \overline{p} $ shows a strong centrality dependence. A larger difference is observed in mid-central collisions than in most central and peripheral collisions at 7.7, 11.5 and 39 GeV. p (3 iq) experiences the whole process where the initial geometry eccentricity is transformed into anisotropy in the momentum space, whereas p (0 iq) may only partly experience this process. The combination of baryon stopping effect and scattering is the cause of the difference of$ v_{2} $ between the transported protons and anti-protons, largest in mid-central collisions. No significant centrality dependence is observed at 200 GeV due to the small difference of$ v_{2} $ between p (3 iq) and$ \overline{p} $ .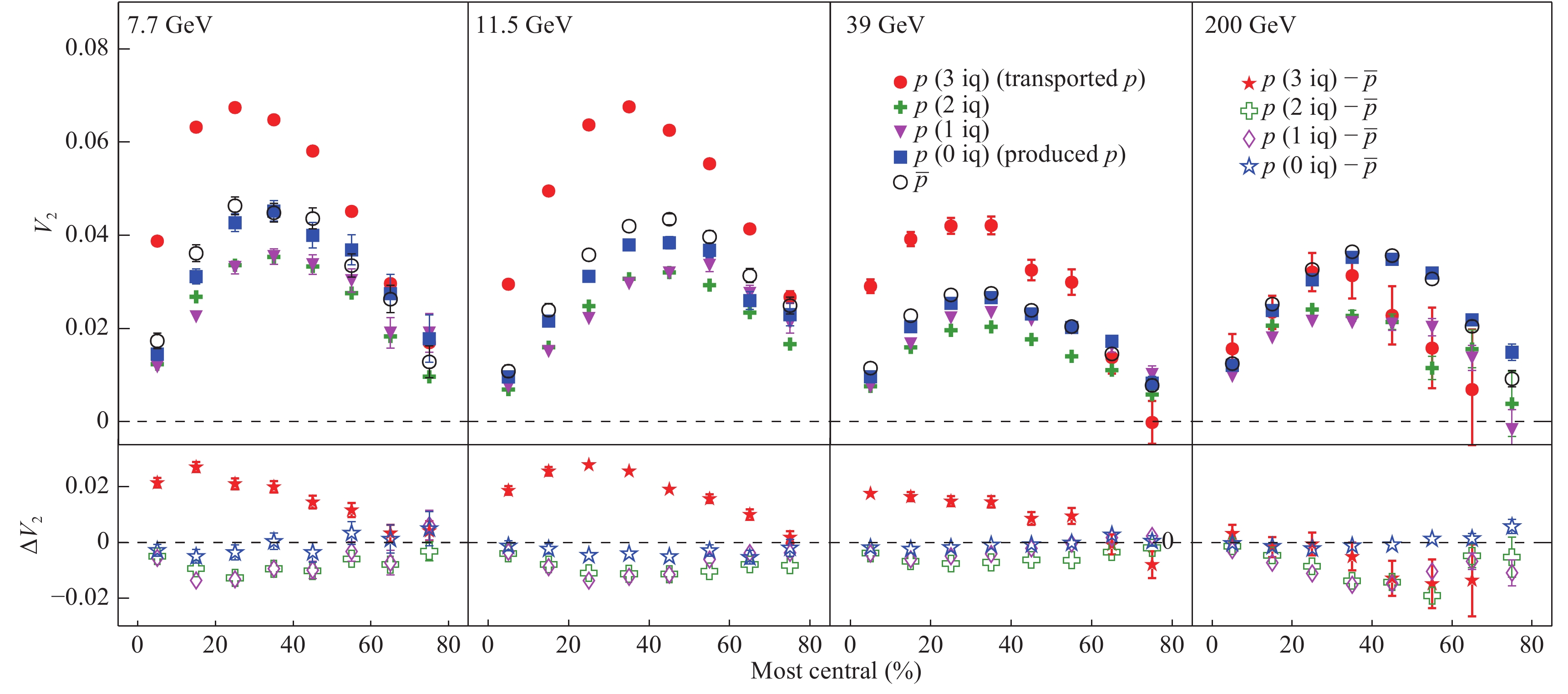
Figure 1. (color online) Upper panel: The elliptic flow of p (3 iq), p (2 iq), p (1 iq), p (0 iq) and
$ \overline{p} $ are plotted as a function of collison centrality in Au+Au collisions at$ \sqrt{s_{{\rm NN}}} $ = 7.7, 11.5, 39, 200 GeV. Lower panel: The difference of$ v_{2} $ between p (3 iq), p (2 iq), p (1 iq), p (0 iq) and$ \overline{p} $ as a function of collision centrality in Au+Au collisions at$ \sqrt{s_{{\rm NN}}} $ = 7.7, 11.5, 39, 200 GeV.The elliptic flow
$ v_{2} $ of p (2 iq) and p (1 iq) show similar centrality dependence as$ v_{2} $ of p (0 iq) and$ \overline{p} $ , but are systematically lower . p (0 iq), p (1 iq), p (2 iq) and$ \overline{p} $ are produced at the same time in the early stage via the string excitation scheme [32], but part of p (1 iq) and p (2 iq) are produced in the decay of unstable baryons. This means that the formation time of p (0 iq) and$ \overline{p} $ should be earlier than of p (1 iq) and p (2 iq). Hence, p (1 iq) and p (2 iq) suffer less interactions than p (0 iq) and$ \overline{p} $ .$ v_{2} $ of p (1 iq) and p (2 iq) are smaller than of p (0 iq) and$ \overline{p} $ . Thus, in the UrQMD model,$ v_{2} $ of the inclusive p is slightly lower than, or consistent with,$ v_{2} $ of$ \overline{p} $ , depending on the collision energy, which is consistent with the results in ref [33].The upper panel of Fig. 2 shows the elliptic flow of p (3 iq), p (2 iq), p (1 iq), p (0 iq) and
$ \overline{p} $ as a function of transverse momentum$ p_{{\rm T}} $ in 0%-80% Au+Au collisions at$ \sqrt{s_{{\rm NN}}} $ = 7.7, 11.5, 39, 200 GeV. The lower panel shows the difference of$ v_{2} $ between p (3 iq), p (2 iq), p (1 iq), p (0 iq) and$ \overline{p} $ . The difference of$ v_{2} $ between p (0 iq) and$ \overline{p} $ does not show a clear$ p_{{\rm T}} $ dependence, and is almost consistent with 0 , except at 7.7 GeV. However, the difference of$ v_{2} $ between p (3 iq) and$ \overline{p} $ shows a weak$ p_{{\rm T}} $ dependence. The splitting of$ v_{2} $ between p (3 iq) and p (0 iq) may be due to the stronger flow of transported quarks, which experience more interactions than produced quarks. This phenomenon is consistent with the study in ref [22], by assuming that$ v_{2} $ of transported quarks is larger than of produced quarks, and results in a splitting of$ v_{2} $ between protons and anti-protons.$ v_{2} $ of p (2 iq) and p (1 iq) increase with$ p_{{\rm T}} $ , but are systematically smaller than of p (3 iq), p (0 iq) and$ \overline{p} $ .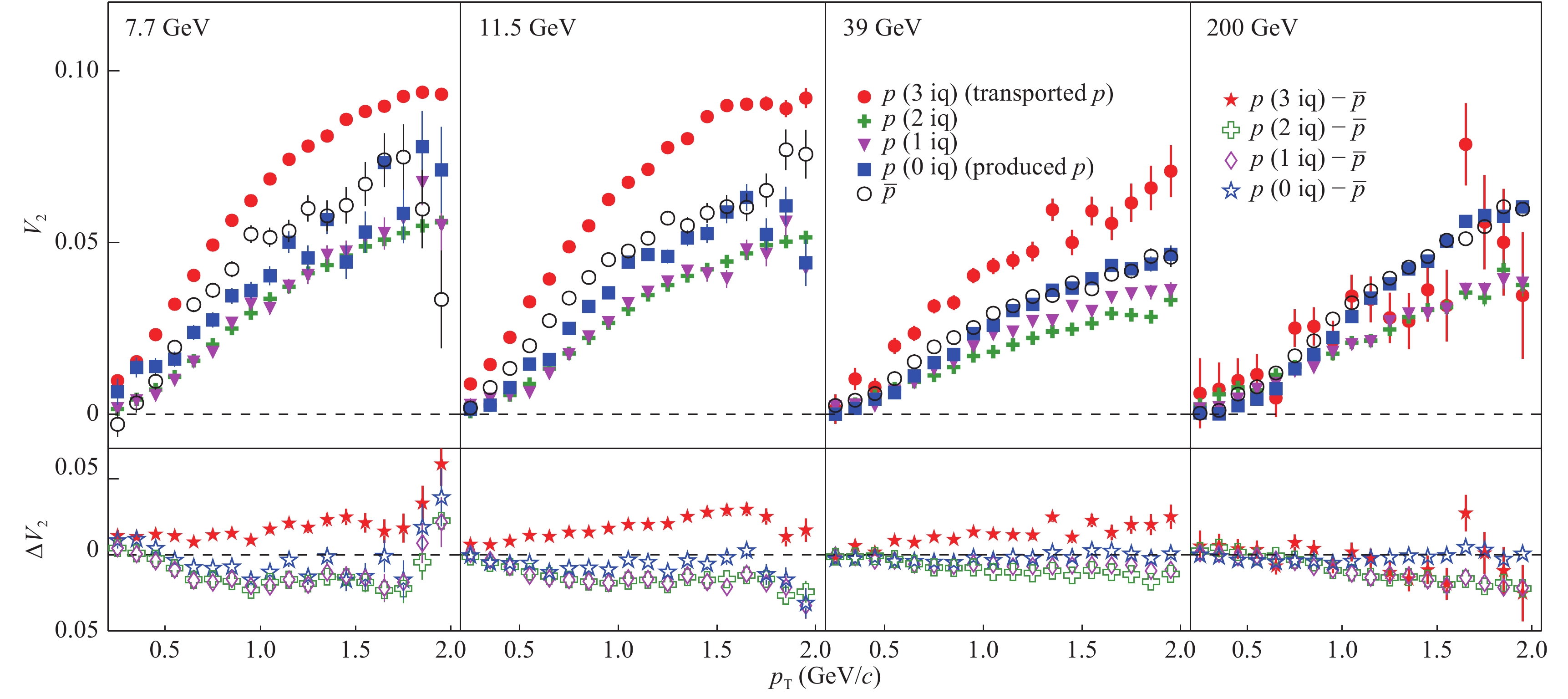
Figure 2. (color online) Upper panel: The elliptic flow of p (3 iq), p (2 iq), p (1 iq), p (0 iq) and
$ \overline{p} $ as a function of the transverse momentum$ p_{{\rm T}} $ for 0%-80% central Au+Au collisions at$ \sqrt{s_{{\rm NN}}} $ = 7.7, 11.5, 39, 200 GeV. The lower panels show the difference of$ v_{2}(p_{{\rm T}}) $ between p (3 iq), p (2 iq), p (1 iq), p (0 iq) and$ \overline{p} $ .In order to compare with the STAR results, we calculate the integrated elliptic flow
$ v_{2} $ of p (3 iq), p (2 iq), p (1 iq), p (0 iq) and$ \overline{p} $ in the interval$ 0.2 < p_{{\rm T}} < 2.0 $ GeV/c . In Fig. 3, panel (a) shows the integrated elliptic flow$ v_{2} $ of p (3 iq), p (2 iq), p (1 iq), p (0 iq) and, panel (b) shows the difference in$ v_{2} $ between the STAR measurements and the UrQMD model, as function of the collision energy in Au+Au collisions.$ v_{2} $ of p (3 iq) is systematically larger than of p (0 iq) and$ \overline{p} $ . Thus, the$ v_{2} $ difference between p (3 iq) and$ \overline{p} $ is larger than 0. The$ v_{2} $ difference between p (0 iq) and$ \overline{p} $ is slightly smaller than 0, or consistent with 0, depending on the collision energy.$ v_{2} $ of p (2 iq) and p (1 iq) are systematically smaller than of p (3 iq), p (0 iq) and$ \overline{p} $ . Therefore, the difference of$ v_{2} $ between p (2 iq)/p (1 iq) and$ \overline{p} $ is smaller than 0. The difference of$ v_2 $ between p (3 iq) and$ \overline{p} $ shows a similar energy dependence as the STAR results. Our results for p (3 iq) -$ \overline{p} $ show good agreement with the STAR results below 11.5 GeV. At 39 GeV, the$ v_{2} $ difference of p (3 iq) and$ \overline{p} $ is not consistent with the STAR results quantitatively. The yield of p (3 iq) is relatively smaller than of p (2 iq) and p (1 iq), and$ v_{2} $ of all protons is much smaller than the STAR result. This indicates that the$ v_{2} $ difference with respect to STAR measurements may be partly due to the$ v_{2} $ difference between p (3 iq) and$ \overline{p} $ . However, it can not explain the STAR results. In principle, the yield of p (3 iq) dominates the yield of protons at low energies. The magnitude of the$ v_{2} $ difference p (3 iq) -$ \overline{p} $ , as the STAR data and the UrQMD model are consistent for Au+Au collisions at 7.7 and 11.5 GeV, suggests that the hadronic interactions are dominant at these collision energies. The$ v_{2} $ difference between the STAR results and our calculations at 39 GeV indicates that the partonic interactions are also important for the increase of$ v_{2} $ at high energies. Additionally, the fact that the fraction of p (3 iq) relative to inclusive protons decreases with increasing energy, can also lead to such a difference.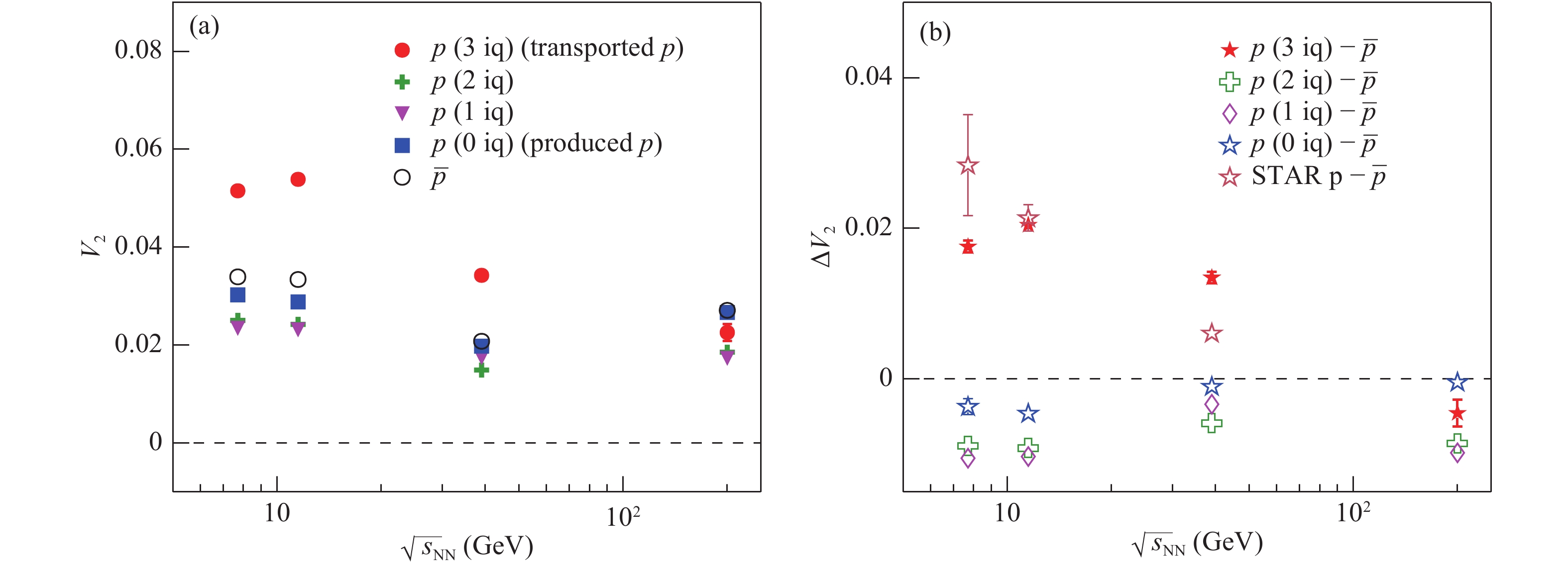
Figure 3. (color online) Panel (a): The integrated
$ v_{2} $ of p (3 iq), p (2 iq), p (1 iq), p (0 iq) and$ \overline{p} $ as a function of collision energy for 0%-80% central Au+Au collisions. Panel (b): The difference in$ v_{2} $ between p (3 iq), p (2 iq), p (1 iq), p (0 iq) and$ \overline{p} $ as a function of collision energy for 0%-80% central Au + Au collisions. -
In summary, by tracing the number of initial quarks in the UrQMD model, p (3 iq), p (2 iq), p (1 iq), p (0 iq) can be distinguished, which provides a way to study the elliptic flow of transported protons and produced protons. We found that the elliptic flow of produced protons shows similar dependence on collision centrality, transverse momentum and collision energy as of anti-protons. The possible explanation is that produced protons and anti-protons are both made of produced quarks. At the same time, the produced protons and anti-protons can only be produced at the early stage of the hadronic evolution of the system. Both experience similar magnitude of interactions in the system, which leads to similar
$ v_{2} $ . For transported protons, the elliptic flow is systematically larger than for anti-protons as a function of collision centrality, transverse momentum and collision energy. This can be explained as following: quarks transported from forward rapidity to mid-rapidity by the baryon stopping effect gain larger$ v_{2} $ than produced quarks.$ v_{2} $ of p (2 iq) and p (1 iq) are systematically smaller than of transported protons, produced protons and anti-protons. Our results with the UrQMD model indicate that the splitting of$ v_{2} $ for protons may partly arise from the difference of$ v_{2} $ between transported quarks and produced quarks. The difference of$ v_{2} $ between transported protons with 3 initial quarks and anti-protons shows good quantitative agreement with that between protons and anti-protons in the STAR measurements at low energies (7.7 and 11.5 GeV), but also large deviation at high energies (≥ 39 GeV). This suggests that hadronic interactions are dominant in collisions at 7.7 and 11.5 GeV. Without partonic interactions in the UrQMD model, it is problematic to reproduce$ v_{2} $ at high energies (≥ 39 GeV). On the other hand, the fraction of transported protons relative to inclusive protons may also contribute to the difference between the STAR data and the UrQMD model.
Elliptic flow of transported and produced protons in Au+Au collisions with the UrQMD model
- Received Date: 2018-11-19
- Accepted Date: 2019-02-25
- Available Online: 2019-05-01
Abstract: Within the framework of the UrQMD model, by tracing the number of initial quarks in protons, we study the elliptic flow of protons with 3, 2, 1, 0 initial quarks and anti-protons in Au+Au collisions at





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF
















 DownLoad:
DownLoad: