-
It is widely believed that with the increase of temperature and/or chemical potential, the strongly-interacting matter undergoes a phase transition from hadronic matter to quark-gluon plasma (QGP), which can be studied in relativistic heavy-ion collisions (RHIC) at CERN (France/Switzerland), BNL (USA), and GSI (Germany) [1, 2]. Theoretically, on the one hand, ab initio lattice QCD [3] simulations found that the transition is a crossover at low chemical potential. On the other hand, QCD effective model [4, 5] calculations generally indicate that the phase transition is of first order at high chemical potential, and that in the middle range of chemical potential there exists a critical end point (CEP) where the first order phase transition stops. One of the important goals in RHIC is to determine the existence and the location of CEP. For this purpose, the second phase of the beam energy scan at RHIC (BNL) will be performed between 2019 and 2021 [6].
It should be noted that many previous calculations of the location of CEP are based on an infinite thermodynamical system. However, the QGP system produced in RHIC has undoubtedly a finite volume. The homogeneous volume before freeze-out in Au-Au and Pb-Pb collisions ranges between approximately
$ 50\sim250 $ fm3 [7], based on the UrQMD transport approach [8]. The smallest quark-gluon plasma (QGP) system produced in RHIC could be as small as 2 fm3 , as estimated in Ref. [9]. Therefore, a theoretical study of whether the finite volume has a significant impact on CEP is important for a RHIC experiment, and it has been studied within the Nambu-Jona-Lasinio (NJL) model [10], Polyakov-Nambu-Jona-Lasinio (PNJL) model [11, 12], quark-meson model [13] and Dyson-Schwinger equations (DSEs) [14-16].It is well known that when the volume of a strongly interacting system is small enough, not only its size but also its shape have an important impact on the QCD phase transition. However, it should be noted that in most calculations, for the sake of convenience, a cube was used to simulate the fireball produced in RHIC, thus ignoring the influence of different shapes on the phase transition. Therefore, in order to get closer to the real shape of the fireball produced in a RHIC experiment, we use a sphere to study, by means of MRE [17], the finite volume phase transition in the DSE framework. Compared to the other effective models, DSE takes quarks and gluons as the fundamental degrees of freedom, and includes both the confinement and dynamical chiral symmetry breaking (DCSB) effects. It has also provided many insights into the QCD phase diagram, for instance, the chiral and deconfinement phase transition [18-20].
This paper is organized as follows: In Sec. 2, we give a brief introduction to the quark gap equation in a finite spherical volume at finite temperature and finite chemical potential. In Sec. 3, we study the effect of finite volume on the chiral phase transition, especially its influence on the behavior of CEP. Finally, we give a brief summary in Sec. 4.
-
DSE is a suitable QCD-connected non-perturbative method and it is widely used in the studies of hadron physics [21,22] and QCD phase diagram. At zero temperature and zero chemical potential, DSE of the quark propagator, namely the quark gap equation, reads [16]①
$ S(p)^{-1} = S_{0}(p)^{-1}+\frac{4}{3}\int\frac{{\rm d}^{4}q}{(2\pi)^4}g^{2}D_{\mu\nu}(p-q)\gamma_{\mu}S(q)\Gamma_{\nu},$

(1) where
$ S(p)^{-1} $ is the inverse of the dressed quark propagator, and$ S_{0}(p)^{-1} $ is the inverse of the free quark propagator.$ g $ is the coupling constant of strong interaction,$ D_{\mu\nu}(p-q) $ is the dressed gluon propagator, and$ \Gamma_{\nu} $ is the one-particle irreducible quark-gluon vertex. According to the Lorentz structure analysis,$ S(p)^{-1} $ can generally be decomposed as [23]$ S(p)^{-1} = i{\not\!p}A(p^{2})+B(p^{2}), $

(2) where
$ A(p^{2}) $ and$ B(p^{2}) $ are scalar functions of$ p^{2} $ . Note that for the free quark propagator$ S_{0}(p)^{-1} $ , the scalar functions are$ A = 1, B = m $ .Next, we extend the quark gap equation to finite
$ T $ and$ \mu $ , so that it reads$ \begin{split} S(\vec{p},\tilde{\omega}_{n})^{-1} = &S_{0}(\vec{p},\tilde{\omega}_{n})^{-1}+\frac{4}{3}T\int\!\!\!\!\!\!\!\!\!\!\!\!\sum g^{2}\\ &\times D_{\mu\nu}(\vec{k},\Omega_{nl})\gamma_{\mu}S(\vec{q},\tilde{\omega}_{l})\Gamma_{\nu}, \end{split} $

(3) where
$S_{0}(\vec{p},\tilde{\omega}_{n})^{-1} = i\vec{\gamma}\cdot \vec{p}+i\gamma_{4}\tilde{\omega}_{n}+m, $

(4) $ \vec{k} = \vec{p}-\vec{q} $ ,$ \Omega_{nl} = \omega_{n}-\omega_{l} $ ,$ \tilde{\omega}_{n} = \omega_{n}+i\mu $ ,$ \omega_{n} = (2n+1)\pi T, $ $ n\in \bf{Z} $ and$ \displaystyle\int\!\!\!\!\!\!\!\!\!\!\!\!\sum $ denotes$ {\sum_{l}}\int\displaystyle\frac{{\rm d}^{3}\vec{q}}{(2\pi)^3} $ . Due to the breaking of$ O(4) $ symmetry down to$ O(3) $ symmetry, the Lorentz structure of$ S(\vec{p},\tilde{\omega}_{n})^{-1} $ is now decomposed as$ \begin{split} S(\vec{p},\tilde{\omega}_{n})^{-1} = & i{\not\!\!\vec{p}}A(\vec{p},\tilde{\omega}_{n})+{\bf{1}}B(\vec{p},\tilde{\omega}_{n})\\ &+i\gamma_{4}\tilde{\omega}_{n}C(\vec{p},\tilde{\omega}_{n})+{\not\!\!\vec{p}}\gamma_{4}\tilde{\omega}_{n}D(\vec{p},\tilde{\omega}_{n}) \end{split}, $

(5) where
$ {\not\!\!\vec{p}} = \vec{\gamma}\cdot\vec{p} $ ,$ \vec{\gamma} = (\gamma_{1}, \gamma_{2}, \gamma_{3}) $ , and the four scalar functions$ F = A, B, C, D $ are complex and satisfy the condition$ F(\vec{p},\tilde{\omega}_{n})^{\ast} = F(\vec{p},\tilde{\omega}_{-n-1}), $

(6) which can be used to verify the accuracy of numerical calculations. In our calculations, we ignore the function
$ D $ because it is power-law suppressed in the ultra-violet region. At zero$ T $ but finite$ \mu $ ,$ D $ vanishes exactly, as shown in [24], because the corresponding tensor has incorrect transformation properties under time reversal. As a result, the widely used structure of$ S(\vec{p},\tilde{\omega}_{n})^{-1} $ is as follows$ \begin{split} S(\vec{p},\tilde{\omega}_{n})^{-1} = &i{\not\!\!\vec{p}}A(\vec{p},\tilde{\omega}_{n})+{\bf{1}}B(\vec{p},\tilde{\omega}_{n})\\ &+i\gamma_{4}\tilde{\omega}_{n}C(\vec{p},\tilde{\omega}_{n}), \end{split} $

(7) We are now ready to introduce the quark gap equation in a finite spherical volume, and for taking the finite volume effects into account we consider the MRE formalism [25-27], which modifies the density of states as follows
$ \rho_{\rm MRE}(p,m,R) = 1+\frac{6\pi^{2}}{pR}f_{S}+\frac{12\pi^{2}}{(pR)^{2}}f_{C}, $

(8) where
$ f_{S} $ denotes the surface contribution to the density of states$ f_{S} = -\frac{1}{8\pi}\left(1-\frac{2}{\pi}\arctan\frac{p}{m}\right), $

(9) The curvature contribution is given by Madsen
$ ^{,} $ s ansatz [27]$ f_{C} = \frac{1}{12\pi^{2}}\left[1-\frac{3p}{2m}\left(\frac{\pi}{2}-\arctan \frac{p}{m}\right)\right], $

(10) which takes into account the finite quark mass. It should be noted that there are different interpretations of
$ m $ in the MRE formula when applied to non-perturbative calculations, for example, in the (P)NJL model, see Refs. [25,26,28]. In this paper, we treat$ m $ as the current quark mass, Refs. [26,28] , instead of the constitute quark mass, Ref. [25].For
$ m\neq 0 $ , the main problem with MRE is that it predicts a negative density of states for small$ p $ , when in reality there are no states at all [29]. Therefore, we introduce the IR cutoff ($ \Lambda_{\rm IR} $ ) in the momentum space, as in Refs. [26,28]. Actually, for anti-periodic boundary conditions in spatial directions, in a cubic box of size$ L $ , we have$ \vec{p}^{2} = \displaystyle\frac{4\pi^{2}}{L^{2}}\sum_{i = 1}^{3}\left(n_{i}+\displaystyle\frac{1}{2}\right)^{2} $ ,$ n_{i} = 0, \pm1, \pm2 \cdot\cdot\cdot $ . The minimum momentum is$ |p_{\min}| = \displaystyle\frac{\pi}{L} $ , similar to$ \Lambda_{\rm IR} $ . In our calculations, the following replacement must be performed.$ \int_{0}^{\Lambda,\infty}\frac{ {\rm d}^{3}\vec{p}}{(2\pi)^3}\cdots\rightarrow\int_{\Lambda_{\rm IR}}^{\Lambda,\infty}\frac{ {\rm d}^{3}\vec{p}}{(2\pi)^3}\rho_{\rm MRE}\cdots, $

(11) where
$ \Lambda_{\rm IR} $ is the largest solution of the equation$ \rho_{\rm MRE}(p,m,R) = 0 $ with respect to momentum$ p $ . Thus, in a finite spherical volume, the quark gap equation becomes$ \begin{split} S(\vec{p},\tilde{\omega}_{n})_{F}^{-1} = &S_{0}(\vec{p},\tilde{\omega}_{n})^{-1}+\frac{4}{3}T\int\!\!\!\!\!\!\!\!\!\!\!\!\sum_{f}g^{2}\rho_{\rm MRE}\\ &\times D_{\mu\nu}(\vec{k},\Omega_{nl})\gamma_{\mu}S(\vec{q},\tilde{\omega}_{l})\Gamma_{\nu}, \end{split} $

(12) where now
$ \displaystyle\int\!\!\!\!\!\!\!\!\!\!\!\!\sum_{f} $ denotes$ \sum_{l}\displaystyle\int_{\Lambda_{\rm IR}}\displaystyle\frac{{\rm d}^{3}\vec{p}}{(2\pi)^3} $ .To solve the quark gap equation, truncations are inevitable. Here, we employ the Rainbow truncation [30,31]
$ \Gamma_{\mu}(p_{n},q_{l}) = \gamma_{\mu}, $

(13) which is widely used in the studies of hadron physics and QCD phase diagram. We also employ the widely used gluon propagator, as in Refs. [32-34], which has the form
$ g^{2}D_{\mu\nu}(k_{\Omega}) = {\cal{G}}(k_{\Omega}^{2})(\delta_{\mu\nu}-k_{\Omega}^{\mu}k_{\Omega}^{\mu}/k_{\Omega}^{2}), $

(14) where
$ {\cal{G}}(k_{\Omega}^{2}) = \frac{4\pi^{2}}{\omega^{6}}D_{0}k_{\Omega}^{2}{\rm e}^{-k_{\Omega}^{2}/\omega^{2}}, $

(15) and
$ k_{\Omega} = (\vec{k},\Omega_{nl}) $ ,$ \delta_{\mu\nu} $ = diag{+1,+1,+1,+1}.The related parameters,
$ D_{0} $ and$ \omega $ , are usually fixed by observables in hadron physics: the pion mass$ m_{\pi}$ = 0.139 GeV and the pion decay constant$ f_{\pi}$ = 0.095 GeV. Here, we use the typical values, that is$ \omega$ = 0.5 GeV,$D_{0} $ = 1.0 GeV2 [15] , and the current quark mass$ m $ = 0.005 GeV. -
In this section, we study the chiral phase transition in a finite spherical volume, and especially discuss its influence on the location of CEP. We first solve the quark gap equation. The procedure is to insert Eqs. (7,13,14,15) into Eq. (12), multiply each side by
$ -i{\not\!\!\vec{p}} $ ,$ -i\gamma_{4}\tilde{\omega}_{n} $ and$ {\bf{1}}_{4} $ , respectively, and then take the trace on both sides. Note that$ S(\vec{p},\tilde{\omega}_{n}) $ and$ S(\vec{p},\tilde{\omega}_{n})^{-1} $ have the same Lorentz structure. The coupled non-linear equations for the scalar functions$ A, B, C $ can then be obtained as follows$ A_{pn} = 1+\frac{4T}{3\vec{p}^{2}}\int\!\!\!\!\!\!\!\!\!\!\!\!\sum_{f}\rho_{\rm MRE}\frac{{\cal{G}}(k_{\Omega}^{2})}{\vec{q}^{2}A^{2}_{ql}+\tilde{\omega}_{l}^{2}C^{2}_{ql}+B^{2}_{ql}}\left\{A_{ql}\left[\vec{p}\cdot\vec{q}+\frac{2(\vec{k}\cdot\vec{p})(\vec{k}\cdot\vec{q})}{k^{2}}\right]+C_{ql}\frac{2\tilde{\omega}_{l}\Omega_{nl}(\vec{k}\cdot\vec{p})}{k^{2}}\right\}, $

(16) $ C_{pn} = 1+\frac{4T}{3\tilde{\omega}_{n}}\int\!\!\!\!\!\!\!\!\!\!\!\!\sum_{f}\rho_{\rm MRE}\frac{{\cal{G}}(k_{\Omega}^{2})}{\vec{q}^{2}A^{2}_{ql}+\tilde{\omega}_{l}^{2}C^{2}_{ql}+B^{2}_{ql}}\left\{A_{ql}\frac{2\Omega_{nl}(\vec{k}\cdot\vec{q})}{k^{2}}+C_{ql}\tilde{\omega}_{l}\left(1+\frac{2\Omega_{nl}^{2}}{k^{2}}\right)\right\} , $

(17) $ B_{pn} = m+\frac{4T}{3}\int\!\!\!\!\!\!\!\!\!\!\!\!\sum_{f}\rho_{\rm MRE}\frac{3{\cal{G}}(k_{\Omega}^{2})B_{ql}}{\vec{q}^{2}A^{2}_{ql}+\tilde{\omega}_{l}^{2}C^{2}_{ql}+B^{2}_{ql}}. $

(18) These coupled equations can be numerically solved by iteration. In Fig. 1, we show
$ B(0,\tilde{\omega}_{0}^{2}) $ as a function of$ T $ for three different volumes. We find that$ B(0,\tilde{\omega}_{0}^{2}) $ decreases continuously with increasing temperature, which means that the transition is a crossover. Furthermore,$ B(0,\tilde{\omega}_{0}) $ decreases as the volume decreases. For example, at$ T$ = 0.05 GeV, we find that$ B(0,\tilde{\omega}_{0}) $ reduces from 0.525 GeV to 0.473 GeV, which means that the DCSB effect becomes weak. This is consistent with the other calculations [12].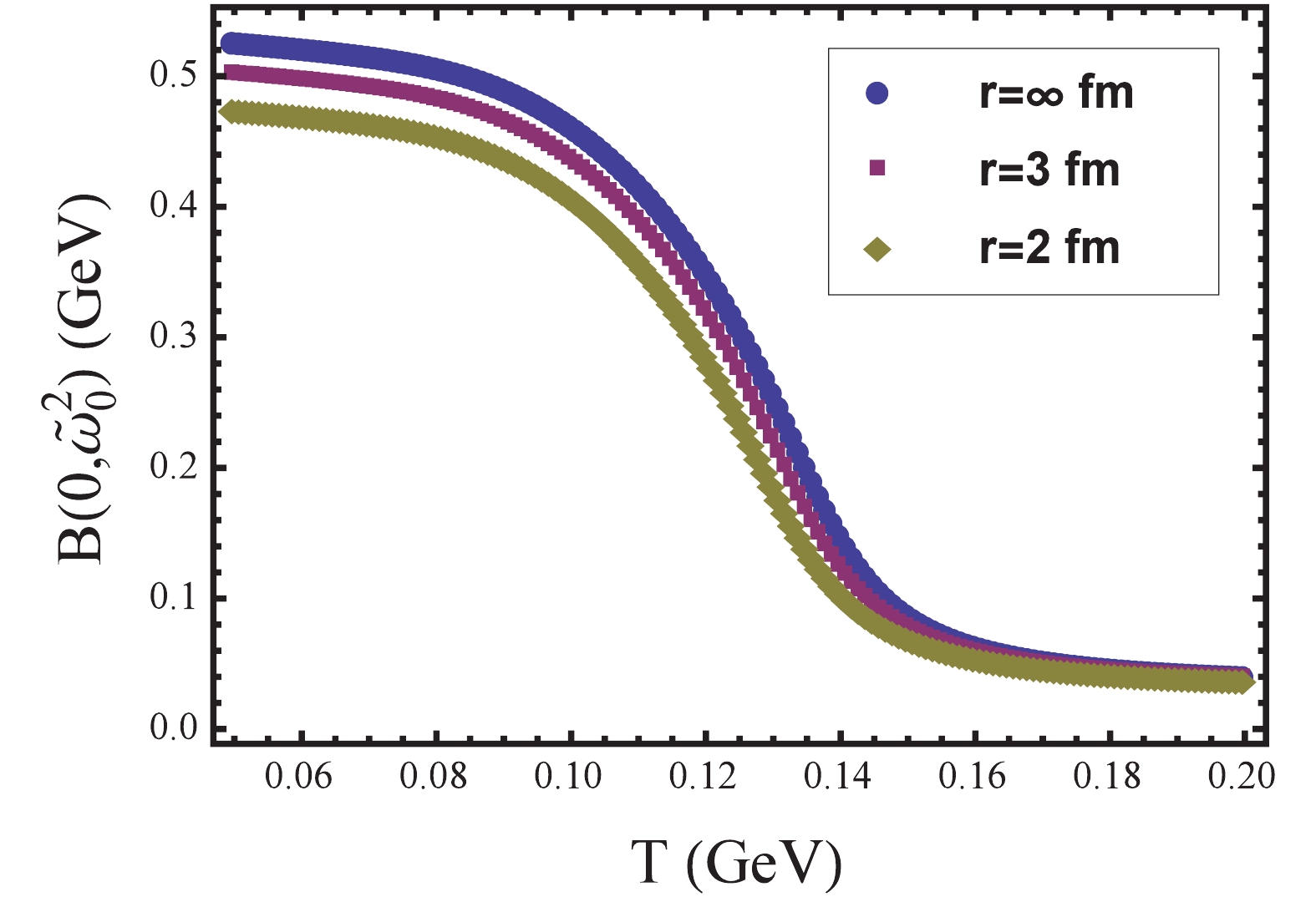
Figure 1. (color online)
$ B(0,\tilde{\omega}_{0}^{2}) $ as a function of$ T $ at$ \mu = 0 $ for three different radii$ r $ .The crossover behavior can be further studied by the chiral susceptibility which is defind as [35]
$ \chi_{m}(T,\mu) = \frac{\partial B(0,\tilde{\omega}_{0}^{2})}{\partial m} $

(19) Its volume dependence is plotted in Fig. 2. We find that the critical temperature
$ T_{c} $ shows a slight volume dependence as it only decreases from 0.14 GeV to 0.135 GeV. We conclude that at zero chemical potential and finite temperature, the influence of finite volume on chiral phase transition is not so obvious. In Fig. 3, we plot$ B(0,\tilde{\omega}_{0}^{2}) $ as a function of$ \mu $ at$ T $ = 0.09 GeV for three different volumes. At infinite volume, there appears a sudden discontinuity in$ B(0,\tilde{\omega}_{0}^{2}) $ at a critical value$ \mu_{c} $ = 0.275 GeV, which indicates a first order phase transition. However, when the radius is reduced to 2 fm,$ B(0,\tilde{\omega}_{0}^{2}) $ changes continuously and a crossover occurrs. This indicates that below$ T$ = 0.09 GeV, the finite size has a significant impact on the phase diagram, i.e. on the location of CEP.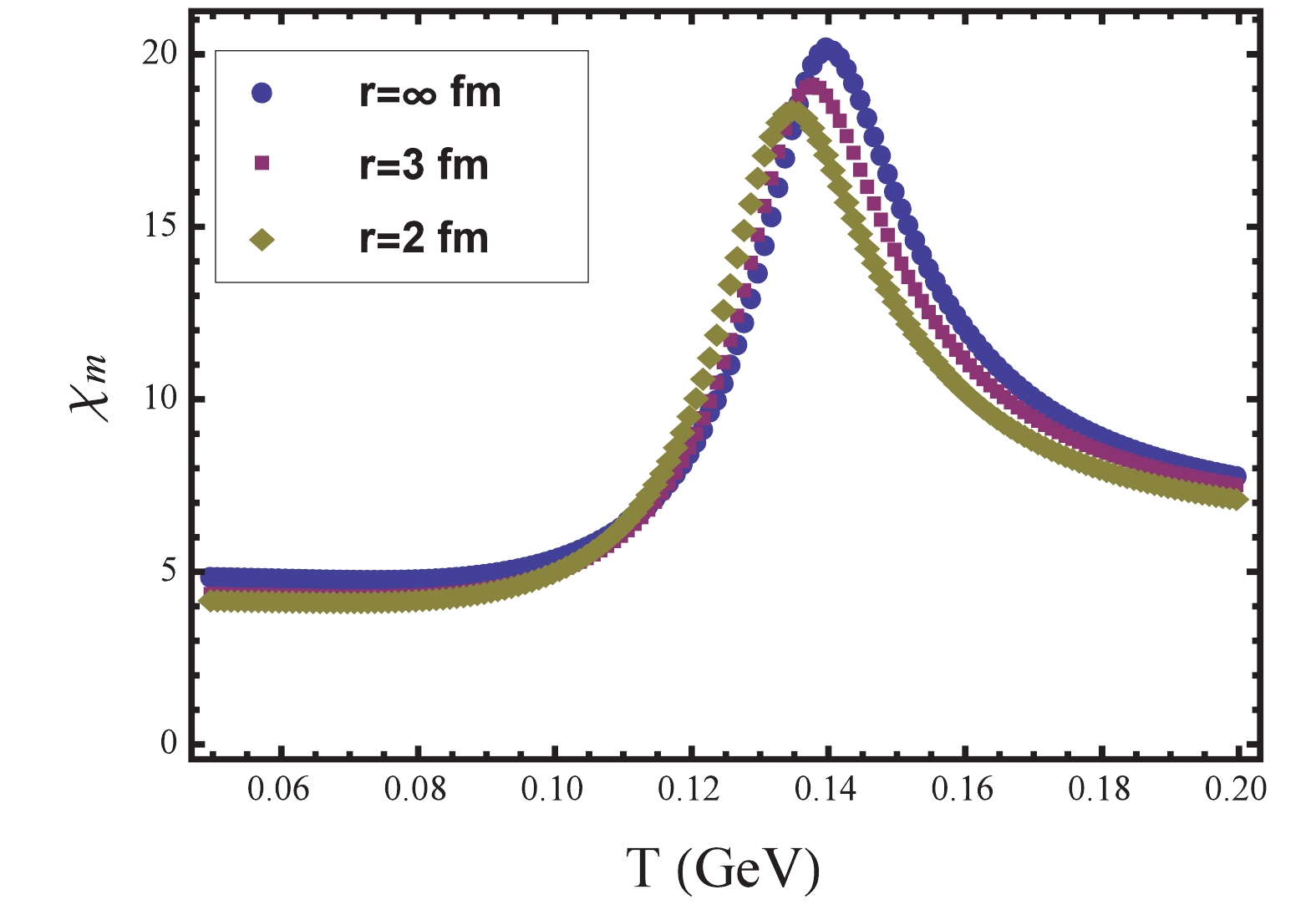
Figure 2. (color online) Chiral susceptibility
$ \chi_{m} $ as a function of$ T $ at$ \mu = 0 $ for three different radii$ r $ .
Figure 3. (color online)
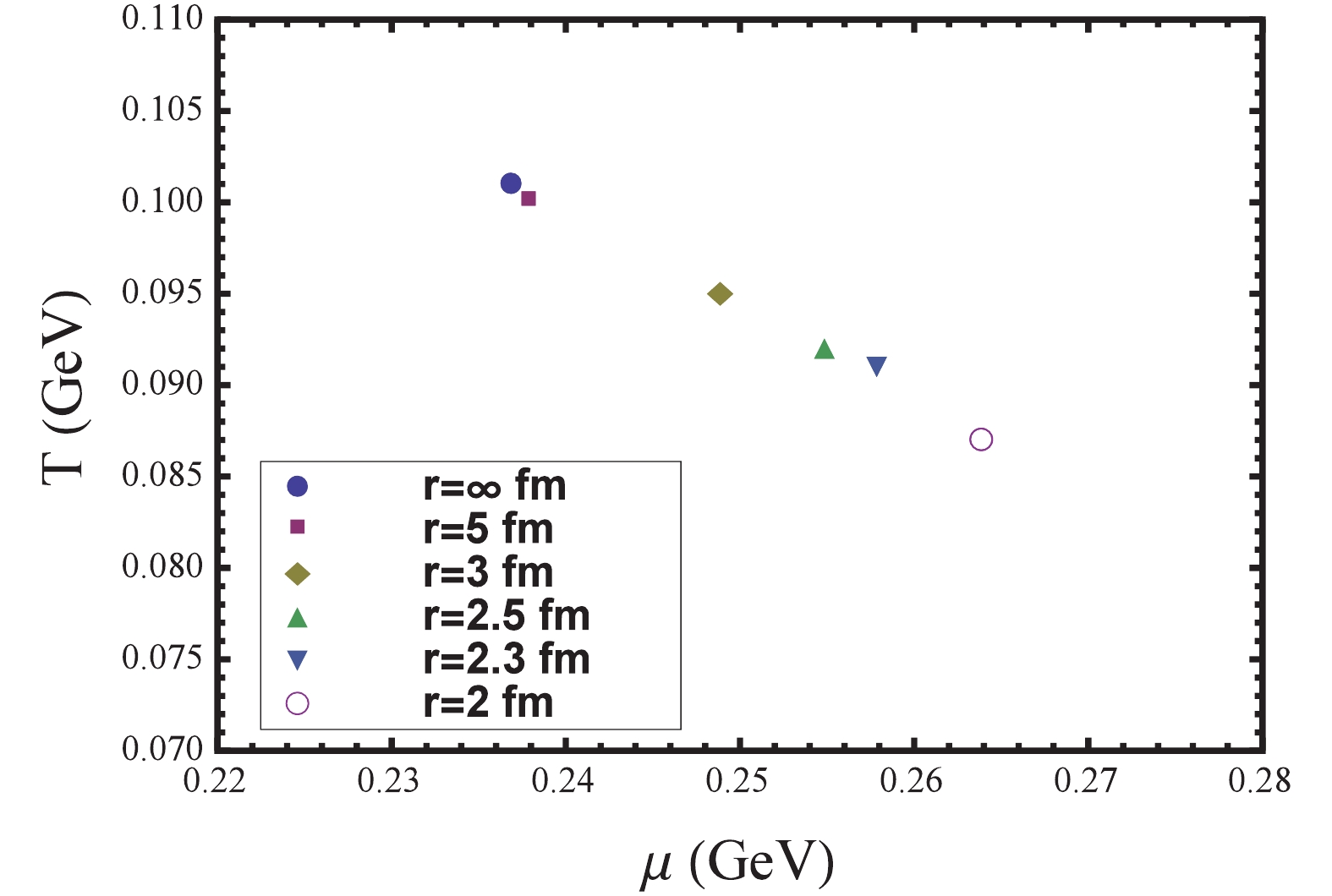
$ B(0,\tilde{\omega}_{0}^{2}) $ as a function of$ \mu $ at$ T$ = 0.09 GeV for three different radii$ r $ .We plot the volume dependence of CEP in Fig. 4. We see that when the radius of spherical volume is larger than 5 fm, the chiral phase diagram is almost the same as for the infinite system. As the radius of spherical volume decreases, we note that CEP shifts towards smaller temperature and higher chemical potential. Thus, for CEP search in RHIC experiments, according to our calculations, when the radius is below 3 fm, the finite volume effects may not be negligible. However, even if the radius is as small as 2 fm, the location of CEP shifts from
$ (\mu_{E},T_{E})$ = (0.237 GeV, 0.101 GeV) to$ (\mu_{E},T_{E})$ = (0.264 GeV, 0.087 GeV) , and the variation does not exceed 20%. It is interesting to compare our results with the other DSE calculations [14,15]. The main difference is that when we take a sphere instead of a cube, we find that the influence of finite volume on phase transitions is much weaker. For instance, in Ref. [15], CEP moves from$ (\mu_{E},T_{E}) $ = (0.24 GeV, 0.10 GeV) at$ L = \infty $ to$ (\mu_{E},T_{E}) $ = (0.37 GeV, 0.025 GeV) at$ L$ = 2.1 fm, and the variation is more than 60%. In Ref. [14], the variation is more than 70%. This reflects the fact that when we study the influence of finite volume on QCD phase transition, we should consider not only the size but also the shape of the volume. Finally, our result is slightly different from the PNJL model [12] , in which the value of$ \mu $ of CEP is almost constant. -
Within the framework of DSE, we consider, for the first time, the influence of the finite volume on the chiral phase transition in a sphere. For taking the finite volume effects into account, we consider the MRE formalism, in which the surface and curvature effects are also properly incorporated. This formalism has been used to study the thermodynamic quantities in the PNJL model [36], and color superconductivity in the NJL model [26]. Our main conclusion is that not only the size of the volume but also its shape have a sizable impact on the phase transition. In relative terms, we find that the influence of finite volume on chiral phase transition in a sphere is not as significant as in a cube. For example, at zero chemical potential and finite temperature,
$ T_{c} $ remains almost the same as the volume decreases. At finite chemical potential and finite temperature, our results show that as the radius of the spherical volume decreases, the location of CEP shifts toward smaller temperature and higher chemical potential. However, the amplitude of the variation does not exceed 20%. Therefore, we should use a shape which is closer to that of the QGP fireball produced in RHIC to better study the finite volume phase transition. Finally, as the next step, we intend to go beyond the bare vertex approximation [37,38] to see if there are any differences.
Chiral phase transition from the Dyson-Schwinger equations in a finite spherical volume
- Received Date: 2019-02-18
- Available Online: 2019-06-01
Abstract: Within the framework of the Dyson-Schwinger equations and by means of Multiple Reflection Expansion, we study the effect of finite volume on the chiral phase transition in a sphere, and discuss in particular its influence on the possible location of the critical end point (CEP). According to our calculations, when we take a sphere instead of a cube, the influence of finite volume on phase transition is not as significant as previously calculated. For instance, as the radius of the spherical volume decreases from infinite to 2 fm, the critical temperature






 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF














 DownLoad:
DownLoad: