-
One of the main fields of precision examination of the perturbative Quantum Chromodynamics (QCD) is the study of hadron production with momentum p (
$ p^2 = m_H^2 $ ) at large transverse momentum$ p_T $ , where$ p_T^2 >> m_H^2 $ . At the leading power of$ 1/p_T $ , the fragmentation mechanism may be dominant so that the differential cross-section can be factorized as (for reviews, see [1-4])$\begin{split} {E_p}\frac{{{\rm d}{\sigma _{A + B \to H + X}}}}{{{{\rm d}^3}p}} \approx & \sum\limits_f {\int {\frac{{{\rm d}z}}{{{z^2}}}} } {D_{f \to H}}(z;\mu ){E_c}\\ & \times \frac{{{\rm d}{\sigma _{A + B \to f({p_c}) + X}}}}{{{{\rm d}^3}p}}\left( {{p_c} = \frac{1}{z}p} \right) ,\end{split}$

(1) where the parton-level differential cross-section
$ {\rm d}\sigma_{A+B\to f(p_c)+X} $ contains the short-distance dynamics, and$ D_{f\to H}(z;\mu) $ is the so-called single parton fragmentation function (FF) of a hadron H from parton f , parametrizing the universal hadronization effects [5, 6]. Generally, the fragmentation functions are non-perturbative, but their renormalized scale-dependence is perturbatively calculable, and can be described by the famous Dokshitzer-Gribov-Lipatov-Altarelli-Parisi (DGLAP) equations which also govern the renormalization group (RG) running of the parton distribution functions (PDFs)$\begin{split}{\mu ^2}\frac{\rm d}{{{\rm d}{\mu ^2}}}{D_{f \to H}}(z;\mu ) = &\sum\limits_{{f^\prime }} {\int_z^1 {\frac{{{\rm d}{z^\prime }}}{{{z^\prime }}}} } {P_{f \leftarrow {f^\prime }}}(z/{z^\prime },{\alpha _s}(\mu ))\\ &\times{D_{{f^\prime } \to H}}({z^\prime };\mu ) ,\end{split}$

(2) where
$ P_{f\leftarrow f^\prime}(z,\alpha_s(\mu)) $ are the celebrated Altarelli-Parisi splitting functions [7, 8].For FFs of quarkonia, which are different from FFs of light mesons which rely completely on the dynamics in the non-perturbative regime of QCD, one believes that they can be further factorized into products of perturbatively calculable parts and non-perturbative behavior of the wave-functions of quarkonia at the origin, due to the nature of quarkonium as a non-relativistic bound state of a heavy quark and anti-quark. The standard theoretical tool to deal with the heavy quark bound state system is the NRQCD factorization [9], where all information about the hadronization of quarkonium is encoded in the NRQCD matrix elements. In the literature [10-16], various single-parton FFs of quarkonia have been calculated. Recently, such fragmentations for quarkonia have been calculated to a higher order of
$ \alpha_s $ and v analytically or numerically [17-26] by implementing the state-of-art multi-loop calculation techniques.$ B_{c} $ mesons are unique as they consist of two heavy quarks of different flavor. Their production in high energy collisions is a hot topic in perturbative QCD since 1990s [27-42]. In these works, a lot of effort has been paid to FFs of$ B_c $ mesons, and most of the calculations were done in the framework of NRQCD factorization, similar to the corresponding calculations for quarkonia. It is worth noting that the first NLO calculation of FF for a heavy-quark to$ B_c^{(*)} $ meson, which is quite non-trivial, was carried out in [38].In this paper, we compute the relativistic corrections of FFs for a heavy-quark to
$ B_c $ and$ B_c^* $ at the leading order of$ \alpha_s $ . These corrections are equally important as the NLO QCD radiative corrections due to the NRQCD power counting rule. Similar results appeared in the Appendix of [15] as a by-product of the calculation of FFs for quarkonia. The differences between this paper and Ref. [15] are listed in the following: 1) we consider a different scheme for calculating the relativistic corrections for the S-wave heavy-quark bound system, in which the mass of$ B_c^{(*)} $ meson appears as an overall factor, which is different from the scheme adopted in [15] where the binding energy is treated as a part of non-relativistic corrections; 2) we consider the contribution from the color-octet NRQCD operators; 3) we calculate FF of a heavy quark to transversely polarized$ B_c^* $ ; 4) we further investigate the DGLAP evolution effects.The paper is organized in the following way. We first present in Sec. 2 the definition of FFs for b quark to
$ B_c^{(*)} $ following Collins and Soper, and the desired NRQCD factorization formula. In Sec. 3, we illustrate the matching procedure, present the explicit expressions for the short-distance distributions, and compare them with those in literature. In Sec. 4, we present the non-singlet and singlet DGLAP evolutions of the obtained FFs. Finally, we summarize in Sec. 5. -
In this section, we briefly review the definition of the fragmentation function which was given by Collins and Soper [5, 6], and present the NRQCD factorization formula for FFs of b-quark to
$ B_c^{(*)} $ .We adopt the following notation for the decompositions of momenta: the 4-velocity of
$ B_c $ is$ v^{\mu} $ with$ v^2 = 1 $ . We also use the same notation v for the non-relativistic expansion parameter, which is a typical value of the relative velocity of a quark and anti-quark inside a$ B_c $ meson. Depending on the context, one should not confuse these two. We also introduce two light-like vectors$ n^{\mu} $ and$ \bar{n}^{\mu} $ such that$ n^{2} = \bar{n}^{2} = 0 $ and$ \bar{n}\cdot n = 1 $ . Any 4-vector$ a^{\mu} $ can be decomposed as$ a^{\mu} = a^{+}\bar{n}^{\mu}+a^{-}{n}^{\mu}+a_{\perp}^{\mu} $ ($ a^{+}\equiv n\cdot a $ and$a^{-}\equiv $ $ \bar{n} \cdot a $ ) with$ n\cdot a_{\perp} = \bar{n}\cdot a_{\perp} = 0 $ . Thus,$ a\cdot b = a^{+}b^{-}+a^{-}b^{+}+ $ $a_{\perp}\cdot b_{\perp} $ . For convenience, we set$ v^{\mu} = v^{+}\bar{n}^{\mu}+v^{-}n^{\mu} $ . Obviously,$v^{+}v^{-} = $ $ 1/2 $ .The d-dimensional fragmentation function of b quark to
$ B_c^{(*)} $ meson is defined as given by Collins and Soper in [5, 6],$\begin{split} {D_{b \to B_c^{(*)}}}(z;\mu ) = & \frac{{{z^{d - 3}}}}{{4{N_c}}}\sum\limits_X {\int\limits_{ - \infty }^\infty {\frac{{{\rm d}{x^ - }}}{{2\pi }}} } {{\rm e}^{ - {\rm i}{p^ + }{x^ - }/z}} \\ &\times{\rm{Tr}}\left[ {\not \!n\langle 0|W(0)b(0)|B_c^{(*)}(p),X\rangle}\right. \\ & \left. \times \langle B_c^{(*)}(p),X|\bar b({x^ - }n){W^\dagger }({x^ - })|0\rangle \right] \\ =& \frac{{{z^{d - 3}}}}{{4{N_c}}}\sum\limits_X \delta ({p^ + }/z - {p^ + } - p_X^ + )\\ &\times{\rm{Tr}}\left[ {\not\! n\langle 0|W(0)b(0)|B_c^{(*)}(p),X\rangle} \right. \\ & \left. \times\langle B_c^{(*)}(p),X|\bar b(0){W^\dagger }(0)|0\rangle \right] , \end{split}$

(3) where
$ b(x) $ is the b quark field in QCD, and the Wilson line along a light-like path is defined as$W({x^ - }) \equiv {\rm{P}}\exp \left( { + {\rm i}{g_s}\int_{{x^ - }}^\infty {\rm d} s{A^ + }(sn)} \right),$

(4) in which
$ g_s $ is the SU(3) gauge coupling and$ A_\mu (x)\equiv A^A_\mu(x) T^A $ ($ T^A $ are the generators of the SU(3) group in the fundamental representation). Since in this paper we never encounter the situation that would need the extra dimension to regulate the ultraviolet or infrared divergences, we always set$ d = 4 $ .Since
$ B_c^{(*)} $ can be regarded as a non-relativistic bound-state of b and anti-c quarks, the contribution of the heavy-quark mass may be further factorized. Therefore, up to$ {\cal O}(v^2) $ , we get the factorization formula within the NRQCD factorization framework,$\begin{split} {D_{b \to {B_c}{(^{2s + 1}}{S_J})}}(z,\mu ) = &2{m_{{B_c}}}\Bigg\{ d_{2s + 1S_J^{[1]}}^{(0)}(z,\mu )\frac{{\langle {\cal O}_1^{{B_c}}{(^{2s + 1}}{S_J})\rangle }}{{{M^4}}} \\ &+ d_{2s + 1S_J^{[8]}}^{(0)}(z,\mu )\frac{{\langle {\cal O}_8^{{B_c}}{(^{2s + 1}}{S_J})\rangle }}{{{M^4}}}\\ & + d_{2s + 1S_J^{[1]}}^{(2)}(z,\mu )\frac{{\langle {\cal P}_1^{{B_c}}{(^{2s + 1}}{S_J})\rangle }}{{{M^6}}}\Bigg\} \\ &+ {\cal O}({v^4}) , \end{split}$

(5) where the mass scale
$ M\equiv m_b+m_c $ is introduced to balance the mass dimensions so that the perturbatively calculated short-distance distributions$ d(z,\mu) $ are dimensionless, and the matrix elements of the singlet and octet NRQCD operators are defined as$\langle {\cal O}_1^{{B_c}}{(^1}{S_0})\rangle = \sum\limits_X {\langle 0|} \chi _c^\dagger {\psi _b}|{B_c} + X\rangle \langle {B_c} + X|\psi _b^\dagger {\chi _c}|0\rangle ,$

(6) $\langle {\cal O}_8^{{B_c}}{(^1}{S_0})\rangle = \sum\limits_X {\langle 0|} \chi _c^\dagger {T^A}{\psi _b}|{B_c} + X\rangle \langle {B_c} + X|\psi _b^\dagger {T^A}{\chi _c}|0\rangle ,$

(7) $\begin{split} \langle {\cal P}_1^{{B_c}}{(^1}{S_0})\rangle =& \frac{1}{2}\left[ {\sum\limits_X {\langle 0|} \chi _c^\dagger {\psi _b}|{B_c} + X\rangle} \right. \\ &\left.\times\langle {B_c} + X|\psi _b^\dagger {{\left( { - \frac{i}{2}\mathop {{ D}}\limits^{\leftrightarrow} } \right)}^2}{\chi _c}|0\rangle + {\rm{h}}.{\rm{c}}. \right],\end{split}$

(8) $\langle {\cal O}_1^{B_c^*}{(^3}{S_1})\rangle = \sum\limits_X {\langle 0|} \chi _c^\dagger {\sigma ^i}{\psi _b}|B_c^* + X\rangle \langle B_c^* + X|\psi _b^\dagger {\sigma ^i}{\chi _c}|0\rangle ,$

(9) $\begin{split} \langle {\cal O}_8^{B_c^*}{(^3}{S_1})\rangle =& \sum\limits_X {\langle 0|} \chi _c^\dagger {T^A}{\sigma ^i}{\psi _b}|{B_c} + X\rangle \\ &\times\langle {B_c} + X|\psi _b^\dagger {T^A}{\sigma ^i}{\chi _c}|0\rangle ,\end{split}$

(10) $\begin{split}\langle {\cal P}_1^{B_c^*}{(^3}{S_1})\rangle =& \frac{1}{2}\left[ {\sum\limits_X {\langle 0|} \chi _c^\dagger {\sigma ^i}{\psi _b}|B_c^* + X\rangle} \right. \\ & \left. \times\langle B_c^* + X|\psi _b^\dagger {\sigma ^i}{{\left( { - \frac{i}{2}\mathop {{D}}\limits^{\leftrightarrow} } \right)}^2}{\chi _c}|0\rangle + {\rm{h}}.{\rm{c}}. \right] ,\end{split}$

(11) where
$ \chi_c $ and$ \psi_b $ are the two-component effective fields in NRQCD for$ \bar c $ and b quarks, respectively,$ \sigma^i $ is the i-th Pauli matrix, and$ {D} = {\nabla}-{ig_s}{A} $ is the covariant derivative. Note that all$ B_c^{(*)} $ states defined in (6-11) are non-relativistically normalized, while such states are relativistically normalized in the definition of FF in (3). The factor$ 2 m_{B_c} $ in the factorization formula (3) is just from the relativistic normalization condition of the single particle states.By using the vacuum saturation approximation, at the leading order of
$ \alpha_s $ , the matrix elements$ \langle {\cal O}_1\rangle $ can be related to the radial wave function of S-wave$ B_c $ meson at the origin$ R_{S}(0) $ in the color-singlet model through$\begin{split}&\langle {\cal O}_1^{{B_c}}{(^1}{S_0})\rangle \simeq \frac{{{N_c}}}{{2\pi }}|{R_S}(0){|^2} ,\\ &\langle {\cal O}_1^{{B_c}}{(^3}{S_1})\rangle \simeq (d - 1)\frac{{{N_c}}}{{2\pi }}|{R_S}(0){|^2} .\end{split}$

(12) However, there is no similarly simple relation for the matrix elements
$ \langle {\cal O}_8\rangle $ . -
In the practical computation of the short-distance distributions
$ d(z,\mu) $ , we replace$ B_c^{(*)} $ with a color-singlet quark pair$ [b\bar c(^{2s+1}S_J^{[1]})] $ ,$|[b\bar c{(^{2s + 1}}S_J^{[1]})](p)\rangle = \sum\limits_{a,b = 1}^{{N_c}} {\frac{{{\delta _{ab}}}}{{\sqrt {{N_c}} }}} |{b^a}({p_b}),{\bar c^b}({p_c})\rangle ,$

(13) or a color-octet quark pair
$ [b\bar c(^{2s+1}S_J^{[8]})] $ $|[b\bar c{(^{2s + 1}}S_J^{[8]})](p)\rangle = \sum\limits_{a,b = 1}^{{N_c}} {\frac{{T_{ab}^A}}{{\sqrt {{T_F}} }}} |{b^a}({p_b}),{\bar c^b}({p_c})\rangle ,$

(14) where a, b are color indices, and
$ T_F = 1/2 $ is the Dynkin index of the SU(3) group in the fundamental representation. We set the momenta as$\begin{split} &{p^\mu } = {M_H}{v^\mu } = p_b^\mu + p_c^\mu ,\;\;\;p_b^2 = m_b^2 ,\;\;p_c^2 = m_c^2 ,\\ & {p_b} = {m_b}{v^\mu } + {k^\mu } ,\;\;{p_c} = {m_c}{v^\mu } + {{\tilde k}^\mu } , \end{split}$

(15) where
$ k^\mu $ and$ \tilde{k}^\mu $ are the residual momenta of b-quark and$ \bar c $ -quark, respectively.At the leading order of
$ \alpha_s $ , we have$\begin{split} {D_{b \to [b\bar c]}}(z;\mu ) =& \frac{z}{{4{N_c}}}\sum\limits_{{\rm{colors\& spins}}} {\int {\frac{{{\rm d}{q^{\rm{ + }}}{{\rm d}^{\rm{2}}}{q_ \bot }}}{{{{({\rm{2}}\pi )}^{\rm{3}}}{\rm{2}}{q^ + }}}}} \\ &\times\theta ({q^{\rm{ + }}})\delta ({p^{\rm{ + }}}{\rm{/}}z{\rm{ - }}{p^{\rm{ + }}}{\rm{ - }}{q^{\rm{ + }}}){{\left| {\cal M} \right|}^{\rm{2}}} ,\end{split}$

(16) with
$\begin{split} {\left| {\cal M} \right|^2} = &{\rm{Tr}}\Big[ {\not \!\!n\langle 0|W(0)b(0)|[b\bar c](p),c(q)\rangle} \\ &\times\langle [b\bar c,c(q)](p),c(q)|\bar b(0){W^\dagger }(0)|0\rangle \Big] ,\end{split}$

(17) where
$ q^2 = m_c^2 $ . Schematically, this is a similar NRQCD factorization formula as in (5), when the$ B_c^{(*)} $ state is replaced by the corresponding$ b\bar c $ pair state.In the light-cone gauge,
$\begin{split} &\langle {b^a}({p_b}),{{\bar c}^b}({p_c}),{c^c}(q)|{\left[ {\bar b(0){W^\dagger }(0)} \right]_d}|0\rangle = - g_s^2T_{ad}^AT_{cb}^A\\ &\left\{ {\frac{{{{\bar u}_c}(q){\gamma ^\mu }{v_c}({p_c}){{\bar u}_b}({p_b}){\gamma _\mu }(\not \!\!p \!+\! \not \!\!q \!+\! {m_b})}}{{[{{(p + q)}^2} - m_b^2][{{({p_c} + q)}^2}]}} - \frac{{{{\bar u}_c}(q)\not \!\!n{v_c}({p_c}){{\bar u}_b}({p_b})}}{{[{{({p_c} \!+\! q)}^2}][{{({p_c}\! +\! q)}^ + }]}}} \right\}, \end{split}$

(18) where we have used various equations of motion to simplify the spin structures. We also checked the expression of this matrix element in the covariant gauge, which is the same as the above expression in the light-cone gauge, as it should be.
Since FF is defined in a Lorenz invariant way, we can do the calculation in any reference frame. For convenience, we choose the rest frame of the
$ b\bar c $ pair, in which we have$ v^\mu = (1,\bf{0}) $ and${k^\mu } = \left( {\frac{{{{{k}}^{{2}}}}}{{2{m_b}}},{{k}}} \right) ,\;\;\;{\tilde k^\mu } = \left( {\frac{{{{{k}}^{{2}}}}}{{2{m_c}}}, - {{k}}} \right) .$

Generally, one applies the replacements
$\begin{split}v({p_c})\bar u({p_b}) &\to {\Pi _0}({p_b},{p_c}) = \\ &i\frac{{\left( {{\rm{ }}{{\not \!\!p}_c} - {m_c}} \right){\gamma _5}(\not \!\!p + {E_b} + {E_c})\left( {{{\not \!\!p}_b} + {m_b}} \right)}}{{2\sqrt {2{E_b}{E_c}} \sqrt {({E_c} + {m_c})({E_b} + {m_b})} 2({E_b} + {E_c})}} ,\end{split}$

(19) $\begin{split}v({p_c})\bar u({p_b}) &\to {\Pi _1}({p_b},{p_c}) =\\ & - \frac{{\left( {{\rm{ }}{{\not \!\!p}_c} - {m_c}} \right){{\not \!\!\varepsilon }^*}({\rm{ }}\not \!\!p + {E_b} + {E_c})\left( {{\rm{ }}{{\not \!\!p}_b} + {m_b}} \right)}}{{2\sqrt {2{E_b}{E_c}} \sqrt {({E_c} + {m_c})({E_b} + {m_b})} 2({E_b} + {E_c})}} ,\end{split}$

(20) to project out the spin-singlet and spin-triplet parts, respectively. Here,
$ \varepsilon^\mu $ denotes the polarization vector of the spin-triplet quark pair, and the energies are$ E_b = $ $ \sqrt{m_b^2+{k}^2} $ and$ E_c = \sqrt{m_c^2+{k}^2} $ . After expanding the resulting matrix element (18) to the second order in momentum k, one can extract the S-wave contributions by neglecting the first order terms in k (which contribute to the P-wave state only) and by making the replacement$ k^i k^j\to { k}^2 \delta^{ij}/3 $ . This leads to the corresponding matrix elements of NRQCD operators at the leading order of$ \alpha_{s} $ ,$\begin{split}\langle {\cal O}_1^{b\bar c}{(^1}{S_0})\rangle \equiv &\sum\limits_X {\langle 0|} \chi _c^\dagger {\psi _b}|[b\bar c]{(^1}S_0^{[1]}) + X\rangle \\ &\times\langle [b\bar c]{(^1}S_0^{[1]}) + X|\psi _b^\dagger {\chi _c}|0\rangle = 2{N_c},\end{split}$

(21) $\begin{split}\langle {\cal O}_8^{b\bar c}{(^1}{S_0})\rangle \equiv &\sum\limits_X {\langle 0|} \chi _c^\dagger {\psi _b}|[b\bar c]{(^1}S_0^{[8]}) + X\rangle \\ &\times\langle [b\bar c]{(^1}S_0^{[8]}) + X|\psi _b^\dagger {\chi _c}|0\rangle = 2{N_c}{C_F},\end{split}$

(22) $\begin{split}\langle {\cal O}_8^{b\bar c}{(^1}{S_0})\rangle \equiv &\sum\limits_X {\langle 0|} \chi _c^\dagger {\psi _b}|[b\bar c]{(^1}S_0^{[8]}) + X\rangle \\ &\times\langle [b\bar c]{(^1}S_0^{[8]}) + X|\psi _b^\dagger {\chi _c}|0\rangle = 2{N_c}{C_F},\end{split}$

(23) $\begin{split}\langle {\cal O}_8^{b\bar c}{(^3}{S_1})\rangle \equiv &\sum\limits_X {\langle 0|} \chi _c^\dagger {\sigma ^i}{\psi _b}|[b\bar c]{(^3}S_1^{[8]}) + X\rangle \\ &\times\langle [b\bar c]{(^3}S_1^{[8]}) + X|\psi _b^\dagger {\sigma ^i}{\chi _c}|0\rangle \\ = &2(d - 1){N_c}{C_F},\end{split}$

(24) $\langle {\cal P}_1^{b\bar c}(n)\rangle = {{{k}}^2}\langle {\cal O}_1^{b\bar c}(n)\rangle ,\;\;n{ = ^1}S_0^{[1]} {,^3}S_1^{[1]} .$

(25) It is worth noting that we are calculating FF for
$ B_{c}^{*} $ by using the replacement rules for the summation of polarization vectors$\sum\limits_{\lambda = 0, \pm 1} {{\varepsilon ^{*\mu }}} (p,\lambda ){\varepsilon ^\nu }(p,\lambda ) \to - {g^{\mu \nu }} + \frac{{{p^\mu }{p^\nu }}}{{{p^2}}} = - {g^{\mu \nu }} + {v^\mu }{v^\nu },$

(26) for the unpolarized case, and
$\begin{split}\sum\limits_{\lambda = \pm 1} {{\varepsilon ^{*\mu }}} &(p,\lambda ){\varepsilon ^\nu }(p,\lambda ) \to - {g^{\mu \nu }} + \frac{{{p^\mu }{n^\nu } + {p^\nu }{n^\mu }}}{{{p^ + }}} - \frac{{{p^2}{n^\mu }{n^\nu }}}{{{{({p^ + })}^2}}} \\ &= - {g^{\mu \nu }} + \frac{{{v^\mu }{n^\nu } + {v^\nu }{n^\mu }}}{{{v^ + }}} - \frac{{{n^\mu }{n^\nu }}}{{{{({v^ + })}^2}}} ,\end{split}$

(27) for the transversely polarized case. We will invoke a superscript T for FF and corresponding short-distance distributions of transversely polarized
$ B_c^* $ .Using the matching equations,
${D_{b \to b\bar c{(^1}S_0^{[1]})}} = \frac{{2{N_c}}}{{{M^4}}}\left( {d_{1S_0^{[1]}}^{(0)} + \frac{{{{{k}}^{\bf{2}}}}}{{{M^2}}}d_{1S_0^{[1]}}^{(2)}} \right),$

(28) ${D_{b \to b\bar c{(^3}S_1^{[1]})}} = \frac{{2(d - 1){N_c}}}{{{M^4}}}\left( {d_{3S_1^{[1]}}^{(0)} + \frac{{{{{k}}^{\bf{2}}}}}{{{M^2}}}d_{3S_1^{[1]}}^{(2)}} \right),$

(29) ${D_{b \to b\bar c{(^1}S_0^{[8]})}} = \frac{{2{N_c}{C_F}}}{{{M^4}}}d_{1S_0^{[8]}}^{(0)},$

(30) ${D_{b \to b\bar c{(^1}S_0^{[8]})}} = \frac{{2{N_c}{C_F}}}{{{M^4}}}d_{1S_0^{[8]}}^{(0)},$

(31) we can extract the short-distance distributions straightforwardly.
-
At the lowest order of v,
$\begin{split} d_{1S_0^{[1]}}^{(0)}(r,z) =& \frac{{C_F^2\alpha _s^2}}{{24N_c^2}}\frac{{z{{(1 - z)}^2}}}{{{r^2}{{(1 - \bar rz)}^6}}}[6 - 18(1 - 2r)z \\ &+ (21 - 74r + 68{r^2}){z^2} - 2\bar r(6 - 19r \\ &+ 18{r^2}){z^3} + 3{{\bar r}^2}(1 - 2r + 2{r^2}){z^4}], \end{split}$

(32) $\begin{split} d_{3S_1^{[1]}}^{(0)}(r,z) =& \frac{{C_F^2\alpha _s^2}}{{24N_c^2}}\frac{{z{{(1 - z)}^2}}}{{{r^2}{{(1 - \bar rz)}^6}}}[2 - 2(3 - 2r)z \\ &+ 3(3 - 2r + 4{r^2}){z^2} - 2\bar r(4 - r + 2{r^2}){z^3} \\ &+ {{\bar r}^2}(3 - 2r + 2{r^2}){z^4}] , \end{split}$

(33) $d_{1S_0^{[8]}}^{(0)}(r,z) = \frac{1}{{2{N_c}C_F^2}}d_{b{ \to ^1}S_0^{[1]}}^{(0)}(r,z),$

(34) $d_{3S_1^{[8]}}^{(0)}(r,z) = \frac{1}{{2{N_c}C_F^2}}d_{b{ \to ^3}S_1^{[1]}}^{(0)}(r,z),$

(35) in which we use
$ r\equiv m_c/(m_b+m_c) $ and$ \bar r\equiv 1-r $ to shorten the expressions. The color factor is$ C_F =$ $ (N_c^2-1)/(2 N_c) $ with$ N_c = 3 $ . Here, we fix$ \alpha_s $ at$ \mu = m_b+m_c $ .$ d^{(0)}_{^{1}{}S_{0}^{[1]}}(r, z) $ and$ d^{(0)}_{ ^{3}{}S_{1}^{[1]}}(r, z) $ agree with the results obtained by Braaten et al in [30] by expressing$ \langle {\cal O}_1\rangle $ in terms of the Schrödinger wave function at the origin.At the order of
$ v^2 $ , we get$\begin{split} d_{1S_0^{[1]}}^{(2)}(r,z) = & - \frac{{\alpha _s^2C_F^2}}{{288N_c^2}}\frac{{z{{(1 - z)}^2}}}{{{r^4}{{\bar r}^2}{{\left( {1 - \bar rz} \right)}^8}}}[66 - 48r \\ &+ \left( {96{r^3} - 504{r^2} + 792r - 330} \right)z\\ & + \left( {904{r^4} - 2624{r^3} + 3810{r^2} - 2738r + 693} \right){z^2}\\ & - 8\bar r\left( {316{r^4} - 576{r^3} + 670{r^2} - 426r + 99} \right){z^3}\\ & + 2{{\bar r}^2}\left( {1064{r^4} - 1744{r^3} + 1919{r^2} - 1158r + 264} \right){z^4}\\ & - 2{{\bar r}^3}\left( {336{r^4} - 524{r^3} + 664{r^2} - 415r + 99} \right){z^5}\\ & + 3{{\bar r}^4}\left( {24{r^4} - 32{r^3} + 58{r^2} - 42r + 11} \right){z^6}], \end{split}$

(36) and
$\begin{split} d_{3S_1^{[1]}}^{(2)}(r,z) = & - \frac{{\alpha _s^2C_F^2}}{{864N_c^2}}\frac{{z{{(1 - z)}^2}}}{{{r^4}{{\bar r}^2}{{(1 - \bar rz)}^8}}}[66 - 96r \\ &+ 48{r^2} + \left( {384{r^3} - 840{r^2} + 768r - 330} \right)z\\ & + \left( {472{r^4} - 2432{r^3} + 3466{r^2} - 2130r + 759} \right){z^2}\\ & - 8\bar r\left( {196{r^4} - 280{r^3} + 492{r^2} - 291r + 132} \right){z^3}\\ & + 2{{\bar r}^2}\left( {560{r^4} - 488{r^3} + 1383{r^2} - 882r + 462} \right){z^4}\\ & - 2{{\bar r}^3}\left( {192{r^4} - 164{r^3} + 692{r^2} - 471r + 231} \right){z^5}\\ & + 3{{\bar r}^4}\left( {40{r^4} - 64{r^3} + 130{r^2} - 82r + 33} \right){z^6}]. \end{split}$

(37) For transversely polarized fragmentation function for
$ B_c^{*} $ , we get the short-distance distributions as$\begin{split}d_{3S_1^{[1]}}^{{\rm{T}}(0)}(r,z) =& \frac{{\alpha _s^2C_F^2}}{{36N_c^2}}\frac{{z{{(1 - z)}^2}}}{{{r^2}{{[1 - \bar rz]}^6}}} \Big[2 + (4r - 6)z \\ &+\left( {10{r^2} - 4r + 9} \right) {z^2} - 2\bar r\left( {r + 4} \right){z^3} + 3{\bar r^2}{z^4}\Big],\end{split}$

(38) $d_{3S_1^{[8]}}^{{\rm{T}}(0)}(r,z) = \frac{1}{{2{N_c}C_F^2}}d_{b{ \to ^3}S_1^{[1]}}^{{\rm{T}}(0)}(r,z) ,$

(39) and
$\begin{split} d_{3S_1^{[1]}}^{{\rm{T}}(2)}(r,z) = & - \frac{{\alpha _s^2C_F^2}}{{864N_c^2}}\frac{{z{{(1 - z)}^2}}}{{{r^4}{{\bar r}^2}{{(1 - \bar rz)}^8}}}\Big[22 - 32r + 16{r^2} \\ &+ 2\left( {64{r^3} - 140{r^2} + 128r - 55} \right)z\\ & + \left( {176{r^4} - 832{r^3} + 1140{r^2} - 692r + 253} \right){z^2}\\ & - 8\bar r\left( {64{r^4} - 90{r^3} + 153{r^2} - 88r + 44} \right){z^3}\\ & + 2{{\bar r}^2}\left( {128{r^4} - 72{r^3} + 375{r^2} - 240r + 154} \right){z^4}\\ & - 2{{\bar r}^3}\left( {44{r^3} + 160{r^2} - 121r + 77} \right){z^5} \\ &+ {{\bar r}^4}\left( {88{r^2} - 64r + 33} \right){z^6}\Big]. \end{split}$

(40) In [30], the authors attribute to
$ \int_0^z D_{b\to B_c^{(*)}}(z) $ a kind of fragmentation probability. It is quite interesting to investigate the ratios among such fragmentation probabilities of b to$ B_c $ , unpolarized$ B_c^{*} $ and transversely polarized$ B_c^{*} $ , which are$\begin{split} {R_{13}}(r) = &\frac{{\int_0^1 {\rm d} z {D_{b \to {B_c}}}(r,z)}}{{\int_0^1 {\rm d} z {D_{b \to B_c^*}}(r,z)}} \approx \frac{1}{3}\frac{{\int_0^1 {\rm d} z d_{1{S_0}}^{(0)}(r,z)}}{{\int_0^1 {\rm d} z d_{3{S_1}}^{(0)}(r,z)}} \\ =&\frac{1}{3} - \left( {\frac{{35}}{{36}} - \frac{{5\ln r}}{6}} \right)r + {\cal O}({r^2}) ,\\ {R_{{\rm{T}}3}}(r) = &\frac{{\int_0^1 {\rm d} z D_{b \to {B_c}}^{\rm{T}}(r,z)}}{{\int_0^1 {\rm d} z {D_{b \to B_c^*}}(r,z)}} \approx \frac{{\int_0^1 {\rm d} z d_{3{S_1}}^{{\rm{T}}(0)}(r,z)}}{{\int_0^1 {\rm d} z d_{3{S_1}}^{(0)}(r,z)}} \\ =& \frac{2}{3} + \frac{5}{{18}}r + {\cal O}({r^2}) . \end{split}$

One can see that such ratios agree in the limit
$ r\to 0 $ with the rough estimates based on arguments of counting the polarization degrees of freedom. Even when the$ {\cal O}(v^2) $ corrections are taken into account, the above limits when r goes to zero still hold.The fragmentation functions
$ D_{\bar c\to B_c^{(*)}} $ can be easily obtained by replacing r with$ 1-r $ in the above expressions. Namely, one has${D_{\bar c \to B_c^{(*)}}}(r,z) = {D_{b \to B_c^{(*)}}}(\bar r,z) ,$

which is just a consequence of a kind of charge-conjugation [30].
-
As mentioned in Sec. 1 in [15], the relativistic corrections of FF have already been calculated. Neglecting the color-octet contribution, and taking into account the Gremm-Kapustin relation [43], which for
$ B_c^{(*)} $ is,${M_{B_c^{(*)}}} = {m_b} + {m_c} + \frac{{{{\langle {{{k}}^{\bf{2}}}\rangle }_{B_c^{(*)}}}}}{{2{m_b}}} + \frac{{{{\langle {{{k}}^{\bf{2}}}\rangle }_{B_c^{(*)}}}}}{{2{m_c}}} + {\cal O}({v^4}),$

(41) where
${\left\langle {{{{k}}^{\bf{2}}}} \right\rangle _{B_c^{(*)}}} \equiv \frac{{\left\langle {{\cal P}_1^{B_c^{(*)}}} \right\rangle }}{{\left\langle {{\cal O}_1^{B_c^{(*)}}} \right\rangle }} ,$

(42) we can derive the same results as in [15].
We note that in many phenomenological applications of the NRQCD factorization, the matrix element
$ \langle {\cal P}^H\rangle $ is treated as a free parameter, which is usually not bounded by the Gremm-Kapustin relation. In this sense, it is inconsistent in the matching procedure to treat the binding energy as a part of the relativistic corrections, which is equivalent to applying the Gremm-Kapustin relation. Our scheme to calculate the relativistic corrections by taking out the meson mass as an overall factor is more relevant and consistent in phenomenological applications. -
In this section, we solve the DGLAP evolution equations numerically by using the 4-th order classical Runge-Kutta method. We consider both the non-singlet and singlet evolution. We neglect the contributions from the color-octet operators.
The singlet DGLAP equations read as
$\begin{split}\mu \frac{\partial }{{\partial \mu }}{D_{f \to {B_c}}}(z;\mu ) = & \frac{{{\alpha _s}({\mu ^2})}}{\pi }\sum\limits_{f' \in (b,\bar c,g)} {\int_z^1 {\frac{{{\rm d}z'}}{{z'}}} }\\ & \times{P_{f' \leftarrow f}}(z/z',{\alpha _s}(\mu )){D_{f' \to {B_c}}}(z';\mu ) ,\\ f =& b,\bar c,g,\end{split}$

(43) where the Altarali-Parisi kernels
$ P_{f'\leftarrow f}(z/z',\alpha_{s}(\mu)) $ are$\begin{array}{*{20}{l}} {{P_{q \leftarrow q}}(z)}{ = {C_F}\left[ {\displaystyle\frac{{1 + {z^2}}}{{{{(1 - z)}_ + }}} + \displaystyle\frac{3}{2}\delta (1 - z)} \right] + {\cal O}(\alpha _s^2),} \end{array}$

(44) $\begin{array}{*{20}{l}} {{P_{g \leftarrow q}}(z)}{ = {C_F}\left[ {\displaystyle\frac{{1 + {{(1 - z)}^2}}}{z}} \right] + {\cal O}(\alpha _s^2),} \end{array}$

(45) $\begin{array}{*{20}{l}} {{P_{q \leftarrow g}}(z)}{ = {T_F}[{z^2} + {{(1 - z)}^2}] + {\cal O}(\alpha _s^2),} \end{array}$

(46) $\begin{split} {P_{g \leftarrow g}}(z) =& \Bigg\{ 2{C_A}\left[ {\frac{z}{{(1 - z)}_ + }} + (1 - z)\left(z + \frac{1}{z}\right) \right] \\ &+ \frac{\beta _0}{2}\delta (1 - z) \Bigg\} + {\cal O}(\alpha _s^2). \end{split}$

(47) where
$ C_A = N_c $ and$ \beta_{0} = 11C_{A}/3-4 T_F n_{f}/3 $ . The non-singlet DGLAP equation can be obtained from the singlet case by neglecting the off-diagonal Altarali-Parisi kernels.Here, the sliding scale
$ \mu $ is rather a factorization scale than a renormalization scale, since eventually such a scale dependence of the fragmentation functions will be canceled by the corresponding factorization scale dependence in the parton-level cross-sections, or partial decay widths after convolution. Of course, the fragmentation function of a heavy-quark to$ B_c $ will also be renormalization scale dependent. However, such dependence should be canceled by the$ \beta $ -function dependent terms (mainly from the virtual vertex corrections and self-energy corrections) in the higher order radiative corrections of these fragmentation functions, which is not the main concern in this work.We take the strong coupling
$ \alpha_s(m_Z) = 0.118 $ with the leading logarithm renormalization running with$ n_f = 5 $ , and the heavy quark pole masses$ m_b = 4.78 $ GeV and$ m_c = 1.67 $ GeV, and$ m_{B_c} = 6.275 $ GeV [44]. We also take the Schrödinger wave function at the origin of$ B_c^{(*)} $ from the potential model in [45], which is$ \vert R_S(0)\vert^2 = $ $ 1.642\;\rm{GeV}^3 $ . This implies that$\langle {\cal O}_1^{{B_c}}{(^1}{S_0})\rangle \simeq 0.784 \;{\rm{Ge}}{{\rm{V}}^3} ,\;\;\;\langle {\cal O}_1^{B_c^*}{(^3}{S_1})\rangle \simeq 2.346\; {\rm{Ge}}{{\rm{V}}^3}.$

We use the Gremm-Kapustin relation and heavy-quark spin symmetry to get the values for
$\begin{split}\langle {\cal P}_1^{{B_c}}{(^1}{S_0})\rangle \simeq & \frac{{2{m_b}{m_c}({M_{{B_c}}} - {m_b} - {m_c})}}{{{m_b} + {m_c}}}\langle {\cal O}_1^{{B_c}}{(^1}{S_0})\rangle \\ =& - 0.330\;{\rm{Ge}}{{\rm{V}}^{\rm{5}}} ,\end{split}$

(48) $\langle {\cal P}_1^{B_c^*}{(^3}{S_1})\rangle \simeq 3\langle {\cal P}_1^{{B_c}}{(^1}{S_0})\rangle = - 0.990\;{\rm{Ge}}{{\rm{V}}^{\rm{5}}} .$

(49) We set FFs at the initial renormalization scale
$ \mu = $ $m_b+ m_c = 6.00 $ GeV , as presented at the end of Sec. 3. The corresponding plots are depicted in Fig. 1. One can see that the relativistic corrections enhance the distributions by about 15% - 20%.
Figure 1. (color online) FF
$ D_{b\to B_c} $ ,$ D_{b\to B_c^*} $ and$ D_{b\to B_c^*}^{\rm T} $ for$ \mu = 6 $ GeV without/with relativistic corrections.Since the behavior of FFs for b to
$ B_c $ , unpolarized$ B_c^* $ and transversely polarized$ B_c^* $ are similar, we only show the effects of the DGLAP evolution for FFs of$ B_c $ . We show the non-singlet DGLAP evolution in Fig. 2. One can see that the evolution effects are sizable, but do not change the behavior of$ D_{b\to B_c} $ very much. The jump around z = 0 is mainly due to the instability of the numerical method. With improved accuracy of the numerical method, such deficiency would be reduced.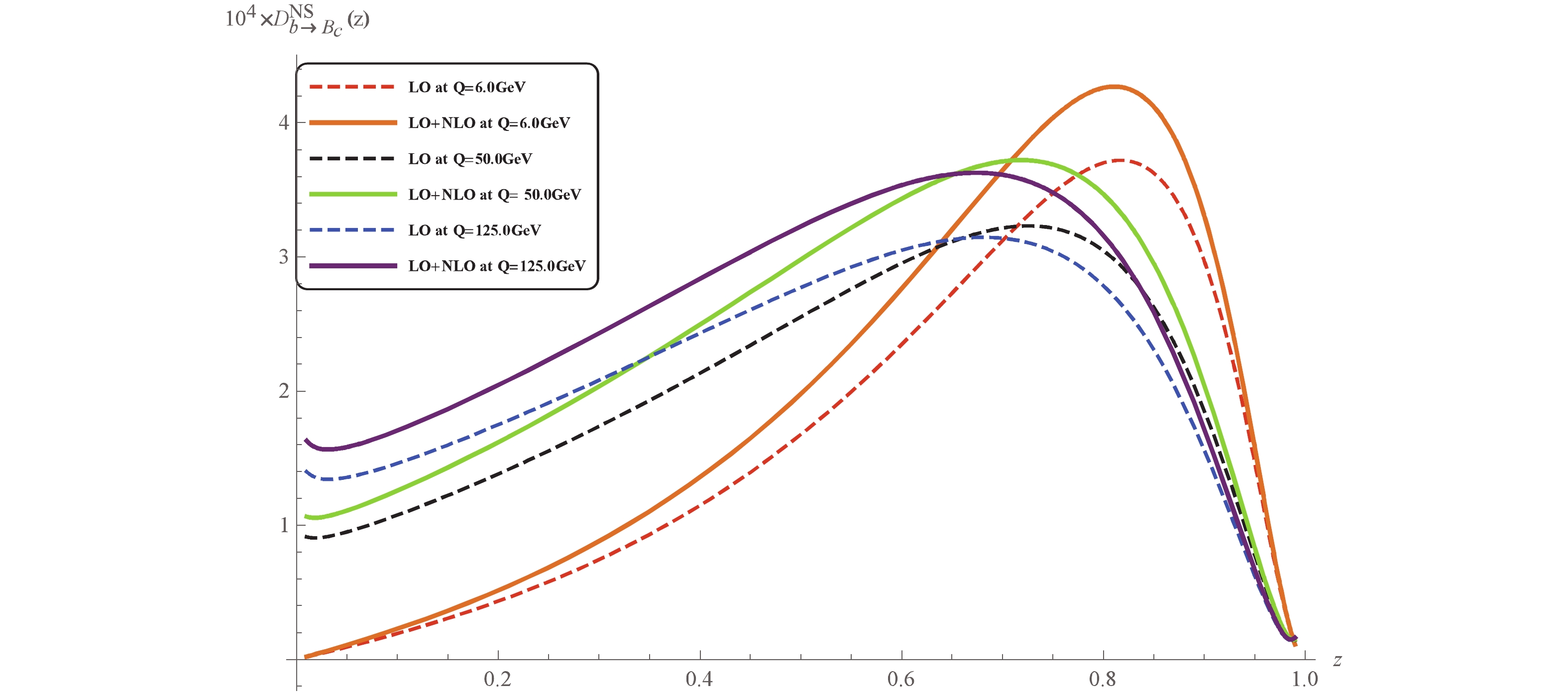
Figure 2. (color online) FF
$ D_{b\to B_c} $ for$ \mu = 6.0 $ GeV,$ \mu = 50.0 $ GeV and$ \mu = 125.0 $ GeV without/with relativistic corrections for the non-singlet DGLAP evolution.The singlet DGLAP evolution of
$ D_{b\to B_c} $ ,$ D_{\bar c \to B_c} $ and$ D_{g\to B_c} $ are shown in Fig. 3, Fig. 4 and Fig. 5, respectively.$ D_{g\to B_c}(z) $ starts from$ {\cal O}(\alpha_s^3) $ , which means that$ D_{g\to B_c}(z) = 0 $ at$ {\cal O}(\alpha_s^2) $ . Therefore, for the consistency of the initial conditions for the RG running, we take$ D_{g\to B_c}(z) = 0 $ at$ \mu = 6 $ GeV as the initial value. From these three diagrams, one can observe that
Figure 3. (color online) FF
$ D_{b\to B_c} $ for$ \mu = 6.0 $ GeV,$ \mu = 50.0 $ GeV and$ \mu = 125.0 $ GeV without/with relativistic corrections for the singlet DGLAP evolution.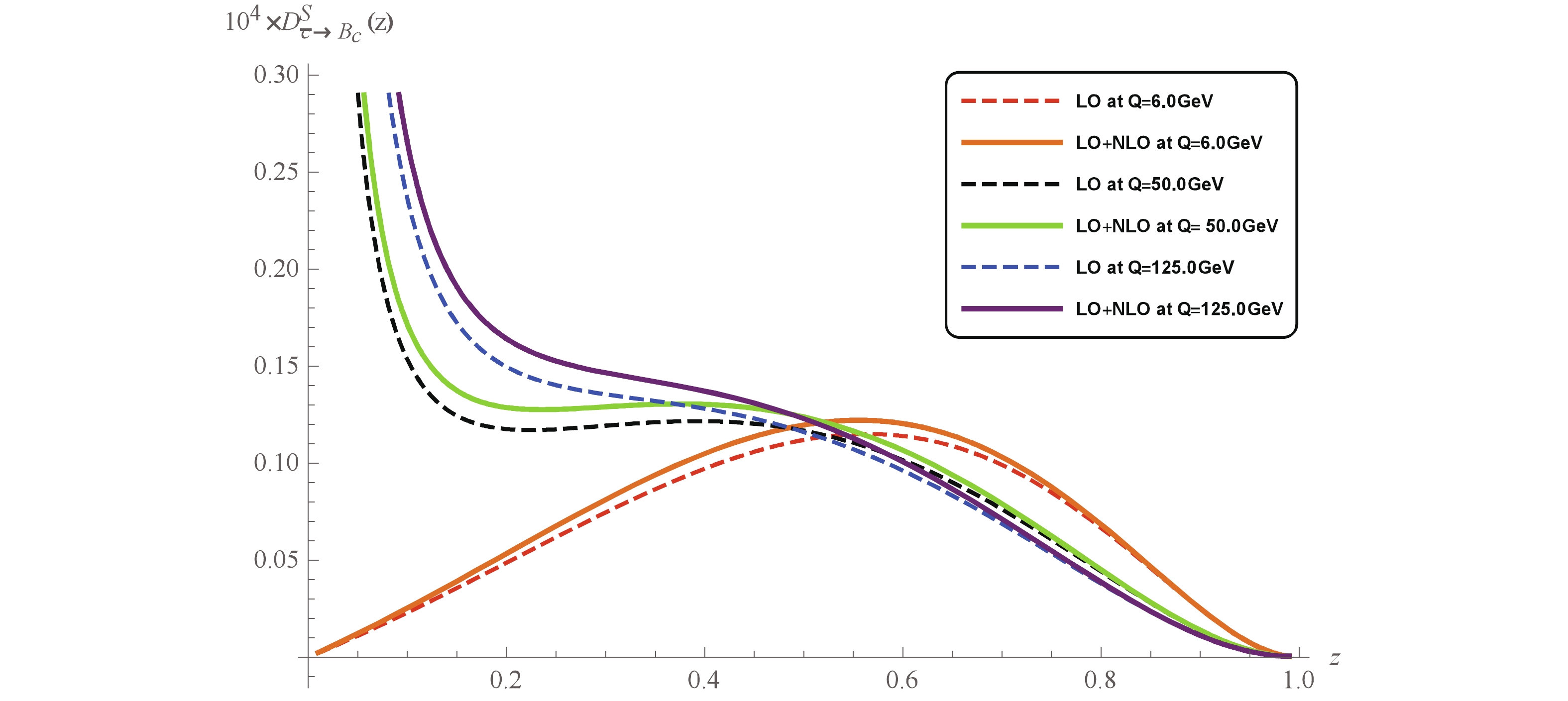
Figure 4. (color online) FF
$ D_{\bar c\to B_c} $ for$ \mu = 6.0 $ GeV,$ \mu = 50.0 $ GeV and$ \mu = 125.0 $ GeV without/with relativistic corrections for the singlet DGLAP evolution.
Figure 5. (color online) FF
$ D_{g\to B_c} $ for$ \mu = 6.0 $ GeV,$ \mu = 50.0 $ GeV and$ \mu = 125.0 $ GeV without/with relativistic corrections for the singlet DGLAP evolution.• all three FFs at z = 0 tend to diverge due to the singlet DGLAP evolution;
• the values of
$ D_{\bar c\to B_c} $ are almost one order of magnitude smaller than$ D_{b \to B_c} $ , which is understandable since it is harder to get a heavier quark from parton fragmentation;• for
$ \mu = 50.0 $ GeV and 125.0 GeV, the values of$ D_{g\to B_c} $ are comparable with$ D_{\bar c\to B_c} $ , which implies that the contribution from gluon fragmentation is needed for more accurate theoretical prediction of$ B_c $ production at large transverse momenta. -
In this paper, we calculated the relativistic corrections of FFs for a heavy quark to
$ B_c $ , and unpolarized and transversely polarized$ B_c^* $ , within the framework of NRQCD factorization at the leading order of$ \alpha_s $ . We showed that by adopting the Gremm-Kapustin relation, we can reproduce the results in the literature. However, we argue that our scheme for counting the relativistic corrections is more consistent in phenomenological applications.We showed that the
$ {\cal O}(v^2) $ corrections are around 15% - 20% as expected, and are as important as the NLO radiative corrections in [38]. We also showed that the DGLAP evolution is equally important for phenomenological applications. The singlet DGLAP evolution can drastically change the behavior of FFs for a heavy quark to$ B_c^{(*)} $ in the small z region. Furthermore, the singlet DGLAP evolution implies that FFs of gluon to$ B_c^{(*)} $ could be as important as the relativistic corrections and NLO radiative corrections of FFs for heavy-quark to$ B_c^{(*)} $ , especially for production in a hadron collider at large transverse momenta. Therefore, this FF deserves further investigation beyond the level of DGLAP evolution.When the transverse momentum is reduced, the so-called double parton fragmentation mechanism becomes more and more important for increasing the predictive power of the model [17]. The color-singlet double parton fragmentation function is closely related to the light-cone distribution amplitude (LCDA) which appears mostly in the exclusive production. LCDAs of
$ B_c $ meson have been studied up to NLO in$ \alpha_s $ and v expansions in [46, 47]. However, the color-octet double fragmentation functions for$ B_c^{(*)} $ are still missing, and it would be important that they are studied.We thank Yu Jia and Wen-Long Sang for valuable discussions.
Relativistic corrections of the fragmentation functions for a heavy quark to Bc and ${{B}_{\!\!{c}}^*}~$
- Received Date: 2019-04-19
- Available Online: 2019-08-01
Abstract: In this paper, we compute the relativistic corrections of the fragmentation functions (FFs) for a heavy quark to Bc and







 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF
















 DownLoad:
DownLoad: