-
Nuclear collective and non-collective rotations are powerful probes for the nuclei structure. Experimentally, massive amounts of spectroscopic data exist, with particularly rich sidebands that are built on excited configurations. Theoretical investigations, e.g., cranking mean-field models, usually focus on ground-state bands because of the difficulty of tracking a given configuration. Among sidebands, multi-quasiparticle high-
$ K $ bands attract attention in particular. Transitions from high-$ K $ to low-$ K $ states are usually forbidden due to the$ K $ selection rule of$ \gamma $ -ray emissions [1]. This can lead to high-$ K $ isomers, i.e., nuclear metastable states [1, 2]. Neutron-rich Mo, Ru, and Pd isotopes are interesting in both theory and experiment. These nuclei are assumed to play an important role in the r-process [3]. Experiments have observed some$ 5^- $ bands in$ ^{102-106}{\rm Mo} $ ,$ ^{108-112}{\rm Ru} $ and$ ^{112-114}{\rm Pd} $ [4-7]. There is no strict half-life requirement for a nuclear excited state to be designed as an isomer [8]. Generally, an excited state with a half-life longer than 1 ns is an isomer. In the mass region, high-$ j $ orbitals, neutron$ \nu{h_{11/2}} $ and proton$ \pi{g_{9/2}} $ , appear near the proton and neutron Fermi surfaces at$ Z\sim42 $ and$ N\sim64 $ . Therefore, we expect high-$ K $ isomeric excited states and their collective rotational bands.The neutron-rich nuclei have abundant properties regarding their structure, e.g., shape transitions [9–13],
$ \gamma $ -vibration [14–17], and triaxial shape [4, 6, 18, 19]. In this region, several high-$ \Omega $ orbitals can be found around the proton and neutron Fermi surfaces, e.g.,$\pi{5/2}[303], $ $ \pi{5/2}[422], \nu{5/2}[532], \nu{5/2}[413], $ $ \nu{5/2}[402] $ , and$ \nu{7/2}[523] $ . These can form various multi-particle high-$ K $ configurations and lead to high-$ K $ rotational sidebands. After the early study of Ref. [20] reported evidence of rotations in the neutron-rich Mo-Pd region, numerous experiments have been devoted to investigate shape transitions and rotational properties of the nuclei. The first systematic high-spin study of collective bands was performed in Ref. [21], which reported deformed configurations in Zr and Mo isotopes. The$ \gamma $ -ray spectroscopy also provides important information on the properties of single-particle orbitals, which are essential for understanding the behaviors of nuclear excitations. A series of$ K^{\pi} = 5^- $ bands have been observed experimentally in even-even Mo, Ru, and Pd isotopes [4–7]. The bandheads of the$ 5^- $ bands have been interpreted as two-particle excitations in experiments [4–6, 22, 23]. The investigations of the multi-particle configurations and spectra can provide abundant information on the properties of single-particle orbits.Several models have been used to investigate the properties of the neutron-rich nuclei, including the Hartree-Fock-Bogoliubov (HFB) [19, 24] method, projected shell model [19, 25, 26], and the cranked shell model [3, 5, 6, 9, 14]. However, most models focus on the ground-state bands. A comprehensive understanding of the nuclei structures is yet to be obtained. Rich sidebands should be studied alongside the yrast band. In an earlier study [3], we investigated some
$ K^\pi = 5^- $ states within the mass region. In the recent works [27–29], we developed the configuration-constrained cranking shell model for sidebands. In the present work, we perform the configuration-constrained cranking Skyrme Hartree-Fock (HF) pairing calculation for the neutron-rich Mo, Ru, and Pd isotopes, focusing the rotations of the$ 5^- $ isomeric states. The paper is organized as follows: a brief formulation of the configuration-constrained cranking pairing Skyrme Hartree-Fock is presented in Section 2. The calculations for Mo, Ru and Pd isotopes are provided in Sec. 3. -
The total cranked Hamiltonian in the cranked Hartree-Fock basis can be expressed as [27]
$ \hat{H}^\omega = E^{\rm HF}_G(\omega)+\sum\limits_{\mu\geq{A+1}}e^\omega_{\mu}b^+_{\mu}b_{\mu}-\sum\limits^A_{\mu = 1}e^\omega_{\mu}b_{\mu}b^+_{\mu}+H_p, $

(1) where
$ E^{\rm HF}_G(\omega) $ is the lowest cranked HF energy at a given rotational frequency$ \omega $ with the Skyrme interaction.The HF wave function ignores the residual two-body correlation, which is usually treated using the Bogoliubov pairing method. The second and third terms yield particle-hole excitations, with$ e^\omega_\mu $ depicting the Skyrme Hartree-Fock single-particle Routhian [27].$ H_p = -G\sum_{\xi{\eta}}a^{+}_{\xi}a^{+}_{\hat{\xi}}a_{\hat{\eta}}a_{\eta} $ depicts the residual two-body pairing interaction. In pairing calculations, only monopole pairing is considered. The pairing strength G is determined by an odd-even mass difference using a three-point formula [30], which includes the mean-field and blocking effects [30, 31]. In this study, the pairing strengths of protons and neutrons are determined:$ G_\nu $ = 0.44 MeV,$ G_\pi $ = 0.61 MeV.Usually, nuclear pairing correlation is treated using the Bogoliubov method. However, in the rotations of broken-pair multi-quasiparticle configurations, the residual pairing is weak, and the Bogoliubov numerical calculation fails. To avoid this problem, a particle-number-conserving (PNC) pairing method was suggested [32-36], which applies the technique of the shell-model diagonalization with a simple pairing Hamiltonian. Previous cranking PNC calculations were performed at fixed deformations [32, 33], without considering the shape evolutions in the rotation processes. This limits the predictive power of the model, as a self-consistent deformation is needed. In our recent works [28, 29], we used PNC pairing to treat the pairing correlation in the total-Routhian-surface (TRS) method with the Woods-Saxon potential. The deformation of a rotational state is determined by minimizing the calculated TRS [28, 29].
However, the Hamiltonian based on a one-body potential raises the double counting problem. In this work, we assume the two-body Skyrme interaction. In our previous study [27], we developed self-consistent configuration-constrained cranking Skyrme HF calculations with the PNC pairing. For the calculations of a configuration-given rotational band, the configurations can be identified and tracked by calculating the occupation probabilities of orbits using averaged Nilsson numbers [37–39]. In the present calculation with the cranking Skyrme HF and PNC pairing, the investigated state can be found with the specific orbits that are almost fully occupied (i.e., with the orbital occupation probability close to one), and their partner orbits that are almost unoccupied (i.e., occupation probabilities nearly zero). Here, several eigenstates would correspond to a given configuration, with similar occupation probabilities of the specific orbits. We usually consider the lowest-energy state. The PNC pairing method [27, 32, 40] diagonalizes the Hamiltonian in a truncated model space, similar to the technique of the "standard" shell model, and preserves the particle number. The details of the calculation can be found in Ref. [27].
-
In the present Skyrme Hartree-Fock calculation, the Skyrme force of SKM* with particle-number-conserved pairing [41] is adopted. Rotational bands built on the levels of 2458.6 keV in 102Mo, 1884.1 keV in 104Mo and 2146.81 keV in 106Mo have been observed with the
$ K^\pi = 5^- $ configurations assigned [6, 23]. Figure 1 shows the calculated kinematic moments of inertia (MoI) for the ground-state bands and the sidebands of two-particle$ K^\pi = 5^- $ configurations, compared with the experimental data in 102, 104, 106Mo.
Figure 1. (color online) Calculated and experimental MoI's for ground-state bands and sidebands built on
$K^\pi = 5^-$ configurations in 102-106Mo. Experimental data are taken from Refs. [6, 7]. The$5^-$ configurations are 2$\nu$ :$\nu 5/2^-[532]\otimes \nu 5/2^+[402]$ , 2$\pi$ :$\pi5/2^+[422]\otimes \pi5/2^-[303]$ .For the
$ K^\pi = 5^- $ bands, we calculated two-neutron$ \nu5/2^-[532]\otimes\nu5/2^+[402] $ and two-proton$ \pi5/2^+[422]\otimes$ $ \pi5/2^-[303] $ configurations. The orbits are close to the Fermi level, and hence lead to the low-lying high-$ K $ two-quasiparticle states. As seen in The MoI's calculated with$ K^\pi = 5^- $ ,$ \pi{5/2^+[422]\otimes\pi5/2^-[303]} $ two-proton configuration give reasonable agreement with the experimental data, as shown in Fig. 1. However, the calculated MoI's of the two-neutron$ \nu5/2^-[532]\otimes\nu 5/2^-[402] $ $ K^\pi = 5^- $ bands are also close to the MoI's extracted experimentally, which indicates a mixing of the two$ K^\pi = 5^- $ configurations. In Ref. [22], the 1883.8 keV level is assigned to$ \pi5/2^+[422]\otimes\pi5/2^-[303] $ in 104Mo. In 102Mo, there is no two-neutron$ \nu5/2^-[532]\otimes\nu5/2^+[402] $ state found in the calculation. This is because the$ 5/2^-[532] $ and$ 5/2^+[402] $ orbits are not close to the neutron Fermi surface. A two-proton$ \pi5/2^+[422]\otimes\pi5/2^-[303] $ configuration was hence suggested. These findings imply that the two-proton$ \pi5/2^+[422]\otimes\pi5/2^-[303] $ configuration is the main component of$ K^\pi = 5^- $ bands.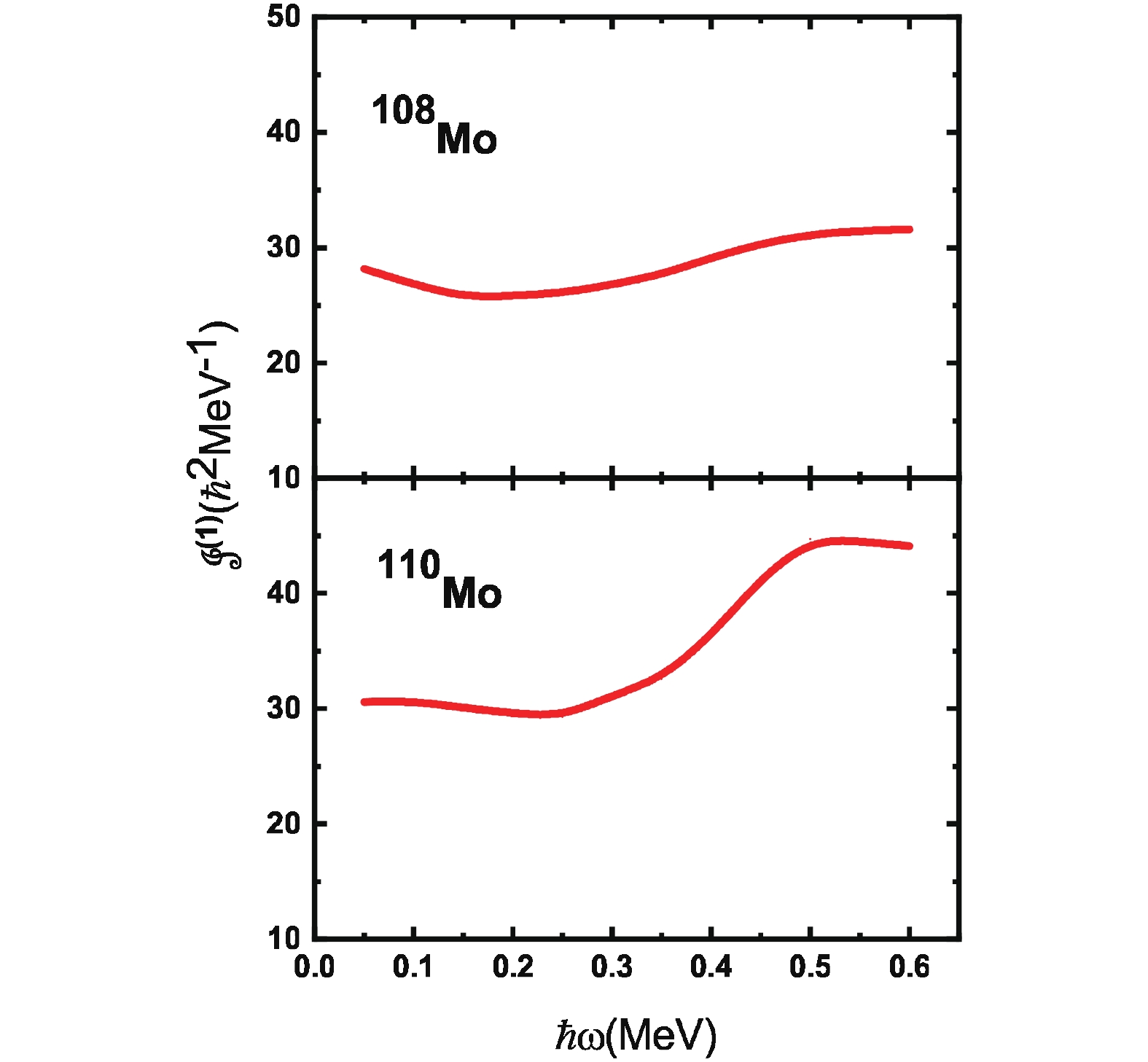
Figure 5. (color online) Calculated MoI's for
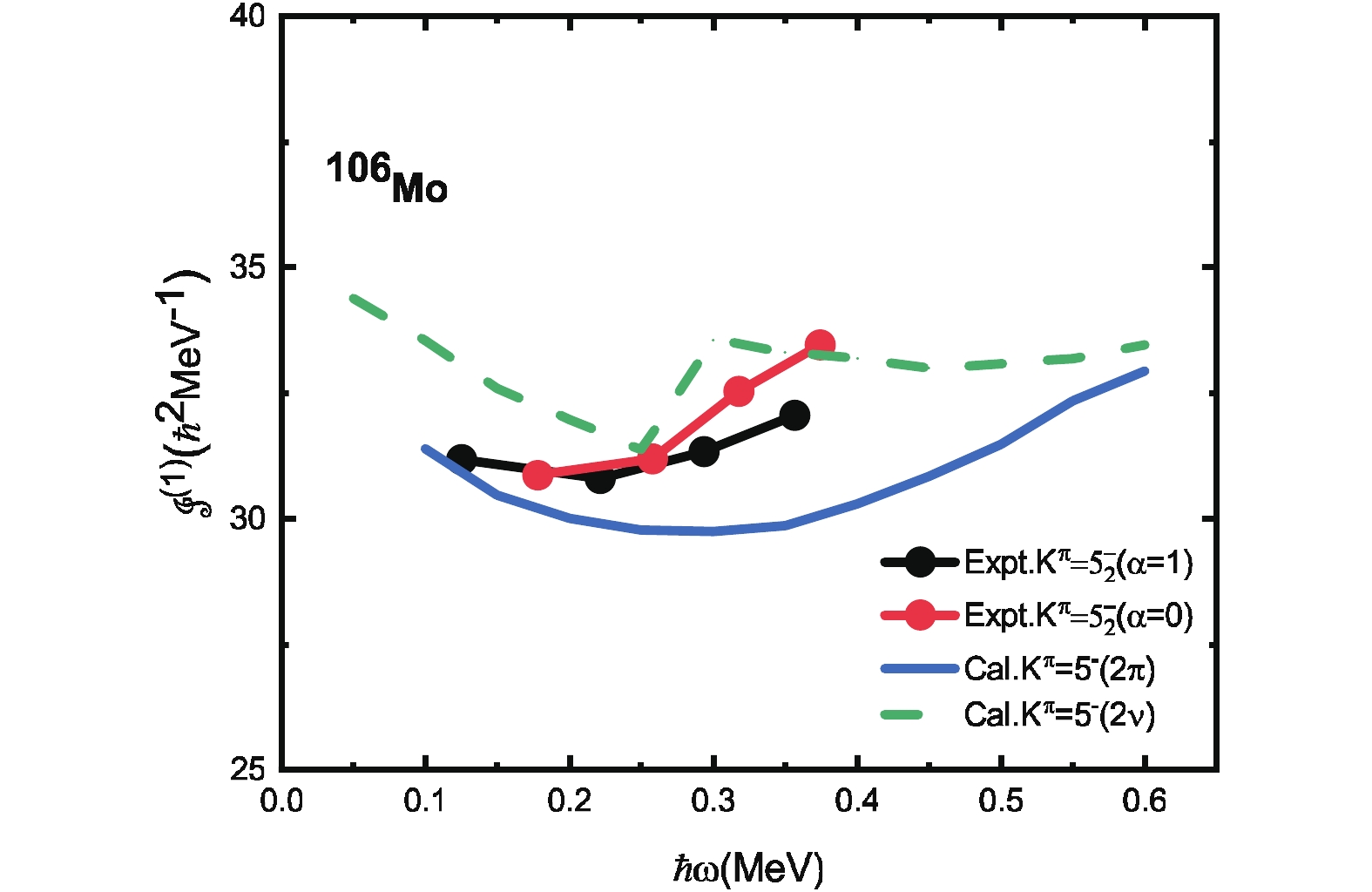
$^{108, 110}{\rm Mo}$ as predictions. The configuration is$\pi{5/2}^-[303]\otimes\pi{5/2}^+[422]$ .A second 5– is observed in 106Mo. The
$ 5^- $ rotational band is built on the 1952 keV level [42]. The experiment [42] separates the band into two branches with different signatures, as shown in Fig. 2. The study of Ref. [23] suggests that the$ 5_2^- $ band in 106Mo is a two-neutron band. However, in this work, the experimental MoI cannot be reproduced by the configuration-constrained cranking HF calculation for the two-neutron or two-proton configuration. The mixing between$ \nu5^- $ and$ \pi5^- $ is possible to appear in this band.Figure 3 shows the experimental and calculated MoI's of the ground-state and two-particle bands in Ru isotopes. The calculations reproduce the ground-state bands reasonably, including the alignments in 108, 110, 112Ru. 108Ru is assumed to be a
$ \gamma $ -soft nucleus, whereas 110, 112Ru are more like rigid triaxial rotors in Ref. [43].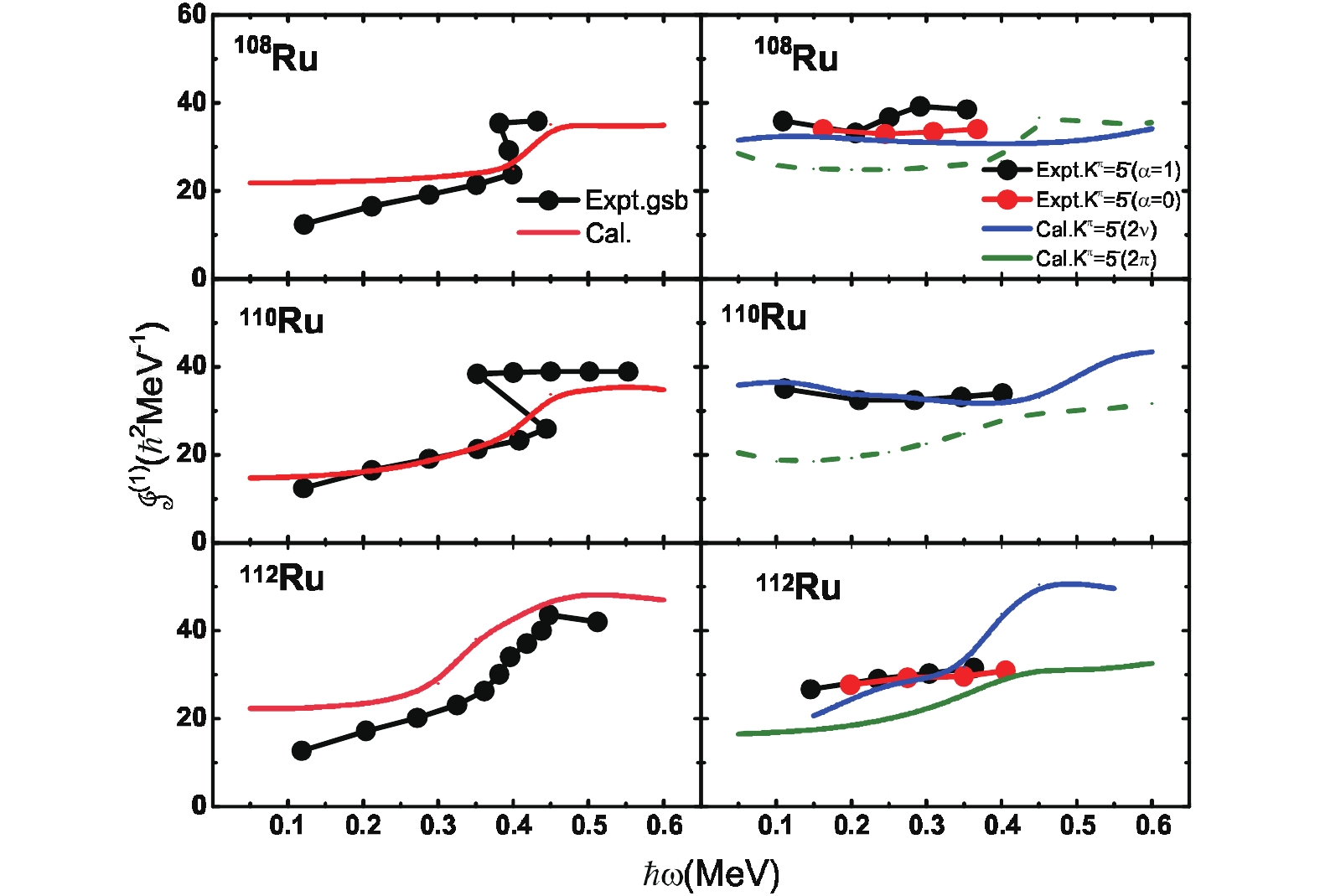
Figure 3. (color online) Calculated and experimental MoI's for ground-state bands and sidebands built on
$K^\pi = 5^-$ in 108-112Ru. Experimental data are taken from Refs. [4, 7]. The configurations are 2$\pi$ :$\pi5/2^+[422]\otimes\pi5/2^-[303]$ , 2$\nu$ :$\nu5/2^-[532]\otimes\nu5/2^+[402]$ for 108Ru and$\nu5/2^-[532]\otimes\nu5/2^+[413]$ for 110, 112Ru.Possible low-lying two-neutron and two-proton
$ K^\pi = 5^- $ states were investigated, as shown in Fig. 3 for Ru isotopes. Rotational bands built on the$ K^\pi = 5^- $ bandheads at 2111.0 keV in 108Ru, 2145.3 keV in 110Ru, and 2003.3 keV in 112Ru were observed [4]. Rotational bands were considered [44] as the two-neutron intrinsic configurations of$ \nu5/2[532]\otimes \nu5/2[402] $ in 108Ru. We performed the configuration-constrained Skyrme HF calculations for the possible low-lying$ 5^- $ configurations of two-neutron$ \nu{5/2}^-[532]\otimes\nu{5/2}^+[402] $ ,$ \nu{5/2}^-[532]\otimes\nu5/2^+[413] $ , and two-proton$ \pi{5/2}^-[303]\otimes $ $ \pi{5/2}^+[422] $ . We see in Figure 3 shows that two-neutron$ 5^- $ configurations provide better quantitative descriptions of data in comparison to the$ 5^- $ two-proton configuration. The negative parity bands are interpreted as two-quasineutron excitations [15, 44, 45]. The two-neutron states lie at lower energy than the two-proton state in this region. The lowest configuration is obtained by exciting a neutron from the highest$ h_{11/2} $ level to the low-lying mixed$ d_{5/2}-g_{7/2} $ levels [15]. For$ ^{108}{\rm Ru} $ , the calculated lowest bandhead of the$ 5^- $ bands is the two-neutron$ \nu{5/2}^-[532]\otimes\nu{5/2}^+[402] $ configuration, which supports the experimental data provided in Ref. [44]. For 110, 112Ru, the configuration of the$ K^\pi = 5^- $ band is$ \nu{5/2}^-[532]\otimes $ $ \nu5/2^+[413] $ . The component of the$ 5^- $ state changes as the number of neutrons increases. The neutron$ 5/2[413] $ orbital is closer to the Fermi surface with increasing neutron number. Our calculations show that the mixture of the$ \nu 5/2[413] $ ($ d_{5/2} $ ) and$ \nu 5/2[402] $ ($ g_{7/2} $ ) orbits is not obvious.Figure 4 shows the calculations of 112Pd and 114Pd. The 5− rotational bands were observed in the two isotopes [5]. The present cranking calculations efficiently reproduce the backbending that is caused by alignment of the
$ h_{11/2} $ neutrons. The two upbendings are predicted around$ \hbar\omega\thickapprox $ 0.55 MeV. The second upbending was observed in 116Pd In Ref. [5]. The second band crossings due to alignments of$ (\pi{g_{9/2}})^2 $ proton pairs were predicted to take place at 0.55 MeV and 0.48 MeV. The present calculation in 114Pd supports the prediction made in Ref. [10].$ K^- = 5^- $ bands were observed in 112, 114Pd as well [5]. As calculated for Ru isotopes, the two-neutron$ K^\pi = 5^- $ configuration was assigned for the observed$ 5^- $ sidebands in 112, 114Pd. The calculated configuration for 112Pd is$ \nu{5/2}^-[532]\otimes\nu{5/2}^+[402] $ , which is different from the case of its isotone 110Ru ($ \nu{5/2}^-[532]\otimes\nu{5/2}^+[413] $ ). The 2184 keV level was assigned to$ K^\pi = 5^- $ in 114Pd, taking the data from Ref. [5]. The calculated MoI's for this band with$ K^\pi = 6^- $ has similar rotational behavior to the experimental$ 5^- $ band. The configuration of the$ K^\pi = 6^- $ state is two-neutron$ \nu{7/2}^-[523]\otimes\nu{5/2}^+[413] $ . The$ K^\pi = 5^- $ state has a relatively pure two-neutron configuration in Pd isotopes.
Figure 4. (color online) Calculated and experimental MoI's for ground-state bands and sidebands built on Kπ=5− in Pd isotopes. The experimental data are taken from Refs. [5, 7]. The configurations are 2
$\nu$ :$\nu{5/2}^-[532]\otimes\nu{5/2}^+[402]$ for 112Pd and$\nu{7/2}^-[523]\otimes$ $\nu{5/2}^+[413]$ for 114Pd.Approaching heavier nuclei in this mass region, our calculations predict the two-proton
$ \pi{5/2}^-[303]\otimes$ $ \pi{5/2}^+[422] $ rotational bands in$ ^{108, 110}{\rm Mo} $ , as shown in Fig. 5. This information should be useful for possible experiments conducted in the future. -
In this study, we have performed self-consistent configuration-constrained cranking Skyrme HF calculations with the particle-number-conserved pairing for Ru, Pd, and Mo isotopes. The calculations reproduce the experimental moments of inertia for both ground-state and
$ K^\pi = 5^- $ bands to a reasonable degree. In the comparison of data, the configurations onto which$ K^\pi = 5^- $ bands are built are discussed in detail. This information is useful for the further understanding of the nuclei structures. These predictions may provide guidance for future experiments in this mass region.We acknowledge the High-performance Computing Platform of Peking University for providing computational resources.
${K^\pi=5^-}$ rotational bands in neutron-rich Mo, Ru, and Pd nuclei
- Received Date: 2019-05-07
- Available Online: 2019-08-01
Abstract: The collective rotations of the






 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF
















 DownLoad:
DownLoad: