-
The Beam Energy Scan (BES) program [1-5] at the Relativistic Heavy Ion Collider (RHIC) has as its goal, among others, to probe the phase structure of Quantum Chromodynamic (QCD) matter and find its critical point [6–15], which is represented by the endpoint of the first order phase transition boundary of the QCD phase diagram [7–9,16–22]. At the critical point, the thermal medium is strongly correlated with divergent fluctuations of various variables [6–9]. The skewness S and kurtosis κ of the net protons diverge with the correlation length by
$ \xi^{4.5} $ and$ \xi^{7} $ , respectively [23]. In the BES experiment, event-by-event multiplicity fluctuations of net protons and net charges were systematically measured at different collision energies [24–28]. The kurtosis κ of net protons presents a non-monotonic behavior and largely deviates from the Poisson baseline at lower collision energies, indicating the discovery potential of the critical point [28, 29].Recently, non-equilibrium effects were found to be significant for an expanding medium near the critical point [30–46]. In particular, the critical slow-down effects largely influence the non-equilibrium fluctuations, which can even reverse the signs of skewness S and kurtosis κ compared with the equilibrium values [37,38]. The soft mode of the critical point was argued to be a diffusive mode, which is a combination of the order parameter field and the conserved quantities [32]. Recently, diffusion dynamics near the critical point were calculated [42,45], which showed that the second order cumulant of the conserved charge exhibits non-monotonic behavior with the change of the rapidity window [42].
For the dynamical model calculations near the critical point, the non-equilibrium fluctuations are non-universal and depend on various free parameters, such as the relaxation time, mapping from the 3D Ising model to the hot QCD medium, etc. In contrast, within the framework of Kibble-Zurek Mechanism (KZM), some universal variables can be constructed near the critical point that are insensitive to some non-universal factors [41,46–51]. The key point behind the KZM is that, due to the critical slow-down effects, the systems inevitably fall out of equilibrium near the critical point, after which these “frozen” systems have correlated regions with characteristic scales, leading to various universal variables. The KZM was first introduced by Kibble in cosmology [52] and then extended by Zurek to condensed matter physics [53]. In relativistic heavy ion collisions, the KZM was first studied in Ref. [41], which constructed universal functions of the order parameter field that are insensitive to the relaxation time and the evolving trajectory of the system. In Ref. [51], we investigated the Kibble-Zurek scaling for both the order parameter field and the multiplicity fluctuations of net protons, using the Langevin dynamics of model A. We found that, compared with the original fluctuations of net protons, the oscillating behavior of the constructed approximately universal functions are strongly suppressed.
In this study, we investigate the critical universal scaling of the conserved charge within the framework of model B. As mentioned above, the soft mode near the QCD critical point is a diffusive mode, which is a linear combination of the order parameter field and the conserved quantities. Moreover, the conserved quantities are directly related to the possible experimental observable. In comparison with our early work [51], which only considers the non-conserved order parameter field, this study explores the possible universal scaling for fluctuations of conserved charge using the stochastic diffusion equation (SDE). We demonstrate that the constructed universal functions for the two-point correlation function and the second-order cumulant of the conserved charge are insensitive to the non-universal factors of two cases 1) the evolving hot medium with different strength of critical component
$ c_c $ , a parameter in the mapping from 3D Ising to QCD critical point; 2) the evolving system with different initial temperature$ T_0 $ . We restrict our attention to the possibility of constructing the universal functions for diffusion dynamics near the critical point, as we only focus on the 1+1-dimensional system with the Bjorken approximation. For realistic universal observables that might be associated with experimental measurements, at least a numerical simulation of the 3+1 dimensional diffusion dynamics and consideration of the higher-order cumulants of fluctuations is necessary. This requires high statistical runs and a large amount of computing resources, which we leave to a future study.The paper is organized as follows: Section 2 briefly reviews the dynamics of conserved charge near the critical point based on the stochastic diffusion equation. In Section 3, we construct the universal functions for two-point correlation function and the second-order cumulant. Section 4 presents and discusses the main results of the constructed universal functions. Section 5 summarizes and concludes this paper.
-
For a dynamical model near the critical point, the slow modes are the relevant and essential modes that largely influence the critical behavior of the evolving system. According to the classification in Ref. [54], the critical dynamics of the non-conserved and conserved order parameter field belong to models A and B, respectively. Meanwhile, model H describes a system with a conserved order parameter field, conserved transverse momentum density, and nonzero Poisson bracket between the two. In general, it is believed that the dynamical system near QCD critical point lies in model H [32,55-57]. However, the related analysis or numerical implementation of model H is complicated, and it has not been fully developed. For simplicity, our previous work [51] only focused on the dynamics and universal scaling of the non-conserved order parameter field within the framework of model A. Recently, the stochastic diffusion dynamics of the conserved charge for model B has been developed by Ref. [42] , which demonstrated that the two-point correlation function and cumulant behave non-monotonically with the change of the rapidity interval and window, respectively. In this study, we explore the universal behavior of the conserved charge based on the stochastic diffusion equation described in Ref. [42].
For simplicity, we focus on the 1+1-dimensional evolution of the conserved charge density
$ n(y,\tau) $ with the proper time$ \tau = \sqrt{t^2-z^2} $ and the spacetime rapidity$ y = \tanh^{-1}(z/t) $ for a boost-invariant Bjorken system. The related stochastic diffusion equation is [42]:$ \begin{align} \frac{\partial}{\partial \tau} \delta n(y,\tau) = D_y(\tau) \frac{\partial^2}{\partial^2 y} \delta n(y,\tau) + \frac{\partial }{\partial y} \zeta(y,\tau) \end{align}. $

(1) Here
$ \delta n(y,\tau) = n(y,\tau)-\langle n(y,\tau)\rangle $ , and$ \langle \cdots\rangle $ denotes the event average. The diffusion coefficient$ D_y(\tau) $ is related to the Cartesian one$ D_C(\tau) $ with$ D_y(\tau) = D_C(\tau)\tau^{-2} $ . The noise$ \zeta(y,\tau) $ satisfies the fluctuation-dissipation theorem:$ \begin{split} &\langle \zeta(y,\tau) \rangle = 0,\\ &\langle \zeta(y_1,\tau_1)\zeta(y_2,\tau_2)\rangle = 2\chi_y(\tau) D_y(\tau) \delta (y_1-y_2) \delta (\tau_1-\tau_2), \end{split} $

(2) where
$ \chi_y(\tau) $ is the susceptibility of the conserved charge per unit rapidity, related to the Cartesian one$ \chi_C(\tau) $ with$ \chi_y(\tau)/\tau = \chi_C(\tau) $ . For notational convenience, these subscripts of the diffusion coefficient and susceptibility are omitted in the following part of this paper, such that$ D(\tau) = D_y(\tau) $ and$ \chi(\tau) = \chi_y(\tau) $ , respectively.After solving the SDE (1), the correlation function is obtained as follows:
$ \begin{split} C(y_1,y_2;\tau)\equiv &\langle \delta n(y_1,\tau)\delta n(y_2,\tau) \rangle\\ =& \chi(\tau) \delta(y_1-y_2)\\ &- \int^\tau_{\tau_0} {\rm d}\tau' \chi'(\tau') G(y_1-y_2;2{\rm d}(\tau',\tau)), \end{split} $

(3) where
$ \chi'(\tau) = {\rm d}\chi(\tau)/{\rm d}\tau $ . Here, the normalized Gaussian distribution is:$ \begin{align} G(\bar{y};d) \equiv \frac{1}{\sqrt{\pi}d} {\rm e}^{-\bar{y}^2/d^2}, \end{align} $

(4) and
$ \begin{align} d(\tau_1,\tau_2)\equiv\left[2\int^{\tau_2}_{\tau_1}{\rm d}\tau' D(\tau')\right]^{1/2} \end{align}, $

(5) represents the diffusion “length” in rapidity space from
$ \tau_1 $ to$ \tau_2 $ with$ \tau_1\leqslant \tau_2 $ .The amount of the charge deposed within a finite rapidity window
$ \Delta y $ at mid-rapidity and at a proper time τ can be calculated as:$ \begin{align} Q_{\Delta y}(\tau) \equiv \int^{\Delta y/2}_{-\Delta y/2} {\rm d}y n(y,\tau). \end{align} $

(6) Correspondingly, the second-order cumulant of
$ Q_{\Delta y}(\tau) $ takes the following form:$ \begin{split} K(\Delta y,\tau)&\equiv \langle \delta Q_{\Delta y}(\tau)^2\rangle/\Delta y\\ & = \frac{1}{\Delta y}\int^{\Delta y/2}_{-\Delta y /2} {\rm d}y_1{\rm d}y_2 \langle \delta n(y_1,\tau) \delta n(y_2,\tau)\rangle\\ & = \chi(\tau)- \int^\tau_{\tau_0} {\rm d}\tau' \chi'(\tau') F\left(\frac{\Delta y}{2{\rm d}(\tau',\tau)}\right), \end{split} $

(7) where
$ \begin{align} F(X)\equiv \frac{2}{\sqrt{\pi}} \int^X_0 {\rm d}z\left(1-\frac{z}{X}\right){\rm e}^{-z^2}. \end{align} $

(8) The detailed derivation is given in Appendix A.
Note that Eq. (1) only considers the two-point interaction. The higher order terms and the kinetic term
$ \partial^4 \delta n /\partial y^4 $ are neglected, and their contributions are considered to be included in the renormalized coefficients$ D(\tau) $ and$ \chi(\tau) $ (See Sec. 2.2) [42]. The advantage of this treatment is that Eq. (1) can be analytically solved, as shown in Eqs. (3) and (7). To obtain proper results, we implement this simplified model slightly off the critical point in the following calculation and consider it as our first attempt to study the Kibble-Zurek scaling for the two-point correlations in the diffusion dynamics. -
Both the correlation function (3) and the cumulant (7) depend on the susceptibility
$ \chi(\tau) $ and diffusion coefficient$ D(\tau) $ , which requires additional parametrizations. In general, the susceptibility$ \chi $ and diffusion coefficient D include both the singular parts$ \chi^{\rm cr} $ ,$ D^{\rm cr}_C $ and the regular parts$ \chi^{\rm reg} $ ,$ D^{\rm reg}_C $ , respectively [42]. As the system evolves near the critical point, the singular contributions become dominant. We thus neglect the regular parts to simplify the following study of the Kibble-Zurek scaling. The susceptibility$ \chi(\tau) $ and diffusion coefficient$ D(\tau) $ with only the singular parts are then written as:$ \begin{align} &\chi(T) = \chi^{\rm cr}(T), \end{align} $

(9) $ \begin{align} &D(T) = D^{\rm cr}_C/\tau^2. \end{align} $

(10) Here, we construct the singular part
$ \chi^{\rm cr} $ and$ D^{\rm cr}_C $ through a mapping between the hot QCD matter and the 3D Ising model. The mapping is non-universal, which has some other strategies for the mapping relation. For illustration purposes, we use the linear parametric model [58,59], in which the magnetization of 3D Ising systems is parameterized with two variables R and θ:$ \begin{align} M(R,\theta) = m_0 R^{1/3}\theta, \end{align} $

(11) where the reduced temperature r and the dimensionless magnetic field H are expressed as:
$ \begin{align} &r(R,\theta) = R(1-\theta^2), \end{align} $

(12) $ \begin{align} &H(R,\theta) = h_0 R^{5/3}\theta(3-2\theta^2), \end{align} $

(13) where we have adopted the values of the Ising critical exponents [60], and the normalization constants
$ m_0 $ and$ h_0 $ are fixed by the conditions$ M(r = -1,H = 0^+) = 1 $ and$ M(r = 0,H = 1) = 1 $ . From Eq. (11), the susceptibility of the 3D Ising model can be calculated:$ \begin{align} \chi_M(r,H) = \frac{\partial M(r,H)}{\partial H} \Bigg|_r = \frac{m_0}{h_0} \frac{1}{R^{4/3}(3+2\theta^2)}. \end{align} $

(14) The susceptibility
$ \chi_{M}(r,H) $ of the 3D Ising system is translated into$ \chi_{M}(T,\mu) $ on the temperature T and chemical potential μ plane$ (T,\mu) $ with the linear mapping as in Refs. [37,42], where T linearly relates to H:$ (T-T_{\rm c})/ $ $\Delta T = H/\Delta H $ , and r is treated as a free parameter to simulate the change of μ [42]. The critical temperature is set to$ T_{\rm c} = 160 $ MeV, and the width of the critical region is set to$ \Delta T/\Delta H = 10 $ MeV. As in Ref. [61], we assume the critical component of the conserved charge for the hot QCD systems$ \chi^{\rm cr}(T,\mu) $ is directly proportional to the Ising component$ \chi_{M}(T,\mu) $ and satisfies similar critical behavior①:$ \begin{align} \frac{\chi^{\rm cr}(T,\mu)}{\chi^H} = c_c \chi_M(T,\mu) = c_c \frac{m_0}{h_0} \frac{1}{R^{4/3}(3+2\theta^2)}, \end{align} $

(15) where the dimensionless factor
$ c_c $ is treated as a free parameter.$ \chi^H $ is the susceptibility in the hadronic medium, which can be absorbed by the definitions$ C'(y_1-y_2;\tau)\equiv $ $ C(y_1-y_2;\tau)/\chi^H $ and$ K'(\Delta y,\tau)\equiv K(\Delta y,\tau)/\chi^H $ . In the following calculations, we omit the prime to simplify the notation.Considering that the evolving hot QCD system belongs to model H in the classification of Ref. [54], we scale the diffusion coefficient
$ D^{\rm cr}_C $ with the correlation length$ \xi $ as:$ D^{\rm cr}_C\sim \xi^{-2-\chi_\eta+\chi_\lambda} $ with the exponents$ \chi_\eta\simeq 0.04 $ and$ \chi_\lambda\simeq 0.916 $ [54]. The correlation length$ \xi $ in$ \tau-y $ frame is connected to the susceptibility$ \chi^{\rm cr} $ as:$ \begin{align} \xi = \xi_0\left(\frac{\chi^{\rm cr}}{\chi^H}\right)^{1/(2-\chi_\eta)}, \end{align} $

(16) where we set
$ \xi_0 = 0.1 $ . Correspondingly, the parameterized$ D^{\rm cr}_C $ is:$ \begin{align} D^{\rm cr}_C(r,H) = d_c \left[\frac{\chi^{\rm cr}(r,H)}{\chi^H}\right]^{(-2+\chi_\eta+\chi_\lambda)/(2-\chi_\eta)} \end{align}, $

(17) where the constant
$ d_c = 1 $ fm, as used in Ref. [42].We only focus on an evolving system in 1+1-dimension with Bjorken expansion. We assume that the heat bath is evolving along a trajectory with fixed r, and the temperature T dropping down with the proper time τ as [37]:
$ \begin{align} T(\tau) = T_0\left(\frac{\tau_0}{\tau}\right)^{c^2_s}, \end{align} $

(18) where the speed of sound is taken as
$ c^2_s = 0.15 $ . The initial time$ \tau_0 $ and the corresponding temperature$ T_0 $ are described in Sec. 4. -
The correlation (3) and cumulant (7) obtained from solving SDE (1) are non-universal and sensitive to some inputs in the parametrization of
$ \chi(\tau) $ and$ D(\tau) $ , such as the strength of the critical component$ c_c $ , initial temperature$ T_0 $ , etc. In Refs. [41] and [51], the universal functions were constructed within the framework of the Kibble-Zurek mechanism for model A, which involves with the evolving non-conserving order parameter field near the critical point. In this section, we study the possible universal behavior of the correlation function (3) and cumulant (7) for the evolving conserved charge of model B.For a dynamical system near the critical point, there are two competitive time scales, namely the relaxation time
$ \tau_{\rm{ rel}} $ that describes the time for the system to equilibrate, and the quench time$ \tau_{\rm{ quench}} $ that characterizes the alteration rate of the external potential.The Bjorken expansion of the hot medium Eq. (18) introduces the variation of the susceptibility
$ \chi(\tau) $ and diffusion coefficient$ D(\tau) $ , with which the quench time can be calculated as:$ \begin{align} \tau_{\rm{ quench}} = \left|\frac{\xi(\tau)}{\partial_\tau \xi(\tau)}\right|. \end{align} $

(19) For a diffusion system near the critical point, the relaxation time of the two-point correlation function takes the form
$ \tau_{\rm{ rel}} = [2 D(\tau) q^2]^{-1} $ for a particular mode q. For the slow modes with$ q\ll \xi^{-1} $ , the relaxation time is large compared to$ \tau_{\rm{ quench}} $ , which leads to these modes moving out of equilibrium as the system evolves near the critical point. For the fast modes with$ q\gg \xi^{-1} $ , the relaxation times are small, which corresponds to sufficiently fast equilibration even near the critical point. In this work, we focus on the mode with$ q\xi = 1 $ , and the relaxation time is given by:$ \begin{align} \tau_{\rm{ rel}} = \frac{\xi^2}{2 D(\tau)}. \end{align} $

(20) The relaxation time
$ \tau_{\rm{ rel}} $ is strongly enhanced as the system cools down to the critical point and the quench time$ \tau_{\rm{ quench}} $ continuously decreases. Consequentially, there exists a point$ \tau^* $ , where the relaxation time equals to quench time, after which the system goes out of equilibrium with the formation of correlated patches. According to the Kibble-Zurek Mechanism, the characteristic time scale$ \tau_{\rm{ KZ}} $ and scale in the longitudinal direction$ l_{\rm{ KZ}} $ are determined by$ \tau^* $ with [41]:$ \begin{align} \tau_{\rm{ KZ}} = \tau_{\rm{ rel}}(\tau^*) = \tau_{\rm{ quench}} (\tau^*), \qquad l_{\rm{ KZ}} = \xi(\tau^*). \end{align} $

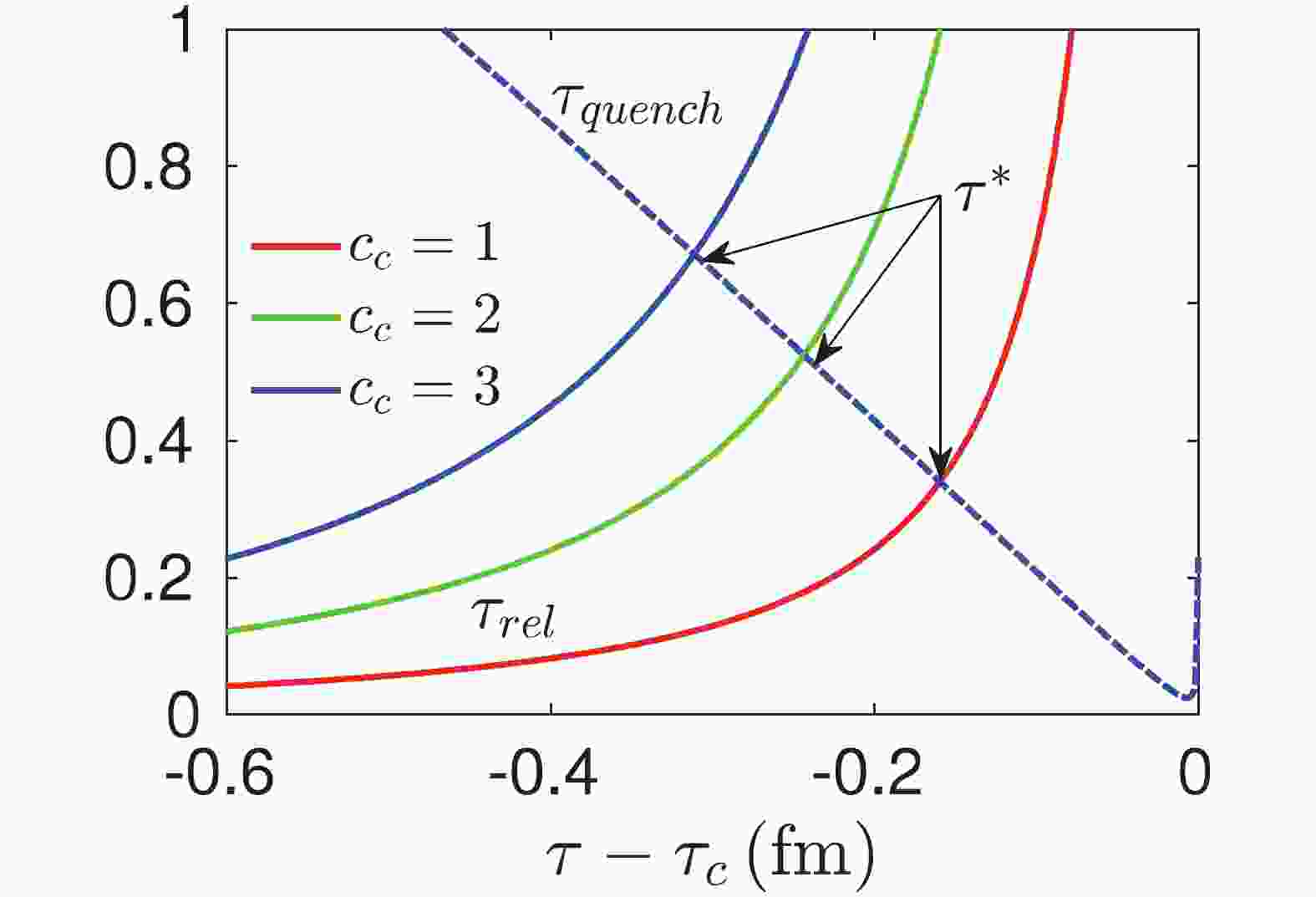
(21) In Fig. 1, we plot the relaxation time
$ \tau_{\rm{ rel}} $ and quench time$ \tau_{\rm{ quench}} $ as functions of$ \tau-\tau_c $ , where$ \tau_c $ is the time when the temperature of the system hits the critical temperature$ T_c $ . It shows that the relaxation time$ \tau_{\rm{ rel}} $ increases and the quench time$ \tau_{\rm{ quench}} $ decreases as the system approaches to the critical point, and the proper time$ \tau^* $ can be determined by Eq. (21).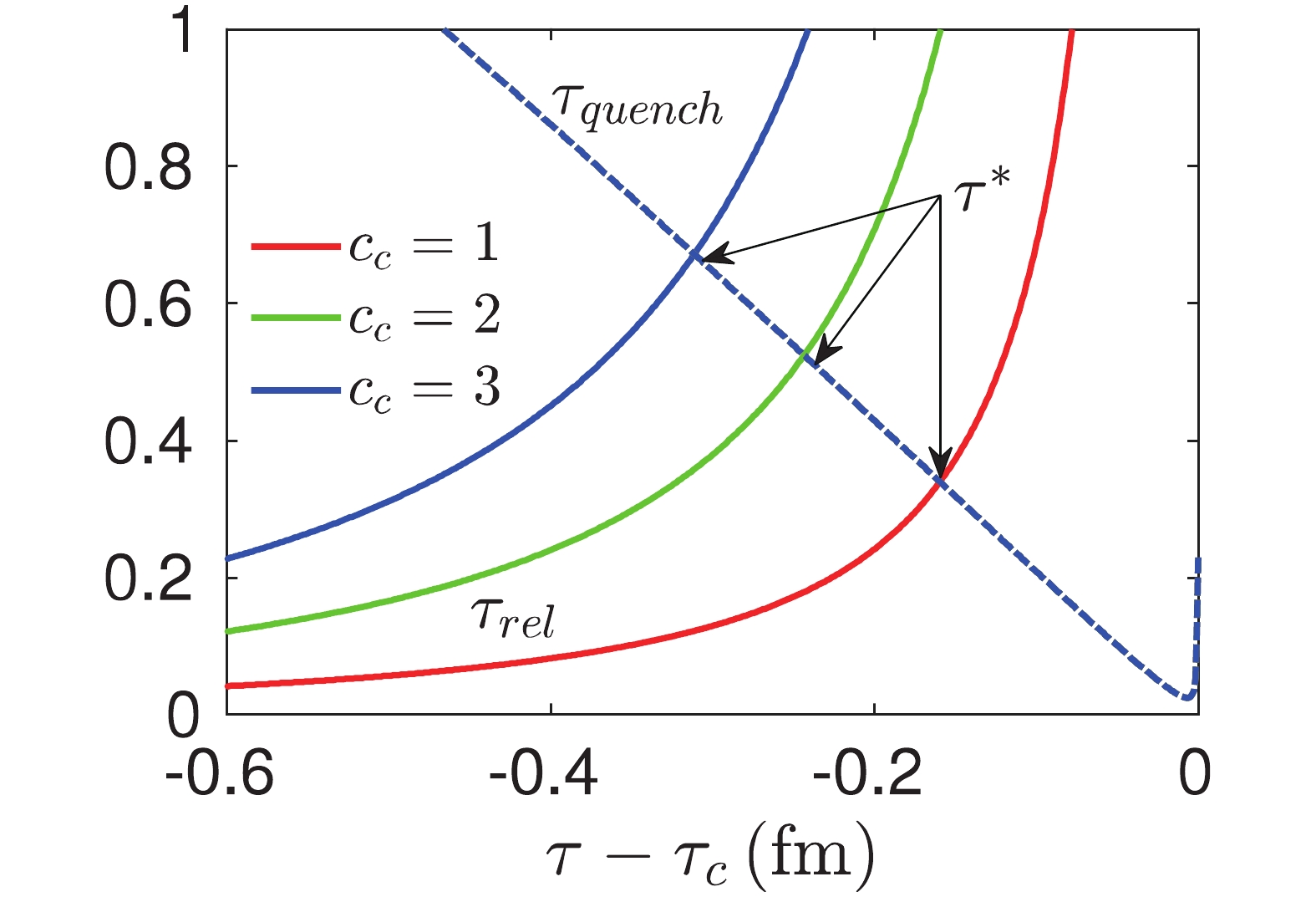
Figure 1. (color online) Temporal evolution of quench time
$\tau_{\rm{quench}}$ and relaxation time$\tau_{\rm{rel}} $ with different$c_c $ . Location of the proper time$\tau^* $ is computed from$\tau_{\rm{rel}}(\tau^*)=\tau_{\rm{quench}}(\tau^*) $ .After obtaining the characteristic scales
$ \tau_{\rm{ KZ}},\,l_{\rm{ KZ}} $ in Eq. (21), the universal function is constructed with the following redefined variables:$ \begin{split} \tilde{\tau}&\equiv (\tau-\tau_c)/\tau_{\rm{ KZ}},\quad \tilde{y}\equiv y/l_{\rm{ KZ}},\quad \tilde{\xi}\equiv \xi/l_{\rm{ KZ}},\quad\\ \tilde{D}&\equiv D/l^{-2+\chi_\eta+\chi_\lambda}_{\rm{ KZ}},\quad \tilde{\chi} \equiv \chi /l^{2-\chi_\eta}_{\rm{ KZ}}. \end{split} $

(22) The rescaled correlation function
$ \tilde{C}(\tilde{y}_1-\tilde{y}_2,\tilde{\tau}) $ and the rescaled function of cumulant$ \tilde{K}\left(\Delta y/l_{\rm{ KZ}}, \tilde{\tau}\right) $ is constructed as$ \begin{split} C(y_1-y_2,\tau) =& l^{1-\chi_\eta}_{\rm{ KZ}}\Bigg\{ \tilde{\chi}(\tilde{\tau}) \delta (\tilde{y}_1-\tilde{y}_2)\\ &-\int^{\tilde{\tau}}_{\tilde{\tau}_0}{\rm d}\tilde{\tau}'\frac{{\rm d}\tilde{\chi}(\tilde{\tau}')}{{\rm d}\tilde{\tau}'}\left[2\pi\int^{\tilde{\tau}}_{\tilde{\tau}'}{\rm d}\tilde{\tau}''\tilde{D}\right]^{-\frac{1}{2}}\\&\times\exp\left[-\frac{(\tilde{y}_1-\tilde{y}_2)^2}{2\int^{\tilde{\tau}}_{\tilde{\tau}'}{\rm d}\tilde{\tau}''\tilde{D}}\right]\Bigg\} \\ \equiv & l^{1-\chi_\eta}_{\rm{ KZ}} \tilde{C}(\tilde{y}_1-\tilde{y}_2,\tilde{\tau}), \end{split} $

(23) $ \begin{align} \begin{aligned} K(\Delta y,\tau) & = l^{2-\chi_\eta}_{\rm{ KZ}} \Bigg\{\tilde{\chi}(\tilde{\tau})-\int^{\tilde{\tau}}_{\tilde{\tau}_0} {\rm d}\tilde{\tau}'\frac{{\rm d}\tilde{\chi}(\tilde{\tau}')}{{\rm d}\tilde{\tau}'}F\bigg(\frac{\Delta y/l_{\rm{ KZ}}}{2[2\int^{\tilde{\tau}}_{\tilde{\tau}'}{\rm d}\tilde{\tau}'' \tilde{D}]^{1/2}}\bigg)\Bigg\}\\ &\equiv l^{2-\chi_\eta}_{\rm{ KZ}} \tilde{K}\left(\frac{\Delta y}{l_{\rm{ KZ}}}, \tilde{\tau}\right). \end{aligned} \end{align} $

(24) The rescaled functions
$ \tilde{C}(\tilde{y}_1-\tilde{y}_2,\tilde{\tau}) $ and$ \tilde{K}\left(\Delta y/l_{\rm{ KZ}}, \tilde{\tau}\right) $ as functions of the redefined variables$ \tilde{y}_1-\tilde{y}_2,\tilde{\tau} $ and$ \Delta y/l_{\rm{ KZ}}, \tilde{\tau} $ are universal and insensitive to some free parameters, which is demonstrated in the following section. The calculated correlation function$ C(y_1-y_2,\tau) $ and cumulant$ K(\Delta y,\tau) $ evolves with respect to proper time τ, while the Kibble-Zurek scaling procedure is with respect to the relative time$ \tau-\tau_c $ as shown in Eq. (21). Therefore, the above rescaling formulae (23) and (24) are valid near the critical point, where the relative time$ \tau-\tau_c $ is small. -
In this section, we demonstrate that the constructed universal functions Eq. (23) and Eq. (24) are insensitive to the free inputs, the strength of critical component
$ c_c $ and the initial temperature$ T_0 $ .First, we numerically calculate the correlation function (3) and cumulant (7) with the parameterizations of susceptibility
$ \chi(\tau) $ and diffusion coefficient$ D(\tau) $ along a particular trajectory with the fixed chemical potential$ r = 0.1 $ . The temperature drops according to Eq. (18) with the initial temperature$ T_0 = 190 $ MeV and the initial time$ \tau_0 $ is set at$ \tilde{\tau}_0\equiv (\tau_0-\tau_c)/\tau_{\rm{ KZ}} = -2.5 $ .The left panel of Fig. 2 presents the correlation function
$ C(y_1-y_2,\tau) $ as a function of$ y_1-y_2 $ with different strengths of the critical component$ c_c = 1,2,3 $ at a fixed rescaled time$ \tilde{\tau} = -0.5 $ , where the corresponding temperature T is larger than, yet close to$ T_c $ . As shown in Ref. [42], the correlation function as a function of$ y_1-y_2 $ has a local minimum at very small$ y_1-y_2 $ due to the$ \delta(y_1-y_2) $ contribution in Eq. (3). As expected, the correlation function (3) is sensitive to the strength of the critical component$ c_c $ . In the right panel of Fig. 2, we investigate the universal behavior of the reconstructed correlation function (23) within the framework of KZM. As shown in Fig. 1, the relaxation time$ \tau_{\rm{rel}} $ is significantly increased as the system approaches the critical point, whereas quench time$ \tau_{\rm quench} $ decreases, resulting in a point$ \tau^* $ where the relaxation time equals to the quench time. With the obtained characteristic scales$ l_{\rm{ KZ}} $ and$ \tau_{\rm{ KZ}} $ at$ \tau^* $ and the redefined variables (22), we construct the universal correlation function according to Eq. (23). The right panel of Fig. 2 plots the constructed universal correlation function$ \tilde{C}(\tilde{y}_1-\tilde{y}_2,\tilde{\tau}) $ at$ \tilde{\tau} = -0.5 $ with different$ c_c $ . Compared with the original correlation function$ C(y_1-y_2,\tau) $ that is sensitive to critical component$ c_c $ , these constructed correlation function$ \tilde{C}(\tilde{y}_1-\tilde{y}_2,\tilde{\tau}) $ perfectly converge into one universal curve.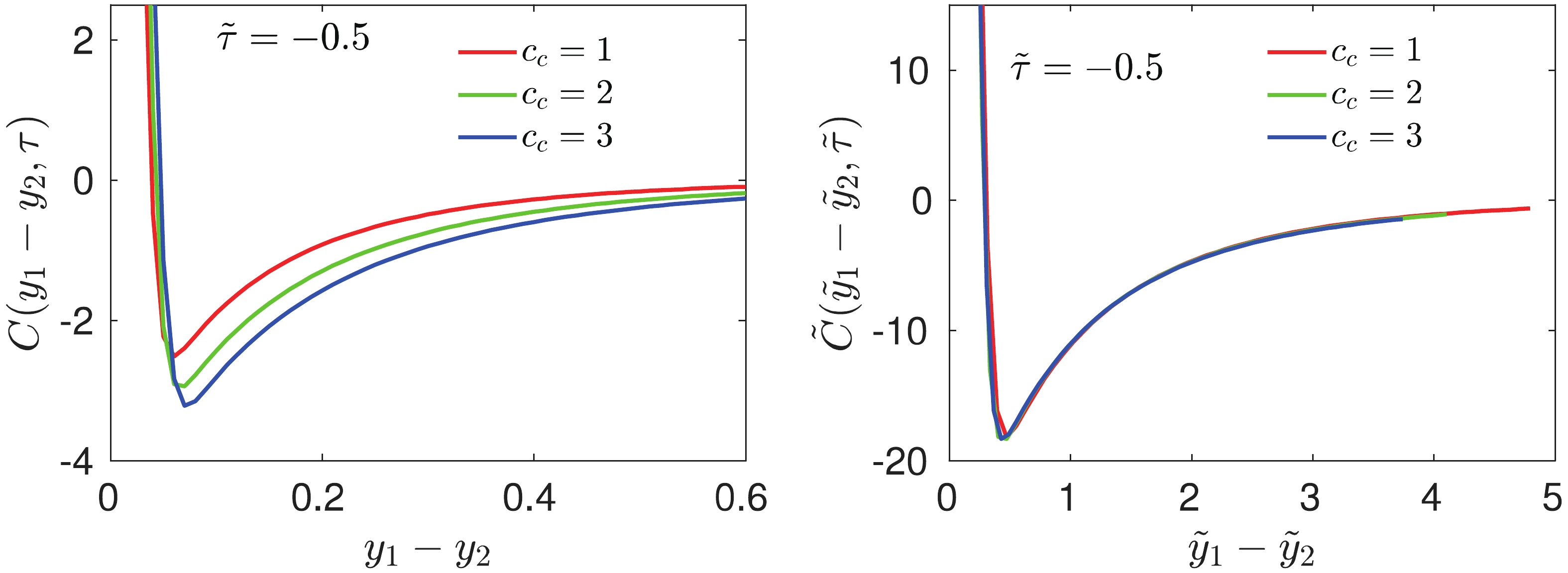
Figure 2. (color online) Left panel: Correlation function
$ C(y_1-y_2,\tau) $ of conserved charge as a function of rapidity interval$ y_1-y_2 $ , with different strengths of critical component$ c_c $ . The rescaled time is fixed at$ \tilde{\tau} = -0.5 $ (where the temperature T is close to, yet above$ T_c $ ). Right panel: Corresponding universal correlation function$ \tilde{C}(\tilde{y}_1-\tilde{y}_2,\tilde{\tau}) $ as a function of$ \tilde{y}_1-\tilde{y}_2 $ .In Fig. 3, we plot the correlation function
$ C(y_1-y_2,\tau) $ as a function of$ y_1-y_2 $ at the rescaled time$ \tilde{\tau} = 0.5 $ , where the temperature T is below$ T_c $ . In contrast to the local minimum of$ C(y_1-y_2,\tau) $ as a function of$ y_1-y_2 $ in Fig. 2, which arises from the$ \delta(y_1-y_2) $ contribution, the local minimum in the left panel of Fig. 3 is due to the changing sign of$ \chi'(\tau) $ in Eq. (3) when$ T<T_c $ , indicating that the susceptibility$ \chi(\tau) $ has a maximum with respect to the proper time τ. Meanwhile,$ C(y_1-y_2,\tau) $ at$ \tilde{\tau} = 0.5 $ also exhibits sensitivity to the strength of the critical component$ c_c $ . After the same scaling procedure as above, the constructed universal correlation function$ \tilde{C}(\tilde{y}_1-\tilde{y}_2,\tilde{\tau}) $ converges into a single curve.
Figure 3. (color online) Similar to Fig. 2, but with the rescaled time is set to
$ \tilde{\tau} = 0.5 $ (where the temperature T is close but below$ T_c $ ).In Fig. 4, we investigate the universal behavior of the cumulant
$ K(\Delta y,\tau) $ according to Eq. (24). The system evolves with the same parameters as the two above cases, where only the chemical potential is changed to$ r = 0.3 $ . The left panel of Fig. 4 shows the temporal evolution of$ K(\Delta y,\tau) $ with different strengths of the critical component$ c_c $ , where$ \Delta y $ is fixed at$ \Delta y/l_{\rm{ KZ}} = 4 $ . Similar to the two above cases of correlation function, the temporal evolution of second-order cumulant$ K(\Delta y,\tau) $ strongly depends on$ c_c $ . After rescaling$ K(\Delta y,\tau) $ and$ \tau-\tau_c $ with$ l^{2-\chi_\eta}_{\rm{ KZ}} $ and$ \tau_{\rm{ KZ}} $ , the constructed universal cumulant$ \tilde{K}(\Delta y/l_{\rm{ KZ}},\tilde{\tau}) $ is independent of the strength of the critical component$ c_c $ , as expected in Eq. (24).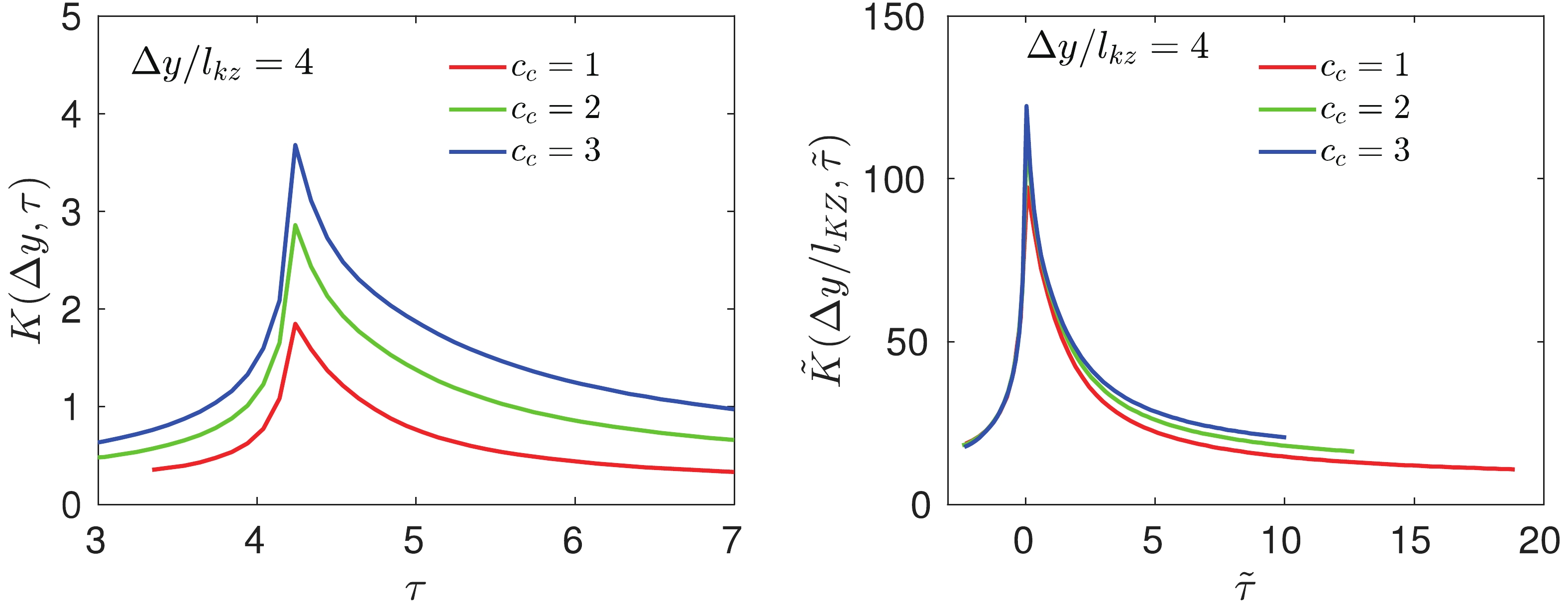
Figure 4. (color online) Temporal evolution of second-order cumulants
$ K(\Delta y,\tau) $ for conserved charge with different strengths of critical component$ c_c = 1,2,3 $ . Right panel: corresponding universal function$ \tilde{K}(\Delta y/l_{\mbox{ KZ}},\tilde{\tau}) $ as a function of rescaled timeFurthermore, we show that the constructed universal function
$ \tilde{K}(\Delta y/l_{\rm{ KZ}},\tilde{\tau}) $ is also not sensitive to the initial temperature$ T_0 $ . For this case, we evolve the systems with different initial temperature$ T_0 = 170,\ 180,\ 190 $ MeV at a fixed initial rescaled time$ \tilde{\tau}_0 = -2.5 $ along a trajectory with fixed chemical potential$ r = 0.3 $ . Once more, we assume one-dimensional Bjorken expansion and the temperature drops according to Eq. (18). The left panel of Fig. 5 plots the temporal evolution of the second-order cumulant$ K(\Delta y,\tau) $ with$ c_c = 3 $ and$ \Delta y/l_{\rm{ KZ}} = 4 $ , which exhibits a significant dependence on the initial temperature$ T_0 $ . After the same rescaling procedure as described above, the universal cumulant$ \tilde{K}(\Delta y/l_{\rm{ KZ}},\tilde{\tau}) $ is constructed, which is insensitive to the initial temperature$ T_0 $ as shown in right panel of Fig. 5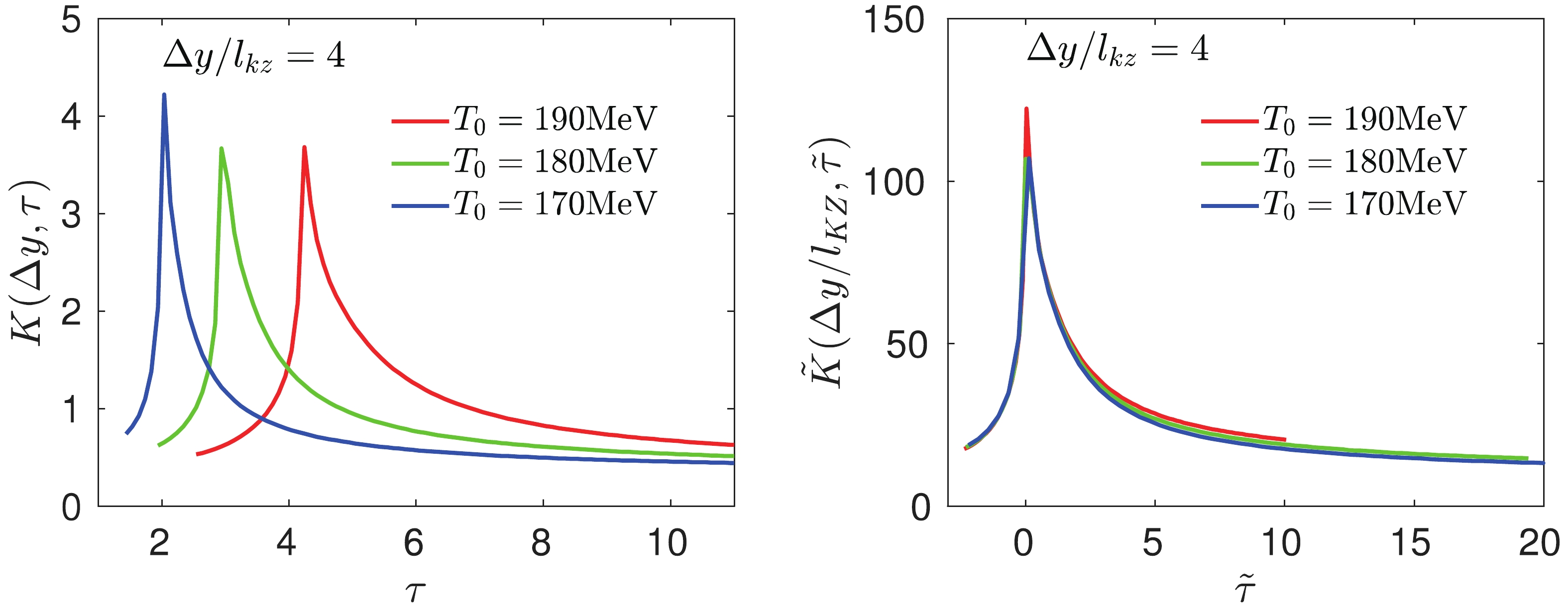
Figure 5. (color online) Similar to Fig. 4, but evolving the system with different initial temperatures
$ T_0 = 170,180,190\ $ MeV. -
We explored the Kibble-Zurek scaling for the critical fluctuation of the conserved charge within the framework of stochastic diffusion dynamics. By analytically solving the stochastic diffusion equation (1), the temporal evolution of the two-point correlation function
$ C(y_1-y_2,\tau) $ and the second-order cumulant$ K(\Delta y,\tau) $ of conserved charge are obtained, which are non-universal in terms of some free inputs in the model calculations, such as the initial temperature$ T_0 $ and the strengths of the critical components$ c_c $ in the mapping between the QCD medium and 3D-Ising model.By determinating the time
$ \tau^* $ , after which the system falls out of equilibrium, we calculated the characteristic scales$ \tau_{\rm{ KZ}} $ and$ l_{\rm{ KZ}} $ of the “frozen” system near the critical point. Using these obtained scales and rescaling the traditional two-point correlation function$ C(y_1-y_2,\tau) $ and cumulant$ K(\Delta y,\tau) $ , we constructed the universal correlation function$ \tilde{C}(\tilde{y}_1-\tilde{y}_2,\tilde{\tau}) $ and cumulant$ \tilde{K}(\Delta y/l_{{\rm KZ}},\tilde{\tau}) $ in terms of the rescaled rapidity$ \tilde{y} $ and proper time$ \tilde{\tau} $ , respectively. These rescaled functions are universal in terms of different free parameters. For instance, we have numerically shown that the universal functions$ \tilde{C}(\tilde{y}_1-\tilde{y}_2,\tilde{\tau}) $ and$ \tilde{K}(\Delta y/l_{\rm{ KZ}},\tilde{\tau}) $ converge into a single curve, and they are insensitive to the strength of critical component$ c_c $ and initial temperature$ T_0 $ , respectively.At last we would like to point out that this work focuses on the universal scaling of the two-point correlation function and second-order cumulant for the conserved charge based on the stochastic diffusion equation without the higher order coupling (1). At current stage, our constructed universal functions cannot be expected to connect with experimental data, since we used the 1+1-dimensional heat bath with the Bjorken approximation to simplify the calculations. In contrast, there are many natural extensions to this current study. For example, with the higher order contribution added to the stochastic diffusion equation of the conserved charge, the universal scaling of the two-point correlation function can be studied, as well as the ones of multi-point correlation functions and related higher-order cumulants. Besides, studying the universal scaling with a more realistic evolving medium are also important for a realistic predictions of the possible observables that might be measured in experiment. These work are complicated, but worthwhile to be investigated in the near future.
We are grateful for the fruitful discussions with F. Yan, D. Teaney, M. Kitazawa, and M. Asakawa. We also gratefully acknowledge the extensive computing resources provided by the Super-computing Center of Chinese Academy of Science (SCCAS), Tianhe-1A from the National Supercomputing Center in Tianjin, China, and the High-performance Computing Platform of Peking University.
-
In this appendix, we present the detailed derivation of the correlation function (3) from the stochastic diffusion equation (1), which is based
${\rm{on}} $ Ref. [42].With the Fourier transform
$\tag{A1} \begin{align} n(q,\tau) = \int {\rm d}y {\rm e}^{-{\rm i}qy}n(y,\tau), \end{align} $

SDE (1) in the Fourier space is written as:
$ \tag{A2}\begin{align} \frac{\partial}{\partial \tau} \delta n(q,\tau) = -D(\tau) q^2 \delta n(q,\tau) + {\rm i}q \zeta(q,\tau), \end{align} $

and the noise satisfies
$ \tag{A3}\begin{split} \begin{aligned} &\langle \zeta(q,\tau) \rangle = 0,\\ &\langle \zeta(q_1,\tau_1) \zeta(q_2,\tau_2) \rangle = 4\pi \chi(\tau) D(\tau) \delta (q_1+q_2) \delta (\tau_1-\tau_2). \end{aligned} \end{split} $

Therefore, one could obtain the temporal evolution of the correlation function in q space :
$ \begin{align} \frac{\partial}{\partial \tau}\langle \delta n(q_1,\tau) \delta n(q_2,\tau) \rangle =& -D(\tau) (q^2_1+q^2_2) \langle \delta n(q_1,\tau) \delta n(q_2,\tau) \rangle\nonumber \\& + 4\pi q_1q_2 \chi(\tau) D(\tau) \delta (q_1+q_2), \end{align} $

based on which the relaxation time of the correlation function is obtained as:
$ \tau_{\mbox{rel}} = [ D(\tau) (q^2_1+q^2_2)]^{-1} $ . With the assumption of the locality in the initial fluctuations$\tag{A4} \begin{align} \langle \delta n(q_1,\tau_0) \delta n(q_2,\tau_0) \rangle = 2\pi \delta(q_1+q_2) \chi(\tau_0), \end{align} $

the solution of Eq. (A4) is calculated to be
$\tag{A5} \begin{split} \langle \delta n(q_1,\tau) \delta n(q_2,\tau) \rangle = 2\pi \delta(q_1+q_2) \bigg (\chi(\tau_0) {\rm e}^{-q^2_1[d(\tau_0,\tau)]^2}+2q^2_1\int^\tau_{\tau_0} {\rm d}\tau' \chi(\tau')D(\tau'){\rm e}^{-q^2_1[d(\tau',\tau)]^2}\bigg). \end{split} $

Then, the correlation function in y space is computed as
$\tag{A6} \begin{split}\langle \delta n(y_1,\tau) \delta n(y_2,\tau) \rangle=& \chi(\tau_0) G(y_1-y_2;2d(\tau_0,\tau)) +\int^\tau_{\tau_0} {\rm d}\tau'\chi(\tau') \frac{\rm d}{{\rm d}\tau'} G(y_1-y_2;2d(\tau',\tau)) \\=& \chi(\tau) \delta(y_1-y_2) - \int^\tau_{\tau_0} {\rm d}\tau' \chi'(\tau') G(y_1-y_2;2d(\tau',\tau)). \end{split} $

Meanwhile, the second order cumulant
$ K(\Delta y,\tau) $ can be straightforwardly calculated, as shown in Eq. (7).
Universal scaling of conserved charge in stochastic diffusion dynamics
- Received Date: 2019-03-15
- Available Online: 2019-08-01
Abstract: We explore the Kibble-Zurek scaling of conserved charge using stochastic diffusion dynamics. The characteristic scales





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF

















 DownLoad:
DownLoad: