-
Most hadrons produced in high energy collisions have a relatively low (transverse) momentum perpendicular to the beam axis. The production of soft hadrons is mainly driven by the soft QCD processes, and in particular the non-perturbative hadronization. Experimental and theoretical studies of soft hadron production are important for understanding the properties of the soft parton system created in collisions, and for testing and/or developing phenomenological models. Heavy-ion physics at the SPS, RHIC and LHC energies shows that quark-gluon plasma (QGP) is created in the early stage of collisions. In
$ pp $ and/or$ p\bar{p} $ collisions, it is usually assumed that QGP is not created, at least not up to the RHIC energies. However, recent measurements at the LHC energies show a series of new hadron production phenomena in$ pp $ collisions, such as the ridge and collectivity behavior [1-3], increased baryon-to-meson ratio, and increased strangeness [4-6]. Theoretical studies of these new phenomena mainly focus on how the features of a small partonic system are related to these observations by considering different mechanisms, such as the color re-connection, string overlap and/or color rope [7-10], or by considering the creation of mini-QGP or the phase transition [11-16].In our latest works [17-21], by studying the available data for the hadronic
$ p_{T} $ spectra and yields, we proposed a new understanding of the novel features of hadron production in small quark/parton systems created in$ pp $ and/or$ p $ -Pb collisions at the LHC energies, i.e. a change of the hadronization mechanism from the traditional fragmentation to quark (re-)combination. In the quark (re-) combination mechanism (QCM), some typical features of the identified hadron production appear, such as the enhanced baryon-to-meson ratio and quark number scaling of hadron elliptical flow at intermediate$ p_{T} $ . These features were observed in the relativistic heavy-ion collisions [22-24], and recently also in$ pp $ and$ p $ -Pb collisions at the LHC energies in the high multiplicity classes [3, 4, 6, 25]. In particular, a quark number scaling property of the hadron transverse momentum spectra was observed in$ p $ -Pb collisions at$ \sqrt{s_{\rm NN}} = 5.02$ TeV [17].Recently, the ALICE collaboration reported
$ p_{T} $ spectra of the identified hadrons in different multiplicity classes in$ pp $ collisions at$ \sqrt{s} = $ 7 TeV [26], and preliminary data for the inelastic events in$ pp $ collisions at$ \sqrt{s} = $ 13 TeV [27]. For the first time, a clear signal of the quark number scaling property in the hadronic$ p_T $ spectra in$ pp $ collisions is seen. Considering the production of baryons$ \Omega^{-}\left(sss\right) $ and mesons$ \phi\left(s\bar{s}\right) $ , the momentum distribution functions$ f\left(p_{T}\right)\equiv {\rm d}N/{\rm d}p_{T} $ in QCM with the equal velocity combination approximation read as$ f_{\Omega}\left(p_{T}\right) = \kappa_{\Omega}\left[f_{s}\left(\frac{p_{T}}{3}\right)\right]^{3}, $

(1) $ f_{\phi}\left(p_{T}\right)= \kappa_{\phi}f_{s}\left(\frac{p_{T}}{2}\right)f_{\bar{s}}\left(\frac{p_{T}}{2}\right) = \kappa_{\phi}\left[f_{s}\left(\frac{p_{T}}{2}\right)\right]^{2}. $

(2) Here,
$ \kappa_{\phi} $ and$ \kappa_{\Omega} $ are coefficients independent of momentum.$ f_{s,\bar{s}}\left(p_{T}\right) $ is the$ s $ ($ \bar{s} $ ) quark distribution at hadronization, and we assume$ f_{s}\left(p_{T}\right) = f_{\bar{s}}\left(p_{T}\right) $ in the center rapidity region at the LHC energies. With the above two formulas, we get a correlation between the production of$ \Omega^{-} $ and$ \phi $ in QCM$ f_{\phi}^{1/2}\left(2p_{T}\right) = \kappa_{\phi,\Omega}f_{\Omega}^{1/3}\left(3p_{T}\right) = \kappa_{\phi}^{1/2}f_{s}\left(p_{T}\right), $

(3) where
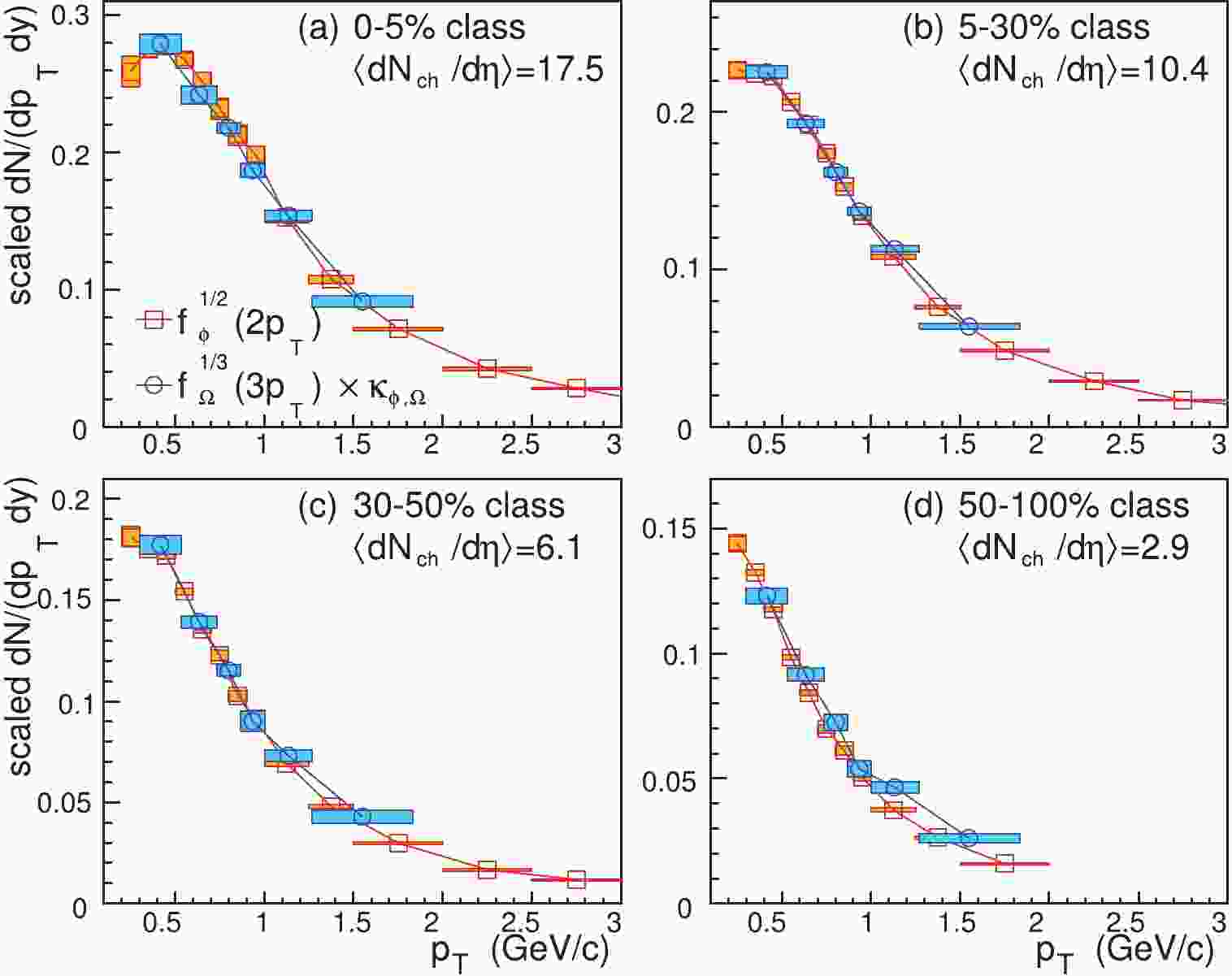
$ \kappa_{\phi,\Omega} = \kappa_{\phi}^{1/2}/\kappa_{\Omega}^{1/3} $ is independent of momentum. In order to check this scaling property, we apply the following operation on the$ {\rm d}N/({\rm d}p_{T}{\rm d}y) $ data for$ \Omega^- $ and$ \phi $ at midrapidity [26]: (i) we divide the$ p_{T} $ bin for$ \Omega^{-} $ ($ \phi $ ) by 3 (2), (ii) take the$ 1/3 $ ($ 1/2) $ power of the measured$ {\rm d}N/({\rm d}p_{T} {\rm d}y) $ for$ \Omega^{-} $ ($ \phi $ ), and (iii) multiply$ \left( {\rm d}N_{\Omega}/ ({\rm d}p_{T}{\rm d}y)\right)^{1/3} $ by a constant factor$ \kappa_{\phi,\Omega} $ , so that the data points for small$ p_T $ ($ p_T\lesssim $ 0.5 GeV/c) are in coincidence with the scaled data for$ \phi $ as much as possible. We show in Fig. 1 the scaled data for$ \Omega^- $ and$ \phi $ in different multiplicity classes in$ pp $ collisions at$ \sqrt{s} = $ 7 TeV. The relative statistical uncertainties of the scaled data are only a few percent, and are shown as rectangles with filled colors in the figure. We see that in the high multiplicity classes, e.g. Fig.1(a) and (b), the scaled data for$ \Omega^{-} $ are consistent with those for$ \phi $ , and therefore the quark number scaling property holds. This verifies our argument in the recent work [21], and is a clear signal of quark combination hadronization in$ pp $ collisions at the LHC energies. In the low multiplicity classes, Fig. 1(c) and (d), the scaled data for$ \Omega^{-} $ are somewhat flatter than for$ \phi $ at$ p_{T}\gtrsim1 $ GeV/c, and the quark number scaling property seems to be broken to a certain extent. We note that this is probably due to the threshold effects of strange quark production [21].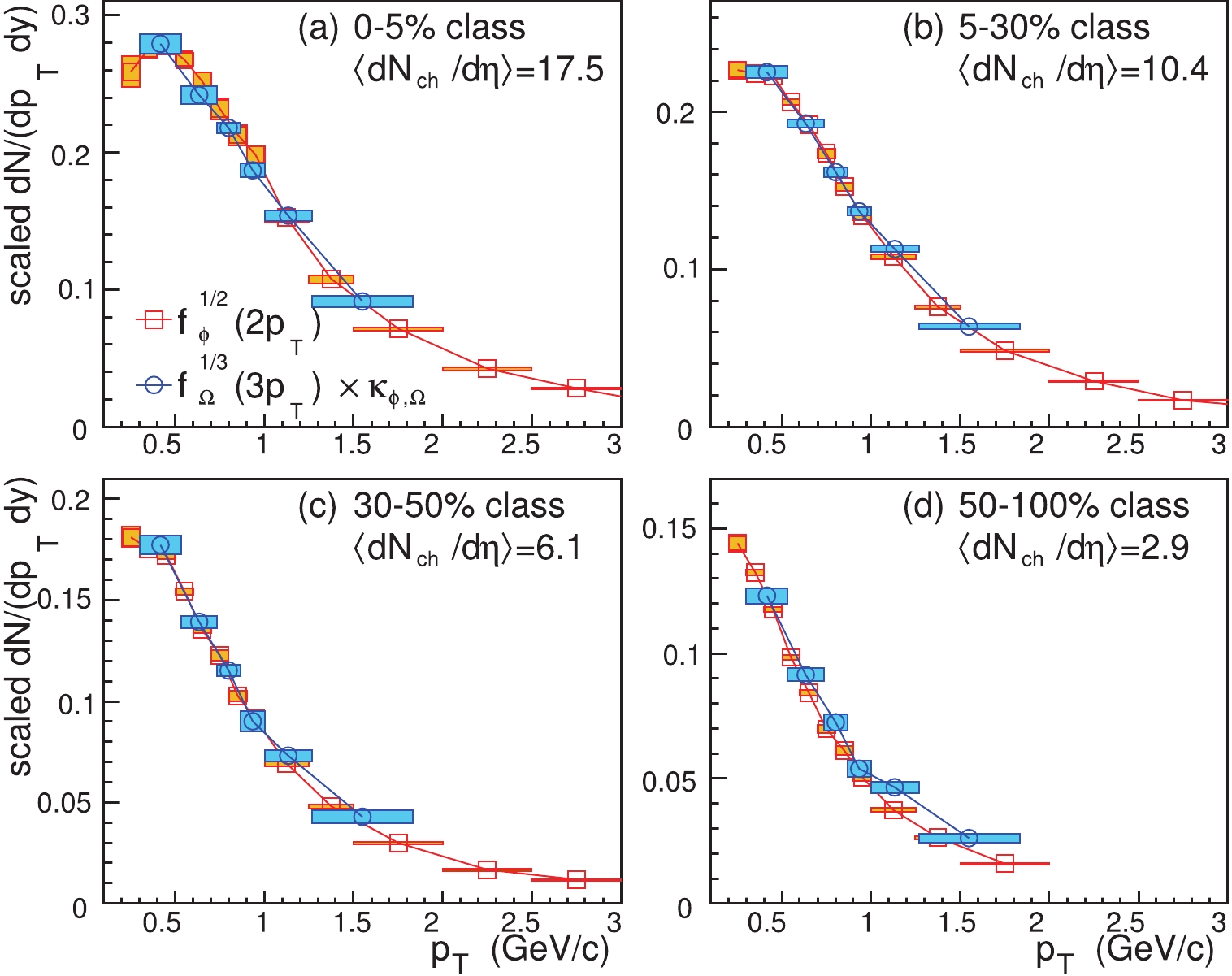
Figure 1. (color online) The scaling property in the
${\rm d}N/{\rm d}p_{T}{\rm d}y$ data for$\Omega^{-}$ and$\phi$ at midrapidity in different multiplicity classes in$pp$ collisions at$\sqrt{s} = 7$ TeV. The coefficient$\kappa_{\phi,\Omega}$ in the four multiplicity classes is taken as (1.76, 1.82, 1.83, 1.93). The data for$\Omega^{-}$ and$\phi$ are taken from Ref. [26].In Fig. 2, we show the scaled data for
$ \Omega^{-} $ and$ \phi $ in$ pp $ collisions at$ \sqrt{s} = $ 7 and 13 TeV [26-29] as a guide for energy dependence. We see that the quark number scaling property in the inelastic events in$ pp $ collisions at$ \sqrt{s} = $ 7 TeV is broken to a certain extent, but it holds well in the inelastic events in$ pp $ collisions at$ \sqrt{s} = $ 13 TeV. This is an indication of the quark combination hadronization at higher collision energies.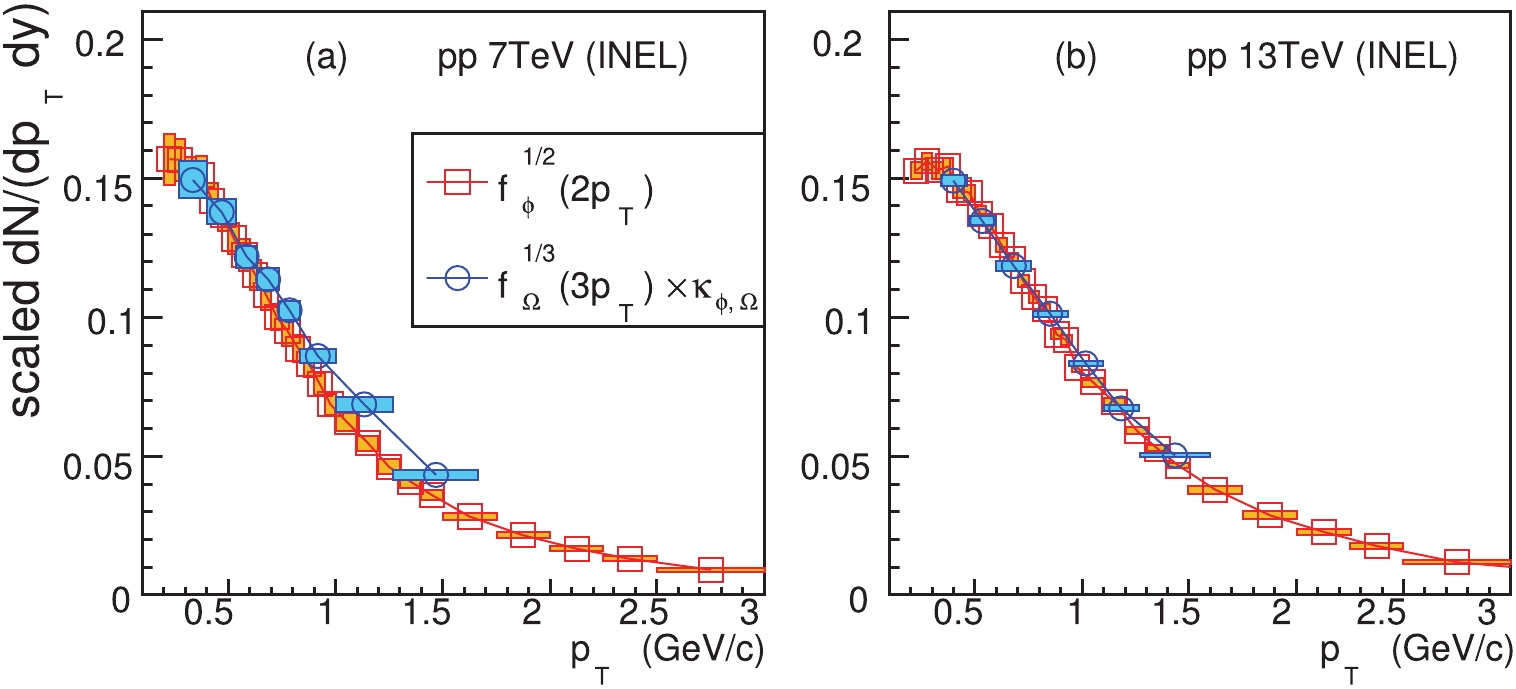
Figure 2. (color online) The scaling property in the
${\rm d}N/{\rm d}p_{T}{\rm d}y$ data for$\Omega^{-}$ and$\phi$ at midrapidity in the inelastic events in$pp$ collisions at$\sqrt{s} = $ 7 and 13 TeV. The coefficient$\kappa_{\phi,\Omega}$ is taken as (2.0, 1.5), respectively. The data for$\Omega^{-}$ and$\phi$ are taken from Refs. [26, 27].On the other hand, we performed a run of event generators Pythia8 [30, 31] and Herwig6.5 as a naive test of the string and cluster fragmentation mechanisms in
$ pp $ collisions at$ \sqrt{s} = 13 $ TeV. Fig. 3 shows the results for the scaled$ p_T $ spectra of$ \Omega $ and$ \phi $ at mid-rapidity given by the two event generators. Here, we adopted the Pythia version 8240 and Herwig version 6521. We chose two event classes, the inelastic non-diffractive events (INEL) and the high multiplicity events with$ {\rm d}N_{\rm ch}/{\rm d}y \geqslant $ 15, to check the multiplicity dependence of the predictions. In the Pythia8 simulations, we further checked the predictions with the default string fragmentation tune (marked as Pythia8 in Fig. 3), and with the rope hadronization mechanism (marked as Pythia8 rope in Fig. 3). Panels (a)-(c) show the scaled spectra of$ \Omega $ and$ \phi $ where the coefficient$ \kappa $ is chosen so that the two spectra are coincident at small$ p_T $ . Panel (d) shows the ratio of the two scaled spectra. We see that the constituent quark number scaling property given by the two event generators with the current tunes is violated by more than 20% at$ p_T \gtrsim $ 1.5 GeV/c.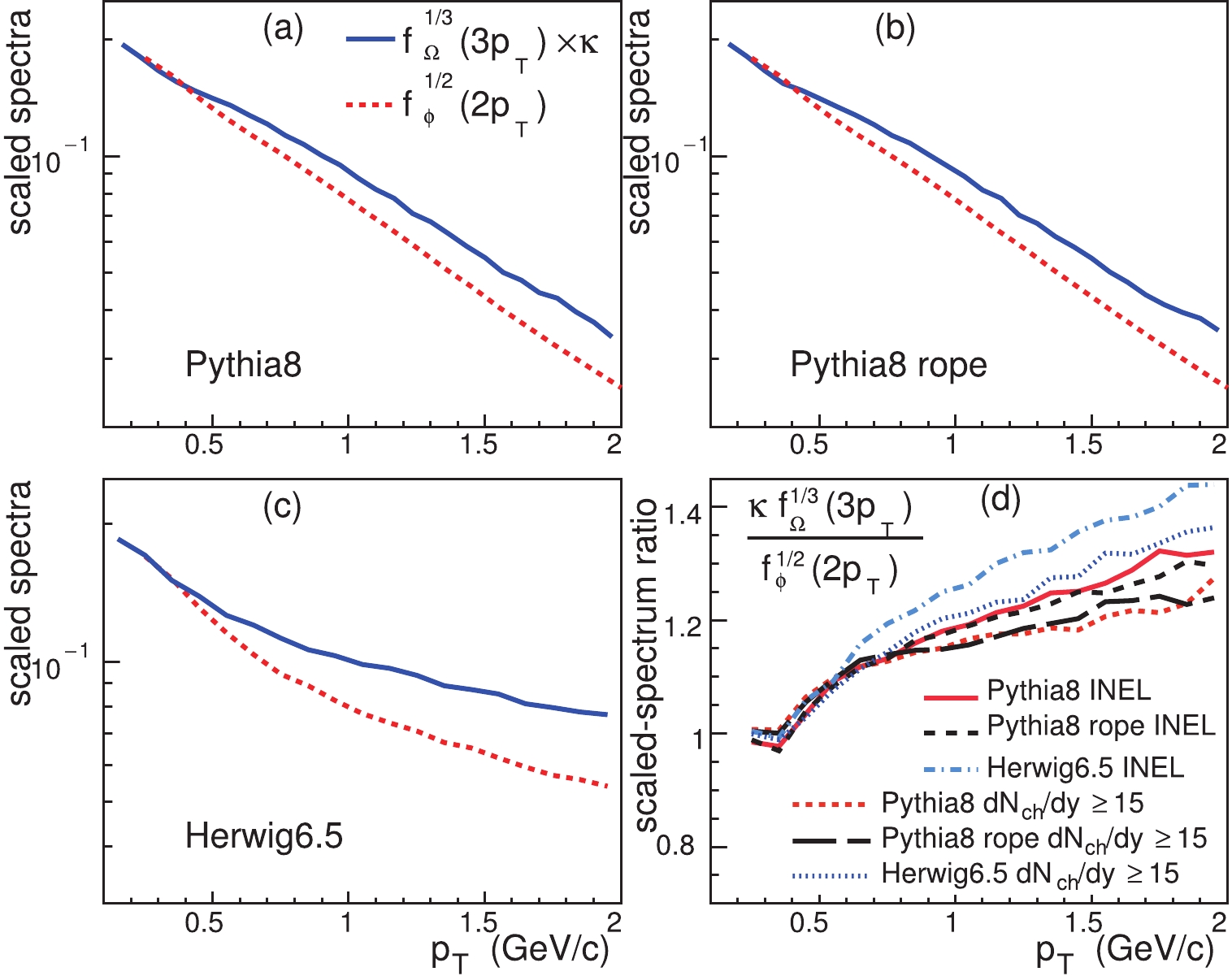
Figure 3. (color online) The scaled
$p_T$ spectra of$\Omega$ and$\phi$ at midrapidity in pp collisions at$\sqrt{s} = $ 13 TeV given by the event generators Pythia8 and Herwig6.5. See the text for detailed explanation.In this paper, we apply the quark combination model proposed in our recent works [17, 21] to systematically study the production of identified hadrons in
$ pp $ collisions at$ \sqrt{s} = $ 13 TeV. We calculate the$ p_{T} $ distributions and yields of identified hadrons and focus on various ratios or correlations of the hadronic yields and$ p_T $ spectra. We compare our results with the available experimental data to test the quark combination hadronization in$ pp $ collisions at the LHC energies. Predictions are made for future tests.The paper is organized as follows: Sec. 2 briefly introduces the model of quark (re)combination mechanism with the equal velocity combination approximation. Sec. 3 and Sec. 4 present our results and relevant discussions for the inelastic events and different multiplicity classes. A summary and discussion is given in Sec. 5.
-
Quark (re-)combination/coalescence mechanism was proposed in the 1970s [32] and has many applications in high energy
$ e^{-}e^{+} $ ,$ pp $ and heavy-ion collisions [33-39]. In particular, ultra-relativistic heavy-ion collisions create deconfined hot quark matter in a large volume whose microscopic hadronization process can be naturally described by QCM [40-45]. In this section, we briefly introduce the quark combination model, proposed in previous works [17, 21] in the framework of QCM with the equal velocity combination approximation. We take the constituent quarks and antiquarks as the effective degrees of freedom of the soft parton system created at hadronization. Combinations of constituent quarks and antiquarks with equal velocity result in formation of identified baryons and/or mesons. -
The momentum distributions of the identified baryons and mesons are denoted as
$ f_{B_{i}}\left(p_{B}\right) = N_{B_{i}}\,f_{B_{i}}^{\left(n\right)}\left(p_{B}\right), $

(4) $ f_{M_{i}}\left(p_{M}\right) = N_{M_{i}}\,f_{M_{i}}^{\left(n\right)}\left(p_{M}\right). $

(5) Here,
$ p_B $ and$ p_M $ are the momenta of baryons$ B_i $ and mesons$ M_i $ , and$ N_{B_{i}} $ and$ N_{M_{i}} $ are the momentum-integrated multiplicities of$ B_i $ and$ M_i $ , respectively. The superscript$ \left(n\right) $ means that the distribution function is normalized to one. In the equal velocity combination approximation, also called co-moving approximation, the momentum distributions of baryons and mesons can be simply obtained as a product of the distributions for the constituent quarks and/or antiquarks. We have, for$ B_{i} $ $ \left(q_{1}q_{2}q_{3}\right) $ $ f_{B_{i}}^{\left(n\right)}\left(p_{B}\right) = A_{B_{i}}\,f_{q_{1}}^{\left(n\right)}\left(x_{1}p_{B}\right)f_{q_{2}}^{\left(n\right)}\left(x_{2}p_{B}\right)f_{q_{3}}^{\left(n\right)}\left(x_{3}p_{B}\right), $

(6) and for
$ M_{i}\left(q_{1}\bar{q}_{2}\right) $ $ f_{M_{i}}^{\left(n\right)}\left(p_{M}\right) = A_{M_{i}}f_{q_{1}}^{\left(n\right)}\left(x_{1}p_{M}\right)f_{\bar{q}_{2}}^{\left(n\right)}\left(x_{2}p_{M}\right), $

(7) where
$ f_{q}^{\left(n\right)}\left(p\right)\equiv {\rm d}n_{q}/{\rm d}p $ is the momentum distribution of quarks normalized to one.$ A_{B_{i}}^{-1} = \int{\rm d}p\prod_{i = 1}^{3}f_{q_{i}}^{\left(n\right)}\left(x_{i}p\right) $ and$ A_{M_{i}}^{-1} = \int{\rm d}pf_{q_{1}}^{\left(n\right)}\left(x_{1}p\right)f_{\bar{q}_{2}}^{\left(n\right)}\left(x_{2}p\right) $ are the normalization coefficients for baryons$ B_{i} $ and mesons$ M_{i} $ , respectively. The momentum fraction$ x $ is given by, recalling that the momentum$ p = m\gamma v\propto m $ ,$ x_{i} = m_{i}\bigg/\sum\limits_{j}m_{j}, $

(8) where indexes
$ i,j = 1,2,3 $ are for baryons, and$ i,j = 1,2 $ for mesons. The quark masses are taken to be the constituent masses$ m_{s} = 500 $ MeV and$ m_{u} = m_{d} = 330 $ MeV.The multiplicities of baryons and mesons are
$ N_{B_{i}} = N_{q_{1}q_{2}q_{3}}P_{q_{1}q_{2}q_{3}\rightarrow B_{i}}, $

(9) $ N_{M_{i}} = N_{q_{1}\bar{q}_{2}}P_{q_{1}\bar{q}_{2}\rightarrow M_{i}}. $

(10) Here,
$ N_{q_{1}q_{2}q_{3}} $ is the number of all possible combinations of three quarks related to the$ B_{i} $ formation, and is taken as$ 6N_{q_{1}}N_{q_{2}}N_{q_{3}} $ ,$ 3N_{q_{1}}\left(N_{q_{1}}-1\right)N_{q_{2}} $ and$ N_{q_{1}}\left(N_{q_{1}}-1\right)\left(N_{q_{1}}-2\right) $ for the case of three different flavors, two identical flavors and three identical flavors, respectively. The factors 6 and 3 are the number of permutations related to the different quark flavors.$ N_{q_{1}\bar{q}_{2}} = N_{q_{1}}N_{\bar{q}_{2}} $ is the number of all possible$ q_{1}\bar{q}_{2} $ pairs related to the$ M_{i} $ formation.Considering the flavor independence of the strong interaction, we assume that the probability of
$ q_{1}q_{2}q_{3} $ forming a baryon and the probability of$ q_{1}\bar{q}_{2} $ forming a meson are flavor independent. The combination probability can then be written as$ P_{q_{1}q_{2}q_{3}\rightarrow B_{i}} = C_{B_{i}}\frac{\overline{N}_{B}}{N_{qqq}}, $

(11) $ P_{q_{1}\bar{q}_{2}\rightarrow M_{i}} = C_{M_{i}}\frac{\overline{N}_{M}}{N_{q\bar{q}}}. $

(12) Here,
$ \overline{N}_{B}/N_{qqq} $ denotes the average (or flavor blinding) probability of three quarks combining into a baryon.$ \overline{N}_{B} $ is the average number of total baryons and$ N_{qqq} = N_{q}(N_{q}-1)(N_{q}-2) $ is the number of all possible three-quark combinations, with$ N_{q} = \sum_{f}N_{f} $ the total quark number.$ C_{B_{i}} $ is the probability of selecting the correct discrete quantum number, such as spin, in the formation of$ B_{i} $ as$ q_{1}q_{2}q_{3} $ is destined to form a baryon. Similarly,$ \overline{N}_{M}/N_{q\bar{q}} $ denotes the average probability for a quark and antiquark to combine into a meson, and$ C_{M_{i}} $ is the branching ratio for the formation of$ M_{i} $ as$ q_{1}\bar{q}_{2} $ is destined to from a meson.$ \overline{N}_{M} $ is the total meson number, and$ N_{q\bar{q}} = N_{q}N_{\bar{q}} $ is the number of all possible quark-antiquark pairs for meson formation.In this paper, we only consider the ground state
$ J^{P} = 0^{-},\,1^{-} $ mesons and$ J^{P} = (1/2)^{+},\,(3/2)^{+} $ baryons in the flavor SU(3) group. For mesons$ C_{M_{j}} = \left\{ \begin{aligned} \frac{1}{1+R_{V/P}}\;\; {\rm{for }}\;\;&J^{P} = 0^{-} \rm{ mesons},\\ \frac{R_{V/P}}{1+R_{V/P}} \;\; \rm{for }\;\;& J^{P} = 1^{-} \rm{ mesons}, \end{aligned}\right. $

(13) where we introduce a parameter
$ R_{V/P} $ , which represents the relative production weight of the$ J^{P} = 1^{-} $ vector mesons to the$ J^{P} = 0^{-} $ pseudo-scalar mesons with the same flavor composition. For baryons$ C_{B_{j}} = \left\{ \begin{aligned} \frac{1}{1+R_{D/O}} \;\; \rm{for }\;\;& J^{P} = ({1}/{2})^{+} \rm{ baryons},\\ \frac{R_{D/O}}{1+R_{D/O}} \;\; \rm{for }\;\;& J^{P} = ({3}/{2})^{+} \rm{ baryons}, \end{aligned}\right. $

(14) except that
$ C_{\Lambda} = C_{\Sigma^{0}} = {1}/{(2+R_{D/O})} $ ,$ C_{\Sigma^{*0}} = {R_{D/O}}/{(2+R_{D/O})} $ ,$ C_{\Delta^{++}} = C_{\Delta^{-}} = C_{\Omega^{-}} = 1 $ . The parameter$ R_{D/O} $ stands for the relative production weight of the$ J^{P} = (3/2)^{+} $ decuplet to the$ J^{P} = (1/2)^{+} $ octet baryons of the same flavor content. Here,$ R_{V/P} $ is taken as 0.45 by fitting the data for the$ K^{*}/K $ ratio in$ pp $ collisions at$ \sqrt{s} = $ 7 TeV and$ p $ -Pb collisions at$ \sqrt{s_{\rm NN}} = $ 5.02 TeV [46], and$ R_{D/O} $ is taken as 0.5 by fitting the data for$ \Xi^{*}/\Xi $ and$ \Sigma^{*}/\Lambda $ [47]. The fraction of baryons relative to mesons is$ N_{B}/N_{M}\approx0.085 $ for vanishing net-quarks [18, 21, 45]. Using the unitarity constraint for hadronization,$ N_{M}+3N_{B} = N_{q} $ ,$ N_{B_{i}} $ and$ N_{M_{i}} $ can be calculated using the above formulas for the given quark numbers at hadronization.We summarize the main underlying dynamics of the model. The constituent quarks and antiquarks are assumed to be the effective degrees of freedom of the soft parton system at hadronization. Combinations of constituent quarks and antiquarks with equal velocity result in the formation of baryons and mesons. This is similar to the constituent quark model, i.e. the sum of the masses (and momenta) of the constituent quarks is used to construct the mass (and momentum) of a hadron. The model parameters
$ R_{V/P} $ and$ R_{D/O} $ contain the non-perturbative dynamics and are obtained by fitting the relevant experimental data. They are assumed to be relatively stable in/at different collision systems/energies. Also, the normalization of the hadronization process is a prerequisite for quark combination. The quark number conservation is not only globally satisfied via$ N_{M}+3N_{B} = N_{q} $ and$ N_{M}+3N_{\bar{B}} = N_{\bar{q}} $ , but is also satisfied for each quark flavor via$ \sum_{h} n_{q_i,h} N_h = N_{q_i} $ . Here,$ h $ runs over all hadron species, and$ q_i = d,u,s,\bar{d}, \bar{u},\bar{s} $ .$ n_{q_i,h} $ is the number of constituent quarks$ q_i $ in a hadron$ h $ . Therefore, this is a statistical model based on the constituent quark degrees of freedom, and is different from the popular parton recombination/coalescence models [40, 41] which adopt the Wigner wave function method with the instantaneous hadronization approximation. -
As the quark number at hadronization is small, the identified hadron production will suffer some threshold effects. For example, baryon production is forbidden for events with
$ N_{q}<3 $ . For events with$ N_{s}<3 $ ,$ \Omega^{-} $ baryon production is forbidden. In$ pp $ collisions at the LHC energies, the event-averaged number of strange quarks is$ \langle N_{s}\rangle\lesssim1 $ in the midrapidity region ($ |y|<0.5 $ ) for the inelastic events and not-too high multiplicity event classes. Therefore, the yield of$ \Omega^{-} $ is no longer completely determined by the average number of strange quarks but is also strongly influenced by the distribution of the strange quark number. The case of$ \Xi $ , which needs two strange quarks, is similar. We use$ {\cal{P}}\left(\left\{ N_{q_{i}}\right\} ,\left\{ \langle N_{q_{i}}\rangle\right\} \right) $ to denote the distribution of the quark number around the event average, and obtain the averaged multiplicity of identified hadrons by$ \langle N_{h_{i}}\rangle = \sum\limits_{\left\{ N_{q_{i}}\right\} }{\cal{P}}\left(\left\{ N_{q_{i}}\right\} ,\left\{ \langle N_{q_{i}}\rangle\right\} \right)N_{h_{i}}, $

(15) where
$ N_{h_{i}} $ is given by Eqs. (9) and (10), and is a function of$ \left\{ N_{q_{i}}\right\} $ .For simplicity, we assume the flavor-independent quark number distribution
$ {\cal{P}}\left(\left\{ N_{q_{i}}\right\} ,\left\{ \langle N_{q_{i}}\rangle\right\} \right) = \prod\limits_{f}{\cal{P}}\left(N_{f},\langle N_{f}\rangle\right), $

(16) where
$ f $ runs over$ u $ ,$ d $ ,$ s $ flavors. We neglect the fluctuation of net-charges and take$ N_{f} = N_{\bar{f}} $ in all events. The distribution of$ u $ and$ d $ quarks is based on the Poisson distribution$ Poi\left(N_{u(d)},\langle N_{u(d)}\rangle\right) $ . As discussed above, we in particular tune the strange quark distribution. Since for the minimum bias events and small multiplicity classes in$ pp $ collisions$ \langle N_{s}\rangle\lesssim1 $ , and the Poisson distribution$ Poi\left(N_{s},\langle N_{s}\rangle\right) $ in this case has a long tail for$ N_{s}\geqslant 3 $ which may over-weight the events with$ N_{s}\geqslant 3 $ , we distort the Poisson distribution by the suppression factor$ \gamma_{s} $ , i.e. we take${\cal{P}}\left(N_{s},\langle N_{s}\rangle\right) = {\cal{N}}Poi\left(N_{s},\langle N_{s}\rangle\right)\times[\gamma_{s}\,\Theta\left(N_{s}-3\right)+ \Theta(3-$ $N_{s})] $ , where$ \Theta\left(x\right) $ is the Heaviside step function and$ {\cal{N}} $ is the normalization constant.$ \gamma_{s} $ is taken as 0.8 for the inelastic (INEL > 0) events and the various multiplicity classes.There are other possible effects of the small number of quarks. For example, in the events with
$ N_{s} = N_{\bar{s}} = 1 $ , as$ s $ and$ \bar{s} $ are most likely created from the same vacuum excitation and therefore are not likely to directly constitute a color singlet, the$ \phi $ production is suppressed. In addition, as the distributions of quark momenta are dependent on the number of quarks (i.e. on the system size), we neglect such dependence in the given multiplicity classes. Their potential effects will be studied in a future work. -
We use the above quark combination model to describe the transverse production of hadrons at midrapidity in
$ pp $ collisions.The approximation of equal velocity combination in the model is reduced to the equal transverse-velocity combination. Here, we only study one dimensional$ p_T $ distribution of hadrons by further integrating over the azimuthal angle. The$ p_T $ distribution functions of quarks at hadronization and at midrapidity are input for the model and are denoted as$ f_{q_i}\left(p_T\right) = \langle N_{q_i} \rangle f_{q_i}^{\left(n\right)}\left(p_{T}\right) $ with$ q_i = d,u,s,\bar{d}, \bar{u}, \bar{s} $ .$ \langle N_{q_i} \rangle $ is the number of$ q_i $ in the rapidity interval$ |y|<0.5 $ , and$ f_{q_i}^{\left(n\right)}\left(p_{T}\right)\equiv {\rm d}n_{q_i}/{\rm d}p_{T} $ is the quark$ p_{T} $ spectrum normalized to one. We assume the iso-spin symmetry between up and down quarks, and also assume the charge conjugation symmetry between a quark and antiquark. Finally, we have only two input functions$ f_u(p_T) $ and$ f_s(p_T) $ , which can be determined by fitting the data for identified hadrons. -
Using the scaling property in Eq. (3) and the experimental data shown in Fig. 2, we can directly obtain the normalized
$ p_{T} $ distribution of strange quarks at hadronization, which can be parametrized in the form$ f_{s}^{\left(n\right)}\left(p_{T}\right) = {\cal{N}}_{s}\left(p_{T}+a_{s}\right)^{b_{s}}\left(1+\frac{\sqrt{p_{T}^{2}+M_{s}^{2}}-M_{s}}{n_{s}c_{s}}\right)^{-n_{s}}, $

(17) where
$ {\cal{N}}_{s} $ is the normalization constant, and the parameters are$ a_{s} = 0.15 $ GeV/c,$ b_{s} = 0.649 $ ,$ n_{s} = 4.14 $ ,$ M_{s} = 0.5 $ GeV and$ c_{s} = 0.346 $ . By fitting the data for the other hadrons such as protons and$ K^{*0} $ , we also obtain the$ p_{T} $ distribution of up/down quarks at hadronization. Taking the parametrization in Eq. (17), the parameters of up/down quarks are$ a_{u} = 0.15 $ GeV/c,$ b_{u} = 0.355 $ ,$ n_{u} = 3.46 $ ,$ M_{u} = 0.33 $ GeV and$ c_{u} = 0.358 $ . In Fig. 4, we plot$ f_{u}^{\left(n\right)}\left(p_{T}\right) $ and$ f_{s}^{\left(n\right)}\left(p_{T}\right) $ as a function of$ p_{T} $ , and their ratio in the inelastic events in$ pp $ collisions at$ \sqrt{s} = $ 13 TeV.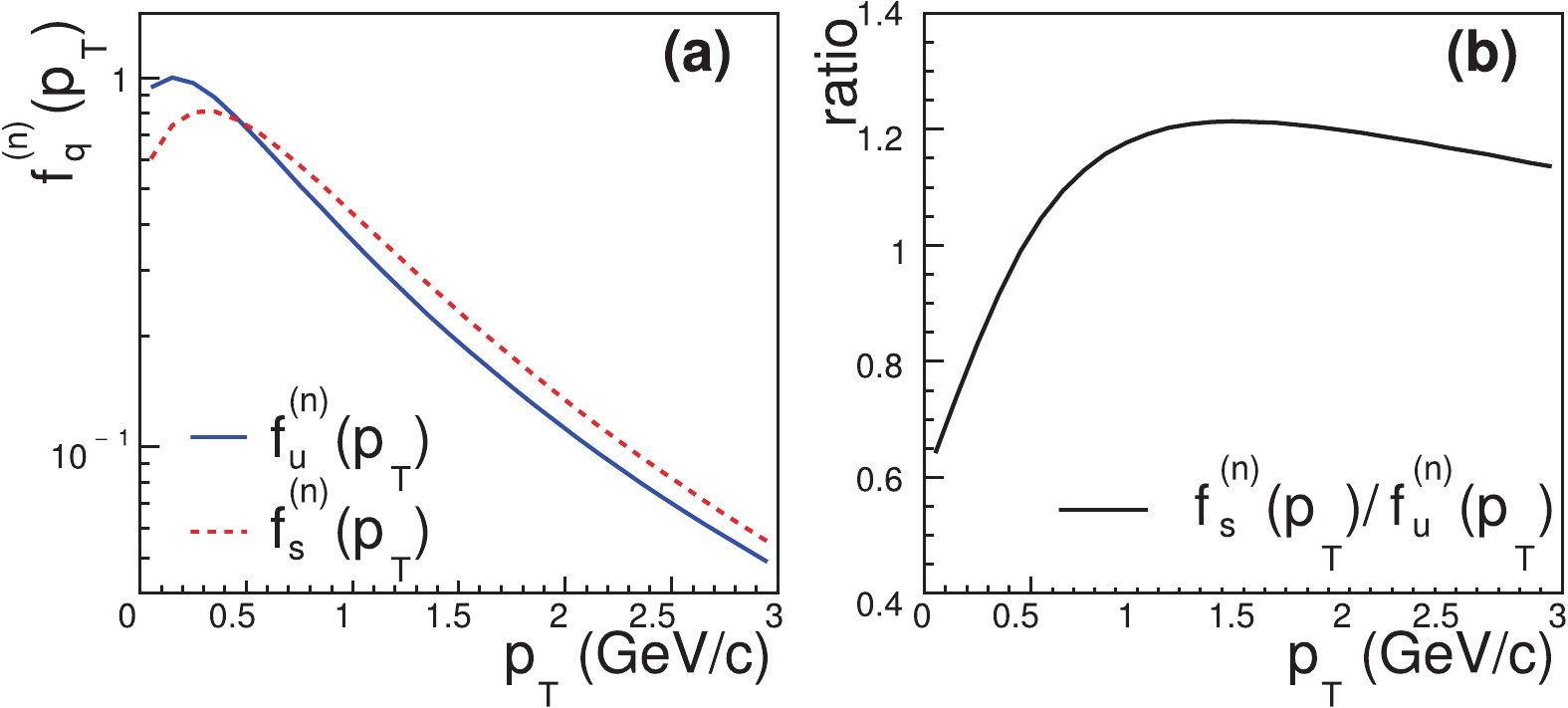
Figure 4. (color online) The
$p_{T}$ spectra of u and s quarks at midrapidity, and their ratio in the inelastic (INEL>0) events in pp collisions at$\sqrt{s} = $ 13 TeV.We emphasize that by taking advantage of the quark number scaling property, we can conveniently extract the momentum distributions of soft quarks at hadronization from the experimental data for the hadronic
$ p_{T} $ spectra. The extracted quark$ p_{T} $ spectra carry important information about the soft parton system created in$ pp $ collisions at the LHC energies. First of all, since the parameters$ b_s $ and$ b_u $ in the quark distribution function in Eq. (17) are obviously smaller than one, the extracted$ f_{u}^{\left(n\right)}\left(p_{T}\right) $ and$ f_{s}^{\left(n\right)}\left(p_{T}\right) $ deviate from the Boltzmann distribution in the low$ p_{T} $ range. This indicates that thermalization may be not reached in the small partonic system created in$ pp $ collisions at the LHC energies. Secondly, we see that the ratio$ f_{s}^{\left(n\right)}\left(p_{T}\right)/f_{u}^{\left(n\right)}\left(p_{T}\right) $ , Fig. 4 (b), increases for small$ p_{T} $ and then saturates (or only slightly decreases) with$ p_{T} $ . This property is similar to that observed in$ pp $ collisions at$ \sqrt{s} = $ 7 TeV [21] and in$ p $ -Pb collisions at$ \sqrt{s_{\rm NN}} = $ 5.02 TeV [17], and in heavy-ion collisions at RHIC and the LHC [48-50]. This information about the constituent quarks provides an important constraint for developing more sophisticated theoretical models of soft parton system created in high energy collisions. -
Among the hadrons that are often measured by experiments, pions and kaons are the most abundant particles. However, because the pion and kaon masses are significantly smaller than the sum of the masses of their constituent (anti-)quarks, the pion and kaon momenta can not be calculated by a simple combination of the constituent (anti-)quark momenta at hadronization [21]. Therefore, the momentum spectra of pions and kaons are not the most direct probes of the quark combination model, and these results are not shown here. On the other hand, protons,
$ \Lambda $ ,$ \Xi^{-} $ ,$ \Omega^{-} $ ,$ \phi $ and$ K^{*0} $ can be constructed from the constituent quarks and antiquarks. These hadrons can be used to effectively test the quark combination model.In Fig. 5, we show the calculated results for the
$ p_T $ spectra of protons,$ \Lambda $ ,$ \Xi^{-} $ ,$ \Omega^{-} $ ,$ \phi $ and$ K^{*0} $ in the inelastic (INEL > 0) events in$ pp $ collisions at$ \sqrt{s} = $ 13 TeV using the quark spectra in Fig. 4 and quark numbers$ \langle N_{u}\rangle = 2.8 $ and$ \langle N_{s}\rangle = 0.86 $ . The quark numbers are fixed by globally fitting the data for the$ p_T $ -integrated yield densities of these hadrons [27]. The solid lines are the QCM results which include the contribution of the strong and electromagnetic decay of the resonances. The symbols are the preliminary data for the hadronic$ p_T $ spectra at midrapidity measured by the ALICE collaboration [27]. We see that the data can in general be fitted well by QCM. Our results for$ K^{*0} $ are slightly below the data. If we multiply the$ K^{*0} $ spectrum by a constant factor, we see that the shape is in good agreement with the data.
Figure 5. (color online) The
$p_{T}$ spectra of identified hadrons at midrapidity in the inelastic (INEL>0) events in$pp$ collisions at$\sqrt{s} = $ 13 TeV. The solid lines are the results of QCM and the symbols are the preliminary data of the ALICE collaboration [27].Besides the scaling property between the
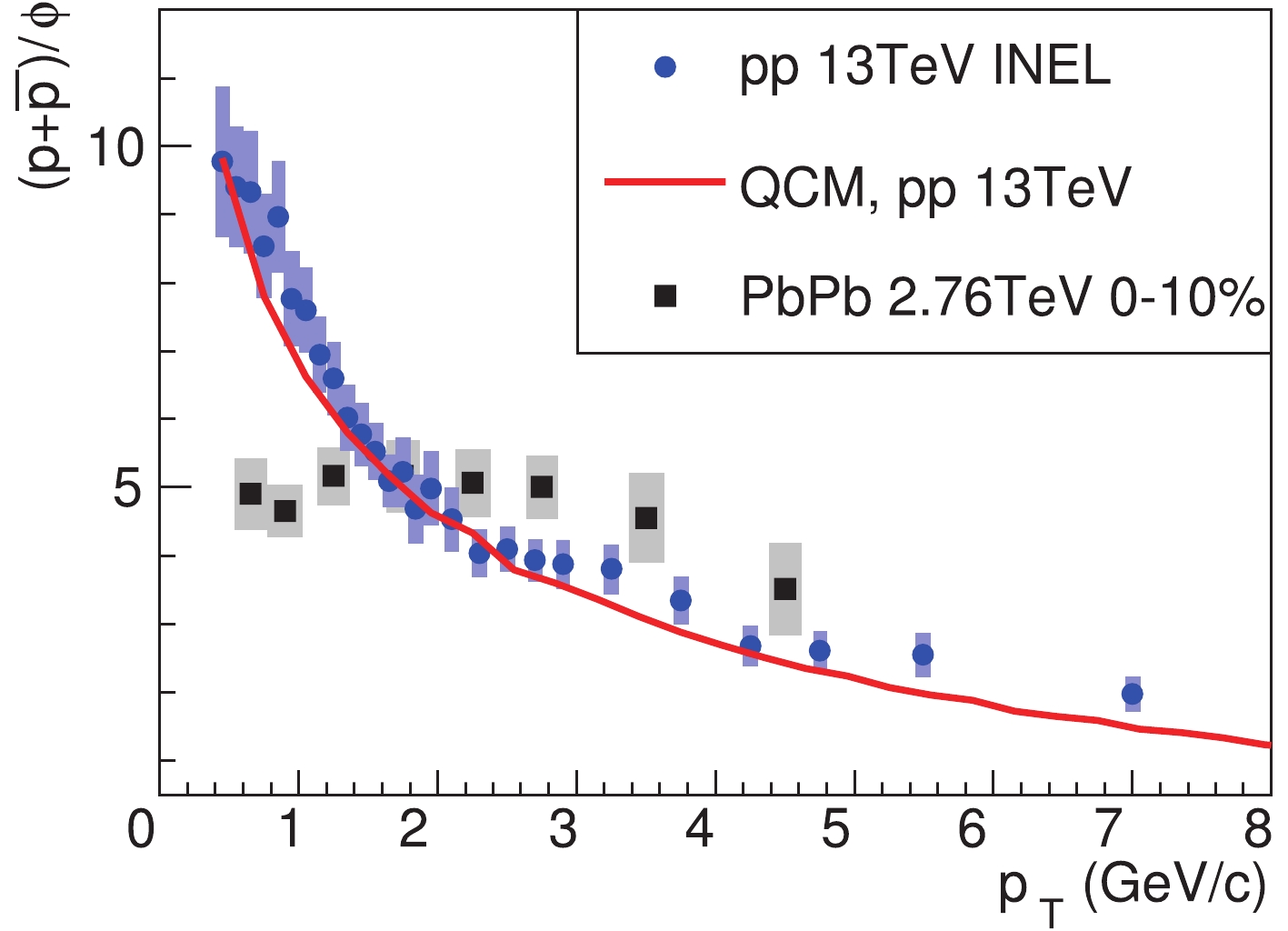
$ p_{T} $ spectra of$ \Omega^{-} $ and$ \phi $ shown in the Introduction, the ratio$ \left(p+\bar{p}\right)/\phi $ as a function of$ p_{T} $ can also give an intuitive picture of the microscopic mechanism of hadron production. Protons and$ \phi $ have similar masses but totally different quark content. In the central (0%-10% centrality) Pb-Pb collisions at$ \sqrt{s_{\rm NN}} = 2.76 $ TeV, the data for the$ \left(p+\bar{p}\right)/\phi $ ratio [51], black squares in Fig. 6, are almost flat with respect to$ p_{T} $ . The flat ratio is related to the similar masses of protons and$ \phi $ , and is usually attributed to the strong radial flow and statistical hadronization in the chemical/thermal equilibrium in relativistic heavy-ion collisions. However, the data for$ \left(p+\bar{p}\right)/\phi $ in the inelastic events in$ pp $ collisions at$ \sqrt{s} = $ 13 TeV [52], solid circles in Fig. 6, show a rapid decrease with increasing$ p_{T} $ . This is an indication of the out-of-thermal equilibrium in$ pp $ collisions. In QCM, the$ p_T $ distributions of identified hadrons are determined by the$ p_T $ spectra of (anti-)quarks at hadronization. The$ \left(p+\bar{p}\right)/\phi $ ratio in QCM reflects the ratio or the correlation between the third power of the$ u $ quark spectrum and the square of the$ s $ quark spectrum. With the quark spectra in Fig. 4 , which self-consistently describe the data for the hadronic$ p_T $ spectra in Fig. 5, the calculated$ p/\phi $ ratio in QCM, solid line in Fig. 6, shows a decreasing behavior with$ p_T $ and is in good agreement with the data for$ pp $ collisions [52].Hyperons
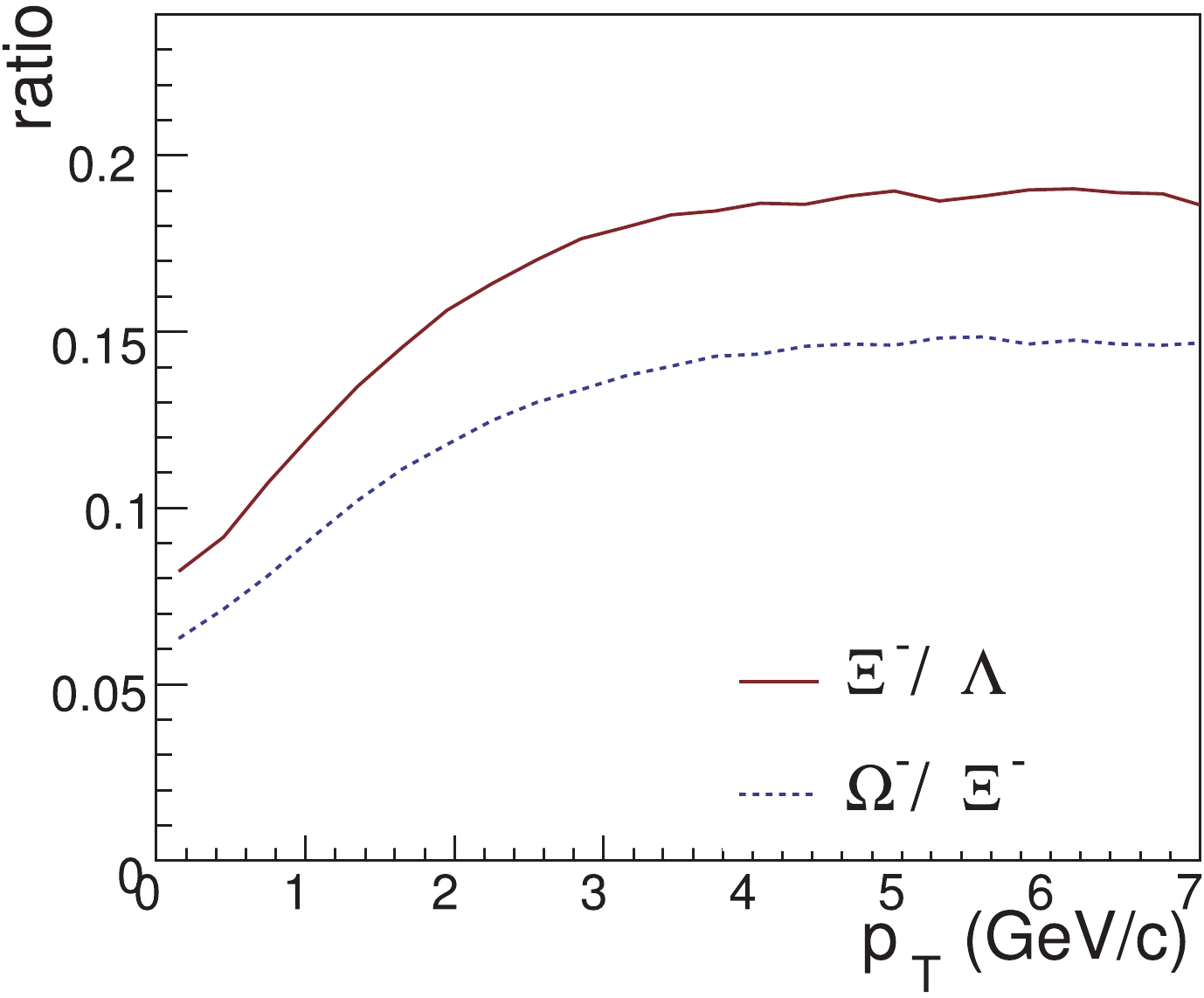
$ \Lambda $ ,$ \Xi^{-} $ and$ \Omega^{-} $ contain one, two and three$ s $ constituent quarks, respectively. Therefore, the ratios$ \Xi^{-}/\Lambda $ and$ \Omega^{-}/\Xi^{-} $ reflect the difference in momentum distributions of$ u $ ($ d $ ) quark and$ s $ quark at hadronization. Fig. 7 shows our prediction for the ratios$ \Xi^{-}/\Lambda $ and$ \Omega^{-}/\Xi^{-} $ as a function of$ p_{T} $ in the inelastic events in$ pp $ collisions at$ \sqrt{s} = $ 13 TeV. We see that the two ratios initally increase with$ p_{T} $ , and then tend to saturate at intermediate$ p_{T}\sim6 $ GeV/c, which is due to the difference between the$ p_T $ spectra of strange quarks and of up/down quarks in the range$ p_T\lesssim 2 $ GeV/c, see the ratio$ f_{s}^{(n)}(p_{T})/f_{u}^{(n)}(p_{T}) $ shown in Fig. 4(b). -
Using the preliminary data for the
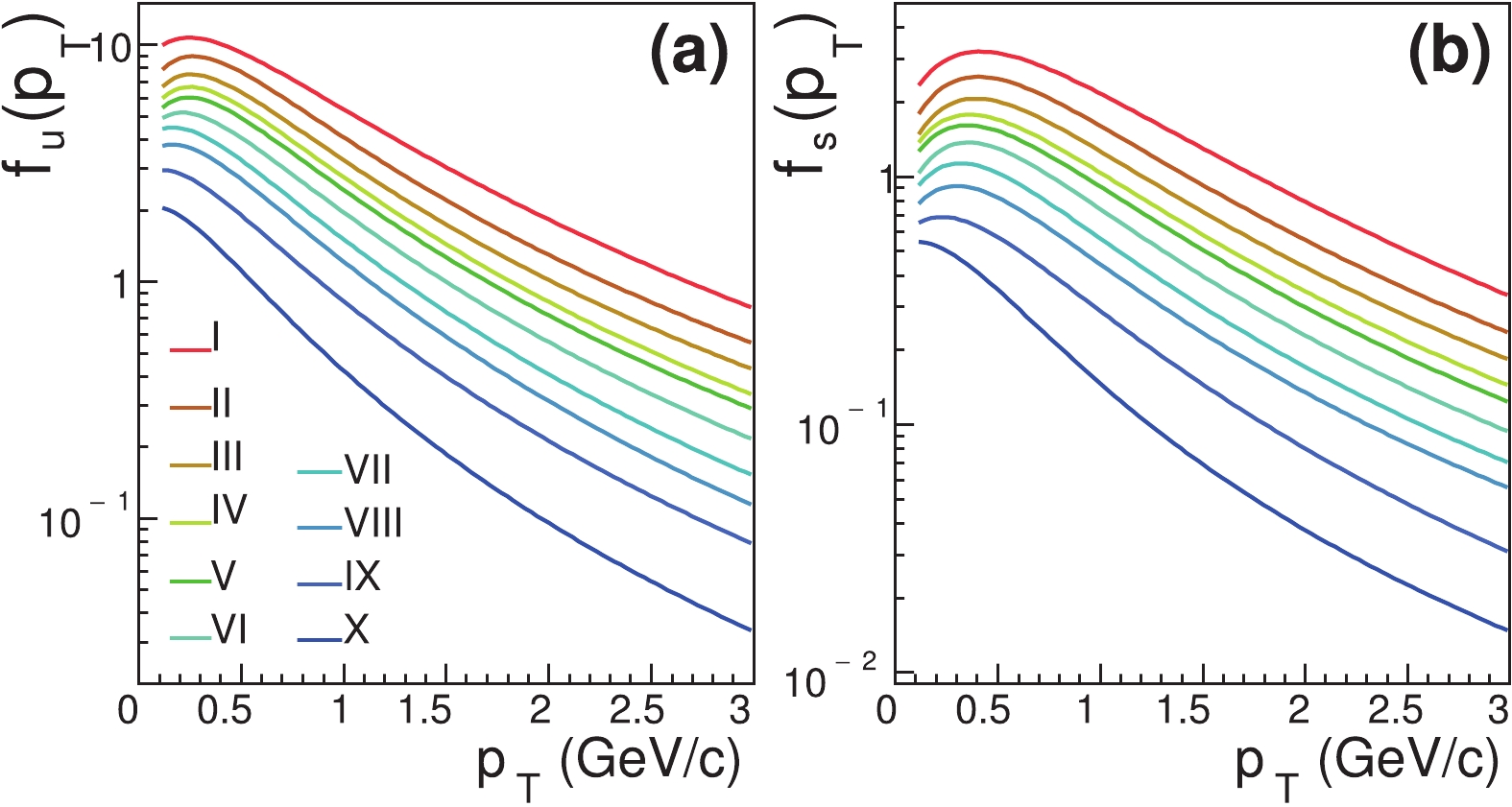
$ p_{T} $ spectra of protons,$ K^{*0} $ and$ \phi $ in different multiplicity classes [52, 53], we can determine the corresponding$ p_{T} $ spectra of constituent quarks at hadronization and predict the$ p_T $ spectra of the other identified hadrons. Fig. 8 shows the extracted quark$ p_{T} $ spectra (using the parametrization in Eq. (17)) at midrapidity in different multiplicity classes. Since the parameter$ b_q $ in the quark spectrum in high multiplicity classes tends to one, the distribution function in Eq. (17) asymptotically tends to the Boltzmann distribution in the low$ p_T $ range, and therefore we see a thermal behavior of the quark spectrum. This is related to the increasing multiple parton interactions in these event classes. In small multiplicity classes, the parameter$ b_q $ is relatively small and the quark spectrum deviates from the thermal behavior. -
In Fig. 9, we show the
$ p_{T} $ -integrated yields of identified hadrons (including kaons)① in different multiplicity classes and compare them with the preliminary data in$ pp $ collisions at$ \sqrt{s} = $ 13 TeV [52, 54]. In general, the results of QCM, solid lines, are in good agreement with the data (with the maximum deviation of about 10%).The yield ratios of different hadrons can considerably cancel the dependence on the model parameters and/or model input. Therefore, they are a more direct test of the basic physics of the model when confronted with the experimental data. In Fig. 10, we show the yield ratios of hyperons
$ \Omega^{-} $ ,$ \Xi^{-} $ and$ \Lambda $ to pions divided by the number of inclusive INEL>0 events. The data for$ pp $ collisions at$ \sqrt{s} = $ 7 [5] and 13 TeV [52], and for$ p $ -Pb collisions at$ \sqrt{s_{\rm NN}} = $ 5.02 TeV [55, 56], are presented in order to get a clear tendency with respect to the multiplicity of charged particles at midrapidity. The solid lines are the numerical results of QCM, which are found to be in agreement with the data. We emphasize that the strangeness-related hierarchy is closely related to the strange quark content of these hyperons at hadronization, which can be easily understood using the analytical relation in QCM. Taking the yield formulas Eqs. (9) and (11) and considering the strong and electromagnetic decays, we have
Figure 10. (color online) The yield ratios of hyperons to pions divided by the number of inclusive
$ {\rm INEL} > 0 $ events. The data for$pp$ collisions at$\sqrt{s} = $ 7 [5] and 13 TeV [52], and$p$ -Pb collisions at$\sqrt{s_{\rm NN}} = $ 5.02 TeV [55, 56], are presented. The solid lines are the numerical results of QCM, and the dotted lines are the analytic approximation in QCM.$ N_{\Omega} \approx\frac{\lambda_{s}^{3}}{\left(2+\lambda_{s}\right)^{3}}\overline{N}_{B}, $

(18) $ N_{\Xi}\approx\frac{3\lambda_{s}^{2}}{\left(2+\lambda_{s}\right)^{3}}\overline{N}_{B}, $

(19) $ \begin{split} N_{\Lambda}\approx &\left(\frac{2+0.88R_{D/O}}{2+R_{D/O}}+0.94\frac{R_{D/O}}{1+R_{D/O}}\right)\frac{6\lambda_{s}}{\left(2+\lambda_{s}\right)^{3}}\overline{N}_{B}\\ \approx & \frac{7.73\lambda_{s}}{\left(2+\lambda_{s}\right)^{3}}\overline{N}_{B}, \end{split}$

(20) where we neglect the effects of small quark numbers, and adopt the strangeness suppression factor
$ \lambda_{s} = \langle N_{s}\rangle/\langle N_{u}\rangle $ . Due to the contribution of complex decays, the pion yield has a complex expression [57], and here we write$ N_{\pi} = a_{\pi}\langle N_{q}\rangle $ with the coefficient$ a_{\pi} $ almost constant. The double ratios in Fig. 10 then have simple approximate expressions$ \frac{N_{\Omega}}{N_{\pi}}\bigg/\left(\frac{N_{\Omega}}{N_{\pi}}\right)_{\rm INEL>0}^{pp} \approx\frac{\lambda_{s}^{3}}{\left(2+\lambda_{s}\right)^{3}}\bigg/\frac{\lambda_{s}^{'3}}{\left(2+\lambda_{s}^{'}\right)^{3}}, $

(21) $ \frac{N_{\Xi}}{N_{\pi}}\bigg/\left(\frac{N_{\Xi}}{N_{\pi}}\right)_{\rm INEL>0}^{pp} \approx\frac{\lambda_{s}^{2}}{\left(2+\lambda_{s}\right)^{3}}\bigg/\frac{\lambda_{s}^{'2}}{\left(2+\lambda_{s}^{'}\right)^{3}}, $

(22) $ \frac{N_{\Lambda}}{N_{\pi}}\bigg/\left(\frac{N_{\Lambda}}{N_{\pi}}\right)_{\rm INEL>0}^{pp} \approx\frac{\lambda_{s}}{\left(2+\lambda_{s}\right)^{3}}\bigg/\frac{\lambda_{s}^{'}}{\left(2+\lambda_{s}^{'}\right)^{3}}, $

(23) where
$ \lambda_{s}^{'} $ is the strangeness suppression factor in the INEL >0 events in$ pp $ collisions. Here, we see a clear hierarchy structure among the three double ratios in terms of$ \lambda_s $ . The dotted lines in Fig. 10 are the results of the above analytic formulas with a naively tuned strangeness suppression$ \lambda_{s} = \lambda_{s}^{'}\left[1+0.165\log\left({\langle {\rm d}N_{\rm ch}/{\rm d}\eta\rangle_{|\eta|<0.5}}/{6.0}\right)\right] $ with$ \lambda_{s}^{'} = 0.31 $ . They fit well the experimental data for the double ratios for$ \langle {\rm d}N_{\rm ch}/{\rm d}\eta\rangle_{|\eta|<0.5} \gtrsim 10 $ . In the small multiplicity classes$ \langle {\rm d}N_{\rm ch}/{\rm d}\eta\rangle_{|\eta|<0.5}\lesssim6 $ , the small quark number effects are not negligible so that the analytic approximations give larger values than the experimental data. Our numerical results include the small quark number effects and are found to be closer to the data.The yield ratio
$ \Xi/\phi $ is also influenced by the small quark number effects. If we neglect them, we have$ N_{\phi}\approx\frac{R_{V/P}}{1+R_{V/P}}\frac{\lambda_{s}^{2}}{\left(2+\lambda_{s}\right)^{2}}\overline{N}_{M} $

(24) and using Eq. (19), we get the ratio
$ \frac{N_{\Xi}+N_{\bar{\Xi}}}{N_{\phi}} = 2\frac{1+R_{V/P}}{R_{V/P}}\frac{3}{2+\lambda_{s}}R_{B/M}\approx\frac{1.7}{2+\lambda_{s}}, $

(25) which slightly decreases with increasing
$ \lambda_{s} $ , and therefore slightly decreases with an increase of multiplicity$ \langle {\rm d}N_{\rm ch}/d\eta\rangle $ because$ \lambda_{s} $ increases with$ \langle {\rm d}N_{\rm ch}/{\rm d}\eta\rangle $ . This is in contradiction with the experimental data. However, taking into account the small quark number effects in QCM, we get the correct behavior of the ratio$ \Xi/\phi $ , as shown by the solid line in Fig. 11. The production of$ \Xi^{-} $ needs not only two$ s $ quarks but also a$ d $ quark, which is different from$ \phi $ which needs only an$ s $ and$ \bar{s} $ . Therefore, in small multiplicity events or for small quark numbers, the formation of$ \Xi^{-} $ is suppressed to a certain extent (or occasionally forbidden) in comparison with$ \phi $ . We see that the calculated ratio$ \Xi/\phi $ using QCM increases with system multiplicity$ \langle {\rm d}N_{\rm ch}/{\rm d}\eta\rangle $ , and is consistent with the experimental data for$ pp $ collisions at$ \sqrt{s} = $ 13 TeV and for$ p $ -Pb collisions at$ \sqrt{s_{\rm NN}} = $ 5.02 TeV [52, 58].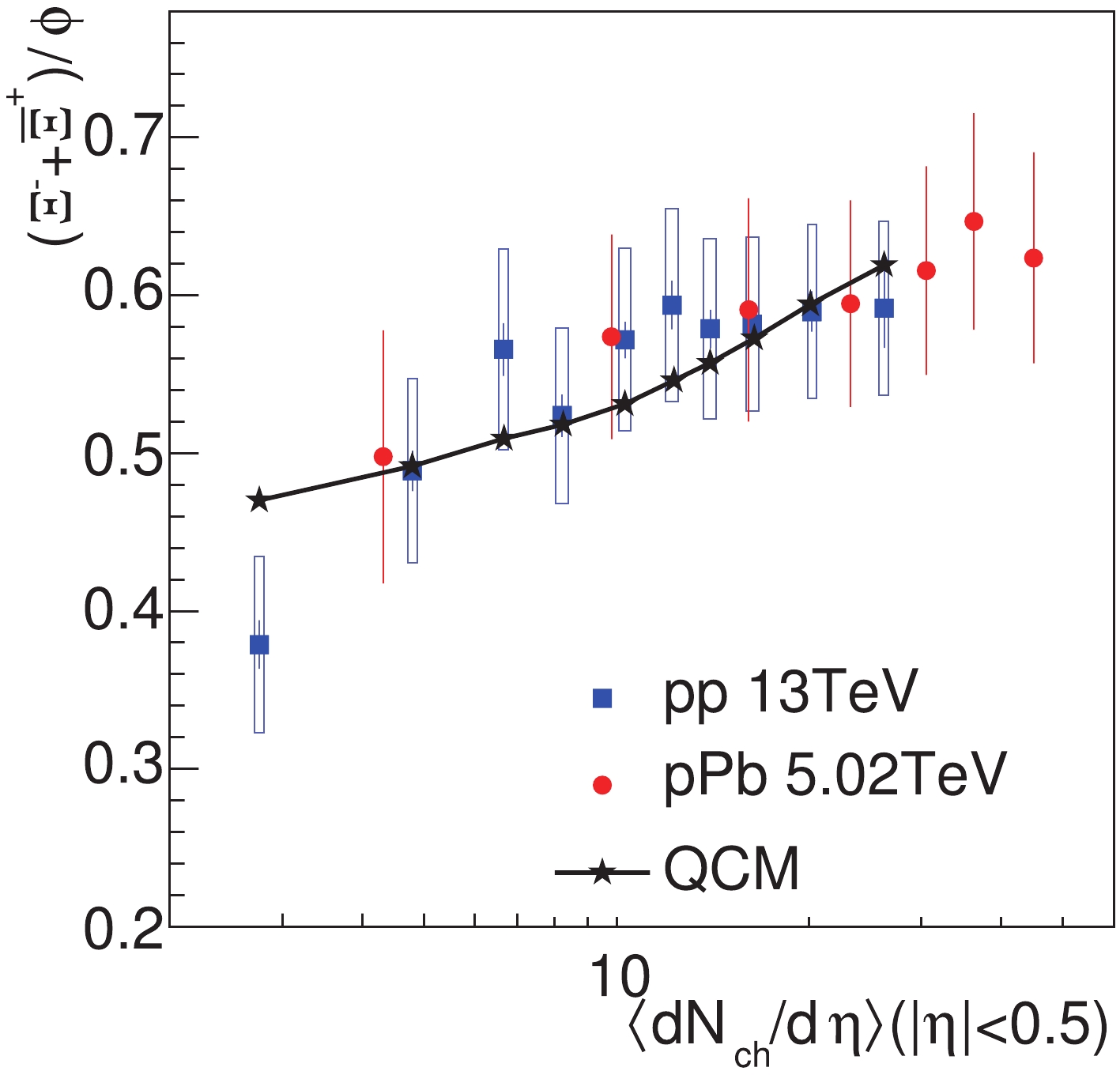
Figure 11. (color online) The yield ratio
$\Xi/\phi$ as a function of$\langle {\rm d}N_{\rm ch}/{\rm d}\eta\rangle_{|\eta|<0.5}$ . The preliminary data for$pp$ collisions at$\sqrt{s} = $ 13 TeV, solid squares, and for$p$ -Pb collisions at$\sqrt{s_{\rm NN}} = $ 5.02 TeV, solid circles, are taken from Refs. [52, 58]. The solid line is the result of QCM.Protons and
$ \phi $ have similar masses but different quark content. The yield ratio$ \phi/p $ can test the flavor-dominated features of hadron production in QCM. Neglecting the small quark number effects, the proton yield, after taking into account the decay of$ \Delta $ resonances, has a simple expression$ N_{p} \approx \frac{1}{4} \frac{1}{\left(2+\lambda_{s}\right)^{3}}\overline{N}_{B}. $

(26) Using Eq. (24), we get the yield ratio
$ \frac{N_{\phi}}{N_{p}} \approx \frac{1}{4} \frac{R_{V/P}}{1+R_{V/P}} \lambda_s^2 (2+\lambda_{s}) \frac{\overline{N}_{M}}{\overline{N}_B} \\ \approx 0.91\lambda_s^2 (2+\lambda_{s}), $

(27) which shows a significant dependence on the strangeness suppression factor
$ \lambda_s $ . We get$ N_{\phi}/N_p\approx0.22 $ with$ \lambda_s = 0.32 $ in the low multiplicity classes, and$ N_{\phi}/N_p\approx0.28 $ with$ \lambda_s = 0.36 $ in the high multiplicity classes. The short dashed lines in Fig. 12 are for the above two values in the analytical approximation. They are slightly lower than the experimental data [52, 58], symbols in the figure. The small quark number effects increase the ratio to a certain extent as they suppress the proton yield. We show the numerical results of our model including the small quark number effects, solid line, and see a good agreement with the data.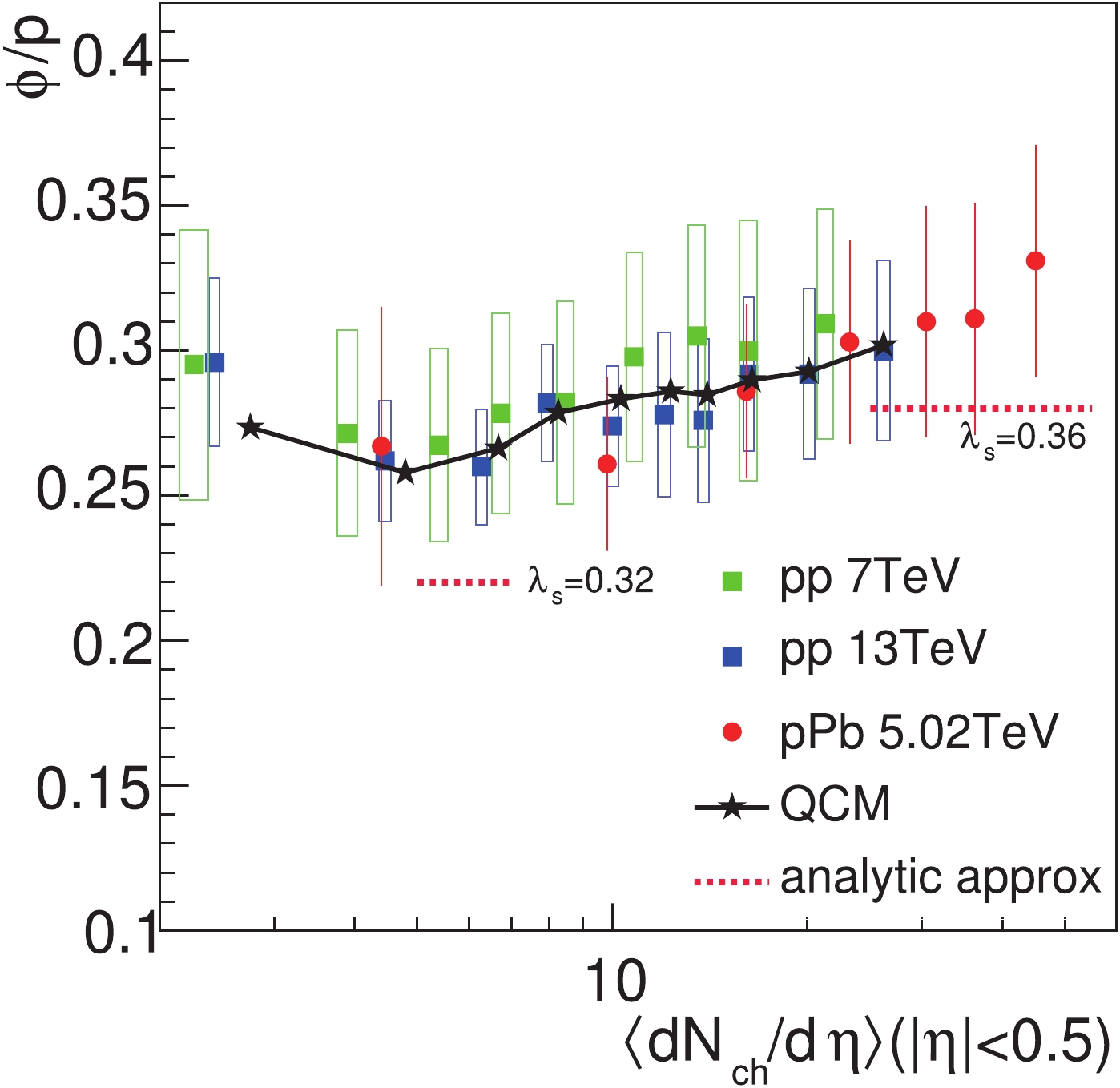
Figure 12. (color online) The yield ratio
$\phi/p$ as a function of$\langle {\rm d}N_{\rm ch}/{\rm d}\eta\rangle_{|\eta|<0.5}$ . The data for$pp$ collisions at$\sqrt{s} = $ 7 and 13 TeV, solid circles and squares, and the data for$p$ -Pb collisions at$\sqrt{s_{\rm NN}} = $ 5.02 TeV, solid circles, are taken from Refs. [52, 58]. The solid line is the numerical result of QCM. The short dashed lines are the analytical approximation. -
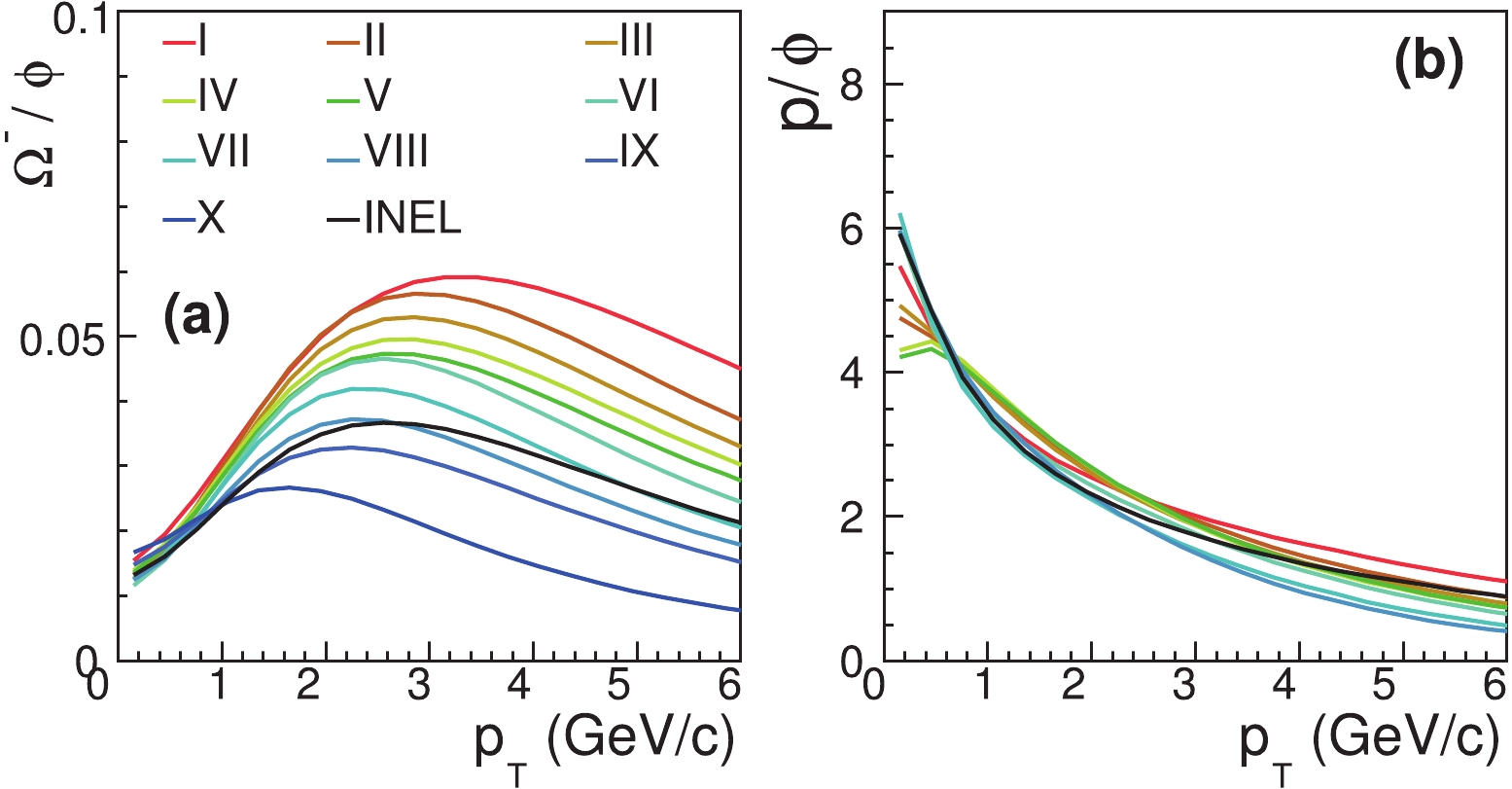
In Fig. 13, we show the fit of the data for the
$ p_{T} $ spectra of protons,$ K^{*0} $ and$ \phi $ [52, 53] using QCM, and the predictions for the other identified hadrons in different multiplicity classes for$ pp $ collisions at$ \sqrt{s} = $ 13 TeV. Note that the classes IV and V are combined for the$ K^{*0} $ data and for our results. Beside comparing the predictions of single hadron spectra with the data, we emphasize that QCM can be more effectively tested by spectrum ratios and/or scaling. The first test is whether the constituent quark number scaling holds in the$ p_{T} $ spectra for$ \Omega^{-} $ and$ \phi $ in different multiplicity classes. The second is to study the ratio$ \Omega^{-}/\phi $ as a function of$ p_{T} $ . The$ \Omega^{-}/\phi $ ratio in QCM is solely determined by the strange quark$ p_{T} $ spectrum at hadronization, and this ratio usually exhibits a nontrivial$ p_{T} $ dependence, as shown in Fig. 14(a), which is a typical behavior of the baryon-to-meson ratio in QCM and is absent or unapparent in the traditional fragmentation picture. We also see that the ratio$ \Omega^{-}/\phi $ in higher multiplicity classes can reach higher peak values. The peak position of$ \Omega^{-}/\phi $ in high multiplicity classes is also enlarged compared with the low multiplicity classes. The third test is to study the ratio$ p/\phi $ as a function of$ p_{T} $ so as to clarify if its$ p_{T} $ dependence is flavor dominated or mass dominated. The results of QCM are shown in Fig. 14(b) , which decrease with$ p_{T} $ and show a relatively weak multiplicity dependence. -
Taking advantage of the available experimental data for the hadronic
$ p_T $ spectra and yields at midrapidity, we have systematically studied the production of soft hadrons in$ pp $ collisions at$ \sqrt{s} = $ 13 TeV in the framework of the quark combination mechanism at hadronization. We applied the quark combination model which assumes that the constituent quarks and antiquarks are the effective degrees of freedom of the parton system at hadronization, and used the equal velocity combination approximation in hadron formation. We applied the model to systematically calculate the$ p_{T} $ spectra and yields of soft strange hadrons in the inelastic events (INEL>0) and in different multiplicity classes.We found several interesting results which are sensitive to the hadronization mechanism. (1) The
$ p_{T} $ spectra of$ \Omega^{-} $ and$ \phi $ in the inelastic events (INEL>0) in$ pp $ collisions at$ \sqrt{s} = $ 13 TeV exhibit a constituent quark number scaling property. The high multiplicity classes in$ pp $ collisions at$ \sqrt{s} $ = 7 TeV also show this scaling property. This is the first time that such a scaling property is observed in high energy$ pp $ collisions, and is an obvious experimental signal of the quark combination mechanism at hadronization in high energy$ pp $ collisions. (2) The$ p/\phi $ ratio in the inelastic events (INEL > 0) in$ pp $ collisions at$ \sqrt{s} = $ 13 TeV shows a clear decrease with increasing$ p_{T} $ , which indicates that the statistical hadronization model is not the reason for this behavior. We demonstrated that the data are naturally explained by the quark combination model. (3) The yield ratios$ \Lambda/\pi $ ,$ \Xi^{-}/\pi $ and$ \Omega^{-}/\pi $ divided by the number of inelastic events as a function of system multiplicity$ \langle {\rm d}N_{\rm ch}/{\rm d}\eta\rangle $ at midrapidity show a strangeness-related hierarchy structure. We demonstrated that the hierarchy structure is closely related to the strange quark content of these hyperons as the result of the combination of strange quarks and up/down quarks during their production.Using the quark number scaling property, the
$ p_T $ spectrum of strange quarks was extracted from the data for$ \Omega $ and$ \phi $ . The$ p_T $ spectra of up/down quarks was extracted from the data for the other hadrons containing up/down constituent quarks. The extracted quark momentum distribution functions are important results which describe the properties of the strongly interacting partonic system at hadronization in the language of constituent quarks.To confirm the new features of hadronization dynamics in high energy
$ pp $ collisions, we should carefully study all related experimental data. We have made predictions of the$ p_{T} $ spectra and spectrum ratios of strange hadrons in$ pp $ collisions at$ \sqrt{s} = $ 13 TeV to further test our model with the experimental data that will be available in the future. On the other hand, compared to our previous study of$ pp $ collisions at$ \sqrt{s} = $ 7 TeV [21] which gave a first indication, the current study provides a stronger signal of quark combination hadronization in high energy$ pp $ collisions. We still need further systematical studies of$ pp $ collisions at the other LHC energies to test the universality of the new hadronization features, and to study their relation with the possible creation of mini-QGP in small collision systems.
Constituent quark number scaling from strange hadron spectra in pp collisions at ${{\sqrt{s}= 13}}$ TeV
- Received Date: 2019-06-03
- Accepted Date: 2019-10-01
- Available Online: 2020-01-01
Abstract: We show that the







 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF



























 DownLoad:
DownLoad: