Antiproton production in heavy-ion collisions at subthreshold energies

Heavy-ion collisions in laboratory provide a unique possibility to create dense hadronic matter for investigating the in-medium properties of hadrons and the nuclear equation of state [1-5]. Particle production at energies below the threshold in nucleon-nucleon collisions can probe the high-density hadronic matter properties, i.e. the chiral symmetry restoration, phase-transition from quark-gluon plasma to hadrons, hadron-nucleon interaction, nuclear equation of state, etc. [6-10]. A number of experiments for subthreshold production of pions, kaons, antikaons and antiprotons in heavy-ion collisions were performed and precise spectra were measured [11-13]. The in-medium properties associated with secondary reactions and the concept of quasiparticles and their propagation in matter were investigated thoroughly. The subthreshold antiproton production is more complicated because of the annihilation process. The first evidence of antiproton production dates back to 1955, obtained at Berkeley in collisions of protons on copper at the energy of 6.2 GeV by Chamberlain, Segrè, Wiegand and Ypsilantis [14]. The experiments at BEVALAC and JINR in the 1980s were performed for subthreshold antiproton production in heavy-ion collisions, and were followed by precise measurements at KEK and GSI. Recently, antiproton pair correlation was investigated by the STAR collaboration in relativistic heavy-ion collisions [15]. The secondary beams of antiprotons were produced at many laboratories, such as CERN, BNL, KEK [16-19], and will be available at PANDA (antiproton annihilation experiment in construction at Darmstadt in Germany) for hypernuclear physics, charmonium physics and hadron spectroscopy. Experiments in antiproton physics are also planned at the future high-intensity heavy-ion accelerator facility (HIAF) in Huizhou, China [20].

The antiproton production in heavy-ion collisions or proton induced reactions at deep subthreshold energies is related to the antiproton-nucleon interaction and also coupled to a number of reaction channels, e.g. the meson-baryon and baryon-baryon collisions, annihilation channels, charge-exchange reaction, elastic and inelastic collisions associated with antiprotons. There have been several approaches for describing the antiproton production, e.g. the fireball model [21], the first-chance nucleon-nucleon collision model [22], the quasicoherent multiparticle collision model [23], and the microscopic transport approaches [24-28]. These models can explain to some extent the antiproton spectra in proton-nucleus and nucleus-nucleus collisions. Self-consistent description of all possible channels that contribute to antiproton production is still needed, in particular of the secondary reactions with annihilation products.

In this work, the microscopic mechanism of antiproton production in heavy-ion collisions at subthreshold energies is investigated with the Lanzhou quantum molecular dynamics (LQMD) transport model. The article is organized as follows. In Section 2, we give a brief description of the model of antiproton production. The calculated results and discussion are presented in Section 3. A summary and perspectives of antiproton physics are outlined in Section 4.

In the Lanzhou quantum molecular dynamics (LQMD), the dynamics of resonances with masses below 2 GeV, hyperons ($ \Lambda $, $ \Sigma $, $ \Xi $) and mesons ($ \pi $, $ \eta $, K, $ \overline{K} $, $ \rho $, $ \omega $), is associated with the mean-field potential and reaction channels, which are coupled in the hadron-hadron collisions, antibaryon-baryon annihilations, decay of resonances [29, 30]. The temporal evolution of all nucleons is described by Hamilton's equations of motion with self-consistently generated two-body interaction. However, the mean-field approach is used for the evolution of all hadrons produced in nucleon-nucleon collisions, which is a one-body interaction. In this work, the antiproton production in nucleon-nucleon collisions is implemented in the model. The antiproton-nucleon potential is evaluated from the dispersion relation as

with $ \Sigma_{\rm S}^{\overline{B}} = \Sigma_{\rm S}^{B} $ and $ \Sigma_{\rm V}^{\overline{B}} = -\Sigma_{\rm V}^{B} $. The nuclear scalar $ \Sigma_{\rm S}^{N} $ and vector $ \Sigma_{\rm V}^{N} $ self-energies are computed from the well-known relativistic mean-field model with the NL3 parameter [31]. The relativistic self-energies are used for the construction of hyperon and antibaryon potentials only. The nuclear density $ \rho $ is obtained from the phase-space density in the model. The antiproton evolves in the mean-field potential of the nuclear medium, which is similar to the Boltzmann-Uehling-Uhlenbeck transport model. Based on the results of the Giessen Boltzmann-Uehling-Uhlenbeck transport model [32], a factor $ \xi $ is introduced in order to control the strength of the phenomenological optical potential as $ \Sigma_{\rm S}^{\overline{N}} = \xi\Sigma_{\rm S}^{N} $ and $ \Sigma_{\rm V}^{\overline{N}} = -\xi\Sigma_{\rm V}^{N} $ with $ \xi $ = 0.25, which leads to the strength of $ V_{\overline{N}} = -164 $ MeV at the normal nuclear density $ \rho_{0} $ = 0.16 fm⁻³. The effective mass $ m^{\ast}_{\overline{p}} = \omega_{\overline{B}}({{p}} = 0,\rho = \rho_{0}) $ is used to evaluate the threshold energy for antiproton production, e.g. the threshold energy in the nucleon-nucleon collisions is $ \sqrt{s_{\rm th}} = m^{\ast}_{\overline{p}} + 3m_{N} $ where $ m_{N} $ is the nucleon mass.

The production and decay of resonances in meson-baryon and baryon-baryon collisions have been implemented in the LQMD model [30], in which the strangeness and vector mesons are created via direct processes. The antiproton production is related to the pion-baryon and nucleon-baryon channels at the subthreshold energy (E$ _{\rm th} $ = 5.62 GeV) as

The cross-sections in the pion-baryon and nucleon-baryon channels are evaluated in the same form as in Ref. [33]

with the parameters $ a = 1 $ mb, $ b = 2.31 $, $ c = 2.3 $ , and $ a = 0.12 $ mb, $ b = 3.5 $, $ c = 2.7 $ , for the pion and nucleon induced reactions, respectively. Isotropic distribution of the produced antiprotons is considered in the calculations.

The annihilation reactions in antibaryon-baryon collisions are described by a statistical model with the SU(3) symmetry of pseudoscalar and vector mesons [34], which takes into account possible combinations in the final state of two to six mesons [35]. Besides the annihilation channels, the charge-exchange reaction (CEX), elastic (EL) and inelastic scattering with antibaryons are also implemented in the model as follows [36].

Here, B stands for the nucleon and $ \Delta $(1232), Y($ \Lambda $, $ \Sigma $, $ \Xi $), K(K⁰, K⁺) and $ \overline{K} $($ \overline{K^{0}} $, K⁻). The line over B (Y) stands for the antiparticles. The cross-sections of these channels are based on the parametrization or extrapolation of the available experimental data. Pions are the main products of the annihilation reactions. The inverse processes in the pion-nucleon and pion-meson ($ \pi, \rho, \omega $) collisions contribute to the antiproton production. The pion-nucleon scattering forming a resonance is included in the LQMD model using the Breit-Wigner formula by fitting the available experimental data [37].

Particles produced in heavy-ion collisions reveal the properties of high-density hadronic matter formed in the compression stage. In Fig. 1, we show the time evolution of mesons ($ \pi^{+} $, $ \eta $, K⁺ and K⁻), hyperons ($ \Lambda $, $ \Sigma^{-} $ and $ \Xi^{-} $), primordial antiprotons and antiprotons in the annihilation channels in central ²⁸Si+²⁸Si collisions at the incident energy of 3 GeV/nucleon in the laboratory frame. It is obvious that most particles are in equilibrium in the collision stage (after 20 fm/c), except K⁻ and annihilation antiprotons. The strangeness exchange process $ K^{-}N\rightarrow \pi Y $ and annihilation reactions reduce the yields of K⁻ and antiprotons, respectively. Pions are the main products of the antiproton annihilation process. Therefore, pion induced reactions contribute to the production of strange particles. The primordial antiprotons with the multiplicity of $ 10^{-5} $ are reduced to about $ 4\times10^{-7} $. Only about 4% of the primordial antiprotons can be emitted from the dense hadronic matter, which is consistent with the results of the relativistic Vlasov-Uehling-Uhlenbeck (RVUU) model [26]. It should be mentioned that meson-baryon collisions are not included in the RVUU model of antiproton production. The contribution of pion-nucleon collisions to the antiproton production is one third of the total antiproton yield.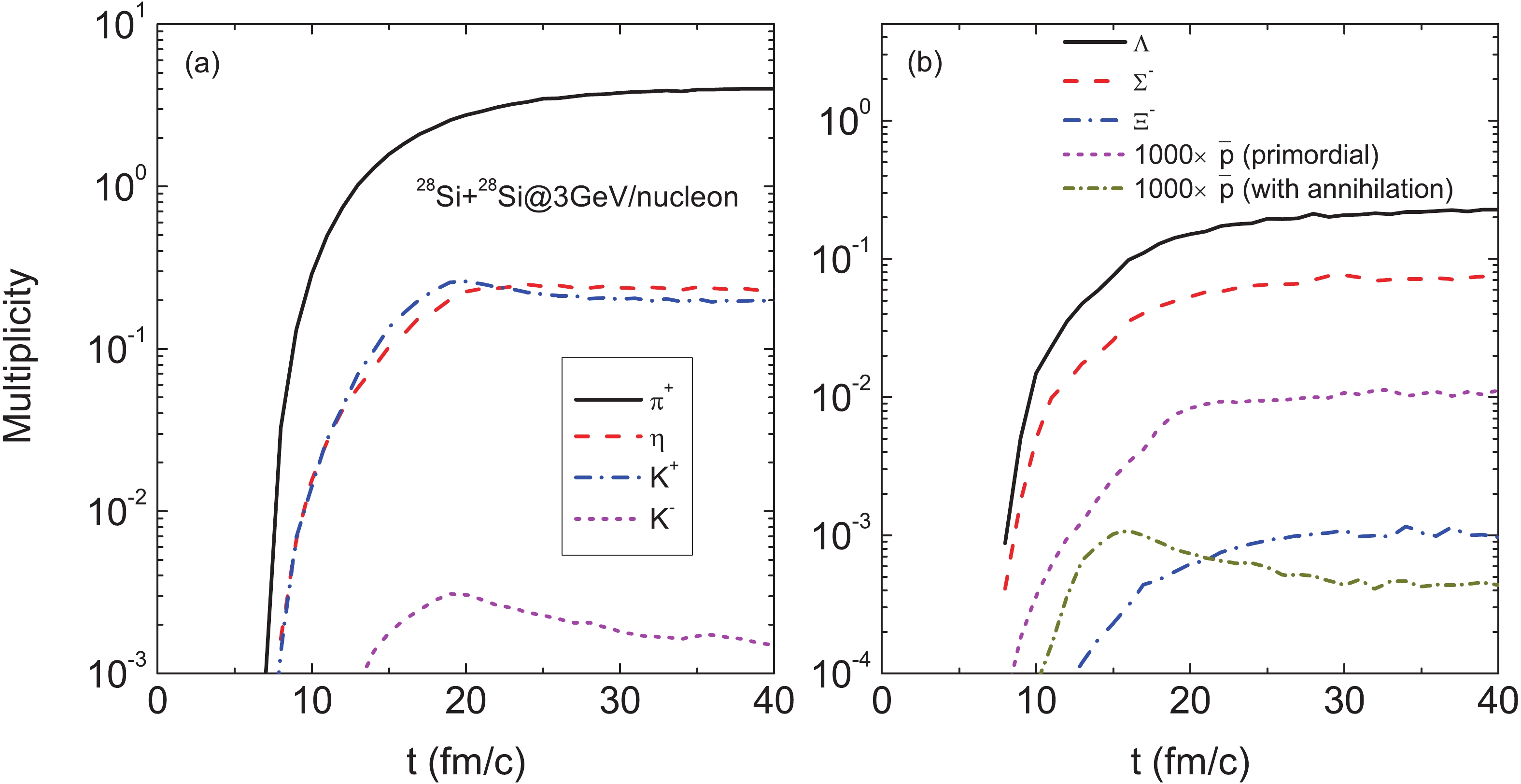

Figure 1.  (color online) Temporal evolution of mesons, hyperons, primordial antiprotons and antiprotons produced in the annihilation channels in central ²⁸Si+²⁸Si collisions at the incident energy of 3 GeV/nucleon.

Hadronic matter formed in heavy-ion collisions has been shown to be related to the reaction system. Heavy nuclei induced reactions enhance the baryon density in the colliding region, which enables subthreshold particle production and more pronounced in-medium effects. Systematic analysis is useful for reducing the uncertainties of some quantities, such as the in-medium cross-section and decay width. We calculated K⁺, K⁻, primordial and annihilation antiprotons in central collisions of ¹²C+¹²C, ²⁸Si+²⁸Si, ⁴⁰Ca+⁴⁰Ca, ⁵⁸Ni+⁵⁸Ni, ¹¹²Sn+¹¹²Sn and ¹⁹⁷Au+¹⁹⁷Au at 2 GeV/nucleon, as shown in Fig. 2. It is obvious that the yields of K⁺ and primordial antiprotons increase monotonically with the mass number of the colliding system. Participant nucleons are available for particle production. However, a plateau appears for K⁻ and annihilation antiprotons because of the secondary collisions. The antiproton-nucleon potential and annihilation effects are analyzed in Fig. 3. The inclusion of the mean-field potential enhances antiproton production due to the reduction of the threshold energy. The fact that the antiproton yields in nucleus-nucleus collisions are underestimated without the correction of the threshold energy was also found in other models. On the other hand, the attractive $ \overline{p} $-N potential leads to the rapid decrease of the antiproton production with increasing momentum. The contribution of the annihilation channel reduces the number of antiprotons, in particular in the domain of low momenta. The enhancement of subthreshold antiproton yields in deuteron induced reactions compared with proton-nucleus collisions was found at KEK [38]. The annihilation mechanism with high-intensity antiproton beams will be investigated by the PANDA experiment in the near future.

Figure 2.  Mass dependence of K⁺, K^-, primordial antiprotons and annihilation antiprotons at the incident energy of 2 GeV/nucleon.

Figure 3.  (color online) Rapidity and transverse momentum spectra of primordial antiprotons and annihilation antiprotons in central ⁴⁰Ca+⁴⁰Ca collisions at the energy of 3 GeV/nucleon.

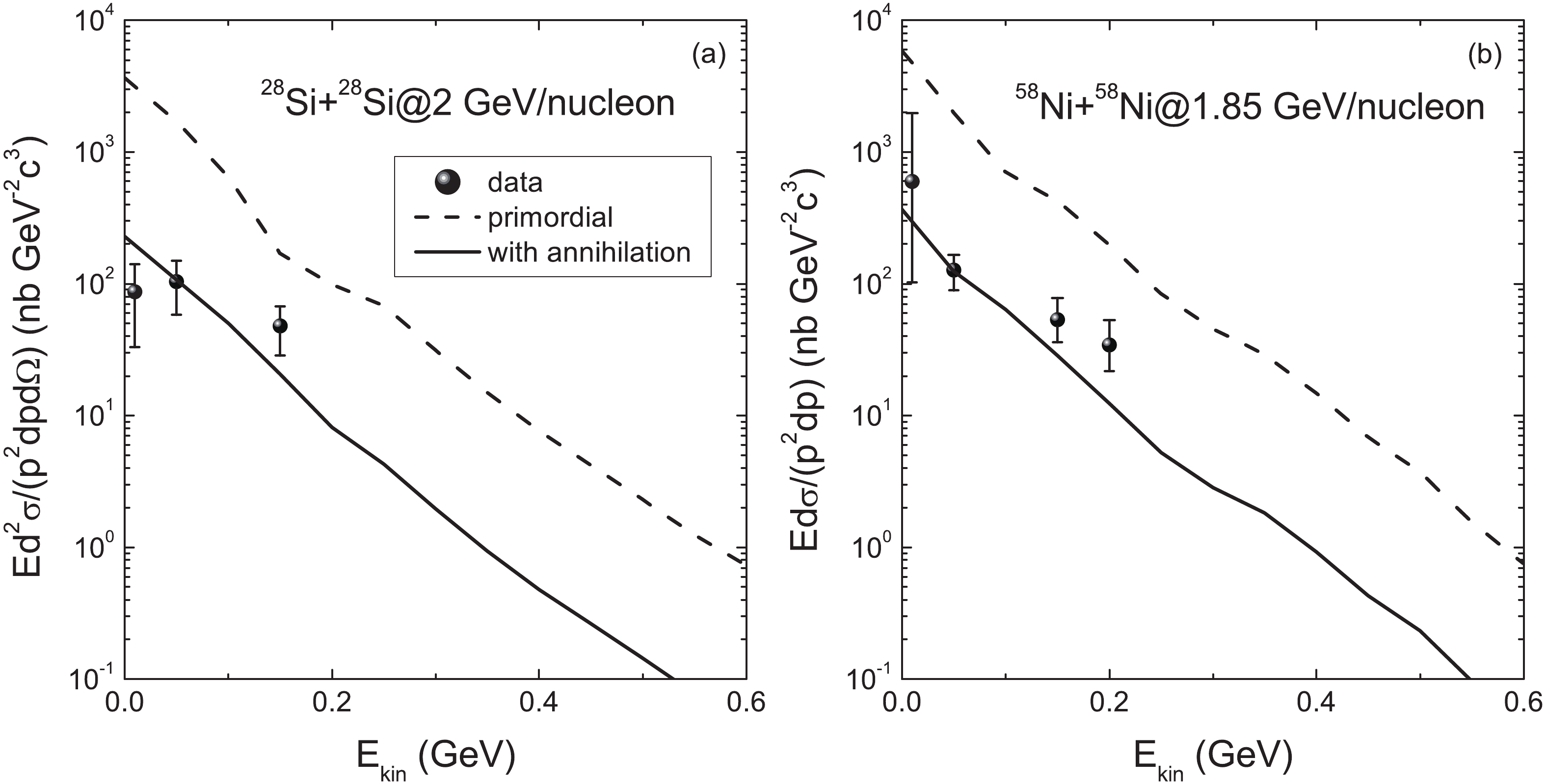
The kinetic energy spectrum of the invariant cross-section reflects the properties of hadronic matter, i.e. the local temperature of particle emission, particle optical potential, nuclear equation of state, etc. In Fig. 4 , we show the inclusive spectra of antiprotons produced in the collisions of ²⁸Si+²⁸Si and ⁵⁸Ni+⁵⁸Ni at the respective incident energies of 2 GeV/nucleon and 1.85 GeV/nucleon compared with the available experimental data [39, 40]. The calculated results are consistent with the data when the annihilation channel is included. The primordial antiprotons are emitted in the early stage of the collisions. Annihilation considerably reduces the antiproton production in the whole energy range and leads to the creation of pions in the dense matter. The collisions of pions with the surrounding nucleons may produce antiprotons, and the multiple processes increase the antiproton production to some extent. The antiproton production in heavy-ion collisions is related to the collision centrality [41]. Central collisions increase the probability of annihilation. Consequently, antiproton yields do not obey a linear dependence on the collision centrality.

Figure 4.  Invariant spectra of antiprotons produced in collisions of ²⁸Si+²⁸Si and ⁵⁸Ni+⁵⁸Ni at the respective incident energies of 2 GeV/nucleon and 1.85 GeV/nucleon compared with the available experimental data [39, 40].

Collective flows in heavy-ion collisions provide azimuthal correlations of emitted particles, which have been used for extracting the properties of high-density baryonic matter. The flow information can be extracted from the Fourier expansion in the phase space, i.e. expressed as $\frac{{\rm d}N}{{\rm d}\phi}(y,p_{t}) = N_{0}(1+2V_{1}(y,p_{t})\cos(\phi)+2V_{2}(y,p_{t}) $$ \cos(2\phi)+\cdots) $, where $ p_{t} = \sqrt{p_{x}^{2}+p_{y}^{2}} $ and y are the transverse momentum and the longitudinal rapidity along the beam direction, respectively. The directed (transverse) flow is defined as the first coefficient and expressed as $ V_{1} = \langle p_{x}/p_{t} \rangle $, which provides information about the azimuthal anisotropy of the transverse emission. The elliptic flow $ V_{2} = \langle (p_{x}/$$ p_{t})^{2}-(p_{y}/p_{t})^{2} \rangle $ gives the competition between the in-plane ($ V_{2}> $0) and out-of-plane ($ V_{2}< $0, squeeze out) emissions. The brackets indicate averaging over all events in accordance with a specific class such as rapidity or transverse momentum cut. The transverse flows of nucleons, light clusters, pions and strange particles in heavy-ion collisions have been investigated for the high-density symmetry energy, in-medium NN cross-section, optical potentials of particles in nuclear matter, particle emission, etc. [8, 30]. To investigate the antiproton azimuthal distribution in the reaction plane, we calculated the spectra of $ \pi^{+} $, K⁺ and antiprotons produced in semi-central collisions of ⁵⁸Ni+⁵⁸Ni (b = 4 fm) at the incident energy of 3 GeV/nucleon, as shown in Fig. 5. It can be seen that the directed flows of $ \pi^{+} $, K⁺ and antiprotons are anti-correlated in comparison to protons. The anti-flow effect in antiproton emission is caused by the annihilation reactions, which enable antiproton absorption by surrounding nucleons (shadowing effect). Only the opposite evolution of antiprotons, away from nucleon emission, can escape from the collision zone and shows anti-correlation in the phase space. The phenomenon is very similar to $ \pi^{+} $ emission. The attractive $ \overline{p} $N potential reduces anti-correlation. It is known that the repulsive potential leads to the anti-flow of K⁺[8]. The competition of the attractive $ K^{-} $N and the strangeness exchange reaction $ K^{-}N\rightarrow \pi Y $ contributes to $ K^{-} $ emission. The anti-correlation of directed flow of antiproton production in heavy-ion collisions was measured at AGS from the transverse momentum spectra [42].

Figure 5.  (color online) Rapidity distribution of directed flows of $ \pi^{+} $, K⁺, K⁻ and antiprotons produced in ⁵⁸Ni+⁵⁸Ni at the incident energy of 3 GeV/nucleon.

In summary, the antiproton dynamics in heavy-ion collisions at deep subthreshold energies was investigated with the LQMD transport model. The collective effects in antiproton production in heavy-ion collisions are more pronounced than in proton induced reactions. The influence of the annihilation and the $ \overline{p} $-N potential on antiproton production was analyzed thoroughly. The inclusion of the $ \overline{p} $-N potential enhances the antiproton abundance because of the decrease of the threshold energy. The available experimental data for invariant spectra are reproduced well by the model after taking into account the contributions of the annihilation reactions and of the optical potential. The pion-nucleon channel slightly enhances the antiproton production. The directed flow of antiprotons is anti-correlated to the proton flow and is caused by the annihilation in the nuclear medium.