-
The existence of multi-quasiparticle configurations is consistently predicted and observed in the low-lying level structures of nuclei near the
$ N = 50 $ closed shell. For the even-Z$ N = 47 $ nuclei, three-quasiparticle excitations from the$ \nu(g_{9/2})^{-3} $ or$ \pi(g_{9/2})^2 \nu(g_{9/2})^{-1} $ configuration are expected to dominate low-lying level schemes. The$ \nu(g_{9/2})^{-3} $ excitations are indeed observed in the$ N = 47 $ 85Sr isotone Z = 38 [1, 2], and they generate the low-lying positive-parity structure up to the yrast state with spin 21/2+, corresponding to the aligned$ \nu(g_{9/2})^{-3}_{J^{\pi}} $ = 21/2+ configuration. However, the level structure of the$ N = 47 $ isotone 89Mo Z = 42 [3] as well as g-factor measurements [4] both indicate that yrast positive-parity states up to 25/2+ in 89Mo are essentially built from the$ \pi(g_{9/2})^{-2} $ $ \nu(g_{9/2})^{-1} $ configuration, showing an evolution from the neutron to the proton alignment in the even-Z$ N = 47 $ isotones with increasing proton number.In contrast, the
$ N = 47 $ nuclei in the$ A \simeq 90 $ mass region, which lie in the vicinity of 100Sn, are particularly suited to study neutron-proton (np) interactions. This specific feature is due the fact that this region is dominated by protons and neutrons particle-hole excitations in the same 1$ g_{9/2} $ orbital. Consequently, the spatial overlap between the proton and neutron single-particle$ g_{9/2} $ wave functions are large, resulting in an enhanced np interaction. This interaction is expected to be strongest in$ N = Z $ nuclei, which have the largest relative number of neutron-proton pairs (see Ref. [5] for a review). As the proton number increases, the low-lying level structure from 85Sr to 89Mo [1–3, 6] undergoes a slight but systematic compression. This systematic trend suggests that effects of the np interaction could increase with Z along the$ N = 47 $ isotonic chain. Investigation of the low-spin level structure in 91Ru would extend the systematic trend in$ N = 47 $ to larger proton numbers, and thus provide a good opportunity for the study of the competition between proton-particle and neutron-hole excitations in the$ g_{9/2} $ orbital, and probe the possible onset of the np interaction effects when approaching the$ N = Z $ line.The excited states of 91Ru were studied by Arnell et al. [7] via the (
$ \alpha $ ,$ xn $ ) reaction. Subsequently, the level scheme was extended up to$ J^{\pi} $ = (41/2−) at 8 MeV excitation energy by Heese and co-workers [8] using the reaction 58Ni (36Ar,$ 2p1n $ ) 91Ru at a beam energy of 149 MeV. More recently, results from$ \beta $ -decay studies of some neutron-deficient nuclei including 91Rh [9, 10] were published, and several new$ \gamma $ -rays were observed.In this study, we report the low- to medium-spin level scheme of 91Ru, including a new observed low-spin positive-parity structure. The experiment and data analysis is briefly described in the following section, which is followed by some details on the shell-model calculations that were performed to interpret our data.
-
Low-spin states in 91Ru were populated by the fusion-evaporation reaction 58Ni ( 36Ar,
$ 2p1n $ ) 91Ru at a bombarding energy of E (36Ar) = 111 MeV [11]. The beam was delivered by the GANIL CIME cyclotron and focused on a 99.83% isotopically enriched 58Ni target of 6.0 mg/cm2 thickness. The charged-particle emission following the decay of the 94Pd compound nucleus was detected using the DIAMANT detector system, which comprises 80 CsI scintillators [12, 13]. The Neutron Wall [14], comprising 50 liquid scintillator detectors and covering a solid angle of$ 1\pi $ in the forward direction, was used for the detection of evaporated neutrons.$ \gamma $ rays emitted from the reaction products were detected using the EXOGAM Ge clover detector array [15]. At the time of the experiment, seven segmented clover detectors were placed at an angle of 90°, and four detectors were placed at an angle of 135° relative to the beam direction, leaving room for the Neutron Wall at forward angles. EXOGAM was used in a close-packed configuration with the front part of the BGO Compton suppression shields removed from the clover detectors. Details regarding the experiment have been described earlier [11]. Events were collected when one or more$ \gamma $ rays was detected in the Ge clover detectors together with at least one neutron in the Neutron Wall. With these conditions, a total of 4$ \times 10^9 $ events were recorded.In the offline analysis, the selected events had one detected neutron along with two detected protons (corresponding to the production of 91Ru). With the particle condition of
$ 2p1n $ , a total of about 2.6$ \times 10^7 $ $ \gamma $ -$ \gamma $ coincidence events were selected. Efficiency and energy calibration for Ge clover detectors was performed with the standard$ \gamma $ -ray 152Eu radioactive source. After the gain matching for all Ge clover detectors, these coincidence data were sorted into symmetric and asymmetric (angle-dependent) matrices for subsequent analysis.Spins and parities of the levels were deduced from the information on directional correlations of the
$ \gamma $ -rays from oriented states (DCO ratios) [16] and the$ \gamma $ -ray polarisation asymmetry [17]. The multipolarity of emitted$ \gamma $ -rays was determined directly from the DCO ratios, and the electromagnetic character was deduced from linear polarization measurements. For these kind of measurements, the EXOGAM Clover geometry has proved very efficient. Details are given in Refs. [11, 18]. -
New transitions were assigned to 91Ru on the basis of coincidence with
$ \gamma $ -rays already known in this nucleus. Typical prompt$ \gamma $ -$ \gamma $ coincidence spectra for 91Ru are shown in Fig. 1. The new$ \gamma $ -rays assigned to 91Ru are listed in Table 1. Their relative intensities were obtained from the total projection of the$ E_{\gamma}-E_{\gamma} $ matrix. In the case where the peak-to-background ratio in the total projection was too low, or where there was a contamination in the peak from other$ \gamma $ -ray transitions, the relevant transition energies were selected in the coincidence matrix, and the obtained projected spectra were used to fit the relative intensities. The transition energies were also measured in the total projection in the matrix. The energy uncertainties presented in the table are a combination of statistical, calibration, and background errors. The level scheme for 91Ru, as shown in Fig. 2, was established by the results from careful analysis of the$ \gamma $ -ray coincidence relationships. The spin-parity assignments are based on measured DCO ratios and Compton asymmetries for the transitions. The stretched quadrupole transitions cannot be distinguished from$ {\Delta}I = 0 $ dipole transitions or certain mixed$ {\Delta}I = 1 $ transitions. In these cases, simultaneously measuring the linear polarization of the transitions could provide supplementary arguments for the spin assignments. These results, as well as the level scheme, were already partially published in Ref. [11].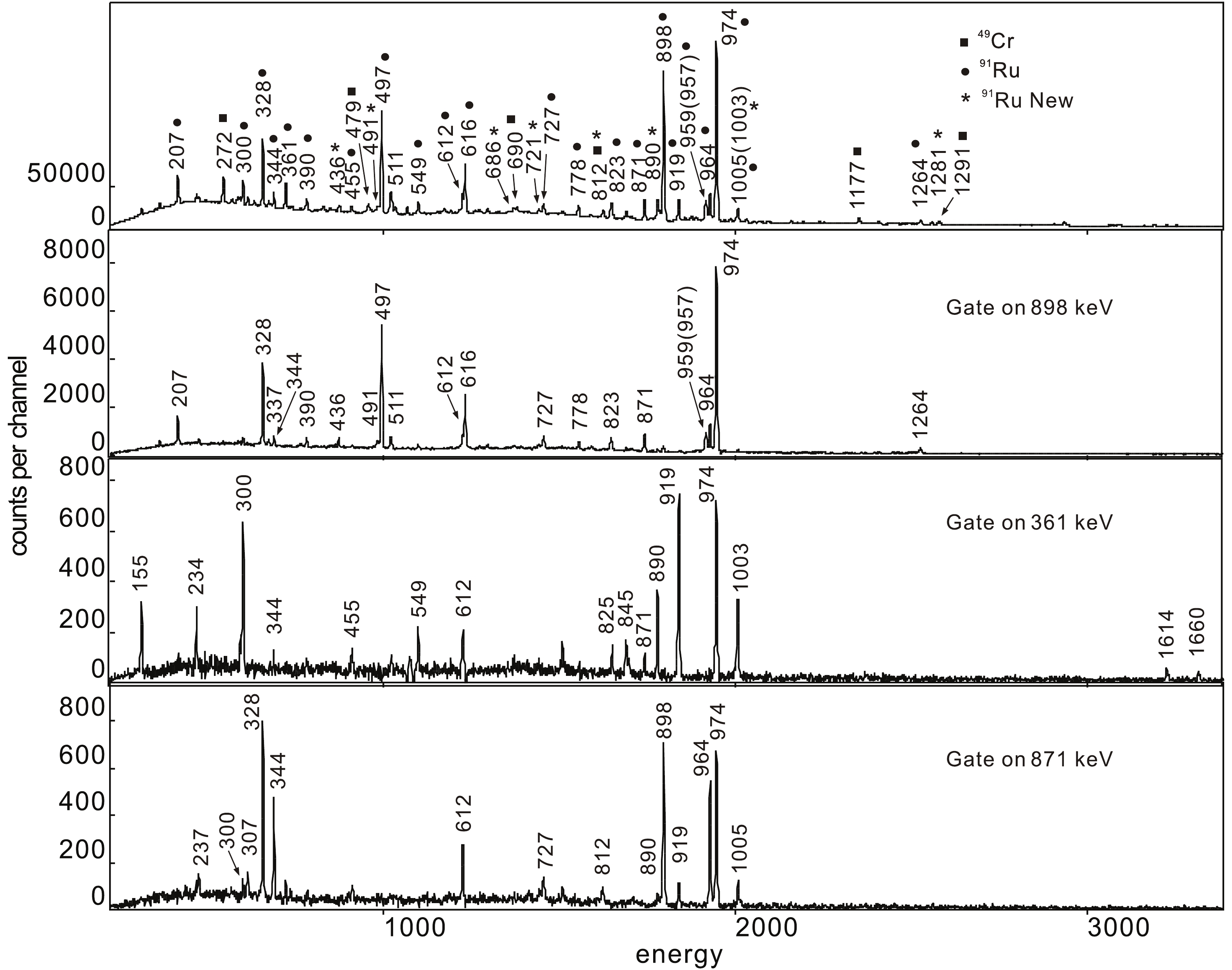
Figure 1. Upper spectrum shows total projection of
$E_{\gamma}-E_{\gamma}$ matrix sorted assuming two detected protons and one detected neutron. Lower panels show typical coincidence spectra for 91Ru gated on 898, 361, and 871 keV$\gamma$ -rays, corresponding to transitions that depopulate$17/2^{+}$ ,$15/2^{-}$ , and$25/2^{-}$ states in 91Ru, respectively.E $_{\gamma}$ /keV

I $_{\gamma}$ (%)

R $_{\rm DCO}$ 

Gate $_{\rm DCO}$ /keV

Asymmetry ${{E}}_{\rm i}$ 

$\rightarrow$ 

${{E}}_{\rm f}$ 

$J^{\pi}_{\rm i}$ 

$\rightarrow$ 

$J^{\pi}_{\rm f}$ 

45.8 46→0 (7/2+)→(9/2+) 233.6 2.7(2) 0.9(2) 361 1893→1660 (13/2−)→( $11/2_{2}^{+}$ )

252.9 < 0.6 5100→4847 ( $29/2_2^{-}$ )→(

$27/2_2^{-}$ )

435.9 2.4(2) 1.02(8) 974 0.17(7) 2799→2363 ( $21/2_2^{+}$ )→

$(17/2_2^{+}$ )

491.4 4.2(2) 0.7(2) 974 0.07(2) 2363→1872 ( $(17/2_2^{+}$ )→(

$(17/2_1^{+}$ )

518.8 2.2(4) 1.1(2) 1614 2179→1660 ( $15/2^{+}$ )→(

$11/2_{2}^{+}$ )

685.8 0.8(1) 0.6(1) 974 −0.12(3) 1660→974 ( $11/2_{2}^{+}$ )→(

$13/2^{+}$ )

720.7 0.7(1) 0.57(10) 871 −0.11(3) 5100→4379 ( $29/2_2^{-}$ )→(

$27/2^{-}$ )

754.5 1.7(2) 3164→2409 ( $21/2_1^{-}$ )→(

$17/2_2^{-}$ )

811.6 0.8(1) 0.55(9) 871 −0.16(5) 4847→4035 ( $27/2_2^{-}$ )→(

$25/2^{-}$ )

844.0 0.4(1) 890→46 ( $11/2_{1}^{+}$ )→(

$7/2^{+}$ )

889.8 7.6(1) 1.05(5) 361 −0.03(1) 890→0 ( $11/2_{1}^{+}$ )→(

$9/2^{+}$ )

1003.6 6.7(3) 0.98(4) 361 0.12(5) 1893→890 ( $13/2^{-}$ )→(

$11/2_{1}^{+}$ )

1126.9 0.8(1) 0.96(9) 497 5097→3970 ( $31/2^{+}$ )→(

$27/2^{+}$ )

1280.7 2.1(8) 0.6(1) 974 0.14(4) 2254→974 ( $15/2^{-}$ )→(

$13/2^{+}$ )

1613.9 1.3(1) 1.58(9) 234 0.18(3) 1660→46 ( $11/2_{2}^{+}$ )→(

$7/2^{+}$ )

1659.7 1.3(1) 1.07(8) 234 −0.07(2) 1660→0 ( $11/2_{2}^{+}$ )→(

$9/2^{+}$ )

Table 1.
$\gamma$ -ray energies, intensities relative to$13/2^{+}\rightarrow9/2^{+}$ 974 keV transition, DCO ratios, Compton asymmetries, and their assignments in 91Ru. Gates used for determination of DCO ratios are indicated. Energy uncertainties are within 0.5 keV. (Only new transitions discussed in this paper are shown).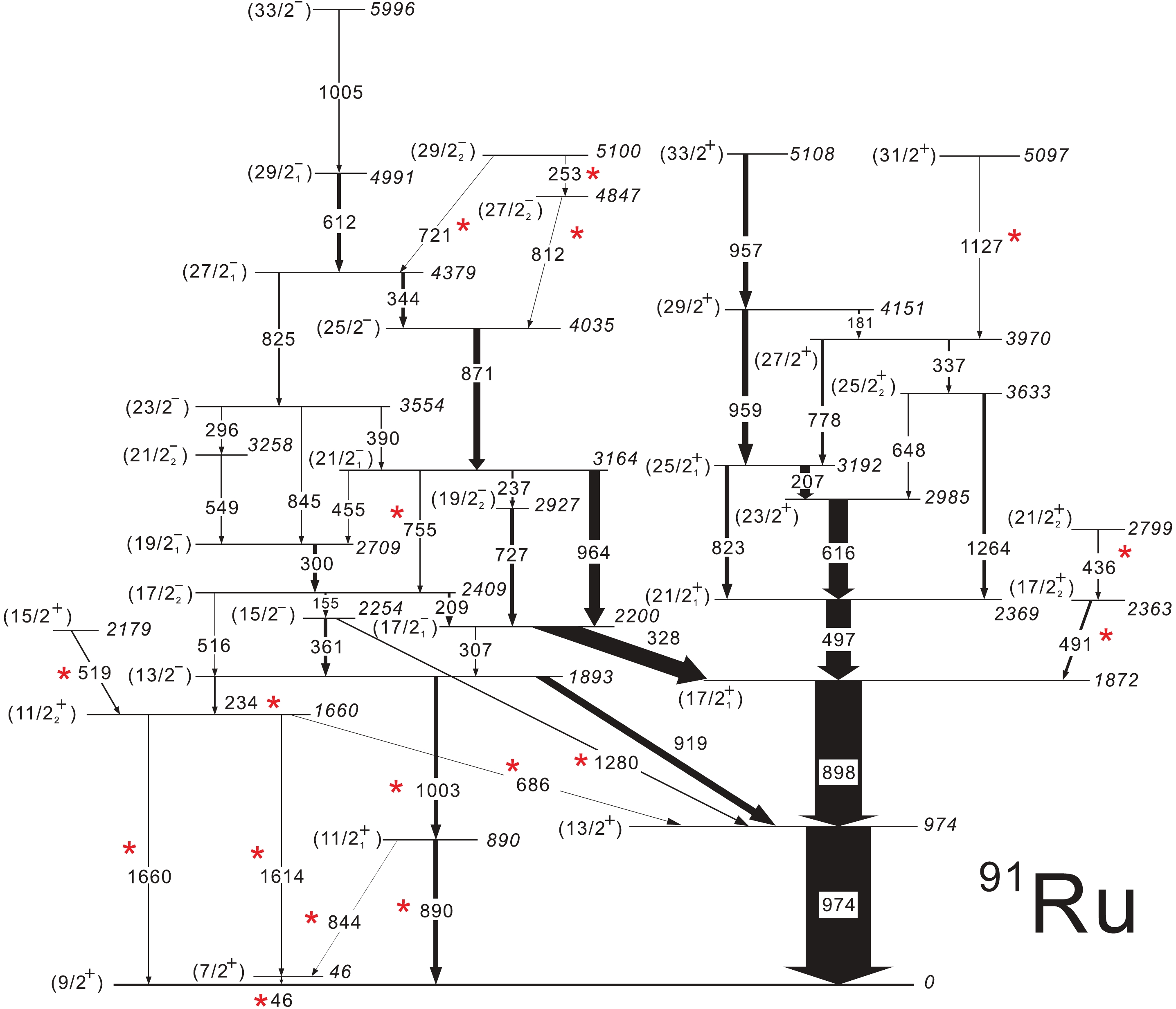
Figure 2. (color online) Level scheme of 91Ru, obtained from present experiment. New
$\gamma$ -ray transitions are marked by asterisks.The present level scheme of 91Ru is consistent with the previous result of Heese et al. [8], with the exception of the
$ 19/2^{-}_{3} $ level. For this particular state, some modifications have been made in the present work. First, the 296 keV transition was found to be a magnetic dipole rather than magnetic$ {\Delta}I = 0 $ dipole, as suggested in Ref. [8]. Furthermore, the ordering of$ \gamma $ -rays in the 549-296 transition sequence was reversed in the present level scheme. This is based on the intensity consideration, since 889 keV and 804 keV crossover transitions were not observed in this work.Below the
$ (13/2^{-}) $ level, a transition sequence consisting of 1003 keV and 890 keV$ \gamma $ -rays was observed feeding the ground state. The order of the two new transitions is determined mainly by comparing their relative intensities. This is further supported by a new observed crossover transition of 844 keV energy, as shown in Fig. 2. The DCO ratio and asymmetry measured for the 890 keV transition are 1.05 and 5, respectively, when gated by the stretched dipole transition, and −0.03 and 1, respectively, indicating a stretched$ M1 $ multipolarity, which leads to the assignment of$ (11/2^{+}) $ for the new state at 890 keV. A stretched$ E1 $ character for the 1003 keV transition is obtained from the results of the DCO ratio ($ 0.98\pm0.04 $ when gated by the stretched dipole transition) and linear polarization measurements ($ 0.12\pm0.05 $ ). Hence, this$ \gamma $ -ray has been assigned to the$ (13/2^{-}) $ $ \rightarrow $ $ (11/2_{1}^{+}) $ transition, which in turn provides a supplementary argument for the previous assignment of the$ (13/2^{-}) $ state at 1893 keV.The newly observed
$ \gamma $ -rays at energies of 234, 1660, and 1614 keV have been assigned to connect the$ (13/2^{-}) $ level and the$ (9/2^{+}) $ ground state. These new transitions are clearly seen in Fig. 1. Based on the obtained DCO ratios and the Compton asymmetries, we assigned the$ M1 $ and$ E2 $ multipolarities to the 1660 and 1614 keV$ \gamma $ -rays, respectively. The DCO ratio analysis shows that the 234 keV transition has a dipole multipolarity (see Table 1). These assignments lead to an identification of the$ (7/2^{+}) $ state at 46 keV excitation energy and the$ (11/2^{+}) $ level at 1660 keV excitation energy. The 46 keV$ \gamma $ -ray, which corresponds to the decay of the excited state to the ground state, cannot be observed in the EXOGAM Clovers, since it is fully absorbed by the material located around the target, including the DIAMANT array. Furthermore, a new transition of 686 keV was observed and assigned to connect the$ (11/2_{2}^{+}) $ level at 1660 keV and the$ (13/2^{+}) $ state at 974 keV. The combination of the DCO ratio and linear polarization data shows that the 686 keV$ \gamma $ -ray contains the$ M1 $ multipolarity, which confirms the spin and parity assignments of the 1660 keV level as$ J^{\pi} = (11/2^{+} $ ). Finally, a 519 keV line has been observed in coincidence with all the above-mentioned new transitions except the one at 234 keV. The measured DCO ratio and asymmetry indicate the$ E2 $ character. This transition reveals the yrast ($ 15/2^{+} $ ) level at 2179 keV. -
As shown in Fig. 2, the level scheme of 91Ru displays a complex structure in the presence of high-energy
$ \gamma $ -rays, irregular level spacings, and many parallel decay branches, indicating that the excited states are formed primarily by the excitations of valence nucleons, which are expected to be suitably described by the shell model. The shell model seems to be an appropriate tool to study the structure of 91Ru. In the earlier study of Heese et al. [8], the yrast positive parity states in 91Ru have been efficiently described by the shell model calculations performed with the code RITSSCHIL, where a 88Sr core was used, and the model space was restricted to the$ g_{9/2} $ and$ p_{1/2} $ orbits outside the 88Sr core. However, despite the success the calculations had in explaining the level structure of 91Ru, the use of the small ($ g_{9/2} $ ,$ p_{1/2} $ ) space has only limited applicability. In the present work, we performed the shell model with extended$ P+QQ $ interaction [19–22] for a more detailed understanding of the observed level scheme of 91Ru. The shell model space has been extended to ($ f_{5/2} $ ,$ p_{3/2} $ ,$ p_{1/2} $ ,$ g_{9/2} $ ). This choice of model space should lead to more accurate descriptions of nuclei with$ A\approx90 $ , especially for those close to the limit of the restricted model space ($ Z\approx38 $ ,$ N\approx50 $ ). It also has the advantage that protons and neutrons are treated on an equal basis. Recently, an extended$ P+QQ $ force was applied to the$ f_{7/2} $ - and$ g_{9/2} $ -shell nuclei. This interaction is schematic, nevertheless it works remarkably well. The conventional$ P+QQ $ force was first proposed by Bohr and Mottelson, and subsequently widely used by Kisslinger and Sorensen, Baranger and Kumar, and numerous authors. Later, the octupole-octupole ($ OO $ ) force was introduced into the extended$ P+QQ $ force model to describe negative-parity states. The$ QQ $ and$ OO $ forces are the long-range and the deformation-driving part of the effective interaction. Contrary to this, the monopole pairing force can be associated with a short-range force, which restores the spherical shape. The extended$ P+QQ $ interaction is isospin-invariant and includes the$ np $ pairing forces in addition to the$ np $ $ QQ $ force, which is considered to be suitable for studying$ N \thickapprox Z $ nuclei. Details regarding this model are described in Refs. [19–22].Hasegawa et al. have carried out shell model calculations using the extended P+QQ model for Ru isotopes including 91Ru. The calculations qualitatively reproduce the overall energy levels observed in the Ru isotopes 88Ru, 90Ru, 91Ru, 92Ru, 93Ru, and 94Ru using a single set of parameters in the model space (
$ f_{5/2} $ ,$ p_{3/2} $ ,$ p_{1/2} $ ,$ g_{9/2} $ ). The same extended$ P+QQ $ model is therefore expected to describe the level structure of 91Ru established in this work.By studying the single-particle energies used by Hasegawa et al. [23], we fixed their energies in MeV as follows:
$ \varepsilon _{g\,_{9/2}} = 0.0 $ ,$ \varepsilon _{p\,_{1/2}} = 1.6 $ ,$ \varepsilon _{p\,_{3/2}} = 6.0 $ ,$ \varepsilon _{f\,_{5/2}} = 5.5 $ for both proton and neutron holes. The energy difference$ \varepsilon _{p\,_{1/2}}-\varepsilon _{g\,_{9/2}} $ = 1.1 applied in Ref. [23] is modified to be 1.6 MeV to correctly reproduce the very low-lying 7/2+ and the 9/2+ ground states in 91Ru. 100Sn is considered as a "core" in these calculations. The strengths of the$ J = 0 $ and$ J = 2 $ pairing forces,$ QQ $ force, and$ OO $ force are determined such that the same set of parameters reproduce the observed energy levels as a whole in Ru isotopes, as well as lighter isotopes of Sr, Zr, and Mo including odd-A and odd-odd nuclei ($ 38\leqslant Z \leqslant44 $ ,$ 45\leqslant N \leqslant50 $ ). We use different force strengths for proton-proton ($ pp $ ), neutron-neutron ($ nn $ ), and neutron-proton ($ np $ ) interactions and impose A dependence on them as usual. We adopt the approximation that the$ pp $ ,$ nn $ , and$ np $ interactions have the same force strengths$ g_{0} $ ,$ g_{2} $ ,$ \chi_{2} $ , and$ \chi_{3} $ to reduce the number of parameters. The fixed parameters are as follows (in MeV):$ g_{0} = 24/ A $ ,$ g_{2} = 225/ A^{5/3} $ ,$ \chi_{2} = 400/ A^{5/3} $ ,$ \chi_{3} = 350/ A^{6} $ for$ pp $ ,$ nn $ , and$ np $ interactions, respectively. Changes of force strengths within 10% do not significantly affect the level scheme of 91Ru. We use the shell model code NuShellX, newly released by Rae [24]. This code first obtains proton and neutron substrates and subsequently diagonalizes$ np $ interactions for their product states. -
The calculated level energies of states in 91Ru are compared with the experimental ones in Fig. 3 for positive- and negative-parity states, where the observed or calculated levels with the same
$ J^{\pi} $ values are connected to each other with dashed lines. The yrast and non-yrast states, as well as the two close lying levels, are separately shown in two columns. The overall agreement between calculation and experiment is generally satisfactory. In Table 2, we show the main components of wave functions (>10%) for the excited states in 91Ru. The leading configurations in these states are given by$ (p^{6})^{\pi}_{J_{p}} $ $ (n^{3})^{\pi}_{J_{n}} $ ($ \pi $ being the parity of proton- and neutron-hole subsystems). Its squared amplitudes and expectation values of proton-hole numbers$ \langle n_{a} \rangle _{p} $ and neutron-hole numbers$ \langle n_{a} \rangle _{n} $ in the respective orbitals a are also shown in Table 2. The configurations contributing to the wave functions were characterized according to their seniority. Fig. 3 and Table 2 show that the present calculations adequately reproduce the level energies and decay patterns of the positive and negative level structure.$J^{\pi}_{i}$ 

leading config proton $\langle n_{a} \rangle_{p}$ 

neutron $\langle n_{a} \rangle _{n}$ 

% $(p^{6})$ 

$_{J_{p}}$ 

$^{\pi}$ 

$(n^{3})$ 

$_{J_{n}}$ 

$^{\pi}$ 

$\nu$ 

$p_{3/2}$ 

$f_{5/2}$ 

$p_{1/2}$ 

$g_{9/2}$ 

$p_{3/2}$ 

$f_{5/2}$ 

$p_{1/2}$ 

$g_{9/2}$ 

$7/2^{+}$ 

52 ${(p^{6})}_0^{+}$ 

${(n^{3})}_{7/2}^{+}$ 

3 0.0 0.0 0.2 5.8 0.0 0.0 0.0 3.0 18 ${(p^{6})}_{2}^{+}$ 

${(n^{3})}_{9/2}^{+}$ 

3 0.0 0.0 0.2 5.8 0.0 0.0 0.0 3.0 17 ${(p^{6})}_{2}^{+}$ 

${(n^{3})}_{7/2}^{+}$ 

5 0.0 0.0 0.2 5.8 0.0 0.0 0.0 3.0 $9/2^{+}$ 

62 ${(p^{6})}_{0}^{+}$ 

${(n^{3})}_{9/2}^{+}$ 

1 0.0 0.0 0.2 5.8 0.0 0.0 0.0 3.0 $11/2_{1}^{+}$ 

29 ${(p^{6})}_{0}^{+}$ 

${(n^{3})}_{11/2}^{+}$ 

3 0.0 0.0 0.2 5.8 0.0 0.0 0.0 3.0 22 ${(p^{6})}_{2}^{+}$ 

${(n^{3})}_{9/2}^{+}$ 

3 0.0 0.0 0.2 5.8 0.0 0.0 0.0 3.0 15 ${(p^{6})}_{2}^{+}$ 

${(n^{3})}_{7/2}^{+}$ 

5 0.0 0.0 0.2 5.8 0.0 0.0 0.0 3.0 14 ${(p^{6})}_{4}^{+}$ 

${(n^{3})}_{7/2}^{+}$ 

5 0.0 0.0 0.2 5.8 0.0 0.0 0.0 3.0 $11/2_{2}^{+}$ 

33 ${(p^{6})}_{2}^{+}$ 

${(n^{3})}_{9/2}^{+}$ 

3 0.0 0.0 0.1 5.9 0.0 0.0 0.0 3.0 26 ${(p^{6})}_{2}^{+}$ 

${(n^{3})}_{7/2}^{+}$ 

5 0.0 0.0 0.1 5.9 0.0 0.0 0.0 3.0 18 ${(p^{6})}_{4}^{+}$ 

${(n^{3})}_{9/2}^{+}$ 

3 0.0 0.0 0.1 5.9 0.0 0.0 0.0 3.0 Continued on next page Table 2. Structure of yrast and non-yrast states in 91Ru. Leading components of configurations
$(p^{6})^{\pi}_{J_{p}}$ $(n^{3})^{\pi}_{J_{n}}$ , and its squared amplitude (in percentages) are tabulated in the second and third column, where the superscript$\pi$ in$(p^{6})^{\pi}_{J_{p}}$ $(n^{3})^{\pi}_{J_{n}}$ indicates parity of 6p and 3n subsystems. Expected values of proton number$\langle n_{a} \rangle _{p}$ (neutron number$\langle n_{a} \rangle _{p}$ ) in four proton orbitals (in four neutron orbitals) are tabulated in columns 5–8 (in columns 9–12).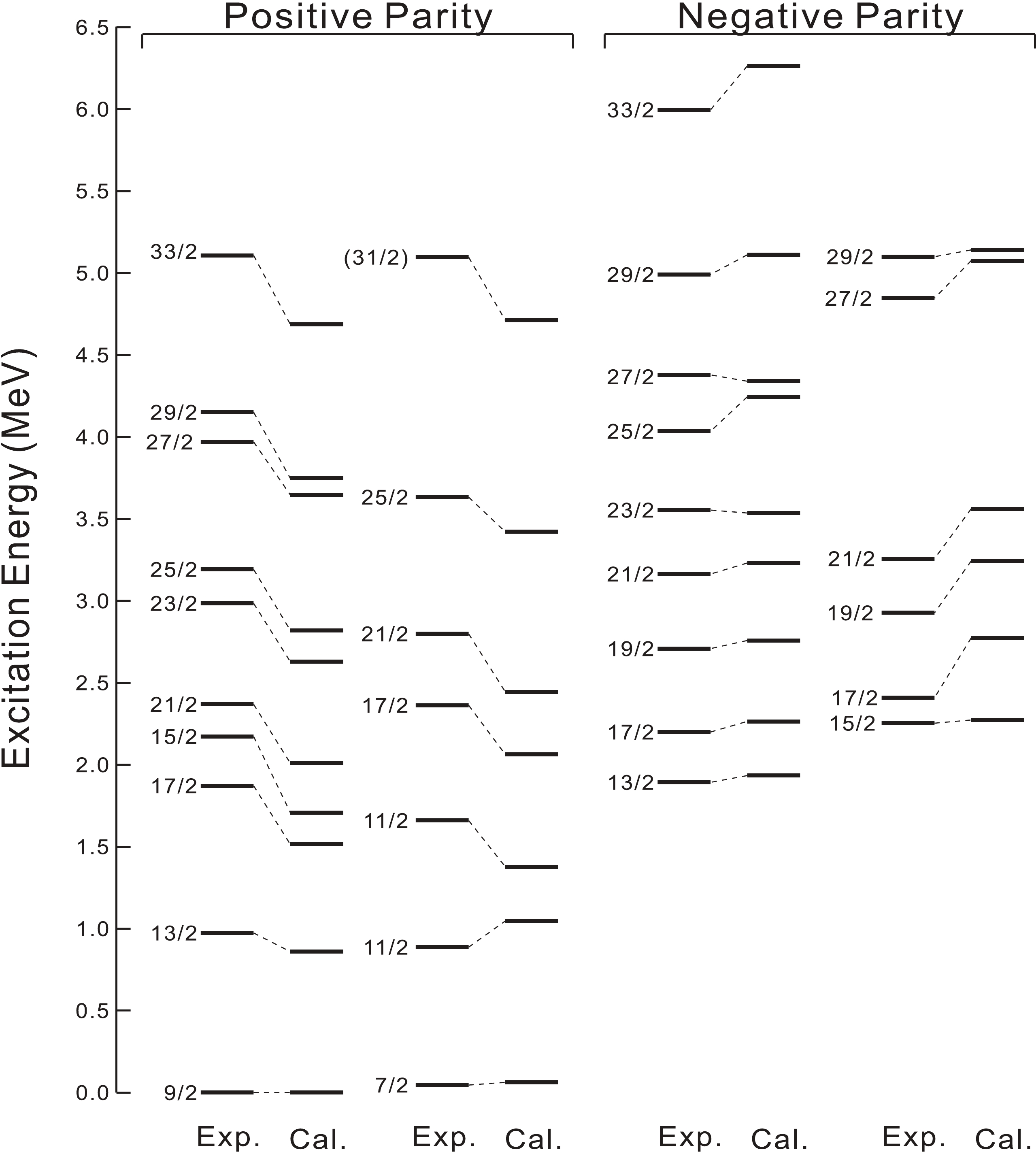
Figure 3. Calculated positive- and negative-parity energy levels of 91Ru, compared with experimental ones.
Table 2-continued from previous page $J^{\pi}_{i}$ 

leading config proton $\langle n_{a} \rangle_{p}$ 

neutron $\langle n_{a} \rangle _{n}$ 

% $(p^{6})$ 

$_{J_{p}}$ 

$^{\pi}$ 

$(n^{3})$ 

$_{J_{n}}$ 

$^{\pi}$ 

$\nu$ 

$p_{3/2}$ 

$f_{5/2}$ 

$p_{1/2}$ 

$g_{9/2}$ 

$p_{3/2}$ 

$f_{5/2}$ 

$p_{1/2}$ 

$g_{9/2}$ 

$11/2_{3}^{+}$ 

19 ${(p^{6})}_{0}^{+}$ 

${(n^{3})}_{11/2}^{+}$ 

3 0.0 0.0 0.1 5.9 0.0 0.0 0.0 3.0 17 ${(p^{6})}_{6}^{+}$ 

${(n^{3})}_{7/2}^{+}$ 

5 0.0 0.0 0.1 5.9 0.0 0.0 0.0 3.0 15 ${(p^{6})}_{4}^{+}$ 

${(n^{3})}_{7/2}^{+}$ 

5 0.0 0.0 0.1 5.9 0.0 0.0 0.0 3.0 15 ${(p^{6})}_{6}^{+}$ 

${(n^{3})}_{9/2}^{+}$ 

3 0.0 0.0 0.1 5.9 0.0 0.0 0.0 3.0 $13/2^{+}$ 

38 ${(p^{6})}_{2}^{+}$ 

${(n^{3})}_{9/2}^{+}$ 

3 0.0 0.0 0.1 5.8 0.0 0.0 0.0 3.0 28 ${(p^{6})}_{0}^{+}$ 

${(n^{3})}_{13/2}^{+}$ 

3 0.0 0.0 0.1 5.8 0.0 0.0 0.0 3.0 $15/2^{+}$ 

25 ${(p^{6})}_{4}^{+}$ 

${(n^{3})}_{7/2}^{+}$ 

5 0.0 0.0 0.1 5.9 0.0 0.0 0.0 3.0 12 ${(p^{6})}_{6}^{+}$ 

${(n^{3})}_{7/2}^{+}$ 

5 0.0 0.0 0.1 5.9 0.0 0.0 0.0 3.0 12 ${(p^{6})}_{4}^{+}$ 

${(n^{3})}_{9/2}^{+}$ 

3 0.0 0.0 0.1 5.9 0.0 0.0 0.0 3.0 15 ${(p^{6})}_{6}^{+}$ 

${(n^{3})}_{9/2}^{+}$ 

3 0.0 0.0 0.1 5.9 0.0 0.0 0.0 3.0 $17/2_{1}^{+}$ 

25 ${(p^{6})}_{4}^{+}$ 

${(n^{3})}_{9/2}^{+}$ 

3 0.0 0.0 0.0 5.9 0.0 0.0 0.0 3.0 16 ${(p^{6})}_{2}^{+}$ 

${(n^{3})}_{13/2}^{+}$ 

5 0.0 0.0 0.0 5.9 0.0 0.0 0.0 3.0 $17/2_{2}^{+}$ 

27 ${(p^{6})}_{0}^{+}$ 

${(n^{3})}_{17/2}^{+}$ 

3 0.0 0.0 0.1 5.9 0.0 0.0 0.0 3.0 11 ${(p^{6})}_{2}^{+}$ 

${(n^{3})}_{13/2}^{+}$ 

5 0.0 0.0 0.1 5.9 0.0 0.0 0.0 3.0 11 ${(p^{6})}_{8}^{+}$ 

${(n^{3})}_{7/2}^{+}$ 

5 0.0 0.0 0.1 5.9 0.0 0.0 0.0 3.0 $21/2_{1}^{+}$ 

20 ${(p^{6})}_{6}^{+}$ 

${(n^{3})}_{9/2}^{+}$ 

3 0.0 0.0 0.1 5.9 0.0 0.0 0.0 3.0 17 ${(p^{6})}_{8}^{+}$ 

${(n^{3})}_{9/2}^{+}$ 

3 0.0 0.0 0.1 5.9 0.0 0.0 0.0 3.0 11 ${(p^{6})}_{4}^{+}$ 

${(n^{3})}_{13/2}^{+}$ 

5 0.0 0.0 0.1 5.9 0.0 0.0 0.0 3.0 $21/2_{2}^{+}$ 

45 ${(p^{6})}_{0}^{+}$ 

${(n^{3})}_{21/2}^{+}$ 

3 0.0 0.0 0.1 5.8 0.0 0.0 0.0 3.0 13 ${(p^{6})}_{2}^{+}$ 

${(n^{3})}_{21/2}^{+}$ 

5 0.0 0.0 0.1 5.8 0.0 0.0 0.0 3.0 11 ${(p^{6})}_{2}^{+}$ 

${(n^{3})}_{17/2}^{+}$ 

5 0.0 0.0 0.1 5.8 0.0 0.0 0.0 3.0 $23/2^{+}$ 

54 ${(p^{6})}_{8}^{+}$ 

${(n^{3})}_{9/2}^{+}$ 

3 0.0 0.0 0.1 5.9 0.0 0.0 0.0 3.0 $25/2_{1}^{+}$ 

52 ${(p^{6})}_{8}^{+}$ 

${(n^{3})}_{9/2}^{+}$ 

3 0.0 0.0 0.1 5.9 0.0 0.0 0.0 3.0 17 ${(p^{6})}_{6}^{+}$ 

${(n^{3})}_{13/2}^{+}$ 

5 0.0 0.0 0.1 5.9 0.0 0.0 0.0 3.0 $25/2_{2}^{+}$ 

21 ${(p^{6})}_{8}^{+}$ 

${(n^{3})}_{9/2}^{+}$ 

3 0.0 0.0 0.1 5.9 0.0 0.0 0.0 3.0 15 ${(p^{6})}_{8}^{+}$ 

${(n^{3})}_{13/2}^{+}$ 

5 0.0 0.0 0.1 5.9 0.0 0.0 0.0 3.0 11 ${(p^{6})}_{2}^{+}$ 

${(n^{3})}_{21/2}^{+}$ 

5 0.0 0.0 0.1 5.9 0.0 0.0 0.0 3.0 $27/2^{+}$ 

30 ${(p^{6})}_{10}^{+}$ 

${(n^{3})}_{9/2}^{+}$ 

5 0.0 0.0 0.0 5.9 0.0 0.0 0.0 3.0 27 ${(p^{6})}_{8}^{+}$ 

${(n^{3})}_{13/2}^{+}$ 

5 0.0 0.0 0.0 5.9 0.0 0.0 0.0 3.0 16 ${(p^{6})}_{8}^{+}$ 

${(n^{3})}_{11/2}^{+}$ 

5 0.0 0.0 0.0 5.9 0.0 0.0 0.0 3.0 $29/2^{+}$ 

42 ${(p^{6})}_{8}^{+}$ 

${(n^{3})}_{13/2}^{+}$ 

5 0.0 0.0 0.0 5.9 0.0 0.0 0.0 3.0 27 ${(p^{6})}_{10}^{+}$ 

${(n^{3})}_{9/2}^{+}$ 

5 0.0 0.0 0.0 5.9 0.0 0.0 0.0 3.0 13 ${(p^{6})}_{6}^{+}$ 

${(n^{3})}_{17/2}^{+}$ 

5 0.0 0.0 0.0 5.9 0.0 0.0 0.0 3.0 $31/2^{+}$ 

25 ${(p^{6})}_{8}^{+}$ 

${(n^{3})}_{17/2}^{+}$ 

5 0.0 0.0 0.0 5.9 0.0 0.0 0.0 3.0 18 ${(p^{6})}_{10}^{+}$ 

${(n^{3})}_{13/2}^{+}$ 

7 0.0 0.0 0.0 5.9 0.0 0.0 0.0 3.0 13 ${(p^{6})}_{12}^{+}$ 

${(n^{3})}_{9/2}^{+}$ 

5 0.0 0.0 0.0 5.9 0.0 0.0 0.0 3.0 $33/2^{+}$ 

36 ${(p^{6})}_{8}^{+}$ 

${(n^{3})}_{17/2}^{+}$ 

5 0.0 0.0 0.0 5.9 0.0 0.0 0.0 3.0 25 ${(p^{6})}_{10}^{+}$ 

${(n^{3})}_{13/2}^{+}$ 

7 0.0 0.0 0.0 5.9 0.0 0.0 0.0 3.0 12 ${(p^{6})}_{6}^{+}$ 

${(n^{3})}_{21/2}^{+}$ 

5 0.0 0.0 0.0 5.9 0.0 0.0 0.0 3.0 One can see in Fig. 3 shows that these calculations efficiently describe the favored positive-parity states at 974, 1872, 2369, 2985, and 3192 keV, which are connected by strong
$ E2 $ or$ M1 $ transitions. The dominant components of these states have six proton holes occupying the$ 1g_{9/2} $ and$ 2p_{1/2} $ orbitals and three neutron holes filling the$ 1g_{9/2} $ orbitals. Up to spin 25/2, the total angular momentum of these dominant components is built up by the successive alignment of two proton holes parallel to the spin of the last unpaired neutron hole in$ 1g_{9/2} $ . The structural change from seniority$ \nu = 3 $ to$ \nu = 5 $ occurs above the 25/2+ state, which reflects in a relatively large spacing between the 25/2+ and 29/2+ states. This is found in the calculations as well as in the experimental observation. The above configuration assignments are consistent with the previous shell-model study by Heese et al. [8]. As illustrated in Fig. 3, the negative-parity states are efficiently and precisely reproduced by the calculations. The dominant components of all the negative-parity levels up to 33/2− have six proton holes mainly occupying the$ 1g_{9/2} $ and$ 2p_{1/2} $ orbitals with small admixtures from the$ 1f_{5/2} $ and/or$ 2p_{3/2} $ orbitals, and three neutron holes filling the$ 1g_{9/2} $ orbitals, which illustrate that an extension of the ($ g_{9/2} $ ,$ p_{1/2} $ ) model space to a larger configuration including the$ f_{5/2} $ ,$ p_{3/2} $ ,$ p_{1/2} $ , and$ g_{9/2} $ orbitals should be taken into account for a more precise shell model description.The new states of 7/2+, 11/2
$ _{1}^{+} $ , and 11/2$ _{2}^{+} $ identified in this study at 46, 890, and 1660 keV, respectively, are grouped into a low-lying positive-parity structure. A similar structure has also been observed in the lighter$ N = 47 $ isotone 89Mo by Kitching et al. [6]. They suggested that the three-neutron-hole$ \nu g_{9/2}^{-3} $ configuration would take an important role in explaining this low-lying structure. Indeed, the 7/2+, 11/2$ _{1}^{+} $ , and 11/2$ _{2}^{+} $ state in 91Ru are reproduced by the shell model states, whose wave function mainly arises from$ \nu $ $ g_{9/2}^{-3} $ (52% for 7/2+, 29% for 11/2$ _{1}^{+} $ , 33% for 11/2$ _{2}^{+} $ ) with a mixture of$ \pi $ $ g_{9/2}^{-2} $ $ \,\nu $ $ g_{9/2}^{-1} $ (18% for 7/2+, 22% for 11/2$ _{1}^{+} $ , 26% for 11/2$ _{2}^{+} $ ). These results indicate that, compared to the 7/2+ state with a quite pure three-neutron-hole configuration, the two 11/2+ states exhibit a larger configuration mixing of proton subconfigurations. -
The excited states in 91Ru were populated via the fusion-evaporation reaction 58Ni (36Ar, 2p1n
$ \gamma $ ) 91Ru at a beam energy of 111 MeV. New low-lying levels were observed in 91Ru for the first time. Spins and parities were assigned to new and previously reported levels in 91Ru by measuring the DCO ratios and linear polarization of$ \gamma $ -rays. We have carried out the shell model calculation for 91Ru in the model space$ \pi \nu $ ($ f_{5/2} $ ,$ p_{3/2} $ ,$ p_{1/2} $ ,$ g_{9/2} $ ). A parameter set of the extended$ P+QQ $ interaction was determined for the$ 38\leqslant Z \leqslant44 $ ,$ 45\leqslant N \leqslant50 $ nuclei including 91Ru. The shell model efficiently explains the overall level scheme observed in 91Ru.Based on the fairly good agreement, we discussed the low-lying positive-parity structure of 91Ru. The shell model results show that the new low-lying positive-parity states of 7/2+, 11/2
$ _{1}^{+} $ , and 11/2$ _{2}^{+} $ can be interpreted as three-quasiparticle excitations, which mainly arise from the three-neutron-hole$ \nu $ $ g_{9/2}^{-3} $ configuration with a mixture of$ \pi $ $ g_{9/2}^{-2} $ $ \,\nu $ $ g_{9/2}^{-1} $ .
Multi-quasiparticle excitations of 91Ru
- Received Date: 2019-11-20
- Available Online: 2020-02-01
Abstract: The level structure in neutron-deficient nucleus 91Ru was investigated via the 58Ni (36Ar, 2p1n





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF



















 DownLoad:
DownLoad: