-
Recently, the BESIII collaboration analyzed the cross section of the
$ e^+e^- \to K^+K^- $ process at the center-of-mass energy of 2.00 to 3.08 GeV. A resonant structure was observed in the line shape, which has a mass of$ 2239.2 \pm 7.1 \pm 11.3\; \rm{MeV} $ and a width of$ 139.8 \pm 12.3 \pm 20.6\; $ MeV [1]. Given the production process, the quantum number of this resonant structure can be assigned as$ J^{PC} = 1^{--} $ .From the Review of Particle Physics, there exist four
$ J^{PC} = 1^{--} $ states observed around 2.2 GeV,$ \phi(2170) $ ,$ \rho(2150) $ ,$ \omega(2205) $ and$ \rho(2270) $ [2]. The$ \phi(2170) $ state with$ I^G(J^{PC}) = 0^-(1^{--}) $ , labeled previously as$ Y(2175) $ , has been investigated using many theoretical models, which include the conventional$ s\bar s $ state [3–7], hybrid state [3, 8], tetraquark state [9 –14],$ \Lambda \bar \Lambda(^3S_1) $ bound state or hexaquark state [15–19], and$ \phi K \bar K $ resonance state [20, 21].$ \rho(2150) $ ,$ \omega(2205) $ and$ \rho(2270) $ were also studied as the conventional radial or orbital excited mesons in the consistent quark model [22–24]. As mentioned by the BESIII collaboration, the newly observed resonant structure, denoted as$ X(2239) $ in the present work, has a different mass and width than$ \phi(2170) $ and$ \rho(2150) $ , and seems to be a new resonance [1]. The other two listed states,$ \omega(2205) $ and$ \rho(2270) $ , are both broad and can not have the same structure as the newly observed state [2].In the conventional quark model, several highly excited
$ 1^{--} $ $ \rho $ ,$ \omega $ , and$ \phi $ states are predicted in this energy region, and their strong decay behavior has been investigated in the quark pair creation model. Due to the large phase space, the predicted total decay widths of these states are rather broad, which suggests that the newly observed state with a width of about$ 140 $ MeV may not be a conventional excited meson. More exotic interpretations, such as a$ ss \bar s \bar s $ tetraquark state, need to be considered to clarify its nature. The P-wave$ ss \bar s \bar s $ system was mostly investigated by the QCD sum rule method [9–12, 25] and the simple quark models [13, 14], and their results are not consistent. Hence, it is essential to study this system in a more realistic potential model.In this work, we first employ a relativized quark model to estimate the masses of
$ ss\bar s \bar s $ tetraquark states. The relativized quark model, proposed by Godfrey, Capstick and Isgur, has been widely used to study the properties of conventional hadrons and gives a unified description of the traditional hadron spectra [26–36]. It has also been extended to various tetraquark systems, such as$ Qq \bar Q \bar q $ and$ Qq \bar q \bar q $ [37–39]. Moreover, relativistic effects are included in this model, which is essential for the up, down and strange quarks. Therefore, it is suitable to deal with the$ ss\bar s \bar s $ tetraquark states, where strange quarks and antiquarks are included. To calculate the tetraquark masses, we focus on the diquark-antidiquark picture, which has been extensively discussed and employed in Refs. [37–51]. We first calculate the masses and wave functions of the axial-vector and vector ss diquarks, and then obtain the mass spectra and diquark-antidiquark wave functions by solving the Schrödinger-type equation between the diquark and antidiquark. The total wave function can be expressed as a product of the diquark, antidiquark, and diquark-antidiquark wave functions. The predicted mass of the lowest$ 1^{--} $ $ ss\bar s \bar s $ tetraquark is 2227 MeV, which is consistent with the experimental value of$ 2239.2 \pm 7.1 \pm 11.3\; \rm{MeV} $ given by the BESIII collaboration. This suggests that the newly observed resonant structure$ X(2239) $ can be assigned as the lowest$ J^{PC} = 1^{--} $ $ ss \bar s \bar s $ tetraquark state. Using the wave functions obtained in the relativized quark model and the electromagnetic transition operator, we estimate the radiative decays of$ ss\bar s \bar s $ tetraquarks. It is found that the radiative decay width of the lowest$ 1^{--} $ $ ss \bar s \bar s $ tetraquark state is 27 keV, which is significant. Furthermore, the strong decay behavior is also discussed, and the ratios of the dominant channels are estimated. The information about the radiative and strong decays may be useful for future experimental searches.The paper is organized as follows. In Sec. 2, the relativized quark model is briefly introduced, and the masses of the
$ ss\bar s \bar s $ tetraquark states are calculated. In Sec. 3, the radiative transitions and strong decays of the$ ss\bar s \bar s $ tetraquark states are numerically estimated. Finally, we give a short summary in the last section. -
The Hamiltonian between the quark and antiquark in the relativized quark model can be expressed as
$ \tilde{H} = H_0+\tilde{V}({ p},{ r}), $

(1) with
$ H_0 = (p^2+m_i^2)^{1/2}+(p^2+m_j^2)^{1/2}, $

(2) $ \tilde{V}({ p},{ r}) = \tilde{H}^{\rm conf}_{ij}+\tilde{H}^{\rm cont}_{ij}+\tilde{H}^{\rm ten}_{ij}+\tilde{H}^{\rm so}_{ij}, $

(3) where
$ \tilde{H}^{\rm conf}_{ij} $ includes the spin-independent linear confinement and the Coulomb-like interaction, and$ \tilde{H}^{\rm cont}_{ij} $ ,$ \tilde{H}^{\rm ten}_{ij} $ , and$ \tilde{H}^{\rm so}_{ij} $ are the color contact term, color tensor interaction and spin-orbit term, respectively.$ \tilde{H} $ represents the operator H taking account the relativistic effects via the relativized procedure. The explicit forms of these interactions and the details of the relativization scheme can be found in Refs. [26, 27]. In the original GI model, the coupled channel or screening effects are ignored, which may influence the properties of the excited mesons and tetraquarks [33, 37, 52–55]. The modified procedure$ br \to b(1-e^{-\mu r})/\mu $ with a new screening parameter$ \mu $ , gives a better description of the meson and tetraquark spectra, especially for the strange quark systems [33, 37]. Hence, we take the screening effects into account for completeness.In the present work, only the antitriplet diquark
$ [\bar 3_c]_{ss} $ is considered, while the$ [6_c]_{ss} $ type diquarks can not be formed in the GI quark model. For the quark-quark interaction in the antitriplet diquark and triplet antidiquark systems, the relation$ \tilde{V}_{ss}({ p},{ r}) = \tilde{V}_{\bar s \bar s}({ p},{ r}) = \tilde{V}_{s\bar s}({ p},{ r})/2 $ is employed. The parameters used in our calculations are the same as in the original work [26]. The structure of$ ss\bar s \bar s $ tetraquarks is illustrated in Fig. 1. The interaction between diquark and antidiquark$ \tilde{V}_{{ss}-{\bar s \bar s}}({ p},{ r}) $ equals to the quark-antiquark interaction$ \tilde{V}_{s\bar s}({ p},{ r}) $ . The ground state of ss diquark in S-wave has the spin-parity$ J^P = 1^+ $ and is named axial-vector diquark. For the excited states, we only consider P-wave ss diquark with spin-parity$ J^P = 1^- $ , which is denoted as vector diquark.It should be mentioned that a constituent diquark naturally has a size as does a constituent quark, although they are treated as point-like in the potential formula [47]. The constituent quark model works whether the constituent quark or diquark has a size or not. A comparison between the diquark picture and the full few-body calculations can be found in Refs. [48, 49]. Investigating P-wave tetraquarks as a four-body system in the relativized quark model is certainly more interesting, convincing and complicated.
Here, we use the Gaussian expansion method to solve the Hamiltonian (1) with the potential
$ \tilde{V}_{ss}({ p},{ r}) $ [56]. The obtained masses of the axial-vector and vector ss diquarks are presented in Table 1. Since a better description of the strange quark system can be obtained with$ \mu = 0.02\; \rm{GeV} $ [33, 37], we use the diquark masses obtained with this value to calculate the masses and wave functions of$ ss\bar s \bar s $ tetraquarks.Quark content Diquark type Mass
(GI model)Mass $(\mu= 0.02~\rm{GeV})$ 

Mass $(\mu= 0.04~\rm{GeV})$ 

$\{s,s\}$ 

A 1.135 1.121 1.108 $\{s,s\}$ 

V 1.424 1.396 1.369 Table 1. Masses of the axial-vector and vector ss diquarks, denoted as A and V . The brace corresponds to the symmetric quark flavor content. The masses are in MeV.
With the diquarks listed in Table 1, the masses of
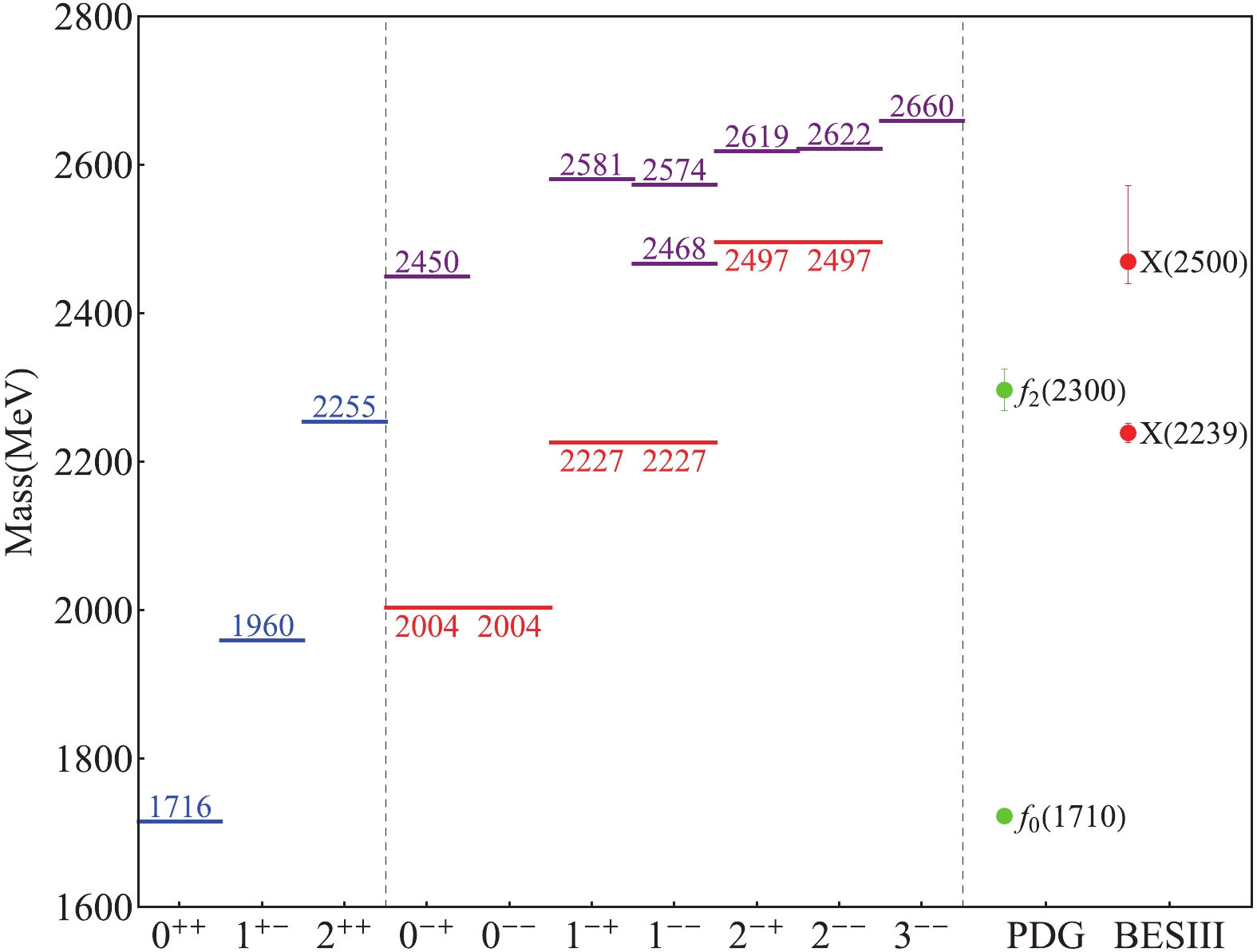
$ ss\bar s \bar s $ tetraquarks and the wave functions between diquarks and anti-diquarks can be calculated. The total wave function of an$ ss\bar s \bar s $ tetraquark can be expressed as a product of the diquark, anti-diquark and relative wave functions. The masses of$ ss\bar s \bar s $ tetraquark states composed of A and V diquarks and antidiquarks are presented in Table 2 and Fig. 2. The predicted mass of the lowest$ 0^{++} $ state is 1716 MeV, which is consistent with the$ f_0(1710) $ state. For the$ 1^{+-} $ $ ss\bar s \bar s $ state, only the$ h_1(1965) $ state listed in PDG lies in this energy region [2]. As$ h_1(1965) $ was observed in the$ \omega \eta $ and$ \omega \pi \pi $ final states, its assignment as a$ 1^{+-} $ $ ss\bar s \bar s $ tetraquark is disfavored. In Refs. [12, 25], it is suggested that the new structure$ X(2063) $ , observed in$ J/\psi \to \phi \eta \eta^\prime $ by the BESIII collaboration [57], is a$ 1^{+-} $ $ ss\bar s \bar s $ tetraquark candidate based on the QCD sum rule method. However, our calculated mass is 100 MeV lower than the experimental value, which does not support this interpretation. Considering the mass, spin, parity and$ \phi \phi $ decay mode of$ f_2(2300) $ , we may assign it as a$ 2^{++} $ $ ss\bar s \bar s $ tetraquark state.$J^{PC}$ 

Diquark Anti-diquark S L Mass Candidate $|0^{++}\rangle$ 

A $\bar A$ 

0 0 1716 $f_0(1710)$ 

$|1^{+-}\rangle$ 

A $\bar A$ 

1 0 1960 $|2^{++}\rangle$ 

A $\bar A$ 

2 0 2255 $f_2(2300)$ 

$|0^{-\pm}\rangle$ 

V $\bar A$ 

0 0 2004 $|1^{-\pm}\rangle$ 

V $\bar A$ 

1 0 2227 $X(2239)$ 

$|2^{-\pm}\rangle$ 

V $\bar A$ 

2 0 2497 $|0^{-+}\rangle$ 

A $\bar A$ 

1 1 2450 $X(2500)$ 

$|1^{-+}\rangle$ 

A $\bar A$ 

1 1 2581 $|1^{--}\rangle$ 

A $\bar A$ 

0 1 2574 $|1^{--}\rangle$ 

A $\bar A$ 

2 1 2468 $|2^{-+}\rangle$ 

A $\bar A$ 

1 1 2619 $|2^{--}\rangle$ 

A $\bar A$ 

2 1 2622 $|3^{--}\rangle$ 

A $\bar A$ 

2 1 2660 For P-wave
$ ss\bar s \bar s $ tetraquarks, we predict three$ 1^{--} $ states. The lowest one has an internal excitation of diquark or antidiquark, while the other two have relative excitations between diquarks and antidiquarks. The three$ 1^{--} $ states, and other theoretical results, are listed in Table 3 . It can be seen that our classification is significantly different from the results based on the QCD sum rule [9–11, 25], and the result of the simple quark model where the internal excitation of diquark or anti-diquark was not considered [13]. The predicted lowest mass is 2227 MeV, which agrees well with$ X(2239) $ observed by the BESIII collaboration [1]. The experimental mass of$ \phi(2170) $ is about 50 MeV lower than our result, and can not be excluded as a$ ss\bar s \bar s $ tetraquark. The two higher$ 1^{--} $ states may have been observed in previous experiments [4, 11, 58–60], or may be discovered in future searches.Table 3. The predicted three
$1^{--}$ $ss\bar s \bar s$ tetraquarks states, and other theoretical results. The masses are in MeV.Furthermore, we predict several higher
$ ss\bar s \bar s $ tetraquarks around 2.5 GeV. For the higher$ 0^{-+} $ state, there exists a candidate$ X(2500) $ with a mass of$ 2470^{+15+101}_{-19-23}\; \rm{MeV} $ observed in the$ J/\psi \to \gamma \phi \phi $ process by the BESIII collaboration [61]. In the conventional quark model,$ X(2500) $ was assigned as the$ \phi(5^1S_0) $ state given its mass and total width [62, 63], but with a tiny$ \phi \phi $ partial decay width. The$ ss\bar s \bar s $ tetraquark interpretation of$ X(2500) $ may avoid this defect due to its decay into the$ \phi \phi $ final state. Other predictions could provide helpful information for future experimental searches. -
Besides the mass spectrum, the decay behavior is also needed to indentify tetraquark states in future experiments. We first calculate the radiative transitions and then estimate the relevant ratios of the dominant strong decay modes. To treat the radiative transitions between
$ ss\bar s \bar s $ tetraquarks, one can adopt the EM transition operator which has been successfully applied to study the radiative decays of quarkonium and baryons [64–66]. In this model, the quark-photon EM coupling at the tree level is taken as$ H_e = -\sum\limits_j e_j \bar \psi_j \gamma_\mu^j A^\mu({ k},{ r}_j) \psi_j, $

(4) where
$ \psi_j $ stands for the jth quark field with coordinate$ { r}_j $ , and$ A^\mu $ is the photon field with three-momentum k. To match the wave functions obtained from the Schrödinger-like equation, we adopt this quark-photon EM coupling in a non-relativistic form. In the initial hadron rest system, the approximate form can be written as [64–72]$ h_e \cong \sum\limits_j \Bigg [ e_j { r}_j \cdot {{\epsilon}} - \frac{e_j}{2m_j} {{\sigma}}_j \cdot ({{\epsilon}} \times {{ {\hat k}}}) \Bigg ] {\rm e}^{-{\rm i}{ k} \cdot { r}_j}, $

(5) where
$ e_j $ ,$ m_j $ , and$ {{\sigma}}_j $ stand for the charge, constituent mass and Pauli spin vector of the jth quark, respectively.$ {{\epsilon}} $ is the polarization vector of the final photon.One can obtain the helicity amplitude
$ {\cal A} $ of the radiative transition as [64, 65]$ {\cal A} = -{\rm i} \sqrt{\frac{\omega_\gamma}{2}} \langle f | h_e | i \rangle. $

(6) We can then estimate the radiative transitions as [64, 65]
$ \Gamma = \frac{|{{ k}}|^2}{\pi} \frac{2}{2J_i+1} \frac{M_f}{M_i} \sum\limits_{J_{fz},J_{iz}} |{\cal A}|^2, $

(7) where
$ J_i $ is the total angular momentum of the initial tetraquarks, and$ J_{fz} $ and$ J_{fi} $ are the components of the total angular momenta along the z axis of the initial and final tetraquarks, respectively. In this work, the masses and wave functions of$ ss\bar s \bar s $ tetraquarks are taken from our theoretical predictions.The estimated radiative transitions of
$ ss\bar s \bar s $ tetraquarks are listed in Table 4, where we eliminate the notation$ AA $ of the three ground states without causing misunderstanding. The predicted radiative transitions between the three ground states$ 0^{++} $ ,$ 1^{+-} $ , and$ 2^{++} $ are respectivelyDecay mode $M_i$ /MeV

$M_f$ /MeV

Width/keV $|1^{+-} \rangle \to |0^{++} \rangle\gamma$ 

1960 1716 157 $|2^{++} \rangle \to |1^{+-} \rangle\gamma$ 

2255 1960 175 $|V\bar{A}, 0^{-+} \rangle \to |1^{+-} \rangle\gamma$ 

2004 1960 0.001 $|V\bar{A}, 1^{--} \rangle \to |0^{++} \rangle\gamma$ 

2227 1716 26.6 $|V\bar{A}, 1^{-+} \rangle \to |1^{+-} \rangle\gamma$ 

2227 1960 3.1 $|V\bar{A}, 2^{--} \rangle \to |0^{++} \rangle\gamma$ 

2497 1716 49.4 $|V\bar{A}, 2^{--} \rangle \to |2^{++} \rangle\gamma$ 

2497 2255 4.6 $|V\bar{A}, 2^{-+} \rangle \to |1^{+-} \rangle\gamma$ 

2497 1960 65.4 $|A\bar{A}, 0^{-+} \rangle \to |1^{+-} \rangle\gamma$ 

2450 1960 1345 $|A\bar{A}, 1^{-+} \rangle \to |1^{+-} \rangle\gamma$ 

2581 1960 1444 $|A\bar{A}, 1^{--} \rangle_{S = 0} \to |0^{++} \rangle\gamma$ 

2574 1716 1137 $|A\bar{A}, 1^{--} \rangle_{S = 0} \to |2^{++} \rangle\gamma$ 

2574 2255 0.0 $|A\bar{A}, 1^{--} \rangle_{S = 2} \to |0^{++} \rangle\gamma$ 

2468 1716 0.0 $|A\bar{A}, 1^{--} \rangle_{S = 2} \to |2^{++} \rangle\gamma$ 

2468 2255 119 $|A\bar{A}, 2^{-+} \rangle \to |1^{+-} \rangle\gamma$ 

2619 1960 954 $|A\bar{A}, 2^{--} \rangle \to |2^{++} \rangle\gamma$ 

2622 2255 809 $|A\bar{A}, 3^{--} \rangle \to |2^{++} \rangle\gamma$ 

2660 2255 606 Table 4. Radiative transitions.
$ \Gamma[|1^{+-} \rangle \to |0^{++} \rangle\gamma] = 157\; \rm{keV}, $

(8) $ \Gamma[|2^{++} \rangle \to |1^{+-} \rangle\gamma] = 175\; \rm{keV}, $

(9) which are significant. As we assign
$ f_0(1710) $ and$ f_2(2300) $ as the$ 0^{++} $ and$ 2^{++} $ states, the rather large radiative decay rates may be useful to search for the missing$ 1^{+-} $ $ ss\bar s \bar s $ tetraquark. As the$ 0^{++} $ state has large branching ratios to$ K\bar K $ and$ \eta \eta $ , more studies of the decay processes$ ss\bar s \bar s(1^{+-}) \to $ $ ss\bar s \bar s(0^{++}) \gamma \to K\bar K \gamma $ and$ss\bar s \bar s(1^{+-}) \to $ $ ss\bar s \bar s(0^{++}) \gamma \to \eta \eta \gamma $ are suggested in future experiments.For the transitions between the
$ V\bar A $ type and ground states, the partial radiative decay widths range from 1 eV to tens of keV. The$ |V\bar{A}, 1^{--} \rangle \to |0^{++} \rangle\gamma $ process has 26.6 keV, which shows that the newly observed$ X(2239) $ state has a significant radiative decay width. The other two$ 1^{--} $ states with relative excitations between diquarks and anti-diquarks can decay into$ 0^{++} $ and$ 2^{++} $ ground states,$ \Gamma[|A\bar{A}, 1^{--} \rangle_{S = 0} \to |0^{++} \rangle\gamma] = 1137\; \rm{keV}, $

(10) $ \Gamma[|A\bar{A}, 1^{--} \rangle_{S = 2} \to |2^{++} \rangle\gamma] = 119\; \rm{keV}, $

(11) where the ten times larger partial width derives from the phase space. The radiative decay of the
$ S = 0 $ state to the$ 2^{++} $ final state is highly suppressed, which is also the case for the$ S = 2 $ state to the$ 0^{++} $ final state. These predictions may be helpful for searching and distinguishing the two higher$ 1^{--} $ $ ss\bar s \bar s $ tetraquark states. Radiative transitions of the excited$ ss\bar s \bar s $ tetraquarks are rarely discussed in literature, and more theoretical and experimental studies can be expected in the future. -
Strong decays can occur if tetraquarks lie above the meson-meson or baryon-antibaryon threshold. With the assignment of
$ Y(2175) $ as a$ ss\bar s \bar s $ tetraquark state, the ratios of the dominant decay modes were estimated in Ref. [13, 14]. In this work, three$ J^{PC} = 1^{--} $ $ ss\bar s \bar s $ tetraquarks are predicted, and the ratios of some of the significant decay channels are as follows.Apparently, the S-wave decay channels between the two final states are more favored than the P-wave channels. Also, the final states with strangeonium seem to be easier than the two kaon states, where the initial two strange quarks annihilate and the two up/down quarks are created simultaneously. For the baryon-antibaryon final states
$ \Lambda \bar \Lambda $ and$ \Sigma \bar \Sigma $ , more quark pairs are annihilated and created. Also, these processes are limited by the phase space, and are not considered in the present work.For the S-wave channels with strangeonium, three possible combinations of final states exist:
$ 1^{--} $ and$ 0^{++} $ ,$ 1^{+-} $ and$ 0^{-+} $ , and$ 1^{++} $ and$ 1^{--} $ . Seven resonances with the$ s\bar s $ component,$ \eta $ ,$ \eta^\prime $ ,$ \omega $ ,$ \phi $ ,$ f_0(980) $ ,$ h_1(1380) $ and$ f_1(1420) $ should be considered. Because of the large mass of$ f_1(1420) $ , the$ 1^{++} $ and$ 1^{--} $ combinations are forbidden or highly limited by the phase space, and are neglected here. Finally, the possible S-wave decay channels with strangeonium are$ \eta h_1(1380) $ ,$ \eta^\prime h_1(1380) $ ,$ f_0(980) \omega $ and$ f_0(980)\phi $ , where the nonet mixing angles$ \theta_P = -11.3^\circ $ and$ \theta_V = 39.2^\circ $ are adopted to determine the$ s\bar s $ components in relevant mesons [2]. Following the route of Refs. [13, 14], our results are listed in Table 5. It is shown that$ f_0(980) \phi $ is the dominant decay mode, and the contribution of$ \eta h_1(1380) $ is significant.$ \eta^\prime h_1(1380) $ may be also important for the two higher states, while the contribution of the$ f_0(980) \omega $ channel is rather small.$J^{PC}$ 

Mass/MeV $\Gamma(\eta h_1)$ :

$\Gamma(\eta^\prime h_1)$ :

$\Gamma(f_0(980) \omega)$ :

$\Gamma( f_0(980) \phi)$ 

$\Gamma(\eta \omega)$ :

$\Gamma(\eta^\prime \omega)$ :

$\Gamma(\eta \phi)$ :

$\Gamma(\eta^\prime \phi)$ 

$\Gamma(K K_1(1270))$ :

$\Gamma(K K_1(1400))$ 

$1^{--}$ 

2227 0.48∶ −− ∶0.01∶1 0.01∶0.01∶1.35∶1 1.19∶1 $1^{--}$ 

2468 0.69∶0.37∶0.01∶1 0.01∶0.01∶1.64∶1 1.54∶1 $1^{--}$ 

2574 0.78∶0.54∶0.01∶1 0.01∶0.01∶1.76∶1 1.68∶1 Table 5. The ratios of strong decay channels of the three predicted
$1^{--}$ $ss\bar s \bar s$ tetraquarks states. The short dash denotes a forbidden channel due to the phase space.Although the P-wave decay channels with strangeonium should contribute less than the S-wave modes, we also estimate their ratios. From Table 5, it can be seen that the
$ \eta \phi $ and$ \eta^\prime \phi $ final states may have significant contributions, while the$ \eta \omega $ and$ \eta^\prime \omega $ channels can be neglected.For the S-wave channels with kaon states, only the
$ 1^+ $ plus$ 0^- $ channels$ K K_1(1270) $ and$ K K_1(1400) $ may play significant roles. The$ 1^- $ plus$ 0^+ $ and$ 1^+ $ plus$ 1^- $ combinations are forbidden or highly suppressed by the phase space. Our results show that the$ K K_1(1270) $ and$ K K_1(1400) $ channels have comparable decay widths for these tetraquark states.To sum up, the dominant channels for the three
$ 1^{--} $ tetraquark states are$ f_0(980) \phi $ and$ \eta h_1(1380) $ , while the$ \eta \phi $ and$ \eta^\prime \phi $ modes may also be important. For the kaon final states, both$ K K_1(1270) $ and$ K K_1(1400) $ channels are important. We hope that future experiments could search for the$ 1^{--} $ $ ss\bar s \bar s $ tetraquark states in these channels. -
In this work, we investigated the masses of the
$ ss \bar s \bar s $ tetraquark states in the relativized quark model proposed by Godfrey and Isgur. Only the antitriplet diquark$ [\bar 3_c]_{cs} $ was considered. The masses of the$ ss \bar s \bar s $ tetraquark states were obtained by solving the Schrödinger-like equation between diquark and antidiquark. The color screening effects were also included in the calculations. It was found that the new resonant structure$ X(2239) $ observed in the$ e^+e^- \to K^+K^- $ process by the BESIII collaboration can be assigned as a P-wave$ 1^{--} $ $ ss \bar s \bar s $ tetraquark state.Besides the mass spectrum, the wave functions of the
$ ss \bar s \bar s $ tetraquark states were obtained, and the radiative transitions between tetraquarks and the ratios of the strong decay channels were estimated. The lowest P-wave$ 1^{--} $ $ ss \bar s \bar s $ tetraquark state radiates to the ground state with a width of 27 keV, and the main strong decay modes include the$ f_0(980) \phi $ and$ \eta h_1(1380) $ final states. The other$ ss \bar s \bar s $ tetraquark candidates$ f_0(1710) $ ,$ f_2(2300) $ , and$ X(2500) $ were also considered. We hope our assignments can be tested in future experiments.We would like to thank Wen-Biao Yan, Xian-Hui Zhong and Dian-Yong Chen for valuable discussions.
The ${{ ss \bar s \bar s}} $ tetraquark states and the structure of X(2239) observed by the BESIII collaboration
- Received Date: 2019-09-14
- Available Online: 2020-02-01
Abstract: We investigate the mass spectrum of the







 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF




































 DownLoad:
DownLoad: