HTML
-
The production and absorption of the
$ \Delta $ resonance in heavy-ion collision around the threshold energy has attracted considerable attention in recent years because the ratio of charged pions which arise from the decay of the$ \Delta $ resonance is assumed to be an observable sensitive to the symmetry energy at the suprasaturation density [1-4]. Different conclusions concerning the constraints of symmetry energy have been obtained with different transport models [2-7], which stimulate further study of the$ \Delta $ production and absorption mechanisms, as well as their sensitivity to the density region probed by the$ \pi^-/\pi^+ $ ratio. Recently, based on the IBUU calculations, Gao-Chan Yong [8] claimed that the$ \pi^{-}/\pi^{+} $ ratio is sensitive to the symmetry energy around the normal density, rather than around the suprasaturation density. The debate concerning the constraints on the symmetry energy at suprasaturation density based on the$ \pi^-/\pi^+ $ ratio indicates that a more careful study of the$ \Delta $ production and absorption cross-sections, as well as of the propagation of$ \pi $ in the reaction, are urgently needed.Generally, in heavy-ion collision at intermediate energies, the production and propagation of pions follow three stages: 1) First,
$ \Delta $ s are produced in$ NN\to N\Delta $ collisions; 2) after about 2 fm/c, which depends on the width of$ \Delta $ -resonances,$ \Delta $ s decay into nucleons and pions, and following them,$ \Delta $ s are absorbed through$ \pi+N\to \Delta $ processes; 3)$ \Delta $ s with a longer lifetime and higher energy participate in the$ N\Delta\to NN $ reactions. The probability of these processes is directly related to their cross-sections or decay widths. Due to the complications in the high-dimensional transport models, most of the transport models adopt Monte-Carlo cascade method to solve the collision partwhere the nucleon-nucleon cross sections and decay widthsare the key inputs. For the stages 1) and 2), the cross-sections and decay widths can be obtained from the experiments, and there is less ambiguity. However, the cross-sections of$ N\Delta \rightarrow NN $ in stage 3) cannot be measured directly, and they have to be calculated using the detailed balance relationship.One of the popular ways to obtain the
$ N\Delta\to NN $ cross-sections is to calculate them from the measured cross-sections of$ NN\to N\Delta $ using the detailed balance [9-16]. The cross-sections of$ NN\to N\Delta $ in free space have been measured [17-21], and are well explained by the one-boson exchange model (OBEM) and the relativistic Boltzmann-Uhling-Uhlenbeck approach [22-27]. The detailed balance means that the scattering matrix elements obtained from the time-reversal invariance are equal, i.e.$ |\mathcal{M}|_{if}^2 $ =$ |\mathcal{M}|_{fi}^2 $ , where i and f are the initial and final states of the scattered particles.Since
$ \Delta $ is a resonance with a broad mass distribution, it requires to consider the$ \Delta$ -mass effects in the calculations of the$ N\Delta\to NN $ cross-sections [9-11, 14, 28, 29]. For example, Danielewicz et al. [10] considered a linear$ m_\Delta $ dependence of$ \overline{|\mathcal{M}|^2} $ (i.e. the$ \Delta $ mass dependence of$ \overline{|\mathcal{M}_D|^2} $ is ignored ① in the$ NN\to N\Delta $ process), and obtained the following relationship for the one-$ \Delta(1232) $ absorption cross-section [10, 14, 16, 22, 30, 31],$ \begin{split} &\sigma^D_{N_{3}\Delta_{4}\to N_{1}N_{2}} = \\ &\;\frac{1}{2}\frac{1}{1+\delta_{N_{1}N_{2}}}\frac{|{{p}}_{\rm{12}}|^2}{|{{p}}_{\rm{34}}(m_\Delta)|} \sigma_{N_1N_2\to N_3\Delta_4}\\ &\;\bigg/{\int_{m_N+m_\pi}^{\sqrt s-m_N} {\rm d}m'_\Delta f(m'_\Delta)|{{p}}_{\rm{34}}(m'_\Delta)|}. \end{split} $

(1) The superscript D means that the
$ N\Delta\to NN $ cross-section is calculated using the method proposed by Danielewicz et al.$ f(m'_\Delta) $ is the$ \Delta $ mass distribution,$ \frac{1}{1+\delta_{N_1N_2}} $ takes into account identical of final two nucleons. If the$ \Delta $ mass dependence of$ |{{p}}_{\rm{34}}| $ is also ignored, this leads to the Wolf et al. formula [11, 12], which we express as,$ \begin{split} \sigma^W_{N_{3}\Delta_{4}\to N_{1}N_{2}} =& \frac{1}{2N}\frac{1}{1+\delta_{N_{1}N_{2}}}\frac{|{{p}}_{\rm{12}}|^2}{|{{p}}_{\rm{34}}(m_\Delta)|^2} \\&\times \sigma_{ N_{1}N_{2}\to N_{3}\Delta_{4}}. \end{split} $

(2) where the factor
$ N = \int^{\sqrt{s}-m_N}_{m_N+m_\pi} f(m'_\Delta) {\rm d}m'_\Delta $ . The two methods of calculating$ \sigma_{N\Delta\to NN} $ based on Eq. (1) and Eq. (2) have been discussed in Refs. [11, 12, 14]. It was found that they can obviously influence the calculation of observables of heavy-ion collisions, such as the rapidity distribution and flow of pions, at beam energies from 0.8 A GeV to 1.35 A GeV. Since both methods ignore the$ \Delta $ mass dependence of$ |\mathcal{M}_{D}|^2 $ or$ |{{p}}_{\rm{34}}| $ , which is thought to be very important near the threshold energy, it would be interesting to evaluate the precision of the two methods and to calculate the$ N\Delta\to NN $ cross-sections taking into account the$ m_\Delta $ dependence of the M matrix and$ |{{p}}_{\rm{34}}| $ .In this work, we first investigate the
$ \Delta $ mass dependence of$ \overline{|\mathcal{M}|^2} $ and$ |{{p}}_{\rm{34}}(m_{\Delta})| $ in the framework of OBEM. The cross-section of$ N\Delta\to NN $ in free space is directly obtained from the M matrix element. It is denoted as$ \sigma^{th}_{N\Delta\to NN} $ , and is chosen as a benchmark for the methods proposed in [10-12], i.e. Eqs. (1) and (2), for calculating$ \sigma_{N\Delta\to NN} $ from$ \sigma_{NN\to N\Delta} $ . Finally, the exact results for$ \sigma_{N\Delta\to NN} $ and the sampling function for the mass of$ \Delta $ in the transport models are given in the framework of OBEM.
-
We adopt the OBEM method with the effective Lagrangian density for nucleons and
$ \Delta $ baryons which interact through$ \sigma $ ,$ \omega $ ,$ \rho $ ,$ \delta $ , and$ \pi $ mesons [22, 27, 32-34]. Different from Ref. [23], we also include the isovector mesons$ \rho $ and$ \delta $ in order to describe the isospin asymmetric nuclear matter and the isospin dependent in-medium$ NN\rightleftharpoons N\Delta $ cross-sections. The cross-section of$ NN\rightleftharpoons N\Delta $ can be calculated from their M matrix [22]. The elementary two-body$ NN\to N\Delta $ cross-section for a given$ m_\Delta $ reads$ \begin{split} \tilde{\sigma}( m_{\Delta}) =& \frac{1}{4F}\int \frac{{\rm d}^3 {{p}}_3}{(2\pi)^3 2E_3 } \frac{{\rm d}^3 {{p}}_4}{(2\pi)^3 2E_4}\\ &\times(2\pi)^4\delta^{4}(p_1+p_2-p_3-p_4)\overline{|\mathcal{M}(m_\Delta)|^2}\\ =& \frac{1}{64\pi^2}\int \frac{|{{p}}_{\rm{34}}(m_\Delta)|}{\sqrt{s_{12}}\sqrt{s_{34}}|{{p}}_{\rm{12}}|} \overline{|\mathcal{M}(m_\Delta)|^2} {\rm d}\Omega, \end{split} $

(3) where
$ \overline{|\mathcal{M}(m_\Delta)|^2} = \frac{1}{(2s_{1}+1)(2s_2+1)}\sum\limits_{s_{1}s_{2}s_{3}s_{4}}|\mathcal{M}(m_\Delta)|^2 $ is for the$ N_1N_2\to$ $ N_3\Delta_4 $ process.$ {{p}}_{\rm{12}} $ and$ {{p}}_{\rm{34}}(m_\Delta) $ are the center-of-mass momenta of the incoming (1 and 2) and the outgoing particles (3 and 4).$ F = \sqrt{(p_{1}p_{2})^2-p^{2}_{1}p^{2}_{2}} = \sqrt{s_{12}}|{{p}}_{\rm{12}}| $ is the invariant flux factor,$ s_{12} = (p_1+p_2)^2 $ , and$ s_{34} = (p_3+p_4)^2 $ ($ s_{12} = s_{34} = s $ in free space). The total cross-section is the elementary two-body cross-section averaged over the mass distribution of$ \Delta $ , i.e.,$ \begin{split} \sigma_{N_{1}N_{2}\to N_{3}\Delta_{4}} =& \frac{1}{64\pi^2} \\&\times\int {\rm d}m_{\Delta} {\rm d}\Omega \frac{|{{p}}_{\rm{34}}(m_\Delta)|}{\sqrt{s_{12}}\sqrt{s_{34}}|{{p}}_{\rm{12}}|} \overline{|\mathcal{M}(m_\Delta)|^2}f(m_{\Delta}) \end{split} $

(4) $ f(m_{\Delta}) $ is the mass distribution of the$ \Delta $ resonance,$ f(m_{\Delta}) = \frac{2}{\pi}\frac{m^{2}_{\Delta}\Gamma(m_{\Delta})}{(m^{2}_{0,\Delta}-m^{2}_{\Delta})^2+m^{2}_{\Delta}\Gamma^2(m_{\Delta}) }. $

(5) Here,
$ m_{0,\Delta} $ is the pole mass of$ \Delta $ . The decay width$ \Gamma(m_\Delta) $ is taken in a parameteric form [23].$ \sigma_{N_{3}\Delta_{4}\to N_{1}N_{2}} $ for a given value of$ m_\Delta $ can be exactly calculated as,$ \begin{split} \sigma^{th}_{N_{3}\Delta_{4}\to N_{1}N_{2}} =& \frac{1}{4F}\int \frac{{\rm d}^3 {{p}}'_2}{(2\pi)^3 2E'_2} \frac{{\rm d}^3 {{p}}'_1}{(2\pi)^3 2E'_1 }\\ &\times(2\pi)^4\delta^{4}(p'_1+p'_2-p'_3-p'_4)\overline{|\mathcal{M}_{N\Delta \to NN}|^2}\\ = &\frac{1}{1+\delta_{N_{1}N_{2}}}\frac{1}{64\pi^2}\int \frac{|{{p}}'_{\rm{12}}|}{\sqrt{s_{\rm{34}}}\sqrt{s_{\rm{12}}}|{{p}}'_{\rm{34}}(m_\Delta)|}\\ &\times \overline{|\mathcal{M}_{N\Delta \to NN}|^2} {\rm d}\Omega, \end{split} $

(6) $ {{p}}'_{\rm{34}} $ is the momentum of the incoming N or$ \Delta $ , and$ {{p}}'_{\rm{12}} $ is the momentum of the outgoing N in the center-of-mass frame. The M matrix is,$ \begin{aligned} \overline{|\mathcal{M}_{N\Delta \to NN}|^2} = \frac{(2s_{1}+1)(2s_2+1)}{(2s_{3}+1)(2s_4+1)}\overline{|\mathcal{M}(m_\Delta)|^2}, \end{aligned} $

(7) where the
$ \Delta $ mass is the same for both processes. The ratio between Eq. (6) and Eq. (4) gives an exact relationship between the cross-sections of$ NN\to N\Delta $ and$ N\Delta \to NN $ . Thus,$ \sigma^{th}_{N\Delta\to NN} $ for given$m_\Delta$ can be written as,$ \begin{split} \sigma^{th}_{N_3\Delta_4\to N_1N_2} = &\frac{\sigma_{N_1N_2\to N_3\Delta_4}}{1+\delta_{N_1N_2}}\frac{(2s_{1}+1)(2s_2+1)}{(2s_{3}+1)(2s_4+1)}\\ &\times\frac{\int {\rm d}\Omega |{{p}}_{12}|^2\overline{|\mathcal{M}(m_{\Delta})|^2}}{\int {\rm d}\Omega |{{p}}'_{34}(m_{\Delta})|\int |{{p}}_{34}(m'_{\Delta})|f(m'_{\Delta})\overline{|\mathcal{M}(m'_{\Delta})|^2}{\rm d}m'_{\Delta}}. \end{split} $

(8) One should note that
$ {{p}}'_{\rm{34}} $ and$ {{p}}'_{\rm{12}} $ are the momenta of$ N_3 $ (or$ \Delta_4 $ ) and$ N_1 $ (or$ N_2 $ ) in the center-of-mass of$ N\Delta\to NN $ , while$ {{p}}_{\rm{12}} $ and$ {{p}}_{\rm{34}} $ are the momenta of$ N_1 $ (or$ N_2 $ ) and$ N_3 $ (or$ \Delta_4 $ ) in$ NN\to N\Delta $ . For a given center-of-mass energy$ \sqrt s $ ,$ |{{p}}_{\rm{12}}| $ =$ |{{p}}'_{\rm{12}}| $ for the ingoing and outgoing nucleons, but$ |{{p}}_{\rm{34}}| $ may not be equal to$ |{{p}}'_{\rm{34}}| $ , depending on whether the mass of$ \Delta $ is equal in the production and absorption processes.
-
We first check the mass dependence of the extracted M matrix, i.e.
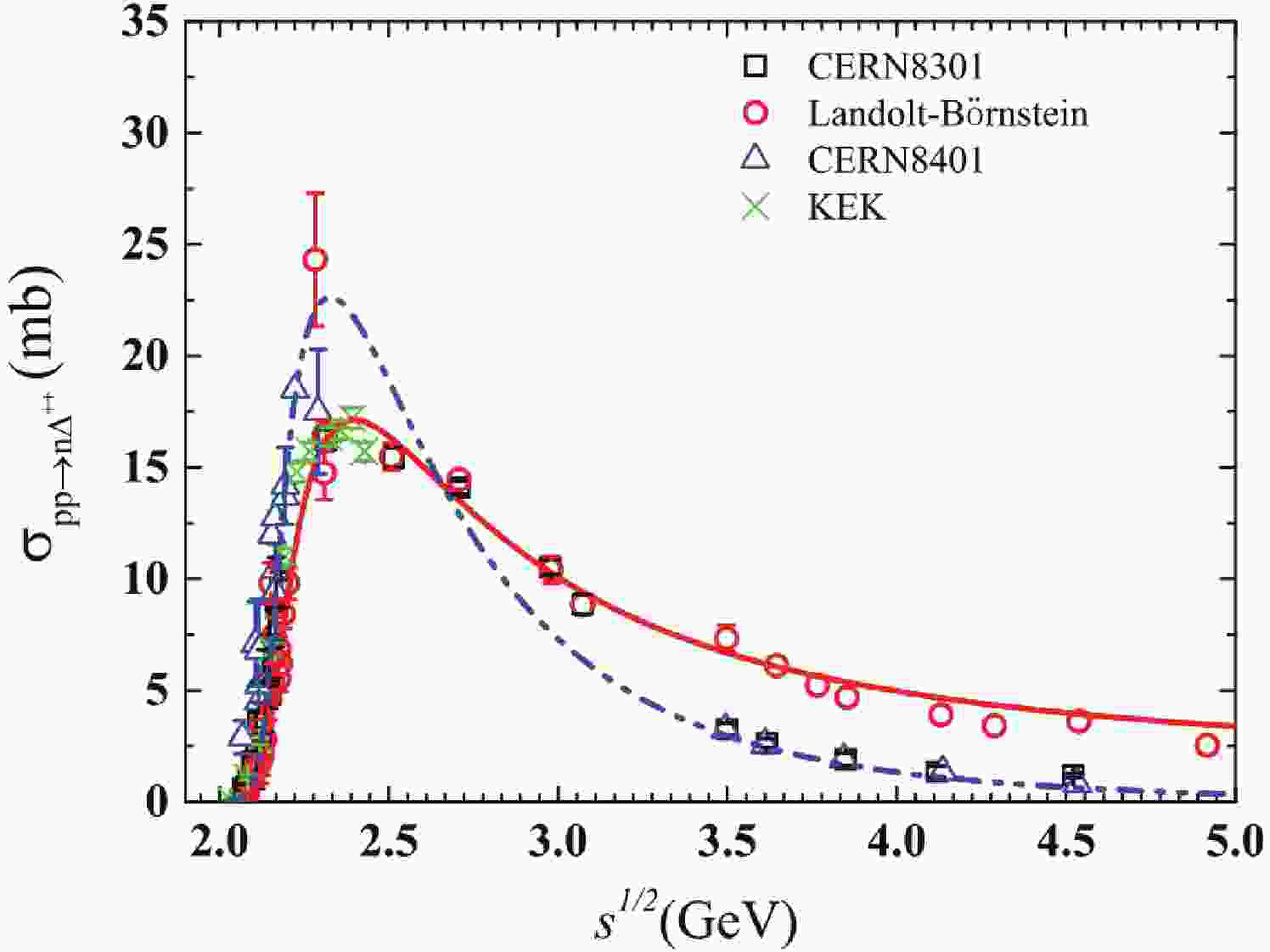
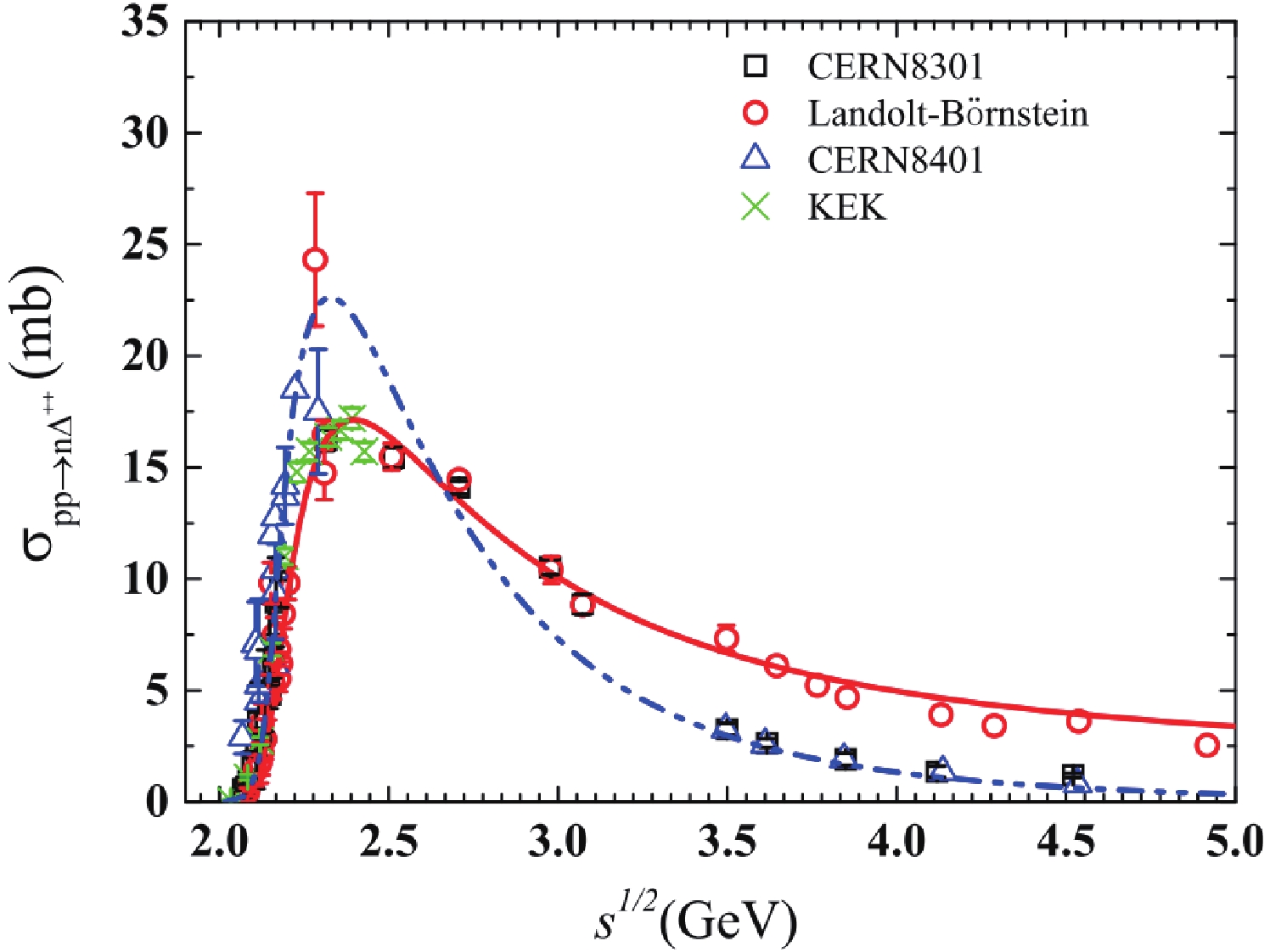
$ \overline{|\mathcal{M}(m_{\Delta})|^2} $ , in free space, based on OBEM. The details of the M matrix calculations can be found in our previous work [27], and the parameters in the expression for$ |\mathcal{M}|^2 $ were determined by fitting the measured cross-sections of$ pp\to n\Delta^{++} $ [17]. Several groups have published measured cross-sections of$ NN\to N\Delta $ [17, 19-21]. As shown in Fig. 1, there is still an uncertainty of 3-5 mb in the measured cross-sections of$ pp\to n\Delta^{++} $ around$ \sqrt s \sim $ 2.2 GeV and above 3.0 GeV. Two typical values of the cross-section of$ pp\to n\Delta^{++} $ , CERN8401 (blue triangles) [20] and Landolt-Börnstein [17] (red circles), were chosen to adjust the parameters of the M matrix, and to understand the uncertainties due to the experimental errors, as they are the two extreme cases in the published data for$ pp\to n\Delta^{++} $ .In Fig. 2 (a), we plot the angular integrated isospin independent M matrix as a function of
$ m_{\Delta} $ for the total energies$ s^{1/2} = $ 2.1, 2.5 and 3.0 GeV. The shadow regions correspond to the M matrix with the experimental uncertainties obtained from CERN8401 [20] and the Landolt-Börnstein data [17]. The range of$ m_\Delta $ is from$ m_N+m_\pi $ to$ \sqrt{s}-m_N $ , where the maximum value of$ m_\Delta $ depends on the energy of the process of$ NN\to N\Delta $ . The isospin independent M matrix is obtained by normalizing the M matrix with the isospin factors, i.e.,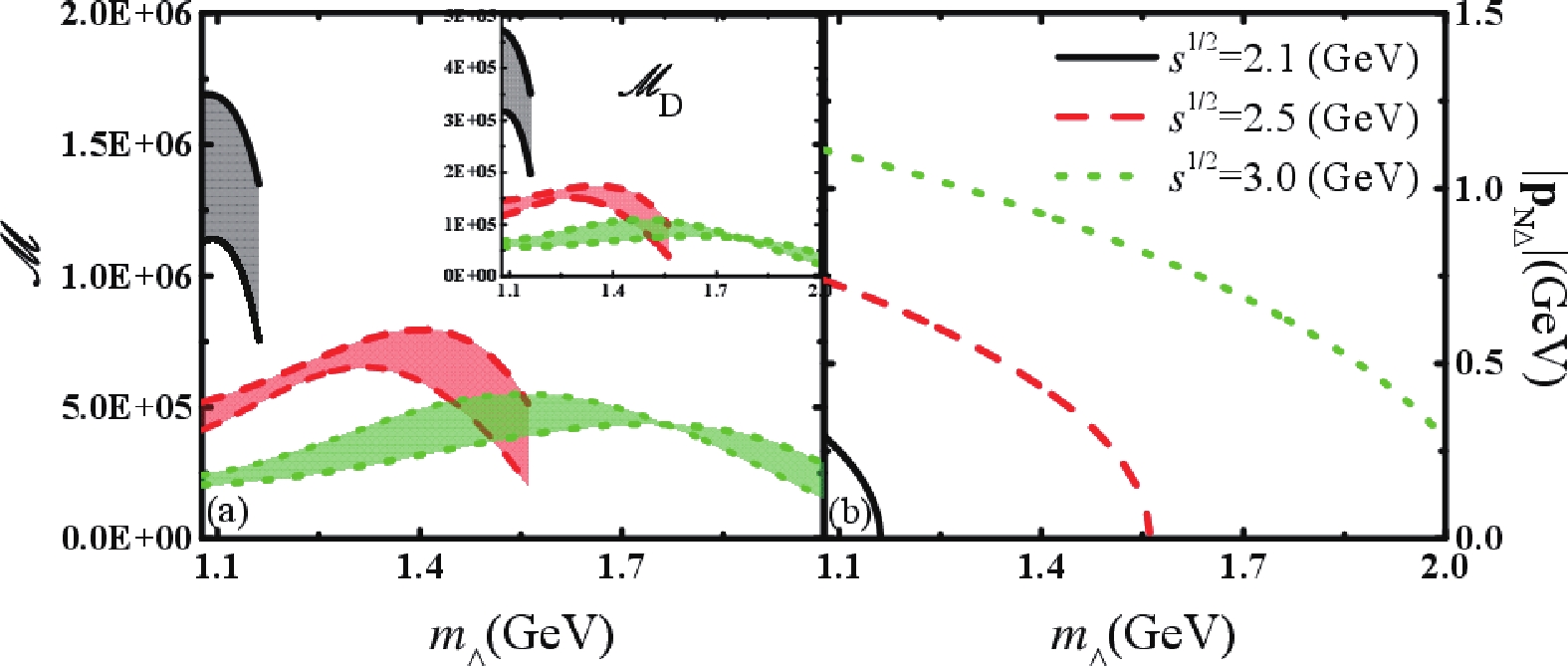
Figure 2. (color online) (a)
${\mathscr{M} } = \frac{1}{I^2_i}\int \sum_{s}|\mathcal{M}|^2 {\rm d}\Omega$ as a function of$m_{\Delta}$ in free space for the energies$s^{1/2}$ of 2.1, 2.5 and 3 GeV. The insert in the figure is$\frac{1}{I^2_i}\int \sum_{s} |\mathcal{M}_{D}|^2 {\rm d}\Omega$ (GeV-4) as in Ref. [10]. (b)$|{\bf{p}}_{N\Delta}|$ as a function of$m_{\Delta}$ in free space.$ {\mathscr{M} }= \frac{1}{I^2_i} \int \sum_{s}|\mathcal{M}|^2 {\rm d}\Omega = \frac{(2s_1+1)(2s_2+1)}{I^2_i} \int \overline{|\mathcal{M}|^2} {\rm d}\Omega. $

(9) $ I_{i = d,e} $ is the isospin factor as in Refs. [27, 32], and$ I^2_{d,e}(n\Delta^{++}\!\!\to \!\! pp) \!= \!I^2_{d,e}(p\Delta^{-}\!\!\to\!\! nn) \!= \!2 $ and$ I^2_{d,e}(\rm{other channels}) = $ 2/3. As shown in the left panel of Fig. 2, the behavior of$ {\mathscr{M} } $ as a function of$ m_\Delta $ in OBEM clearly shows that$ \overline{|\mathcal{M}(m_{\Delta})|^2} $ depends on$ m_\Delta $ irrespective of the experimental data used. In order to understand the assumption of mass dependence of the M matrix in the method of Danielewicz at al. [10], we also show$ {\mathscr{M} }_{D} = \frac{1}{I_i^2}\int|\mathcal{M}_{D}|^2 {\rm d}\Omega $ in the inset of Fig. 2(a), which has the same convention as in Ref. [10] in GeV-4. For the energy range selected, our calculations show that$ |\mathcal{M}_D|^2 $ clearly depends on$ m_\Delta $ in all mass regions where$ \Delta $ can be produced. This can be understood from the formula for the M matrix, Eq. (22) in Ref. [32]. For example, the exponent of$ m_\Delta $ in the M-matrix is roughly$ m_\Delta^2 $ . For higher energies, the$ \Delta $ mass dependence of the M matrix becomes weak, which means that the assumption for calculating$ N\Delta\to NN $ in Ref. [10] is reasonable.Another point which needs to be investigated is the mass dependence of
$ |{{p}}_{N\Delta}(m_\Delta)| $ (here$ |{{p}}_{N\Delta}(m_\Delta)| $ is$ |{{p}}_{34}(m_\Delta)| $ ) in Eq. (8). In Fig. 2(b), we present the mass dependence of$ |{{p}}_{N\Delta}(m_\Delta)| $ for different energies, where one can see that$ |{{p}}_{N\Delta}(m_\Delta)| $ decreases with the mass of$ \Delta $ , and that the mass dependence is much sharper for lower energies than for higher energies. The panels in Fig. 2 show that both$ \overline{|\mathcal{M}(m_{\Delta})|^2} $ and$ |{p}_{N\Delta}(m_{\Delta})| $ in Eq. (8) depend on the mass of$ \Delta $ , especially for lower energies.Clearly, Fig. 2 shows that the
$ \Delta $ mass dependence (which in turn depends on the system energy) of the M matrix and$ |{{p}}_{N\Delta}(m_\Delta)| $ cannot be ignored, and can influence the accuracy of calculations of the$ N\Delta\to NN $ cross-sections based on the detailed balance using Eq. (1) or Eq. (2). We select three typical values of$ m_\Delta $ to understand the precision of the different methods of estimating$ \sigma_{N\Delta \to NN} $ : the minimum mass of$ \Delta $ ($ m_{\Delta} = m_{\rm{min},\Delta} = 1.077 $ GeV), the pole mass ($ m_{0,\Delta} = 1.232 $ GeV); and$ m_\Delta = 1.387 $ GeV, which corresponds to the maximum mass of$ \Delta $ produced in heavy-ion collisions with the beam energy of 1 GeV. Since other data give a similar$ m_{\Delta} $ dependence of the M matrix as shown in Fig. 2, we use in the following the M matrix parameters extracted from the Landolt-Börnstein data [17].Figure 3 (a)-(c) present the results of
$ \sigma_{n\Delta^{++} \rightarrow pp } $ as a function of$ s^{1/2} $ in free space for$ m_\Delta = 1.077 $ , 1.232 and 1.387 GeV. The black solid lines are$ \sigma^{th}_{n\Delta^{++} \rightarrow pp} $ which are directly calculated from the M matrix element of$ N\Delta\to NN $ based on the scattering theory. The red dashed lines are$ \sigma^{W}_{n\Delta^{++} \rightarrow pp} $ obtained with the method adopted by Wolf et al. [11-13], i.e. Eq. (2), without taking into account the mass dependence of$ |{{p}}_{N\Delta}| $ . The green dotted lines are$ \sigma^{D}_{n\Delta^{++} \rightarrow pp} $ obtained by Danielewicz et al. [10], i.e. Eq. (1), where the mass dependence of$ |\mathcal{M}|^2 $ is neglected. All methods predict a large$ \Delta $ absorption cross-section around the threshold energy of the$ n\Delta^{++} \rightarrow pp $ process which increases with$ m_\Delta $ , while$ \sigma_{n\Delta^{++} \rightarrow pp} $ decreases with energy. However, the methods of Wolf [11-13] and Danielewicz [10] do not reproduce well$ \sigma_{n\Delta^{++} \rightarrow pp} $ around the threshold energy if the$ \Delta $ mass is far from the pole$ m_\Delta = m_{0,\Delta} $ = 1.232 GeV. Other channels of$ N\Delta\to NN $ give similar results since the differences come only from the isospin factor.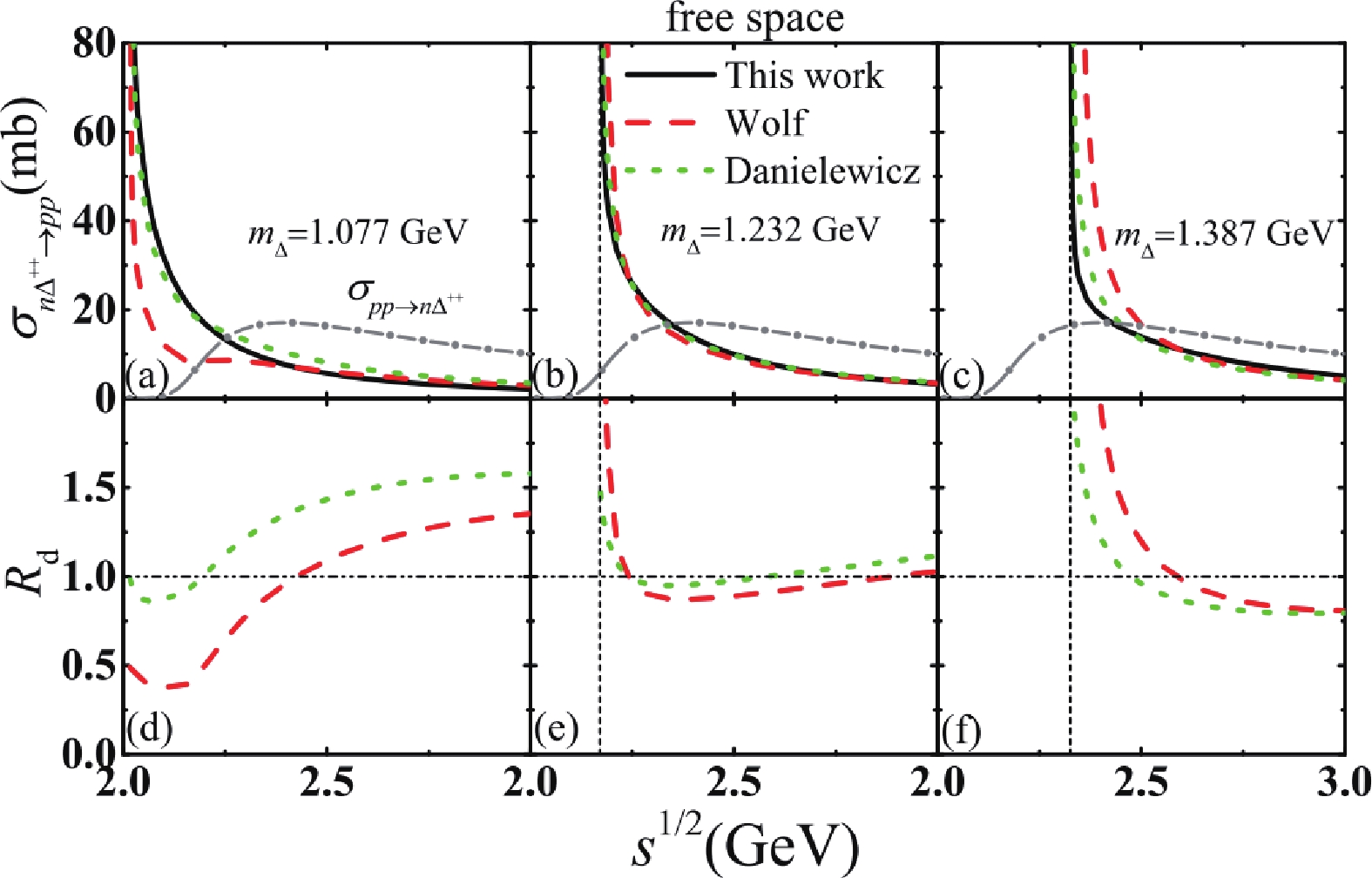
Figure 3. (color online) Panels (a)-(c):
$\sigma_{n\Delta^{++}\rightarrow pp }$ in free space as a function of$s^{1/2}$ for different detailed balance methods and for three values of$m_{\Delta}$ . Panels (d)-(f):$R_{d}$ as a function$s^{1/2}$ corresponding to the upper panels.In order to see the deviations clearly, we present in Fig. 3(d)-(f) the ratio defined as
$ R_{d} = \sigma_{\Delta N\to NN}^{i}/\sigma_{\Delta N\to NN}^{th} $ ($ \sigma_{\Delta N\to NN}^{W} $ $ \,\mathrm{for} \,\, i = W ,\, \sigma_{\Delta N\to NN}^{D}\,\,\mathrm{for}\,\, i = D $ ) for different masses of$ \Delta $ .$ R_d $ has the same value in all channels of$ N\Delta\to NN $ since the contributions from the isospin factor cancel in the ratio.$ R_d = 1 $ means the proposed detailed balance can well describe the$ N\Delta\to NN $ cross section. Red dashed lines are the results of$ \sigma^{W}_{\Delta N\to NN}/\sigma^{th}_{\Delta N\to NN} $ , and green dotted lines$ \sigma^{D}_{\Delta N\to NN}/\sigma^{th}_{\Delta N\to NN} $ . For$ m_{\Delta} = m_{0,\Delta} $ , both methods reproduce well the values of$ \sigma^{th}_{N\Delta\to NN} $ , except for$ s^{1/2}<2.2 $ GeV, where the Danielewicz method is much closer to the precise result than the Wolf method. If$ m_\Delta = 1.076 $ or 1.387 GeV, larger deviations are found near the threshold energy of the$ N\Delta\to NN $ process (close to the vertical dashed lines). For example, if$ m_\Delta $ is close to the minimum mass of$ \Delta $ , both methods in Refs. [10, 11] underestimate the$ \Delta $ absorption cross-section for$ s^{1/2}<2.2 $ GeV, and the deviation is less than 20% for the Danielewicz method and larger than 50% for the Wolf approach. Both methods overestimate the$ \Delta $ absorption cross-section, and the deviation is close to 50% for the Danielewicz method while the Wolf approach gives the deviation is less than 40% for$ s^{1/2}>2.5 $ GeV. In the large mass region of$ \Delta $ , both methods overestimate the$ \Delta $ absorption cross-section for$ s^{1/2}<2.47 $ GeV, but underestimate it for$ s^{1/2}>2.6 $ GeV. Furthermore, the cross-sections of$ N\Delta\to NN $ in free space can be changed by using different coupling constants [32]. The mass dependence of the M matrix should exist and cannot be simply ignored near the threshold energy, since the M matrix is determined by fitting the$ NN\to N\Delta $ data. The above comparison suggests that the mass dependence of the M matrix and$ |{{p}}_{N\Delta}(m_\Delta)| $ should be taken into account for precise calculations of the$ N\Delta\to NN $ cross-sections.Using the isospin independent matrix
$ {\mathscr{M} } $ in Eq. (9), the cross-section of$ N\Delta\to NN $ can be expressed as,$ \begin{aligned} \sigma_{N\Delta\to NN}^{th} = \frac{1}{64\pi^2s} \frac{|{{p}}_{\rm{12}}|}{|{{p}}_{N\Delta}(m_\Delta)|}\frac{I^2_i{\mathscr{M} }}{(2s_3+1)(2s_4+1)}\frac{1}{1+\delta_{N_1N_2}}. \end{aligned} $

(10) The form of
$ {\mathscr{M} } $ can be found in Ref. [35]. For the$ n\Delta^{++}\to pp $ and$ p\Delta^{-}\to nn $ channels,$ I_i^2 = 2 $ , while for the$ n\Delta^+\to np $ ,$ n\Delta^0\to nn $ ,$ p\Delta^+\to pp $ ,$ p\Delta^0\to np $ channels,$ I_i^2 = 2/3 $ . Hence, the ratio$ \sigma_{n\Delta^{++}\to pp} $ :$ \sigma_{p\Delta^{-}\to nn} $ :$ \sigma_{n\Delta^+\to np} $ :$ \sigma_{p\Delta^0\to np} $ :$ \sigma_{n\Delta^0\to nn} $ :$ \sigma_{p\Delta^+\to pp} $ is 3:3:2:2:1:1. Since the mass dependence of the M matrix is considered, the mass of$ \Delta $ in the process$ NN\to N\Delta $ should be sampled by considering the mass dependence of$ |\mathcal{M}|^2 $ . Therefore, the$ \Delta $ mass should be sampled as,$ P(m_\Delta) = \frac{\displaystyle\int_{m_{N}+m_{\pi}}^{m_\Delta}|{{p}}_{N\Delta}(m'_\Delta)|\times I^2_i{\mathscr{M} }\times f(m'_\Delta){\rm d}m'_\Delta}{\displaystyle\int_{m_{N}+m_{\pi}}^{\sqrt s-m_N}|{{p}}_{N\Delta}(m_\Delta)|\times I^2_i{\mathscr{M} }\times f(m_\Delta) {\rm d}m_\Delta} . $

(11) Since the in-medium cross-sections are adopted in the simulations of heavy-ion collisions, it is necessary to check the isospin effects and the precision of the calculations of the in-medium cross-sections of
$ N\Delta\to NN $ using the methods proposed in [10, 11]. The in-medium cross-sections of$ NN\to N\Delta $ are calculated in the same way as in Refs. [27, 32], and depend on the coupling constants and isospin asymmetry. As a result of the isospin splitting of the in-medium$ NN\to N\Delta $ cross-section, one can expect that$ R_d $ also depends on the isospin asymmetry and the channel of the$ N\Delta\to NN $ . In Fig. 4, we present$ R_d $ as a function of$ s^{1/2} $ for two times normal density ($ 2\rho_0 $ ) and for three$ m^*_\Delta $ values. The upper panels are the results in symmetric nuclear matter, i.e.$ \alpha = (\rho_n-\rho_p)/(\rho_n+\rho_p) = 0 $ . The panels (d)-(i) are the results in isospin asymmetric nuclear matter with$ \alpha = 0.2 $ , where (d), (e) and (f) panels are for$ n\Delta^{++}\to pp $ , and (g), (h) and (i) panels are for$ p\Delta^{-}\to nn $ . The selected three values of$ m^*_\Delta $ are the effective masses, which depend on the density, isospin asymmetry, and the charge state of$ \Delta $ . Similarly to the results in free space, the deviations in the low and high$ \Delta $ mass regions are larger than in the pole mass region. and the$ R_d $ values depend on$ m^*_\Delta $ ,$ s^{1/2} $ and the channels of$ N\Delta\to NN $ . As shown in Fig. 4 (d) and (g), one can see that the$ m^*_\Delta $ dependence of the M matrix influences the$ p\Delta^-\to nn $ cross-section more than that of$ n\Delta^{++}\to pp $ near the threshold energy in neutron-rich matter. The effect of isospin on$ R_d $ of in-medium$ N\Delta\to NN $ can be understood from the ratio between Eq. (1) and Eq. (8), or between Eq. (2) and Eq. (8), where the effective mass splitting of the$ \Delta $ and nucleon in the M matrix leads to different$ R_d $ for different channels of$ N\Delta\to NN $ . Hence, the$ \Delta $ mass dependence of the M matrix for in-medium$ N\Delta\to NN $ cross-sections also depends on the channels of$ N\Delta\to NN $ .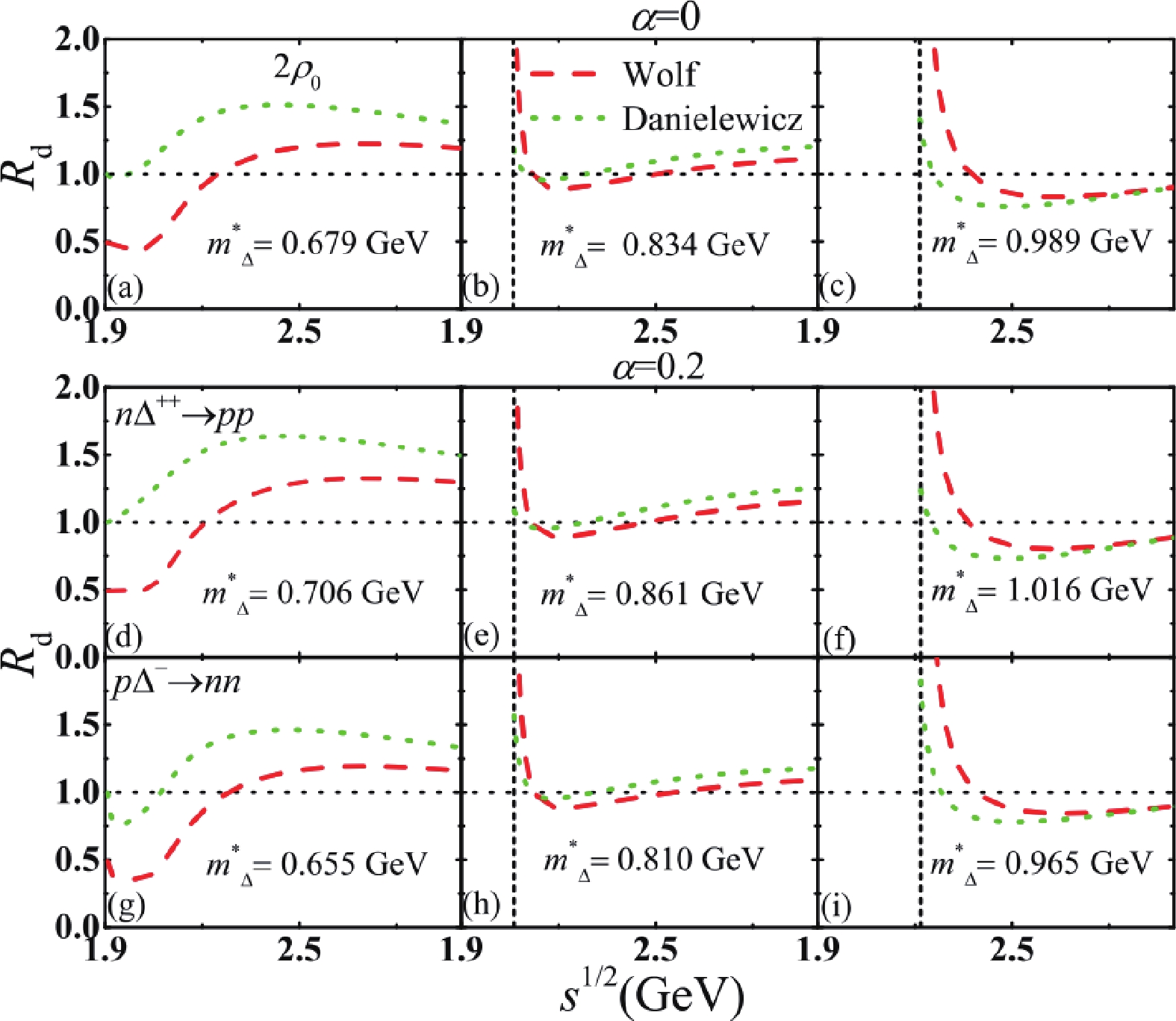
Figure 4. (color online) Panel (a)-(c):
$R_d$ as a function of$s^{1/2}$ for$2\rho_0$ , different types of detailed balance and three values of$m^*_{\Delta}$ , in symmetric nuclear matter$\alpha$ = 0. Panel (d)-(f):$R_d$ as a function of$s^{1/2}$ for$n\Delta^{++}\to pp$ , and (g)-(i) for$p\Delta^{-}\to nn$ , for$2 \rho_0$ and different values of$m^{*}_{\Delta}$ , in asymmetric nuclear matter ($\alpha$ = 0.2).
-
In summary, we have evaluated the methods of calculating
$ \sigma_{N\Delta\rightarrow NN} $ from$ \sigma_{NN \rightarrow N\Delta} $ in the framework of OBEM. Comparing$ \sigma_{N\Delta\rightarrow NN} $ obtained with the methods proposed in [10] and [12] with$ \sigma^{th}_{N\Delta\rightarrow NN} $ , which is the exact result using the M matrix in OBEM, we showed that the methods in Refs. [10] and [12] underestimate the low mass and overestimate the large mass$ \Delta $ absorption cross-sections near the threshold. We found that the mass dependence of the M matrix should be taken into account, especially around the threshold energy.The role of accurate calculations of
$ \sigma_{N\Delta\to NN} $ in transport models of heavy-ion collisions near the threshold energy should also be investigated, since most of the$ \Delta $ resonances participating in the processes$ N\Delta\to NN $ are low mass$ \Delta $ s. Another interesting work for the future is to evaluate the effect of the resonances with a much broader width, which could be useful to better understand the mechanisms of particle production in high energy heavy-ion collisions.






 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF
















 DownLoad:
DownLoad: