-
The greatest advancement in physics, achieved by Einstein's theory of relativity, validated its stature after 103 years, when the image of a supermassive black hole was released on April 10, 2019 [1]. Black holes have captivated the scientific community since LIGO successfully detected gravitational waves from two merging black holes [2-4]. While subsequent attempts to enhance the detector sensitivity for further detections are underway, the event horizon telescope revolutionized physics by pioneering the first look at M87* [1]. This marked a new era in theoretical cosmology, attracting the interest of numerous researchers towards black holes [5-9].
A black hole is one of the objects that gives rise to the unique phenomenon of gravitational lensing. According to Einstein, when light encounters a cluster of massive objects in its trajectory towards an observer, the cluster bends the light rays, forming a gravitational lens. Galaxy clusters tend to deflect passing light with their gravitational fields, which causes distortions of the source in the background. Strong lensing produces arcs and rings like Einstein's ring, while weak lensing is a result of minor distortions with magnifications that are too small to detect, unless averaged over a number of galaxies. Although weak lensing distortions are considered futile for individual galaxies, they can be used to distinguish between various mass distributions and can therefore be used to study the characteristics of the infant universe and the geometry of the cosmic web [10].
To utilize this subtle property of differential deflection exhibited by weak lensing, it is customary to first calculate the angle of deflection of light, which depends on the mass distribution of the lensing system. The Gauss-Bonnet theorem (GBT), introduced by Gibbons and Werner (GW), was first used to calculate the deflection angle so as to account for the optical geometry [11,12], using a domain outside the trajectory of light. The optical metric consists of light rays treated as spatial geodesics, inducing a topological effect [13,14]. Then, the new GW method is applied to a variety of spacetime metric of black holes and wormholes [15-39]. Defining the Euler characteristic of the topology as
$ \chi $ and a Riemannian metric of the symmetric lens' manifold as$ g $ , the domain of the surface can be written as$ (D, \chi, g) $ . For Gaussian curvature,$ K $ , and geodesics curvature,$ \kappa $ , GBT is formulated as [12]:$ \int \int_D K {\rm d}S + \int_{\partial D} \kappa {\rm d}t + \sum\limits_i \alpha_i = 2\pi \chi(D) $

(1) where,
$ \alpha_i $ is the exterior angle with$ i^{\rm{th}} $ vertex.The deflection angle was calculated by Gibbons and Werner [12] through this method for a Schwarzschild black hole. When the source and the observer are asymptotically flat, the deflection angle is presumed to be very small. Thus, the asymptotic deflection angle is given by [12]:
$ \hat{\alpha} = - \int \int_D K {\rm d}S. $

(2) A major conundrum associated with black holes is the information paradox. Quantum mechanics predicts that the information (or the specific state) of a particle plummeting into a black hole cannot be lost; more precisely, the quantum wave function that acts as the fingerprint of the falling particle is always preserved on the surface of the black hole for billions of years. In 1974, Stephen Hawking proposed that the black holes evaporate over time releasing their mass and energy back into the universe in the form of black body radiation, known as Hawking radiation [40,41]. This arises from the fact that black holes have temperatures and implies that the information of the engulfed object vanishes with the black hole. Clearly, quantum mechanics and general relativity contradict each other in this case, leading to the information paradox.
Among the few conjectures that solve the information paradox, the most plausible explanation was provided by Hawking. He suggested that the information of the falling objects could escape from being absorbed into the black hole, by leaking out of its radiation field through quantum fluctuations. The outgoing radiation returns to the universe with the particle (perhaps, distorted) information imprinted on it. These quantum perturbations in the event horizon require quantum gravity corrections, such that their spacetimes are consistent. These quantum effects infer that the black holes obey quantum mechanics.
In this article, our aim is to employ this approach to determine the quantum gravity effects on the deflection angle. This paper is organized as follows: in Section 2, we briefly review the spacetime described by an extended uncertainty principle-corrected black hole. In Section 3, we calculate the deflection angle by the EUP black hole using the Gauss-Bonnet theorem in weak field regions. In Section 4, we extend our studies for the deflection of light by the EUP black hole in a plasma medium. We conclude our findings in Section 5. Natural units are used throughout this paper:
$ G = \hbar = c = 1 $ . -
Consider the hydrogen atom. The kinetic energy of the electron balances out its negative potential energy, thus preventing the electron from collapsing into the nucleus. Heisenberg stated this by the uncertainty principle. Since black holes are now recognized as quantum objects, Ronald J. Adler argues that the same idea can be applied to them: the generalized uncertainty principle [42] might prevent a black hole from evaporating. Mathematically, the Heisenberg relation contains an extra term proportional to the square of momentum uncertainty. Alternatively, the Heisenberg relation can be modified with an extra term proportional to the square of position uncertainty, yielding the extended uncertainty principle (EUP). If the contributions from the EUP corrections are adequate, they can be used at a large scale to compute dark matter effects, properties of the black hole, size of its photosphere, etc.
For a fundamental distance scale,
$ L $ , the Heisenberg relation with the EUP correction for position uncertainty [43] can be written as:$ \Delta x \Delta p \geqslant 1 + \alpha \frac{\Delta x^2}{L^2}, $

(3) where
$ \alpha $ is a coupling constant.It is emphasized that the uncertainty principle remains retrievable due to the condition
$ L \gg \Delta x $ . It also implies that [44] the effects of quantum gravity manifest themselves over large distances, hence validating the notion of quantum effects on macroscopic scales.The line element of a spherically symmetric black hole with mass, M, subjected to the EUP correction is defined [45] as:
$ {\rm d}s^2 = - f(r) {\rm d}t^2 + f(r)^{-1} {\rm d}r^2 + r^2 ({\rm d}\theta^2 + \sin^2 \theta {\rm d}\phi^2), $

(4) where:
$ f(r) \equiv 1- \frac{2M}{r} \left(1+\frac{4\alpha M^2}{L^2} \right). $

(5) The corresponding expression [46] for the deflection angle of a photon verging on this black hole with the distance of closest approach,
$ r_0 $ , is written as:$ \hat{\alpha}(r_0) = -\pi + 2 \int_{r_0}^\infty {\rm d}r \frac{\sqrt{f(r)^{-1}}}{r \sqrt{\dfrac{r^2}{r_0^2}\dfrac{f(r_0)}{f(r)}-1}}. $

(6) If
$ M/r_0 \ll 1 $ , the deflection angle is too small: this implies weak deflection lensing [47]. Subsequently,$ \alpha $ increases as$ r_0 $ approaches the photosphere until it diverges, generating strong deflection lensing. -
Taking
$ \theta = \pi/2 $ for equatorial plane, Equation (4) reduces to the optical metric for null geodesics:$ {\rm d}t^2 = \frac{{\rm d}r^2}{f(r)^2} + \frac{r^2}{f(r)} {\rm d}\phi^2. $

(7) Following the computation of non-zero Christoffel symbols, the Gaussian curvature (proportional to the Ricci scalar) can be written as:
$ K = \frac{R}{2} \approx - {\frac {8{M}^{3}\alpha}{{r}^{3}{L}^{2}}} - {\frac {2M}{{r}^{3}}} +{\cal{O}}(M^{4}). $

(8) Using the straight line approximation [12] as
$ r = u/ \sin \phi $ , where$ u $ is the impact parameter, Equation (2) of GBT suggests that:$ \hat{\alpha} = - \int_0^\pi \int_{\textstyle{\frac{u}{\sin \phi}}}^\infty K {\rm d}S, $

(9) where
$ {\rm d}S = r{\rm d}r {\rm d}\phi $ . Ignoring the higher order terms, Equations (8) and (9) simplify to the following expression for the deflection angle, due to weak lensing with EUP corrections:$ \hat{\alpha}_{w} = {\frac {4M}{u}}+{\frac {16{M}^{3}\alpha}{u{L}^{2}}} $

(10) for weak-field limits. Thus, the EUP parameter
$ \alpha $ increases the deflection angle, and deflection angle reduces to the case of Schwarzschild black hole when$ \alpha = 0 $ . The deflection angle in the leading order terms is seen to be in agreement with [45]. -
Lensing in vacuum does not entail dispersive properties of a photon. However, lenses are usually besieged [48] by plasma, which divulges a non-trivial component for the deflection angle. Gravitational deflection in a plasma medium fosters refraction inducing more deflection. This change in medium is specified by the refractive index [49] accounting for the auxiliary component that is essentially small but not negligible, especially in the radio regime. To incorporate the effects of plasma, consider the case when light travels from vacuum to a hot, ionized gas medium. Let
$ v $ be the velocity of light through the plasma. The refractive index,$ n(r) $ is described by:$ n(r) \equiv \frac{c}{v} = \frac{1}{{\rm d}r/{\rm d}t} \quad \quad\quad\quad\{\because c = 1\}. $

(11) The refractive index
$ n(r) $ for an EUP-corrected black hole is obtained as [25],$ n(r) = \sqrt{1-\frac{\omega_e^2}{{\omega_\infty^2}} \left[1- \frac{2M}{r} \left(1+\frac{4\alpha M^2}{L^2} \right)\right]}, $

(12) where
$ \omega_{e} $ is the electron plasma frequency, and$ \omega_{\infty} $ is the photon frequency measured by an observer at infinity. The line element in Equation (4) can be re-written as:$\begin{split} {\rm d} \sigma ^ { 2 } =& g _ { i j } ^ { \rm { opt } } {\rm d} x ^ { i } {\rm d} x ^ { j }\\ =& \frac { n ^ { 2 } ( r ) } { 1- \dfrac{2M}{r} \left(1+\dfrac{4\alpha M^2}{L^2} \right)} \left[ \frac{{\rm d} r ^ { 2 }}{1- \dfrac{2M}{r} \left(1+\dfrac{4\alpha M^2}{L^2} \right)} + r^2 {\rm d} \phi ^ { 2 }\right]. \end{split}$

(13) Therefore, the optical Gaussian curvature becomes:
$\begin{split} K \approx& -{\frac {2M}{{r}^{3}}}+{\frac {3{M}^{2}}{{r}^{4}}}-{\frac {8{M}^{3}\alpha}{{L}^{2}{r}^{3}}}+ -{\frac {M\omega_e^2}{{\omega_\infty^2}r^3}}+{\frac {4{M}^{2}\omega_e^2}{{\omega_\infty^2}{r}^{4}}} \\ & -\left( {\frac {4\alpha}{{\omega_\infty^2}{L}^{2}{r}^{3}}}+ {\frac {4}{{\omega_\infty^2}{r}^{5}}} \right) {M}^{3} {\omega_e^2}. \end{split}$

(14) Consequently, the deflection angle becomes:
$ \hat{\alpha}_{w_{n}} \approx {\frac {4M}{u}} + {\frac{2M{\omega_e^2}}{u{\omega_\infty^2}}} + {\frac {16\alpha{M}^{3}}{u{L}^{2}}}+{\frac {8\alpha{M}^{3}{\omega_e^2}}{u{L}^{2}{\omega_\infty^2}}} . $

(15) In an attempt to graphically depict the variation indicated by Equation (15), the deflection angle was plotted against the impact parameter to obtain Fig. 1.
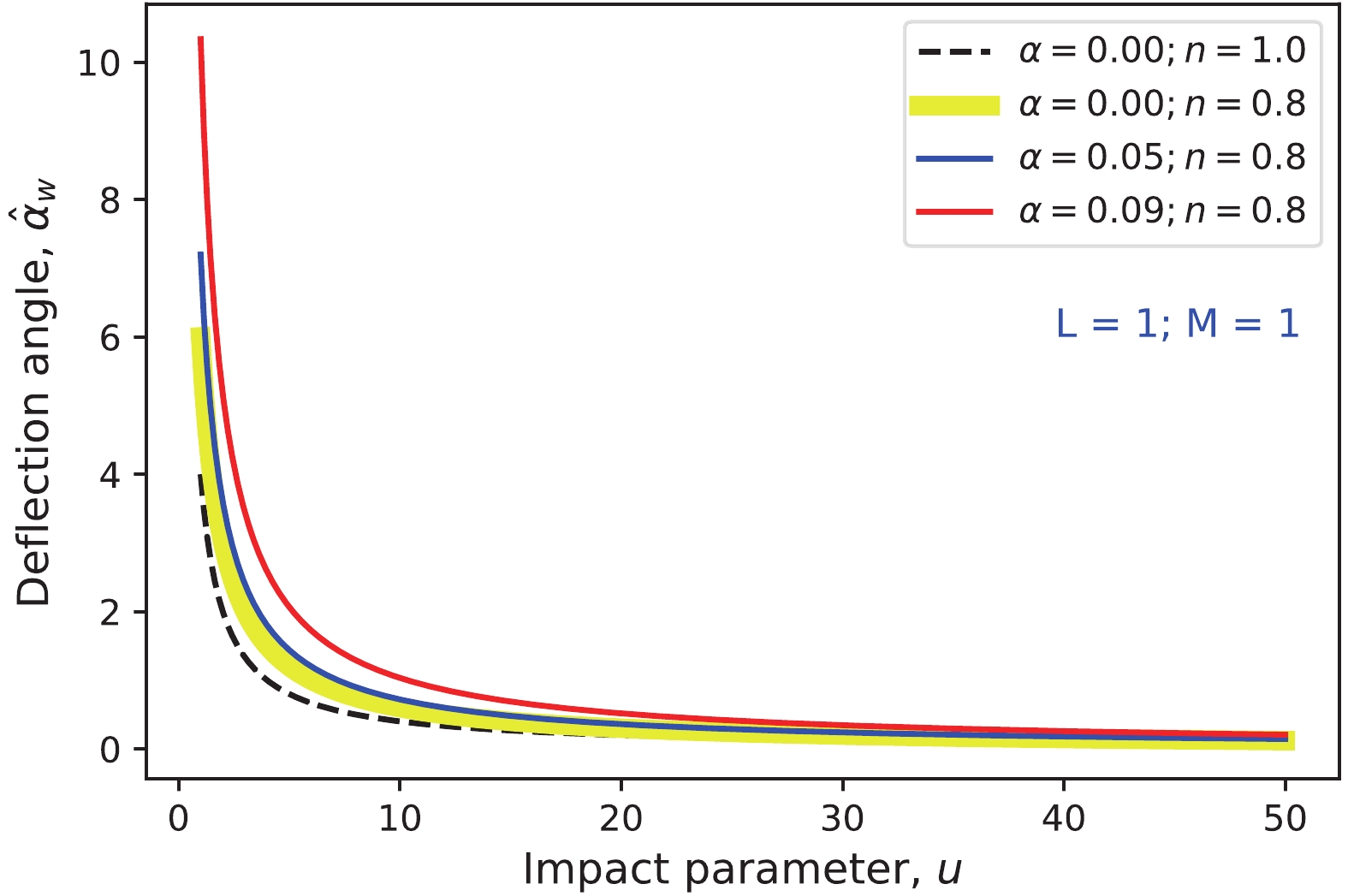
Figure 1. (color online) Deflection angle vs impact parameter for various values of coupling constant,
$ \alpha $ , with refractive index,$ n = 0.8 .$ In Fig. 1, the deflection angle is subject to quantum effects for low values of the impact parameter. Evidently, the contribution of these effects (characterized by the EUP parameter,
$ \alpha $ ) is not negligible. Thus, the deflection angle increases when the photon rays move through a medium of homogeneous plasma. The graph shows a significant increase in the deflection angle for the case of plasma medium, compared to the typical$ \hat{\alpha}_w $ that corresponds to the case of vacuum where EUP corrections are not considered. However, for a high impact parameter, all behaviors seem to be in close agreement. Furthermore, the results show that as$ \omega_e/\omega_\infty\to 0 $ , Equation (15) reduces to Equation (10), removing the influence of plasma. This indicates the standard case and is represented by the dashed line in Fig. 1.The deflection angle of EUP black hole in Equation (15) reduces to the following form in the weak field approach:
$ \hat{\alpha}_{w_{n}} \approx{\frac {4M(1+\alpha l^2)}{u}}+{\frac {2M{\omega_e^2}}{u{\omega_\infty^2}}}+{\frac {8\alpha{M}^{3}{\omega_e^2}}{u{L}^{2}{\omega_\infty^2}}}, $

(16) where
$ l = 2M/L $ .The first term of the deflection angle given in 16 is known as the deflection angle of post-Newtonian approach,
$ \alpha_{\rm{PPN}} = 2(1+\gamma) M / u $ . By comparing the deflection angle of the EUP black hole without the influence of plasma, we have$ \gamma-1 = 2l^2 $ , where using the constraint of solar system$ |\gamma-1| \lesssim 2.1 \times 10^{-5} $ , one can obtain the lower bound of EUP parameter as follows$ L \gtrsim 9.1 \times 10^{5} {\rm{ m}} $ [45].The scope of this work deals with regular, homogeneous plasma. This can be extended to cope with magnetic effects, known as the "Zeeman effect", potentially augmented by combining this epitome of magnetized plasma with the instances of homogeneous and inhomogeneous cases, as demonstrated by Ref. [50].
-
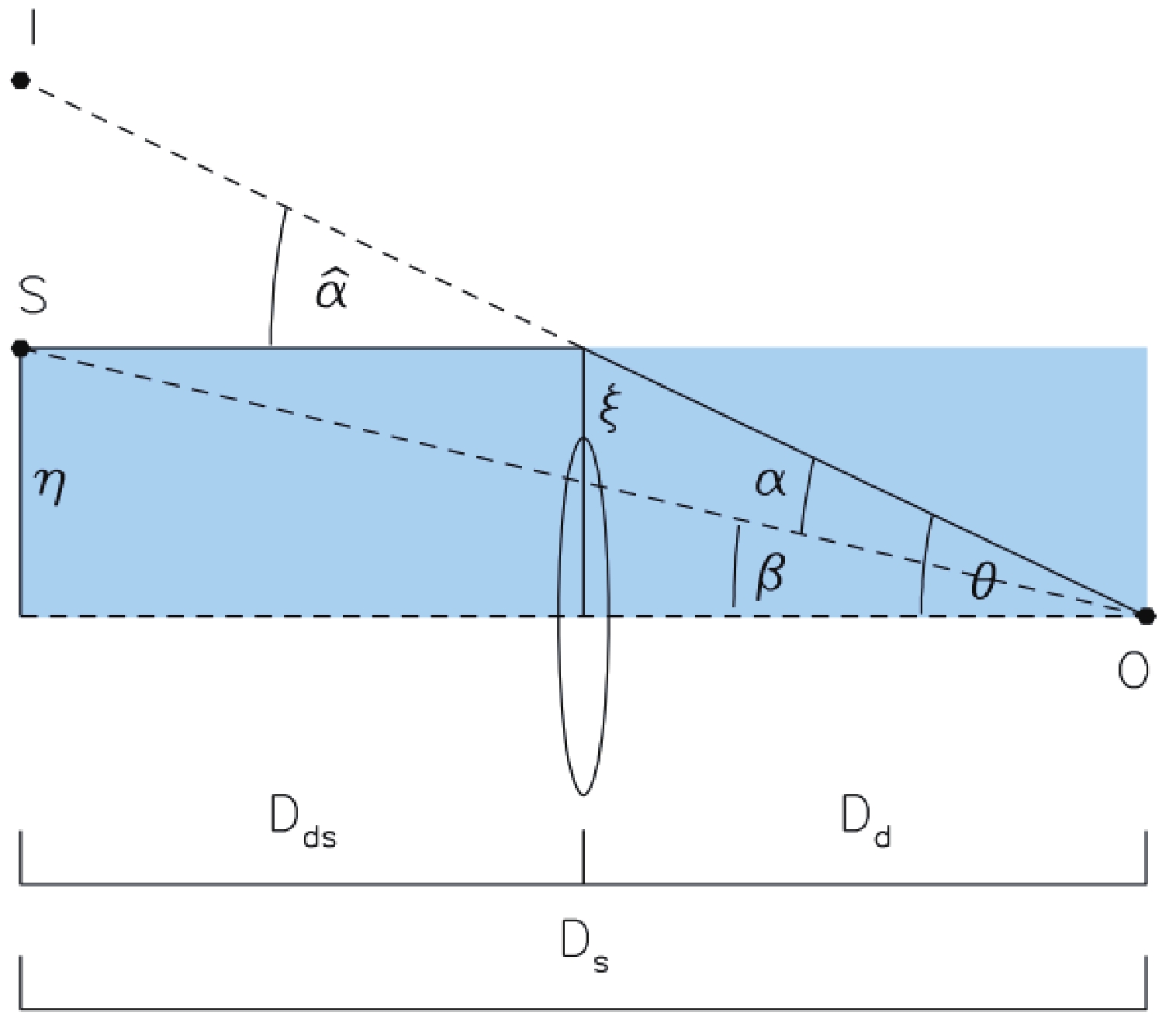
Here, we focus on the observational relevance (positions, magnifications, and differential time delays between lensed images) of the results derived in previous sections. The gravitational lensing effects we use here in the weak deflection limit have a setting, such that the massive compact object (the lens L) is located between a point source of light (S) and an observer (O), in an asymptotically flat region of the spacetime shown in Fig. 2, where the corresponding lens equation (or ray-tracing equation) with the angular positions of the images (
$ \theta $ ), and the actual position of the source ($ \beta $ ) is as follows [45]:$ \tan \beta = \tan \theta -D\ \left[ \tan \theta +\tan (\hat{\alpha}-\theta )\right], $

(17) where
$ D $ is the ratio of the distance from the lens to the source,$ d_{\rm LS} $ and the distance from the observer to the source,$ d_{\rm S} $ :$ D\equiv d_{\rm LS}/d_{\rm S} $ . Then, in the weak lens approximation ($ \alpha D_{s} \simeq \hat{\alpha} D_{d s} $ ), the above lens equation ($ \beta = \theta-\frac{D_{d s}}{D_{s}} \hat{\alpha}(\theta) $ ) for the EUP black hole with Einstein angle$ \theta_{\rm E} $ , is calculated as follows [45]:$ \beta = \theta-\left(1+\alpha l^{2}\right) \frac{\theta_{\rm{E}}^{2}}{\theta}, $

(18) where the impact parameter,
$ u = D_{d} \theta $ , and the Einstein angle (for the position consistent with$ \beta = 0 $ ) is$ \theta_{\rm{E}} = \sqrt{\frac{4 M D_{\rm{LS}}}{D_{\rm{L}} D_{\rm{S}}}}, $

(19) while the Einstein radius is
$ R_{E} = \theta_{E} D_{d}. $

(20) Using the Einstein angle in Eq. (19) in Eq. (18), we obtain
$ \beta \theta = \theta^{2}-\theta_{\rm E}^{2} $ . Subsequently, the corresponding angular position of images is obtained as follows:$ \theta_{\pm} = \frac{1}{2}\left[\beta \pm \sqrt{\beta^{2}+4\left(1+\alpha l^{2}\right) \theta_{\rm{E}}^{2}}\right], $

(21) and the angular separation between the two images are
$ \Delta \theta = \theta_{+}-\theta_{-} = \sqrt{\beta^{2}+4\left(1+\alpha l^{2}\right) \theta_{\rm{E}}^{2}}. $

(22) Magnification
$ \mu \left( \theta \right) $ of images takes place because the bending of light by the lens focuses more light rays from the source into a solid angle at the observer brightening up the image. It is defined by [45]$ \mu \left( \theta \right) = \left[ \frac{\sin \beta }{\sin \theta }\frac{{\rm d}\beta }{{\rm d}\theta }\right] ^{-1}, $

(23) and the magnification for the EUP black hole is calculated as follows:
$ \mu_{\pm} = \frac{\beta^{2}+2\left(1+\alpha l^{2}\right) \theta_{\rm{E}}^{2}}{2 \beta \sqrt{\beta^{2}+4\left(1+\alpha l^{2}\right) \theta_{\rm{E}}^{2}}} \pm \frac{1}{2}. $

(24) Moreover, one can calculate the total flux of images (with the original flux of the source
$ F_{\rm{src}} $ ), using the magnification as follows:$ F_{\rm{tot}} = \left(\mu_{+}+\mu_{-}\right) F_{\rm{src}} \\ = \frac{\beta^{2}+2\left(1+\alpha l^{2}\right) \theta_{\rm{E}}^{2}}{\beta \sqrt{\beta^{2}+4\left(1+\alpha l^{2}\right) \theta_{\rm{E}}^{2}}} F_{\rm{src}}. $

(25) The last important observable for the weak gravitational lensing is the time delay, which can be calculated using the following equation: [45]
$ T = \int_{R_{\rm{src}}}^{r_{0}} \frac{{\rm{d}} t}{{\rm{d}} r} {\rm{d}} r+\int_{r_{0}}^{R_{\rm{obs}}} \frac{{\rm{d}} t}{{\rm{d}} r} {\rm{d}} r, $

(26) where
$ \frac{{\rm{d}} t}{{\rm{d}} r} = \frac{\sqrt{f(r)^{-1} r^2 f(r_0)}}{f(r) \sqrt{r_{0}} \sqrt{\dfrac{r^2}{r_0} \dfrac{f(r_0)}{f(r)}-1}}, $

(27) and further, using
$ u = D_{\rm{L}} \sin \theta $ , the corresponding differential time delay for the EUP black hole is obtained as follows:$\ \begin{split} \Delta T =& {T_ + } - {T_ - } = 4M\left[ {\frac{\beta }{{2\theta _{\rm{E}}^2}}\sqrt {{\beta ^2} + 4\left( {1 + \alpha {l^2}} \right)\theta _{\rm{E}}^2} } \right.\\ &\left. { + \left( {1 + \alpha {l^2}} \right)\ln \left( {\frac{{\sqrt {{\beta ^2} + 4\left( {1 + \alpha {l^2}} \right)\theta _{\rm{E}}^2} + \beta }}{{\sqrt {{\beta ^2} + 4\left( {1 + \alpha {l^2}} \right)\theta _{\rm{E}}^2} - \beta }}} \right)} \right]. \end{split} $

(28) The angular position of images for the homogeneous magnetized plasma is
$ \theta = \frac{1}{2}(\beta \pm \sqrt{\beta^{2}+4 \Theta_{\pm}^{2}}) $

(29) with
$ \Theta_{\pm} = \theta_{E} \sqrt{\frac{1}{2}\left\{1+\left[1-\frac{\omega_{e}^{2}}{\omega_{\infty}^{2}}\left(1-\xi(1+\alpha l^2) \right) \right]^{-1}\right\}}. $

(30) If the source, lens, and observer are lined up at
$ \beta $ = 0, the image of the source forms the so-called Einstein ring [51]. Hence, using the above angular position and repeating the calculations, the presence of the plasma is found to cause a shift in the angular position of images as shown in Fig. 1 [50]. For example, the vicissitudes of plasma on the angular position in the case of an Einstein ring is different in Ref. [25].The impacts of gravitational lensing on the deflection angle due to the bending of trajectories of massive objects for various criteria, explored by Ref. [51], highlights the enormity of infinitesimal corrections. Furthermore, in Ref. [52], the authors addressed the coupling of photons to the Weyl tensor in a Schwarzschild black hole for weak deflection lensing and deduced that measuring the variation of the total flux of two images caused by a black hole (in this case, Sagittarius A*) might be a promising way to test this outlook in the future. As per Ref. [53], in the weak field regime, deviations of observables are too minute to be detected in the aspect of modified gravity versus general relativity; the differential time delay - which seems to produce a significant increase - is seen to be the only prominently detectable observable. The work by C.-Y. Wang, et. al in Ref. [54] encompasses weak deflection lensing observables for the charged Horndeski black holes: their findings for Sagittarius A* as the lens insinuates that the deviations of these observables from those of the Schwarzschild black hole are either too small to detect or easily to be wiped out by the flares of Sagittarius A*, albeit the angular separation, angular difference, and flux difference between the two lensed images prevailing within the thresholds of current technology. Further, weak lensing by the regular non-minimal Einstein–Yang–Mills black hole has been studied by Ref. [55] and construed to be the same as that of the Reissner–Nordström black hole. Nevertheless, all past analyses agree on the common assertion that the current technology is insufficient to validate the procured corollaries.
-
In this study, we investigated the quantum gravity effects in the vicinity of a black hole, so as to preserve the specific state of an object falling into it, hence solving the information paradox. These quantum effects, in the presence of a plasma medium, are found to induce substantial changes in the deflection angle, as in the case study of the supermassive black holes, Sagittarius A* and M87 [45]; this claim is also supported by the calculations of Ref. [50], where observables show a potent contribution from the plasma medium. This variation can be utilized to develop the precision of differential deflection, established by typical assumptions of weak lensing. The nature of Equation (15) to adapt between vacuum and plasma advocates flexibility to modify the result for a wide range of analyses. It is concluded that the EUP corrections are indeed sufficiently high to determine various parameters on a large scale. Finally, we determined the impacts of plasma on three salient observables, namely, position, magnification, and time delay. It is inferred that their consequences are indeed conspicuous.
Weak deflection angle of extended uncertainty principle black holes
- Received Date: 2019-08-26
- Accepted Date: 2019-11-26
- Available Online: 2020-02-01
Abstract: We discuss the effects of quantum fluctuations spewed by a black hole on its deflection angle. The Gauss-Bonnet theorem (GBT) is exploited with quantum corrections through the extended uncertainty principle (EUP), and the corresponding deflection angle is obtained. Moreover, we have attempted to broaden the scope of our work by subsuming the effects of plasma medium on the deflection angle. To demonstrate the degree of difference, the acquired results are compared with the prevailing findings.





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF













 DownLoad:
DownLoad: