-
In recent decades, theoretical and experimental physicists have made progress in studying the heavy-light meson spectrum with the observation of a large number of charmed and bottom mesons. In particular, the charmed meson spectrum has been mapped with high precision with the observation of many new charmed states such as
$ D_{1}^{*}(2680) $ ,$ D_{2}^{*}(2460) $ ,$ D_{J}(2580) $ ,$ D_{J}^{*}(2650) $ ,$ D_{J}^{*}(2760) $ ,$ D_{J}(2740) $ ,$ D_{J}(3000) $ ,$ D_{J}^{*}(3000) $ [1-3]. In our previous work, we studied the strong decay of some charmed states with the$ ^{3}P_{0} $ decay model and the heavy meson effective theory, and identified the quantum numbers of these charmed states [4-6]. In the bottom sector, only the ground states,$ B^{0}(5279) $ ,$ B^{\pm}(5279) $ ,$ B^{*}(5324) $ ,$ B_{s}(5366) $ and$ B_{s}^{*}(5415) $ , and a few of the low lying excited states,$ B_{1}(5721) $ and$ B_{2}^{*}(5747) $ , have been identified in PDG [7]. Compared to the charmed mesons, there is little information about the excited bottom states.Fortunately, the LHCb collaboration has observed some new bottom states in recent years, such as
$ B_{J}(5840)^{0} $ ,$ B_{J}(5840)^{+} $ ,$ B_{J}(5970)^{0} $ and$ B_{J}(5970)^{+} $ [8-11]. Besides, the CDF, D0 and LHCb collaborations have also observed two bottom-strange mesons,$ B_{s1}(5830) $ and$ B_{s2}^{*}(5840) $ [12-14], and assigned their$ J^{P} $ as$ 1^{+} $ and$ 2^{+} $ , respectively. The masses and widths of these newly observed bottom and bottom-strange mesons are listed in Table 1. For these mesons, it is important to assign the quantum numbers and identify their position in the bottom meson spectrum. Several approaches have been used for this work, such as the quark model [15-23], the heavy quark effective theory (HQET) [5, 24], lattice QCD [25], and the$ ^{3}P_{0} $ model [26-28]. However, the predictions of different theoretical approaches, even with the same theoretical method but different parameters, are not completely consistent with each other.States Mass/(MeV/c2) Width/MeV $ J^{PC} $ 

Decay channels $ B_{1}(5721)^{+} $ [7]

$ 5725.9^{+2.5}_{-2.7} $ 

$ 31\pm6 $ 

$ 1^{+} $ 

$ B^{*0}\pi^{+} $ 

$ B_{1}(5721)^{0} $ [7]

$ 5726.1\pm1.3 $ 

$ 27.5\pm3.4 $ 

$ 1^{+} $ 

$ B^{*+}\pi^{-} $ 

$ B_{2}^{*}(5747)^{+} $ [7]

$ 5737.2\pm0.7 $ 

$ 20\pm5 $ 

$ 2^{+}(1^{3}P_{2}) $ 

$ B^{0}\pi^{+} $ ,

$ B^{*0}\pi^{+} $ 

$ B_{2}^{*}(5747)^{0} $ [7]

$ 5739.5\pm0.7 $ 

$ 24.2\pm1.7 $ 

$ 2^{+}(1^{3}P_{2}) $ 

$ B^{+}\pi^{-} $ ,

$ B^{*+}\pi^{-} $ 

$ B_{J}(5970)^{+} $ [7]

$ 5964\pm5 $ 

$ 62\pm20 $ 

- $ B^{*0}\pi^{+} $ , [

$ B^{0}\pi^{+} $ ]

$ B_{J}(5970)^{0} $ [7]

$ 5971\pm5 $ [7]

$ 81\pm12 $ 

- $ B^{*0}\pi^{+} $ , [

$ B^{+}\pi^{-} $ ]

$ B_{J}(5840)^{+} $ [11]

$ 5862.9\pm5.0 $ 

$ 224\pm80 $ 

- $ B^{*0}\pi^{+} $ , [

$ B^{0}\pi^{+} $ ]

$ B_{J}(5840)^{0} $ [11]

$ 5862.9\pm5.0 $ 

$ 127.4\pm16.7 $ 

- $ B^{*0}\pi^{+} $ , [

$ B^{+}\pi^{-} $ ]

$ B_{s1}(5830) $ [7]

$ 5828.7\pm0.1 $ 

$ 0.5\pm0.3 $ 

$ 1^{+} $ 

$ B^{*}K $ 

$ B_{s2}^{*}(5840) $ [7]

$ 5839.85\pm0.7 $ 

$ 1.40\pm0.4 $ 

$ 2^{+}(1^{3}P_{2}) $ 

$ B^{*}K $ ,

$ BK $ 

Table 1. Experimental information about the newly observed excited bottom and bottom-strange states.
Since the discovery of bottom mesons
$ B_{1}(5721) $ and$ B_{2}^{*}(5747) $ by the D0 collaboration in 2007 [8], their nature was studies using different models, and they were identified as the$ 1^{+} $ and$ 2^{+} $ bottom states in PDG [7]. However, the assignment of$ B_{1}(5721) $ meson still needs further confirmation because it is a mixture of the$ ^{3}P_{1} $ and$ ^{1}P_{1} $ states.$ B_{J}(5970) $ bottom meson was explained as a$ 2S1^{-} $ or$ 1D3^{-} $ state by different theoretical approaches [29-37], but its spin-parity still remains undetermined in PDG, which only lists its mass and decay width. Furthermore, we note that$ B_{J}(5840) $ meson is omitted from the summary tables in PDG, which indicates that its assignment needs additional theoretical and experimental verifications. As for$ B_{s2}^{*}(5840) $ and$ B_{s1}(5830) $ bottom-strange mesons, they are assigned as the strange partners of$ B_{2}^{*}(5747) $ and$ B_{1}(5721) $ with quantum numbers$ 2^{+} $ and$ 1^{+} $ [7, 38-41].In Refs. [34-37], the assignments of some excited B and
$ B_{s} $ mesons were analyzed with the quark model and the$ ^{3}P_{0} $ model. As different parameters were used, their conclusions are not consistent with each other. In addition, we studied the two-body strong decay of$ B_{1}(5721) $ ,$ B_{2}^{*}(5747) $ ,$ B(5970) $ ,$ B_{s1}(5830) $ and$ B_{s2}^{*}(5840) $ with the heavy meson effective theory at the leading order approximation, and designated the states$ 2S1^{-} $ ,$ 1D1^{-} $ and$ 1D3^{-} $ as candidates for$ B_{J}(5970) $ [29]. As a continuation of our previous work, we study the strong decay of other bottom mesons with the$ ^{3}P_{0} $ decay model and give a simple discussion of their quantum numbers. The calculated strong decay widths in this work may be confronted to the future experimental data, and will be helpful in determining the nature of these heavy-light mesons. The paper is arranged as follows. In Sec. 2, we give a brief review of the$ ^{3}P_{0} $ decay model. In Sec. 3, we study the strong decay of$ B_{1}(5721) $ ,$ B_{2}^{*}(5747) $ ,$ B_{s1}(5830) $ ,$ B_{s2}^{*}(5840) $ ,$ B_{J}(5840) $ and$ B_{J}(5970) $ , and identify the assignments of these states. In Sec. 4, we present our conclusions. -
In the analysis of strong decay of mesons, the
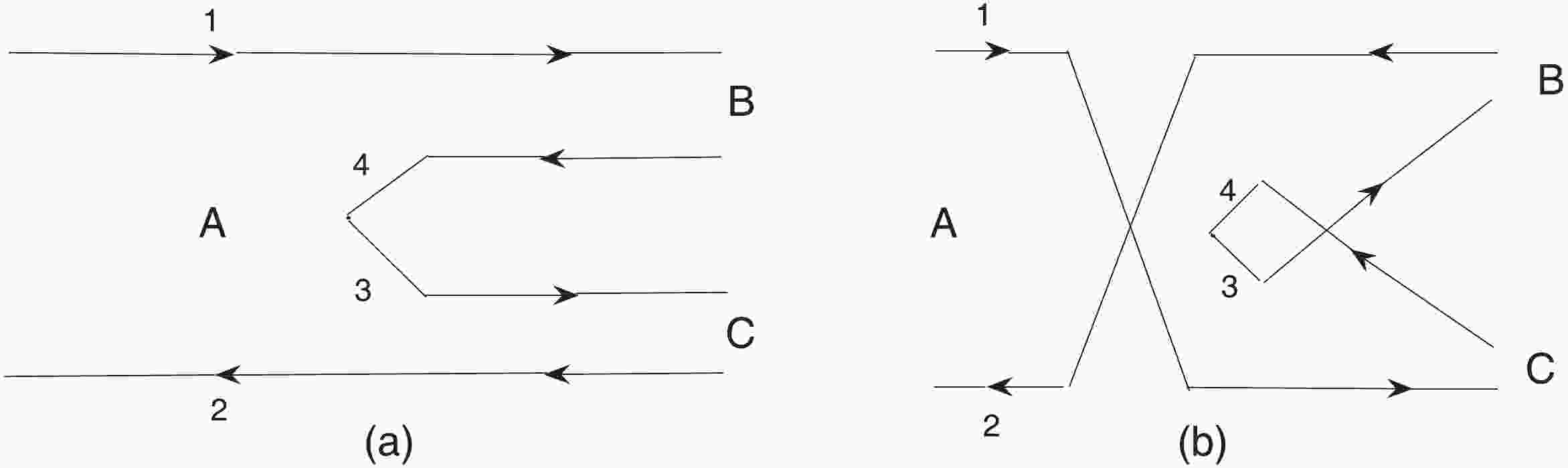
$ ^{3}P_{0} $ decay model is an effective and simple method which can give a good prediction of the decay behavior of many hadrons [42-46]. This model was introduced by Micu in 1969 [26], and further developed by Le Yaouanc and other collaborations [27, 28]. In Ref. [47], Barnes et al. performed a comprehensive study of the strong decay of light mesons with the$ ^{3}P_{0} $ model. This model has been extensively used to describe the strong decay of heavy mesons in the charmonium [48-51] and bottommonium systems [52-54], of baryons [55] and even of the teraquark states [56].At first, an alternative phenomenological model was considered for studying the strong decay in which quark-antiquark pairs are produced with the
$ ^{3}S_{1} $ quantum number. However, this possibility was disfavored by measurements of the ratio of partial wave amplitudes [57]. In the$ ^{3}P_{0} $ decay model, it is now generally accepted that a quark-antiquark pair ($ q_{3}\overline{q}_{4} $ ) with the$ 0^{++} $ quantum number (in the$ ^{3}P_{0} $ state) is created from vacuum [26-28, 42]. For a meson decay process A→BC, the quark-antiquark pair ($ q_{3}\overline{q}_{4} $ ) regroups into final state mesons (BC) with$ q_{1}\overline{q}_{2} $ from the initial meson A. This process is illustrated in Fig. 1, and its transition operator in the nonrelativistic limit is written as,$\begin{split}T =& - 3\gamma \sum\limits_m {\langle 1m1 - m\mid 00\rangle } \int {{\rm d^3}} {\vec p_3}{\rm d^3}{\vec p_4}{\delta ^3}({\vec p_3} + {\vec p_4})\\&\times{\cal Y}_1^m\left(\frac{{{{\vec p}_3} - {{\vec p}_4}}}{2}\right)\chi _{1 - m}^{34}\varphi _0^{34}\omega _0^{34}q_3^\dagger ({\vec p_3})q_4^\dagger ({\vec p_4}) , \end{split}$

(1) where
$ q_{3}^{\dagger} $ and$ q_{4}^{\dagger} $ are the creation operators in the momentum space of the quark-antiquark$ q_{3}\overline{q}_{4} $ pair.$ \gamma $ is a dimensionless parameter reflecting the creation strength of the quark-antiquark pair.$ \varphi_{0}^{34} $ ,$ \omega_{0}^{34} $ and$ \chi_{1-m}^{34} $ denote its flavor, color and spin wave functions, respectively.In the c.m. frame, the amplitude of a decay process
$ A\rightarrow BC $ can be written as,$\begin{split} {{\cal M}^{{M_{{J_A}}}{M_{{J_B}}}{M_{{J_C}}}}}(\vec P) =& \gamma \sqrt {8{E_A}{E_B}{E_C}} \displaystyle\sum\limits_{\scriptstyle{M_{{L_A}}},{M_{{S_A}}},\atop {\scriptstyle{M_{{L_B}}},{M_{{S_B}}},\atop \scriptstyle{M_{{L_C}}},{M_{{S_C}}},m}} \langle {L_A}{M_{{L_A}}}{S_A}{M_{{S_A}}}\mid {J_A}{M_{{J_A}}}\rangle \langle {L_B}{M_{{L_B}}}{S_B}{M_{{S_B}}}\mid {J_B}{M_{{J_B}}}\rangle \\ & \times \langle {L_C}{M_{{L_C}}}{S_C}{M_{{S_C}}}\mid {J_C}{M_{{J_C}}}\rangle \langle 1m1 - m\mid 00\rangle \langle \chi _{{S_B}{M_{{S_B}}}}^{14}\chi _{{S_C}{M_{{S_C}}}}^{32}\mid \chi _{{S_A}{M_{{S_A}}}}^{12}\chi _{1 - m}^{34}\rangle \\&\times [\langle \phi _B^{14}\phi _C^{32}\mid \phi _A^{12}\phi _0^{34}\rangle I(\vec P,{m_1},{m_2},{m_3})\\ & + {( - 1)^{1 + {S_A} + {S_B} + {S_C}}}\langle \phi _B^{32}\phi _C^{14}\mid \phi _A^{12}\phi _0^{34}\rangle I( - \vec P,{m_2},{m_1},{m_3})], \end{split}$

(2) where
$ \langle\chi_{S_{B}M_{S_{B}}}^{14}\chi_{S_{C}M_{S_{C}}}^{32}\mid \chi_{S_{A}M_{S_{A}}}^{12}\chi_{1-m}^{34}\rangle $ ,$ \langle \phi_{B}^{14}\phi_{C}^{32}\mid \phi_{A}^{12}\phi_{0}^{34}\rangle $ are the spin and flavor matrix elements. The two terms in the last factor correspond to the two diagrams in Fig. 1. The momentum space integral$ I(\vec P,m_{1},m_{2},m_{3}) $ is given by$\begin{split} I(\vec P,{m_1},{m_2},{m_3}) =& \int {{\rm d^3}} \vec p\psi _{{n_B}{L_B}{M_{{L_B}}}}^*\left(\frac{{{m_3}}}{{{m_1} + {m_2}}}{{\vec P}_B} + \vec p \right) \psi _{{n_C}{L_C}{M_{{L_C}}}}^*\\&\times\left(\frac{{{m_3}}}{{{m_2} + {m_3}}}{{\vec P}_B} + \vec p\right) {\psi _{{n_A}{L_A}{M_{{L_A}}}}}({{\vec P}_B} + \vec p){\cal Y}_1^m(\vec p), \end{split}$

(3) where
$ \vec P = \vec P_{B} = -\vec P_{C}, \vec p = \vec p_{3} $ , and$ m_{3} $ is the mass of the created quark$ q_{3} $ . In Eq. (3),$ \psi $ is the meson space wave function which is used to describe the space part of the meson. We commonly employ the simple harmonic oscillator (SHO) as an approximation of the meson space wave function. In the momentum space, it is defined as$\begin{split}{\Psi _{nL{M_L}}}(\vec p) =& {( - 1)^n}{( - i)^L}{R^{L + \frac{3}{2}}}\sqrt {\frac{{2n!}}{{\Gamma (n + L + \frac{3}{2})}}} \\&\times\exp \left( - \frac{{{R^2}{p^2}}}{2}\right) L_n^{L + \frac{1}{2}}({R^2}{p^2}){{\cal Y}_{L{M_L}}}(\vec p), \end{split}$

(4) where R is the scale parameter of SHO. Using the Jacob-Wick formula, we can convert the helicity amplitude into the partial wave amplitude [58]
$\begin{split}{{\cal M}^{JL}}(\vec P) =& \frac{{\sqrt {4\pi (2L + 1)} }}{{2{J_A} + 1}}\sum\limits_{{M_{{J_B}}}{M_{{J_C}}}} {\langle L0J{M_{{J_A}}}|{J_A}{M_{{J_A}}}\rangle } \\&\times\langle {J_B}{M_{{J_B}}}{J_C}{M_{{J_C}}}|J{M_{{J_A}}}\rangle {{\cal M}^{{M_{{J_A}}}{M_{{J_B}}}{M_{{J_C}}}}}(\vec P), \end{split}$

(5) where
$ M_{J_{A}} = M_{J_{B}}+M_{J_{C}} $ ,${{J}} = {{{J}}_{{B}}} + {{{J}}_{{C}}}$ and${{{J}}_{{A}}} = {{{J}}_{{B}}} + {{{J}}_{{C}}} + {{L}}$ .$ {L} $ is the relative angular momentum between the final states B and C.In terms of the partial wave amplitudes, the decay width in the relativistic phase space is
$\Gamma = \frac{\pi }{4}\frac{{|\vec P|}}{{M_A^2}}\sum\limits_{JL} | {{\cal M}^{JL}}{|^2} , $

(6) where
$ |\vec P| = \frac{\sqrt{[M_{A}^{2}-(M_{B}+M_{C})^{2}][M_{A}^{2}-(M_{B}-M_{C})^{2}]}}{2M_{A}} $ is the three-momentum of the daughter meson in the c.m. frame.$ M_{A} $ ,$ M_{B} $ , and$ M_{C} $ are the masses of mesons A, B, and C. More details of the decay model can be found in Refs. [26-28, 42]. -
The parameters in the
$ ^{3}P_{0} $ model include the light quark pair ($ q\overline{q} $ ) creation strength$ \gamma $ , the SHO wave function scale parameter R, and the masses of the mesons and constituent quarks. The quark masses are taken as$ m_{u} = m_{d} = 0.22 $ GeV,$ m_{s} = 0.42 $ GeV and$ m_{b} = 4.81 $ GeV [7]. The value of the factor$ \gamma $ , which describes the strength of the quark-antiquark pair creation from vacuum, may be different when studying the decay of different hadrons, for example, light mesons, heavy-light mesons and heavy mesons. In fact, different studies employed different values, for example the value of 8.77 was used in reference [44], 13.4 in Refs. [59, 60] and$ 6.25 $ in Refs. [42, 61]. However, there is no definitive conclusion about the value of$ \gamma $ for different hadrons. Its value is related not only to the hadron itself, but also to quarks created in vacuum. In Ref. [42], H.G.Blundel et al. carried out a series of least squares fits of model predictions of decay widths of 28 best known meson decays. The fitted$ \gamma $ value of 6.25 was suggested as the optimal for$ u/d $ quarks, and$ \gamma_{s\overline{s}} = \gamma/\sqrt{3} $ for s quark. In this work, we adopt this value, which is higher than that used by Kokoski and Isgur by a factor of$ \sqrt{96\pi} $ due to different field theory conventions, constant factors in T, etc. [62].The input parameter R has a significant influence on the shape of the radial wave function, which leads to the sensitivity of the spatial integral in Eq. (3) on the value of the parameter R. Thus, the decay width given by the
$ ^{3}P_{0} $ decay model is also sensitive to R. Taking the strong decay of$ B_{2}^{*}(5747) $ as an example, we plot the decay width as a function of the parameter R in Fig. 2, and the partial decay ratio in Fig. 3. From the two figures, we can see that the partial decay ratio given by the$ ^{3}P_{0} $ model is insensitive to the parameter R, but the decay widths strongly depend on this parameter. If$ R_{B^{0}} $ ,$ R_{B^{+}} $ ,$ R_{B^{*0}} $ ,$ R_{B^{*+}} $ and$ R_{\pi} $ are fixed to 2.5$ {\rm GeV}^{-1} $ , the decay width of$ B_{2}^{*}(5747) $ changes by several times as the value of$ R_{B_{2}^{*}(5747)} $ changes from 2.0$ {\rm GeV}^{-1} $ to 3.0${\rm GeV}^{-1} $ . To proceed, there are two possibilities, one is to take the common value, and the other the effective value. The effective value is determined such to reproduce the realistic rms radius by solving the Schrodinger equation [22, 23]. In these references, the linear potential was used, which can be written as,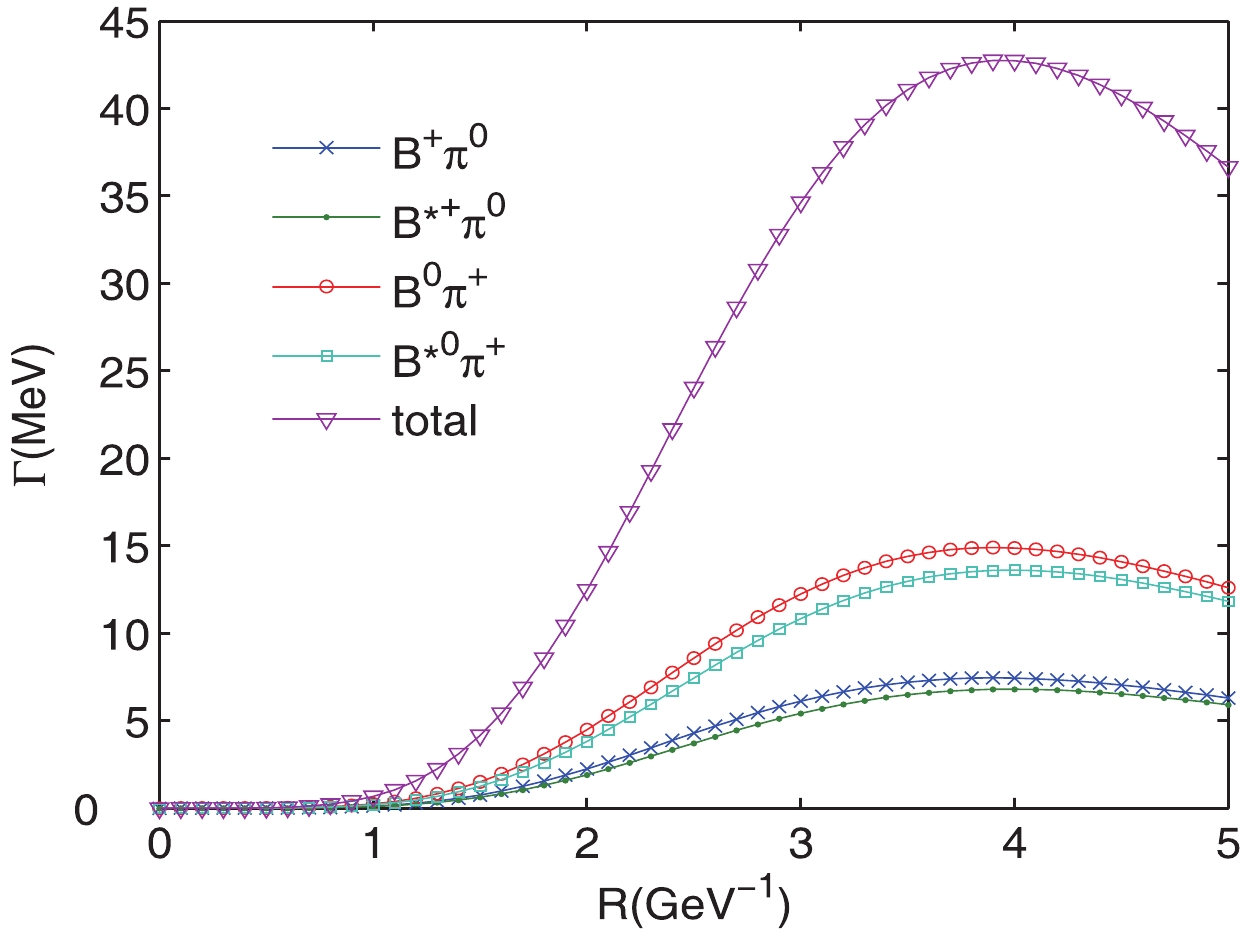
Figure 2. (color online) Strong decay width of
$ B^{*+}_{2}(5747) $ as the$ 1^{3}P_{2} $ state as a function of the scale parameter R.
Figure 3. Partial decay ratio
$ \frac{\Gamma_{B^{*+}_{2}(5747)\rightarrow B^{+}\pi^{0}}}{\Gamma_{B^{*+}_{2}(5747)\rightarrow B^{*+}\pi^{0}}} $ of the$ 1^{3}P_{2} $ state as a function of the scale parameter R.$ V_{\rm scr}(r) = V_{V}(r)+V_{s}(r), $

(7) where
$ V_{V}(r) = -\frac{4}{3}\frac{\alpha_{c}}{r} , $

(8) $ V_{s}(r) = \lambda\left(\frac{1-e^{-\mu r}}{\mu}\right). $

(9) More details about the potential model can be found in Refs. [18-23]. For the common value, H.G. Blunder et al. [42] suggested
$ R = 2.5 $ GeV-1 as the optimal value by fitting the experimental data. In our previous work, we studied the strong decay of some charmed mesons using the common value and obtained results consistent with the experimental data. Thus, we continue to use the common value for the parameter R in this work.The meson mass also has a significant influence on its strong decay. Taking
$ B_{2}^{*}(5747) $ as an example, if the masses of the daughter mesons are the standard values in PDG, the decay width of$ B_{2}^{*}(5747) $ varies greatly with its mass, as can be seen in Fig. 4. The masses of bottom mesons, especially the newly observed bottom states, are updated from time to time. In this work, we take the recently updated values in PDG [7], as listed in Table 2. For the newly observed bottom states which are not included in PDG, we take the experimental data as input.States $ \pi^{\pm} $ 

$ \pi^{0} $ 

$ \eta $ 

$ B^{\pm} $ 

$ B^{0} $ 

Mass/MeV $ 139.6 $ 

$ 135.0 $ 

$ 547.9 $ 

$ 5279.3 $ 

5279.6 States $ B^{*} $ 

$ B_{s}^{0} $ 

$ B_{s}^{*} $ 

$ K^{\pm} $ 

$ \overline{K^{0}} $ 

Mass/MeV $ 5324.7 $ 

$ 5366.9 $ 

$ 5415.4 $ 

$ 493.67 $ 

$ 497.61 $ 

Table 2. The masses of hadrons used in these calculations.

Figure 4. (color online) Strong decay width of
$ B^{*+}_{2}(5747) $ as the$ 1^{3}P_{2} $ state as a function of its mass.The
$ ^{3}P_{0} $ model is a simplified model of a complicated theory and it is not surprising that the predictions are not very accurate. Once the optimal values of all input parameters are determined, the best predictions of the$ ^{3}P_{0} $ decay model are expected to be within a factor of 2. A detailed analysis of the uncertainties of the results can be found in Ref. [42].It should be noted that mixing can occur between states with
$ J = L $ and$ S = 1 $ or$ S = 0 $ . The relation between the heavy quark symmetric states and the non-relativistic states$ ^{3}L_{L} $ and$ ^{1}L_{L} $ is written as [63],$\left( {\begin{array}{*{20}{c}} {|{s_l} = L + \dfrac{1}{2},{L^P}\rangle }\\ {|{s_l} = L - \dfrac{1}{2},{L^P}\rangle } \end{array}} \right) = \frac{1}{{\sqrt {2L + 1} }}\left( {\begin{array}{*{20}{c}} {\sqrt {L + 1} }&{ - \sqrt L }\\ {\sqrt L }&{\sqrt {L + 1} } \end{array}} \right)\left( {\begin{array}{*{20}{c}} {{|^3}{L_L}}\\ {{|^1}{L_L}} \end{array}} \right). $

(10) Using this relation, we get the mixing angle
$ \theta = 35.3^{\circ} $ for the states$ J = L = 1 $ , and thus this relation transforms to$\left( {\begin{array}{*{20}{c}} {|\dfrac{3}{2},{1^ + }\rangle }\\ {|\dfrac{1}{2},{1^ + }\rangle } \end{array}} \right) = \left( {\begin{array}{*{20}{c}} {\cos \theta }&{ - \sin \theta }\\ {\sin \theta }&{\cos \theta } \end{array}} \right)\left( {\begin{array}{*{20}{c}} {{|^3}{P_1}}\\ {{|^1}{P_1}} \end{array}} \right).$

(11) For a decay process
$ A\rightarrow BC $ , if the initial states$ A(l^{P} ) $ are a mixture, the partial wave amplitude can be written as$\left( {\begin{array}{*{20}{c}} {{\cal M}_{|l + \frac{1}{2},{l^P}\rangle \to BC}^{JL}}\\ {{\cal M}_{|l - \frac{1}{2},{l^P}\rangle \to BC}^{JL}} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} {\cos \theta }&{ - \sin \theta }\\ {\sin \theta }&{\cos \theta } \end{array}} \right)\left( {\begin{array}{*{20}{c}} {{\cal M}_{{|^3}{l_l}\rangle \to BC}^{JL}}\\ {{\cal M}_{{|^1}{l_l}\rangle \to BC}^{JL}} \end{array}} \right). $

(12) In our calculations, the states
$ B_{1}(5721) $ and$ B_{s1}(5830) $ are the$ 1^{+} $ bottom and bottom-strange states, and each of them is a mixture of$ ^{3}P_{1} $ and$ ^{1}P_{1} $ states. In addition, we study the strong decay of$ B_{J}(5970) $ as the$ 2^{-} $ state, which is the mixture of$ ^{3}D_{2} $ and$ ^{1}D_{2} $ states. Since for these states$ J = L = 2 $ , their mixing angle can also be determined using Eq. (10). Considering the mixture of initial states, the decay width can be expressed as,$\begin{split} \Gamma (|l + \frac{1}{2},{l^P}\rangle \to BC) =& \frac{\pi }{4}\frac{{|\vec P|}}{{M_A^2}}\sum\limits_{JL} | \cos \theta {\cal M}_{{|^3}{L_L} \to BC}^{JL} \\&- \sin \theta {\cal M}_{{|^1}{L_L} \to BC}^{JL}{|^2}, \\ \Gamma (|l - \frac{1}{2},{l^P}\rangle \to BC) =& \frac{\pi }{4}\frac{{|\vec P|}}{{M_A^2}}\sum\limits_{JL} | \sin \theta {\cal M}_{{|^3}{L_L} \to BC}^{JL} \\&+ \cos \theta {\cal M}_{{|^1}{L_L} \to BC}^{JL}{|^2}. \end{split}$

(13) -
The bottom mesons
$ B_{2}^{*+}(5747) $ and$ B_{2}^{*0}(5747) $ are both assigned as the$ 2^{+} $ states with total decay widths of$ 20\pm5 $ MeV and$ 24.2\pm1.7 $ MeV, respectively. As$ 1^{3}P_{2}(2^{+}) $ states, we calculate the strong decay widths of$ B_{2}^{*+}(5747) $ and$ B_{2}^{*0}(5747) $ as 23.9 MeV and 24.7 MeV, which is consistent with the experimental data. As a further confirmation of this assignment, we take the ratio of the partial widths for the decays into$ B^{0}\pi^{+} $ and$ B^{*0}\pi^{+} $ . The predicted ratio$\frac{{{\Gamma _{B_2^{* + }(5747) \to {B^0}{\pi ^ + }}}}}{{{\Gamma _{B_2^{* + }(5747) \to {B^{*0}}{\pi ^ + }}}}} = 1.18$

is in good agreement with the experimental ratio of 1.12, as is the ratio for
$ B_{2}^{*0}(5747) $ . As for$ B_{1}^{+}(5721) $ and$ B_{1}^{0}(5721) $ mesons, each of them is a mixture of bottom states$ ^{3}P_{1} $ and$ ^{1}P_{1} $ . In Table 3 and Table 4, the$ 1P_{1} $ and$ 1P_{1}' $ states denote the$ j_{q} = \frac{1}{2} $ and$ j_{q} = \frac{3}{2} $ states. We can see that the results for the$ j_{q} = \frac{3}{2}(1P_{1}') $ bottom states with the total decay widths of 39.8 MeV and 37.9 MeV, are roughly compatible with the experimental data of$ 31\pm6 $ MeV and$ 27.5\pm3.4 $ MeV. These results favor$ B_{1}(5721) $ as the$ j_{q} = \frac{3}{2} $ spin partner of the$ B_{2}^{*}(5747) $ state,$ B_{2}^{*+}(5747) $ 

$ B_{1}^{+'}(5721) $ 

$ B_{1}^{+}(5721) $ 

$ B^{*+}_{0} $ 

State $ 1^{3}P_{2} $ 

$ 1 P_{1}' $ 

$ 1P_{1} $ 

$ 1 ^{3}P_{0} $ 

Mass $ 5737.2 $ [7]

$ 5726.0 $ [7]

$ 5726.0 $ [7]

$ 5697.4 $ [35]

$ B^{+}\pi^{0} $ 

$ 4.3 $ 

$ - $ 

$ - $ 

$ 76.3 $ 

$ B^{*+}\pi^{0} $ 

$ 3.7 $ 

$ 26.5 $ 

$ 138.8 $ 

$ - $ 

$ B^{0}\pi^{+} $ 

$ 8.6 $ 

$ - $ 

$ - $ 

$ 155.1 $ 

$ B^{*0}\pi^{+} $ 

$ 7.3 $ 

$ 13.3 $ 

$ 69.4 $ 

$ - $ 

total $ 23.9 $ 

$ 39.8 $ 

$ 208.2 $ 

$ 231.4 $ 

Table 3. Strong decay widths of
$ B_{2}^{*}(5747) $ ,$ B_{1}(5721) $ and$ B^{*}_{0} $ with possible assignments. The symbol "-" means that the decay is forbidden by the selection rules, or that the decay cannot take place because it is below the threshold. All values are in units of MeV.$ B_{2}^{*0}(5747) $ 

$ B_{1}^{0'}(5721) $ 

$ B_{1}^{0}(5721) $ 

$ B^{*0}_{0} $ 

State $ 1^{3}P_{2} $ 

$ 1 P_{1}' $ 

$ 1 P_{1} $ 

$ 1 ^{3}P_{0} $ 

Mass $ 5739.5 $ [7]

$ 5726.1 $ [7]

$ 5726.1 $ [7]

$ 5697.4 $ [35]

$ B^{+}\pi^{-} $ 

$ 8.9 $ 

$ - $ 

$ - $ 

$ 78.3 $ 

$ B^{*+}\pi^{-} $ 

$ 7.6 $ 

$ 25.3 $ 

$ 134.9 $ 

$ - $ 

$ B^{0}\pi^{0} $ 

$ 4.4 $ 

$ - $ 

$ - $ 

$ 156.5 $ 

$ B^{*0}\pi^{0} $ 

$ 3.8 $ 

$ 12.6 $ 

$ 67.6 $ 

$ - $ 

total $ 24.7 $ 

$ 37.9 $ 

$ 202.5 $ 

$ 234.8 $ 

Table 4. Strong decay widths of
$ B_{2}^{*}(5747) $ ,$ B_{1}(5721) $ and$ B^{*}_{0} $ with possible assignments. The symbol "-" means that the decay is forbidden by the selection rules, or that the decay cannot take place because it is below the threshold. All values are in units of MeV.$({B_1}(5721),B_2^*(5747)) = {({1^ + },{2^ + })_{\frac{3}{2}}}\qquad n = 1,L = 1$

After identifying the
$ 1P_{1}' $ assignment, the remaining$ 1P_{1} $ and the$ 1^{3}P_{0} $ state are the spin doublet with$ j_{q} = \frac{1}{2} $ . The total width of$ 1^{3}P_{0} $ is predicted as 231.4 MeV, which is broader than the$ j_{q} = \frac{3}{2} $ P wave doublet. This prediction is consistent with the heavy quark limit (HQL). -
We note that PDG only reports
$ B_{J}(5970) $ bottom meson and omits the$ B_{J}(5840) $ state from the summary tables, while the spin-parity of$ B_{J}(5970) $ remains unknown. Thus, we study the strong decay with the$ 2^{1}S_{0} $ and$ 2^{3}S_{1} $ assignments for the$ B_{J}(5840) $ state and$ 2^{3}S_{1} $ ,$ 1^{3}D_{1} $ ,$ 1^{3}D_{3} $ ,$ 1D_{2}' $ and$ 1D_{2} $ assignments for the$ B_{J}(5970) $ state. The results are shown in Table 5 and Table 6. The LHCb collaboration suggested that the$ B_{J}(5840) $ and$ B_{J}(5970) $ signals should be identified as the$ 2^{1}S_{0} $ and$ 2^{3}S_{1} $ bottom states. We note also that the strong decay into$ B\pi $ is reported by LHCb as 'possibly seen' for$ B_{J}(5840) $ and$ B_{J}(5970) $ . However, our analysis indicates that the decay into$ B\pi $ is forbidden for$ B_{J}(5840) $ as a$ 2^{1}S_{0} $ state. If the decay into$ B\pi $ is confirmed in the future, the$ 2^{1}S_{0} $ assignment can be ruled out. As for the$ 2^{3}S_{1} $ assignment of$ B_{J}^{+}(5840) $ and$ B_{J}^{0}(5840) $ , their total decay widths are 121.9 MeV and 117.5 MeV, which is compatible with the experimental data. Therefore, we tentatively take$ 2^{3}S_{1} $ as the assignment for$ B_{J}(5840) $ .$ B_{J}^{+}(5840) $ 

$ B_{J}^{+}(5970) $ 

States $ 2^{1}S_{0} $ 

$ 2^{3}S_{1} $ 

$ 2^{3}S_{1} $ 

$ 1^{3}D_{1} $ 

$ 1^{3}D_{3} $ 

$ 1D_{2}' $ 

$ 1D_{2} $ 

Mass $ 5862.9 $ [11]

$ 5964 $ [7]

$ B^{+}\pi^{0} $ 

$ - $ 

$ 12.9 $ 

$ 10.2 $ 

$ 27.3 $ 

$ 6.5 $ 

$ - $ 

$ - $ 

$ B^{*+}\pi^{0} $ 

$ 38.1 $ 

$ 25.4 $ 

$ 23.7 $ 

$ 14.1 $ 

$ 6.0 $ 

$ 23 $ 

$ 80.9 $ 

$ B^{0}\pi^{+} $ 

$ - $ 

$ 25.8 $ 

$ 20.4 $ 

$ 54.6 $ 

$ 13.1 $ 

$ - $ 

$ - $ 

$ B^{0*}\pi^{+} $ 

$ 76.1 $ 

$ 50.8 $ 

$ 47.4 $ 

$ 28.2 $ 

$ 11.9 $ 

$ 11.6 $ 

$ 40.5 $ 

$ B^{+}\eta $ 

$ - $ 

$ 2.7 $ 

$ 14.4 $ 

$ 25.8 $ 

$ 0.5 $ 

$ - $ 

$ - $ 

$ B^{*+}\eta $ 

$ - $ 

$ 1.6 $ 

$ 20.0 $ 

$ 8.5 $ 

$ 0.5 $ 

$ 1.2 $ 

$ 23.4 $ 

$ B_{S}^{0}K^{+} $ 

$ - $ 

$ - $ 

$ 13.1 $ 

$ 21.4 $ 

$ 0.2 $ 

$ - $ 

$ - $ 

$ B_{S}^{0*}K^{+} $ 

$ - $ 

$ - $ 

$ 12.3 $ 

$ 4.9 $ 

$ 0.03 $ 

$ 0.6 $ 

$ 13.9 $ 

$ B_{1}(1P_{1})\pi $ 

$ - $ 

$ - $ 

$ 0.51 $ 

60.2 0.12 0.82 0.38 $ B_{1}(1P^{'}_{1})\pi $ 

$ - $ 

$ - $ 

$ 0.22 $ 

0.51 0.07 0.01 0.06 $ B_{2}^{*}\pi $ 

$ - $ 

$ - $ 

$ 0.24 $ 

0.73 0.54 75.03 0.13 total $ 114.2 $ 

$ 121.9 $ 

$ 172.4 $ 

$ 255.7 $ 

$ 39.43 $ 

$ 112.3 $ 

$ 159.27 $ 

Table 5. Strong decay widths of
$ B_{J}^{+}(5840) $ and$ B_{J}^{+}(5970) $ with possible assignments. The symbol "-" means that the decay is forbidden by the selection rules, or that the decay cannot take place because it is below the threshold. All values are in units of MeV.$ B_{J}^{0}(5840) $ [11]

$ B_{J}^{0}(5970) $ 

States $ 2^{1}S_{0} $ 

$ 2^{3}S_{1} $ 

$ 2^{3}S_{1} $ 

$ 1^{3}D_{1} $ 

$ 1^{3}D_{3} $ 

$ 1D_{2}' $ 

$ 1D_{2} $ 

Mass $ 5862.9 $ [11]

$ 5971.0 $ [7]

$ B^{+}\pi^{-} $ 

$ - $ 

$ 25.8 $ 

$ 20.0 $ 

$ 54.3 $ 

$ 13.4 $ 

$ - $ 

$ - $ 

$ B^{*+}\pi^{-} $ 

$ 76.1 $ 

$ 50.8 $ 

$ 46.7 $ 

$ 28.3 $ 

$ 12.2 $ 

$ 22.9 $ 

$ 80.9 $ 

$ B^{0}\pi^{0} $ 

$ - $ 

$ 12.9 $ 

$ 10.0 $ 

$ 27.1 $ 

$ 6.7 $ 

$ - $ 

$ - $ 

$ B^{0*}\pi^{0} $ 

$ 38.0 $ 

$ 25.3 $ 

$ 23.3 $ 

$ 14.1 $ 

$ 6.1 $ 

$ 11.4 $ 

$ 40.5 $ 

$ B^{0}\eta $ 

$ - $ 

$ 2.7 $ 

$ 14.7 $ 

$ 26.3 $ 

$ 0.5 $ 

$ - $ 

$ - $ 

$ B^{*0}\eta $ 

$ - $ 

$ - $ 

$ 20.9 $ 

$ 8.9 $ 

$ 0.2 $ 

$ 1.3 $ 

$ 23.9 $ 

$ B_{S}^{0}K^{+} $ 

$ - $ 

$ - $ 

$ 13.7 $ 

$ 22.1 $ 

$ 0.2 $ 

$ - $ 

$ - $ 

$ B_{S}^{0*}K^{+} $ 

$ - $ 

$ - $ 

$ 13.5 $ 

$ 5.2 $ 

$ 0.03 $ 

$ 0.6 $ 

$ 13.5 $ 

$ B_{1}(1P_{1})\pi $ 

$ - $ 

$ - $ 

$ 0.55 $ 

61.4 0.15 0.91 0.42 $ B_{1}(1P^{'}_{1})\pi $ 

$ - $ 

$ - $ 

$ 0.22 $ 

0.50 0.07 0.01 0.05 $ B_{2}^{*}\pi $ 

$ - $ 

$ - $ 

$ 0.25 $ 

0.81 0.60 73.03 0.15 total $ 114.1 $ 

$ 117.5 $ 

$ 163.8 $ 

$ 249.01 $ 

$ 40.12 $ 

$ 110.15 $ 

$ 159.42 $ 

Table 6. Strong decay widths of
$ B_{J}^{0}(5840) $ and$ B_{J}^{0}(5970) $ with possible assignments. The symbol "-" means that the decay is forbidden by the selection rules, or that the decay cannot take place because it is below the threshold. All values are in units of MeV.The situation is the same for
$ B_{J}(5840) $ . The decay channel$ B\pi $ of$ B_{J}(5970) $ is 'possibly seen' in experiments, and the assignments$ 1D_{2}' $ and$ 1D_{2} $ are tentatively ruled out as the decay into$ B\pi $ is forbidden. The experiments suggest that the total decay widths of$ B_{J}^{+}(5970) $ and$ B_{J}^{0}(5970) $ are$ 62\pm20 $ MeV and$ 81\pm12 $ MeV. For the assignments$ 1^{3}D_{3} $ and$ 1^{3}D_{1} $ , we can see that the predicted total widths of 39.43 MeV and 40.12 MeV in the case of the$ 1^{3}D_{3} $ assignment are consistent with the experiments within the predictive power of the model and the experimental uncertainties. Thus, we slightly prefer the$ 1^{3}D_{3} $ assignment for$ B_{J}(5970) $ . -
The bottom-strange mesons
$ B_{s1}(5830) $ and$ B_{s2}^{*}(5840) $ are assigned as$ 1^{+} $ and$ 2^{+} $ states in PDG, but it is noted that$ J^{P} $ needs confirmation [7]. In order to provide further information, we study the strong decay of$ B_{s2}^{*}(5840) $ as the$ 1^{3}P_{2} $ assignment, and$ B_{s1}(5830) $ as the$ 1P_{1}' $ and$ 1P_{1} $ assignments. The predicted total decay width of$ B_{s2}^{*}(5840) $ is 1.35 MeV, which is consistent with the experimental value of$ 1.40\pm0.4 $ MeV. In addition, the predicted partial decay ratio is$\frac{{{\Gamma _{B_{s2}^*(5840) \to {B^{* + }}{K^ - }}}}}{{{\Gamma _{B_{s2}^*(5840) \to {B^ + }{K^ - }}}}} = 0.15.$

(14) This value is roughly compatible with the experimental value of
$ 0.093\pm0.018 $ , which supports the$ 1^{3}P_{2} $ assignment for$ B_{s2}^{*}(5840) $ . As a$ 1^{+} $ state,$ B_{s1}(5830) $ meson is a mixture of$ 1^{3}P_{1} $ and$ 1^{1}P_{1} $ . From Table 7, we can see that the predicted total decay width of$ 1P_{1}' $ is 3.1 MeV. Although this is higher than the experimental value of$ 0.5\pm0.4 $ MeV, it is still compatible with the experiment within the predictive power of the model. Thus,$ 1P_{1}' $ is the optimal assignment for$ B_{s1}(5830) $ , and we conclude that$ B_{s1}(5830) $ and$ B_{s2}^{*}(5840) $ are the$ j_{q} = \frac{3}{2} $ doublet,$ B_{s2}^{*}(5840) $ 

$ B_{s0}^{*} $ 

$ B_{s1}(5830) $ 

States $ 1^{3}P_{2} $ 

$ 1^{3}P_{0} $ 

$ 1P_{1}' $ 

$ 1P_{1} $ 

Mass $ 5839.85 $ [7]

$ 5794.8 $ [35]

$ 5828.7 $ [7]

$ 5828.7 $ [7]

$ B^{+}K^{-} $ 

$ 0.6 $ 

$ 217 $ 

$ - $ 

$ - $ 

$ B^{*+}K^{-} $ 

$ 0.09 $ 

$ - $ 

$ 1.59 $ 

$ 31.9 $ 

$ B_{0}\overline{K^{0}} $ 

$ 0.6 $ 

$ 217 $ 

$ - $ 

$ - $ 

$ B_{0}^{*}\overline{K^{0}} $ 

$ 0.06 $ 

$ - $ 

$ 1.51 $ 

$ 30.2 $ 

total $ 1.35 $ 

$ 434 $ 

$ 3.1 $ 

$ 62.1 $ 

Table 7. Strong decay widths of
$ B_{s2}^{*}(5840) $ ,$ B_{s0}^{*} $ and$ B_{s1}(5830) $ with possible assignments. The symbol "-" means that the decay is forbidden by the selection rules, or that the decay cannot take place because it is below the threshold. All values are in units of MeV.$({B_{s1}}(5830),B_{s2}^*(5840)) = {({1^ + },{2^ + })_{\frac{3}{2}}}\qquad n = 1,L = 1$

The remaining states
$ 1P_{1} $ and$ 1^{3}P_{0} $ in Table 7 are the spin doublet with$ j_{q} = \frac{1}{2} $ and their total decay widths are much larger than of the spin doublet with$ j_{q} = \frac{3}{2} $ . -
In Refs. [34-37], the properties of bottom and bottom-strange mesons were analyzed with the relativized quark model and the
$ ^{3}P_{0} $ decay model. In Ref. [37], the harmonic oscillator wave function parameter R was taken with the same value as in our study (2.5 GeV−1). As for the pair-creation strength$ \gamma $ , it was replaced by an effective value$ \gamma_{0}^{\rm eff} = \frac{m_{n}}{m_{i}}\gamma_{0} $ . In Refs. [35, 36], the effective oscillator parameter$ R_{\rm eff} $ was obtained by equating the rms radius of the harmonic oscillator wave function for the given (n, l) quantum numbers with the relativized quark model, and the value of$ \gamma = 0.4 $ was used in the calculations.Some of our conclusions concerning the assignments of the bottom mesons are consistent with those of the above works, but there are some differences. For example,
$ B_{1}(5721) $ and$ B_{2}^{*}(5747) $ are unanimously identified as the spin doublet$ (1^{+},2^{+})_{\frac{3}{2}} $ with$ n = 1 $ ,$ L = 1 $ , while$ B_{s1}(5830) $ and$ B_{s2}^{*}(5840) $ are identified as the strange partners of$ B_{1}(5721) $ and$ B_{2}^{*}(5747) $ . However, our results for the total width of these mesons are$ 39.8 $ MeV,$ 23.9 $ MeV,$ 3.1 $ MeV,$ 1.35 $ MeV, respectively, while the results in Ref. [35] are$ 6.9 $ MeV,$ 11.4 $ MeV,$ 0.11 $ MeV,$ 0.78 $ MeV. In comparison with the latest data in Ref. [7], our results for$ B_{1}(5721) $ and$ B_{2}^{*}(5747) $ are closer to the experimental values, while the results for$ B_{s1}(5830) $ and$ B_{s2}^{*}(5840) $ in Ref. [35] are more accurate. For$ B_{J}(5840) $ and$ B_{J}(5970) $ , our analysis indicates that the possible assignments for these two mesons are$ 2^{3}S_{1} $ and$ 1^{3}D_{3} $ , which needs further confirmation by experiments. In particular, the decay modes$ B_{J}(5840)\rightarrow B\pi $ and$ B_{J}(5970)\rightarrow B\pi $ are crucial for identifying the optimal assignment of these two states. In Refs. [35, 36],$ B_{J}(5840) $ was identified as the$ 2^{3}S_{1} $ or$ 2^{1}S_{0} $ state, and$ B_{J}(5970) $ as the$ 1^{3}D_{3} $ or$ 1D_{2}' $ state. These conclusions also depend on whether these mesons are confirmed to decay into$ B\pi $ . In Ref. [37], it is suggested that the most likely assignment for$ B_{J}(5970) $ is$ 2^{3}S_{1} $ .In summary, we obtained assignments that are consistent with the other collaborations for
$ B_{1}(5721)^{0} $ ,$ B_{1}(5721)^{+} $ ,$ B_{2}^{*}(5747)^{0} $ ,$ B_{2}^{*}(5747)^{+} $ ,$ B_{J}(5840)^{0} $ ,$ B_{J}(5840)^{+} $ ,$ B_{J}(5970)^{0} $ ,$ B_{J}(5970)^{+} $ ,$ B_{s1}(5830) $ and$ B_{s2}^{*}(5840) $ . Our analysis supports that$ B_{1}(5721) $ and$ B_{2}^{*}(5747) $ are the spin doublet$ (1^{+},2^{+})_{\frac{3}{2}} $ with$ n = 1 $ ,$ L = 1 $ , and that$ B_{s1}(5830) $ and$ B_{s2}^{*}(5840) $ are the strange partners of$ B_{1}(5721) $ and$ B_{2}^{*}(5747) $ . The possible assignments of$ B_{J}(5840) $ and$ B_{J}(5970) $ are$ 2^{3}S_{1} $ and$ 1^{3}D_{3} $ . There are certainly differences in the final results because of the different choices of parameters. The final assignments of the above mesons, especially of$ B_{J}(5840) $ and$ B_{J}(5970) $ , need further confirmation by experiments.
Analysis of the excited bottom and bottom-strange states B1(5721), ${{ B_{2}^{*}(5747) }}$ , ${{ B_{s1}(5830)}} $ , $ {{B_{s2}^{*}(5840) }}$ , ${{ B_{J}(5840) }}$ and $ {{B_{J}(5970) }}$ of the B meson family
- Received Date: 2020-01-04
- Available Online: 2020-03-01
Abstract: In order to make a further confirmation of the assignments of the excited bottom and bottom-strange mesons











 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF

































 DownLoad:
DownLoad: