-
Heavy-ion fusion reactions have attracted much attention in recent years [1-4], because they are not only one of the important ways to synthesize new super-heavy elements (SHE), but also an important method to study nuclear structure and nuclear reaction mechanisms. With rare radioactive beams provided by many laboratories in the world, it is possible to study the properties of nuclei located near the drip lines, and to study nuclear reactions by using projectiles with exotic properties, considerably different from those along the
$ \beta $ stability line. Because of new phenomena in weakly bound nuclei [5-12], such as increased probability of neutron transfer and fusion [13] and increased breakup probability, one of the hot topics in SHE synthesis is the fusion with weakly bound nuclei, especially with halo nuclei.Halo nuclei, in which the valence neutron(s) or proton(s) are very weakly bound, are expected to give rise to new phenomena in nuclear reactions. In the semiclassical picture, the nucleus with a low binding energy usually has a larger radius, and the probabilities of specific reaction channels, such as neutron transfer and fusion, increase [13]. However, the experiments with the proton drip line nucleus 17F on 208Pb at energies around the Coulomb barrier do not observe enhancement of the fusion cross-section due to breakup or to the large interaction radius [14]. For the reaction 17F+208Pb at energies around the Coulomb barrier, Liang showed that the influence of breakup of 17F on the fusion cross-section is quite weak [5]. One of the hypothesis to explain the experimental data is the so-called "shielding effect". In the reaction, 17F is excited to the first excited state, becomes a proton-halo nucleus (hereafter denoted as 17F*), and is polarized as the valence proton is repelled by the reaction partner, and is shielded by the 16O core. With such a shielding effect, the effective interaction radius is smaller than one of 17F in the first excited state, and the fusion rate does not increase as expected.
In this work, using the improved quantum molecular dynamics model (ImQMD) and taking 17F+ 208Pb as an example, we try to verify the existence of the shielding effect of the valence proton in fusion reactions, and investigate its influence on the effective interaction potential. The paper is organized as follows. In Sec. 2, we briefly introduce the model. In Sec. 3, we present the improvement of the ImQMD model needed to describe the halo nucleus and the shielding effect in fusion reactions. Finally, a brief summary is given in Sec. 4.
-
The quantum molecular dynamics (QMD) model built by Aichelin and Peilert et al. [15, 16], which intuitively describes the microscopic dynamics of a nuclear reaction, is a powerful tool for studying heavy-ion collisions (HICs) at intermediate energies. Several versions of the QMD model, such as ImQMD, IQMD, IQMD-BNU, IQMD-IMP, IQMD-SINAP, JAM, JQMD, TuQMD, UrQMD, have been developed and successfully applied in various research fields. A detailed discussion of the QMD models can be found in Refs. [17-19]. The ImQMD model [20-26], used in this work, is briefly described below.
In the ImQMD model, the nucleon is represented by a Gaussian wave packet, which reads
$ \phi_{i}({{r}}) = \frac{1}{(2\pi\sigma_{r}^{2})^{3/4}} \exp\left[-\frac{({{r}}-{{r}}_{i})^{2}}{4\sigma_{r}^{2}} +\frac{i}{\hbar}{{r}}\cdot{{p}}_{i}\right], $

(1) where
$ {{r}}_{i} $ ,$ {{p}}_{i} $ is the center of the wave packet of the ith nucleon in the coordinate and momentum spaces, and$ \sigma_{r} $ is the width of the wave packet in the coordinate space. Considering the size of the system,$ \sigma_r $ can be expressed as$ \sigma_{r} = \sigma_{0}A^{1/3}+\sigma_{1}, $

(2) where A is the nucleon number, and
$ \sigma_{0} $ and$ \sigma_{1} $ are the parameters obtained by fitting the properties of many$ \beta $ stable nuclei. Using the Wigner transform of the nucleon wave function and summing over all nucleons, one can get the phase space distribution function of the nuclear system, which reads$ \begin{split} f({{r}},{{p}}) =& \sum \limits_{i}^{A} f_{i}({{r}},{{p}}) = \sum\limits_{i = 1}^{A}\frac{1}{(\pi\hbar)^3} \exp\left[-\frac{({{r}}-{{r}}_i)^2}{2\sigma_{r}^{2}}\right] \\&\times \exp\left[-\frac{({{p}}-{{p}}_i)^2}{2\sigma_{p}^{2}}\right], \end{split}$

(3) where
$ \sigma_{p} $ is the width of the wave packet in the momentum space, which satisfies the minimum uncertainty relation$ \sigma_r \cdot \sigma_p = {\hbar \over 2} $ . The center of the wave packet for each nucleon evolves following the Hamilton canonical equations,$ \dot{{{r}}}_{i} = \frac{\partial H}{\partial{{p}}_{i}},\; \; \; \; \; \; \dot{{{p}}}_{i} = -\frac{\partial H}{\partial{{r}}_{i}}. $

(4) The Hamiltonian, including the kinetic energy, Coulomb energy and nuclear local potential energy, reads
$ H = T+U_{\rm{Coul}}+U_{\rm{loc}}. $

(5) Each term of the Hamiltonian is written as
$ T = \sum\limits_{i}^{A}\frac{p_i^2}{2m}, $

(6) $ U_{\rm Coul} = \frac{1}{2}\int\rho_p({ r})\frac{e^2}{|{{ r}-{{ r}'}}|}\rho_p({ r}'){\rm d}{ r}{\rm d}{{ r}'}, $

(7) $ U_{\rm loc} = \int V_{\rm loc}{\rm d}{ r}, $

(8) where
$ V_{\rm{loc}} $ is the Skyrme potential energy density functional without the spin-orbit term, which can be expressed as$\begin{split} V_{\rm{loc}} =& \frac{\alpha}{2}\frac{\rho^{2}}{\rho_{0}}+ \frac{\beta}{\gamma+1}\frac{\rho^{\gamma+1}}{\rho_{0}^{\gamma}}+ \frac{g_{\rm sur}}{2}(\bigtriangledown\rho)^{2} \\& +g_{\tau}\frac{\rho^{\eta+1}}{\rho_{0}^{\eta}}+ \frac{C_{\rm s}}{2\rho_{0}}[\rho^{2}-\kappa_{\rm s}(\bigtriangledown\rho)^{2}]\delta^{2}. \end{split}$

(9) Here,
$ \rho $ and$ \rho_0 $ are the nucleon density and the saturation density, respectively, and$ \delta = (\rho_n -\rho_p)/\rho $ is the isospin asymmetry. The parameter set used in Eq. (9), called IQ3a, which has been successfully applied to the study of fusion reactions [27, 28], is listed in Table 1.$\alpha $ /MeV

$\beta $ /MeV

$\gamma $ 

$g_{\rm{sur}}$ /(

${\rm MeV\ fm}^{2}$ )

$ g_{\tau }$ /MeV

$\eta $ 

$C_{\rm{s}}$ /MeV

$\kappa _{\rm{s}}$ /

${\rm fm}^{2}$ 

$\rho_{0}$ /

${\rm fm}^{-3}$ 

$\sigma_0$ /fm

$\sigma_1$ /fm

$-207$ 

138 7/6 16.5 14.0 5/3 34.0 0.4 0.165 0.02 0.94 Table 1. The model parameter set IQ3a.
-
The first step to simulate the reaction with the ImQMD model is the initialization of the projectile and target nuclei. As is well known, a good initial nucleus is very important for QMD calculations, especially for reactions at low energies. A typical method for preparing the initial nucleus in QMD is the following: first, the position of each nucleon is determined by Monte Carlo sampling according to the size of the nucleus. Second, based on the density distribution
$ \rho({{r}}) = \int{f({{r}},{{p}})}{\rm d}{ p} = \frac{1}{(2\pi\sigma_{r}^{2})^{3/2}} \sum\limits_{i = 1}^{A}\exp\left[-\frac{({{r}}-{{r}}_{i})^{2}}{2\sigma_{r}^{2}}\right], $

(10) the local Fermi momentum is obtained in the local density approximation
$ P_F = ( {3\pi^2 \over 2}\rho)^{1/3}-\Delta p_F $ , where$ \Delta P_F $ is the contribution of the width of the wave packet and is determined by the binding energy. The initial momentum of each nucleon is sampled randomly in the range 0-$ P_F $ . To check the stability of the prepared nucleus, the prepared nuclear system is evolved on its own for a short or long period of time, depending on the type of reaction. Only those nuclei with satisfactory properties, such as the root-mean-square (rms) radius, binding energy, and time evolution, and for which there is no spurious particle emission for a sufficiently long time, are selected as "good initial nuclei".In order to describe the halo-nucleus, which is a weakly bound nucleus, with such a semi-classical model, special treatment in ImQMD must be used. The halo-nucleus is usually considered as a system with a loose valence nucleon moving around a tight core. Taking the proton-halo nucleus
$^{17}{\rm{F}}^*$ , its rms radius is$ 2.71\pm0.18 $ fm, and the rms radius of the valence proton is 5.33 fm [29-31]. Hence,$^{17}{\rm{F}}^*$ is considered as a system with a 16O core and a valence proton. To save CPU time in ImQMD calculations, the initial distance between the projectile and the target is not infinity, as in the real situation, but has a finite value of 40 fm. There is a very large probability for 17F to be excited by the heavy target nucleus at such a short distance. Therefore, we sample the$^{17}{\rm{F}}^*$ nuclei in the initial state. In the ImQMD model, the$ ^{16}{\rm O} $ core is prepared by the standard method. The experimental value of the rms radius of the neutron in the first excited state of$^{17}{\rm{F}}^*$ is 2.478 fm, meaning that the$ ^{16}{\rm O} $ core of$^{17}{\rm{F}}^*$ is smaller than the ordinary$ ^{16}{\rm O} $ nucleus, which has an rms radius of 2.710 fm. As a result, the radius and the wave packet width calculated using the ordinary 16O, are both multiplied by 0.9 in the sampling of the 16O core. In order to set the valence proton with reasonable properties, two factors are considered. One is the position of the valence proton, which should be far away from the core in order to form the halo. The other is the wave packet width of the valence proton, which reflects the range of the nuclear force and has a clear effect on nucleus surface diffusion [32]. It is obvious that Eq. (2) for the wave packet width of the ordinary nucleon is not suitable for the loosely bound valence proton. The extreme surface diffusion structure of 17F*, i.e. its halo, requires a relatively large width of the valence proton wave packet. By optimally fitting the experimental data for 17F*, the initial distance between the valence proton and the center-of-mass of the core is set to$ R = R_{\rm p}+1.6 $ fm, where$ R_{\rm p} $ is the radius of the proton distribution of the 16O core [33, 34]. The wave packet width and the initial momentum is set to$ \sqrt{2} $ fm and 25 MeV/c, respectively.The ImQMD model is a semiclassical model with the Skyrme
$ \delta $ -type interaction. It is quite difficult for a weakly bound nucleus, such as a halo nucleus, to be stable for a long time in this kind of model. The valence proton will finally fall into the core due to its strong attraction. To maintain a stable halo, the so-called "sphere-shell constraint" is introduced into the model. If the valence proton is too close to the core and tends to move towards the core, or if it is too far and tends to move back to the core, its momentum direction is changed randomly by elastic scattering with the nucleon nearby.Modifications of the method of preparing the initial nucleus and the introduction of the sphere-shell constraint, allow to get
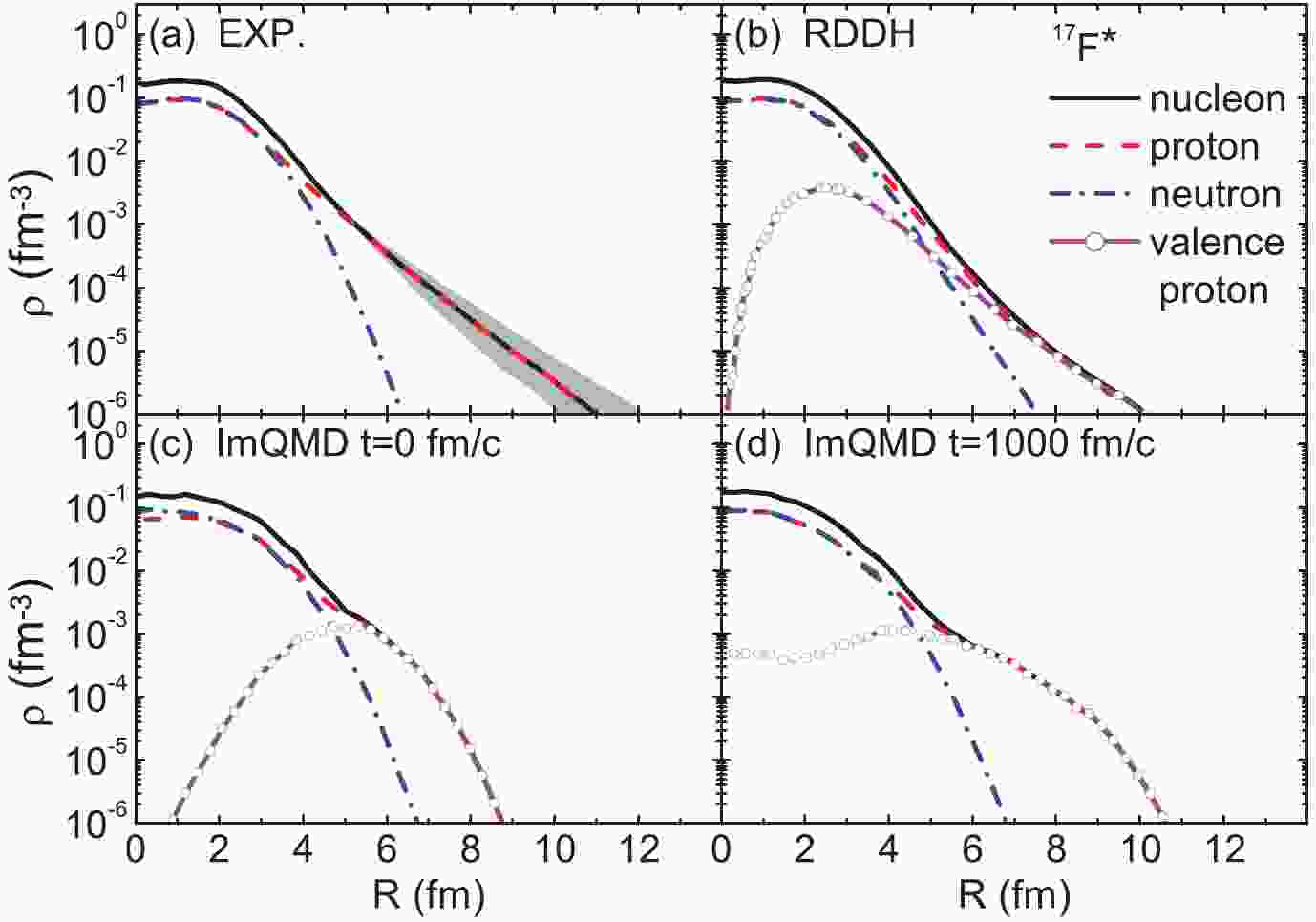
$^{17}{\rm{F}}^*$ which has sufficiently good properties and is stable enough. In Fig. 1, the density distributions of the nucleons, protons, neutrons and the valence protons in$^{17}{\rm{F}}^*$ at 0 and 1000 fm/c are shown. The experimental data [30] and the relativistic density dependent Hartree theory (RDDH) [30, 35], are also shown for comparison. It can be seen that although the halo of the initial$^{17}{\rm{F}}^*$ is small, the distributions given by the ImQMD model are reasonable. As the nucleons self-adjust with time, the ImQMD model gives quite a good distribution, close to the experimental results and the RDDH theory.
Figure 1. (color online) Density distributions of the nucleons, protons, neutrons and the valence protons in
$^{17}{\rm{F}}^*$ from experiments (a), relativistic density dependent Hartree(RDDH) theory (b), and the ImQMD calculations (c) (d).In Fig. 2 , we show the time evolution of the deviation of the binding energy and of the rms radii of nucleons, protons, and neutrons in 17F*. The binding energy and the rms radii remain stable, with small fluctuations, for a sufficiently long time.
-
To obtain a stable halo structure, the sphere-shell constraint, which is not a self-consistent treatment, was introduced into the model. The halo structure is easily destroyed when the halo nucleus enters the field of the target nucleus. Hence, the sphere-shell constraint should be switched off at a proper moment in the simulation, and the valence proton can then move self-consistently in the field of the system. To select a proper switch-off time, the time evolution of the ratio between the force on the valence proton from 208Pb and from the core 16O was investigated, shown in Fig. 3 by the solid curve. For comparison, we also calculated the ratio between the Coulomb force on the valence proton from 208Pb and from the core 16O, shown by the dashed curve, assuming that the projectile and target are two charged points located at their individual center-of-mass, and that they move with their initial velocities. One can see that at the early stage, the effect from the target is quite weak and that the Coulomb force dominates. The influence of the target becomes rapidly stronger from 150 fm/c, and the effect of the nuclear force becomes obvious. Therefore, the sphere-shell constraint is switched off at 150 fm/c in the following calculations.
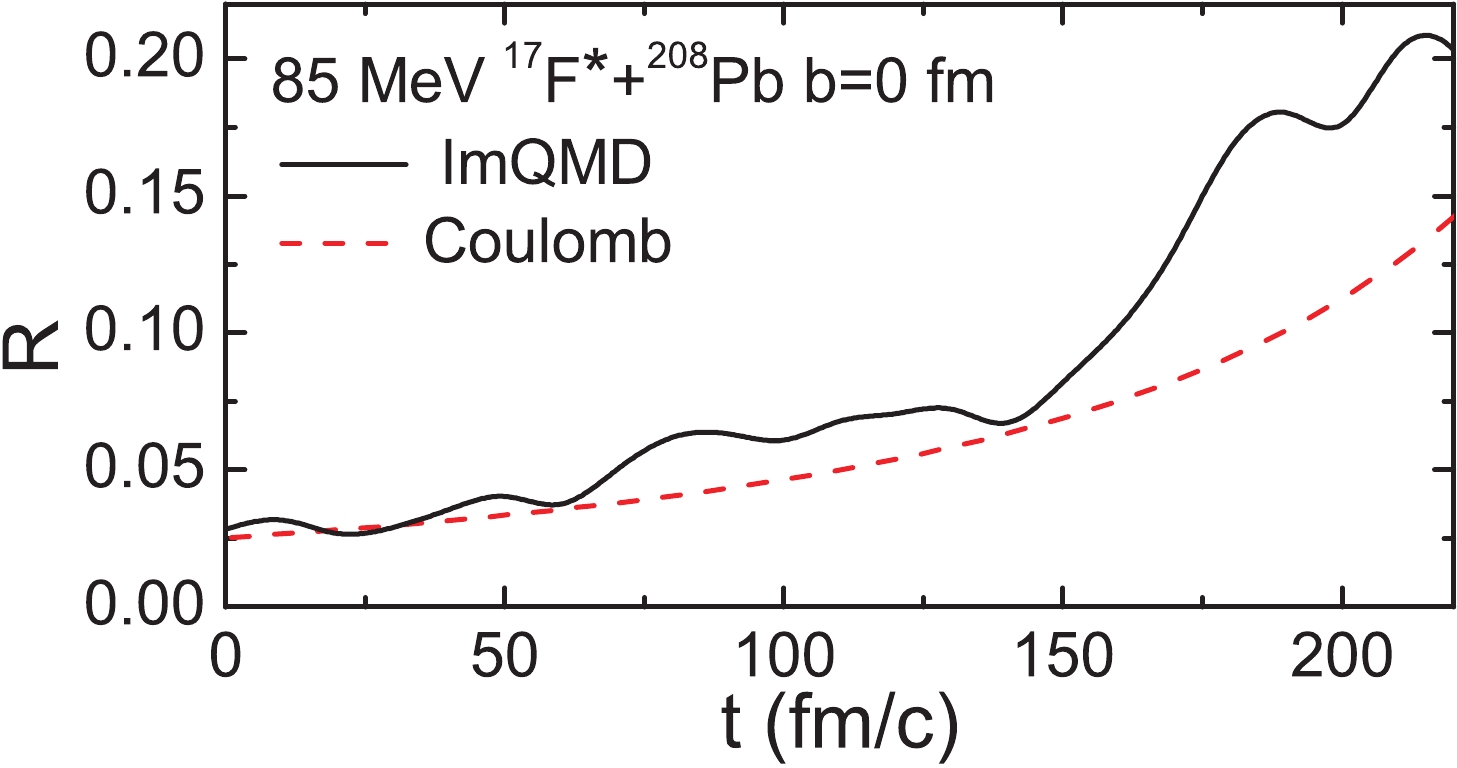
Figure 3. (color online) Time evolution of the ratio between the force on the valence proton from 208Pb and from the core of 17F*.
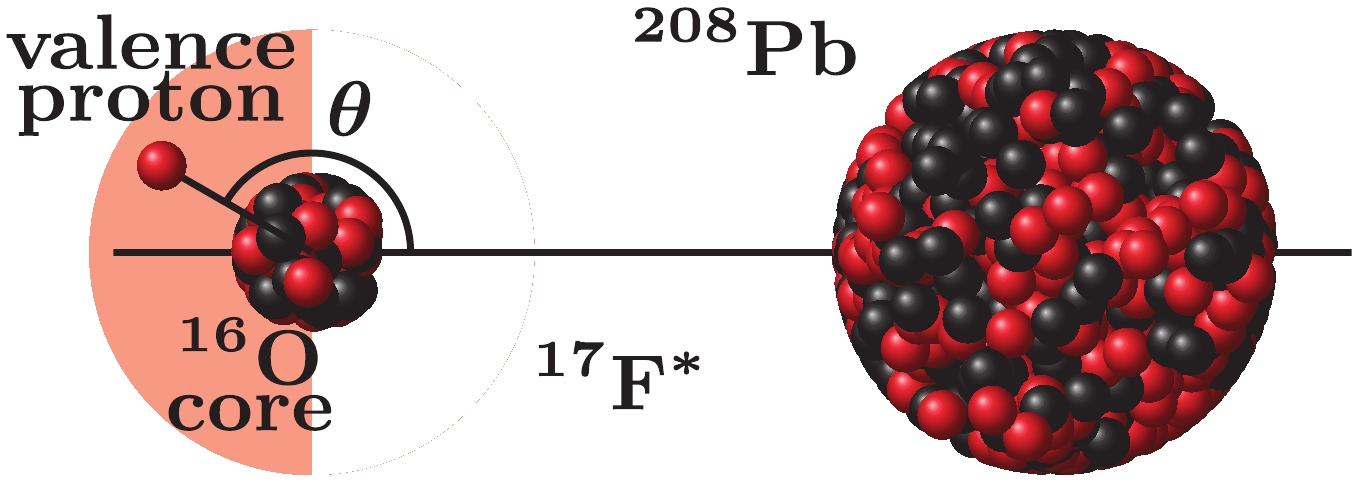
We first checked the shielding of the valence proton by the 16O core in the reaction 17F*+208Pb at the energy
$ E_{\rm c.m.} = $ 85 MeV and$ b = 0 $ fm. As illustrated in Fig. 4, the angle$ \theta $ between the position vector of the valence proton and the center-of-mass of 16O could be a criterion for shielding. If$ \cos \theta <0 $ , the valence proton is considered to be shielded by the 16O core.The proportion of valence protons which are shielded is defined as the ratio
$ N_{\rm{s}}/N_{\rm{t}} $ , which is shown in Fig. 5.$ N_{\rm{s}} $ and$ N_{\rm{t}} $ are the number of events in which the valence proton is shielded during the reaction and the total number of events, respectively. The case for the individual$^{17}{\rm{F}}^*$ is also shown for reference. One can see that for the individual 17F*, the valence proton is distributed uniformly in the halo. In the early stage of the 17F*+208Pb reaction, when the projectile is far from the target, there is no obvious shielding effect. As the projectile moves closer to the target, the shielded proportion increases. From 500 fm/c, there are more events with the valence proton shielded by the core. After 700 fm/c, when 16O is absorbed by the target to form the compound nucleus or is elastically scattered, the shielding effect is disturbed.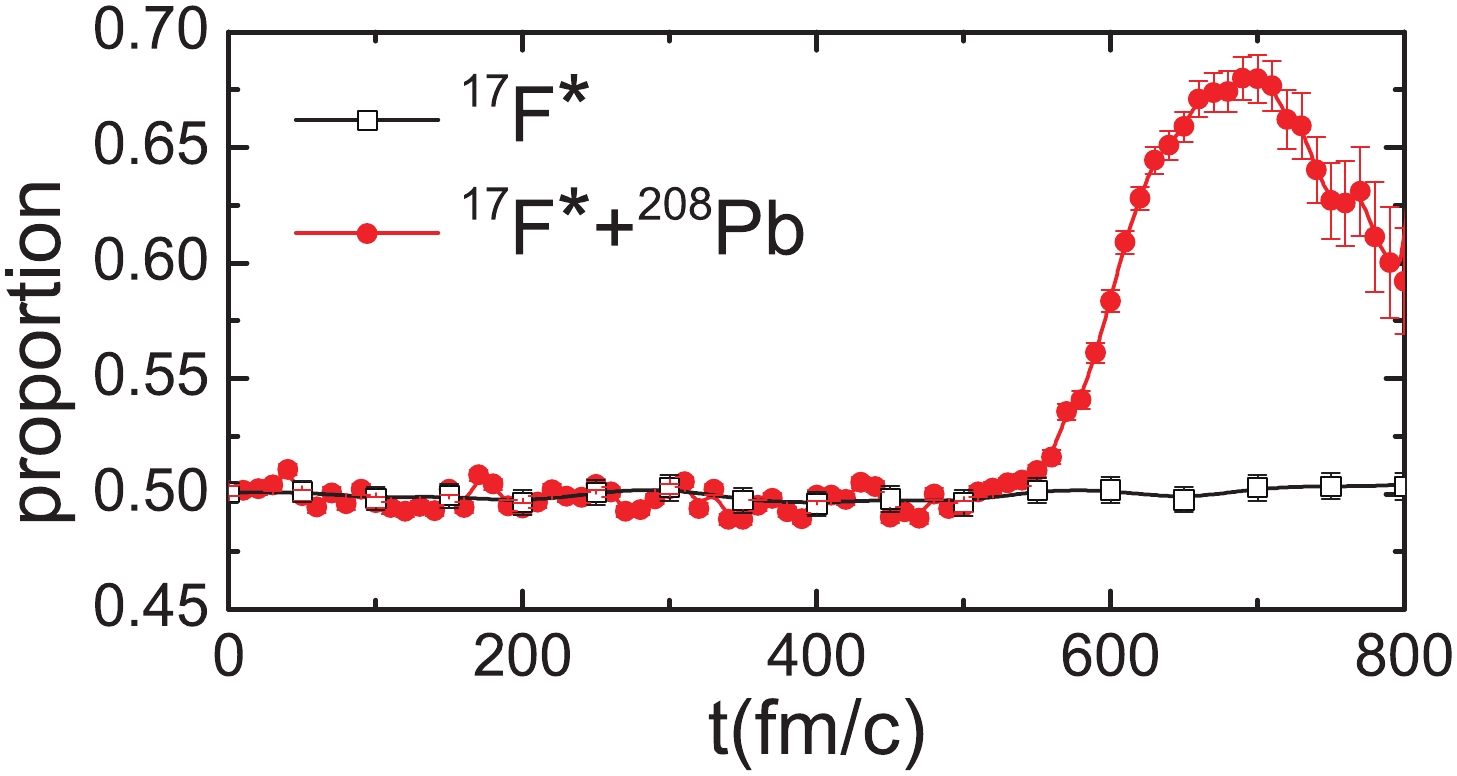
Figure 5. (color online) Time evolution of the proportion of events in which the valence proton is shielded by the core.
By generating a large number of events at each incident energy
$ E_{\rm c.m.} $ and each impact parameter b and counting the number of fusion events, the fusion probability$ g_{\rm fus} $ ($ E_{\rm c.m.}, b $ ) can be obtained and the corresponding fusion cross-section calculated as$ \begin{split} \sigma_{\rm fus}(E_{\rm c.m.}) =& 2\pi \int g_{\rm fus}(E_{\rm c.m.}, b) b {\rm d}b \\ \simeq & 2\pi \sum g_{\rm fus}(E_{\rm c.m.}, b_i) b_i \Delta b , \end{split}$

(11) where
$ \Delta b $ = 1 fm. An event is counted as a fusion (capture) event if the center-to-center distance between the two nuclei is smaller than the nuclear radius of the compound nuclei. Here, the quasi-fission probability for the considered reaction systems is neglected [27].In Fig. 6, we show the fusion excitation functions of 17F*+208Pb and 16O+208Pb calculated by the ImQMD model. The experimental data are shown for comparison. The results for 16O+208Pb are shifted in energy by the factor 9/8 (the ratio of charges of F and O). The fusion cross-section around and above the Coulomb barrier is reproduced quite well. Below the Coulomb barrier, the fusion cross-section of 17F*+208Pb is slightly higher than of 16O+208Pb, but both overestimate the experimental data, which is probably due to the fact that many quantum effects, such as the shell effect and the tunneling effect, cannot be simulated in the present semi-classical ImQMD model. Although the present version of ImQMD cannot describe fusion reactions at very low energies, it is still reasonable to investigate the shielding effect by comparing the fusion cross-sections of 17F*+208Pb and 16O+208Pb. From Fig. 6, one can see that the fusion cross-sections of 17F*+208Pb and 16O+208Pb are close to each other, with no enhancement above or below the Coulomb barrier.
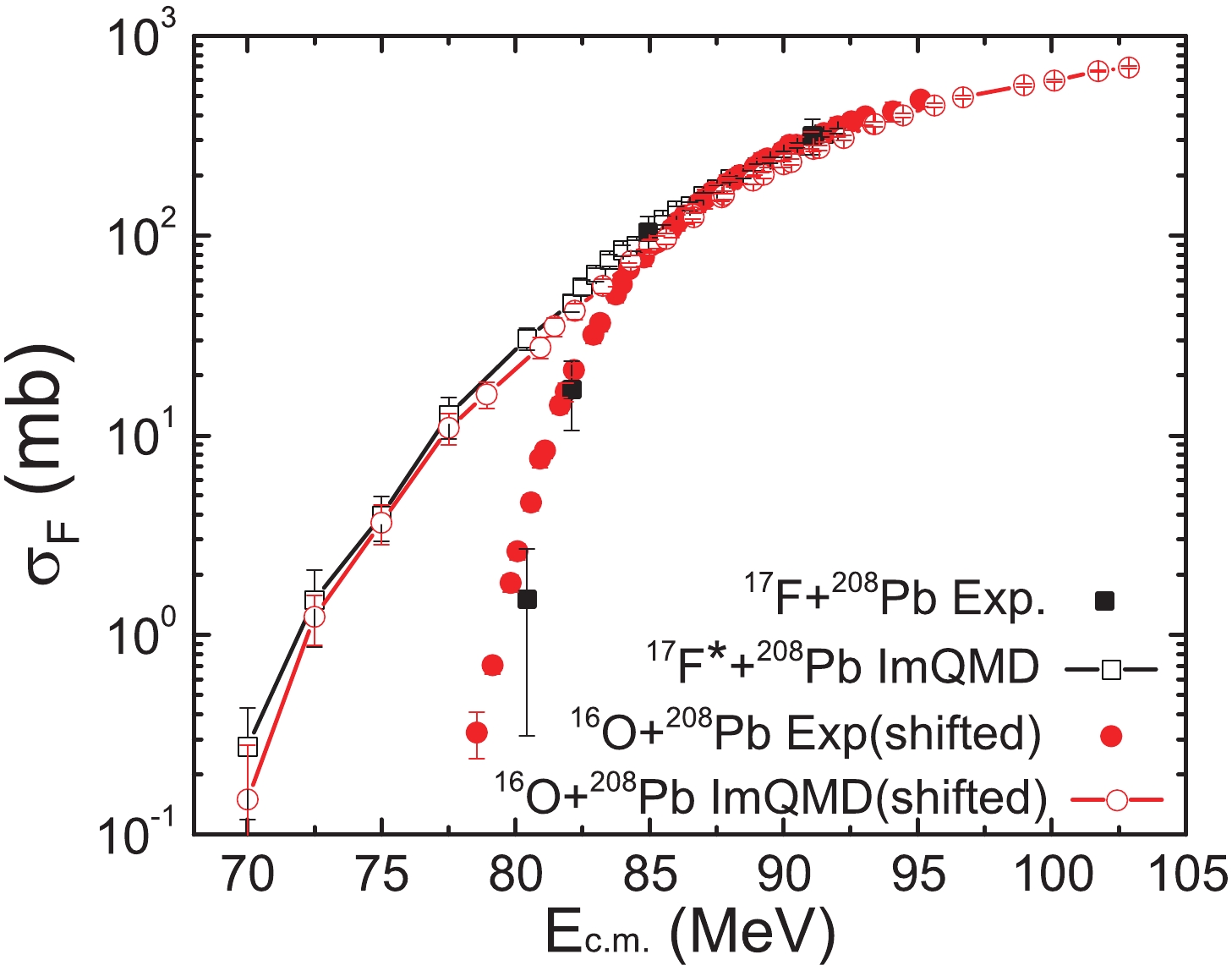
Figure 6. (color online) Fusion excitation functions of 17F*+208Pb and 16O+208Pb calculated by the ImQMD model and compared to the experimental data. The results of 16O+208Pb are shifted in energy by the factor 9/8.
As is well known, the classical fusion cross-section is
$ \sigma_{\rm fus} = \pi R_{\rm eff}^2 $ , where$ R_{\rm eff} $ is the effective interaction radius which is directly related to the radii of the projectile and target. The system with a larger projectile and target nuclei will have a larger fusion cross-section. The rms radii of 17F and 16O are similar in the ground state. Once 17F is excited by 208Pb to a proton-halo nucleus with a larger radius, the fusion cross-section should be enhanced compared to 16O+208Pb. However, the enhancement is not observed in experiments. Taking the shielding effect into consideration, the valence proton is pushed toward or even behind the 16O core, and the thickness of the halo facing the target becomes smaller. This effect reduces the effective interaction radius and changes the effective interaction potential between the projectile and target nuclei. In Fig. 7, we show the effective interaction potential for the fusion reaction 17F*+208Pb at the energy$ E_{\rm c.m.} = $ 85 MeV and$ b = 0 $ fm, for the valence proton distributed uniformly, and for two extreme cases, the valence proton located in front of the 16O core ($ \theta = 0 $ ) and totally shielded ($ \theta = \pi $ ). One can see that before the projectile touches the target, the effective interaction potential is larger for$ \theta = 0 $ than for$ \theta = \pi $ , while after the projectile touches the target, the effective interaction potential is larger for$ \theta = \pi $ than for$ \theta = 0 $ . The competition between effective shielding and no shielding of the valence proton may be one of the possible reasons why the enhancement of the fusion cross-section is not observed. The result for 16O+208Pb at the energy$ E_{\rm c.m.} = $ 76 MeV and$ b = 0 $ fm is also shown in the figure, shifted in energy by the factor 9/8. The similarity of the effective interaction potentials of 17F*+208Pb and 16O+208Pb indicates that these two systems essentially have the same behavior, as indicated by the fusion excitation functions. -
Experiments have shown that the fusion cross-section of a proton-halo nucleus with a heavy target nucleus is not enhanced compared to the regular nucleus as was expected. A reasonable hypothesis is that the valence proton moves away from the target nucleus and is shielded by the core of the halo nucleus, which is the so-called shielding effect. In this work, this effect was verified in fusion reactions by using the ImQMD model. To obtain satisfactory initial proton-halo nucleus, a special sampling method of the initial nucleus was introduced in ImQMD. The shielding phenomenon was verified in the reaction 17F*+208Pb by tracing the relative position of the valence proton with respect to the core 16O in microscopic dynamics simulations. The probability of shielding of the valence proton increases when the projectile and target get closer together. It is found that before the projectile and target touch, the shielding effect reduces the effective interaction potential, while after they touch, the shielding effect increases the effective interaction potential. The fact that the effective interaction potentials for 17F+208Pb and 16O+208Pb are similar leads to similar fusion excitation functions of these two systems.
The authors thank Dr. Ning Wang for careful reading of the manuscript and valuable discussions.
Shielding effects in fusion reactions with a proton-halo nucleus
- Received Date: 2019-11-21
- Accepted Date: 2020-01-18
- Available Online: 2020-05-01
Abstract: To explain the experimental observation that the fusion cross-section of a proton-halo nucleus with a heavy target nucleus is not enhanced as expected, the shielding hypothesis was proposed, where the proton-halo nucleus is polarized and the valence proton shielded by the core. In the frame of the improved quantum molecular dynamics model, the fusion reaction 17F on 208Pb around the Coulomb barrier is simulated. The existence of the shielding effect is verified by the microscopic dynamics simulations. Its influence on the effective interaction potential is also investigated.





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF















 DownLoad:
DownLoad: