-
The large-scale structure of the universe (
$ > 1 {\rm Mpc}$ ) can be successfully described by the ΛCDM (Lambda cold dark matter) cosmological model. However, the observation of small-scale structures [1], such as the Milky Way and dwarf galaxies, seems to be in tension with the simulations of collisionless cold dark matter. This dilemma is usually presented as three issues: missing satellites [2-4], cusp vs core [5, 6] and too big to fail [7, 8]. A possible common solution of these issues is a cold dark matter with nontrivial self-interactions, that is a self-interacting dark matter (SIDM). Such SIDM can be realized in the DM models with a light mediator [9–11].Note that the SIDM models with a light force carrier (
$ \lesssim $ 100 MeV) can have a non-trivial velocity-dependent scattering cross-section which may explain the small-scale structure problems [12–15]. These models have been widely studied in the past few years. However, if the interaction between the DM particles and the target nuclei is induced by a light mediator, the scattering cross-section will be enhanced at low momentum transfer [16–19]. The current DM direct detection experiments have reached impressive sensitivities and are approaching the irreducible background neutrino floor. The null results produced strong constraints for various DM models. In particular, the PandaX-II collaboration has recently searched for the nuclear recoil signals of DM with light mediators [20]. Using the data collected in 2016 and 2017, PandaX-II set strong upper limits on the DM-nucleon cross-section for different mediator masses. On the other hand, if the light mediator mainly decays into the SM particles, such as$ \gamma\gamma $ and$ e^+e^- $ , the injection of sizable energy densities into the visible sector thermal bath after the light elements are generated would spoil the success of the big bang nucleosynthesis (BBN). This requirement produces a lower limit on the couplings between the mediator and the SM particles and could lead to a tension with direct detection experiments.In this work, we investigate the implication of the PandaX limits on the parameter space of the singlet extension of MSSM with or without
$ Z_3 $ symmetry [21–38]. Such models can alleviate the little hierarchy problem by pushing up the SM-like Higgs boson mass to 125 GeV without heavy top-squarks [39], and the model with$ Z_3 $ symmetry, the so-called NMSSM, can solve the notorious$ \mu $ problem in MSSM [40] by dynamically generating the SUSY-preserving$ \mu $ term. For a rather small$ \lambda $ (the coupling between the singlet and doublet Higgs fields), the singlet sector can be almost decoupled from the electroweak symmetry breaking sector and becomes a hidden sector of the model. The singlino-like DM will dominantly annihilate into the SM particles through the s channel light singlet-like Higgs bosons to produce the correct DM relic density [41–45]. Note that the presence of a light mediator can lead to long-range attractive forces between DM particles and enhance the DM annihilation cross-section via the Sommerfeld effect at low temperature [46]. The previous study [46] showed that the general singlet extension of MSSM without$ Z_3 $ symmetry (hereafter called GNMSSM) can have a sufficient DM self-interaction to solve the small-scale structure problem, while NMSSM can give a light DM with the correct relic density but without sufficient self-interaction to solve the small-scale structure problem.The paper is organized as follows. In Sec. 2, we focus on NMSSM and examine the limits on the parameter space of the light dark matter with a light mediator. In Sec. 3, we first show the parameter space of GNMSSM which can solve the small-scale structure problem, and then check the PandaX limits on the parameter space. The conclusions are given in Sec. 4.
-
Since NMSSM with
$ Z_3 $ symmetry can give a light DM with the correct relic density but without sufficient self-interaction to solve the small-scale structure problem [46], in the following we do not require that it solves the small-scale structure problem.In NMSSM, the superpotential of the doublet and singlet Higgs fields is given by
$ \lambda\hat{S}\hat{H_u}\cdot\hat{H_d}+\frac{\kappa}{3}\hat{S}^3 \, , $

(1) where
$ \hat{H}_u $ and$ \hat{H}_d $ are the Higgs doublet superfields,$ \hat{S} $ is the singlet superfield, and$ \lambda $ and$ \kappa $ are dimensionless couplings. The$ Z_3 $ symmetry is imposed on the superpotential to forbid terms other than the singlet. The corresponding soft SUSY breaking terms are given by$ A_\lambda \lambda S H_u\cdot H_d+\frac{A_\kappa}{3}\kappa S^3 +{\rm h.c.}\, . $

(2) $ A_\lambda $ and$ A_\kappa $ are the soft breaking trilinear masses. After spontaneous symmetry breaking, we can get three CP-even Higgs bosons (denoted as$ h_{1,2,3} $ ), two CP-odd Higgs bosons (denoted as$ a_{1,2} $ ) and a pair of charged Higgs bosons. From Eq. (1), we can also see that the interactions between the singlet and the SM sector are controlled by the parameter$ \lambda $ . The constraints on the singlet-like Higgs bosons and singlino-like DM from the collider and dark matter detection experiments can be satisfied if$ \lambda $ is sufficiently small. Since the spectrum of NMSSM has been widely studied in literature [23-31], we concentrate here on the dark singlet sector.In NMSSM, the dark matter can have three components: gaugino, higgsino and singlino. Assuming the gaugino unification relation
$ M_2/M_1\approx 2 $ , there are three dark matter scenarios: the bino-dominant dark matter, higgsino-dominant dark matter and singlino-dominant dark matter. Detailed discussion of these scenarios can be found in Refs. [47–50]. The first two scenarios are almost the same as MSSM, only the singlet-dominant dark matter scenario, which is realized in Peccei-Quinnn limit, can give the correct relic density in the light mass region (less than 10 GeV) of the dark matter parameter space. [51] Besides explaining the observations of CoGeNT and DAMA/ LIBRA [52], this parameter space is also consistent with the experimental constraints from LEP, Tevatron,$ \Upsilon $ and flavor physics. This scenario is also called the Dark Light Higgs (DLH) scenario. The direct detection limits give stringent constraints on the couplings between dark matter and the SM particles, resulting in a small$ \lambda $ , which leads to a$ \sigma_\chi/m_\chi $ too small to explain the small cosmological scale simulations [46].In the following, we check the PandaX constraints on the DLH scenario, which can give light singlino-like DM and light singlet-like Higgs bosons as the mediators. The light singlino-like DM particles mainly annihilate to SM particles via the resonance of the singlet-like pseudo-scalar
$ a_1 $ . DM scatters off the nucleon with the light CP-even singlet-like Higgs boson$ h_1 $ as the mediator, and the scattering cross-section is subject to the PandaX limits. Following Ref. [51], in order to approach the PQ symmetry limit, we define the parameter$ \varepsilon\equiv {\lambda \mu}/{m_Z} $ ,$\varepsilon' \equiv{A_\lambda}/ $ $ {\mu\tan\beta} -1 $ . We perform a random scan over the parameter space:$ 2\leqslant \tan\beta\leqslant 50 $ ,$ 0.05\leqslant\lambda\leqslant 0.2 $ ,$0.0005\leqslant $ $ \kappa\leqslant 0.05 $ ,$ -0.1\leqslant\varepsilon \leqslant 0.1 $ ,$ \varepsilon \sim \varepsilon' $ ,$ |A_\kappa|<500\;{\rm GeV} $ , and$ |\mu|<1000\;{\rm GeV} $ . The sfermion sector parameters are set at 6 TeV so that we can get a 125 GeV SM Higgs boson easily. Note that we did not use the machine learning scan [53, 54] because the parameter space is not too large. In our scan we use the package NMSSMTools [55] to obtain the parameter space with a singlet-like Higgs boson$ h_1 $ lighter than 2 GeV. We require the DM thermal relic density in the 2$ \sigma $ range of the Planck value [56], and the mass of the SM-like Higgs$ h_2 $ in the range of 123-127 GeV.The results are shown in Fig. 1, in which we set the mass of
$ h_1 $ to 1 MeV, 10 MeV and 1 GeV. In each panel, we show the detection limits of PandaX corresponding to the mediator masses. For comparison, we also show the detection limits of CDEX-10 [57], CDMSlite Run 2 SI [58], CRESST-III [59], LUX Combined [60], and XENON1T [61]. We can see that the SI cross-section is enhanced greatly as the mass of the light mediator decreases. This can be understood from the cross-section [51]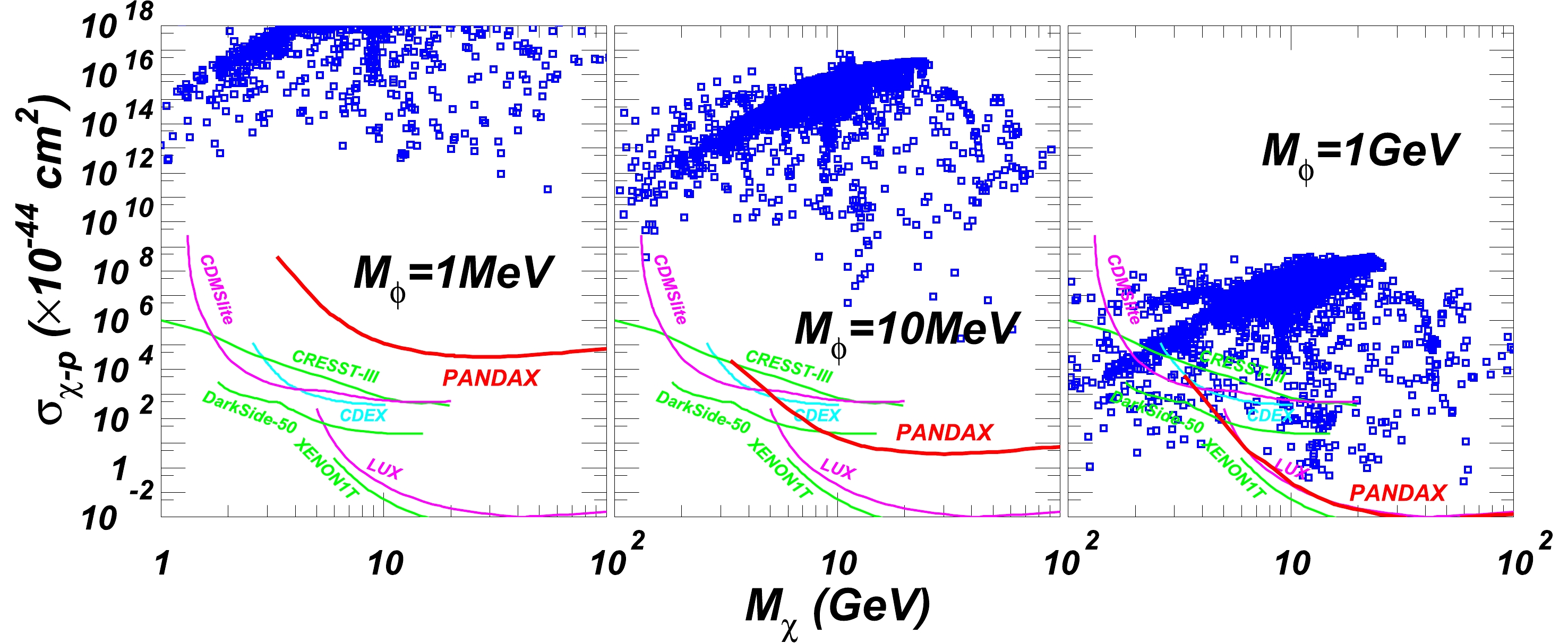
Figure 1. (color online) Scatter plots showing the spin-independent cross-section for dark matter scattering off the nucleon with different mediator masses in the DLH scenario of NMSSM with
$ Z_3 $ symmetry. The light mediator$ \phi $ is the lightest CP-even Higgs boson$ h_1 $ which is singlet dominant. All points satisfy the constraints of the DM relic density with the SM like Higgs boson$ h_2 $ in the range of 123-127 GeV. The detection limits of PandaX [20] on the light mediator are shown by the red lines. The detection limits of CDEX-10 [57], CDMSlite Run 2 SI [58], CRESST-III [59], LUX Combined [60], and XENON1T [61] are also shown.$ {\sigma _{{\rm{SI}}}} \approx \frac{{{{\left[ {\left( {\dfrac{\varepsilon }{{0.04}}} \right) + 0.46\left( {\dfrac{\lambda }{{0.1}}} \right)\left( {\dfrac{{\;v}}{\mu }} \right)} \right]}^2}{{\left( {\dfrac{{{y_{{h_1}\chi \chi }}}}{{0.003}}} \right)}^2}{{10}^{ - 40}}{\rm{c}}{{\rm{m}}^2}}}{{{{\left( {\;\dfrac{{{m_{{h_1}}}}}{{1~{\rm{GeV}}}}} \right)}^4}}}, $

(3) where
$ y_{h_1\chi\chi} $ is the coupling strength of the Higgs boson$ h_1 $ and dark matter. This relation implies that the cross-section increases as the fourth power of the inverse mass of the light mediator. If the mass of the mediator is of the order of MeV, a large number of samples exceed the detection limits, and thus the DLH scenario of NMSSM is severely constrained by PandaX and other experiments (except for the region outside the detection sensitivity, where the dark matter is lighter than 3.5 GeV for the PandaX results). Such stringent constraints are due to the correlation between the dark matter relic density and the dark matter-nucleon scattering cross-section: a proper relic density implies a non-negligible coupling$ a_1f\bar f $ so that the parameter$ \lambda $ can not be too small. The SI cross-section is then greatly enhanced by the mediator mass, as shown in the equation above.From Fig. 1, we see that the dark matter with a mediator of the order of MeV is also excluded by other direct detection experiments. Only a small parameter space with a mediator mass around GeV and a dark matter mass around several GeV is compatible with all direct detection limits.
-
We turn now to the dark Higgs sector of the general singlet extension of MSSM (GNMSSM) for an explanation of the small cosmological structure problem. In GNMSSM, the
$ Z_3 $ discrete symmetry is not imposed and the$ \mu $ term can exist in the superpotential together with the$ \lambda S H_u \cdot H_d $ term (several other terms of the singlet superfield can also exist in the superpotential). Consequently, the dark Higgs sector (including a singlino-dominant dark matter) can be easily realized in GNMSSM without the need for the condition$ \kappa \ll \lambda $ . This means that a singlino-dominant dark matter can be obtained with a sizable$ \kappa $ , and in this case the coupling$ h_1\chi\chi $ in the dark matter self-interaction, which is proportional to$ \kappa $ , can be large. The renormalizable superpotential for the singlet is given by$ W = \eta \widehat{S} +\frac{1}{2}\, \mu_s \widehat{S}^2 + \frac{1}{3} \kappa \widehat{S}^3 \ , $

(4) and the soft SUSY breaking terms take the form
$ -{\cal L}_{\rm{soft}} = m_s^2 | S |^2 + \left( C_\eta \eta S +\frac{1}{2}\, B_s \mu_s S^2 + \frac{1}{3}\, \kappa A_\kappa\ S^3 + {\rm{h.c.}} \right). $

(5) where
$ \eta, \mu_s, m_s^2, C_\eta, B_s $ are additional input parameters in GNMSSM besides those for NMSSM. After the scalar component gets a VEV, we can also get one CP-even Higgs h and one CP-odd Higgs a. The details of the spectrum and the Feynman rules can be found in [46]. Although this singlet sector is a dark sector, it can give the correct relic density of dark matter and a proper self-interaction for the solution of the small-scale structure problem.A detailed study of the solutions of the small cosmological scale anomalies in GNMSSM was presented in [46]. Here, we just show the parameter space in Fig. 2. We can see that part of the parameter space can satisfy simultaneously the requirements for solving the small scale anomalies at the dwarf, the Milky Way and galaxy cluster scales. In this part of the parameter space, the masses of dark matter and its mediator are quite restrained.
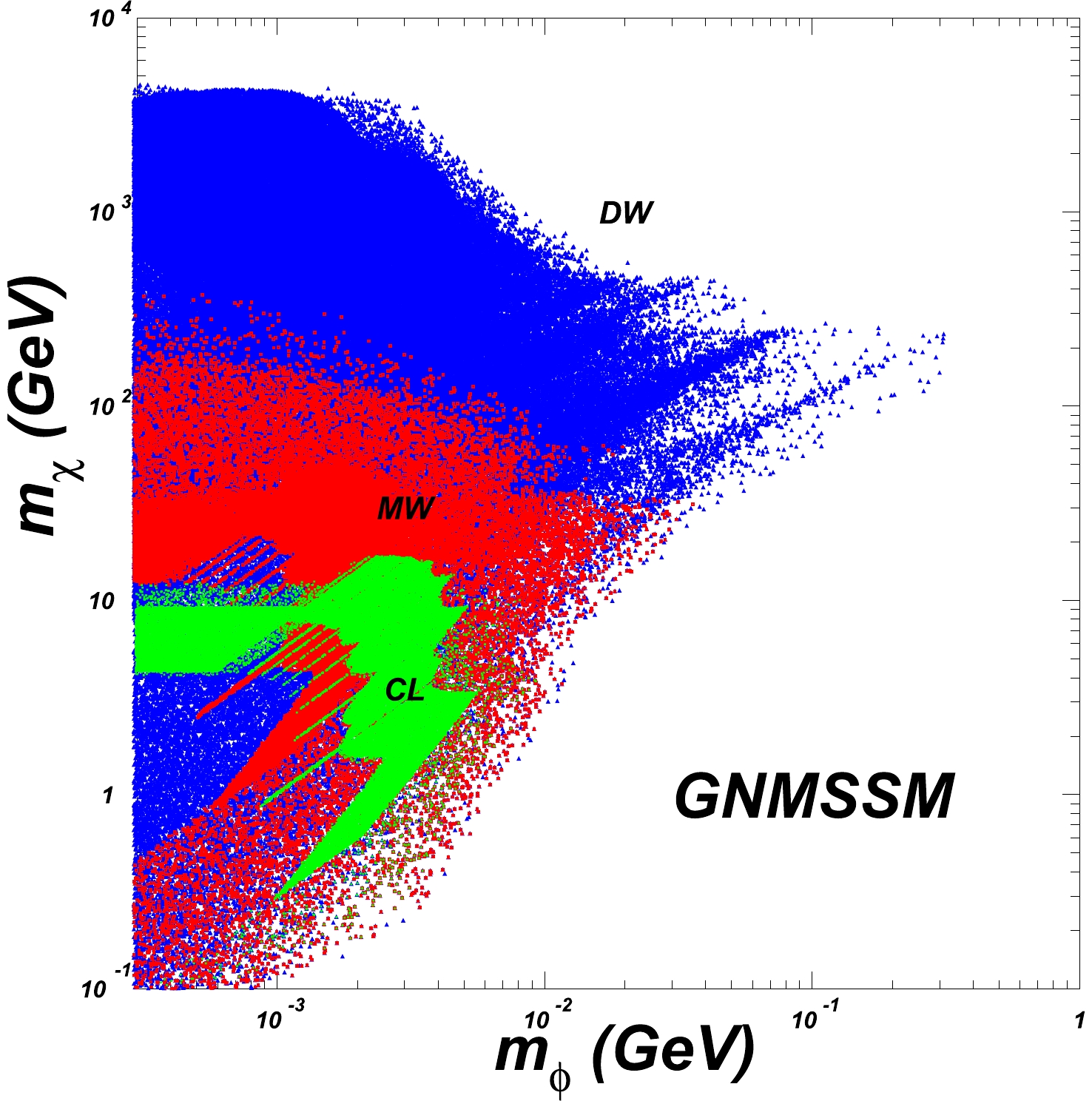
Figure 2. (color online) Parameter space of GNMSSM satisfying the DM relic density, taken from [46]. The blue points are simulations for the dwarf scale, and the red and green points are simulations for the Milky Way with a characteristic velocity of 200 km/s and 1000 km/s, respectively.
In the case of a connection between the electroweak sector and the dark light singlet sector, the mixing angles between the singlet and doublet fields depend on the off-diagonal elements divided by the difference between the diagonal elements. For example, the mixing between
$ H_d $ and S is proportional to$ \theta_{ds}\sim \frac{{\cal M}_{S,13}^2}{\left|{\cal M}_{S,11}^2 -{\cal M}_{S,33}^2\right|} \sim \lambda \times \left({{\rm{electro-weak}}\; {\rm{variables}}}\right), $

(6) where
$ {\cal M} $ is the$ 3\times 3 $ Higgs mass matrix [21–38]. If the mediator$ h_1 $ is around several MeV, the input electroweak parameters give$ {\cal M}_{S,13}^2 $ and$ {\cal M}_{S,33}^2 $ much smaller than the electroweak scale. Thus, we can define the following two angles for the mixing between the singlet and doublet fields$ \theta_{ds} = \lambda \alpha_d \cos\beta,\quad \theta_{us} = \lambda \alpha_u \sin\beta, $

(7) where
$ \alpha_d $ and$ \alpha_u $ are two new parameters for the mixing angles. With such a parametrization, we can calculate the corresponding cross-section. For example, the coupling strength between the singlet and the up-type quarks is given by$ Y_q \lambda \alpha_u\sin\beta, $

(8) and for the down-type quarks, it is given by
$ Y_q \lambda \alpha_d\cos\beta. $

(9) With the parametrizations above, we can calculate the spin-independent DM-nucleon scattering cross-section [62, 63]:
$ \sigma^{SI} = \frac{4 m_r^2}{\pi} f_N^2, $

(10) where
$ m_r = \frac{m_\chi m_N}{ m_\chi + m_N } $

(11) is the reduced dark matter mass, and
$ f_N $ is the effective coupling of DM with the nucleon. Since the singlet sector is much lighter than the electroweak scale, we can neglect the contribution of squarks and of the supersymmetric loop. Thus,$ f_N $ can be written as$ \frac{{{f_N}}}{{{m_N}}} = \sum\limits_{q = u,d,s} {\frac{{f_{Tq}^N}}{{{m_q}}}} {f_q} + \frac{2}{{27}}f_{TG}^N\sum\limits_{q = c,b,t} {\frac{{f_q^H}}{{{m_q}}}} ,$

(12) where
$ f_{Tq}^N $ denotes the fraction of the nucleon mass$ m_N $ that is due to the light quark q, and$ f_{TG}^N = \frac{2}{27}( 1 - f_{Tu}^N - f_{Td}^N - f_{Ts}^N ) $

(13) is the heavy quark contribution to
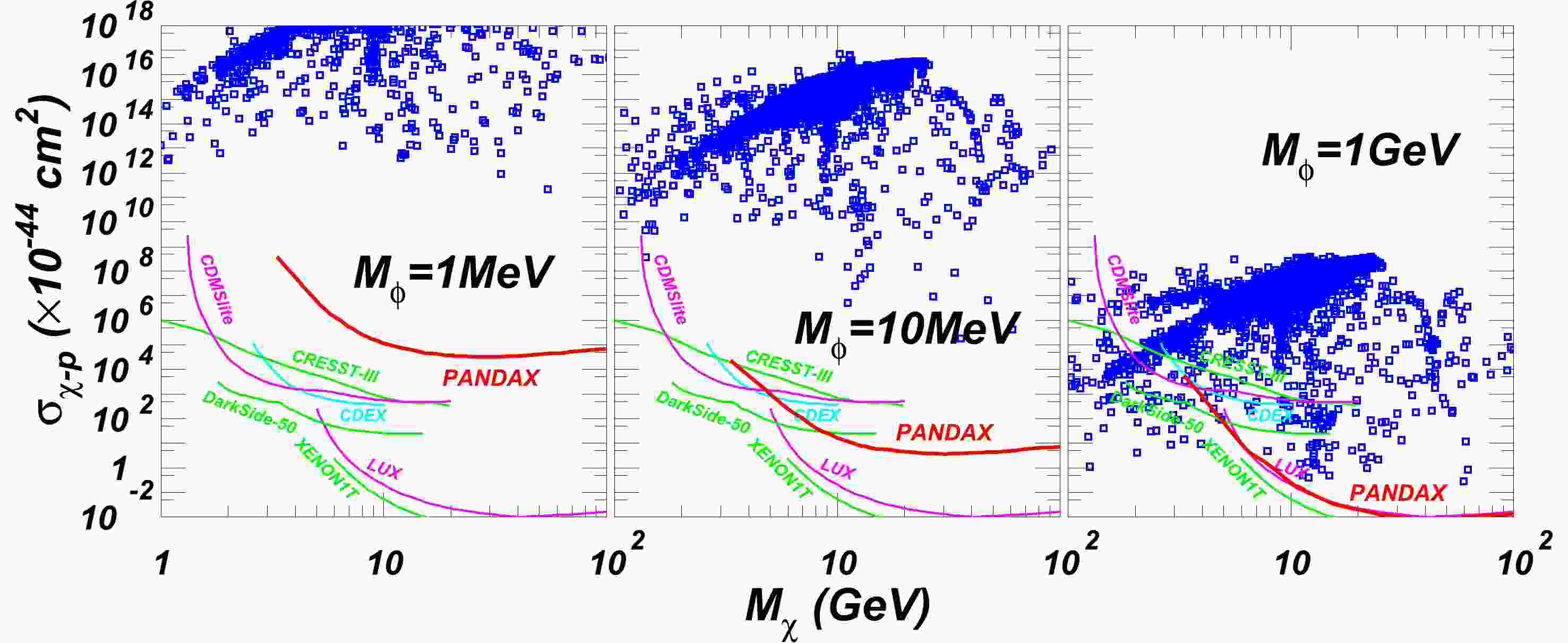
$ m_N $ , which is induced via gluon exchange. A detailed calculation of parameters$ f_{Tq} $ can be found in [62]. In our calculation, we use$ \sigma_{\pi N} = 64 $ MeV and$ \sigma_0 = 35 $ MeV to get the values of$ f_{Tq}^N $ .Figure 3 shows the PandaX constraints on the GNMSSM parameter space in which all points satisfy the DM relic density and the scattering cross-section for small cosmological structures. Here, we set
$ \tan\beta = 2 $ and$ \alpha_u = \alpha_d = 0.001 $ as an example. We also checked the results for different values of$ \tan\beta $ and$ \alpha_u, \alpha_d $ , and found that they are similar. We can see that when$ \lambda $ is less than$ 10^{-5} $ , the dark sector can survive safely. As$ \lambda $ increases, the constraints become stringent.
Figure 3. (color online) Parameter space of GNMSSM satisfying the dark matter relic density and solving the small cosmological structure problem, displayed in the plane of dark matter mass versus mediator mass. The red points are excluded by the PandaX limits.
Note that with the light singlet Higgs bosons and singlino-like DM, the SM-like Higgs has additional decay channels
$ h_{\rm SM}\to h_1 h_1 $ ,$ h_{\rm SM}\to a_1 a_1 $ and$ h_{\rm SM}\to \chi \chi $ . The first two channels are exotic decays and the last one is an invisible decay. Their branching ratios are determined by the coupling parameters$ \lambda $ and$ \kappa $ . These decays can give interesting phenomenology [64].We also note that the singlet CP-even Higgs boson can not be too dark and that it must decay before the start of the Big Bang Nucleosynthesis (BBN) (
$ \sim 1 $ sec), so that its decay products do not affect BBN. However, if the singlet Higgs couples strongly to the SM particles then the direct detection rate of dark matter would be greatly enhanced by the light mediator. One way to solve this obstacle is to add a right-handed neutrino to GNMSSM [65]. Another point is that the light dark matter in our analysis is around the GeV scale. For sub-GeV ultra light dark matter, the dark matter particles could be boosted by the cosmic rays and the detection sensitivity could be considerably enhanced [66-69]. Also, for a heavy dark matter above TeV, the DAMPE collaboration recently reported the cosmic$ e^+ + e^- $ flux excess [70] which seems to favor a TeV scale leptophilic dark matter [71-73]. -
Using the newest limits on the zero-momentum dark matter-nucleon cross-section given by the PandaX collaboration, we checked their implication on the supersymmetric dark models, especially on the parameter space of the light dark matter and its mediator. We first analyzed the spectrum of NMSSM with
$ Z_3 $ symmetry and GNMSSM without$ Z_3 $ symmetry, and found a way to parametrize the connection between the singlet sector and the SM sector. We then examined the parameter space of the two models using the limits of PandaX and other direct detection experiments. We arrived to the following conclusions:• The PandaX limits exclude the case of dark matter above 3.5 GeV. The remaining space is excluded by the requirement of self-interaction, which gives stringent constraints on the mass of the mediator, due to the correlation between the dark matter relic density and the dark matter nucleon cross-section. Thus, NMSSM with
$ Z_3 $ symmetry is excluded by PandaX and the requirement that it should solve the small structure problem.• It is easy to realize self-interaction in GNMSSM, in which the singlet sector can be a dark sector. In the dark sector, the correct relic density and a proper self-interaction can be obtained. Compared to the simple one-mediator model, the supersymmetric model can have a larger parameter space, and the mass of dark matter and its mediator can be relaxed.
• With our parametrization of the connection between the singlet sector and the SM sector, we found that PandaX results can give a constraint on the coupling strength between the two sectors. Only a very small
$ \lambda $ is allowed.In summary, the PandaX limits are a very good test for the self-interaction dark matter models. Additional precision measurements of the light mediator and dark matter, together with self-interaction physics studies, are needed for further advances.
PandaX limits on the light dark matter with a light mediator in the singlet extension of MSSM
- Received Date: 2020-01-21
- Available Online: 2020-06-01
Abstract: Using the latest PandaX limits on the light dark matter (DM) with a light mediator, we check their implication on the parameter space of the general singlet extension of MSSM (without Z3 symmetry), which can have a sufficient DM self-interaction to solve the small-scale structure problem. We find that the PandaX limits can tightly constrain the parameter space, depending on the coupling λ between the singlet and doublet Higgs fields. For the singlet extension of MSSM with Z3 symmetry, the so-called NMSSM, we also demonstrate the PandaX constraints on its parameter space, which gives a light DM with the correct relic density but without sufficient self-interaction to solve the small-scale structure problem. We find that in NMSSM, the GeV dark matter with a sub-GeV mediator is tightly constrained.






 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF
















 DownLoad:
DownLoad: