-
The process of accretion of matter onto a black hole is a hot topic in theoretical physics. This process is mainly responsible for the formation of Quasi-periodic oscillations and emission of gravitational waves. The accretion phenomena plays a role in the formation of astronomical objects, such as stars, planets, galaxies, quasars, etc. The most significant phenomena in the universe, including gamma-ray bursts, X-ray binaries, active glactic nuclei, tidal disruption events mainly occur because of the accretion of gas onto black holes. An accretion disk forms when gaseous matter rotates and accumulates around the black hole. In the past century, it was realized that gravity powers most luminous objects in the universe through accretion. Our main aim is to study accretion onto black holes, known to be the strongest gravitating objects responsible for emitting high-energy fluxes from astronomical objects. Moreover, black holes have an event horizons that act as borders that are traversed by fluids that enter them.
Research on the accretion process in Newtonian gravity began in 1952 by Bondi [1] and later on by Michel [2] in 1972 in the context of general relativity. The difference between the Bondi and the relativistic accretion models is that the former allows stellar winds or ejecta
$ (v>0) $ from the stellar surface, which is the opposite of the accretion$ (v<0) $ , whereas the same process of ejecta does not directly apply to black holes, since black holes are not composed of gas and have no gaseous surface. Any kind of ejection, such as jets from the black holes, occurs only in the presence of charged plasma floating around the black hole under the effect of strong magnetic fields. We have disregarded these considerations in this study. According to Michel's approach, the discussion of critical points in relation to accretion is provided in Ref. [3]. A detail study of the accretion process onto spherically symmetric black holes in general relativity and other theories of gravities can be found in [4-17], and the references therein. Babichev et. al. [18, 19] have shown that phantom accretion onto a black hole decreases its mass. In contrast, if the black hole solutions are considered in the Friedmann-Robertson-Walker universe, it is observed that the black hole accretion may increase the mass of gravitational objects [20].Black holes that exist as a fundamental part of our universe provide the most intriguing solutions to Einstein's field equations. Einstein's general theory of relativity explains very well the exterior and horizons of black holes, whereas it fails to describe the physics of the deep central region, which is is strongly affected by quantum effects. In this context, Weinberg [21] proposed a theory of asymptotic safe gravity (ASG), which embeds gravity in the quantum field theory framework. As its central property, the effective average action satisfies a formally exact functional renormalization group equation. Presently, it has accumulated substantial evidence that the gravitational renormalization group flow possesses a nontrivial fixed point, which could provide the ultra-violet completion of gravity at trans-Planckian energies. The concept of an asymptotically safe gravitational theory has been applied to theories of gravity (such as the Einstein gravity [22] and
$ f(R) $ gravity [23]), cosmology [24, 25], and black holes [26]. In this study, we investigate the relativistic accretion problem in the context of an infra-red limit of an asymptotically safe scenario. We follow the Hamiltonian dynamical formalism in the phase space$ (r,n) $ , where r is the areal radius, and n is the particle density of the fluid. We assume that the improved version of the Schwarzschild black hole is surrounded by a special type of perfect fluid, namely the isothermal type. We then investigate the matter particle dynamics by deriving solutions at critical points. The solutions we obtain for the accretion problem describe the Michel flow and the critical point through which it passes. Hence, to discuss critical flows, we investigate the effect of ASG on the accretion process, which is the main purpose of this work.By expressing accreting matter by the isothermal equation of state, we provide a complete description of the fluid flow behavior near the black hole.
The remainder of this paper is structured as follows: in Section 2 we provide a brief review of field equations to define the static, spherically symmetric black hole metric in ASG within the infra-red limit. We also present some fundamental equations related to accretion to explain a steady-state, radial perfect fluid flow by specifying our assumptions on the fluid equation of state and presenting our results. In Section 3, governing equations for improved Schwarzschild black hole accretion and conservation laws are presented. We then evalute our results at sonic points by considering the isothermal fluid and analyze its flow by choosing suitable values of the state parameter. We also formulate fluid equations as two-dimensional Hamiltonian dynamical systems on the phase space
$ (r,n) $ by assuming that the Hamiltonian depends on the accretion rate in Section 4. We perform a detailed analysis by providing numerical plots for the phase flow of isothermal fluid on modified Schwarzschild background and discuss the effect of coupling parameter. Conclusions are presented in the last section. -
Recently, Cai and Easson [27] found black hole solution in ASG scenario considering higher derivative terms in their investigation. They discuss how the inclusion of quantum corrections modifies the Schwarzschild black hole solution. According to Ref. [27], the geometry of a static spherically symmetric Schwarzschild (anti)-de Sitter black hole in ASG in the IR limit is given by
$\begin{split}{\rm d}{s^2} =& - \left(1 - \frac{{2GM}}{r} + \frac{{2{G^2}M\xi }}{{{r^3}}}\right){\rm d}{t^2}\\& + {\left(1 - \frac{{2GM}}{r} + \frac{{2{G^2}M\xi }}{{{r^3}}}\right)^{ - 1}}{\rm d}{r^2} + {r^2}{\rm d}{\theta ^2} + {r^2}\sin^2 \theta {\rm d}{\phi ^2},\end{split}$

(1) where G and M denotes the gravitational constant and mass of the black hole, respectively. The outer horizon, which is merely the null hypersurface of the modified version Eq. (1) of the Schwarzschild black hole taking quantum corrections into account can be written in approximate form as
$\begin{split}{r_h} = \frac{{2GM}}{3}\left[1 - 2\cosh \left(\frac{1}{3}{\cosh ^{ - 1}}\beta \right)\right],\end{split}$

(2) where
$ \beta = \frac{27\xi}{8GM^2}-1 $ .$ r_h $ given in Eq. (2) is the only real root of$ 1-\frac{2GM}{r}+\frac{2G^2M\xi}{r^3} = 0 $ , which can be calculated using the Weierstrass Polynomial$ r = z+\frac{2GM}{3} $ . By expanding Eq. (2) to the leading order of$ \xi $ , we can approximate it as [27]${r_{IR}} \simeq 2GM - \frac{\xi }{{2M}}.$

(3) If we insert the running coupling parameter
$ \xi = 0 $ into Eqs. (1) and (3), we can retrieve the classical Schwrazschild black hole metric and the corresponding event horizon, respectively. Here, we review some important equations describing the steady state Michel flow on a Schwrazschild (anti) de Sitter black hole in ASG. Further detail and generalization to an even more general static spherically symmetric black hole background is provided in Refs. [16, 28, 29].As described in the introduction, we model the flow of a perfect relativistic fluid, neglecting the effects related to viscosity or heat transport, and further assume that the fluid's energy density is sufficiently small, such that its self-gravity can be neglected. We assume that the flow of the perfect fluid onto the improved Schwrazschild black hole is steady-state flowing in the radial direction, described by the particle density n (also called baryonic number density), pressure p, and the energy density e by an observer moving along the fluid four-velocity
$ u^\alpha u_\alpha = -1 $ . To investigate the accretion process onto high derivative black hole, as described above, we need to review the fundamental equations of accretion for the underlying geometry of the spacetime.The accretion dynamics of a perfect matter is governed by the following conservation laws
${\nabla _\alpha }{J^\alpha } = 0,$

(4) ${\nabla _\alpha }{T^{\alpha \beta }} = 0,$

(5) where
$ J^{\alpha} = nu^{\alpha} $ is the particle current density, and$ T^{\alpha \beta} = nhu^{\alpha}u^{\beta}+pg^{\alpha\beta} $ is the stress energy tensor.$ \nabla $ refers to the covariant derivative with respect to the spacetime metric. Here and onwards, we assume that h denotes the enthalpy per particle defined by$ h = \frac{p+e}{n} $ [30] where$ h = h(n) $ is a function of the particle density n only. In the spherical symmetry stationary case, the above Eqs. (4) and (5) reduce to${r^2}nu = {\rm const} = K,$

(6) $h{\left(1 - \frac{{2GM}}{r} + \frac{{2{G^2}M\xi }}{{{r^3}}} + {u^2}\right)^{1/2}} = {\rm const} = L,$

(7) which expresses the conservation of particle and energy flux through a sphere of constant areal radius r. We stress here that to analyze the perfect fluid flow, Eqs. (6) and (7) will play the main role in the background of improved Schawrzschild black hole, as they will be helpful to convert the present problem into a Hamiltonian dynamical system.
-
Physically, a critical point
$ r = r_c $ describes the transition of the flow's radial velocity measured by the static observer from subsonic to supersonic. If we consider the barotropic fluid for which there is a constant pressure throughout (i.e.$ h = h(n) $ ), then its equation of state can be expressed as [30]$\frac{{{\rm d}h}}{h} = {a^2}\frac{{{\rm d}n}}{n},$

(8) where a denotes the local speed of sound.
Differentiating Eqs. (6) and (7) with respect to r, we obtain
$\begin{aligned}\frac{{{\rm d}u}}{{{\rm d}r}} = \frac{{2u}}{r}\;.\;\frac{{c_s^2\left(1 - \dfrac{{2GM}}{r} + \dfrac{{2{G^2}M\xi }}{{{r^3}}} + {u^2}\right) - \dfrac{{GM}}{{2r}} - \dfrac{{3{G^2}M\xi }}{{2{r^3}}}}}{{{u^2} - c_s^2\left(1 - \dfrac{{2GM}}{r} + \dfrac{{2{G^2}M\xi }}{{{r^3}}} + {u^2}\right)}},\end{aligned}$

(9) where
$ c_{s}^{2} = k $ is the square of the speed of sound, and k is a state parameter for the isothermal equation of state (EoS)$ p = ke $ . The above Eq. (9) can be converted into a two-dimensional autonomous Hamiltonian dynamical system:${f_1}(r,u) = \frac{{{\rm d}r}}{{{\rm d}l}} = r\left\{ {u^2} - c_s^2\left(1 - \frac{{2GM}}{r} + \frac{{2{G^2}M\xi }}{{{r^3}}} + {u^2}\right)\right\} ,$

(10) $ \begin{split} {f_2}(r,u) =& \frac{{{\rm d}u}}{{{\rm d}l}} = 2u\left\{ c_s^2\left(1 - \frac{{2GM}}{r} + \frac{{2{G^2}M\xi }}{{{r^3}}} + {u^2}\right)\right. \\&- \left.\frac{{GM}}{{2r}} - \frac{{3{G^2}M\xi }}{{2{r^3}}}\right\} ,\end{split}$

(11) with an arbitrary parameter l, whose phase portraits consist of r versus s, indicate solutions of Eqs. (6) and (7). To obtain critical points, we set the right hand side of Eqs. (10) and (11) equal to zero, which after solving yield
$u_c^2 = \frac{{GM}}{{2{r_c}}} + \frac{{3{G^2}M\xi }}{{2r_c^3}},$

(12) $c_s^2 = \frac{{\dfrac{{GM}}{{2{r_c}}} + \dfrac{{3{G^2}M\xi }}{{2r_c^3}}}}{{1 - \dfrac{{3GM}}{{2r_c^2}} + \dfrac{{7{G^2}M\xi }}{{2r_c^3}}}}.$

(13) By using Eqs. (12) and (13), we can obtain the sonic points, which refer to the critical points of the dynamical systems of Eqs. (10) and (11). From Eqs. (6) and (7), after performing several intermediate steps, one can arrive at very important equation, which is helpful to describe the critical flows of the fluid under consideration
$\sqrt {1 - \frac{{2GM}}{r} + \frac{{2{G^2}M\xi }}{{{r^3}}} + {{(u)}^2}} = A{r^{2k}}{u^k}.$

(14) For the standard equation of state, the critical point
$ (r_{c},u_{c}) $ is the saddle point, and thus the solution must pass through it. The detailed discussion of this critical point will be presented in the forthcoming sections. -
To analyze the perfect matter flow, it is useful to employ a dynamical system whose orbits consist of graphs of solutions of the system Eqs. (6) and (7). Such a system can be defined conveniently in terms of r and v (where v is the three-velocity of the fluid). We formulate our problem in terms of the Hamiltonian dynamical system on the phase space
$ (r,n) $ , where the vector field describing the dynamics is the Hamiltonian vector field associated with the function$ F(r,n) $ . By assumption, F is constant along the trajectories of phase flow and thus meets the definition of level curves. The main usefulness of converting the accretion problem into a dynamical system is that the fluid behavior near the critical point of F can be analyzed using standard tools of the theory of dynamical systems [31, 32].In Eqs. (6) and (7), we used two integrals of motion K and L. We stress here that any one of them , or any combination of these integrals can be utilized as Hamiltonian system for the fluid flow. Assuming that the Hamiltonian system is a function of two variables r and v and square of the left hand side of Eq. (7), i.e.,
${\cal H}(r,v) = {h^2}\left(1 - \frac{{2GM}}{r} + \frac{{2{G^2}M\xi }}{{{r^3}}} + {u^2}\right),$

(15) which in a more general form can be written as
${\cal H}(r,v) = \frac{{{h^2}(r,v)(f(r) + {u^2})}}{{1 - {v^2}}}.$

(16) We introduce the following pair of a dynamical system
$\dot r = {{\cal H}_{,v}}\;\;\;\;\;\;\;\dot v = - {{\cal H}_{,r}}\;,$

(17) where the dots denote the
$ \tilde{t} $ derivatives, and the$ {\cal H}_{,r} $ and$ {\cal H}_{,v} $ denote partial derivatives of$ {\cal H} $ with respect to r and v, respectively. By solving the right-hand-side of the above equation and subsequently equating to zero results in the desired critical point$ (r_c, u_c) $ , we obtain the following fundamental pair of equations$v_c^2 = a_c^2,\;\;\;\;\;\;{r_c}(1 - a_c^2){f_c},{r_c} = 4{f_c}a_c^2,$

(18) which are thus helpful to derive the following important equations
$(a_c^2 = k)\left[\frac{1}{4}{r_c}{f_{c,{r_c}}} + {f_ * }\right] = \left[\frac{1}{4}{r_c}{f_{c,{r_c}}}\right],$

(19) ${(u_c^r)^2} = \frac{1}{4}{r_c}{f_{c,{r_c}}}.$

(20) We point out here that the above pair of Eqs. (19) and (20) is equivalent to Eqs. (12) and (13) and provide the critical radius and critical speed of the moving fluid. Thus, we shall use these equations to locate the position of the critical point
$ (r_\ast, u_\ast^r) $ . We know that one of the most appreciative tools for energy conservation is the Hamiltonian. In the current study, the precise form of the general Hamiltonian Eq. (15) in terms of the variables r and v for the isothermal test fluid can be expressed as${\cal H}(r,v) = \frac{{{{\left(1 - \dfrac{{2GM}}{r} + \dfrac{{2{G^2}M\xi }}{{{r^3}}}\right)}^{1 - k}}}}{{{{(1 - {v^2})}^{1 - k}}{v^{2k}}{r^{4k}}}},$

(21) where k is the state parameter, and v is the ordinary three-dimensional speed of the fluid, which is given by
${v^2} = \frac{{{u^2}}}{{1 - \dfrac{{2GM}}{r} + \dfrac{{2{G^2}M\xi }}{{{r^3}}} + {u^2}}}.$

(22) We remark here that u is well-defined everywhere, and the velocity v is defined outside the horizon. Complete derivation of these fundamental equations is provided in Refs. [33-35].
-
Expressing accreting matter by the isothermal equation of state (EoS)
$ P = ke $ (where k is a state parameter), we present a complete description of the fluid flow behavior near the black hole.1) The fluid at which isotropic pressure and the energy density of the fluid particles is same is referred to as ultra stiff fluid. In this case, the state parameter has the value
$ k = 1 $ . This value of the state parameter reduces Eq. (19) to$ f_c = 0 $ , which yields$ r_c = r_h $ , i.e., the critical radius and event horizon coincide. In this case, the Hamiltonian in Eq. (21) reduces to${\cal H} = \frac{1}{{{v^2}{r^4}}}.$

(23) As above, the Hamiltonian shows constant of motion i.e.,
$ {\cal H} = {\cal H}_0 $ , and we observe that v behaves as$ \frac{1}{r} $ . To explain the physical behavior of the fluid flow, we need to sketch contour plots of$ {\cal H}(r_c,v_c) = {\cal H}_c $ . From the Fig. 1 on top left, the black curve indicates the solution for$ {\cal H} = {\cal H}_{c} $ , the red curve indicates the solution for$ {\cal H} = {\cal H}_{c}+0.005 $ , the green curve shows the solution for$ {\cal H} = {\cal H}_{c}+0.02999 $ , the magenta curve depicts$ {\cal H} = $ $ {\cal H}_{c}-0.0001 $ , and the blue curve depicts$ {\cal H} = {\cal H}_{c}-0.09 $ . In summary, we observe that for$ v>0 $ , there is particle emission, and$ v<0 $ depicts the fluid accretion.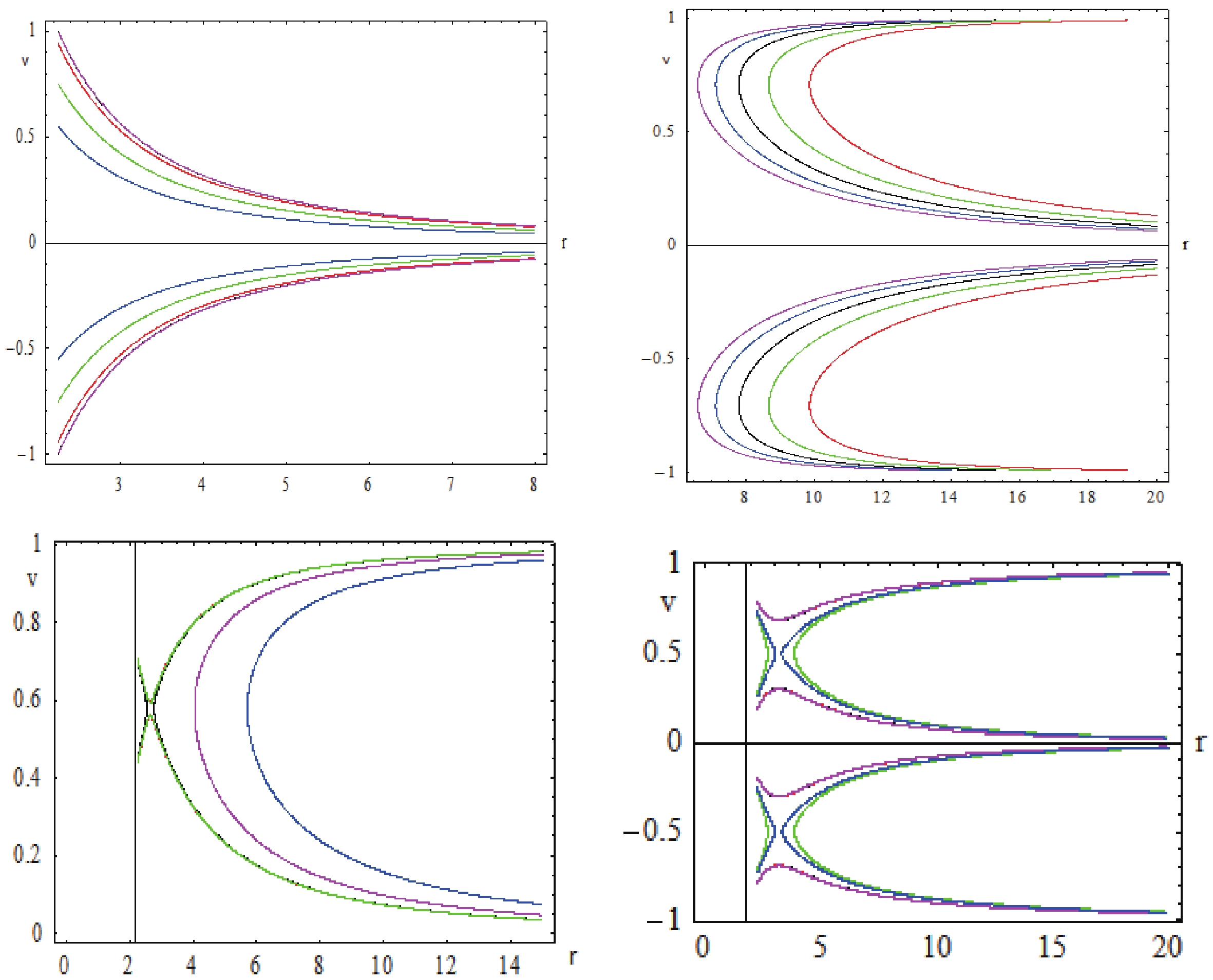
Figure 1. (color online) Contour plot of Hamiltonian
$ {\cal H}(21) $ for ultra-stiff$ (k = 1) $ , ultra-relativistic$ (k = 1/2) $ , radiation$ (k = 1/3) $ and sub-relativistic$ (k = 1/4) $ fluids where$ M = 1, G, \xi = 0.5 $ . The black curve in these graphs depicts the curve that passes through the critical saddle point i.e.$ {\cal H} = {\cal H}_{\ast} .$ 2) If the isotropic pressure is less than the energy density, it has characteristics of an ultra-relativistic fluid. In this type of fluid, the EoS takes the form
$ p = e/2 $ . After setting$ k = 1/2 $ in Eq. (19), we obtain the following expression for the critical radius${r_c} \simeq \frac{5}{2}GM - \frac{{14}}{{25}}\frac{\xi }{M}.$

(24) The Hamiltonian in Eq. (21) in this case reduces to
${\cal H} = \frac{{\sqrt {\left(1 - \dfrac{{2GM}}{r} + \dfrac{{2{G^2}M\xi }}{{{r^3}}}\right)} }}{{{r^2}v\sqrt {1 - {v^2}} }}.$

(25) We can observe that
$ {\cal H} $ in Eq. (25) is not defined for$ (r,v^2) = (r_h,1) $ . However, for some constant values of$ {\cal H} = {\cal H}_0 $ , one can solve it for$ v^2 $ . The five trajectories of solutions to Eq. (25) in the phase space are shown in top right diagram of Fig. 1. Here, the black curve indicates the solution for$ {\cal H} = {\cal H}_{c} $ , the red curve depicts the solution for$ {\cal H} = {\cal H}_{c}-0.01 $ , the green curve for$ {\cal H} = $ ${\cal H}_{c}-0.005 $ , the magenta curve for$ {\cal H} = {\cal H}_{c}+0.01 $ , and the blue curve for$ {\cal H} = {\cal H}_{c}+0.005087 $ . From the contour plots, we see that they are doubly-valued and show unphysical behavior, such we can say that there is no physical significance of such fluid in ASG.3) For the radiation fluid, we have the state parameter
$ k = 1/3 $ . This fluid has the property to absorb the radiations emitted by the black hole. The insertion of$ k = 1/3 $ in Eq. (19) results in the following real approximation of the critical radius${r_c} \simeq 3GM - \frac{5}{9}\frac{\xi }{M},$

(26) while the Hamiltonian in Eq. (21) takes the form
${\cal H} = \frac{{{{\left(1 - \dfrac{{2GM}}{r} + \dfrac{{2{G^2}M\xi }}{{{r^3}}}\right)}^{2/3}}}}{{{r^{4/3}}{v^{2/3}}{{(1 - {v^2})}^{2/3}}}}.$

(27) From above Hamiltonian, we see that the point
$ (r,v^2) = (r_h,1) $ is not a critical point of the dynamical Hamiltonian system. However, the expression for$ v^2 $ can be obtained by fixing$ H = H_0 $ . The characteristics of solution curves are depicted in the left lower picture, where the black curve shows the solution for$ {\cal H} = {\cal H}_{c} $ , the red curve for$ {\cal H} = {\cal H}_{c}+0.00099 $ , the green curve for$ {\cal H} = {\cal H}_{c}+0.0009 $ , the magenta curve for$ {\cal H} = {\cal H}_{c}-0.04 $ , and the blue curve for$ {\cal H} = {\cal H}_{c}-0.09 $ .Here, for the radiation fluid, we find some surprising characteristics as it gets closer to the black hole. The black, magenta, and blue curves exhibit unphysical behavior, however, the green curves describe highly interesting behavior of the transonic type. The fluid has supersonic velocity before the critical point, but as soon as it approaches the critical point, the speed becomes subsonic.
4) In sub-relativistic fluids, energy density exceeds the isotropic pressure, and the assigned value to the state parameter is
$ k = 1/4 $ . Repeating previous steps, we obtain an approximation of the critical radius as${r_c} \simeq \frac{7}{2}GM - \frac{{26}}{{49}}\frac{\xi }{M}.$

(28) The insertion of Eq. (28) into Eq. (20) provides the desired critical point
$ (r_c,u_c) $ .In this case of a sub-relativistic fluid, the Hamiltonian Eq. (24) takes the following form
${\cal H} = \frac{{{{\left(1 - \dfrac{{2GM}}{r} + \dfrac{{2{G^2}M\xi }}{{{r^3}}}\right)}^{3/4}}}}{{r{v^{1/2}}{{(1 - {v^2})}^{3/4}}}}.$

(29) From above equation, it is evident that the point
$ (r,v^2) = (r_h,1) $ is not a critical point of the dynamical system. Now, we draw contour plots of$ {\cal H} $ in the$ (r,v) $ plane by fixing$ {\cal H} = {\cal H}_c $ which describes the following behavior of the moving fluid. The black curve shows the solution for$ {\cal H} = {\cal H}_{c} $ , the red curve for$ {\cal H} = {\cal H}_{c}+0.03 $ , the green curve for$ {\cal H} = {\cal H}_{c}-0.0399 $ , the magenta curve for$ {\cal H} = {\cal H}_{c}+0.0009 $ , and the blue curve for$ {\cal H} = {\cal H}_{c}-0.0317999 $ . The curves shown in the lower right figure describe the behavior of the moving fluid as follows: in the blue and green curves, the fluid reaches near the critical point to show transonic behavior, but surprisingly fails to do so. Hence, in this scenario, we define this motion as unphysical behavior of the fluid (as they show velocity as a double valued function). However, blue and magenta curves show the supersonic accretion motion in the region$ v>v_c $ and subsonic motion in the region where$ v<v_c $ . -
Unlike the Schawrzschild black hole, the quantum gravity affects the accreting fluid near the improved version of Schawrzschild black hole. Furthermore, if we do not entertain the quantum gravity effects, the above presented results are easily reducible to what already been published in [2]. We discuss the asymptotic behavior of isothermal fluids with EoS
$ p = ke $ , such that$ 0<k<1 $ . Eq. (13) can be written in the following form$\frac{{GM}}{{2{r_c}}} + \frac{{3{G^2}M\xi }}{{2r_c^3}} = k\left(1 - \frac{{3GM}}{{2r_c^2}} + \frac{{7{G^2}M\xi }}{{2r_c^3}}\right),$

(30) which can again be reduced to a depressed cubic equation by introducing the Wierstrass polynomial
$ r = t+\frac{7GM}{6} $ , which is equivalently expressed as$t_c^3 - p{t_c} - q = 0,$

(31) where
$p = \frac{{49{G^2}{M^2}}}{{12}},\;\;\;\;\;q = \frac{{343{G^3}{M^3}}}{{108}}.$

(32) Here, Eq. (31) has three roots: one real root and the other two will be complex conjugates of each other. This follows directly from the Cardano formula
${r_c} = \sqrt[3]{{ - q + \iota \sqrt W }} + \sqrt[3]{{ - q - \iota \sqrt W }},$

(33) where
$ W = \sqrt{p^{3}+q^{2}} $ . We can perform a detailed analysis by computing the Jacobian matrix for the Eqs. (10) and (11), for instance$J = \left( {\begin{array}{*{20}{c}} {\dfrac{{\partial {f_1}}}{{\partial r}}}&{\dfrac{{\partial {f_1}}}{{\partial u}}}\\ {\dfrac{{\partial {f_2}}}{{\partial r}}}&{\dfrac{{\partial {f_1}}}{{\partial u}}} \end{array}} \right). $

(34) With the help of the above Jacobian matrix, one can determine that either the critical values are center, saddle, or spiral. If both eigenvalues are real and have different signs, we have a saddle point. If the real part of the complex eigenvalues is negative, then we have a spiral and if the real part of the complex number is zero, we have a center.
Hence, using Eqs. (19) and (20), one can obtain
$ r_c $ and$ u_c^r $ , respectively (velocity of the fluid at sonic point). Then, after putting$ (r_c,u^r_c) $ in Eq. (14), we find the constant$ A $ to obtain u in an explicit form. Moreover, from the normalization of the four-velocity vector, one can also derive an expression for$ u_t(r) $ . Thus, after finding the explicit forms of u and$ u_t $ , one can sketch$ \Big(\frac{u}{u_t}\Big)^2 $ along the$ r$ -axis to see whether for each case k = 1, 1/2, 1/3, 1/4, the fluid passes through the sonic point, as sketched in Fig. 2. In Fig. 1, we have discussed non-transonic solutions, but we have also plotted the transonic solutions for the isothermal fluid in Fig. 2. The transonic solutions yield a maximum accretion rate, because they pass through the critical point. In Fig. 2, we see that the fluid trajectories may form an orbit for$ k = 1/4 $ near the Cauchy and event horizon. -
The model of spherical accretion is used generally to test various theories of modified gravity. To test these theories from the astrophysical perspective, we must investigate how the behaviour of fluids is modified under the change of parameters of modified gravity appearing in the metric of black holes. By varying these free parameters of modified gravity, the positions of critical points might shift, and the speed of fluid flow might enhance or decay near the black hole. Moreover, the fluid behavior might shift from supersonic to subsonic. In the literature, the spherical accretion on black holes has been studied under the frameworks of different modified gravities, like the braneworld gravity [36], Horava-Lifshitz gravity [37], f(R) gravity [33] and f(T) gravity [34], to list a few. In the present study, we were motivated to test another candidate theory of quantum gravity namely, the higher derivative asymptotic safe gravity in the infra-red limit. From Eq. (3) of our paper, the size of black holes in the ASG theory is smaller compared to the Schwarzschild BH. Furthermore, Eq. (26) suggests that the position of the critical point shifts further towards the BH, and it is smaller than the respective critical point for the Schwarzschild BH. Thus, one can compare and distinguish the relativistic accretion models from Schwarzschild BH from a ASG BH by changing the
$ \xi $ parameter.In this study, we adapt the Hamiltonian method of Michel type accretion as developed by several authors of this work [33]. This method is more general than the original method of Michel. Here, we use the general equations for spherical accretion including conservation laws for the ASG BH static metric. The pressure of the perfect fluid for such spherically symmetric flows is, up to a sign, the Legendre transform of the energy density. This leads to a simple differential equation allowing the determination of the energy density, enthalpy, or pressure knowing one of the equations of state. Furthermore, Bondi's model of accretion on a normal star is the oldest model of spherical accretion employing Newtonian mechanics. In that model, the fluid is adiabatic and non-viscous, and the flow is always transonic, thus it allows the existence of critical point. The Bondi model also allows the outflows during accretion, which can explain the jet phenomenon from certain active galactic galaxies, see for details [38]. However, we found that the fluid flow can be more general than Bondi model. The fluid flow can have subsonic, supersonic, and transonic regimes. Also, because of relativistic treatment, more than one critical point might exist, which allows the heteroclinic flows as well.
In our study, we investigated both adiabatic and isothermal fluid flows, since both of them have important astrophysical relevance, see Refs. [38]. Thus, there are astrophysical situations where either entropy is constant and temperature varying (adiabatic) or vice versa (isothermal). In the isothermal case, the sound speed of accretion flow at any radii is always equivalent to the sound speed at a sonic point. Hence, if the temperature of the flow is known, one can easily compute the critical point.
In the Newtonian stellar accretion model, the size of critical radius is considerably larger than the relevant Schwarzschild radius of the star (several hundreds or thousands times the Schwarzschild radius of the star), while the corresponding critical radius for the ASG improved black hole is between 2M and 6M, or comparable to three times the Schwarzschild radius. Therefore, for accretion over black holes, the fluid experiences transonic or ultra-sonic flow just seconds before entering the horizon. The ASG black holes are predicted to be smaller in size compared to the Schwarzschild black hole, while both have same mass. Thus, the relevant transitions from sonic to supersonic to ultrasonic flows occur at a significantly faster rate for ASG black holes. In the study of accretion near the black hole, we found that no physical significance of the radiation fluid exists in asymptotic safe gravity. We observe that the effect of ASG parameter affects the fluid behavior for small values of radial parameter. Moreover, in the critical analysis of the isothermal test fluids, we observe that the fluid trajectories may form a closed orbit for
$ k = 1/4 $ near the Cauchy horizon. It is interesting to consider astronomical observation effects, such as accretion rate and temperature, as done in Refs. [17, 39, 40], which we aim to address our future research.The authors would like to thank the anonymous referee for providing insightful comments.
Accretion on high derivative asymptotically safe black holes
- Received Date: 2019-11-11
- Accepted Date: 2020-01-29
- Available Online: 2020-06-01
Abstract: Asymptotically safe gravity is an effective approach to quantum gravity. It is important to differentiate modified gravity, which is inspired by asymptotically safe gravity. In this study, we examine particle dynamics near the improved version of a Schwarzschild black hole. We assume that in the context of an asymptotically safe gravity scenario, the ambient matter surrounding the black hole is of isothermal nature, and we investigate the spherical accretion of matter by deriving solutions at critical points. The analysis of various values of the state parameter for isothermal test fluids, viz., k = 1, 1/2, 1/3, 1/4 show the possibility of accretion onto an asymptotically safe black hole. We formulate the accretion problem as Hamiltonian dynamical system and explain its phase flow in detail, which reveals interesting results in the asymptotically safe gravity theory.





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF














 DownLoad:
DownLoad: