-
The thermodynamic properties of black holes have become an important bridge for the study of general relativity, thermodynamics and quantum gravity. Black holes are a topic of widespread interest since Hawking discovered that black holes could thermodynamically emit particles, and various thermodynamic properties of black holes have been extensively studied [1-6]. Interestingly, it has been found that black holes as thermodynamic systems have many similarities with general thermodynamics systems. These similarities are more obvious and precise for black holes in the AdS space. The research of AdS black hole thermodynamics began with the pioneering paper of Hawking and Page, where a phase transition was found between the Schwarzschild-AdS black hole and the thermal AdS space [7]. Subsequently, attention has focused on the Hawking radiation and phase transitions of various black holes [8-15].
Recently, the cosmological constant was proposed as the thermodynamic pressure, and its conjugate quantity as the thermodynamic volume, i.e.
$ P = -\frac{\Lambda}{8\pi},\; \; \; V = {\left(\frac{\partial M}{\partial P}\right)}_{S,Q,J}. $

(1) Based on this proposal, the
$ P-V $ critical behavior of charged AdS black holes has been studied by investigating the black hole thermodynamics in the extended phase space [16-28]. The results show that the phase transitions of charged AdS black holes are similar to the van der Waals liquid-gas. Furthermore, black holes have the same critical exponents as the van der Waals system.In the AdS space, in addition to studying phase transitions and critical phenomena, there has been a growing interest in the Joule-Thomson expansion of black holes. Recently, Özgür Ökcü and Ekrem Aydiner developed the black hole thermodynamics in the extended phase space related to the Joule-Thomson expansion [29]. In the Joule-Thomson expansion, gas enters the low pressure region through a porous plug, and enthalpy remains constant during the process. In the Joule-Thomson expansion of a charged AdS black hole, the T−P diagram is divided in two parts by the inversion curve, corresponding to the heating region and the cooling region. The inversion curve has a positive slope only, which is different from the van der Waals fluid where the slope of the inversion curve is positive in one segment of the curve and negative in the other. Subsequently, the Joule-Thomson expansion was promoted rapidly to various black holes, such as the Kerr-AdS black holes [30], AdS black holes with a global monopole [31], d-dimensional AdS black holes [32], AdS black holes in Lovelock gravity [33], and charged Gauss-Bonnet black holes in AdS space [34], etc [35-40].
Einstein's general relativity is the most successful and beautiful theory of gravity. In General Relativity, the geometry and matter fields are coupled minimally, which results in the covariant conservation relation of the energy-momentum tensor. However, this relation is only verified in the Minkowaski flat or weak field regime. Based on this idea, Rastall proposed a modified theory of Einstein's gravity theory in 1972 [41]. Rastall considered that in curved space-time, the covariant derivative of the energy-momentum tensor is no longer zero. Indeed, a non-minimal coupling of the matter field to the space-time geometry was considered such that
$ T^{\mu \nu}_{\; \; ;\mu} = \lambda R^{,\nu}, $

(2) so that Einstein's field equation is modified to
$ G_{\mu \nu}+\kappa \lambda g_{\mu \nu}R = \kappa T_{\mu \nu}, $

(3) where
$ \lambda $ and$ \kappa $ are the Rastall parameter and the Rastall gravitational coupling constant, respectively. It should be emphasized that the parameter$ \lambda $ measures the potential deviation of the Rastall theory from Einstein's general relativity, and shows a tendency of curvature-matter coupling in a non-minimal way [27]. Moreover, the divergence of the energy-momentum tensor can be non-zero in a curved space-time [42]. An interesting inference from the Rastall gravity is that the coupling between geometry and pressureless matter fields can theoretically describe the current accelerated and inflation phases of the universe without introducing strange sources [43-46].In recent decades, studies have shown the advantages of the Rastall gravity in comparison with Einstein's gravity. For example, in the cosmological model ΛCDM, it was found that the Rastall parameters can modify the density parameters in the collapsed region, the non-linear term of the density spectrum of matter and the transformation function of the cosmic disturbance [47]. The problem of dark energy was also studied using the Rastall theory in cosmology [48,49], and it was found that the Rastall theory could give a stable Einstein static cosmological model under certain conditions [50]. Therefore, it appears that the Rastall theory is more advantageous than Einstein's theory for certain astronomical observations. Recently, much attention has been focused on the thermodynamic properties in the Rastall theory, such as the
$ P-V $ criticality of d-dimensional AdS black holes surrounded by a perfect fluid [27], thermodynamics of black holes [51], thermodynamics of flat FLRW universe [52], etc. [53-55].The Rastall theory contains richer physics in comparison with Einstein's theory since the latter is just a special case (
$ \lambda = 0 $ ) of the former. The thermodynamic behavior of black holes in the Rastall gravity is therefore more general, and can better reflect the nature of gravity as a thermodynamic system. On the other hand, the non-minimal coupling between geometry and matter fields in the Rastall theory can have notable effects on the equation-of-state of the usual (Einstein) gravity system with minimal coupling. Hence, it is necessary to check whether the thermodynamic evolution in the Rastall gravity behaves as in the van der Waals fluid and the Einstein gravity. In this paper, by studying the$ P-V $ criticality and the Joule-Thomson expansion of a charged AdS black hole in the Rastall gravity, we attempt to find the effects of the non-minimal coupling between geometry and matter fields on the thermodynamic behavior of gravity. The paper is organized as follows. In Sec. 2, we study the$ P-V $ criticality of a charged AdS black hole in the Rastall gravity, and obtain the critical exponents. In Sec. 3, we study the Joule-Thomson expansion of a charged AdS black hole in the Rastall gravity, and obtain the inverse temperatures and curves. Our conclusions are presented in Sec. 4. -
In this section, we study the
$ P-V $ criticality of charged AdS black hole in the Rastall gravity. The line element of the static space-time of a four-dimensional spherically symmetric black hole can be considered as$ {\rm d}s^2 = -h(r){\rm d}t^{2}+\frac{{\rm d}r^{2}}{h(r)}+r^{2}({\rm d}\theta^{2}+\sin^{2}\theta{{\rm d}\phi^{2}}), $

(4) where
$ h(r) $ is given by [56]$ h(r) = 1-\frac{2M}{r}+\frac{Q^2}{r^2}-\frac{\Lambda r^2}{3-12\lambda}. $

(5) Here,
$ \lambda $ is the Rastall parameter, and$ \Lambda $ ,$ M $ and$ Q $ are the cosmological constant, mass and charge of the black hole. According to [56], we know that$ \lambda<\frac{1}{4} $ corresponds to the anti-de Sitter space-time, so we only consider$ \lambda<\frac{1}{4} $ in the following discussion. The horizon radius is defined by$ h(r) = 0 $ . The mass of the black hole is then given by$ M = \frac{Q^2}{2r_+}+\frac{r_+}{2}+\frac{\Lambda r_+^{3}}{6(4\lambda-1)}, $

(6) and its entropy is
$ A = 4\pi r_+^2, \; \; \; \; S = \frac{A}{4} = \pi r_+^{2}. $

(7) The Hawking temperature of the black hole is given as
$ T = {\Big(\frac{\partial M}{\partial S}\Big)}_{P,Q} = \frac{(1-4\lambda)Q^{2}+(4\lambda-1)r_+^{2}+\Lambda r_+^4}{4(4\lambda-1)\pi r_+^3}, $

(8) and the thermodynamic volume is
$ V = {\Big(\frac{\partial M}{\partial P}\Big)}_{Q,S} = \frac{1}{1-4\lambda}\frac{4\pi r_+^3}{3}. $

(9) The first law of black hole thermodynamics can now be written as
$ {\rm d}M = T {\rm d}S+\Phi {\rm d}Q+V {\rm d}P, $

(10) and the corresponding Smarr relation is
$ M = 2(T S-P V)+\Phi Q, $

(11) where
$ P = -\frac{\Lambda}{8\pi} $ and$ \Phi = \frac{Q}{r} $ . In the extended phase space, according to Eq. (8), the equation-of-state is given as$ P = \frac{(4\lambda-1)(v^{2}-4Q^{2})}{2\pi v^4}-\frac{(4\lambda-1)T}{v}, $

(12) where
$ v = 2r_+ $ . The critical point can be calculated from the relations$ \frac{\partial P}{\partial v} = 0, \; \; \; \frac{\partial^{2}P}{\partial v^2} = 0, $

(13) so that the critical temperature, volume and pressure are respectively
$ T_c = \frac{1}{3\sqrt{6}\pi Q},\; \; \; v_c = 2\sqrt{6}Q,\; \; \; P_c = \frac{1-4\lambda}{96\pi Q^{2}}. $

(14) Using these critical quantities, the universal constant of a charged AdS black hole in the Rastall gravity is given by
$ \epsilon = \frac{P_c v_c}{T_c} = \frac{3}{8} (1-4\lambda). $

(15) Obviously, compared with a charged AdS black hole in the Einstein gravity, the universal constant of a charged AdS black hole in the Rastall gravity contains a term
$ \lambda $ related to the Rastall theory. We can also calculate the critical exponents of charged AdS black holes in the Rastall gravity. Defining$ p = \frac{P}{P_c},\; \; \; \nu = \frac{v}{v_c},\; \; \; \tau = \frac{T}{T_c},\; \; \; t = \tau-1, $

(16) we rewrite the equation-of-state Eq. (12) as
$ p = \frac{8\tau}{3\nu}-\frac{2}{\nu ^2}+\frac{1}{3\nu ^4}. $

(17) This equation-of-state can also be found in [16] for a charged AdS black hole in the Einstein gravity. The critical exponents
$ \alpha $ ,$ \beta $ ,$ \gamma $ ,$ \delta $ are defined as follows:The critical exponent
$ \alpha $ is related to the specific heat capacity at constant volume,$ C_v = T \frac{\partial S}{\partial T}\Big|_V\propto|t|^{-\alpha}. $

(18) The critical exponent
$ \beta $ governs the quantity$ \eta = v_g-v_l $ with the relation,$ \eta = v_g-v_l\propto|t|^{\beta}. $

(19) The critical exponent
$ \gamma $ describes the variation of the isothermal compressibility$ \kappa _T $ with time,$ \kappa_T = -\frac{1}{V} \frac{\partial V}{\partial P}\Big|_T\propto|t|^{-\gamma}. $

(20) The critical exponent
$ \delta $ is related to the pressure at the critical isotherm$ T = T_c $ ,$ |P-P_c|\propto|v-v_c|^{\delta}. $

(21) We easily obtain
$ \alpha = 0 $ ,$ \beta = \frac{1}{2} $ ,$ \gamma = 1 $ ,$ \delta = 3 $ , which are the same as for a charged AdS black hole in the Einstein gravity. We conclude that the Rastall constant does not change the critical exponents.To conclude, although the equation-of-state of a charged AdS black hole in the Rastall gravity is related to the Rastall parameter
$ \lambda $ , its reduced equation-of-state at the critical point is independent of the Rastall parameter$ \lambda $ , as is the case for the Einstein gravity where$ \lambda = 0 $ . This is the reason why the critical exponents are the same as in the Einstein gravity. -
In this section, we consider the Joule-Thomson expansion of a charged AdS black hole in the Rastall gravity. In [29], the Joule-Thomson expansion is considered as a process with constant enthalpy, and the black hole mass is taken as the enthalpy in the AdS space. The Joule-Thomson coefficient
$ \mu $ is then given by$ \mu = {\Big(\frac{\partial T}{\partial P}\Big)}_{H} = {\Big(\frac{\partial T}{\partial P}\Big)}_{M}. $

(22) We can determine the cooling-heating regions from the sign of
$ \mu $ . The pressure always decreases during expansion, so the change in pressure is always negative. However, the temperature may decrease or increase during the expansion. Therefore, the change in temperature determines the sign of$ \mu $ . If$ \mu $ is negative (positive), heating (cooling) occurs, and the gas warms (cools).The Joule-Thomson coefficient can also be given by [29]
$ \mu = {\Big(\frac{\partial T}{\partial P}\Big)}_{H} = \frac{1}{C_p}\Big[T \Big({\frac{\partial V}{\partial T}}\Big)_p-V\Big]. $

(23) Setting
$ \mu = 0 $ , we obtain the inversion temperature of the black hole, i.e.$ T_{i} = V {\Big(\frac{\partial T}{\partial V}\Big)}_{P}. $

(24) Combining Eq. (8) and Eq. (9), the inversion temperature Eq. (24) is given by
$ T_i = \frac{Q^{2}}{4\pi r_+^{3}}-\frac{1}{12\pi r_+}-\frac{2P r_+}{3(4\lambda-1)}. $

(25) On the other hand, according to the definition of the temperature Eq. (8), the inversion temperature can also be given by
$ T_i = -\frac{Q^{2}}{4\pi r_+^{3}}+\frac{1}{4\pi r_+}-\frac{2P r_+}{4\lambda-1}. $

(26) Subtracting Eq. (25) from Eq. (26), yields the identity
$ -3Q^{2}+2r_+^{2}+\frac{8\pi P r_+^{4}}{1-4\lambda} = 0. $

(27) Solving Eq. (27), we get four roots of
$ r_+ $ . Only one root is physically meaningful, and is given by$ r_+ = \frac{1}{2\sqrt{2}}\sqrt{\frac{4\lambda-1}{P\pi}+\sqrt{\frac{(4\lambda-1)(4\lambda-1-24P \pi Q^{2})}{P\pi}}}. $

(28) Substituting the radius
$ r_+ $ from Eq. (28) into Eq. (26), we obtain$ T_i = \frac{1-4\lambda+16\pi P Q^2-\sqrt{(4\lambda-1)(4\lambda-1-24\pi P Q^2)}}{\sqrt{2\pi}P\big(\frac{4\lambda-1+\sqrt{(4\lambda-1)(4\lambda-1-24P\pi Q^{2})}}{P}\big)^{\frac{3}{2}}}. $

(29) The minimum inversion temperature occurs at the point
$ P_i = 0 $ [29], and is given by$ {T_{i}}^{\rm min} = \frac{1}{6\sqrt{6}\pi Q}. $

(30) Therefore, for a charged AdS black hole in the Rastall gravity, the inversion temperature
$ {T_{i}} $ is related to the Rastall parameter$ \lambda $ , but the minimum inversion temperature$ {T_{i}}^{\rm min} $ is independent of the Rastall parameter$ \lambda $ , as is the case for the Einstein gravity where$ \lambda = 0 $ .The ratio between the minimum inversion temperature and the critical temperature is
$ \varepsilon = \frac{{T_{i}}^{\rm min}}{T_{c}} = \frac{1}{2}. $

(31) Obviously, the ratio
$ \varepsilon $ between the minimum inversion temperature and the critical temperature of a charged AdS black hole in the Rastall gravity is independent of the Rastall parameter$ \lambda $ .We plot the inversion curves in the
$ T-P $ plane in Fig. 1. For$ \lambda = -1 $ , we show the inversion curves for different charges$ Q $ . Obviously, the inversion temperature increases with increasing$ Q $ for the same inversion pressure. The inversion curves have a positive slope, which is consistent with AdS black holes in the Einstein gravity.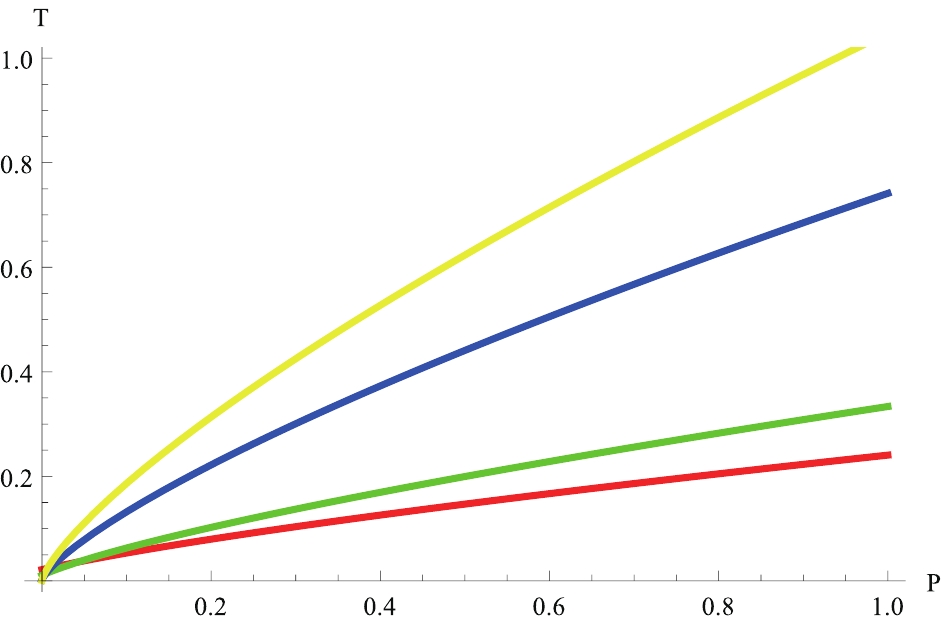
Figure 1. (color online) Inversion curves for
$\lambda = -1$ . From bottom to top, the inversion curves correspond to Q = 1,2,10,20.In Fig. 2, the inversion curves are shown for
$ Q = 1 $ and for Rastall parameters$ \lambda = -0.2, -0.1, 0, 0.1,0.2 $ . Clearly, the inversion temperature increases with increasing$ \lambda $ for the same inversion pressure. When$ \lambda $ decreases, we also find that the slope of the inversion curves decreases. In other words, for the same pressure, a smaller$ \lambda $ implies a lower inversion temperature.
Figure 2. (color online) Inversion curves for Q = 1. From bottom to top, the inversion curves correspond to
$\lambda = -0.2,-0.1,0,0.1,0.2$ .In Fig. 3, we show the isenthalpic and inversion curves of a charged AdS black hole in the Rastall gravity. The isenthalpic curves are divided by the inversion curves into two parts: the upper part is the cooling region, and the lower part is the heating region. The inversion points of the isenthalpic curves increase with increasing
$ M $ and the Rastall parameter$ \lambda $ .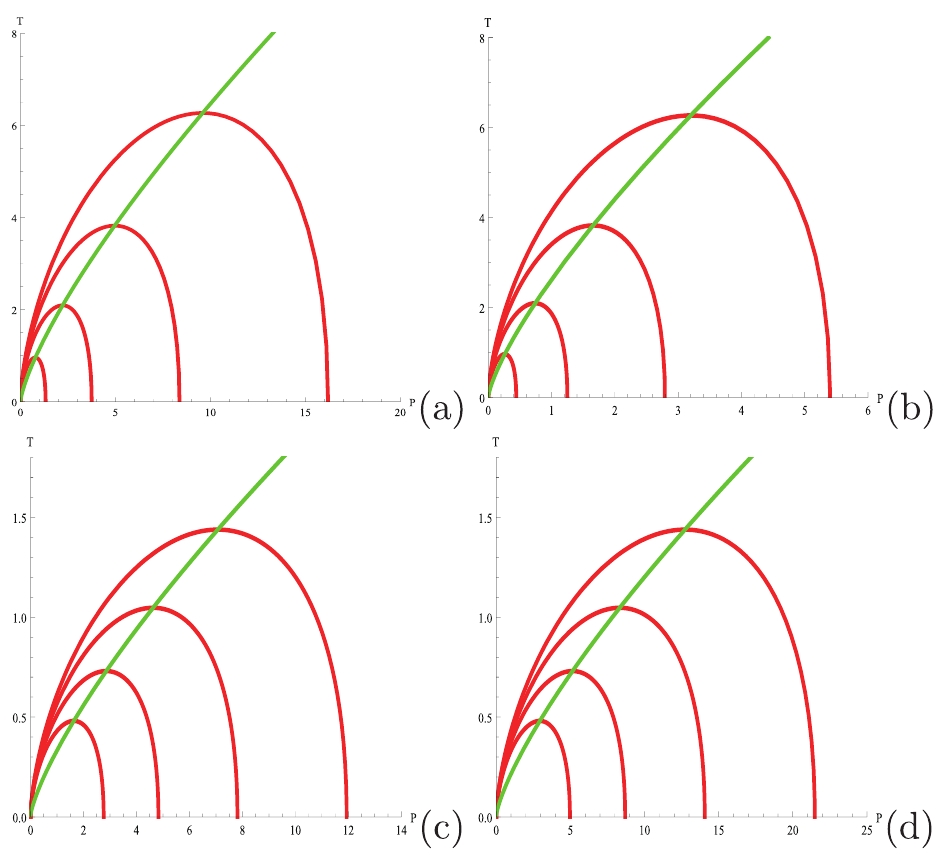
Figure 3. (color online) Isenthalpic and inversion curves of a charged AdS black hole in the Rastall gravity. The green lines are the inversion curves. From bottom to top, the red isenthalpic curves correspond to the increasing values of M. (a)
$Q = 1$ ,$\lambda = 0.1$ and$M = 2,2.5,3,3.5$ , (b)$Q = 1$ ,$\lambda = 0.2$ and$M = 2, 2.5, 3, 3.5$ , (c)$Q = 2$ ,$\lambda = -1$ and$M = 4,4.5,5,5.5$ , (d)$Q = 2$ ,$\lambda = -2$ and$M = 4,4.5,5,5.5 .$ -
In this paper, we discussed the
$ P-V $ criticality and the Joule-Thomson expansion of charged AdS black holes in the Rastall gravity. The Rastall theory contains richer physics in comparison with the Einstein theory since the latter is a special case ($ \lambda = 0 $ ) of the former. The thermodynamic behavior of black holes in the Rastall gravity is therefore more general, and better reflects the nature of gravity as a thermodynamic system. We found that although the equation-of-state of a charged AdS black hole in the Rastall gravity is related to the Rastall parameter$ \lambda $ , its reduced equation-of-state at the critical point is independent of the Rastall parameter$ \lambda $ , which is also the case in the Einstein gravity where$ \lambda = 0 $ . This is the reason why the critical exponents are not related to the Rastall parameter$ \lambda $ . On the other hand, the inversion temperature$ {T_{i}} $ is related to the Rastall parameter$ \lambda $ , but the minimum inversion temperature$ {T_{i}}^{\rm min} $ and the ratio$ \varepsilon $ between the minimum inversion temperature and the critical temperature are both independent of the Rastall parameter$ \lambda $ . Therefore, the thermodynamic evolution of a charged AdS black hole in the Rastall gravity behaves at the critical point as in the van der Waals fluid and charged AdS black hole in the Einstein gravity.We also studied the Rastall parameter
$ \lambda $ by investigating its effect on the isenthalpic and inversion curves in Figs. 1, 2, 3. For$ \lambda = -1 $ , we found from Fig. 1 that the inversion temperature increases with increasing$ Q $ for the same inversion pressure. For$ Q = 1 $ in Fig. 2, the inversion temperature increases with increasing$ \lambda $ for the same inversion pressure. When$ \lambda $ decreases, we found that the slope of the inversion curves also decreases. In other words, for the same inversion pressure, a smaller$ \lambda $ implies a lower inversion temperature. We also obtained the isenthalpic and inversion curves of a charged AdS black hole in the Rastall gravity. The isenthalpic curves are divided into two parts by the inversion curves: the upper part is the cooling region, and the lower part is the heating region. The inversion points of the isenthalpic curves increase with increasing$ M $ and the Rastall parameter$ \lambda $ .
P-V criticality and Joule-Thomson expansion of charged AdS black holes in the Rastall gravity
- Received Date: 2019-12-23
- Available Online: 2020-06-01
Abstract: We discuss the





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF




















 DownLoad:
DownLoad: