-
The observation of gravitational waves (GWs) from binary compact objects symbolizes the beginning of an era of GW astronomy as a branch of observational astronomy with considerable precision. In terms of fundamental physics, we finally have the experimental observables at our disposal for testing whether a quantum theory of gravity is plausible. The GW is an incisive tool for the study of the structure of the black holes and other compact objects. In particular, it may unwrap the enigma about the quantum structure of the spacetime beyond the horizon. With regard to the quantum effects, it is believed that the spacetime is no longer a smooth manifold; it may possess a specific non-trivial structure when the quantum fluctuations become significant [1]. In fact, a structure of the black hole horizon was suggested to solve the black hole information problem, for example, in terms of the fuzzball model [2] and the firewall model [3, 4]. Such a speculated structure may be detected by the GWs emitted from binary black holes [5].
In these models, the horizon is not a smooth sphere, but a shell with a finite thickness. Consequently, tail wavelets referred to as "echoes" may appear after emission of the main GWs [6-9]. The waveform of the echo model suggested in [6] may be ruled out by analysis in [10, 11]. However, the tail wavelet may assume a different form compared with Ref. [6]. This problem can be dealt with from an opposite direction, that is, to find what happens if there is absolutely no signal in the data after the main wave [10, 11]. A detailed analysis in Ref. [12] demonstrates that signals appear for several GW events with a p-value of order 1% or occasionally significantly less. Further approaches for the signal reconnaissance of tail wavelets are presented in Ref. [13]. In this context, observation of the tail wavelets in GW events of the binary neutron stars, besides those of binary black holes, is surprising. While explanations are given in terms of the resulting black hole remnant [14], the observed events also imply the possibility that the tail wavelet may be related to specific generic properties of the binary system rather than the near-horizon quantum structure [15]. In fact, it is quite challenging to interpret the appearance of tail wavelets in terms of the properties of the horizon if the latter does not exist in the first place.
Following this train of thought, we proceed by discussing some of the generic properties of compact objects, which might potentially give rise to tail wavelets. Generally, a black hole/neutron star is surrounded by dark matter, whose density is significantly higher than that of the average value in the universe. We show later that dark matter distributed in the vicinity of the compact object can provide a mechanism for the observed tail wavelets. Further quantitative studies of the wavelets may be helpful to extract the distribution of dark matter around the compact objects. Extensive studies were conducted on the distribution of dark matter around celestial bodies. Some pioneering studies [16, 17] explored specific properties of the dark matter distribution in the halos of various mass scales. A remarkable feature of the distribution of the dark matter is its universality. Halos of different scales, namely, from the mass of the celestial body to that of a cluster of galaxies, all exhibit similar distributions [18, 19]. The density profile of supermassive black holes in elliptical galaxies and barred/ordinary spiral galaxies, such as our Milky Way, is studied quantitatively [20, 21]. For the stellar mass black holes, direct observation of the dark matter halo is still absent. The distribution of dark matter around neutron stars, whose space environment is very similar to stellar mass black holes, was studied in detail [22–24]. Regarding the universal distribution of dark matter halos, it is reasonable that binary compact stars/black holes are immersed within them.
Our proposed scenario is described as follows. The passage of the main GWs from the binary system merger pushes up the dark matter to a certain altitude. After the initial waves traverse through, the matter falls back towards the black hole region and subsequently produces the tail wavelets. The relevant physical quantities include the energy density, pressure, energy flux of the GWs. For linear plane GWs with frequency
$ \omega $ and amplitude$ A $ , the energy density$ \rho $ is found to be [1]$ \rho = \dfrac{\omega^2}{32\pi}(A_{+}^2+A_{\times}^2) $ , while the energy flux$ b $ in the direction of propagation reads$ b = \dfrac{\omega^2}{32\pi}(A_{+}^2+A_{\times}^2). $ The above expressions are the same with the Landau-Lifshitz pseudo-tensor for GWs.In a general case, the stress-energy tensor for the GWs can be defined as a second order perturbation of the Einstein tensor. The general definition of GWs in the strong field region leads to some uncertainties, which depend on the specific choice of the background for the GWs in question. For example, the obtained waves exhibit different forms when the metric about a Minkowski spacetime is expanded as compared to about a Schwarzschild spacetime. Nonetheless, the relation between power per area
$ S = b $ and the pressure$ P $ satisfies$ P = S/c, $

(1) for massless fluctuations (gravitons). Here, we recover the luminous velocity
$ c $ . Notably, Eq. (1) is valid for GWs in a general sense, independent of the background metric. The total energy radiated from a binary object can be calculated, enabling determination of the corresponding pressure. In what follows, we estimate the order of magnitude of the pressure by considering the GW150914 event as an example. The system emits an amount of energy equivalent to three solar masses in about 0.1 seconds. The GW emission is "directional". However, its directivity is significantly weaker than electromagnetic radiation, as the lowest order radiation is of the quadrupole. Thus, if the GWs’ directivity is omitted, the emission can be approximated as isotropic, and the pressure of GW at the horizon is estimated by$ P = \frac{w}{4\pi r_h^2 c}\sim \frac{3\times 10^{49}}{4\pi (62\times 3\times 10^3)^2\times 3\times 10^8} = 2.3\times 10^{29} {\rm {Pa}}. $

(2) With regard to the comparisons, the pressure at the center of a neutron star can reach 1033 to 1034Pa. Thus, the estimated value of the GW pressure is found to be comparable to those of the interior of stellar systems.
At the region near the horizon, the Newton gravity fails. We only make an assumption to determine which force, i.e., pressure or attraction, dominates for an object around the black hole. Considering an object whose mass is 1 kg and area is 1
$ {\rm m}^2 $ , for GW150914, it is attracted by the black hole with force at the horizon$ F = G\dfrac{m_1m_2}{r^2} = 2\times 10^{11}N $ . At same time, the pressure it senses is$ F' = 2.3\times 10^{29}N $ when the main wave passes. The repulsive force is clearly significantly larger than the attractive force for this object. Both the repulsive and attractive force decrease with$ r^{-2} $ . Thus, at large distances, the ratio between the repulsive and attractive force is exactly$ F'/F $ , if the wave is completely absorbed by the object.Furthermore, we assume that the surrounding matter can only absorb a tiny fraction of GW. A rigorous treatment of the scattering between the graviton and matter demands a full-fledged theory of quantum gravity, which remains unknown. Tree level calculations may also be affected by loop corrections. Nevertheless, some preliminary studies on the scattering of gravitons have been carried out, for example in studies of Refs. [25, 26]. By very generic arguments, similar to those for earlier approaches of quantum physics, one can estimate the lower bound of total cross-section of a graviton scattered by a matter particle
$ \sigma\sim 10^{-68} {\rm m}^2 $ [27]. According to known GW events, a typical event emits energy of several solar masses, and the characteristic frequency of the GW is about 100 Hz. Thus, for a typical GW event, the number of gravitons is approximately$ N\; \sim\dfrac{3\times M_{\bigodot}c^2}{h \nu} = $ $10^{79} $ . We estimate the number of collisions of a graviton. The graviton-dark matter system is significantly different from an ordinary molecular system in thermal equilibrium. The graviton does not walk randomly, but almost in a straight line, as it only losses a tiny portion of its momentum with every collision. Thus, the number of collisions is simplified to the number of dark matter particles in such a cylinder, whose bottom is a disk with a radius of the half-wavelength of the graviton, and the height is the thickness of the dark matter in consideration. An unavoidable problem of further calculations is that the mass of the dark matter particles is unknown. It may be from several TeV to even 10−20eV. We take 100 GeV as an example. Further, we assume the mass of the surrounded dark matter is$ 0.3M_{\odot} $ . As we point out in the following section, this is sufficient to excite the tail wavelet. For more detailed numerical calculations, we assume that the thickness of the dark matter is 105 km, and that it distributes homogeneously. With these assumptions, we obtain an upper bound for the number of collisions of a single graviton is$ 7\times 10^{53} $ , in which we assume that the graviton interacts with every particle in the travelling cylinder. The lower bound is$ 10^{17} $ , where we assume that the graviton collides with only one particle in one step. The total scattering cross-section between gravitational radiations and dark matter is therefore, 1028 to 1064 m2. In comparison, the total scattering section of the radiation emitted by the sun in 0.1 seconds is 1016 m2. The radiation pressure in the interior of the Sun is about 10−3 of the total pressure. The momentum per solar photon is$ 5\times 10^{12} $ times the momentum per graviton. This is equivalent to stating that we need a cross-section of gravitons of 1031 m2 to support the mass of the sun. We estimated the total cross section to be about 1028 to 1064 m2. An accurate value requires details of the interaction between graviton and dark matter particles, which remains unknown. Nevertheless, it is highly possible that the gravitons can push away dark matter around one solar mass for GW150914. Furthermore, the sunken region of the gravitational potential may concentrate a large number of dark matter particles, as studied in numerous previous studies. Therefore, the total energy transferred from GW to the surrounding dark matter can be considerable.Because a rigorous approach is not yet feasible, in the remainder of the present study, we carry out a phenomenological approach to investigate this interaction between GWs and dark matter.
-
The surrounding dark matter may lead to modifications of geometry (backreaction). Various modifications were studied in detail in a fairly sophisticated study [28]. The result indicates that environmental effects do not spoil main waves from binary compact objects. In this study, we take two typical modifications to study possible corrections to the tail wavelet QNMs. The first one is Schwarzschild-de Sitter, which describes a black hole with a small amount dark matter (compared to the black hole mass) as a fine approximation,
$ {\rm d}s^2 = -f{\rm d}t^2+f^{-1}{\rm d}r^2+r^2{\rm d}\Omega^2,\; $

(3) where
$ f = 1-2M/r-\Lambda_{\rm {eff}} r^2/3 $ . The effective cosmological constant is related to the density of dark matter,$ \rho_{DM} = \dfrac{\Lambda_{\rm {eff}}}{8\pi} $ . We call it the SdS case.The second one is a short-hair black hole, which describes non-homogeneous fluids [29], where
$ f = 1-2M/r+Q_m^{2k}/r^{2k}. $

(4) Here
$ k $ is the equation of state of the dark matter parameter. The density and pressure of dark matter are$ \rho_m = (2k-1)Q_m^{2k}/(8\pi r^{2k+2}) $ and$ P_m = k\rho_m $ , respectively. The softest matter with$ k = -1 $ is a cosmological constant, and the stiffest matter with$ k = 1 $ mimics electromagnetic fields.We estimate the amplitude of the GW around the horizon. The energy density is proportional to the inverse square of the distance from the source
$ L $ . Thus, around the horizon, we obtain$ \dfrac{\rho_{r_h}}{\rho_{L}} = \dfrac{L_0^2}{r_h^2} $ , where$ L_0 $ denotes the distance from the Earth to the source of GW150914. If the energy loss of the GWs is insignificant, the energy density is inversely proportional to the square of the distance from the center, namely,$ \dfrac{A_{r_h}}{A_{L_0}} = \dfrac{L_0}{r_h} $ . For the event GW150914, we have$ r_h = 1.8\times 10^5 $ m,$ L_0 = 1.2\times 10^{25} $ m, and$ A_{L_0} = 10^{-21} $ . Here,$ A_{L_0} $ is the amplitude measured on the Earth. Then, one obtains$ A_{r_h} = \dfrac{1}{15} $ . Hence, it is reasonable to consider that the amplitude of the initial main GWs is$ A_{r_h}\sim 0.1 $ .From previous studies on tail wavelets (echoes), we estate that the amplitude of the wavelet is one tenth of the main wave or smaller. Thus, the energy carried by the wavelet is about
$ 0.03M_{\bigodot} $ or smaller. The energy conversion from the rest mass energy to the gravitational wave energy can be very efficient in the process of splashing down, i.e., up to 42% [30]. As a conservative estimate, we assume that 10% of the total rest mass of the dark matter is transferred to the gravitational energy of the wavelet. Thus, the mass of dark matter involved to excite the wavelet is approximately$ 0.3M_{\bigodot} $ . Using this parameter, we obtain the exact form of backreactions of dark matter to a Schwarzschild black hole and present the waveform of tail wavelets in the cases of SdS and a short-haired black hole, respectively. We find the fine distinction between the cases of a dressed black hole and a bare one, although it is insignificant.Before presenting the waveform of the wavelet, we explore the time scale between the emission of the main GWs and tail wavelets. This can be estimated by simply investigating the equation of motion of a free-falling particle from a given height. For simplicity, we consider motions along radial geodesics. The results are presented in Fig. 1. There, we consider a particle splashing down from an initial altitude of
$ R $ towards the horizon$ r_h $ . The epoch is observed to be slightly advanced in the modified geometries. The dark matter halo strengthens gravity.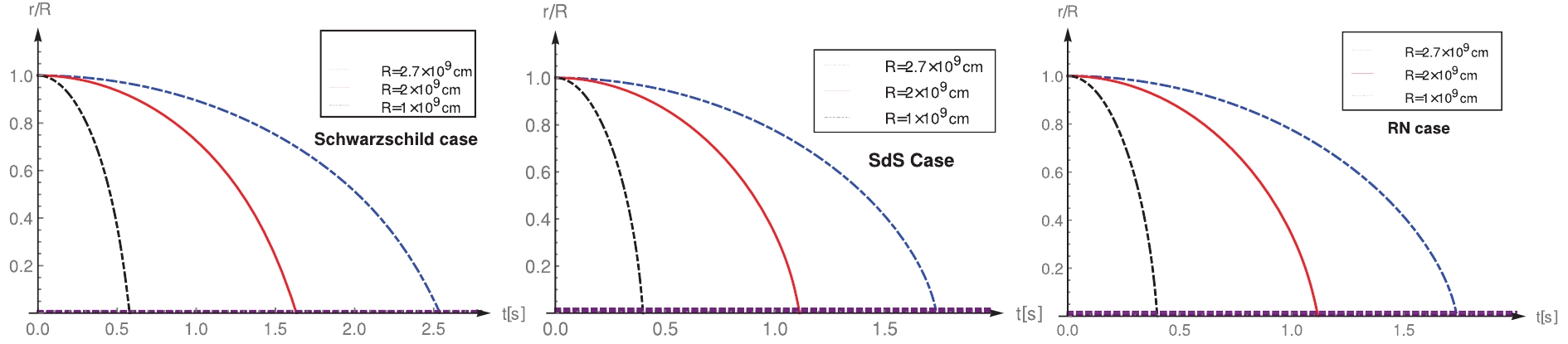
Figure 1. (color online) Estimation of epochs of tail wavelets after the main GWs. Left panel: case without backreaction, i.e., Schwarzschild. Middle panel: Black hole with DM halos, i.e., case of SdS. Right panel: Black hole with short-hair. Location of event horizon is depicted by horizontal dashed purple line.
The waveform of the tail wavelet generated by the infalling of the matter is similar to that of the ordinary quasinormal modes [31–33]. Therefore, in our model, the observed tail wavelets are also a manifestation of the black hole quasinormal modes. However, there is a subtlety. Because the infalling process is continuous, the initial disturbance period carries the information not only on the black hole itself, but also on the matter distribution surrounding it. It is therefore expected that the waveform in the initial disturbance period will be characteristically different from the ordinary quasinormal modes. The Navarro-Frenk-White (NFW) profile is the mostly studied distribution of dark matter around galaxies and clusters [18, 19]. As a more realistic study, we consider an NFW distribution of dark matter around the hole. The NFW distribution can be described by,
$ \rho(r) = \frac{\rho_0}{\dfrac{r}{R_s}\left(1+\dfrac{r}{R_s}\right)^2}. $

(5) Setting
$ x = r/r_h,\; K = r_h/R_s $ , we obtain,$ \rho(x) = \frac{\rho_0}{Kx(1+Kx)^2}. $

(6) We assume that dark matter suffuses between
$ r_h $ and$ 100r_h $ . Thus, the total mass of dark matter (including the mass gravitational field) reads [34],$\begin{split} M_d = 4\pi\int_{r_h}^{100r_h} {\rm d}r r^2 \rho(r) = 4r_h^3\pi\int_{1}^{100}{\rm d}x x^2 \rho(x) = 4\pi r_h^3 \rho_0\int_{1}^{100}{\rm d}x \frac{x^2}{Kx(1+Kx)^2} = 4\pi r_h^3 \rho_0 \frac{1}{K^3}\left(\frac{1}{1+100K}-\frac{1}{1+K}+\ln \frac{1+100K}{1+K}\right). \end{split}$

(7) We require that the total amount of the dark matter is equivalent to the previous homogeneous case, where the total mass is
$ M_{dh} = \rho_{0h}4\pi\int_{r_h}^{100r_h} {\rm d}r r^2 = \rho_{0h}\frac{4\pi}{3}10^6 r_h^3.$

(8) Given a relation between
$ \rho_0 $ and$ \rho_{0h} $ , we obtain a corresponding$ K $ . For example, we assume$ \rho_0 = 10\rho_{0h} $ , and thus we obtain$ r_h = 0.0254R_s $ .In this section, we present numerical calculations of the waveform associated with the gravitational perturbation of the metric owing to the infalling of matter.
The radial master equation of the gravitational fluctuation around the black hole reads [35, 36]
$ f(r)\frac{\partial}{\partial r} \left(f(r)\frac{\partial\Phi}{\partial r}\right)-\frac{1}{c^2}\frac{\partial^2\Phi}{\partial t^2}-V(r)\Phi = 0. $

(9) Here,
$ V $ denotes the potential of the black hole.$ V $ is rather complicated; for even and odd modes, the exact form of$ V $ is provided in Refs. [31-33].$ f(r) $ takes different forms in the cases of Schwarzschild, SdS, and short-hair black holes, as shown above.Based on the analysis in the previous sections, we assume the following initial conditions. For convenience, we choose
$ \eta = ct/r_h $ and consider the following different cases:Case I,
$ \Phi = 0.01 $ as$ \eta \in (0,5) $ .Case II,
$ \Phi = 0.01 $ as$ \eta = 0. $ The first case denotes dark matter that is initially in a homogeneous distribution. For comparison, we plot the second case, which displays a pulse excitation that is the ordinary QNM of the black hole. Figs. 2 and 3 demonstrate the waveforms of the odd and even fluctuations for all geometries, including the Schwarzschild, the geometry with backreaction of dark matter halos (SdS), and the geometry of a short-hair black hole. According to the present estimations, the magnitude of the tail wavelets is at most ~10% of the main GWs [12, 13]. Thus, we take the initial perturbation to be
$ \Phi = 0.01 $ for our calculations. We observe that the waveforms generated by some distribution of dark matter are different from those triggered by a pulse, where the latter corresponds to the ordinary quasinormal mode, which only carries information on the black hole itself. Furthermore, the effects of geometry modifications are not significant compared to the case of a Schwarzschild black hole. In particular, the two modifications present almost the same wavelet, which is slightly different from a "bare" Schwarzschild wavelet.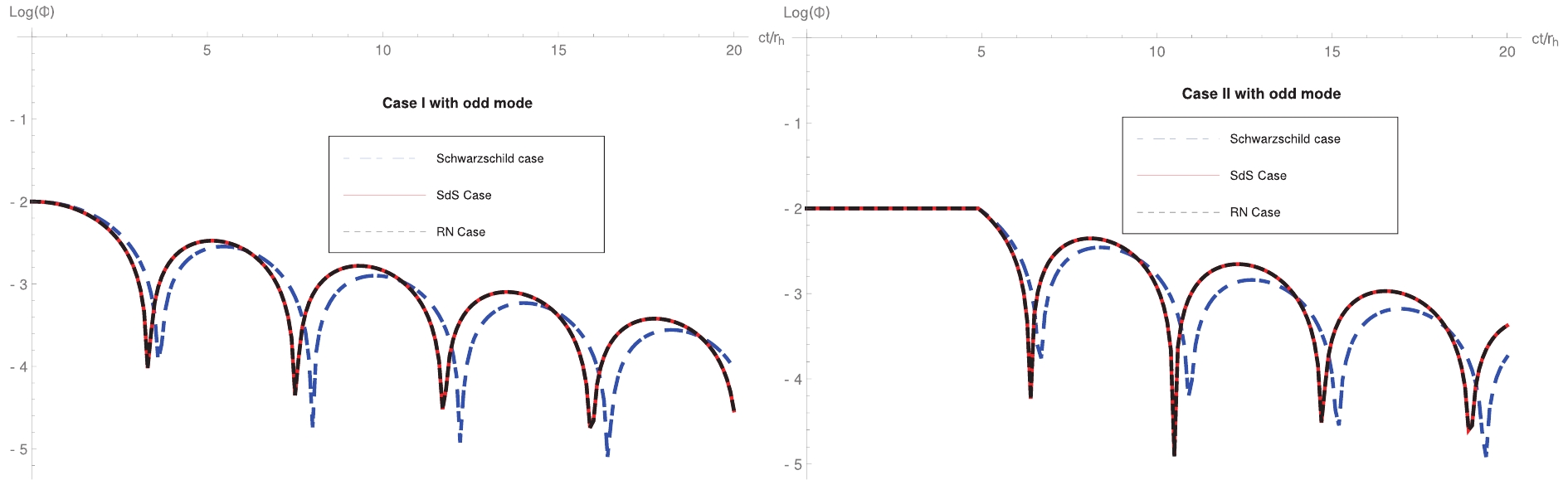
Figure 2. (color online) Waveform of odd gravitational fluctuations, including cases of a bare Schwarzschild black hole and dressed black holes, i.e., SdS and short-haired black hole.

Figure 3. (color online) Waveform of even gravitational fluctuations, including cases of a bare Schwarzschild black hole and dressed black holes, i.e., SdS and short-haired black hole.
We expect that forthcoming data with a better resolution for the waveform, especially those from the third generation GW detectors like the Einstein Telescope [37, 38] and Cosmic Explorer [39], may shed light on the feasibility of the present model.
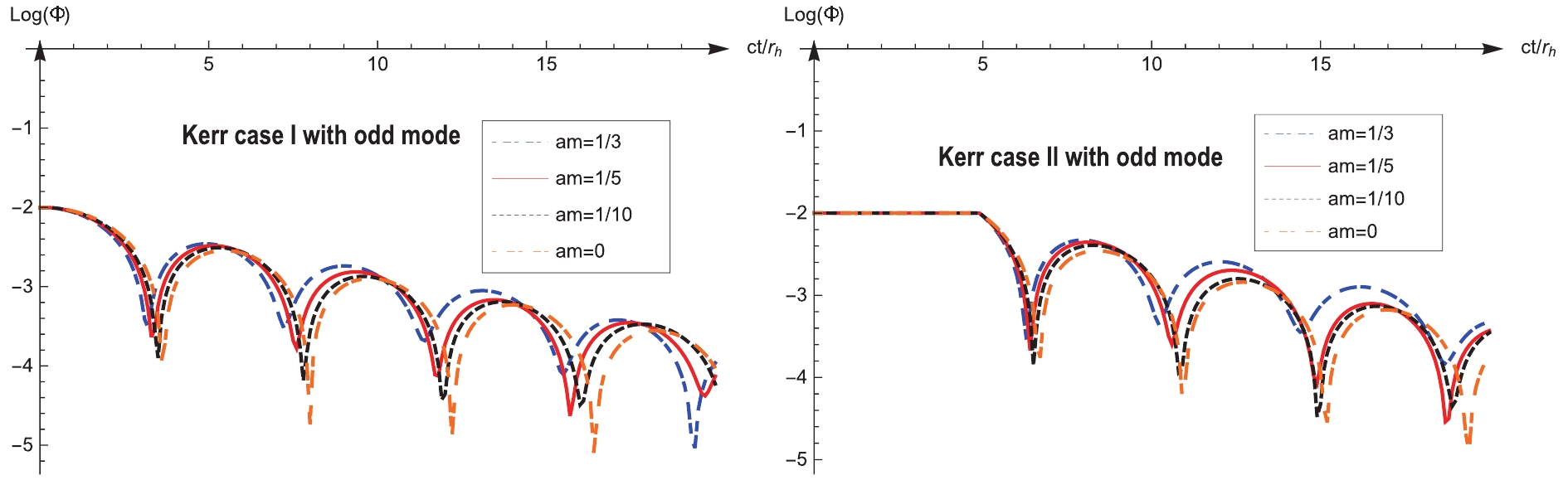
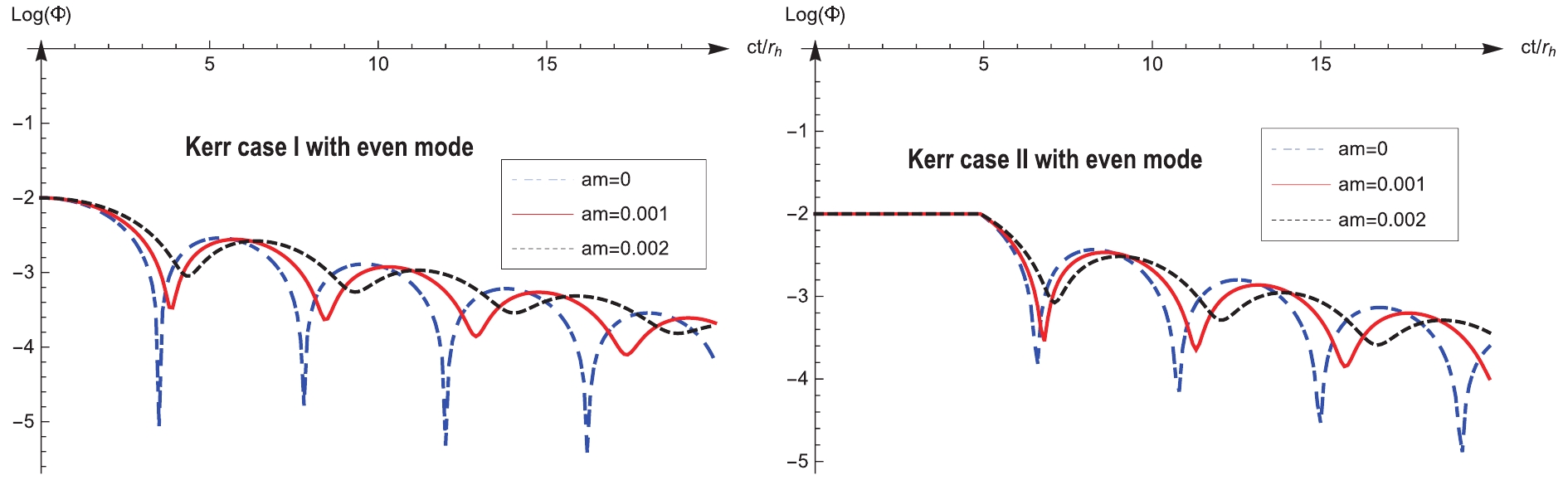
Generally, the astrophysical black hole is a Kerr black hole. We study the Schwarzschild black hole as an approximation of the realistic case. Hence, we present a preliminary investigation of rotating black holes. We plot the corresponding wavelets for the Kerr holes in Fig. 4 and Fig. 5.
-
The data analysis implies that there might be tail wavelets occurring after the main GWs from the merger of binary systems. These tail wavelets exist not only for the GW events of binary black holes, but also for those of binary neutron stars. Therefore, it is speculated that the physical mechanism behind the phenomenon might not be related to the quantum structure of the black hole horizon, but is rather associated with certain generic properties of the collapsing binary system. The main characteristic of our approach is that the explanation is given within the framework of Einstein’s general relativity, rather than originated from a modified theory of gravity or quantum effect.
Following this line of thought, in this work, we present a more natural and straightforward scenario for the generation of tail wavelets. In our model, the cause of the phenomenon is attributed to the matter or dark matter surrounding the binary system. In particular, the dark matter distribution around a compact object has been studied at different scales for many years. We carefully investigate the pressure of the GWs and demonstrate that they can perturb and even push away the matter distributed around a compact star. After the main wave traverses through, the matter falls back towards the black hole horizon, which in turn excites the tail wavelets. Based on our analysis, we assume four different initial conditions for the related gravitational perturbations and evaluate the corresponding waveforms. Furthermore, we make a preliminary exploration of the wavelet for Kerr black holes.
In this study, we concentrate on the physics after inspirals. We explore the effects of energy emission in the merge process and particularly the splashing down of dark matter to the black hole. This is not closely related to the physics before merging. According to the previous studies of intermediate-mass-ratio inspirals (IMRI) without dark matter [40], and especially an upcoming study [41], there is almost no wavelet in IMRI. However, we show that dark matter in such a system can produce significant tail wavelets in the merger of binary compact objects. The effect of dark matter in the inspiraling stage of the IMRI system was investigated in Ref. [42], which demonstrates that dark matter significantly enhances the merging process. We show that dark matter has a significant effect after the merging process.
We look forward to testing the proposed model against forthcoming data from the GW detectors of the third generation. Further studies concerning specific dark matter distributions are in progress. Furthermore, in the frame of this model, we investigate the distribution of dark matter surrounding the black holes by analyzing the waveform of the tail wavelet from the forthcoming data at better resolution, especially those from the third generation GW detectors.
Our heartfelt thanks to Professor Anzhong Wang, Zhoujian Cao, and Wenbiao Han for helpful discussions.
Tail wavelets in merger of binary compact objects
- Received Date: 2020-01-17
- Available Online: 2020-07-01
Abstract: We present a model for tail wavelets, a phenomenon known as “echo” in the literature. The tail wavelet may appear in signal reconnaissances in the merger of binary compact objects, including black holes and neutron stars. We show that the dark matter surrounding the compact objects lead to a speculated tail wavelet following the main gravitational wave (GW). We demonstrate that the radiation pressure of the main wave is fully capable of pushing away the surrounding matter to some altitude, and splashing down of the matter excites the tail wavelet after ringing down of the main wave. We illustrate this concept in a simplified model, where numerical estimations are conducted on the specific distribution of dark matter outside the black hole horizon and the threshold values in accordance with observations. We study the full back reaction of the surrounding dark matter to the metric and find that the effect on to the tail wavelets is insignificant. We reveal the fine difference between the tail wavelets of a dressed and a bare black hole. We demonstrate that the tail wavelet can appear as a natural phenomenon in the frame of general relativity, without invoking modified gravities or quantum effects.





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF














 DownLoad:
DownLoad: