-
The B meson decays into heavy vector particles with charmonia and a kaon-pion pair, i.e.,
$B \to J/\psi K\pi, $ $ \psi(2S)K\pi $ , (etc.). Understanding these three-body hadronic B decays has triggered considerable experimental and theoretical interest. This focus on the polarization and$ CP $ -asymmetry measurements in$ B \to \psi K^* $ decays is motivated by their potential sensitivity to the new physics beyond the standard model (SM) in the$ b \to s $ transition. In the SM, the$ CP $ violation in$ b \to s $ transitions is expected to be very small. Thus, any significant observation of$ CP $ violation may indicate a signal beyond the SM. Because the precision is far from the measurements using the tree level processes, this is a new area of research in B physics, leaving room for contributions from novel physics. Furthermore, the mixing-induced$ CP $ -violating asymmetry is measured in the$ B^0 \to J/\psi K^{*0} $ decay, where angular analysis allows the separation of$ CP $ -eigenstate amplitudes. This resolves the sign ambiguity of the$ \cos 2\beta $ term, which appears in the time-dependent angular distribution due to the interference of parity-even and parity-odd terms. The detailed amplitude analyses of the$ B \to \psi K\pi $ decays have been performed by BABAR [1-3], Belle [4–8], LHCb [9-12], CDF [13-17], CLEO [18], and the D0 Collaboration [19].In theory, the three-body B meson decays receive both resonant and nonresonant contributions, as well as the possible significant final-state interactions (FSIs) [20-22]. Because the nonresonant contributions and possible FSIs can not be reliably evaluated, the analysis for the three-body hadronic decays of the B meson is significantly more complicated than that for the two-body decays. Fortunately, the validity of factorization for these kinds of B decays can be assumed in the quasi-two-body mechanism, where all possible interactions between the pair of mesons are included, and interactions between the bachelor particle and daughter mesons from the resonance are ignored. Several theoretical approaches have been developed to describe the three-body hadronic decays of the B meson based on the symmetry principles and factorization theorems. The QCD-improved factorization (QCDF) [23-26] has been widely applied in the study of the three-body charmless hadronic decays of the B meson [27-37]. The U-spin and flavor
$ SU(3) $ symmetries were also adopted to analyze the three-body decays in Refs. [38-43].There are several theoretical approaches that can be used to calculate the hadronic B meson decays, such as the QCD-improved factorization (QCDF) [23-26], the perturbative QCD (PQCD) factorization approach [44-46], and the soft-collinear-effective theory (SCET) [47-51]. For most
$ B \to h_1 h_2 $ decay channels, the theoretical predictions obtained by adopting these different factorization approaches are in good agreement with each other and consistent with the data within errors. The naive factorization assumption (FA) does not apply to exclusive B meson decays into charmonia, such as$ B \to J/\psi K $ [52], which belongs to the color-suppressed mode. For a color-suppressed mode, a significant impact of non-factorizable contribution is expected. The predictions from FA for such decay channels are consistently small, as they neglect the non-factorizable effects. Thus, numerous attempts to resolve this puzzle have been made in more sophisticated approaches (for a review, see Ref. [46]). Although non-factorizable corrections to the FA have been included in QCDF approach, their predictions are too small to explain the data. QCDF is based on the collinear factorization, in which B meson transition form factors suffer the end-point singularity. The end-point singularity may render the estimation of the non-factorizable contributions out of control. Further details are provided in Ref. [53]. Based on the$ k_T $ factorization theorem, the perturbative QCD (PQCD) approach [54, 55] is suitable for describing different types of heavy hadron decays. The transverse-momentum-dependent hadronic wave function is introduced to remove the potential light-cone divergence and the rapidity singularity [56, 57]. Consequently, both factorizable and non-factorizable contributions can be calculated without end-point singularity. The Sudakov resummation has also been introduced to effectively suppress the long-distance contributions. Therefore, the PQCD approach is a self-consistent framework and has a good predictive power. In the previous studies [53, 58-62], the two-body decays of the$ B (B_c) $ mesons to$ \psi $ and a light vector meson have been studied in the PQCD framework, where the PQCD predictions are in good agreement with the data. However, the width of the resonant state and the interactions between final states associated with the resonances play an important role on the branching ratios and direct$ CP $ violations of the quasi-two-body decays in Refs. [63-71]. Hence, it seems more appropriate to treat a light vector meson as an intermediate resonance.In this study, with the help of the P-wave kaon-pion DAs and the time-like form factor
$ F_{K\pi} $ , which contains the final-state interactions between the kaon-pion pair, the quasi-two-body decays$ B\to \psi [K^*(892),K^*(1410), $ $K^*(1680)]\to \psi K\pi $ , as shown in Fig. 1, are investigated by the PQCD approach, utilizing the framework discussed in Refs. [72, 73], albeit the underlying$ k_T $ factorization has not been rigorously demonstrated [33, 34]. Throughout the remainder of the paper, the symbol$ K^* $ is used to denote the$ K^*(892) $ resonance. As the spin of$ \psi $ meson is 1, there are three possible polarizations generating the longitudinal (0), parallel ($ \parallel $ ), and perpendicular ($ \perp $ ) amplitudes. Therefore, the$ K\pi $ DAs involving both longitudinal and transverse polarizations are nontrivial nonperturbative inputs in our calculations. The two-pion (two-kaon) DAs corresponding to both longitudinal and transverse polarizations have been constructed to capture important final state interactions in the processes involving the resonant$ \rho $ ($ \phi $ ) in our previous studies [74, 75]. The P-wave kaon-pion DAs are introduced in a manner similar to the two-pion DAs [74], and the SU(3) flavor symmetry breaking effect for the kaon-pion pair is considered, which plays an important role in the longitudinal polarization.
Figure 1. Typical leading-order Feynman diagrams for quasi-two-body decays
$B \to \psi (K^* \to) K \pi$ , with$q=(u,d,s)$ . Diagrams (a) and (b) represent factorizable contributions, and diagrams (c) and (d) depict non-factorizable contributions.For the considered three-body hadronic B meson decays, the leading contributions are identified by defining power counting rules for various topologies of amplitudes [72]. Presently, there is no proof of factorization for the three-body B decays. We can only restrict ourselves to specific kinematical configurations, which form the basis of our study. The Dalitz plot contains different regions with "specific'' kinematics. The central region corresponds to the case where all three final particles fly apart with large energy, and none of them moves collinearly to any other. This situation, referred to as a genuine three-body decay, which contains two hard gluons, is power and
$ \alpha_s $ suppressed compared to the leading contribution. The corners correspond to the case in which one final particle is approximately at rest (i.e. soft), and the other two are fast and back-to-back. The central part of the edges corresponds to the case in which two particles move collinearly, and the other particle recoils. Further details are provided in Refs. [27, 76]. The significance of these special kinematic configurations is that different theoretical approaches may be applicable in different regions. The specific kinematic configuration, where two particles are collinear and generate a small invariant mass recoiling against the third one, yields a dominant contribution. This situation occurs particularly in the low$ \pi\pi $ or$ K\pi $ invariant mass region ($ \lesssim $ 2 GeV) of the Dalitz plot. The validity of factorization for this quasi-two-body B meson decay seems like an appropriate assumption. Consequently, it is reasonable to assume that the dynamics associated with the pair of final state mesons can be factorized into a two-meson distribution amplitude$ \Phi_{h_1h_2} $ [77-83]. The contribution from the soft kaon or pion region is included in the two-meson DA, as it also corresponds to the region with a small invariant mass.The typical PQCD factorization formula for a
$ B\to \psi K\pi $ decay amplitude is written in the following form [72],$ {\cal{A}} = \Phi_B\otimes H\otimes \Phi_{K\pi}\otimes\Phi_{\psi}. $

(1) The hard kernel H includes the dynamics of strong and electroweak interactions in three-body hadronic decays in a similar manner as the one for the corresponding two-body decays. The
$ \Phi_B $ ($ \Phi_{\psi} $ ) denotes the wave function for the B meson (the final state meson$ \psi $ ). The$ \Phi_{K\pi} $ is the two-hadron distribution amplitude, which absorbs the nonperturbative dynamics in the K-$ \pi $ hadronization process.The layout of the present paper is as follows. In Sec. 2, we briefly introduce the theoretical framework. The numerical results and discussions are presented in Sec. 3. Section 4 presents our conclusions. The Appendix collects explicit PQCD factorization formulas for all decay amplitudes.
-
We study the B meson rest frame and employ the light-cone coordinates for momentum variables. The B meson momentum
$ p_{B} $ , the total momentum of the kaon-pion pair,$ p = p_1+p_2 $ , the final-state$ \psi $ momentum$ p_3 $ , and the quark momentum$ k_i $ in each meson are chosen as$ \begin{split} p_{B} =& \frac{m_{B}}{\sqrt 2}(1,1,0_{\rm{T}}),\; \quad p = \frac{m_{B}}{\sqrt2}(1-r^2,\eta,0_{\rm{T}}),\; \\ p_3 =& \frac{m_{B}}{\sqrt 2}(r^2,1-\eta,0_{\rm{T}}), \\ k_{B} =& \left(0,x_B \frac{m_{B}}{\sqrt2} ,k_{B {\rm{T}}}\right),\quad k = \left( z (1-r^2)\frac{m_{B}}{\sqrt2},0,k_{\rm{T}}\right), \\ k_3 =& \left(r^2x_3\frac{m_B}{\sqrt{2}},(1-\eta)x_3 \frac{m_B}{\sqrt{2}},k_{3{\rm{T}}}\right),\end{split} $

(2) where
$ m_{B} $ is the mass of the B meson,$ \eta = \frac{\omega^2}{(1-r^2)m^2_{B}} $ with$ r = m_{\psi}/m_{B} $ ,$ m_{\psi} $ is the mass of charmonia, and the invariant mass squared$ \omega^2 = p^2 $ . The momentum fractions$ x_{B} $ , z, and$ x_3 $ run from zero to unity.We define the momentum
$ p_1 $ and$ p_2 $ of kaon-pion pair conventionally as$ \begin{split} p_1 =& \left (\zeta p^+, (1-\zeta)\eta p^+, \sqrt{\zeta(1-\zeta)}\omega,p_{1{\rm{T}}} \right ), \\ p_2 =& \left ( (1-\zeta) p^+, \zeta\eta p^+, -\sqrt{\zeta(1-\zeta)}\omega,p_{2{\rm{T}}} \right ), \end{split}$

(3) where
$ \zeta = p_1^+/P^+ $ characterizes the distribution of the longitudinal momentum of the kaon.The kaon-pion DAs can be related to the single kaon and pion through a perturbative evaluation of the matrix elements [68, 73],
$ \langle K(p_1)\pi(p_2)|\bar{q}_1(y^-)\Gamma q_2(0)|0\rangle, $

(4) as a time-like kaon-pion production process, where
$ \Gamma $ denotes the possible spin projectors I,$ \gamma_5 $ ,$ \gamma_{\mu} $ ,$ \gamma_{\mu}\gamma_5 $ ,$ \sigma_{\mu\nu} $ , and$ \sigma_{\mu\nu}\gamma_5 $ . All these projectors, except for the vector projector, are evaluated in the same way as the two-pion projectors [74]. Meanwhile, the vector current matrix elements must be reanalyzed in this study, because the significant SU(3) flavor symmetry breaking effect is included.The matrix element for the transition from vacuum to the
$ K\pi $ state via the vector current is defined in terms of the vector$ F^{\parallel}_{K\pi}(s) $ and scalar$ F^0_{K\pi}(s) $ form factors as follows,$ \begin{split} \langle K(p_1)\pi(p_2)|\bar{q}_1\gamma_{\mu}q_2|0\rangle = \left[(p_1-p_2)_{\mu}-\frac{m^2_{K}-m^2_{\pi}}{(p_1+p_2)^2}(p_1+p_2)_{\mu}\right] F^{\parallel}_{K\pi}(s) +\frac{m^2_K-m^2_{\pi}}{(p_1+p_2)^2}(p_1+p_2)_{\mu}F^0_{K\pi}(s), \end{split}$

(5) with the invariant mass squared
$ s = \omega^2 = (p_1+p_2)^2 $ . The scalar strange resonances contribute to the scalar form factor$ F^0_{K\pi}(s) $ , whereas the vector resonances contribute to the vector form factor$ F^{\parallel}_{K\pi}(s) $ . This study focuses on the vector strange resonances$ K^*(892),K^*(1410),K^*(1680) $ . Notably, the second term in the bracket appears because of the unequal mass between K and$ \pi $ . The term$ (m^2_{K}-m^2_{\pi})/(p_1+p_2)^2 $ describes the SU(3) symmetry breaking effect.The parametrization for the longitudinal and transverse components corresponding to the
$ \gamma_{\mu} $ spin projector is applied.$ (1) $ For the case$ \mu = + $ , we obtain$ (p_1-p_2)_\mu = $ $ (2\zeta-1 ) p^+ $ ,$ (p_1+p_2)_\mu = p^+ $ ; the twist-2 DA of longitudinal polarization can be described as$ {\not\!\! p} \left [P_1(2\zeta-1)-\frac{m^2_{K}-m^2_{\pi}}{\omega^2}P_0(2\zeta-1)\right ]\phi^0, $

(6) where
$ P_0(2\zeta-1) = 1 $ and$ P_1(2\zeta-1) = 2\zeta-1 $ are two Legendre Polynomials.$ (2) $ For the case$ \mu = x $ , we obtain$\begin{split}& (p_1-p_2)^x = 2 p_1^x = -2\sqrt{\zeta(1-\zeta)}\omega \frac{\epsilon^{x\nu\rho\sigma} \epsilon_{T\nu} p_{\rho} n_{-\sigma}}{p\cdot n_-}, \\& (p_1+p_2)^x = 0, \end{split}$

(7) where the transverse polarization vector is normalized to [74]
$ \epsilon_{T\mu} = \frac{\epsilon_{\mu\nu\rho\sigma} p_1^{\nu} p^{\rho} n_{-}^{\sigma}}{\sqrt{\zeta(1-\zeta)}\; \omega p\cdot n_-}. $

(8) Obviously, the SU(3) asymmetry term contributes to the longitudinal twist-2 DA, but not the transverse one.
Following the prescription in Refs. [74, 84], the expansions of nonlocal matrix elements for various spin projectors
$ \Gamma $ up to twist-3 are listed below:$ \begin{split} \langle K(p_1)\pi(p_2) |\bar{q}_1(y^-)\gamma_{\mu}q_2(0)|0\rangle=&(2\zeta-1-\frac{m^2_{K}-m^2_{\pi}}{\omega^2})p_{\mu}\int_0^1 {\rm d}z{\rm e}^{{\rm i}zP\cdot y}\phi^0(z,\omega)\\ &-2\sqrt{\zeta(1-\zeta)}\omega \frac{\epsilon^{\mu\nu\rho\sigma}\epsilon_{T\nu}p_{\rho}n_{-\sigma}}{p\cdot n_-} \int_0^1 {\rm d}z{\rm e}^{{\rm i}zp\cdot y}\phi^v(z,\omega), \end{split} $

(9) $ \langle K(p_1)\pi(p_2)|\bar{q}_1(y^-)Iq_2(0)|0\rangle = \omega \int_0^1 {\rm d}z{\rm e}^{{\rm i}zp\cdot y}\phi^s(z,\omega), $

(10) $ \langle K(p_1)\pi(p_2) |\bar{q}_1(y^-)\sigma_{\mu\nu}q_2(0)|0\rangle = -{\rm i} \frac{p_{1\mu}p_{2\nu}-p_{1\nu}p_{2\mu}}{\omega } \int_0^1 {\rm d}z{\rm e}^{{\rm i}zp\cdot y}\phi^t(z,\omega), $

(11) $ \langle K(p_1)\pi(p_2) |\bar{q}_1(y^-)\sigma_{\mu\nu}\gamma_5q_2(0)|0\rangle = -\sqrt{\zeta(1-\zeta)} \epsilon_{T\nu}p_{\mu} \int_0^1 {\rm d}z{\rm e}^{{\rm i}zp\cdot y}\phi^T(z,\omega), $

(12) $ \langle K(p_1)\pi(p_2) |\bar{q}_1(y^-)\gamma_{\mu}\gamma_5q_2(0)|0\rangle = {\rm i}\sqrt{\zeta(1-\zeta)}\omega \epsilon_{T\mu} \int_0^1 {\rm d}z{\rm e}^{{\rm i}zp\cdot y}\phi^a(z,\omega), $

(13) $ \langle K(p_1)\pi(p_2) |\bar{q}_1(y^-)\gamma_5q_2(0)|0\rangle = 0, $

(14) with the kaon-pion DAs
$ \phi^{0,T} $ and$ \phi^{s,t,v,a} $ being of twist-2 and twist-3, respectively. The SU(3) asymmetry factor$ (m^2_{K}-m^2_{\pi})/\omega^2 $ only exist in the longitudinal DA$ \phi^0 $ , but not in the other DAs up to twist 3.The P-wave kaon-pion DAs related to both longitudinal and transverse polarizations are introduced in analogy with the case of two-pion DAs [74],
$ \begin{split} \Phi_{K\pi}^{L} =& \frac{1}{\sqrt{2N_c}} \left [{ {\not\!\! p} }\phi^0(z,\zeta,\omega^2)+\omega\phi^s(z,\zeta,\omega^2) +\frac{{{\not\!\! p}}_1{{\not\!\! p}}_2 -{{\not\!\! p}}_2{{\not\!\! p}}_1}{\omega(2\zeta-1)}\phi^t(z,\zeta,\omega^2) \right ] \;, \\ \Phi_{K\pi}^{T} =& \frac{1}{\sqrt{2N_c}} \Big [\gamma_5{{\not\!\! {\epsilon}}}_{T}{ {\not\!\! p} } \phi^T(z,\zeta,\omega^2) +\omega \gamma_5{{\not\!\! {\epsilon}}}_{T} \phi^a(z,\zeta,\omega^2) + {\rm i}\omega\frac{\epsilon^{\mu\nu\rho\sigma}\gamma_{\mu} \epsilon_{T\nu}P_{\rho}n_{-\sigma}}{P\cdot n_-} \phi^v(z,\zeta,\omega^2) \Big ]. \end{split} $

(15) The aim of our study is to obtain the expressions of
$ \phi^0(z,\zeta,\omega^2) $ . According to Eq. (2.9) in Ref. [81], we decompose the kaon-pion DA into eigenfunctions of the evolution equation (Gegenbauer polynomials$ C_n^{\frac{3}{2}}(2z-1) $ ). Eventually, the explicit expression of$ \phi^0(z,\zeta,\omega^2) $ is written in the following form:$ \phi^0(z,\zeta,\omega^2) = \frac{F^{\parallel}_{K\pi}}{2\sqrt{2}}6z(1-z)\left[\sum a_nC_n^{\frac{3}{2}}(2z-1)\right](2\zeta-1-\alpha). $

(16) Below, we label the SU(3) symmetry breaking effect
$ (m^2_{K}-m^2_{\pi})/\omega^2 $ by$ \alpha $ for simplicity.Various twist DAs
$ \phi^i $ assume similar forms as the corresponding DAs for the$ K^* $ meson [53] by replacing the decay constants with the time-like form factor,$ \begin{split} \phi^0(z,\zeta,\omega^2) =& \frac{3F_{K\pi}^{\parallel}(\omega^2)}{\sqrt{2N_c}} z(1-z)\left[1+a_{1K^*}^{||}3t+a_{2K^*}^{||}\frac{3}{2}(5t^2-1)\right]\\&\times(2\zeta-1-\alpha)\;, \end{split} $

(17) $ \phi^s(z,\zeta,\omega^2) = \frac{3F_{K\pi}^{\perp}(\omega^2)}{2\sqrt{2N_c}}\bigg\{ t\left[1+a_{1s}^{\perp} t\right]-a_{1s}^{\perp}2z(1-z)\bigg\}(2\zeta-1) \;, $

(18) $ \phi^t(z,\zeta,\omega^2) = \frac{3F_{K\pi}^{\perp}(\omega^2)}{2\sqrt{2N_c}} t\left[ t+a_{1t}^{\perp}(3 t^2-1)\right](2\zeta-1) \;, $

(19) $\begin{split} \phi^T(z,\zeta,\omega^2) =& \frac{3F_{K\pi}^{\perp}(\omega^2)}{\sqrt{2N_c}}z(1-z)\left[1+a_{1K^*}^{\perp}3 t+ a_{2K^*}^{\perp}\frac{3}{2}(5 t^2-1)\right]\\&\times\sqrt{\zeta(1-\zeta)}\;, \end{split} $

(20) $ \phi^a(z,\zeta,\omega^2) = \frac{3F_{K\pi}^{\parallel}(\omega^2)}{4\sqrt{2N_c}}\bigg\{ t\left[1+a_{1a}^{\parallel} t\right]-a_{1a}^{\parallel}2z(1-z)\bigg\}\sqrt{\zeta(1-\zeta)}\;, $

(21) $ \phi^v(z,\zeta,\omega^2) = \frac{3F_{K\pi}^{\parallel}(\omega^2)}{8\sqrt{2N_c}}\left[1+ t^2+a_{1v}^{\parallel} t^3\right]\sqrt{\zeta(1-\zeta)}\;, $

(22) where
$ t = (1-2z) $ . Two Gegenbauer moments$ a_1 $ and$ a_2 $ are introduced for the twist-2 DAs and one Gegenbauer moment$ a_1 $ for each twist-3 DA. The B meson and$ \psi $ DAs are the same as those widely adopted in the PQCD approach [59-62, 74].The relativistic Breit-Wigner (RBW) line shape is adopted for the P-wave resonance
$ K^*(892), $ $ K^*(1410) $ , and$ K^*(1680) $ to parameterize the time-like form factor$ F_{K\pi}^{\parallel}(s) $ , which is widely adopted in the experimental data analysis. The explicit expression is in the following form [85],$ \begin{split} F_{K\pi}^{\parallel}(s) =& \frac{c_1 m_{K^*(892)}^2}{m^2_{K^*(892)} -s-{\rm i}m_{K^*(892)}\Gamma_1(s)} \\&+\frac{c_2 m_{K^*(1410)}^2}{m^2_{K^*(1410)} -s-{\rm i}m_{K^*(1410)}\Gamma_2(s)} \\ &+ \frac{c_3 m_{K^*(1680)}^2}{m^2_{K^*(1680)} -s-{\rm i}m_{K^*(1680)}\Gamma_3(s)}\;, \end{split} $

(23) where
$ c_i $ (i = 1,2,3) are the corresponding weight coefficients and satisfy$ c_1+c_2+c_3 = 1 $ due to the normalization condition$ F_{K\pi}^{\parallel}(0) = 1 $ . The three terms describe the contributions from$ K^*(892) $ ,$ K^*(1410) $ , and$ K^*(1680) $ , respectively. We find that there is no existing data for the interferences among these resonances. Thus, as a first order approximation, we only determine the modules of the complex weight coefficients$ c_i $ (i = 1,2,3) and ignore their phases.Here, the mass-dependent width
$ \Gamma_i(s) $ is defined by$ \Gamma_i(s) = \Gamma_i\frac{m_i}{\sqrt{s}}\left(\frac{|\overrightarrow{p_1}|}{|\overrightarrow{p_0}|}\right)^{(2L_R+1)}, $

(24) where
$ |\overrightarrow{p_1}| $ is the momentum vector of the resonance decay product measured in the resonance rest frame, and$ |\overrightarrow{p_0}| $ is the value of$ |\overrightarrow{p_1}| $ when$ \sqrt{s} = m_{K^*} $ .$ L_R $ is the orbital angular momentum in the$ K\pi $ system, and$ L_R = 0,1,2,... $ corresponds to the$ S,P,D,... $ partial-wave resonances. Because the vector resonance has spin-1, and kaon (pion) has spin-0, when the$ K\pi $ system forms a spin-1 resonance, the orbital angular momentum between the kaon and pion must be$ L_R = 1 $ , which refers to a P wave configuration.$ m_i $ and$ \Gamma_i $ are the pole mass and width of the corresponding resonance, respectively, where$ i = 1,2,3 $ represents the resonance$ K^*(892) $ ,$ K^*(1410) $ and$ K^*(1680) $ , respectively. According to Ref. [63], we also assume that$ F_{K\pi}^{\perp}(s)/F_{K\pi}^{\parallel}(s)\approx f_{K^*}^T/f_{K^*}, $

(25) with
$ f_{K^*} = 0.217 \pm 0.005 \;{\rm{GeV}}, f^T_{K^*} = 0.185 \pm 0.010\;{\rm{GeV}} $ [86-88]. Because of the limited studies on the decay constants of$ K^*(1410) $ and$ K^*(1680) $ , we use the two decay constants of$ K^*(892) $ to determine the ratio$ F_{K\pi}^{\perp}(s)/F_{K\pi}^{\parallel}(s) $ . -
The differential branching fraction for the
$ B\rightarrow \psi K\pi $ decays into the P-wave kaon-pion pair is expressed as$ \frac{{\rm d} {\cal{B}}}{{\rm d} \omega} = \frac{\tau_B \omega|\vec{p}_1||\vec{p}_3|}{32\pi^3M^3} \sum\limits_{i = 0,\parallel,\perp}|{\cal{A}}_i|^2, $

(26) where the kaon and charmonium three-momenta in the
$ K\pi $ center-of-mass frame are given by$ |\overrightarrow{p_1}| = \frac{\sqrt{\lambda(\omega^2,m_K^2,m_{\pi}^2)}}{2\omega}, \; \quad |\overrightarrow{p_3}| = \frac{\sqrt{\lambda(m_B^2,m_{\psi}^2,\omega^2)}}{2\omega}, $

(27) with the kaon (pion) mass
$ m_K $ ($ m_{\pi}) $ and the K$ \ddot{a} $ ll$ \acute{e} $ n function$ \lambda (a,b,c) = a^2+b^2+c^2-2(ab+ac+bc) $ . The terms$ {\cal{A}}_0 $ ,$ {\cal{A}}_{\parallel} $ , and$ {\cal{A}}_{\perp} $ represent the longitudinal, parallel, and perpendicular polarization amplitudes in the transversity basis, respectively, which are related to$ {\cal{A}}_{L,N,T} $ in the Appendix. The polarization fraction$ f_{\lambda} $ with$ \lambda = 0 $ ,$ \parallel $ , and$ \perp $ is described by$ f_{\lambda} = \frac{|{\cal{A}}_{\lambda}|^2}{|{\cal{A}}_0|^2 +|{\cal{A}}_{\parallel}|^2+|{\cal{A}}_{\perp}|^2}, $

(28) with the normalization relation
$ f_0+f_{\parallel}+f_{\perp} = 1 $ .Before proceeding with the numerical analysis, the meson masses and widths (in units of GeV) are collected below for the numerical calculation [89]:
$ \begin{split} & m_{B} = 5.280, \quad m_{B_s} = 5.367, \quad m_{K^{*0}} = 0.89555, \\ & m_{K^*(1410)} = 1.421,\quad m_{K^*(1680)} = 1.718, \quad m_{J/\psi} = 3.097, \\& m_{\psi(2S)} = 3.686, \quad m_{\pi^{\pm}} = 0.140, \quad m_{K^{\pm}} = 0.494, \\ &\Gamma_{K^*} = 0.0473, \quad \Gamma_{K^*(1410)} = 0.236,\quad \Gamma_{K^*(1680)} = 0.322. \end{split}$

(29) The values of the Wolfenstein parameters are adopted from Ref. [89]:
$ A = 0.836\pm0.015, \lambda = 0.22453\pm $ $ 0.00044 $ ,$ \bar{\rho} = 0.122^{+0.018}_{-0.017} $ ,$ \bar{\eta} = 0.355^{+0.012}_{-0.011} $ . The decay constants (in units of GeV) and the B meson lifetimes (in units of ps) are chosen as [59, 60, 64]$ \begin{split} & f_B = 0.19, \quad f_{B_s} = 0.23, \quad f_{J/\psi} = 0.405, \quad f_{\psi(2S)} = 0.296,\\& f_{K^*} = 0.217, \quad f^T_{K^*} = 0.185,\quad \tau_{B^0} = 1.519,\quad \tau_{B^{\pm}} = 1.638, \\& \tau_{B_{s}} = 1.512. \end{split}$

(30) The Gegenbauer moments and coefficients
$ c_i $ (i = 1,2,3) are determined on the basis of the existing data for the$ B\to \psi K\pi $ branching ratios and polarization fractions from PDG2018 [89],$\begin{split} & a_{1K^*}^{\parallel} = 0.2, \quad a_{2K^*}^{\parallel} = 0.5, \quad a_{1s}^{\perp} = -0.2, \quad a_{1t}^{\perp} = 0.2,\\ & a_{1K^*}^{\perp} = 0.3, \quad a_{2K^*}^{\perp} = 0.8, \quad a_{1a}^{\parallel} = -0.3, \quad a_{1v}^{\parallel} = 0.3,\\ & c_1 = 0.72, \; \quad c_2 = 0.135, \; \quad c_3 = 0.145. \end{split}$

(31) In place of the asymptotic forms of the twist-3 DAs used in the two-body study [58], we introduce one Gegenbauer moment
$ a_1 $ for each twist-3 DA in analogy to the cases for the resonance$ \rho $ in Ref. [74]. We also include an important asymmetric factor$ \alpha $ , which has strong influence on the Gegenbauer moments of twist-2 DAs. The combined effect differentiates the Gegenbauer moments of twist-2 DAs in the quasi-two-body framework from those in the two-body framework [58]. In this study, we fix the Gegenbauer moments of the kaon-pion DAs by matching the theoretical results to experimental data. To determine the four longitudinal Gegenbauer moments$ a_{1K^*}^{\parallel} $ ,$ a_{2K^*}^{\parallel} $ ,$ a_{1s}^{\perp} $ , and$ a_{1t}^{\perp} $ , we pick up the four branching ratios associated with the longitudinal polarization of the$ B^0 \to J/\psi (K^{*}(892)^{0} \to)K^+\pi^- $ and$ B^0 \to \psi(2S) (K^{*}(892)^{0}\to) $ $ K^+\pi^- $ decays from [89], and of the$B^0_s \to J/\psi $ $ (\bar{K}^{*}(892)^{0} \to)K^-\pi^+$ decay measured by LHCb [11], as well as the branching ratio of the$B^0 \to \eta_c(1S) $ $ (K^{*}(892)^{0} \to)K^+\pi^- $ decay [89] as the data inputs. Thus, we can solve the four longitudinal Gegenbauer moments from the four inputs. Similarly, the four transverse Gegenbauer moments can be constrained by the transverse polarization fractions of the two decay modes$B^0 \to $ $ J/\psi (K^{*}(892)^{0} \to)K^+\pi^- $ and$B^0 \to \psi(2S) (K^{*}(892)^{0} \to) $ $ K^+\pi^- $ . Each decay channel has parallel and perpendicular components. We solve the four transverse Gegenbauer moments from the four inputs as well. Naturally, considering experimental uncertainties, it is difficult to precisely restrict these parameters. We merely make the theoretical branching ratios compatible with the experimental ones by adjusting the corresponding Gegenbauer moments. Apart from the results for the$ B^0 \to J/\psi $ $ (K^{*}(892)^{0} \to) K^+\pi^- $ and$ B^0 \to \psi(2S) (K^{*}(892)^{0} \to) K^+\pi^- $ decays from [89] and the branching ratio of the$ B^0_s \to J/\psi (\bar{K}^{*}(892)^{0} \to)K^-\pi^+ $ decay associated with the longitudinal polarization [11], other results shown in Tables 1 and 2 are our predictions based on the determined parameters.Modes PQCD predictions Experimenta $B^0 \to J/\psi (K^{*}(892)^{0} \to)K^+\pi^- $ 

$\mathcal{B}(10^{-4})$ 

$8.31^{+3.34+2.32+1.89+1.81+0.00}_{-2.41-1.77-1.78-1.22-0.14}$ 

$8.47\pm0.03$ 

$f_0$ (%)

$55.9^{+13.4+14.2+0.0+1.8+0.0}_{-16.6-12.9-0.5-0.9-0.1}$ 

$57.1\pm0.7$ 

$f_{\parallel}$ (%)

$21.1^{+8.0+7.2+0.1+0.3+0.1}_{-6.4-8.2-0.1-1.0-0.1}$ 

$-$ 

$f_{\perp}$ (%)

$23.0^{+8.7+5.6+0.4+0.6+0.1}_{-6.9-6.2-0.0-0.8-0.0}$ 

$21.1\pm0.8$ 

$B^0 \to J/\psi (K^{*}(1410)^{0} \to)K^+\pi^- $ 

$\mathcal{B}(10^{-5})$ 

$1.98^{+0.72+0.52+0.33+0.68+0.02}_{-0.46-0.24-0.28-0.38-0.02}$ 

$-$ 

$f_0$ (%)

$53.1^{+13.2+11.3+2.3+2.9+0.6}_{-13.3-11.6-0.8-2.1-0.2}$ 

$-$ 

$f_{\parallel}$ (%)

$20.1^{+5.8+8.3+0.7+0.4+0.2}_{-5.8-8.7-1.1-1.1-0.7}$ 

$-$ 

$f_{\perp}$ (%)

$26.8^{+7.6+3.5+0.1+1.7+0.1}_{-7.6-2.8-1.1-1.2-0.1}$ 

$-$ 

$B^0 \to J/\psi (K^{*}(1680)^{0} \to)K^+\pi^- $ 

$\mathcal{B}(10^{-5})$ 

$2.02^{+0.66+0.54+0.36+0.71+0.02}_{-0.67-0.54-0.52-0.62-0.03}$ 

$-$ 

$f_0$ (%)

$51.2^{+12.9+10.8+1.4+2.9+1.4}_{-14.4-11.4-0.9-4.0-0.2}$ 

$-$ 

$f_{\parallel}$ (%)

$19.7^{+5.8+10.5+0.7+1.8+0.5}_{-5.2-9.4-0.2-0.8-0.3}$ 

$-$ 

$f_{\perp}$ (%)

$29.1^{+8.7+1.5+0.2+2.2+0.0}_{-7.7-2.4-1.2-2.1-1.1}$ 

$-$ 

$B^0_s \to J/\psi (\bar{K}^{*}(892)^{0} \to)K^-\pi^+ $ 

$\mathcal{B}(10^{-5})$ 

$2.29^{+1.26+0.87+0.79+0.50+0.05}_{-0.74-0.58-0.52-0.27-0.00}$ 

$2.73\pm0.27$ 

$f_0$ (%)

$54.3^{+17.5+17.6+1.0+1.9+1.7}_{-19.7-15.9-0.0-0.0-0.0}$ 

$49.7\pm3.5$ 

$f_{\parallel}$ (%)

$24.7^{+10.6+8.8+0.1+0.0+0.0}_{-9.5-9.5-0.1-0.9-0.6}$ 

$17.9\pm3.0$ 

$f_{\perp}$ (%)

$21.0^{+8.9+7.1+0.0+0.0+0.0}_{-8.1-7.3-0.9-1.0-1.1}$ 

$-$ 

$B^0_s \to J/\psi (\bar{K}^{*}(1410)^{0} \to)K^-\pi^+ $ 

$\mathcal{B}(10^{-7})$ 

$7.22^{+2.64+2.24+1.56+1.78+0.00}_{-2.71-1.28-1.43-1.20-0.02}$ 

$-$ 

$f_0$ (%)

$48.3^{+14.7+10.4+0.3+1.4+0.3}_{-15.9-12.1-0.0-1.4-0.0}$ 

$-$ 

$f_{\parallel}$ (%)

$27.8^{+8.6+8.7+0.0+0.0+0.2}_{-7.9-8.7-0.2-0.6-0.3}$ 

$-$ 

$f_{\perp}$ (%)

$23.9^{+7.4+3.6+0.2+1.5+0.0}_{-6.7-2.1-0.1-0.7-0.2}$ 

$-$ 

$B^0_s \to J/\psi (\bar{K}^{*}(1680)^{0} \to)K^-\pi^+ $ 

$\mathcal{B}(10^{-7})$ 

$7.36^{+2.44+2.37+1.29+2.18+0.03}_{-1.46-1.27-1.38-1.05-0.04}$ 

$-$ 

$f_0$ (%)

$42.6^{+14.8+7.6+0.0+2.4+0.2}_{-13.5-11.1-0.9-0.8-0.4}$ 

$-$ 

$f_{\parallel}$ (%)

$29.6^{+7.2+10.5+0.9+0.0+0.5}_{-7.7-8.0-0.1-0.6-0.6}$ 

$-$ 

$f_{\perp}$ (%)

$27.8^{+6.6+2.2+0.1+0.4+0.1}_{-7.2-1.0-0.1-1.3-0.1}$ 

$-$ 

a Experimental results are obtained by multiplying the relevant measured two-body branching ratios according to Eq. (32). Table 1. PQCD predictions for branching ratios and polarization fractions defined in Eq. (28) of P-wave resonance channels in
$B^0_{(s)} \to J/\psi K^{\pm} \pi^{\mp}$ decay along with experimental data [89]. Theoretical errors are attributed to the variation of the longitudinal ($a_{1K^*}^{||}$ and$a_{2K^*}^{||}$ ) and transverse ($a_{1K^*}^{\perp}$ and$a_{2K^*}^{\perp}$ ) Gegenbauer moments, the shape parameters$\omega_{B_{(s)}}$ in the wave function of$B_{(s)}$ meson and the hard scale t, and the parameters in the wave functions of charmonium.Modes PQCD predictions Experimenta $B^0 \to \psi(2S)(K^{*}(892)^{0} \to)K^+\pi^- $ 

$\mathcal{B}(10^{-4})$ 

$3.38^{+1.03+0.97+0.89+0.79+0.03}_{-0.84-0.74-0.77-0.58-0.01}$ 

$3.93\pm0.27$ 

$f_0$ (%)

$46.4^{+18.7+12.4+0.0+1.1+0.2}_{-16.6-10.4-1.0-2.6-0.0}$ 

$46.3^{+2.8}_{-4.0}$ 

$f_{\parallel}$ (%)

$25.4^{+7.9+7.5+0.5+1.4+0.0}_{-6.3-8.5-0.2-0.7-0.3}$ 

$-$ 

$f_{\perp}$ (%)

$28.2^{+8.8+3.5+0.5+1.2+0.0}_{-6.9-4.0-0.0-0.4-0.1}$ 

$30.0\pm6.0$ 

$B^0 \to \psi(2S)(K^{*}(1410)^{0} \to)K^+\pi^- $ 

$\mathcal{B}(10^{-6})$ 

$4.88^{+1.41+1.33+1.08+1.85+0.09}_{-1.11-0.93-0.81-1.02-0.01}$ 

$-$ 

$f_0$ (%)

$44.8^{+13.3+10.1+1.1+3.0+0.9}_{-15.2-10.2-1.4-2.9-0.5}$ 

$-$ 

$f_{\parallel}$ (%)

$23.2^{+7.3+10.2+1.2+1.1+0.6}_{-5.5-10.6-0.8-1.3-0.5}$ 

$-$ 

$f_{\perp}$ (%)

$32.0^{+8.8+1.3+0.3+1.8+0.0}_{-7.7-0.7-0.3-1.7-0.3}$ 

$-$ 

$B^0_s \to \psi(2S) (\bar{K}^{*}(892)^{0} \to)K^-\pi^+ $ 

$\mathcal{B}(10^{-6})$ 

$7.69^{+3.02+3.32+1.53+1.80+0.05}_{-1.93-2.26-1.75-1.21-0.00}$ 

$22.0\pm3.3$ 

$f_0$ (%)

$39.4^{+17.7+14.9+0.8+1.6+0.2}_{-18.9-12.7-1.3-2.0-0.5}$ 

$52.0\pm6.0$ 

$f_{\parallel}$ (%)

$32.0^{+10.0+8.2+0.8+0.7+0.3}_{-9.4-10.4-0.5-0.9-0.8}$ 

$-$ 

$f_{\perp}$ (%)

$28.6^{+8.9+4.5+0.5+1.3+1.2}_{-8.3-4.6-0.3-0.7-0.5}$ 

$-$ 

$B^0_s \to \psi(2S) (\bar{K}^{*}(1410)^{0} \to)K^-\pi^+ $ 

$\mathcal{B}(10^{-7})$ 

$1.50^{+0.51+0.54+0.37+0.47+0.00}_{-0.30-0.36-0.29-0.20-0.01}$ 

$-$ 

$f_0$ (%)

$28.5^{+17.8+8.1+0.5+2.5+0.8}_{-17.3-8.2-0.0-1.3-0.0}$ 

$-$ 

$f_{\parallel}$ (%)

$34.1^{+8.3+10.7+0.2+0.1+0.1}_{-8.5-11.2-0.1-0.8-1.0}$ 

$-$ 

$f_{\perp}$ (%)

$37.4^{+8.9+3.2+0.0+2.1+0.7}_{-9.3-2.6-0.6-2.7-0.9}$ 

$-$ 

a Experimental results are obtained by multiplying the relevant measured two-body branching ratios according to Eq. (32). Table 2. PQCD predictions for branching ratios and polarization fractions defined in Eq. (28) of the P-wave resonance channels in the
$B^0_{(s)} \to \psi(2S) K^{\pm} \pi^{\mp}$ decay along with experimental data [89]. Theoretical errors are attributed to the variation of the longitudinal ($a_{1K^*}^{||}$ and$a_{2K^*}^{||}$ ) and transverse ($a_{1K^*}^{\perp}$ and$a_{2K^*}^{\perp}$ ) Gegenbauer moments, the shape parameters$\omega_{B_{(s)}}$ in the wave function of$B_{(s)}$ meson and the hard scale t, and the parameters in the wave functions of charmonium.The SU(3) asymmetric term
$ \alpha = (m^2_{K}-m^2_{\pi})/\omega^2 $ plays an important role in the longitudinal polarization fraction$ f_0 $ , as it appears in the expression of the longitudinal twist-2 kaon-pion DA. We also estimate the average value of the asymmetric factor$ \alpha $ to lie within the range from 0.05 to 0.6 using the relation$ \alpha = (m^2_{K}-m^2_{\pi})/\omega^2 $ with the kinematic bounds on the value of$ \omega $ [$ (m_K+m_\pi) \leqslant \omega\leqslant (m_B-m_\psi ) $ ]. We find that the average value of$ \alpha $ is effectively approximately 0.2, as shown in Fig. 2, where the curves for the central values of$ B^0 \to J/\psi (K^{*}(892)^{0} \to)K^+\pi^- $ (the gray dashed line) and$ B^0 \to \psi(2S) (K^{*}(892)^{0} \to)K^+\pi^- $ (the gray dash-dotted line) decays associated with longitudinal polarization fractions from data [89], and the curves for the$ B^0 \to J/\psi $ $(K^{*}(892)^{0} \to)K^+\pi^- $ (the red solid line) and the$B^0 \to \psi(2S) $ $ (K^{*}(892)^{0} \to)K^+\pi^- $ (the blue dotted line) decays are obtained by varying$ \alpha $ as a free parameter.
Figure 2. (color online) Longitudinal polarization fraction
$f_0$ as a function of asymmetric factor$\alpha$ for the$B^0 \to J/\psi (K^{*}(892)^{0} \to)$ $K^+\pi^- $ (red solid line) and$B^0 \to \psi(2S) $ $ (K^{*}(892)^{0} \to)K^+\pi^- $ (blue dotted line) decays. The gray dashed and dash-dotted lines represent the central values of the experimental data [89] for their corresponding decay modes. Shaded bands indicate experimental errors.Because the
$ K^*(892) $ components in both$ J/\psi $ and$ \psi(2S) $ modes are efficiently measured with a high significance by the Belle Collaboration [6, 8], we can exactly determine its weight coefficient$ c_1 = 0.72 $ based on its fit fraction. However, the significance of the two high-mass$ K^* $ states is too low for precise determination of$ c_2 $ and$ c_3 $ . For example, the fit fractions for the$ K^*(1410) $ and$ K^*(1680) $ components in the$ \psi(2S) $ channel are$ 5.5^{+8.8}_{-1.5} $ % and$ 2.8^{+5.8}_{-1.0} $ % (statistical errors only), respectively. The corresponding measurements in the$ J/\psi $ mode for the two components are both$ 0.3^{+0.2}_{-0.1} $ % (statistical error only). LHCb made the first Dalitz plot analysis for$ B^0\rightarrow \eta_c(1S) K^+\pi^- $ decays [90]. Their fitting model yields almost equal fit fractions of$ K^*(1410) $ and$ K^*(1680) $ (Table 7 of Ref. [90]), which is very similar to the situation in the$ J/\psi $ mode, as mentioned above. Therefore, it is reasonable to assume that the branching ratios of$ B \to \psi K^*(1410)^0 \to \psi K^+\pi^- $ and$ B \to \psi K^*(1680)^0\to \psi K^+\pi^- $ are approximately equal, and employ the normalization of$ c_1+c_2+c_3 = 1 $ . Then,$ c_2 $ and$ c_3 $ are determined as$ 0.135 $ and$ 0.145 $ , respectively. The small gap between them is understandable with respect to the different nominal masses and widths of$ K^*(1410) $ and$ K^*(1680) $ . We emphasize that our predictions on the excited state channels are only rough estimates of the magnitude, which need to be tested precisely in future experiments.Using Eqs. (26)–(28), the decay amplitudes in the Appendix and all input quantities, the resultant branching ratios
$ {\cal{B}} $ and the polarization fractions$ f_{\lambda} $ , along with the available experimental measurements are summarized in Table 1, while those values for$ \psi(2S) $ are listed in Table 2. Because charged B meson decays differ from the neutral decays only with regard to the lifetimes and the isospin factor in our formalism, we can derive the branching ratios for the$ B^+ $ meson by multiplying those for the$ B^0 $ meson by the ratio$ \tau_{B^+}/\tau_{B^0} $ . For the color-suppressed decays, it is expected that the factorizable diagram contribution is suppressed due to the cancellation of Wilson coefficients$ C_1 + C_2/3 $ . After the inclusion of the vertex corrections, the factorizable diagram contributions in Fig. 1(a) and (b) become comparable with the nonfactorizable ones in Fig. 1(c) and (d).In our numerical calculations for branching ratios and polarization fractions, the first two theoretical errors originate from the Gegenbauer moments in the longitudinal and transverse twist-2 kaon-pion DAs, namely,
$ a_{1K^*}^{||} = 0.2\pm0.2, a_{2K^*}^{||} = 0.5\pm0.5 $ and$a_{1K^*}^{\perp} = 0.3\pm0.3, a_{2K^*}^{\perp} =$ $ 0.8\pm0.8 $ , respectively. For the hadronic charmonium B decays, the energy release may not be sufficiently high to justify the PQCD leading order (LO) calculation, and the theoretical accuracy must be improved. Here, significant vertex corrections are included, such that the Gegenbauer momenta$ a_{1K^*}^{\parallel}, a_{2K^*}^{\parallel} $ in Eq. (17) are redefined and different from those in our previous study [69], for which the hard kernels are evaluated only up to the LO level. Therefore, a wide variation of the Gegenbauer moments is considered for the error estimation, such as$a_{1K^*}^{||} = 0.2\pm0.2 $ ,$ a_{2K^*}^{||} = 0.5\pm0.5 $ , which covers the previously determined central value$ a_{1K^*}^{||} = 0.05, a_{2K^*}^{||} = 0.15 $ . The third theoretical uncertainty results from the shape parameter$ \omega_{B_{(s)}} $ of the$ B_{(s)} $ meson distribution amplitude. We adopt the value$ \omega_B = 0.40\pm $ $0.04 $ GeV or$ \omega_{B_s} = 0.50\pm0.05 $ GeV and vary its value within a 10% range, which is supported by intensive PQCD studies [44, 45, 91, 92]. The fourth error is caused by the variation of the hard scale t from$ 0.75t $ to$ 1.25t $ (without changing$ 1/b_i $ ), which characterizes the effect of the high order QCD contributions. The last error is attributed to the hadronic parameter$ \omega_c = 0.60\pm0.06 $ ($ \omega_c = 0.20\pm0.02 $ ) GeV for$ J/\psi $ ($ \psi(2S) $ ) meson [61, 62] from the wave functions of charmonium.The main uncertainties in our approach originate from the Gegenbauer moments, as listed in Table 1 and Table 2, which can reach a total of about 60% in magnitude. The scale-dependent uncertainty is less than 25% due to the inclusion of the NLO vertex corrections. We evaluated the sensitivity of our results with respect to the choice of the shape parameter
$ \omega_c $ in the charmonia meson wave function. The variation in$ \omega_c $ results in small changes of the branching ratio and polarization fractions, less than approximately 10%. We also examined the sensitivity of our results with respect to the choices of other Gegenbauer moments ($ a_{1s}^{\perp}, a_{1t}^{\perp}, a_{1a}^{\parallel}, a_{1v}^{\parallel} $ ) in the twist-3 DAs. These Gegenbauer moments in the twist-3 DAs have a smaller impact on the total branching ratios than those in the twist-2 DAs. With the increase (decrease) of$ a_{1s}^{\perp}, a_{1t}^{\perp}, a_{1a}^{\parallel}, a_{1v}^{\parallel} $ , the total branching ratios and the longitudinal polarization fractions become larger for the$ B^0 $ ($ B^0_s $ ) decay modes. The opposite pattern of the B and$ B_s $ modes is understood, as they decay into different$ K\pi $ pairs. The positive$ a_1^{\perp,\parallel} $ related to a$ K^+\pi^- $ pair carries an$ \bar s $ quark, while$ a_1^{\perp,\parallel} $ must change the sign for the$ K^-\pi^+ $ pair with an s quark. The errors due to uncertainties in$ m_c $ and CKM matrix elements are very small and can be safely neglected.Our predictions of the branching ratios for the involved
$ J/\psi $ channels are in good agreement with the available data [89] in Table 1. For the$ B^0 \to \psi(2S) (K^{*0} \to) $ $K^+\pi^- $ decay, the PQCD prediction for its branching ratio is consistent with the world average$ (3.93\pm 0.27) \times $ $ 10^{-4} $ within errors. Meanwhile, for the$ B^0_s \to \psi(2S) \bar{K}^{*0} \to \psi K^-\pi^+ $ decay process, the central value of our theoretical prediction the branching ratio is slightly smaller than that of the PDG number [89], within errors. However, the PDG result is obtained by multiplying the best value$ {\cal{B}}(B^{0}\to \psi(2S) K^+\pi^-) $ with the measured ratio$ {\cal{B}}(\bar{B}_s^{0}\to \psi(2S) K^+\pi^-)/ {\cal{B}}(B^{0}\to\psi(2S) K^+\pi^-) $ via an intermediate state$ K^*(892)^0 $ from the LHCb collaboration [12]. We hope that the experiment will provide a direct measurement of this decay mode in the future.The two-body branching fraction
$ {\cal B}(B \to \psi K^{*0}) $ can be extracted from the corresponding quasi-two-body decay modes in Tables 1 and 2 under the narrow width approximation relation$ {\cal{B}}(B \to \psi K^{*0}\to \psi K^+ \pi^- ) = {\cal{B}}( B \to \psi K^{*0}) \cdot {\cal{B}}(K^{*0} \to K^+\pi^-), $

(32) where we assume the
$ K^{*0}\to K\pi $ branching fraction to be 100%. Isospin conservation is assumed for the strong decays of an$ I = 1/2 $ resonance$ K^{*0} $ to$ K\pi $ when branching fractions of the quasi-two-body process$ B \to \psi K^{*0}\to \psi K^+\pi^- $ are computed, as follows:$ \frac{\Gamma(K^{*0} \to K^+\pi^-)}{\Gamma(K^{*0} \to K\pi)} = 2/3, \; \quad \frac{\Gamma(K^{*0} \to K^0\pi^0)}{\Gamma(K^{*0} \to K\pi)} = 1/3. $

(33) When compared with previous theoretical predictions for
$ B \to \psi K^* $ in the two-body framework both in the PQCD approach [53, 58, 61] and in the QCDF approach [93], we find that the branching ratios of the quasi-two-body decay modes are in good agreement with those two-body analyses based on the PQCD approach [58, 61]. Taking$ B^0 \to J/\psi K^{*0} $ decay as an example, we obtain the$ {\cal B}( B^0 \to J/\psi K^{*0}) \approx 1.25 \times 10^{-3} $ from the value as listed in the first section of Table 1, which agrees well with the theoretical prediction$ {\cal B}( B^0 \to J/\psi K^{*0}) = (1.23^{+0.42}_{-0.36}) \times 10^{-3} $ as provided in Ref. [58], and with the world average of the measured ones from BABAR, CDF, and Belle Collaborations [2, 8, 14]:$ (1.3\pm 0.06) \times 10^{-3} $ from HFLAV [94]. The consistency of the PQCD predictions for the branching ratios supports the usability of the PQCD factorization for exclusive hadronic B meson decays. Our PQCD predictions for branching ratios are also consistent with those in the QCDF approach [93] within errors.In Fig. 3(a), we show the
$ \omega $ -dependence of the differential decay rate$ {\rm d}{\cal B}(B^0 \to J/\psi K^+\pi^-)/{\rm d}\omega $ after the inclusion of possible contributions from the resonant states$ K^* $ (the solid curve),$ K^*(1410) $ (the dashed curve),$ K^*(1680) $ (the dotted curve). Similarly, we display the PQCD prediction for$ {\rm d}{\cal B}/{\rm d}\omega $ for$ B^0 \to \psi(2S)K^{*0}\to \psi(2S)K^+\pi^- $ (solid curve) and$ B^0 \to \psi(2S)K^*(1410)^0\to \psi(2S)K^+\pi^- $ (blue dashed curve) in Fig. 3(b). For the considered decay modes$ B^0 \to \psi K^+\pi^- $ , the dynamical limit on the value of invariant mass$ \omega $ is$ (m_{K^+}+m_{\pi^-}) \leqslant \omega \leqslant (m_B-m_{\psi}) $ . For$ B^0 \to \psi(2S) K^+\pi^- $ decays, as$ m_{K^*(1680)} > \omega_{\max} = $ $(m_B- m_{\psi(2S)}) $ , the resonance$ K^*(1680) $ does not contribute to this decay. Evidently, the differential branching ratios of these decays exhibit peaks at the pole mass of the resonant states. Thus, the main portion of the branching ratios lies, as expected, in the region around the resonance. For$ B^0 \to J/\psi K^{*0} \to J/\psi K^+\pi^- $ decay, the central values of the branching ratio$ {\cal B} $ are$ 4.29\times10^{-4} $ and$ 6.49\times 10^{-4} $ when the integration over$ \omega $ is limited in the range of$ \omega = [m_{K^*}-0.5\Gamma_{K^*}, m_{K^*}+0.5\Gamma_{K^*}] $ or$ \omega = [m_{K^*}-\Gamma_{K^*}, m_{K^*}+\Gamma_{K^*}] $ respectively, which amount to a respective 51.6% and 78.1% of the total branching ratio$ {\cal B} = 8.31\times10^{-4} $ , as listed in Table 1. The peak of$ K^*(1680) $ has slightly smaller strength than the$ K^*(1410) $ , while its broader width compensates the integrated strength over the entire phase space. Therefore, the branching ratios of the two components are of a comparable size, as predicted in our work.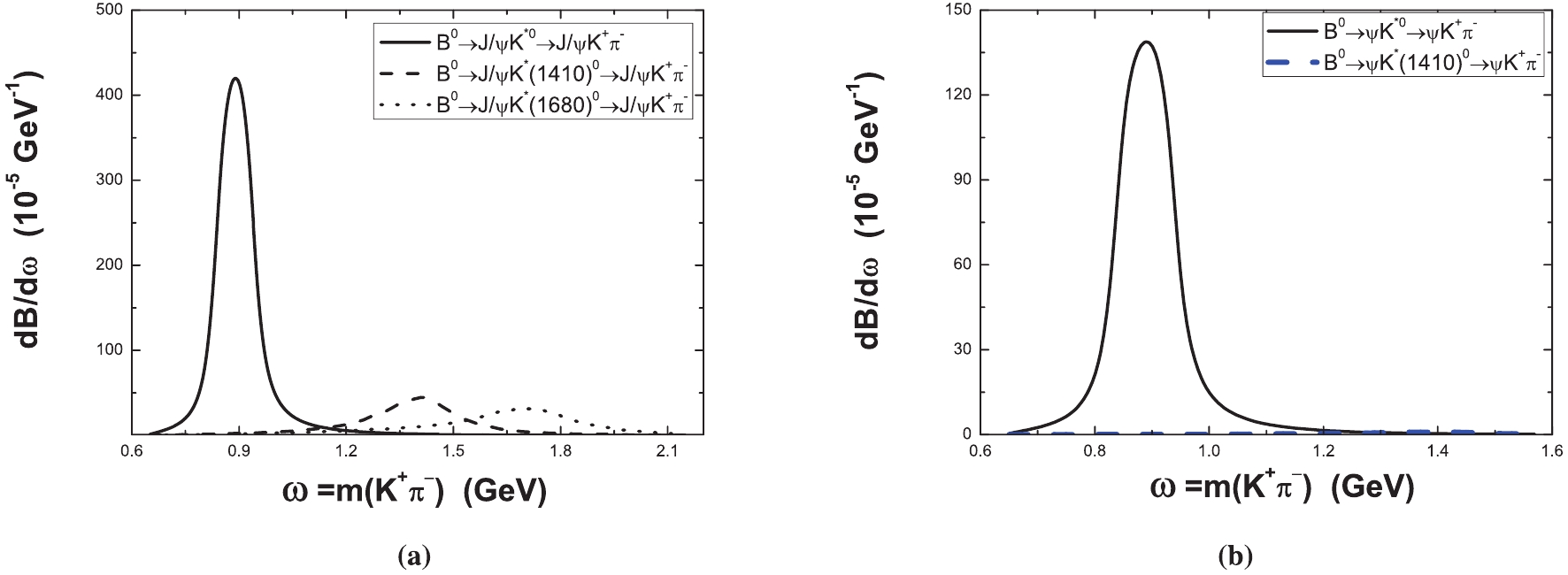
Figure 3. (color online) (a) Differential branching ratios for the
$B^0\to J/\psi [K^{*0},K^*(1410)^0, K^*(1680)^0\to]K^+\pi^-$ decays, and (b) Differential branching ratios for the$B^0\to \psi(2S) [K^{*0},K^*(1410)^0 \to]K^+\pi^-$ decays.From the numerical results as given in Tables 1 and 2, we predict the relative ratio
$ R_1 $ between the branching ratios of B meson decays involving$ \psi(2S) $ and$ J/\psi $ with the resonance$ K^*(1410)^{0} $ ,$\begin{split} R_1(K^*(1410)) =& \frac{{\cal B}(B^0 \to \psi(2S)(K^{*}(1410) ^{0}\to) K^+\pi^-)}{{\cal B}(B^0 \to J/\psi(K^{*}(1410) ^{0} \to) K^+\pi^-)}\\=& 0.25^{+0.01}_{-0.03}, \end{split} $

(34) which is smaller than the corresponding ratio of
$ K^* $ reported by the LHCb measurement [9],$ R_1^{\rm exp} = \frac{{\cal B}(\bar{B}^0 \to \psi(2S) K^{*0})}{{\cal B}(\bar{B}^0 \to J/\psi K^{*0})} = 0.476 \pm 0.014 \pm0.010 \pm 0.012. $

(35) The gap is governed by the different masses and widths in the Breit-Wigner functions of
$ K^* $ and$ K^*(1410) $ . The forthcoming LHCb and Belle-II experiments are expected to provide a direct measurement of$ R_1(K^*(1410)) $ .The polarization fractions defined in Eq. (28) associated with the available data are also listed in Tables 1 and 2, which have the same origin of theoretical uncertainties as the branching ratios. For these decays, the contributions from the non-factorizable tree diagrams in Fig. 1(c,d) are comparable with those of the color-suppressed tree diagrams, although the latter are enhanced by the involving vertex corrections. The fraction of the longitudinal polarization is generally reduced to about ~50%, while the parallel and perpendicular fractions are roughly equal. In particular for the
$ B_s\rightarrow \psi(2S) $ modes, all the three transversity amplitudes are of comparable magnitude. The results are quite different from the expectation in the factorization assumption that the longitudinal polarization should dominate based on the quark helicity analysis [95, 96]. We adopt the helicity amplitudes$ ({\cal{A}}_{0},{\cal{A}}_{+},{\cal{A}}_{-}) $ , which are related to the spin amplitudes$ ({\cal{A}}_{0},{\cal{A}}_{\parallel},{\cal{A}}_{\perp}) $ in the Appendix by$ {\cal{A}}_{\pm} = \frac{{\cal{A}}_{\parallel}\pm{\cal{A}}_{\perp}}{\sqrt{2}}, $

(36) where
$ {\cal{A}}_{0} $ is common to both bases. From the results of Tables 1 and 2 and Eq. (36), there is a hierarchy of helicity amplitudes$ |{\cal{A}}_0|\sim|{\cal{A}}_+|>|{\cal{A}}_{-}| $ , which is similar to the case of two-body charmonium B decays [61].The PQCD predictions for polarization fractions of most considered
$ B^0_{(s)} \to \psi K^* \to \psi K\pi $ agree with currently available data within errors. For the$ B^0_s \to \psi(2S) (\bar{K}^{*} $ $(892)^{0} \to)K^-\pi^+ $ decay, although the central value of$ f_0\approx $ 39.4% is slightly smaller than the measured one$ f_0^{\rm exp} = 52 $ %, they are nevertheless in agreement due to large theoretical and experimental uncertainties. As stressed above, we expect a systematic angular analysis of the$ B^0_s \to \psi(2S) (\bar{K}^{*0} \to)K^-\pi^+ $ decay mode to accurately extract various polarization amplitudes. According to Table 2 and Eq. (9) from Belle collaboration [8], the central values of longitudinal, parallel polarization fractions are 46.3% and 24.8% for$ \bar{B}^0 \to J/\psi K^*(1410)^0 \to $ $ J/\psi K^-\pi^+ $ , and 37.2% and 31.9% for$\bar{B}^0 \to J/\psi K^* $ $ (1680)^0 \to J/\psi K^-\pi^+ $ . In comparison to our predictions in Tables 1 and 2, their longitudinal polarizations are small, whereas the parallel ones are large. As mentioned before, as the tensor and vector decay constants for$ K^*(1410) $ or$ K^*(1680) $ are not known, we use the decay constants of$ K^* $ to define the ratio$ F_{K\pi}^{\perp}(s)/F_{K\pi}^{\parallel}(s) $ . In fact, the ratios$ F_{K\pi}^{\perp}(s)/F_{K\pi}^{\parallel}(s) $ should be regarded as free parameters and determined by fitting to the data in the absence of any theoretical and experimental bases. However, the statistical errors in Ref. [8] are large, and the corresponding systematic errors are still absent; hence, it is not possible to perform a global fitting from the current data. More precise measurements of such decay channels are expected to help us test and improve our theoretical calculations. -
We studied the quasi-two-body decays
$B^0_{(s)} \to $ $ \psi [K^{*0}, K^*(1410)^0, K^*(1680)^0 $ $ \to] K\pi $ in the PQCD factorization approach by introducing the kaon-pion DAs. Analogous to the case of the P-wave pion pair in the final state, the kaon-pion DAs corresponding to the longitudinal and transverse polarizations are constructed through a perturbative evaluation of the hadronic matrix elements associated with various spin projectors.The SU(3) flavor symmetry breaking term has a significant influence on the longitudinal polarizations of the kaon-pion pair. Furthermore, we also fixed the hadronic parameters involved in the kaon-pion DAs on the basis of the data for the branching ratios and polarization fractions of the relevant decay modes.
Our PQCD predictions for the branching ratios and polarization fractions for the considered
$ B^0 \to \psi (K^* \to) K\pi $ decays are in good agreement with the existing data. The clear differences between the PQCD predictions and the measured values for the$ B^0_s \to \psi(2S) (\bar{K}^{*0} \to) K^-\pi^+ $ decay can be tested in the future experiments. The branching ratios of the two-body$ B \to \psi K^* $ can be extracted from the corresponding quasi-two-body modes by employing the narrow width approximation.We also calculated the branching ratios and polarization fractions of the
$ B^0_{(s)} \to \psi[K^*(1410), $ $ K^*(1680)\to] K\pi $ decays, and defined the new ratio$ R_1(K^*(1410)) $ among the branching ratios of the considered decay modes. These predictions can be tested by the future experimental measurements.Many thanks to Hsiang-nan Li and Wen-Fei Wang for valuable discussions.
-
The contributions from the longitudinal polarization, the normal polarization, and the transverse polarization are marked by the subscripts L, N, and T, respectively. The superscript
$ LL $ ,$ LR $ , and$ SP $ refers to the contributions from$ (V-A)\otimes(V-A) $ ,$ (V-A)\otimes(V+A) $ , and$ (S-P)\otimes(S+P) $ operators, respectively. The total decay amplitude is decomposed into$\tag{A1} {\cal{A}} = {\cal{A}}_L+{\cal{A}}_N \epsilon_{T}\cdot \epsilon_{3T} +{\rm i} {\cal{A}}_T \epsilon_{\alpha\beta\rho\sigma} n_+^{\alpha} n_-^{\beta} \epsilon_{T}^{\rho} \epsilon_{3T}^{\sigma}, $

(A1) where the three individual polarization amplitudes are written as
$\tag{A2}\begin{split} {\cal{A}}_{L,N,T}(B^0_{(s)}\to \psi K\pi) =& \frac{G_F}{\sqrt{2}}\Big\{V^*_{cb}V_{cs(cd)} \Big [\Big(C_1+\frac{1}{3}C_2\Big){\cal{F}}_{L,N,T}^{LL}+C_2{\cal{M}}_{L,N,T}^{LL} \Big]\\ &-V^*_{tb}V_{ts(td)}\Big [\Big(C_3+\frac{1}{3}C_4+C_9+\frac{1}{3}C_{10}\Big){\cal{F}}_{L,N,T}^{LL} \\ &+\Big(C_5+\frac{1}{3}C_6+C_7+\frac{1}{3}C_{8}\Big){\cal{F}}_{L,N,T}^{LR}\\ &+ (C_4+C_{10}){\cal{M}}_{L,N,T}^{LL}+(C_6+C_8){\cal{M}}_{L,N,T}^{SP}\Big ]\Big\}, \end{split}$

(A2) with the CKM matrix elements
$ V_{ij} $ and the Fermi coupling constant$ G_F $ . The Wilson coefficients$ C_i $ encode the hard dynamics of weak decays. The above amplitudes are related to those in Eq. (26) via$ \tag{A3}\begin{split} {\cal{A}}_0 =& {\cal{A}}_L, \\ {\cal{A}}_{\parallel} =& \sqrt{2}{\cal{A}}_{N}, \\ {\cal{A}}_{\perp} =& \sqrt{2}{\cal{A}}_{T}. \end{split} $

(39) The explicit amplitudes
$ {{\cal{F}}({\cal{M}})} $ from the factorizable (nonfactorizable) diagrams in Fig. 1 can be obtained in a straightforward manner just by replacing the twist-2 or twist-3 DAs of the$ \pi\pi $ system with the corresponding twists of the$ K\pi $ in Eqs. (17)–(22), as the P-wave kaon-pion DA in Eq. (15) has the same Lorentz structure as that of two-pion DAs in Ref. [74].
P-wave contributions to B(s)→ψKπ decays in perturbative QCD approach
- Received Date: 2020-02-10
- Available Online: 2020-07-01
Abstract: We study the quasi-two-body decays






 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF























 DownLoad:
DownLoad: