-
Properties of neutron-rich nuclei, in particular, the location of the neutron drip line, play an important role not only in understanding nuclear stability with respect to the isospin in hereto unexplored regions of the nuclear chart [1], but also in numerous related scientific issues of current interest. For instance, the r-process nucleosynthesis of heavy elements in stellar evolution crucially depends on the values of beta decay rates and neutron capture cross sections in neutron-rich nuclei that do not exist in terrestrial conditions [2–4]. The masses of neutron-rich nuclei impose stringent constraints on the equation of state of neutron-rich nuclear matter, which is key to understanding the properties of neutron stars and supernovae explosions [5–9].
New generation facilities, such as the Facility for Rare Isotope Beams (FRIB) at Michigan State University and the Radioactive Isotope Beam Factory (RIBF) at RIKEN, have helped in conducting studies of nuclei up to extreme isospin symmetry in the last two decades [10–13]. At the RIBF, the heaviest fluorine and neon isotopes were recently determined to be 31F and 34Ne [14], extending the neutron drip line from
$ Z = 8 $ [15–19], determined twenty years ago, to$ Z = 10 $ .Numerous theoretical studies on the location of the neutron drip line have been conducted. Table 1 presents a partial list of various theoretical predictions in comparison with the experimental data. Clearly, not all of the theoretical results agree with those of the experiments and with each other. This is well understood, as the exact location of the neutron drip line is sensitive to the details of the structure of nuclei, such as the shell evolution, coupling between the continuum and bound states, deformation effect, and three-body force. For example, the authors of Ref. [47] argued that the neutron drip line is related to closing (sub)shell orbitals, and therefore, the drip line of fluorine and neon may be due to the closure of the
$ 2p_{3/2} $ orbital, which results in formation of the drip line nuclei of 31F and 34Ne with$ N = 24 $ [14]. In Refs. [48–50], the extra stability of the neutron-rich isotopes of fluorine and neon relative to oxygen isotopes were attributed to the emergence of the island of inversion ($ Z = 10-12 $ ,$ N = 20-22 $ , and their neighbors), where the ground states gain energy by strong deformation. In Ref. [51], the three-body force was shown to be responsible for moving the oxygen drip line from 28O to 24O.theory experiment $ Z=8 $ 

24O [20, 21], 26O [22], 28O [7, 8, 23-26] 24O [15-18, 27 28] $ Z=9 $ 

29F [7, 8, 21, 23, 24], 31F [29, 30], 33F [31] 31F [14, 27] $ Z=10 $ 

30Ne [25], 32Ne [32], 34Ne [7, 8, 20, 21, 24, 29, 31, 33, 34], 38Ne [35], 40Ne [23], 42Ne [26] 34Ne [14] $ Z=11 $ 

37Na [21, 33, 34], 39Na [25], 45Na [26, 36] $ {^{39}{\rm{Na}}} $ (only one event) [14]

$ Z=12 $ 

40Mg [21, 29, 37-41], 42Mg [25, 42-45], 44Mg [46], 46Mg [26, 35, 45] Table 1. Last bound neutron-rich nuclei with
$ Z = 8-12 $ predicted by various theoretical models in comparison with experimental data.At the mean field level, pairing correlations and continuum effects play an important role in describing the ground-state properties of drip-line nuclei [23, 52-64]. Pairing correlations are responsible for scattering nucleon pairs located at the single-particle level below the Fermi surface into the level above with low orbital angular momentum. Although the Bogoliubov method is arguably more appropriate to deal with the pairing correlations in dripline nuclei [57, 65], the BCS method, if treated properly, can offer a reasonable description [66–69]. However, both methods have the drawback that the particle number is not conserved. Around the Fermi surface, only few nucleons play an important role in determining the properties of neutron-rich nuclei, and the non-conservation of particle number may become particularly relevant. Therefore, the restoration of the particle number conservation is preferred, as shown in the present study.
Based on these considerations, in the present work, we study fluorine, neon, sodium, and magnesium isotopes in the relativistic mean field model and employ the recently developed particular number conservation BCS (FBCS) approach to deal with pairing correlations [70]. We focus on the differences between the results obtained by the RMF+BCS and RMF+FBCS approaches to explore the relevance of the latter in the description of neutron-rich nuclei and in terms of predicting the location of the neutron drip line.
This paper is organized as follows. In Sec. 2, we briefly describe the relativistic mean field model and the FBCS approach. In Sec. 3, we present the results for fluorine, neon, sodium, and magnesium isotopes and discuss the differences between the BCS and FBCS approaches. A short summary and outlook are provided in Sec. 4.
-
The relativistic mean field models or covariant density functional theories have made remarkable progress in describing various nuclear physics phenomena. Refs. [71–79] provide further detail on this topic. In the present study, we take the more conventional meson-exchange formulation, starting from the Lagrangian density expressed as Eq. (1), which contains the nucleon and the exchanged
$ \sigma $ ,$ \rho $ ,$ \omega $ meson, and the photon fields.$ \begin{split} {\cal{L}} =&\bar{\psi}[{\rm i}\gamma^\mu\partial_\mu-M-g_\sigma\sigma -\gamma^\mu(g_\omega\omega_\mu+g_\rho\vec {\tau}\cdot p\vec{\rho}_{\mu}\\ &+e\frac{1-\tau_3}{2}A_\mu) -\frac{f_\pi}{m_\pi}\gamma_5\gamma^\mu\partial_\mu \overrightarrow{\pi}\cdot p\overrightarrow{\tau}]\psi\\ &+\frac{1}{2}\partial^\mu\sigma\partial_\mu\sigma-\frac{1}{2}m_\sigma^2\sigma^2 -\frac{1}{3}g_{2}\sigma^{3}-\frac{1}{4}g_{3}\sigma^{4} \end{split} $

$ \begin{split}& \;\;\;\;\;\;\;\;\;-\frac{1}{4}\Omega^{\mu\nu}\Omega_{\mu\nu}+\frac{1}{2}m_{\omega}^2\omega_\mu\omega^\mu +\frac{1}{4}c_{3}(\omega^{\mu}\omega_{\mu})^{2}\\ &\;\;\;\;\;\;\;\;\;-\frac{1}{4}\vec{R}_{\mu\nu}\cdot p\vec{R}^{\mu\nu}+\frac{1}{2}m_\rho^2\vec{\rho}^\mu\cdot p\vec{\rho}_\mu +\frac{1}{4}d_{3}(\vec{\rho}^{\mu}\vec{\rho}_{\mu})^{2}\\ &\;\;\;\;\;\;\;\;\;-\frac{1}{4}F^{\mu\nu}F_{\mu\nu}, \end{split} $

(1) where M depicts the mass of the nucleon and
$ m_{\sigma} $ ,$ m_{\omega} $ , and$ m_{\rho} $ are the masses of the$ \sigma $ ,$ \omega $ , and$ \rho $ mesons, respectively. Here,$ g_{\sigma} $ ,$ g_{\omega} $ ,$ g_{\rho} $ ,$ g_2 $ ,$ g_3 $ ,$ c_3 $ ,$ d_3 $ , and$ e^{2}/4\pi $ are coupling constants for the$ \sigma $ ,$ \omega $ ,$ \rho $ mesons and photon.$ \psi $ is the Dirac spinor for the nucleon. The field tensors for vector mesons and the photon are defined as$ \Omega_{\mu\nu} = \partial_{\mu}\omega_{\nu}-\partial_{\nu}\omega_{\mu} $ ,$ \vec{R}_{\mu\nu} = \partial_{\mu}\vec{\rho}_{\nu}-\partial_{\nu}\vec{\rho}_{\mu}-g_{\rho}(\vec{\rho}_{\mu}\times\vec{\rho}_{\nu}) $ , and$ F_{\mu\nu} = \partial_{\mu}A_{\nu}-\partial_{\nu}A_{\mu} $ .In the present study, we employ the parameter set PK1 [80] for the mean-field effective interactions. The PK1 parameter set is obtained by fitting to the masses of a number of spherical nuclei and the compression modulus, baryonic density at saturation, and asymmetry energy of nuclear matter. It could provide a description of both the empirical properties of nuclear matter and the ground-state properties of finite nuclei better than most other parameter sets of the same group [80]. Because our main interest is to study the impact of the pairing correlation, particularly the particle number conservation, on the prediction of the dripline, we should only compare results obtained with the same mean-field effective force. Nevertheless, we performed studies using the NL3 parameter set, as in Ref. [70], and our conclusion remains qualitatively unchanged. In the future, one may evaluate whether the impact of the particle number conservation on drip-line nuclei remains in the point-coupling version of the RMF model.
From the Lagrangian density, by employing the so-called no-sea and mean-field approximations, the Dirac equation can be obtained for the nucleon, and the Klein–Gordon equations can be obtained for the mesons. These equations can be solved self-consistently either in coordinate space or using the basis expansion method. In the present study, we adopt the harmonic oscillator basis expansion method described in Refs. [81, 82], where the axial deformation degrees of freedom are taken into account. In the numerical calculation, 12 shells are used to expand the fermion fields and 20 shells for the meson fields, which was found to be sufficient for the relatively small mass nuclei of this study [68].
To deal with pairing correlations, we employ the variational BCS approach [83, 84]. To restore the particle number conservation, we adopt the variation after the projection BCS method or the so-called FBCS method, which has been recently implemented in the RMF model [70]. The corresponding FBCS equation reads
$2(\widetilde{\varepsilon_{j}}+\Lambda_{j})\mu_{j}\nu_{j}+\Delta_{j}(\nu_{j}^{2}-\mu_{j}^{2}) = 0, $

(2) where the quantities
$ \tilde{\varepsilon}_{j} $ ,$ \Lambda_{j} $ , and$ \Delta_{j} $ are defined as follows:$ \begin{split} \widetilde{\varepsilon_{j}} =&(\varepsilon_{j}-G_{jj}\nu_{j}^{2})\frac{R_{1}^{1}}{R^{0}_{0}},\\ \Delta_{j} =&\sum\limits_{k>0}G_{jk}\mu_{k}\nu_{k}\frac{R_{1}^{2}(j,k)}{R^{0}_{0}}(\nu_{j}^{2}-\mu_{j}^{2}),\\ \Lambda_{j} =&\sum\limits_{k>0}(\varepsilon_{j}-\frac{1}{2}G_{kk}\nu_{k}^{2})\nu_{k}^{2}\frac{R^{0}_{0}(R_{2}^{2} -R_{1}^{2})-R_{1}^{1}(R_{1}^{1}-R_{0}^{1})}{(R^{0}_{0})^{2}}\\ &-\frac{1}{2}\sum\limits_{k_{1},k_{2}>0}G_{k_{1}k_{2}}\mu_{k_{1}}\nu_{k_{1}}\mu_{k_{2}}\nu_{k_{2}}\frac{R^{0}_{0}(R_{2}^{3}-R_{1}^{3})}{(R^{0}_{0})^{2}}\\ &+\frac{1}{2}\sum\limits_{k_{1},k_{2}>0}G_{k_{1}k_{2}}\mu_{k_{1}}\nu_{k_{1}}\mu_{k_{2}}\nu_{k_{2}}\frac{R_{1}^{2}(R_{1}^{1}-R_{0}^{1})}{(R^{0}_{0})^{2}}. \end{split} $

(3) In the above equations,
$ \epsilon_j $ is the single-particle energy,$ \nu_j^2 $ ($ \mu_j^2 = 1-\nu_j^2 $ ) is the occupation probability of the j orbit and its time reversal partner, and$ G_{j_{1} j_{2}} = -\bar{V}_{j_{1}, \bar{j}_{1}, j_{2}, \bar{j}_{2}} $ is the pairing interaction matrix element with V the pairing interaction, for which, in the present study, we adopt a density-independent delta interaction. The residual integrals,$ R_{0}^{0} $ ,$ R_{0}^{1} $ ,$ R_{1}^{1} $ ,$ R_{1}^{2} $ ,$ R_{2}^{2} $ ,$ R_{1}^{3} $ , and$ R_{2}^{3} $ , can be easily calculated, as explained in Ref. [70]. -
To solve the RMF+BCS/FBCS equations, we apply a pairing window of 12 MeV both above and below the Fermi surface and adopt the density-independent contact delta interaction
$ V = -V_{0}\delta(\vec{r}_{1}-\vec{r}_{2}) $ in the particle–particle channel [68]. The only free parameter in the particle–particle channel is the pairing strength$ V_{0} $ , which is often adjusted to reproduce the odd–even mass staggerings. Here, we use the three-point formula for such a purpose [83, 84]:$ \Delta =\frac{1}{2}[B(N-1,Z)-2B(N,Z)+B(N+1,Z)],\\ $

(4) where
$ B(N,Z) $ is the binding energy for a nucleus of neutron number N and proton number Z. For each isotopic chain studied in either the BCS or the FBCS method, the pairing strength is fixed, as explained above, and it is provided in Table 2. We chose to fix the pairing strength by fitting to the odd–even staggerings of a few stable nuclei, as specified in Table 2, instead of fitting to the whole isotopic chain including the drip line nuclei. The reason is that our main purpose is to study the impact of the particle number conservation on the prediction of the drip line, but not to provide the best description of the existing data, which might require fine-tuning of the mean-field effective force and consideration of beyond mean field effects, such as configuration mixing and rotation corrections.$ ^{20-24}{\rm{F}} $ 

$ ^{22-26} {\rm{Ne}}$ 

$ ^{26-30} {\rm{Na}}$ 

$ ^{26-30}{\rm{Mg}} $ 

RMF+BCS $ 380 $ 

$ 580 $ 

$ 480 $ 

$ 480 $ 

RMF+FBCS $ 380 $ 

$ 480 $ 

$ 380 $ 

$ 380 $ 

Table 2. Nuclei fitted to fix pairing interaction and corresponding pairing strength
$ V_0 $ in units of MeV·fm-3.To determine the position of the drip line, we employ one- and two-neutron separation energies, given by Eqs. (5) and (6), respectively, as follows:
$ S_{N}(N,Z) = B(N,Z)-B(N-1,Z), $

(5) $ S_{2N}(N,Z) = B(N,Z)-B(N-2,Z). $

(6) The first unbound nucleus clearly has a negative
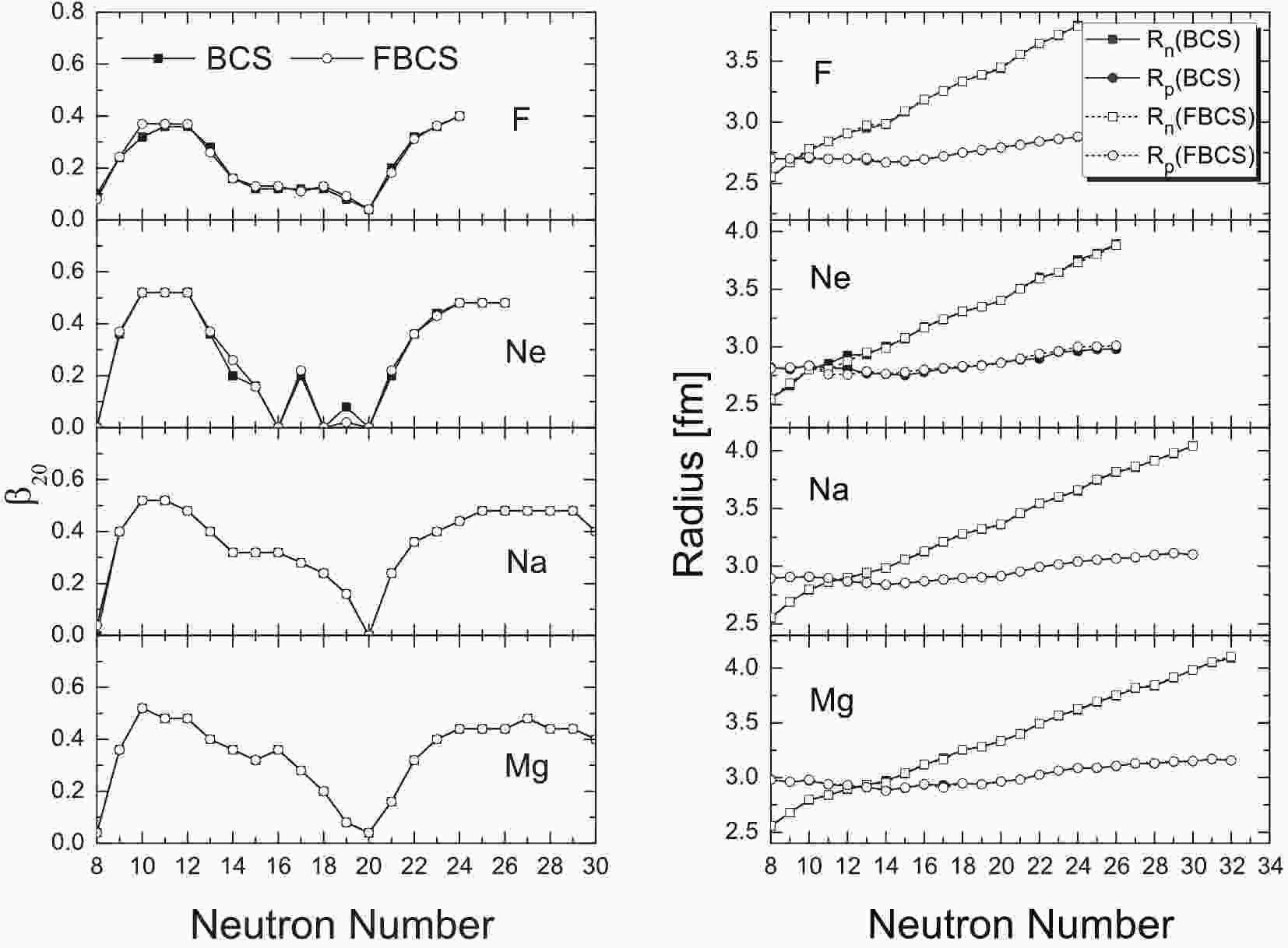
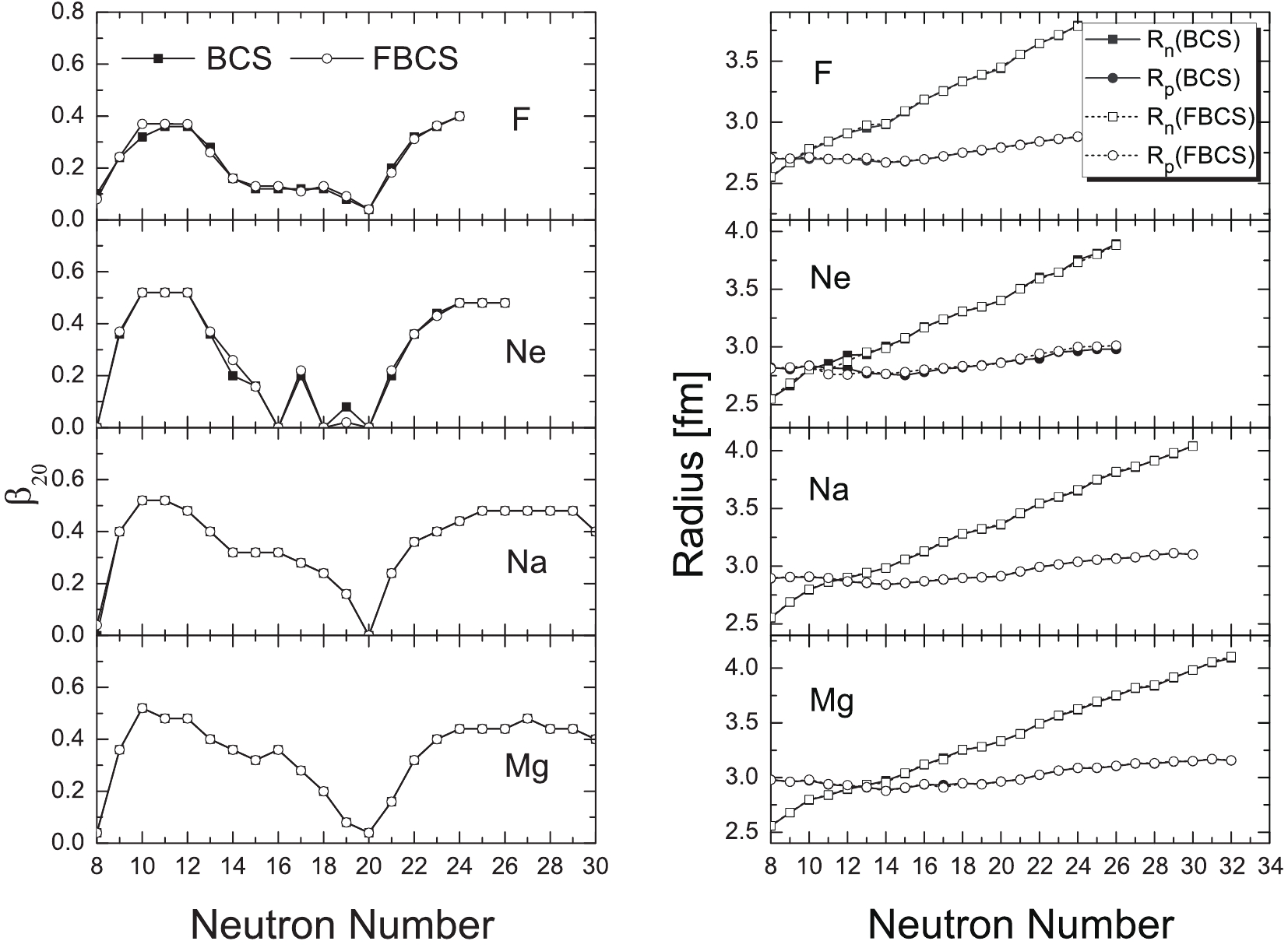
$ S_N $ . For nuclei with an even neutron number, one should also verify$ S_{2N} $ due to the pairing correlation, as$ S_N $ might be negative, whereas$ S_{2N} $ could be positive.In the following, we mainly concentrate on the odd–even staggerings, one-, and two-neutron separation energies, as the quadrupole deformations and neutron/proton radii of the fluorine, neon, sodium, and magnesium isotopes are almost the same in the RMF+FBCS and RMF+BCS approaches, as shown in Fig. 1. Clearly, most neutron-rich nuclei are deformed.① Therefore, one could imagine that spherical calculations may not be able to correctly predict/reproduce the drip line.
-
In Fig. 2, the odd–even mass staggerings of the fluorine isotopes obtained in the RMF+BCS and RMF+FBCS methods are compared with the experimental data. Note that the pairing strengths are fixed by fitting the odd–even mass staggerings of
$ ^{20-24} {\rm{F}}$ , as shown in Table 2. The difference between the RMF+BCS results and those of the RMF+FBCS becomes larger for neutron-rich nuclei, which certainly affects the prediction of the drip line.
Figure 2. Odd–even mass staggerings of fluorine isotopes obtained by RMF+BCS (open circles) and RMF+FBCS (open diamonds) methods, in comparison with experimental data (solid circles) [85].
In Fig. 3, the theoretical one- and two-neutron separation energies of the fluorine isotopes are compared with the experimental data. The two-neutron separation energy is overestimated for
$ N = 20 $ , similar to the finite-range droplet model [86]. For the drip-line nucleus, the RMF+BCS approach yields$ N = 20 $ . In contrast, 31F was experimentally determined as the last bound fluorine isotope [14]. The two extra nucelons located above the closed$ 1d_{3/2} $ orbit with$ N = 22 $ . The FBCS method, which restores the particle number conservation, yields 31F with$ N = 22 $ as the last bound fluorine isotope②.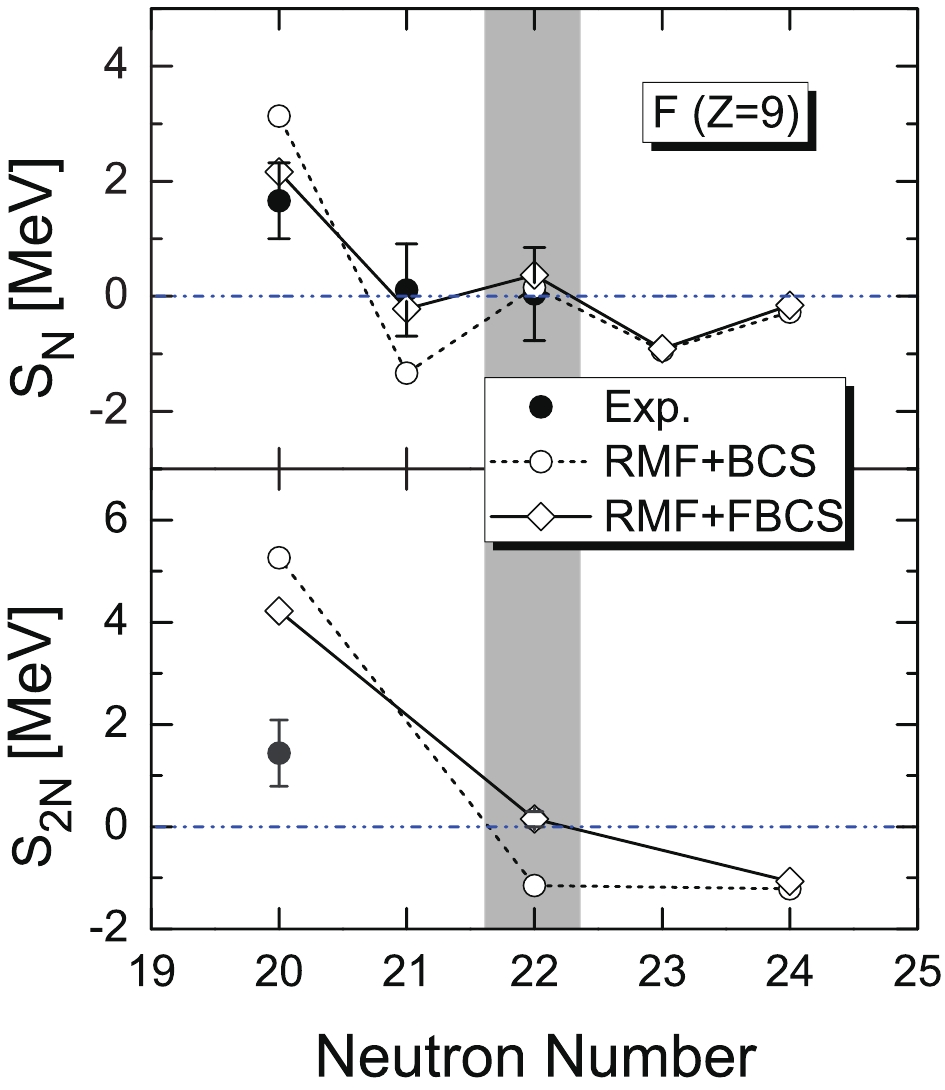
Figure 3. One- (top panel) and two-neutron (bottom panel) separation energies of fluorine isotopes obtained by RMF+BCS (open circles) and RMF+ FBCS (open diamonds) methods, in comparison with experimental data (solid circles) [85].
In Ref. [47], it was argued that if a nucleus is deformed, the Nilsson model is applicable, and the single-particle states with a given asymptotic quantum number have a degeneracy of two. Then, the drip-line nucleus in the present case would be
$ N = 22 $ . Therefore, the experiment result [14] indicates that the neutron-rich fluorine isotopes are deformed. In contrast, although 31F is strongly deformed in both the RMF+BCS and RFM+FBCS methods (see Fig. 1), only the latter yields results consistent with the data. This can be attributed to the restored particle number conservation in the FBCS approach. We note that the pairing energy for 31F in the FBCS method is approximately$ 2.5\; $ MeV, whereas it is only$ 0.2\; $ MeV in the BCS case.It was argued in Ref. [87] that the restoration of particle number before variation can stabilize neutron-rich nuclei, thereby pushing the drip line further away, which agrees with our RMF+FBCS result.
-
In Fig. 4, we demonstrate the odd-even mass staggerings of neon isotopes. The theoretical results are consistent with experimental data, with the exception of 20Ne for the BCS method. We note that in the BCS method, only the orbital
$ 2s_{1/2} $ is occupied. However, in the FBCS approach, both$ 2s_{1/2} $ and$ 1d_{5/2} $ orbitals are occupied. This explains why the FBCS approach can better reproduce the empirical pairing gap of 20Ne.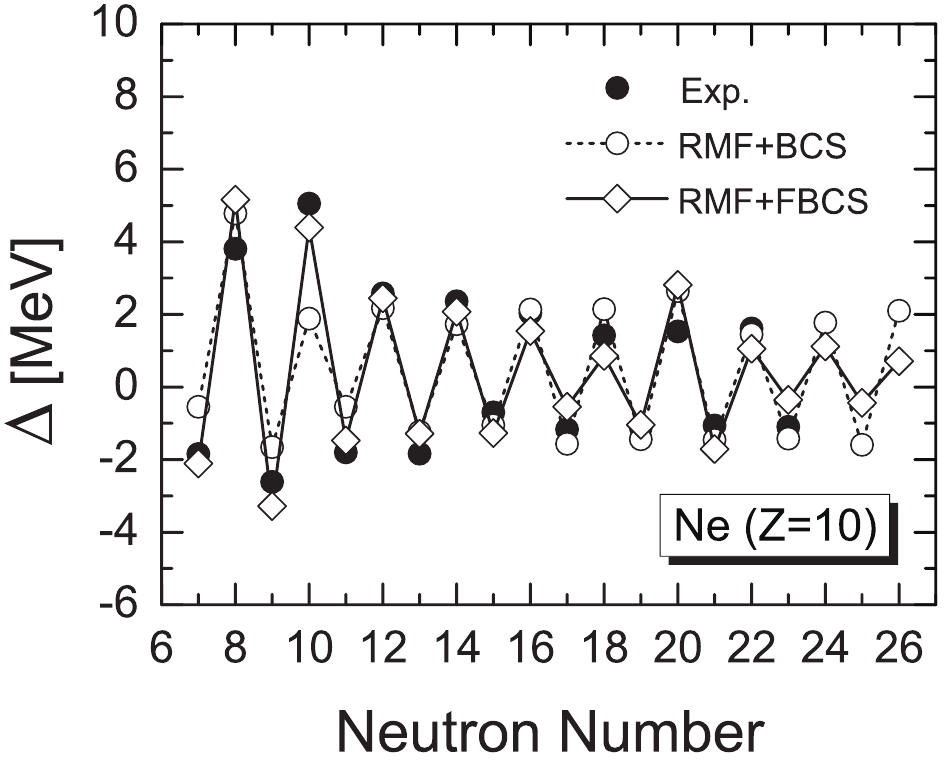
Figure 4. Same as Fig. 2, for neon isotopes.
In Fig. 5, the one- and two-neutron separation energies of neon isotopes are compared with the experimental data. The overall agreement is reasonable, with the exception of 30Ne. For the drip-line nucleus, the BCS method predicts
$ N = 26 $ , while the FBCS method predicts$ N = 24 $ . The experimental$ S_{2N} $ for 34Ne almost vanishes. Our FBCS result is qualitatively consistent with the latest experimental data [14]. The authors of Ref. [31] also conjectured 34Ne to be a neutron drip-line nucleus for neon isotopes, the same as the Monte Carlo Shell Model (MCSM) with various particle–hole excitations taken into account [20].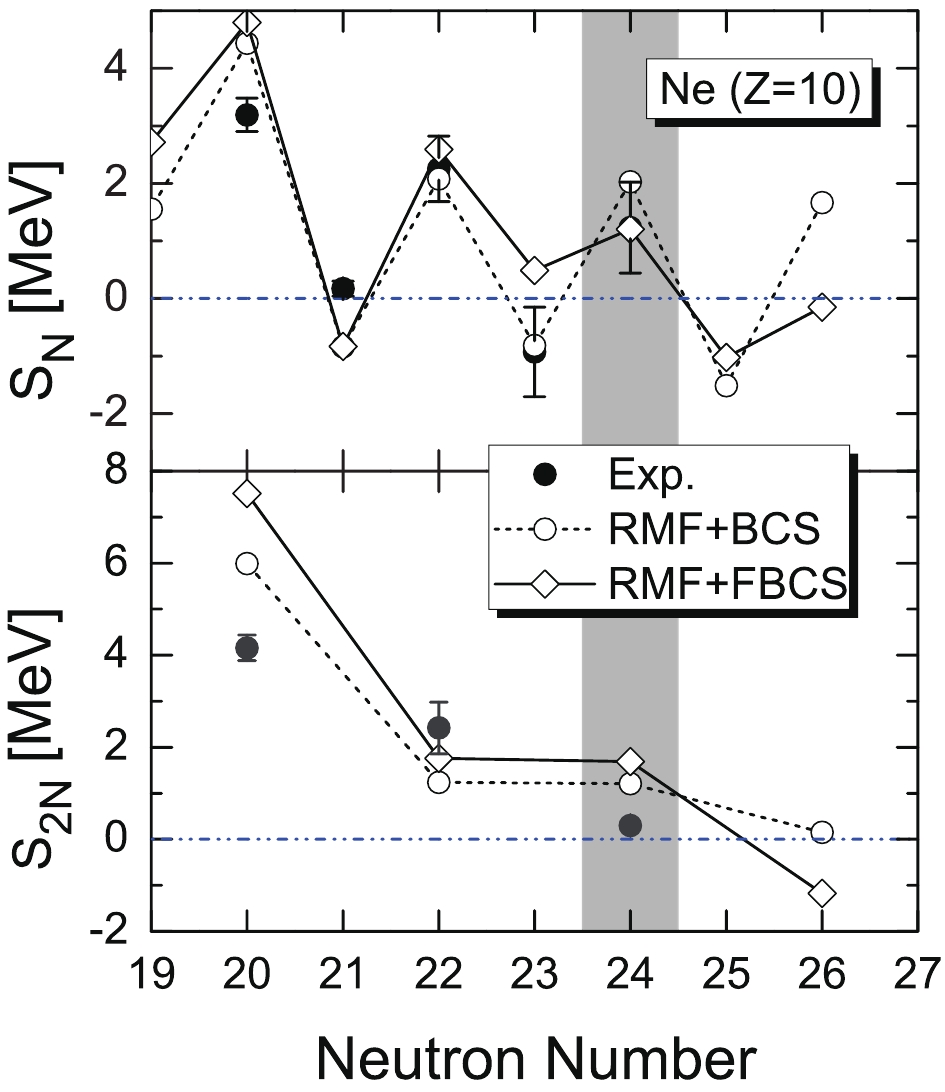
Figure 5. Same as Fig. 3, for neon isotopes.
-
In Fig. 6, we show the odd–even mass staggerings, and in Fig. 7, the one- and two-neutron separation energies of the sodium isotopes in comparison with the experimental data are shown. Interestingly, both the FBCS and BCS methods indicate that 39Na is the last bound sodium isotope from the perspective of the two-neutron separation energy, though the
$ S_{2N} $ for 39Na almost vanishes using the BCS method. Indeed, the recent RIBF experiment detected one event for 39Na [14].
Figure 6. Same as Fig. 2, for sodium isotopes.
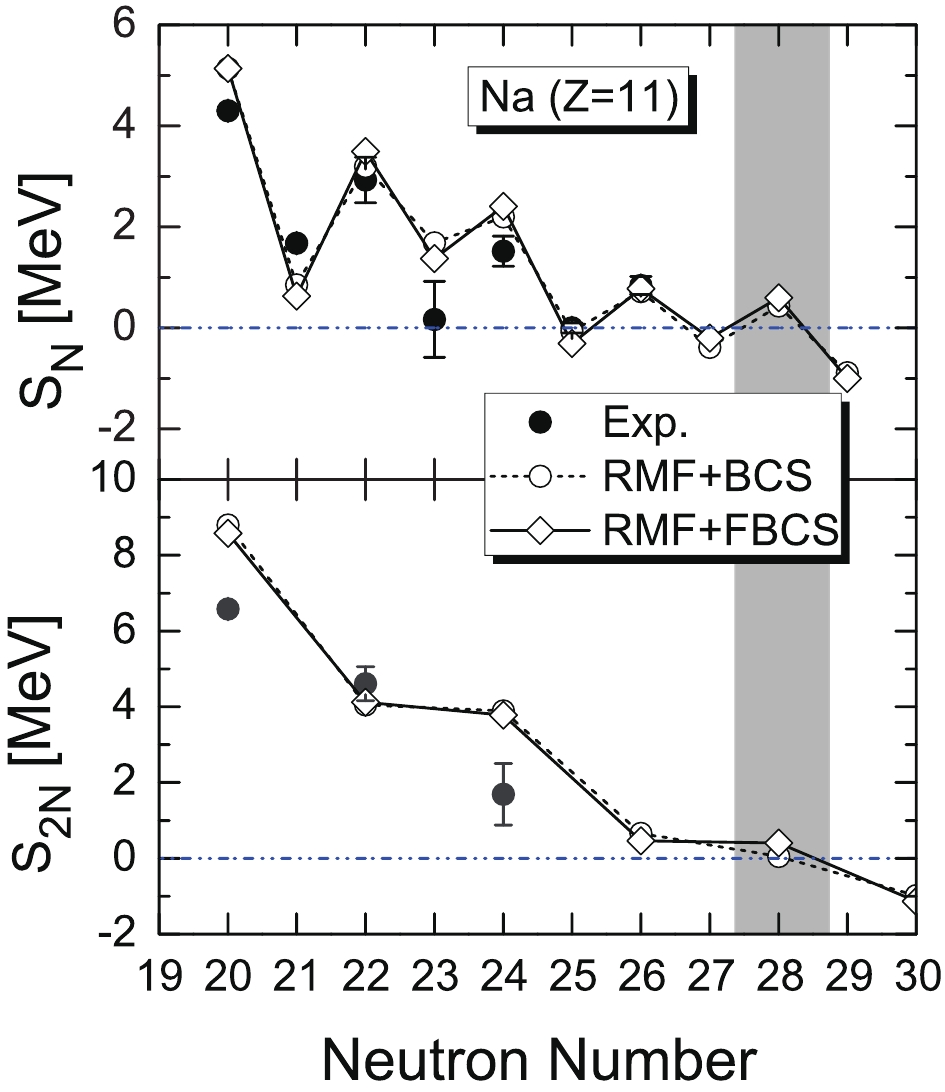
Figure 7. Same as Fig. 3, for sodium isotopes.
The sodium isotopes provide a good opportunity to study the neutron density distributions over a wide range of neutron numbers. In Ref. [36], a systematic study of nuclear density distributions in the sodium isotopes within the RMF model is discussed, with the pairing and blocking effect for odd particle systems properly described by the relativistic Hartree–Bogoliubov (HB) theory in coordinate space. In this study, the neutron drip-line nucleus was predicted to be 45Na. As the orbital
$ 1f_{7/2} $ is very close to the continuum, the$ N = 28 $ closed shell for stable nuclei fails to appear due to the lowering of the$ 2p_{3/2} $ and$ 2p_{1/2} $ orbitals. These results are consistent with the global study using the PC-PK1 parameter set [26]. However, the influence of deformation is neglected in both studies [26, 36], while the latest RIBF result indicates that deformation effects are important in this part of the nuclear chart. -
The odd–even mass staggerings and one- and two-neutron separation energies of the magnesium isotopes are shown in Figs. 8 and 9. From the two-neutron separation energies, we conclude that 40Mg is the last bound magnesium isotope. In the BCS approach, 42Mg is the last bound magnesium isotope. From Table 1, it is clear that model predictions differ significantly, yielding either 40Mg, 42Mg, or 46Mg as the last bound magnesium isotope. Future experiments are required to settle this issue.
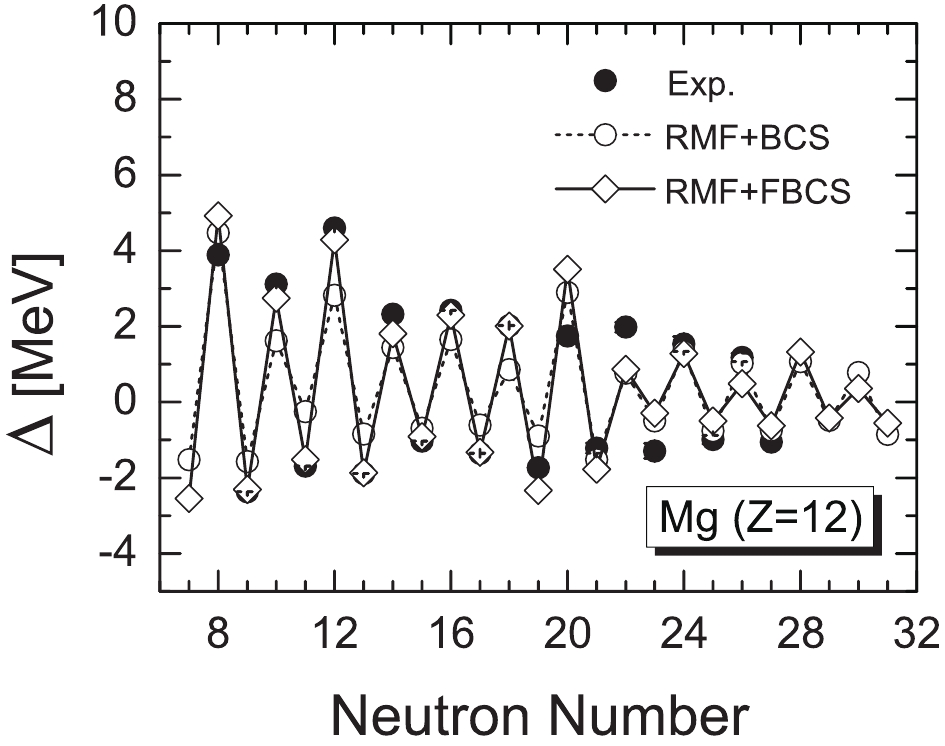
Figure 8. Same as Fig. 2, for magnesium isotopes.
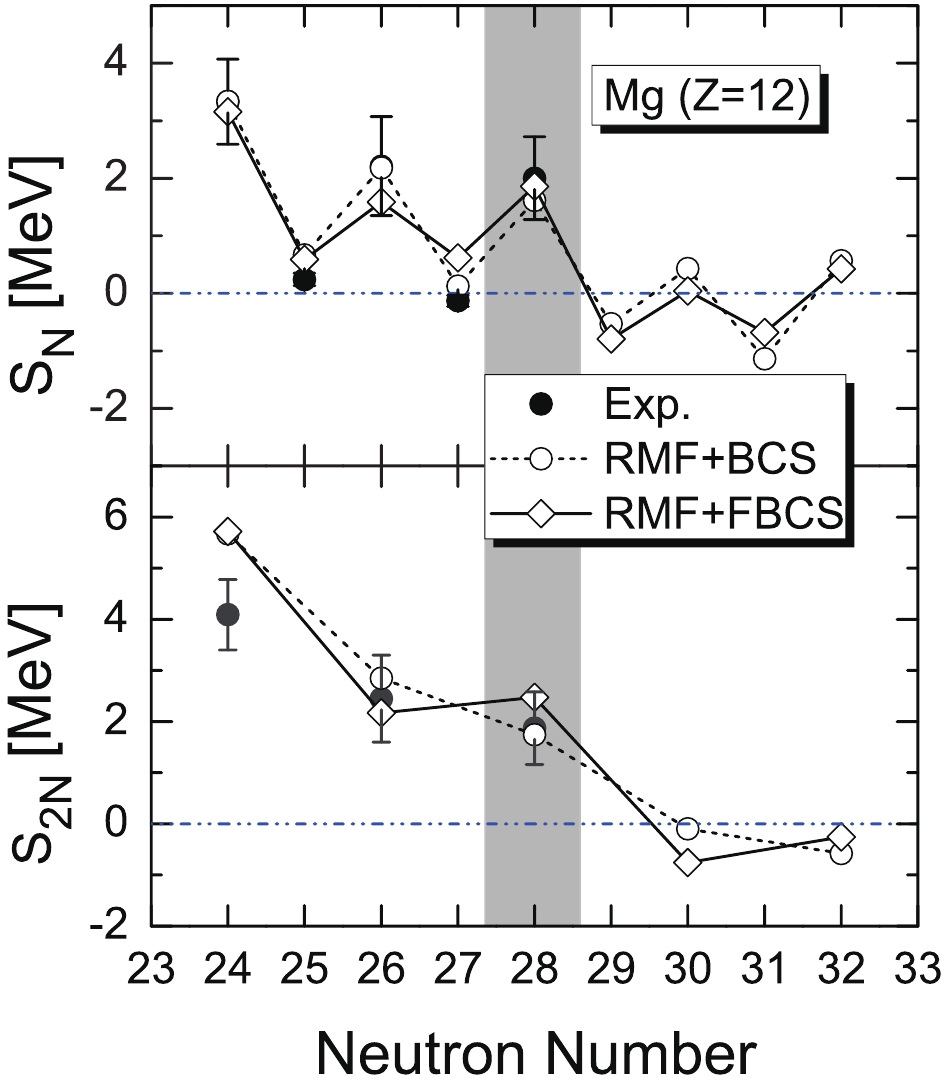
Figure 9. Same as Fig. 3, for magnesium isotopes.
Interestingly, we note from Table 1 that the macroscopic–microscopic mass formula WS4 yields the correct drip-line nuclei 24O and 34Ne, except for 31F. For sodium isotopes, it predicts 37Na as the last bound neutron-rich nucleus, which is different from our prediction, 39Na. For the case of magnesium, it predicts 40Mg as the drip-line nucleus, which is in agreement with the RMF+FBCS approach. Moreover, the WS4 mass formula achieved a description of all existing data at that time with a root-mean-square deviation of 298 keV [21].
-
Inspired by the latest RIBF experiment that identified the neutron drip line of fluorine and neon isotopes for the first time in twenty years, we studied the impact of particle number conservation in one- and two-neutron separation energies. We employed the recently developed RMF+FBCS approach and studied fluorine, neon, sodium, and magnesium isotopes. We showed that proper treatment of both the pairing correlations and deformation effects plays an important role in reproducing experimental results, particularly, the drip-line nuclei of the fluorine and neon isotopes. For the sodium and magnesium isotopes, we predict the drip-line nuclei to be 39Na and 40Mg.
We employed the expansion method based on the harmonic oscillator basis, which may not be sufficient to account for the continuum effect, though the correct reproduction of the fluorine and neon drip line provide us some confidence in the present study. In the future, the deformed relativistic Hartree-Bogoliubov theory in continuum (DRHBc) may need to be applied [35, 45] to study the impact of the continuum. However, a proper treatment of pairing correlations, particularly from the perspective of particle number conservation, needs to be implemented. In the present study, we adopted the density-independent contact delta interaction in the particle–particle channel; however, we do not anticipate that our conclusion will change if other forms of the pairing interaction, such as finite range or density-dependent pairing interactions, are considered. Nevertheless, this should be explicitly studied in the future.
As demonstrated in the present study, a proper description of drip-line phenomena is challenging. It requires a proper treatment of numerous effects, including but not limited to the pairing correlation, as well as the deformation and continuum effects. This study shows that the particle number conservation effect can play a relevant role in identifying the position of the drip line. Further studies are required in the future to corroborate these findings.
Neutron drip line of Z = 9–11 isotopic chains
- Received Date: 2020-02-05
- Available Online: 2020-07-01
Abstract: A recent experimental breakthrough identified the last bound neutron-rich nuclei in fluorine and neon isotopes. Based on this finding, we perform a theoretical study of Z = 9, 10, 11, 12 isotopes in the relativistic mean field (RMF) model. The mean field parameters are assumed from the PK1 parameterization, and the pairing correlation is described by the particle number conservation BCS (FBCS) method recently formulated in the RMF model. We show that the FBCS approach plays an essential role in reproducing experimental results of fluorine and neon isotopes. Furthermore, we predict 39Na and 40Mg to be the last bound neutron-rich nuclei in sodium and magnesium isotopes.





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF













 DownLoad:
DownLoad: