-
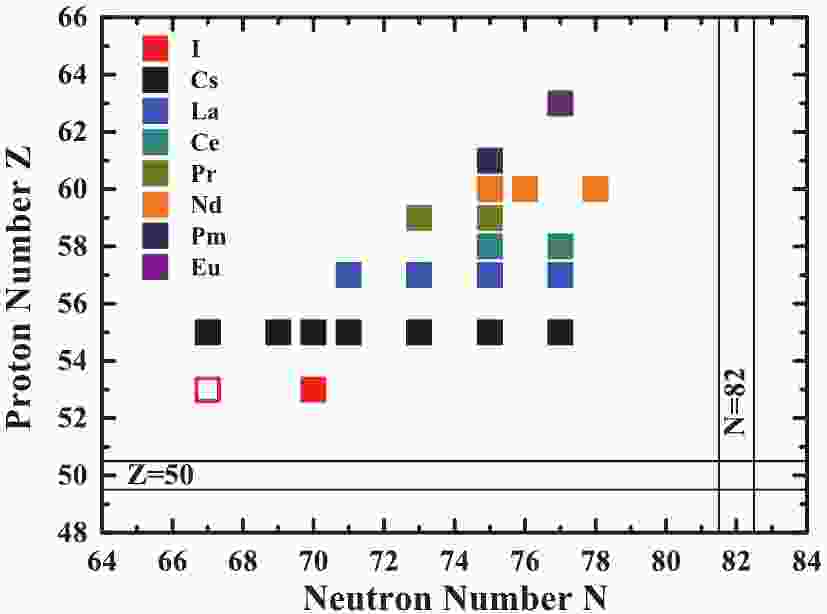
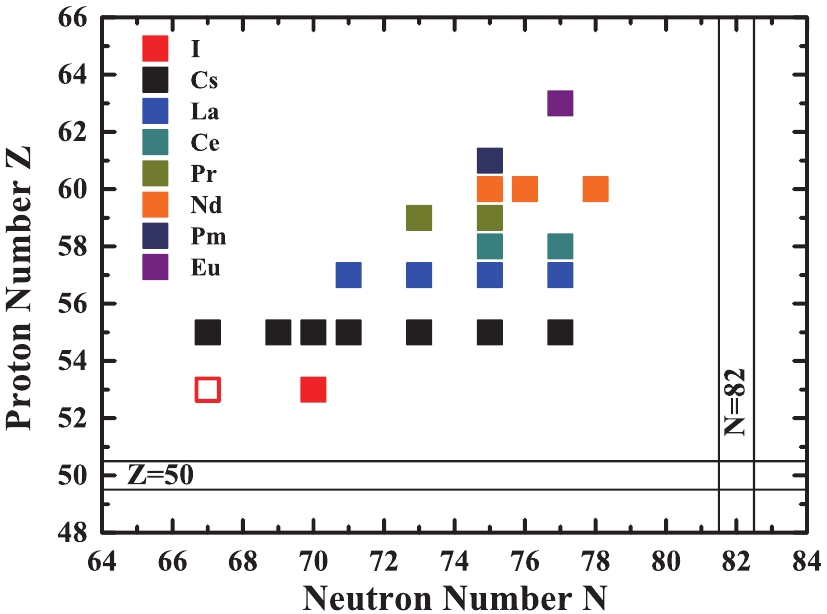
Chirality is a topic of general interest in natural sciences, including chemistry, biology, and physics. In nuclear structure physics, the occurrence of chirality was suggested for triaxially deformed nuclei in 1997 [1], and the predicted patterns of spectra exhibiting chirality, i.e., chiral doublet bands, were experimentally observed in 2001 [2], indicating the existence of one pair of
$ \Delta I = 1 $ nearly degenerate bands with the same parity. Furthermore, the possible existence of two pairs or more of chiral doublet bands in one nucleus, i.e., multiple chiral doublet bands, was demonstrated, and the acronym M$ \chi $ D was introduced by searching for triaxial chiral configurations in Rh isotopes based on constrained relativistic mean-field calculations in Ref. [3]. Hereto, nuclear chirality has become a hot topic in the current frontier of nuclear structure physics, and many chiral candidate nuclei, including several nuclei with MχD phenomenon [4–15], were reported experimentally in the A ≈ 80, 100, 130, and 190 mass regions of the nuclear chart; see e.g., the reviews in Refs. [16, 17] and data tables [18].In the entire nuclear chart, most reported candidate chiral nuclei are located in the A ≈ 130 mass region, where an island of chiral candidates was previously suggested in Ref. [2], and the available reported candidates in I, Cs, La, Ce, Pr, Nd, Pm, and Eu [8, 19–41] are portrayed in Fig. 1. Therefore, it is highly interesting to investigate the boundary of the chiral island. In the A ≈ 130 mass region, the iodine isotopes lie on the lower edge of the present chiral island. In 2003, based on the similar energy spectrum, Moon et al. [42] suggested the presence of chiral doublet bands in 120I. In 2013, Li et al. extended both the yrast and side bands up to state
$ 23^{+} $ and$ 17^{+} $ , respectively [43]. Recently, according to the experimental properties of doublet bands in Ref. [42], Moon et al. [44] discussed the chiral characteristics and doubling of states for the$ \pi h_{11/2} \otimes \nu h_{11/2} $ configuration based on the large-scale spherical shell model and total Routhian energy surface calculations, and further suggested a chiral-like pair band in 120I. Therefore, it is necessary to study the rotational mechanism for the occurrence of the chirality in 120I and extend the boundary of the island of chirality.On the theoretical side, different models of nuclear structure have been applied to study nuclear chirality. Among them, the particle rotor model (PRM) [1, 45–53] and the titled axis cranking (TAC) model including various versions [54–59] are the most widely used. In this article, the experimental characteristics and configuration assignments for the doublet bands in 120I, including energy differences, rotational alignment, and self-consistent tilted axis cranking relativistic mean-field (TAC-RMF) calculation [57, 60-62], are discussed first. Then, the triaxial quasiparticles rotor model (PRM) [45] are adopted to investigate the rotational structure and possible chirality in doublet bands. Finally, a brief summary is given.
-
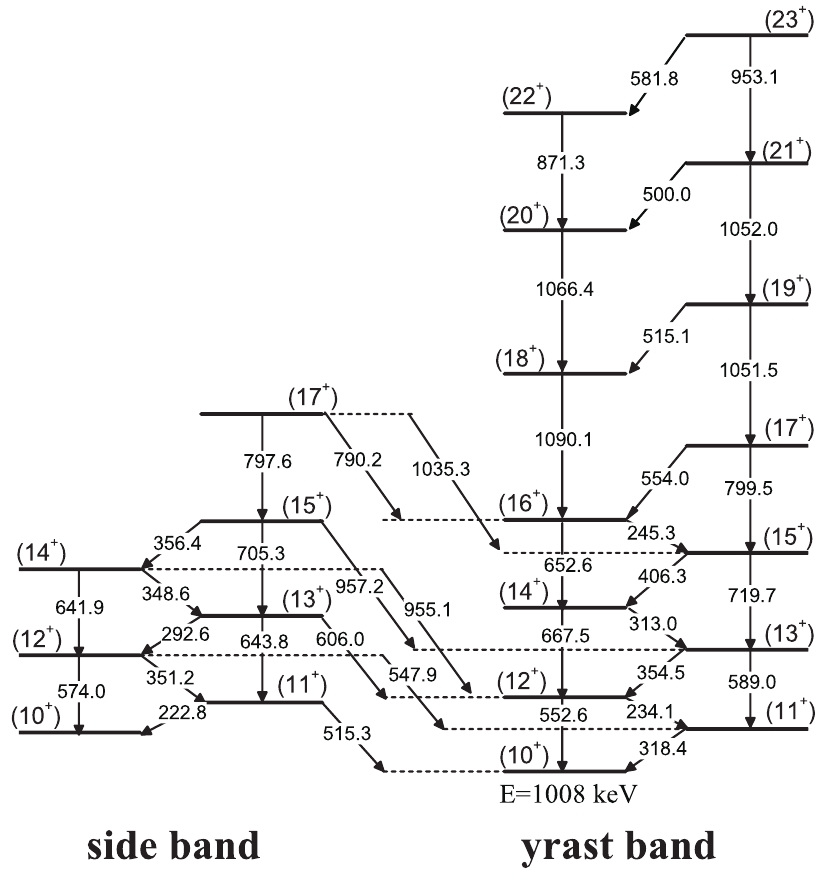
Partial level scheme for 120I derived from Refs. [43, 63] is shown in Fig. 2, where the yrast band and the side band, as well as the linking transitions between them, are adopted from Ref. [43, 63]. The experiment was performed at the HI-13 tandem accelerator of the China Institute of Atomic Energy, and high-spin states in 120I were populated using the fusion-evaporation reaction 114Cd (11B, 5n) at a beam energy of 70 MeV. The yrast band built on the (
$ 10^+ $ ) level at 1008 keV has been extended up to the$ (23^+) $ state, while the side band likewise built on the ($ 10^+ $ ) state is extended up to ($ 17^+ $ ). Apart from the similarity of energy spectra for the doublet bands, the existence of linking transitions multipolarities E2 and$ M1/E2 $ between the two bands also supports the judgment that the side band has the same parity and configuration as that of the yrast band.To study the characteristics of doublet bands, the rotational alignment of the doublet bands in 120I are shown in Fig. 3, compared with the neighboring chiral doublet bands in 122Cs [19] and 124Cs [20]. To subtract the angular momentum of the core, the Harris parameters [64], i.e.,
$ J_{0} = 17.0\;\; \hbar^{2}/ $ MeV,$ J_{1} = 25.8\;\; \hbar^{4}/ $ MeV3, are adopted. In Fig. 3, the large initial alignments ($ \sim6\;\hbar $ ) for the yrast band and side band in 120I indicate that the$ h_{11/2}[550]1/2^{-} $ proton, which can donate a large alignment ($ \sim5.5\;\hbar $ ) is involved in the configuration of the yrast band and side band. In the neighboring isotone 121Xe, the$ h_{11/2} $ neutron rotational band is closer to the yrast line than the$ d_{5/2} $ and$ d_{3/2} $ neutron rotational band [65]. Therefore, the odd neutron in 120I may have the priority to occupy the$ h_{11/2} $ orbit, and the same configuration$ \pi h_{11/2}\otimes \nu h_{11/2} $ as in the assignments in Ref. [44] is favored for the doublet bands in 120I.
Figure 3. (color online) Rotational alignment of yrast and side bands in 120I, compared with 122Cs and 124Cs. Harris parameters [64](
$J_{0} = 17.0\;\;\hbar^{2}/$ MeV,$J_{1} = 25.8\;\;\hbar^{4}/$ MeV3) are used to subtract the angular momentum of the core.In contrast, Fig. 3 shows that the alignment values of the doublet bands in 120I are very close to those in 122Cs and 124Cs during the rotational frequency between 0.25 MeV and 0.34 MeV. This indicates that the configurations of the doublet bands in 120I in the frequency range from 0.25 to 0.34 MeV should be same as those of the doublet bands in 122Cs and 124Cs, i.e., the high-
$ j $ $ h_{11/2} $ proton particle and neutron hole configuration. Therefore, these doublet bands have a similar band structure and angular momentum alignment, indicating that they have the same configuration.Moreover, the alignment of the yrast band in 120I suddenly increases by about 2
$ \hbar $ at around the rotational frequency 0.34 MeV, and then gradually decreases until 0.53 MeV where the backbending phenomenon occurs. This may be attributed to the non-aligned proton$ \pi g_{7/2} $ and neutron$ \nu h_{11/2} $ excitation in the core. Such excitation has been observed in 118Te, i.e., the core of 120I, and its isotope 120Te [66, 67]. When the paired$ g_{7/2} $ protons are excited, the deformation of the nucleus in 120I begins to change and gradually becomes oblate, and the moment of inertia becomes smaller. This is likely the reason behind the decrease in the alignment value at the rotational frequencies of approximately 0.3–0.5 MeV, as discussed in Ref. [63].To further investigate the configuration of the doublet bands in 120I, TAC-RMF calculations were performed. In the past few decades, the relativistic mean field (RMF) theory has had great success in describing properties of nuclei and numerous nuclear phenomena [17, 68–71]. Based on the RMF theory, the tilted axis cranking relativistic mean-field (TAC-RMF) theory was developed to describe numerous nuclear rotational phenomenona, such as magnetic, antimagnetic, and chiral rotation [17, 38, 57, 62, 72]. In the TAC-RMF theory, nuclei are characterized by the relativistic fields
$ S({{r}}) $ and$ V^{\mu}({{r}}) $ in the Dirac equation in the rotating frame with a constant angular velocity vector$ {\bf{\Omega}} $ as$ \begin{array}{l} [{{\alpha}}\cdot(-{\rm i}\nabla- {{V}} ) +\beta (m + S)+V - {\bf{\Omega}}\cdot {\hat{{J}}}]\psi_i = \varepsilon_i\psi_i, \end{array} $

(1) where
$ {\hat{{J}}} = {\hat{{L}}}+\frac{1}{2}{\hat{{\Sigma}}} $ is the total angular momentum of the nucleon spinors, and$ \varepsilon_i $ represents the single-particle Routhians for nucleons. The detailed formalism and numerical techniques are provided in Refs. [60, 61, 73]. A spherical harmonic oscillator basis with ten major shells is adopted to solve the Dirac equation. The point-coupling interaction PC-PK1 [74] is employed for the Lagrangian. Because of the suppression of pairing effects for the high- j two-quasiparticle configuration, the pairing correlations are herein neglected for simplicity. The pairing correlation implemented in a fully self-consistent and microscopic approach in TAC-RMF plays an important role in the description of the energy spectrum and electromagnetic transitions in nuclear rotation [75–78]. Therefore, it is very desirable to perform unified and self-consistent investigations of nuclear chirality within the tilted axis cranking covariant density functional theory with the pairing correlation in the future.In Fig. 4, the single-particle Routhians for the protons (a) and neutrons (b) in 120I are shown as a function of rotational frequency. In principle, broken time-reversal symmetry by the cranking field will be recovered without the cranking field at
$ \Omega = 0 $ , i.e., the levels will be degenerated again, as already shown in Fig. 4. There are three protons and seventeen neutrons above the$ N = 50 $ shell in 120I. Fig. 4(a) clearly shows that the last unpaired proton is occupying in the lower part of$ h_{11/2} $ in an ascending order of energy. Fig. 4(b) shows that the last unpaired neutron is kept fixed in the upper part of$ h_{11/2} $ for a large range of rotational frequency. The other remaining sixteen neutrons are treated self-consistently by filling the orbits according to their energies and distributing them across the$ h_{11/2} $ and$ {g_{7/2}}/{d_{5/2}} $ shells. In summary, the high- j proton-particle and neutron-hole configurations favored the doublet bands in 120I, whereas seven neutrons occupying the$ h_{11/2} $ orbital indicates that the character of neutron-hole is not ideal, which may be the reason that the valence neutron is not obviously considered to have the characteristics of a hole, as discussed in Ref. [44].
Figure 4. (color online) Single-proton (upper panel) and single-neutron (lower panel) Routhians near Fermi surface in 120I as a function of rotational frequency for configuration
$\pi h_{11/2}\otimes\nu h^{-1}_{11/2}$ in TAC-RMF calculation. Levels of$\nu{g_{7/2}}/{d_{5/2}}$ ,$\nu h_{11/2}$ ,$\nu{d_{3/2}/s_{1/2}}$ and$\pi{g_{9/2}}$ are marked by solid black, dashed red, solid green, and blue lines, respectively. Filled olive circles indicate occupied levels.It can be deduced from Fig. 4 that when the neutron number decreases in the iodine isotopes, i.e., the neutron number
$ N $ less than 67, the last odd neutron will occupy in the lower part of$ h_{11/2} $ shell and the neutron$ h_{11/2} $ hole character may not be favored. Similarly, when the proton number$ Z $ is lower than 53, there will be no proton occupying in the$ h_{11/2} $ orbit, and a high-$ j $ $ h_{11/2} $ proton particle is likewise not expected. Considering the proper high-$ j $ particle and hole configuration as a necessary condition for the appearance of chiral doublet bands, 120I could be the edge of island of chiral candidates in the A ≈ 130 mass region. Furthermore, it is naturally interesting to find and predict nuclear chirality in more neighbouring nuclei of 120I. -
The present configuration assignments of the high- j proton-particle and neutron-hole configurations for the doublet bands in 120I are favorable for the chirality. Configuration components are almost the same components of chiral bands in the neighboring odd-odd nuclei 124-128Cs. Therefore, a systematic comparison of their experimental features is performed. In Fig. 5, the energy differences
$ \Delta{E} $ for the doublet bands, i.e.,$ E(I)_{\rm side}-E(I)_{\rm yrast} $ , in 120I and 124-128Cs are shown. The energy differences for these doublet bands are very similar. They exhibit a slight undulation and gradually decrease from 360 to 160 keV with the spin increases from 14 to$ 17\;\hbar $ . 124Cs is particularly similar to 120I, i.e., the energy difference$ \Delta{E} $ is almost the same (greater than 200 keV) and is relatively larger than 126,128,130Cs, which implies that 120I and 124Cs [79] may exhibit a similar chiral geometry, i.e., might correspond to a typical chiral vibration pattern. Furthermore, the gradual decrease in the energy differences of 120I may indicate that the chiral vibration patterns of the nucleus gradually form and tend to stabilize the chirality.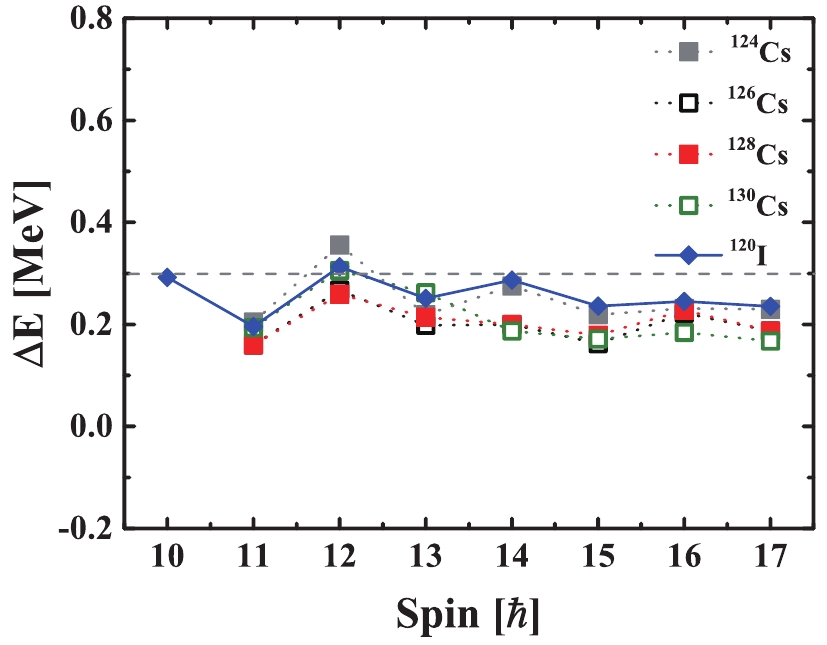
Figure 5. (color online) Comparison of energy differences
$\Delta{E}$ , i.e.,$E(I)_{\rm side}-E(I)_{\rm yrast}$ as a function of spin for doublet bands in 120I and 124,126,128,130Cs.To investigate the existence of nuclear chirality in 120I, the particle rotor model (PRM) with a quasi-proton and a quasi-neutron coupled with a triaxial rotor [45] was adopted. The PRM, as a quantal model describing a system in the laboratory reference frame and comprising collective rotation as well as intrinsic single particle motions, can be applied in a straightforward manner to investigate the angular momentum geometries of chiral doublet bands. In the PRM, the total Hamiltonian is diagonalized with total angular momentum as a good quantum number, and the energy splitting and quantum tunneling between the doublet bands is obtained directly. Its Hamiltonian for an odd-odd nucleus can be written as [45]
$ \begin{array}{l} H = H_{\rm coll}+H^{p}_{\rm intr}+H^{n}_{\rm intr}, \end{array} $

(2) where
$ p $ and$ n $ refer to the proton and neuron, respectively. Further, the configuration of multi-particles sitting in a high-$ j $ shell can be simulated by adjusting the Fermi energy by considering a pairing correlation by a BCS approximation [45]. For a detailed formalism of PRM, see Refs. [1, 45-48].The quadrupole deformation parameter
$ \beta = 0.36 $ for the configuration$ \pi h _{11/2}\otimes \nu h ^{-1}_{11/2} $ was adopted, which is obtained from both the triaxial relativistic mean-field (RMF) [3, 4, 6] and TAC-RMF calculations [60, 61, 80]. The triaxial deformation parameter$ \gamma = 20^{\circ} $ is employed to achieve a better description of the experimental ratios of reduced transition probabilities$ B(M1)/B(E2) $ . The single-$ j $ shell Hamiltonian parameter was taken as [81]$ \begin{split} C = \left(\frac{123}{8}\sqrt{\frac{5}{\pi}}\right) \frac{2N+3}{j(j+1)}A^{-1/3}\beta. \end{split} $

(3) The moment of inertia
$ {\cal{J}} = 25\;\hbar^{2}/ $ MeV is adjusted according to the experimental energy spectra. Following the empirical formula$ \Delta = 12/\sqrt{A} $ , the pairing gap$ \Delta = 1.1 $ MeV is used for both protons and neutrons. As the valence proton Fermi level in 120I is expected at the beginning of$ \pi h_{11/2} $ subshell, the proton Fermi energy$ \lambda_{p} $ assumes the value of$ -3.518 $ MeV. Considering the neutron Fermi level lying in the middle of the$ \nu_{11/2} $ subshell, the neutron Fermi energy$ \lambda_{n} $ is 0.765 MeV by simulating the effect of multivalence neutrons, similar to Refs. [45, 82]. For the electromagnetic transition, the empirical intrinsic quadrupole moment$ Q_{0} = (3/\sqrt{5\pi})R_{0}^{2}Ze\beta = 4.3 $ eb. The gyromagnetic ratio for the collective rotator is given by$ g_{R} = Z/A = 0.44 $ .$ g_{p} = 1.21 $ and$ g_{n} = -0.21 $ are adopted for the proton and neutron, respectively, obtained from the Schmidt magnetic moment formula of the$ h_{11/2} $ orbital with an effective spin gyromagnetic ratio$ g_s = 0.6\,g_s^{\mathrm{free}} $ , as used in the Refs. [14, 53, 83].Fig. 6 presents the calculated energy spectra
$ E(I) $ and energy staggering parameter$ S(I) $ , i.e.,$ [E(I)-E(I-1)]/2I $ , within the PRM calculations for the doublet bands in 120I, in comparison with the corresponding experimental results. The calculated energy spectra and energy staggering parameter$ S(I) $ efficiently reproduce experimental results in the spin region$ 10-15\;\hbar $ . One of the experimental fingerprints for nuclear chirality is that$ S(I) $ varies smoothly with increasing spin, which results from a highly reduced Coriolis interaction [84]. As shown in Fig. 6,$ S(I) $ exhibits a fairly smooth variation, supporting nuclear chirality for the present doublet bands [44]. Further, Fig. 6 shows that$ S(I) $ values of the doublet bands gradually approach each other with increasing spin, exhibiting a slight staggering that gradually becomes weak. Moreover, the behaviors of$ S(I) $ are similar to those for the chiral bands in 124,126,128,130Cs, indicating that the Coriolis interaction may decrease gradually, thereby suggesting that an aplanar rotation gradually appears in the triaxial nuclei. Hence, the chiral vibration pattern of the nucleus may gradually form and approach static chirality.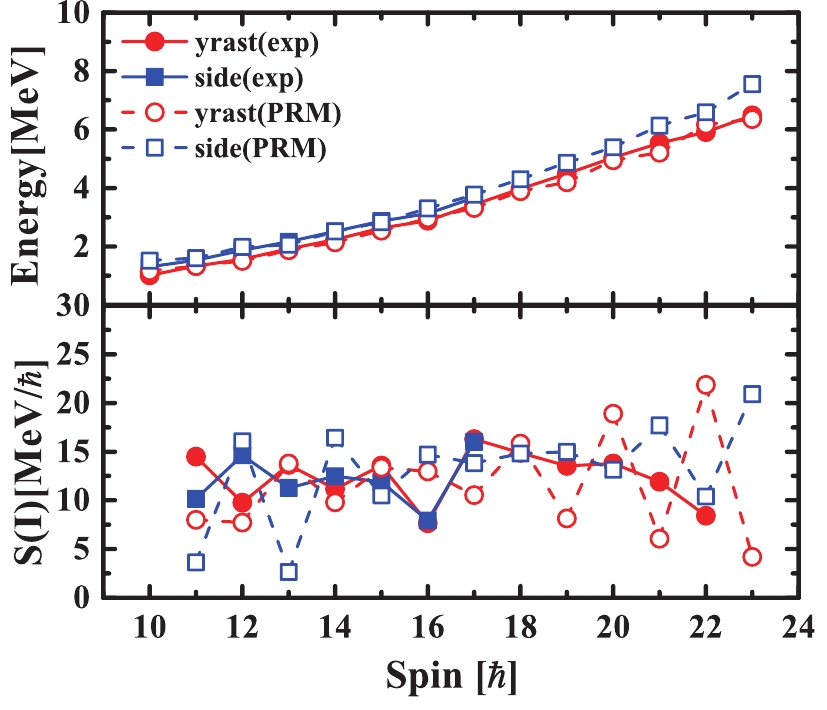
Figure 6. (color online) Excitation energy (upper panel) and staggering parameter
$S(I) = [E(I)-E(I-1)]/2I$ (lower panel) as a function of spin for yrast and side band in 120I. Filled (open) symbols connected by solid (dashed) lines depict experimental (theoretical) values. The yrast and side band are shown by circles and squares, respectively.The calculated in-band
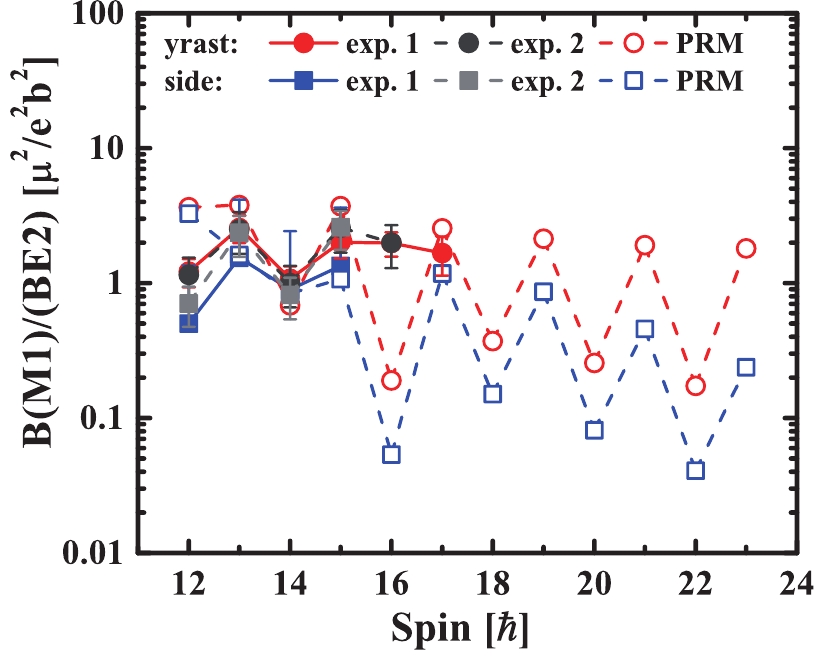
$ B(M1)/B(E2) $ ratios and the corresponding available data extracted from Ref. [63] (marked as exp. 1) for the yrast and side band in 120I are presented in Fig. 7. The corresponding data from Ref. [44] (marked as exp. 2) are also given for comparison. The$ B(M1)/B(E2) $ ratios of the doublet bands from Ref. [63] and Ref. [44] are very close to each other, and both meet the important experimental criteria of chiral double bands. Thus, the$ B(M1)/B(E2) $ ratios of chiral doublet bands should be similar and show staggering behavior with increasing spin. Furthermore, the feature of the$ B(M1)/B(E2) $ is reproduced well by the present PRM calculation, including the magnitude and staggering of the ratios with spin. The success in reproducing the energy spectra, the energy staggering parameter$ S(I) $ and transition probabilities for the doublet bands in 120I suggests that the present calculation must correctly account for the structure of the states in the spin region$ 10-15\;\hbar $ .To shed light on the chirality of 120I, the effective angels
$ \theta_{pn} $ ,$ \theta_{Rp} $ , and$ \theta_{Rn} $ obtained from the PRM calculations are displayed as a function of the spin for the doublet bands in Fig. 8. In the PRM, the effective angle$ \theta $ refers to the angle between the angular momentum orientations of the nuclei in the intrinsic reference frame. For example, the effective angle$ \theta_{pn} $ , which refers to the angle between the proton ($ {{j}_{p}} $ ) and neutron ($ {{j}_{n}} $ ) angular momenta, is defined as [27]$\cos\theta_{pn} = \langle{j}_{p}\cdot{j}_{n}\rangle/ $ $ \sqrt{(j_{p}^{2})(j_{n}^{2})} $ , and similarly for$ \theta_{Rp} $ and$ \theta_{Rn} $ . Here, the subscripts$ p, n $ , and$ R $ denote the proton, neutron, and rotor, respectively. By analyzing effective angles, the chiral geometry represented by a remarkable and similar aplanar rotation between doublet bands can be revealed by a quantum approach.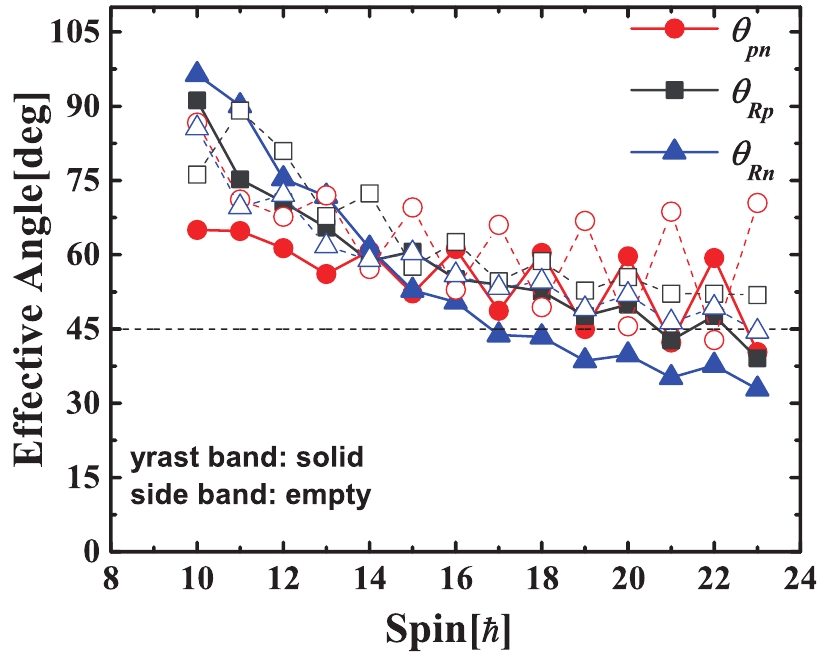
Figure 8. (color online) Effective angles
$\theta_{pn}$ ,$\theta_{Rp}$ , and$\theta_{Rn}$ as a function of spin for doublet bands in 120I. See text for further details.Fig. 8 shows that the effective angles
$ \theta_{pn} $ ,$ \theta_{Rp} $ , and$ \theta_{Rn} $ are greater than$ 60^{\circ} $ around$ I = 10\;\hbar $ , i.e., the angular momenta$ {{j}_{p}} $ ,$ {{j}_{n}} $ , and$ {{R}} $ are nearly perpendicular to each other at the band head, which also appears in 124,126Cs [79, 82]. In the spin region$ 10-15\;\hbar $ , the values of three effective angles for both yrast and side bands are larger than$ 45^{{\circ}} $ , which indicates a obvious aplanar rotation in 120I and provides additional support for the existence of chiral doublet bands in 120I.For the sake of presenting the chiral picture more clearly and examining the evolution of the chiral geometry with angular momentum, the probability distributions for the projection
$ K $ of the total angular momenta ($ K \;plots $ ) of the doublet bands in 120I are calculated in a similar manner as in Refs. [46, 46, 79, 85, 86]. The$ K\; plots $ , i.e, the probability distributions for the projection$ K $ of total angular momenta along long ($ l $ ), intermediate ($ i $ ), and short ($ s $ ) axes are displayed in Fig. 9. At the band head$ I = 10\;\hbar $ , the probability distributions along the$ i $ axis, i.e.,$ K_{i} $ for the doublet bands are different. For the yrast band, the maximum probability$ K_{i} $ appears at$ K_{i} = 0 $ , whereas the$ K_{i} $ for the side band is at its minimum at$ K_{i} = 0 $ , with its peak at$ K_{i}\approx8 $ . This is in accordance with the interpretation of the chiral vibration with respect to the$ s-l $ plane, where the zero-phonon state (yrast band) is symmetric with respect to$ K_{i} = 0 $ , and the one-phone state (side band) is antisymmetric [46, 85].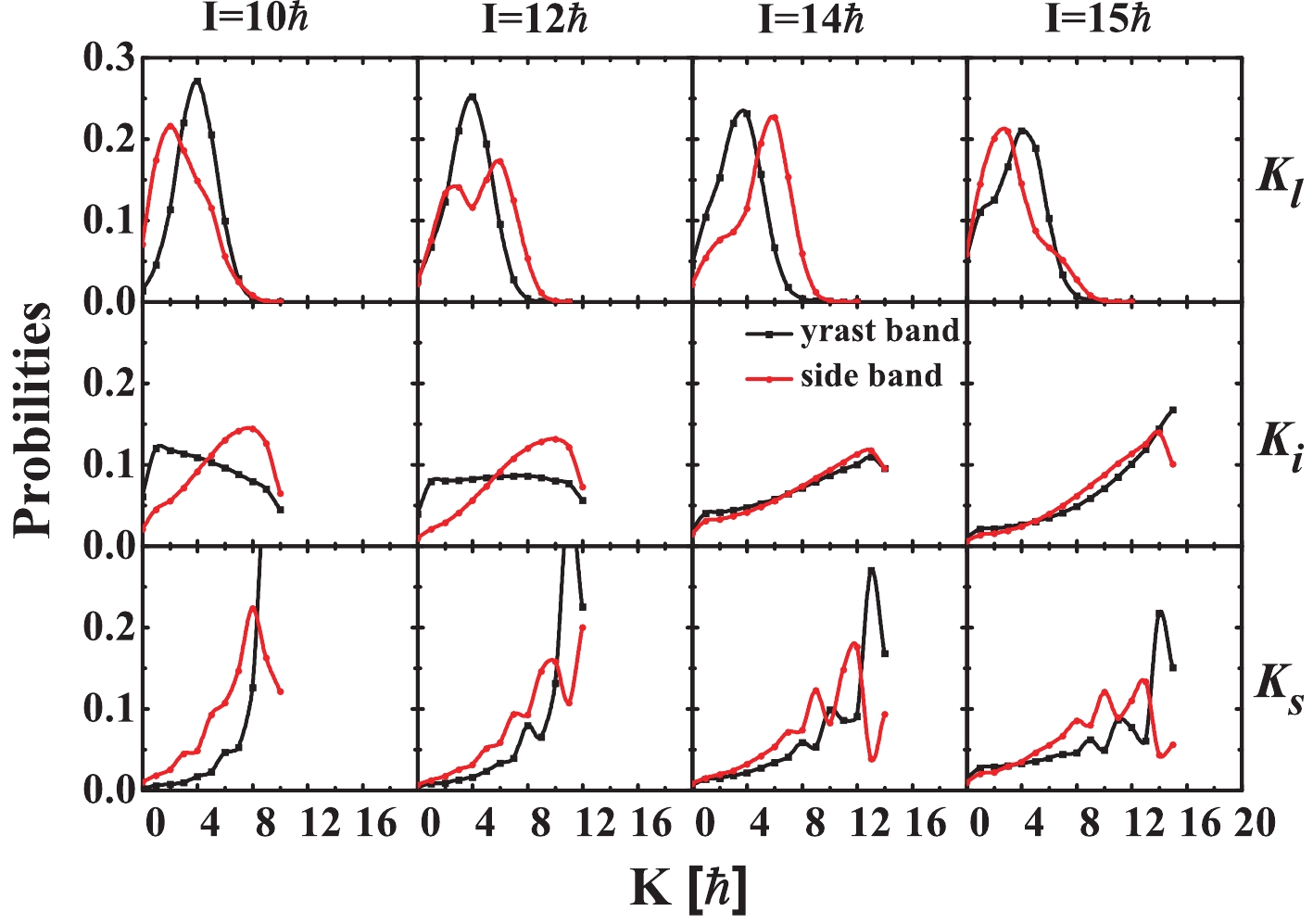
Figure 9. (color online) Probability distributions for projection K of total angular momenta on long (l), intermediate (i), and short (s) axes in PRM for doublet bands in 120I.
As the angular momentum increases,
$ K_{i} $ values for the doublet bands approach each other at the spin region$ 14-15\;\hbar $ , indicating that the chiral vibration through$ s-l $ is weakening and tends towards static chirality. Moreover, the maximum$ K_{s} $ distribution appears at a different position for the doublet bands, indicating that the motion contains a vibration of the vector$ I $ through the$ l-i $ plane. The overall$ K\;plots $ with increasing spin show the peak value of$ K_{l}\approx4 $ , while the peak values of both$ K_{i} $ and$ K_{s} $ increase slightly and are greater than 4, indicating that the total angular momentum gradually deviates from the$ l $ axis. This is highly similar to 124Cs [79], and it is interpreted as a typical chiral vibration pattern across the entire spin region based on present calculations. -
Based on the reported positive-parity doublet bands in 120I, the corresponding experimental characteristics including rotational alignment were extracted and discussed, and the corresponding configuration of the doublet bands is reexamined as
$ \pi h _{11/2}\otimes\nu h^{-1} _{11/2} $ after performing TAC-RMF calculations. For the sake of high-$ j $ particle hole configuration, the TAC-RMF calculation indicates that 120I is located at the borders of the$ A \approx 130 $ island of chiral candidates with configuration$ \pi h _{11/2}\otimes \nu h ^{-1}_{11/2} $ . However, a larger number of neighbouring nuclei should be investigated to obtain a clearer conclusion. Moreover, the positive-parity doublet bands based on the$ \pi h _{11/2}\otimes\nu h^{-1} _{11/2} $ configuration in 120I were studied in two quasiparticles coupled with a triaxial rotor model. The calculated energy spectra, energy staggering parameter$ S(I) $ , and the intraband$ B(M1)/B(E2) $ are in good agreement with the available experimental data. Furthermore, the calculated effective angles between the angular momenta of the core, valence proton and neutron, and probability distributions for the projection of total angular momenta also indicate an obvious chiral geometry of the aplanar rotation. Thus, we propose the reported positive-parity doublet bands in 120I as a candidate of chiral doublet bands.The authors would like to thank Prof. J. Meng and S. Q. Zhang as well as Dr. Q. B. Chen for helpful discussions during the completion of this work.
Doublet bands at borders of A ≈ 130 island of chiral candidates: Case study of 120I
- Received Date: 2020-01-17
- Available Online: 2020-07-01
Abstract: Positive-parity doublet bands were reported in 120I. Based on these, we discuss the corresponding experimental characteristics, including rotational alignment, and re-examine the corresponding configuration assignment. The self-consistent tilted axis cranking relativistic mean-field calculations indicate that the doublet bands are built on the configuration





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF















 DownLoad:
DownLoad: