-
Since the introduction of the concept of neutron stars and their observation, the equation of state (EOS) of the quark matter at finite density with vanishing temperature has been the subject of extensive research. Once the EOS is obtained, the neutron star mass-radius relationship can be calculated by solving the Tolman-Oppenheimer-Volkoff equations [1]. By comparing the theoretical mass-radius relationship with the results obtained from astronomical observations, the theory of strong interaction can be proven.
The basic theory of the strong interactions is described by quantum chromodynamics (QCD). Nevertheless, because of the invalidation of the perturbative QCD method in the low-energy region, it is difficult to obtain a reliable EOS from the first principles of QCD. To solve this problem, several approximate methods that incorporate the basic features of QCD are adopted to calculate the EOS of the quark matter, such as the MIT bag model and Nambu–Jona-Lasinio (NJL) model. Although all these models have their own weaknesses, they play an important role in the study of the EOS of the quark matter.
The NJL model was initially proposed by Nambu and Jona-Lasinio in 1961 [2, 3]. After continuous development, the NJL model has been widely adopted as a quark model to describe cold dense matter in neutron and quark stars [4, 5]. To calculate the relevant physical quantities, we need to apply mean field approximation in the NJL model [4].
The Fierz transformation is a mathematically equivalent transformation, where the original Lagrangian,
$ {\cal{L}} $ , and transformed Lagrangian,$ {\cal{L}}_F $ , are equivalent. Nevertheless, when we employ the mean field approximation, we observe that$ \langle{\cal{L}}\rangle $ is no longer equal to$ \langle{\cal{L}}_F\rangle $ , because the Fierz transformation and mean field approximation are not commutative (notation$ \langle\; \cdot\; \rangle $ denotes the mean field approximation). Apart from these two forms, we can also construct multiple new refined equivalent Lagrangians by calculating the linear combination of$ {\cal{L}} $ and$ {\cal{L}}_F $ :$ {\cal{L}} _R = \left(1-\alpha \right){\cal{L}} + \alpha {\cal{L}} _F , $

(1) where
$ \alpha $ is an arbitrary complex number. Therefore, an important question arises: What effective Lagrangian should be theoretically assumed for the mean field approximation? To obseve this more clearly, we recall the mean field approximation employed in previous studies within the framework of the NJL model. In the original mean field approximation, the Fierz transformation is not performed, indicating that$ \alpha $ is zero in our model. However, as the authors point out in Refs. [6, 7], this approximation is theoretically not self-consistent at the level of the mean field approximation. Refs. [6, 7] indicate that to obtain a self-consistent result in the sense of a mean field approximation, the contribution of the Fierz transformed Lagrangian must be taken into account. Afterwards,$ \alpha = 1/2 $ is adopted in the effective Lagrangian, proposed in Ref. [4]. However, there is no physical requirement that the value of$ \alpha $ must be$ 1/2 $ .Consequently, the authors of Ref. [8] propose that the value of
$ \alpha $ cannot be determined in advance by the mean field approach, but in principle must be determined by experiments or astronomy observations. For example, if the NJL model is applied to describe cold, dense matter in neutron stars, parameter$ \alpha $ may be constrained by the discovery of two-solar-mass neutron stars [9-12] and the gravitational-wave signal from the neutron star merger GW170817 [13–17]. Hence, our novel self-consistent mean field approximation differs from the previous mean field approximation only with respect to the value of$ \alpha $ . Notably, the value of parameter$ \alpha $ is determined by relevant experiments of finite density in our theoretical model, that is,$ \alpha $ depends on the density. This is because parameter$ \alpha $ essentially reflects the weight of the vector channels under finite density [18], and the vector channels with different densities also have different weights. However, due to the lack of experimental data, in this paper we consider$ \alpha $ as a free parameter and study the effects of this free parameter on the phase transition of strong interaction matter. By applying the self-consistent mean field approximation in the two-flavor NJL model, Ref. [8] has noted that parameter$ \alpha $ plays a crucial role in the study of the strong interaction phase diagram. Furthermore, Ref. [18] presents a conclusion that the stiffness of the EOS obtained from two-flavor NJL model can increase significantly to support a two-solar-mass pure quark star as$ \alpha $ increases.In this paper, we extend the self-consistent mean field method described above from 2 flavors to 2 + 1 flavors strong interaction matter at finite density and zero-temperature, and explore the effect of
$ \alpha $ on the phase transition of three-flavor quark matter. Because most studies on the inner structure of neutron stars have assumed that the neutron stars are composed of u, d, and s three-flavor quarks, we believe that this work will aid in studying the EOS of neutron stars. Moreover, we compare the properties of the two-flavor and three-flavor quark matter in the framework of self-consistent mean-field approximation.Notably, the Minkowski space metric,
$g_{\mu\nu} = \{1, -1, -1,$ $ -1\} $ , is adopted, and we selected the three-momentum non-covariant cutoff scheme as the regularization scheme. -
The standard two-flavor NJL Lagrangian with interaction terms in scalar and pseudoscalar-isovector channels is obtained by [4]
$ {\cal{L}} = \bar{\psi}( {\rm{i}}\gamma^\mu \partial_\mu-m)\psi+G\left[(\bar{\psi}\psi)^2+(\bar{\psi} {\rm{i}}\gamma^5{{\tau}}\psi)^2\right], $

(2) where
$ m = $ diag$ (m_u,\; m_d) $ is the current quark mass, which satisfies$ m_u = m_d = m_0 $ ;$ \tau_i(i = 1,\; 2,\; 3) $ are the three Pauli matrices acting in isospin space, and G denotes the coupling constant. The Fierz identity of the Lagrangian is [4]$ \begin{split} {\cal{L}}_F = & \bar{\psi}( {\rm{i}}\gamma^\mu \partial_\mu-m)\psi+\dfrac{G}{4N_c}\bigg[(\bar{\psi}\psi)^2-2(\bar{\psi}\gamma^\mu\psi)^2\\ & +\dfrac12(\bar{\psi}\sigma^{\mu\nu}\psi)^2+2(\bar{\psi}\gamma_\mu\gamma_5\psi)^2-(\bar{\psi} {\rm{i}}\gamma_5\psi)^2\\ & -(\bar{\psi}{{\tau}}\psi)^2-\dfrac12(\bar{\psi}\sigma^{\mu\nu}{{\tau}}\psi)^2+(\bar{\psi} {\rm{i}}\gamma_5{{\tau}}\psi)^2\bigg]. \end{split}$

(3) Our redefined mean field Lagrangian is:
$ \langle{\cal{L}} _R \rangle = \left(1-\alpha \right)\langle{\cal{L}} \rangle + \alpha\langle{\cal{L}} _F \rangle. $

(4) Based on our new Lagranian, we assume that the temperature is zero. Then, the two-flavor gap equation is expressed as:
$ \begin{split} m_f^* = &m_f+ {\rm{i}} g[2(1-\alpha)N_c+\alpha/2]\sum\limits_{f' = u, d}{\rm{tr}}S^{f'}\\ =& m_0+ {\rm{i}} G(2N_c+1/2)\sum\limits_{f' = u,\; d}{\rm{tr}}S^{f'}, \end{split} $

(5) where
$ m^*_f(f = u, d) $ are the constituent quark masses,$ f' $ is a summation index,$ N_c = 3 $ ,$ g = \frac{13G}{12-11\alpha} $ , and$ {\rm{tr}}S^f = -2 {\rm{i}} m_f^*\int^{\Lambda}\dfrac{ {\rm{d}}^3 {{p}}}{(2\pi)^3}\dfrac{1}{E^f_{{{p}}}}\Big[1-\theta(\mu_f^*-E^f_{{p}})\Big]. $

(6) Here,
$ \theta $ is the unit step function,$ E_{{{p}}}^f = \sqrt{{{p}}^2+(m^*_f)^2} $ , and$ \Lambda $ is the three-momentum cutoff. By calculating this integral, we obtain$ \begin{split} {\rm{tr}}S^f = &-\dfrac{ {\rm{i}} m^*_f}{2\pi^2}\Bigg[\Lambda\sqrt{\Lambda^2+(m_f^*)^2}-(m_f^*)^2\sinh^{-1}\dfrac{\Lambda}{m_f^*}\\ &-\Lambda_f^*\sqrt{(\Lambda_f^*)^2+(m_f^*)^2}+(m_f^*)^2\sinh^{-1}\dfrac{\Lambda_f^*}{m_f^*}\Bigg], \end{split} $

(7) where
$ \Lambda^*_f = \sqrt{(\mu^*_f)^2-(m^*_f)^2}\cdot\theta(\mu^*_f-m^*_f), $

(8) and
$ \mu^*_f $ is the effective chemical potential that satisfies$ \mu_f^* = \mu_f-\dfrac{\alpha g}{3\pi^2}\sum\limits_{f' = u,\; d}(\Lambda_{f'}^*)^3. $

(9) -
The three-flavor NJL model with the scalar-pseudoscalar and six fermion interaction is obtained by [5]
$ {\cal{L}} = \bar{\psi}( {\rm{i}}\gamma^\mu \partial_\mu-m)\psi+{\cal{L}}^{(4)}+{\cal{L}}^{(6)}, $

(10) where
$ \psi = (\psi_u,\; \psi_d,\; \psi_s)^{\rm{T}} $ denotes a quark field with three flavors, and$ m = {\rm{diag}}(m_u,\; m_d,\; m_s) $ is the corresponding mass matrix. We assume isospin symmetry on the Lagrangian level,$ m_u = m_d $ , whereas$ m_s $ is in general different. The Lagrangian contains two independent interaction terms, which are calculated by$ {\cal{L}}^{(4)} = G\sum\limits_{i = 0}^8\left[(\bar{\psi}\lambda^i\psi)^2+(\bar{\psi} {\rm{i}}\gamma_5\lambda^i\psi)^2\right], $

(11) $ {\cal{L}}^{(6)} = -K\left[{\rm{det}}\bar{\psi}(1+\gamma_5)\psi+{\rm{det}}\bar{\psi}(1-\gamma_5)\psi\right], $

(12) where
$ \lambda^0 = \sqrt{\frac23}{\bf{1}} $ and$ \lambda^i(i = 1,\; \cdots,\; 8) $ are eight Gell-Mann matrices.The Fierz identity of
$ {\cal{L}}^{(4)} $ is [4]$ {\cal{L}}_F^{(4)} = -\dfrac{3G}{2N_c}\big[(\bar{\psi}\gamma_\mu\lambda^0\psi)^2-(\bar{\psi}\gamma_\mu\gamma_5\lambda^0\psi)^2\big]. $

(13) As for
$ {\cal{L}}^{(6)} $ , we express the six-fermion Lagrange density as an effective four-fermion interaction, such that [4]$ \begin{split} {\cal{L}}^{(6)\rightarrow(4)} =& \sum\limits_{i = 0}^8K_i\Big[(\bar{\psi}\lambda^i\psi)^2-(\bar{\psi} {\rm{i}}\gamma_5\lambda^i\psi)^2\Big]\\&+K_m\Big[(\bar{\psi}\lambda^8\psi)(\bar{\psi}\lambda^0\psi)+(\bar{\psi}\lambda^0\psi)(\bar{\psi}\lambda^8\psi)\Big]\\ &-K_m\Big[(\bar{\psi} {\rm{i}}\gamma_5\lambda^8\psi)(\bar{\psi} {\rm{i}}\gamma_5\lambda^0\psi)+(\bar{\psi} {\rm{i}}\gamma_5\lambda^0\psi)(\bar{\psi} {\rm{i}}\gamma_5\lambda^8\psi)\Big], \end{split}$

(14) and the Fierz identity of
$ {\cal{L}}^{(6)\rightarrow(4)} $ is$ \begin{split} {\cal{L}}^{(6)\rightarrow(4)}_F =& \dfrac{1}{2N_c}\Bigg\{K_m\bigg[(\bar{\psi}\lambda^8\psi)(\bar{\psi}\lambda^0\psi)+\dfrac{1}{2}(\bar{\psi}\sigma^{\mu\nu}\lambda^8\psi)(\bar{\psi}\sigma^{\mu\nu}\lambda^0\psi)-(\bar{\psi} {\rm{i}}\gamma_5\lambda^8\psi)(\bar{\psi} {\rm{i}}\gamma_5\lambda^0\psi)\bigg]\\ &+K_m\bigg[(\bar{\psi}\lambda^0\psi)(\bar{\psi}\lambda^8\psi)+\dfrac{1}{2}(\bar{\psi}\sigma^{\mu\nu}\lambda^0\psi)(\bar{\psi}\sigma^{\mu\nu}\lambda^8\psi)-(\bar{\psi} {\rm{i}}\gamma_5\lambda^0\psi)(\bar{\psi} {\rm{i}}\gamma_5\lambda^8\psi)\bigg]\\ &+\sum\limits_{i = 0}^8K_i\bigg[(\bar{\psi}\lambda^i\psi)^2+\dfrac{1}{2}(\bar{\psi}\sigma^{\mu\nu}\lambda^i\psi)^2-(\bar{\psi} {\rm{i}}\gamma_5\lambda^i\psi)^2\bigg]\Bigg\}, \end{split} $

(15) where
$ \begin{split} K_0 = \dfrac13 {\rm{i}} (N_c+1)K({\rm{tr}}S^s+2{\rm{tr}}S^u),\\ K_1 = K_2 = K_3 = -\dfrac12 {\rm{i}} (N_c+1)K{\rm{tr}}S^s,\\ K_4 = K_5 = K_6 = K_7 = -\dfrac12 {\rm{i}} (N_c+1)K{\rm{tr}}S^u,\\ K_8 = \dfrac16 {\rm{i}} (N_c+1)K({\rm{tr}}S^s-4{\rm{tr}}S^u),\\ K_m = \dfrac{\sqrt{2}}{6} {\rm{i}} (N_c+1)K({\rm{tr}}S^s-{\rm{tr}}S^u). \end{split}$

(16) Based on the self-consistent mean field approximation, the three-flavor gap equation is obtained by:
$\begin{split} m_i^* =&{ {m_i} + (1 - \alpha )4{\rm{i}}g{N_c}{\rm{tr}}{S^i}}\\ &{ - 2k[2{N_c}(1 - \alpha ) + \alpha ]({N_c} + 1){\rm{tr}}{S^j}{\rm{tr}}{S^k}{\rm{ }}}\\ =&{ {m_i} + 4{\rm{i}}G{N_c}{\rm{tr}}{S^i} - 2KN_c^2{\rm{tr}}{S^j}{\rm{tr}}{S^k},} \end{split}$

(17) where
$ (i,\; j,\; k) $ can be any permutation of$ (u,\; d,\; s) $ ,$ g = \dfrac{G}{1-\alpha} $ ,$ k = \dfrac{9K}{4(6-5\alpha)} $ ,$ {\rm{tr}}S^f $ is obtained from Eqs. (7) and (8), and the effective chemical potential satisfies$ \mu^*_i = \mu_i-\dfrac{2\alpha g}{3\pi^2}\sum\limits_{f' = u,\; d,\; s}(\Lambda_{f'}^*)^3. $

(18) -
Due to the lack of experimental data at large chemical potentials, parameter
$ \alpha $ cannot be determined using the experimental results; hence, we regard$ \alpha $ as a free parameter. As a preliminary study, we only consider the case where$ \alpha $ is a real number.In Fig. 1 and Fig. 2, the constituent quark masses,
$ m_f^* $ (left panel), and chiral susceptibilities [19]
Figure 1. (color online) Two flavor quark matter properties as functions of a common quark chemical potential,
$ \mu $ , at zero temperature. (Parameters are expressed as$ \Lambda = 631 $ MeV,$ G\Lambda^2 = 2.02 $ ,$ m_u = m_d = m = 5.5 $ MeV [4].) Left: Constituent quark masses$ m^*_u = m^*_d $ . Right: Chiral susceptibilities$ \chi_{mu} $ =$ \chi_{md} $ .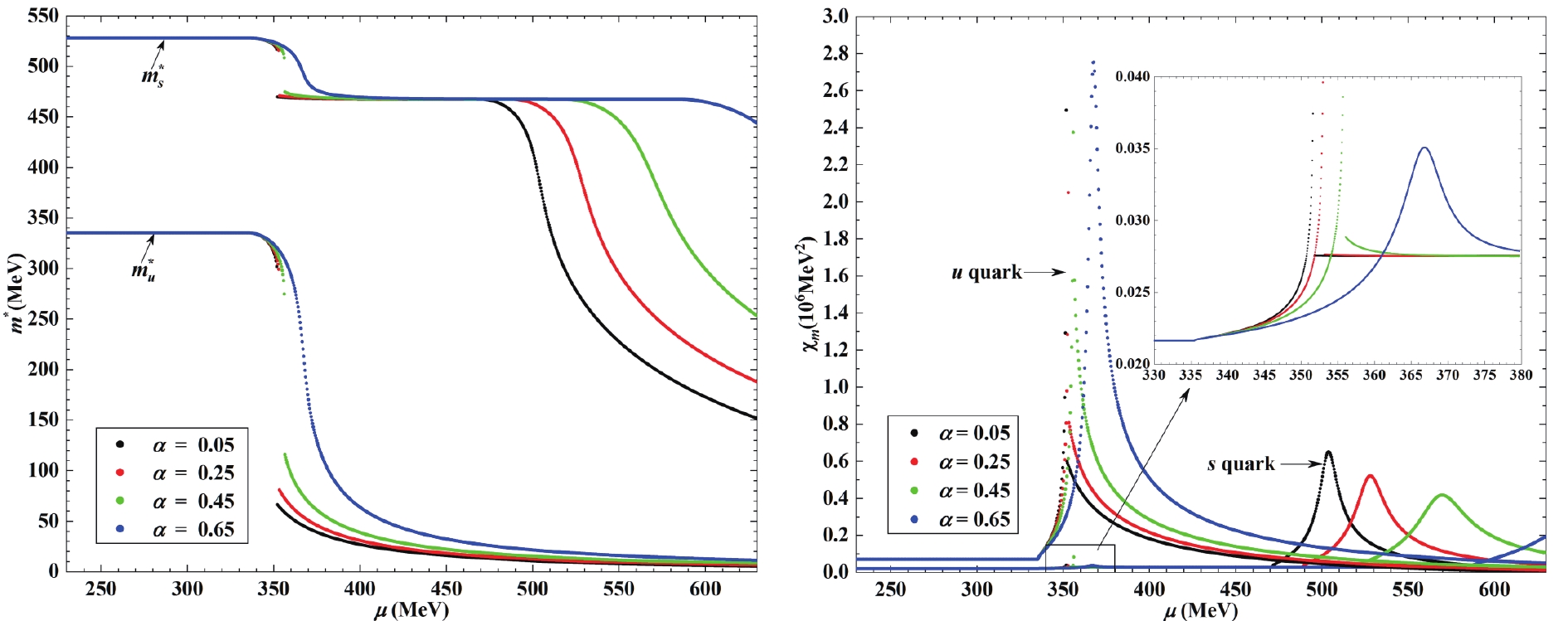
Figure 2. (color online) Three flavor quark matter properties as functions of a common quark chemical potential,
$ \mu $ , at zero temperature. (Parameters are expressed as$ \Lambda = 631.4 $ MeV,$ G\Lambda^2 = 1.835 $ ,$ K\Lambda^5 = 9.29 $ ,$ m_u = m_d = 5.5 $ MeV,$ m_s = 135.7 $ MeV [5].) Left: Constituent quark masses$ m^*_u = m^*_d $ and$ m^*_s $ . Right: Chiral susceptibilities$ \chi_{mu} $ =$ \chi_{md} $ and$ \chi_{ms} $ .$ \chi_{mf} = -\dfrac{ \partial\langle\bar{\psi}_f\psi_f\rangle}{ \partial m_f} , $

(19) (right panel) are plotted as functions of a common quark chemical potential,
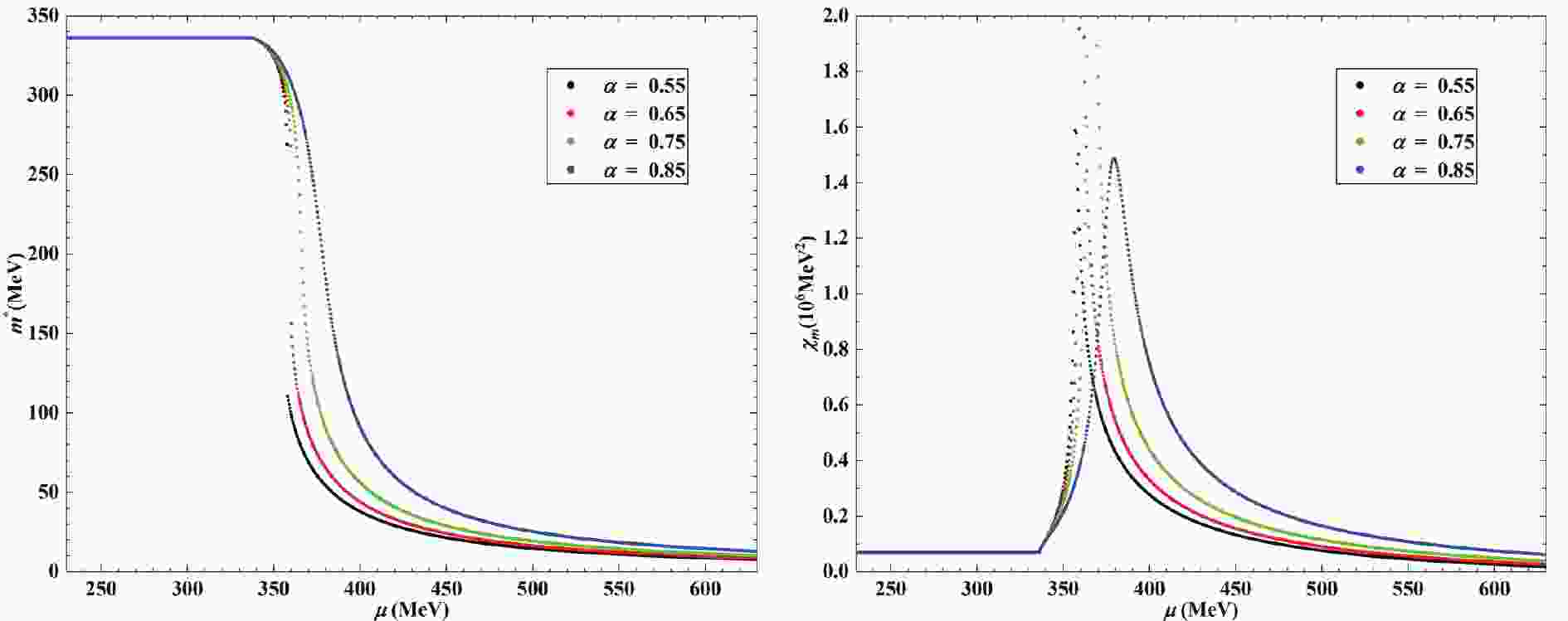
$ \mu $ , and numerous interesting results are observed. Ref. [8] discussed the two-flavor NJL model extensively; hence, we concentrate on the three-flavor model in this study.First, the behavior of the constituent masses,
$ m^*_u = m^*_d $ , and chiral susceptibilities,$ \chi_{mu} $ =$ \chi_{md} $ , exhibits some similarities with the two-flavor model. For example, the chiral susceptibility exhibits different behaviors with different$ \alpha $ . As$ \alpha $ is lower than the critical value,$ \alpha_c $ , ($ \alpha_c $ is approximately 0.55 in the three-flavor NJL model, while is approximately 0.69 in the two-flavor model) the chiral susceptibility is discontinuous at the chiral phase transition point,$ \mu_c $ , which indicates that the phase transition is a first order phase transition. With the increase of$ \alpha $ , the chiral phase transition point increases, the chiral susceptibility exhibits a smooth peak at the pseudo-critical chemical potential, and the phase transition is a crossover.Second, because the flavor symmetry is broken by unequal masses, the behavior of the strange quark exhibits some differences with the u and d quarks. Furthermore, the strange quark will incur a phase transition where the constituent mass of the strange quark,
$ m^*_s $ , drops from 528.1 MeV to 467.7 MeV (properties of the phase transition, such as the chiral phase transition point and order of the phase transition are similar to the phase transition of the other two quarks). The above$ \mu_c $ contributions of tr$ S^u $ and tr$ S^d $ to$ m^*_s $ are negligible, and$ m^*_s $ remains almost constant before point$ \mu_{0s} $ , where$ \mu $ exceeds$ m^*_s $ .$ \mu_{0s} $ increases with parameter$ \alpha $ .Finally, we study the number densities of different quarks (see Fig. 3)
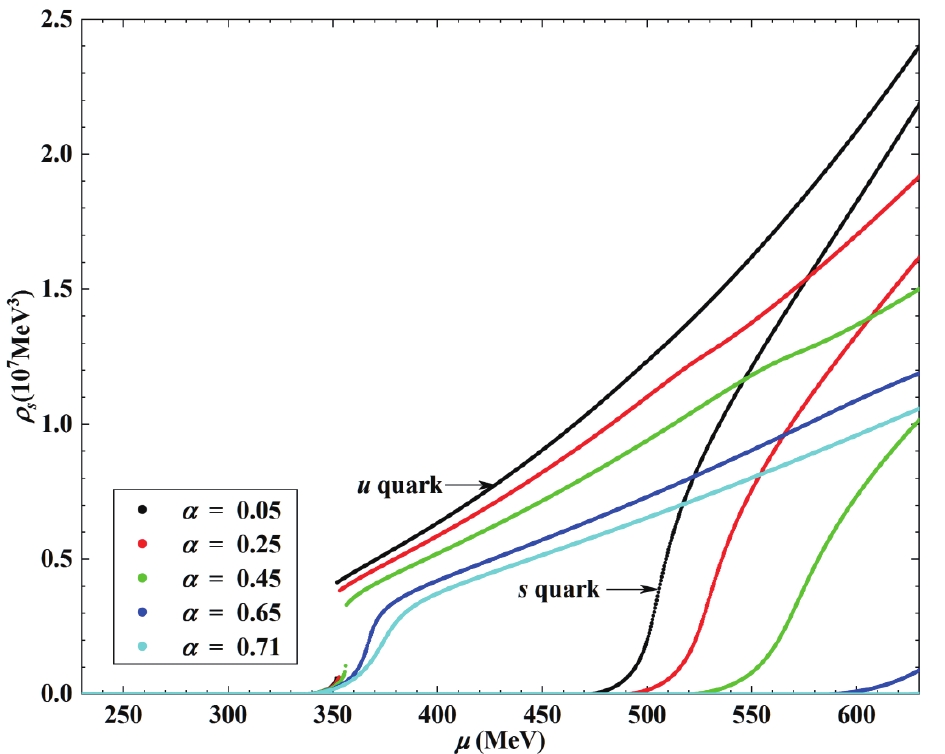
Figure 3. (color online) Number density of different quarks
$ \rho_f $ as a function of a common quark chemical potential,$ \mu $ . (Parameters are presented in Fig. 2.)$ \rho_f = \dfrac{1}{\pi^2}(\Lambda_{f}^*)^3, $

(20) in the three-flavor NJL model. Irrespective of the magnitude of
$ \alpha $ , the number density of the u and d quarks,$ \rho_u = \rho_d $ , is zero unless the chemical potential is greater than a critical value,$ \mu_0 $ , which is independent on parameter$ \alpha $ . Based on the model parameters adopted in this study,$ \mu_0 $ is always equal to 335.5 MeV. (The two-flavor NJL model leads to the same conclusion. Based on the model parameters adopted in this paper,$ \mu_0 $ is always equal to 336.1 MeV in the two-flavor model.) This result was expected, and the authors of Ref. [20] demonstrated this as a model-indepent result. The number density of strange quarks,$ \rho_s $ , is likewise zero until$ \mu $ exceeds$ \mu_{0s} $ . As pointed out earlier,$ \mu_{0s} $ increases with$ \alpha $ , which is different in the case of the u and d quarks. When$ \alpha>0.71 $ ,$ \mu_{0s} $ is even greater than cutoff$ \Lambda $ . Notably, the NJL model is effective and can only be applied under certain energy scales, with parameter$ \Lambda $ defining this energy scale. Therefore, the quark chemical potential studied herein cannot be larger than parameter$ \Lambda $ . This indicates that the strange quark will not contribute to the quark matter if$ \mu $ is not sufficiently large when a large$ \alpha $ is introduced. Furthermore,$ \rho_f $ will decrease at the same$ \mu $ with increasing$ \alpha $ . This will influence the pressure and EOS of the quark matter. -
To obtain the EOS of the quark matter, we should consider the chemical equilibrium [21, 22]. However, we assumed that three different quarks have a common chemical potential in this study. Our calculation, presented below, is still based on this assumption. In this case, the pressure of the strong interaction matter is
$ P(\mu) = P(\mu = 0)+\sum\limits_{f'}\int^\mu_0\rho_{f'}(\mu') {\rm{d}}\mu'. $

(21) The energy density of the strong interaction matter is [23, 24]
$ \varepsilon = -P+\sum\limits_{f'}\mu_{f'}\rho_{f'}. $

(22) Using these two equations, we can obtain the EOS of the three-flavor quark matter (Fig. 4).
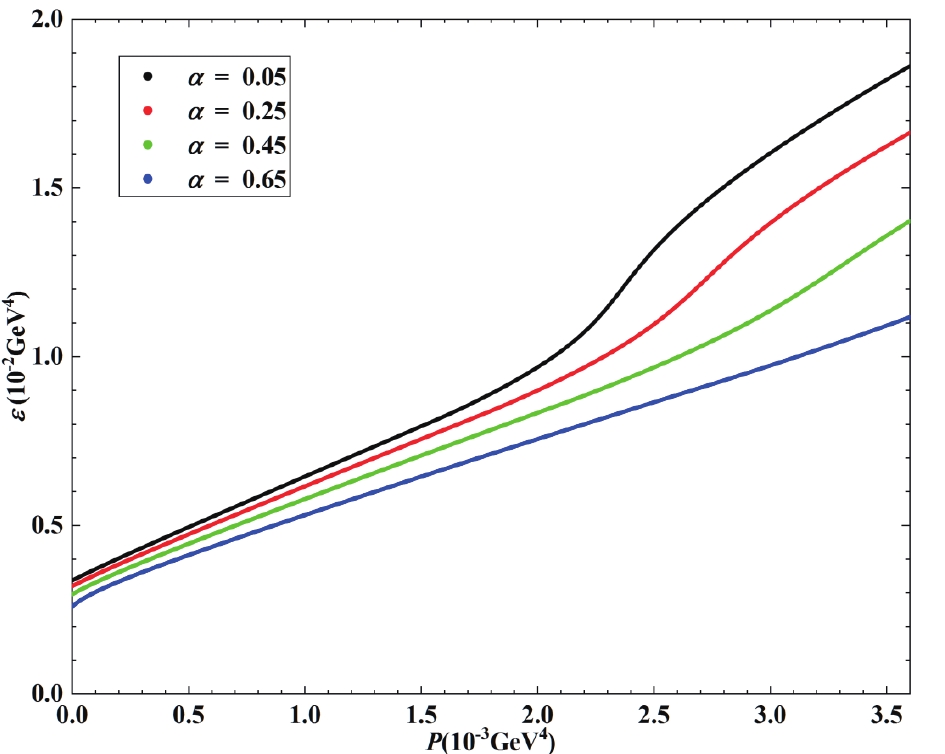
Figure 4. (color online) EOS of three-flavor quark matter. (Parameter
$ P(\mu = 0) $ is$ -(100\;{\rm{MeV}})^4 $ , other parameters are presented in Fig. 2.)To determine the stiffness of the EOS of three-flavor quark matter, we must calculate the sound velocity, which is obtained by
$ v_s = \sqrt{\dfrac{ {\rm{d}} P}{ {\rm{d}} \varepsilon}}. $

(23) To compare these two NJL models, we calculate the results of both two and three flavor quark matter, as shown in Fig. 5.

Figure 5. (color online) Sound velocity in quark matter
$ v_s $ as a function of common quark chemical potential$ \mu $ . Left: Two-flavor quark matter. (Parameter$ P(\mu = 0) $ is$ -(100\;{\rm{MeV}})^4 $ , other parameters are presented in Fig. 1.) Right: Three-flavor quark matter. (Parameters are presented in Fig. 4.)Comparing the two graphs, we obtain the following results. First, with increasing
$ \alpha $ , the velocity can be significantly large, which indicates that if we want to obtain an EOS that supports the existence of two-solar-mass neutron stars, we must introduce a large$ \alpha $ . Second, the relation of the sound velocity with the chemical potential is not monotonic. The velocity of sound becomes non-zero with the production of u and d quarks. With the increase in the chemical potential, the sound velocity will also increase until the phase transition occurs. Subsequently, the sound velocity of the two-flavor quark matter will increase again. In contrast, the three flavor quark matter exhibits another downward peak. Evidently, the point where the sound velocity starts to decrease is where the number density of the strange quark starts to become non-zero. This indicates that the production of s quarks reduces the sound velocity.Fig. 5 shows that the speed of sound,
$ v_s $ , exceeds the conformal limit,$ c/\sqrt{3} $ , in some cases (c denotes the velocity of light). Notably, the conformal limit,$ c/\sqrt{3} $ , only corresponds to that of the gases comprising ultra-relativistic massless particles, whereas real strong interaction systems are far more complicated [25]. For example, the authors of Ref. [26] have noted that the sound velocity might first increase, then decrease after reaching a maximum (possibly even up to$ 0.9c $ [27]), and finally approach the conformal limit from below. In fact, the sound velocity,$ v_s $ , exhibits an uncertain modification at high density, which is undoubtedly worthy of future study. -
We applied a self-consistent mean field approximation by introducing a novel free parameter,
$ \alpha $ , to the NJL model. We observed that parameter$ \alpha $ plays an important role in the study of both two and three flavor strong interaction phase transitions. Specifically, with the increase in$ \alpha $ , the chiral phase transition point increases, the chiral susceptibility exhibits a smooth peak at the chiral phase transition point, and the phase transition is a crossover. Further, increasing$ \alpha $ will decrease the number densities of the different quarks and increase the chemical potential at which the number density of the strange quark is non-zero. This study provides two important implications. 1. From our model, even if the original Lagrangian of the NJL model is not changed, a sufficiently difficult EOS can be obtained by introducing our new mean field approximation method. 2. By comparing the different normalization schemes (such as Pauli–Villars regularization in Ref. [28] and proper time regularization in Ref. [29]), a larger alpha leads to a more difficult EOS, which is independent of the normalization scheme.Finally, some prospects for further studies are as follows: First, we can extend the above approach from zero temperature to finite temperature, which will lead to more interesting results. Second, the regularization scheme we selected is the three-momentum cutoff scheme; therefore, we cannot discuss the case where the chemical potential of quark matter is too high. Hence, a better regularization scheme needs to be introduced. Third, we intend to study how parameter
$ \alpha $ affects the EOS of the quark matter. Ref. [18] concludes that the stiffness of the EOS for the two-flavor quark matter increases significantly to support a two-solar-mass pure quark star, if the critical chemical potential is enhanced when a larger$ \alpha $ is introduced. The three-flavor quark matter will arguably exhibit similar properties. As mentioned above, if a larger$ \alpha $ is introduced, the strange quark does not contribute to the quark matter in the case of an insufficiently large$ \mu $ , which may support the existence of two-flavor quark stars. This issue requires further study and discussion.
Self-consistent mean field approximation and application in three-flavor NJL model
- Received Date: 2019-09-29
- Accepted Date: 2020-01-01
- Available Online: 2020-07-01
Abstract: In this study, we apply a self-consistent mean field approximation of the three-flavor Nambu–Jona-Lasinio (NJL) model and compare it with the two-flavor NJL model. The self-consistent mean field approximation introduces a new parameter,





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF















 DownLoad:
DownLoad: