-
Perturbative Quantum Chromodynamics (pQCD) predicts that the gluon density inside a hadron grows rapidly with increasing energy (or decreasing Bjorken-x) and saturates eventually at sufficiently high energies, forming a new state of high density gluonic matter called Color Glass Condensate (CGC) [1]. The rapidity evolution of the CGC matter is known to be described by the Balitsky-JIMWLK① equation [2-5], whose mean field version is the Balitsky-Kovchegov (BK) equation [6, 7]. One of the hallmarks of the BK equation is the geometric scaling. The experimental data on the total cross-section of the electron-proton deep inelastic scattering (DIS) at HEAR in the small x (
$ x<0.01 $ ) region exhibits geometric scaling behavior [8], which provides strong evidence of the CGC theory. However, a study based on the DGLAP evolution also exhibits geometric scaling behavior [9]. It is difficult to distinguish which (CGC or DGLAP) is the dominant mechanism to dictate the evolution of the partonic system. To obtain more evidence to support the CGC mechanism, numerous studies were carried out during the past years. On the one hand, a series of improved QCD evolution equations were proposed, such as the running coupling BK (rcBK) equation [10, 11], and the full next-to-leading-order (NLO) BK equation [12]. On the other hand, the CGC theory has been used to describe experimental observables, like the proton structure function and the differential cross-section for vector meson production, both from inclusive processes [13-17] and exclusive processes [18-20], which may offer more evidence for the gluon saturation phenomenon.In the field of CGC studies, the investigation of exclusive photoproduction of the vector meson is particularly important, as it is highly sensitive to small x gluons, thus it can offer an unique approach to probe the gluon saturation [21, 22]. In particular, the quarkonia, such as
$ J/\psi $ and$ \phi $ , are of significant interest, because they can explore not only the perturbative but also non-perturbative regimes. In recent years, these mesons have been investigated both experimentally and theoretically. In the experiments, the exclusive$ J/\psi $ and$ \phi $ photoproductions have been measured by H1 and ZEUS collaborations at HERA [23-26]. For higher energies, the LHCb collaboration at LHC has output the exclusive$ J/\psi $ production data in proton-proton (pp) collisions at$ \sqrt{s} = 7 $ and$ \sqrt{s} = 13 $ TeV [27, 28], which enter an even smaller x region ($ x\sim 10^{-6} $ ) and provide high precision experimental data to test the gluon saturation physics.In the theory, the pioneer study of gluon saturation using diffractive DIS at HERA based on the Mueller's dipole model [29] can be traced back to two decades ago, when the Geolec-Biernat and Wusthoff (GBW) model was first proposed to search the saturation effect [30]. From then onwards, significant effort was devoted to investigate the phenomenon of gluon saturation via diffraction in DIS. A dipole saturation model, which is impact-parameter dependent, was developed to describe the differential diffractive
$ J/\psi $ production data at HERA [18, 31]. The t-distributions of differential cross-sections are sensitive to saturation phenomena. An investigation in Ref. [32] showed that a good description of the diffractive DIS data is obtained by combing the dipole model with the Good and Walker picture. The diffractive observables discriminate between the predictions of different models in the saturation region using an unique approach. Based on the framework of the BK equation at non-zero momentum transfer, the authors in Ref. [33] used the momentum transfer q instead of the impact parameter b in the saturation scale to devise an elegant formalism, which is particularly convenient for the comparison between theoretical calculations and experimental data, as the data are directly measured as a function of$ t = -{{q}}^2 $ . To investigate whether the diffractive photoproduction of the vector meson is a sensitive probe of gluon saturation, a systematic study of the vector meson production was performed with two impact parameter dependent models [34], the IP-Sat [31] and b-CGC [35]. The results further confirm that the t-distribution of differential cross-sections of vector meson productions provides an unique method to discriminate among saturation and non-saturation models owing to the appearance of a pronounced dip in the t-distribution [34]. The aforementioned formulism was extended to study the vector meson productions in proton-proton and nucleus-nucleus collisions at LHC energies [20], which demonstrated that gluon saturation models can provide a good qualitative description of the experimental data. However, all the above-mentioned saturation models for the vector meson production are based on the leading-order (LO) dipole amplitude, which is inspired by the non-linear BK evolution equation at leading logarithmic accuracy in pQCD, and these are insufficient for direct applications to phenomenology. The evolution speed of the dipole amplitude resulting from the LO BK equation was found to be too fast to yield a precise description of the HERA data, like proton structure functions [36, 37].Over the past decades, it has been shown that the higher order corrections have a significant contribution to the leading order BK equation. Furthermore, the LO evolution kernel is modified by the running coupling effect, which leads to the rcBK equation [10]. We note that although the kernel of the evolution equation is modified, the rcBK equation has the same structure as the LO BK equation. Our studies on the analytic solution to the rcBK equation have demonstrated that the quadratic rapidity dependence in the exponent of the S-matrix in the LO case is replaced by the linear rapidity dependence once the running coupling correction is included, which indicates that the evolution speed of the dipole scattering amplitude is significantly suppressed by the running coupling effects [38, 39]. The complete NLO corrections to the evolution equation, which include the quark loop (running coupling) and gluon loop contributions, were calculated by Balitsky and Chirilli in Ref. [12]. The authors found that the kernel and structure of the evolution equation are changed by the full NLO effects. The full NLO BK equation is unstable due to a large double transverse logarithm [40], it can be stabilized by the resummation of the double logarithms leading to a collinearly-improved (ci) BK equation [41]. To see the influence of the full NLO corrections on the dipole scattering amplitude, we analytically solved the full NLO BK equation in the saturation region [42]. Our result shows that the rapidity evolution of the dipole scattering amplitude is still suppressed by the full NLO effects; however, the evolution speed is rebound as compared to the running coupling case due to a compensation effect made by gluon loops. Furthermore, our recent studies regarding the dependence of the dipole scattering amplitude on the running coupling prescriptions have shown that the argument of the coupling has a significant impact on the dipole amplitude [43]. We find that the rapidity evolution speed of the dipole amplitude is significantly slowed down by the smallest dipole size running the coupling prescription.
Some of the above-mentioned NLO theories of the high-energy scattering have been directly applied to phenomenology in the inclusive process. The authors in Refs. [44, 45] used the dipole amplitude resulting from the rcBK equation to fit the inclusive small x HERA data. They obtained a rather good description of the data, because the running coupling effect significantly slows down the growth of the dipole amplitude with increasing energy. Soon after the collinearly-improved BK equation was established, several groups compared the resummed equation with recent HERA data [36, 46, 47], they found that the fit is rather successful and exhibits good stability up to virtualities as large as
$ Q^2 = 400 \;{\rm{GeV}}^2 $ for the exchanged photon. Although the NLO corrections have proved to be significant in the inclusive process, they are almost not applied to the vector meson production in the exclusive process in the literature. Based on the aforementioned applications of the NLO effects in the inclusive process, we argue that the higher order corrections are also important in the diffractive vector meson production process. In this work, we find that the$ \chi^2/d.o.f $ for the elastic cross-section (2.159) and differential cross-section (2.056) in the leading logarithmic approximation are significantly improved after including one of the NLO corrections, running coupling (1.097 for the elastic cross section and 1.449 for the differential cross-section). This outcome indicates that the higher order corrections play an important role in the quantitative description of the diffractive vector meson production data. To ensure that the outcome is confident, we study the diffractive vector meson production with the dipole amplitude resulting from the collinearly-improved NLO BK equation. The results show that our theoretical calculations are in good agreement with the experimental measurement with$ \chi^2/d.o.f $ 0.932 for the elastic cross-section and 1.357 for the differential cross-section.We extend our model, which includes higher order corrections, to study the diffractive vector meson productions at LHC energies. We find that the model can provide a rather good description of the
$ J/\psi $ data from 7 TeV and 13 TeV proton-proton peripheral collisions. The predictions of the diffractive$ \phi $ production are provided with our model for 7 TeV and 13 TeV proton-proton peripheral collisions at LHC, as listed in Table 5. One can find that the model with LO dipole amplitude provides a larger total cross-section, which would not be favored by the data, than the one obtained by NLO dipole amplitude. Again, we see that the high-order corrections suppress the evolution of the dipole amplitude. -
In this section, we provide a brief review of the formalism for exclusive vector meson photoproduction in the dipole model. We first introduce the dipole model for calculation of the vector meson productions at non-zero momentum transfer in the CGC framework. We then present the evolution equations of the dipole amplitude, which is a key ingredient in the dipole model. The vector meson wavefunctions, which are also a portion of the dipole model, are provided in the last part of this section.
-
In terms of the dipole model, the vector meson production in an exclusive diffractive
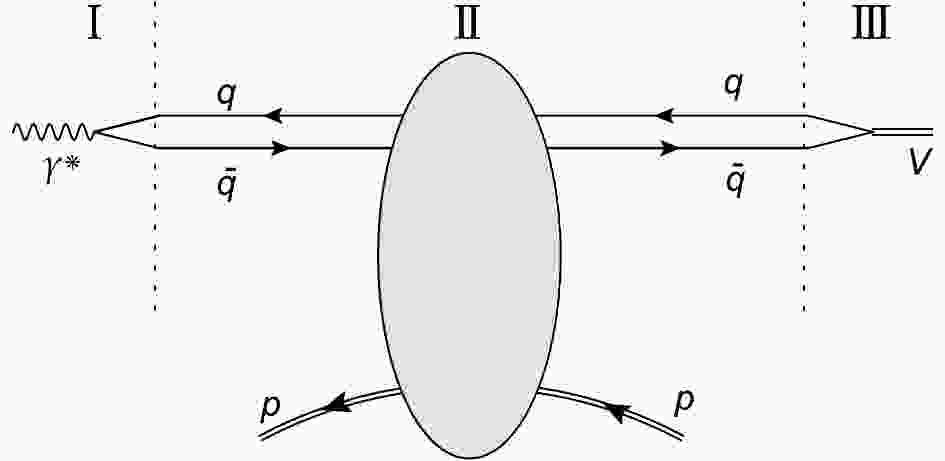
$ \gamma^* p\rightarrow Vp $ scattering can be viewed as three separated subprocesses [48], as shown in Fig. 1. The first subprocess is the formation of a dipole (a quark-antiquark pair) derived from a virtual photon fluctuation. The second subprocess is the interaction between the dipole and the proton via exchanging gluons. The last subprocess is the recombination of the outgoing quark-antiquark pair to generate a final vector meson. Therefore, the scattering amplitude of the diffractive process can be factorized into three ingredients: the photon wave function, the dipole-proton scattering amplitude, and the vector meson wave function. Placing all ingredients together, one can write the imaginary part of the scattering amplitude for a vector meson production as
Figure 1. Schematic diagram of a vector meson production in
$\gamma^* p\rightarrow Vp$ within the dipole model. Three separated subprocesses were denoted by I, II, and III, respectively.$\begin{split} {\cal{A}}^{\gamma^* p\rightarrow Vp}_{T,L}(x,Q^2,{{q}}) =& {\rm{i}}\int_0^1\frac{{\rm d}z}{4\pi}\int {\rm d}^{2}{{r}} \int {\rm d}^{2}{{b}}(\Psi_{V}^{*}\Psi)_{T,L} {\rm{e}}^{-{\rm{i}}{{b}}\cdot{{q}}}\\&\times 2[1-S(x,{{r}},{{b}})], \end{split} $

(1) where z is the longitudinal momentum fraction of the incoming photon carried by a quark, x is the Bjorken variable, and
$ Q^2 $ is the photon virtuality. The variable q denotes the momentum transfer, whose relationship with the squared momentum transfer is$ t = -{{q}}^2 $ . The remaining two dimensional vectors r and b are the transverse size of the quark-antiquark dipole and the impact parameter, respectively.$ \Psi $ is the wave function of the incoming photon, which can be accurately calculated by QED, and it is well known in the literature [49, 50].$ \Psi_{V}^{*} $ denotes the final vector meson wave function, unlike the photon wave function, it has various prescriptions as we shall discuss at the end of this section.$ (\Psi_{V}^{*}\Psi)_{T,L} $ represent the transverse and longitudinal overlap function between the photon and vector meson, respectively.We note that Eq. (1) is a scattering amplitude containing only the forward component. To obtain the nonforward scattering amplitude, one can multiply the forward wave functions by a phase factor
$ \exp[\pm{\rm{i}}(1-z){{r}}\cdot{{q}}/2] $ , as was done in Ref. [51]. Using this approach and assuming that the S-matrix is purely real (or the amplitude is purely imaginary), the scattering amplitude can be written as$\begin{split} {\cal{A}}^{\gamma^* p\rightarrow Vp}_{T,L}(x,Q^2,{{q}}) =& {\rm{i}}\int_0^1\frac{{\rm d}z}{4\pi}\int {\rm d}^{2}{{r}} \int {\rm d}^{2}{{b}}(\Psi_{V}^{*}\Psi)_{T,L}\\&\times {\rm{e}}^{-{\rm{i}}[{{b}}-(1-z){{r}}]\cdot{{q}}} T(x,{{r}},{{b}}), \end{split}$

(2) where
$ T(x,{{r}},{{b}}) = 1-S(x,{{r}},{{b}}) $ describes the scattering amplitude between the dipole and proton, which contains all basic information regarding the strong interactions between the dipole and proton. By taking into account the corrections from the real part of the scattering amplitude and the skewness effect, the differential cross-section of an exclusive vector meson photoproduction can be written as [18]:$ \frac{{\rm d}\sigma^{\gamma^* p\rightarrow Vp}_{T,L}}{{\rm d}t} = \frac{(1+\beta^{2})R_{g}^{2}}{16\pi}\mid{\cal{A}}^{\gamma^* p\rightarrow Vp}_{T,L}(x,Q^2,{{q}})\mid^{2}, $

(3) where
$ \beta $ is the ratio of the real to imaginary part of the scattering amplitude, and the factor$ (1+\beta^{2}) $ is to include the correction from the missing real part of the scattering amplitude due to the amplitude,$ {\cal{A}}^{\gamma^* p\rightarrow Vp}_{T,L} $ , in Eq. (2), only considering the contribution from the imaginary part. The skewness effect factor$ R_{g} $ is derived from the fact that the momentum fraction of the exchanging gluons between the proton and dipole legs can be different. The parameters associated with these two corrections can be expressed by the imaginary part as follows:$ \beta = \tan\left(\frac{\pi\delta}{2}\right),\; \;\;\; {}\; \; \;\; R_g = \frac{2^{2\delta+3}}{\sqrt{\pi}}\frac{\Gamma(\delta+5/2)}{\Gamma(\delta+4)}, $

(4) with
$ \delta \equiv \frac{\partial\ln({\cal{A}}_{T,L}^{\gamma^* p\rightarrow Vp})}{\partial\ln(1/x)}. $

(5) The dipole-proton scattering amplitude originates from the solution to the evolution equations, such as the IIM model [52] inspired by the LO BK equation. In most cases, the impact parameter dependence is disregarded in the BK equation, as the dipole amplitude develops a power-like b behaviour, called Coulomb tails, which yield unphysical results, i.e., the total cross-section violation of the Froissart unitarity bound. To avoid the above-mentioned difficulty, a general strategy is to build an impact parameter independent dipole amplitude inspired by the BK equation, then a model is employed to include the impact parameter dependence, such as two typical models IP-Sat [31] and b-CGC [35]. In this study, we use almost the same scheme as described, albeit with an impact-parameter-independent dipole amplitude resulting from a numerical solution to the LO, rc, ci BK evolution equations. We introduce the impact parameter via multiplying the numerical dipole amplitude with a Gaussian b dependence. In view of the advantage of the method②, which was proposed in Ref. [33] by Marquet, Peschanski, and Soyez (MPS), in study the t-distribution of differential cross sections of photoproduction of vector mesons, we shall follow the MPS strategy in this study. Following Ref. [33], the dipole-proton scattering amplitude can be rewritten in terms of the momentum transfer q instead of the impact parameter b by using the Fourier transform
$ \widetilde{T}(x,{{r}},{{q}}) = \int {\rm d}^{2}{{b}}{\rm{e}}^{-{\rm{i}}{{b}}\cdot{{q}}} T(x,{{r}},{{b}}). $

(6) Substituting Eq. (6) into Eq. (2), the scattering amplitude for
$ \gamma^* p\rightarrow Vp $ exclusive diffractive process becomes$ {\cal{A}}^{\gamma^* p\rightarrow Vp}_{T,L}(x,Q^2,{{q}}) = {\rm{i}}\int_0^1\frac{{\rm d}z}{4\pi}\int {\rm d}^{2}{{r}} (\Psi_{V}^{*}\Psi)_{T,L} {\rm{e}}^{{\rm{i}}z{{r}}\cdot{{q}}} \widetilde{T}(x,{{r}},{{q}}). $

(7) For the Fourier-transformed dipole-proton scattering amplitude
$ \widetilde{T}(x,{{r}},{{q}}) $ , we adopt a generalized formalism$ \widetilde{T}(x,{{r}},{{q}}) = 2\pi R^{2}{\rm{e}}^{-B{{q}}^{2}} {\cal{N}}(r,x), $

(8) where the factor
$ {\rm{e}}^{-B{{q}}^{2}} $ originates from the nonperturbative effects, R can be interpreted as the radius of proton and$ {\cal{N}}(r,x) $ is an impact parameter independent dipole amplitude. We would like to point out that B and R are free parameters in our fit, which shall be determined by fitting to HERA data. -
A key ingredient to calculate the differential cross-section is the dipole-proton scattering amplitude. It is known that almost all past studies on the differential cross-section of vector meson production in the framework of CGC were hovered on the LO level in the literature [53, 54]. Although the LO dipole amplitude can describe the diffractive vector meson production experimental data at HERA at certain uncertainties [33, 55], the precision of the model has to be improved to distinguish the dynamic mechanism of the CGC evolution from the DGLAP evolution, as the DGLAP formulism also provides a good description of the data [34]. Indeed numerous efforts have been made to improve the accuracy of the CGC theory by including other higher order corrections, such as quark loops [10, 11], gluon loops [12], and pomeron loops [56]. The running coupling effects dramatically slow down the evolution of the gluon system, which yield a good description of the latest data from HERA on reduced cross-sections [45]. Similarly, the direct numerical solution of the full NLO BK equation also shows that it slows down the evolution [40]. Based on the significance of the NLO corrections, we extend the LO vector meson production formalism to the NLO of this study. In the next section, we demonstrate that the descriptions of the experimental data are dramatically improved once the NLO corrections are included.
The LO BK equation describes the evolution of a quark-antiquark (with a quark at
$ x_{\bot} $ and an antiquark at$ y_{\bot} $ ) dipole with the rapidity Y by the emission of a soft gluon. In the large$ N_c $ limit, this can be written as$\begin{split} \frac{\partial N(r,Y)}{\partial Y} =& \int {\rm d}^2z_{\bot} K^{{\rm{LO}}} [ N(r_1,Y) + N(r_2,Y)\\& -N(r,Y)- N(r_1,Y)N(r_2,Y) ] , \end{split}$

(9) with the evolution kernel
$ K^{{\rm{LO}}} = \frac{\bar{\alpha}_s}{2 \pi} \frac{r^2}{r_1^2r_2^2}, $

(10) where
$ \bar{\alpha}_s = \alpha_sN_c/\pi $ . Here,$ z_{\bot} $ denotes the transverse coordinate of emitted gluon in the evolution. In Eq. (9), we used the notation$ {{r}} = x_{\bot}-y_{\bot} $ ,$ {{r}}_1 = x_{\bot}-z_{\bot} $ , and$ {{r}}_2 = z_{\bot}-y_{\bot} $ to denote the transverse size of the parent and new daughter dipoles, respectively. The BK equation is obtained at a leading logarithmic approximation, and it has been found that it is insufficient when compared with experimental data [44, 45, 57]. Therefore, significant efforts have been made to improve the understanding of the dipole's evolution at NLO accuracy.The first improvement to the LO BK equation was performed by including quark loops. After resumming
$ \alpha_s N_f $ to all orders, one can obtain an evolution equation with running coupling corrections [10, 11], which is called an rcBK equation. The rcBK equation is given by$\begin{split} \frac{\partial N(r,Y)}{\partial Y} =& \int {\rm d}^2z_{\bot}K^{{\rm{rc}}} [ N(r_1,Y) + N(r_2,Y)\\&-N(r,Y)- N(r_1,Y) N(r_2,Y) ] , \end{split}$

(11) with a modified evolution kernel
$ K^{{\rm{rc}}} = \frac{\bar{\alpha}_s}{2 \pi} \left[\frac{r^2}{r_1^2\,r_2^2}+ \frac{1}{r_1^2}\left(\frac{\alpha_s(r_1^2)}{\alpha_s(r_2^2)}-1\right)+ \frac{1}{r_2^2}\left(\frac{\alpha_s(r_2^2)}{\alpha_s(r_1^2)}-1\right) \right]. $

(12) The numerical solution of the rcBK equation was obtained by Albacete et al. [44, 45]. They found that the proton structure function can be efficiently described under this evolution equation. However, the quark loops corrections are not the only source of the higher order corrections, the complete NLO corrections should also include the contributions from gluon loops and the tree gluon diagrams with quadratic and cubic nonlinearities [12]. Considering all these contributions, we obtain the full NLO BK evolution equation
$ \begin{split} \frac{\partial N(r, Y)}{\partial Y} =& \frac{\bar{\alpha}_s}{2\pi}\int {\rm d}^2r_1K_1[ N(r_1,Y) + N(r_2,Y)-N(r,Y)\\&- N(r_1,Y)N(r_2,Y) ] + \frac{\bar{\alpha}_s^2}{8\pi^2}\int {\rm d}^2r_1{\rm d}^2r_2'K_2 \\ & \times [ N(r_3,Y) + N(r_2',Y) + N(r_1,Y) N(r_2,Y) \\&+ N(r_1,Y)N(r_3,Y)N(r_2',Y)-N(r_2,Y) \\&- N(r_1,Y)N(r_3,Y)- N(r_1,Y)N(r_2',Y)\\& - N(r_3,Y)N(r_2',Y)] + \frac{\bar{\alpha}_s^2N_f}{8\pi^2N_c}\int {\rm d}^2r_1{\rm d}^2r_2' K_3 \\ & \times [ N(r_1',Y) + N(r_1,Y)N(r_2,Y) \\&- N(r_1,Y) - N(r_1',Y)N(r_2,Y) ], \end{split} $

(13) where the kernels are
$\begin{split} K_1 = & \frac{r^2}{r_1^2r_2^2} + \frac{1}{r_1^2}\bigg(\frac{\alpha_s(r_1^2)}{\alpha_s(r_2^2)}-1\bigg)+\frac{1}{r_2^2}\bigg(\frac{\alpha_s(r_2^2)}{\alpha_s(r_1^2)}-1\bigg) \\&+\frac{\bar{\alpha}_s(r^2)r^2}{r_1^2r_2^2}\bigg(\frac{67}{36} - \frac{\pi^2}{12} - \frac{5N_f}{18N_c} - \frac{1}{2}\ln\frac{r_1^2}{r^2}\ln\frac{r_2^2}{r^2}\bigg), \end{split} $

(14) $\begin{split} K_2 =& -\frac{2}{r_3^4} + \bigg[\frac{r_1^2r_2'^2 + r_1'^2r_2^2 - 4r^2r_3^2}{r_3^4(r_1^2r_2'^2-r_1'^2r_2^2)} + \frac{r^4}{r_1^2r_2'^2(r_1^2r_2'^2 - r_1'^2r_2^2)}\\& + \frac{r^2}{r_1^2r_2'^2r_3^2}\bigg]\ln\frac{r_1^2r_2'^2}{r_1'^2r_2^2}, \end{split}$

(15) $ K_3 = \frac{2}{r_3^4} - \frac{r_1'^2r_2^2 + r_2'^2r_1^2 - r^2r_3^2}{r_3^4(r_1^2r_2'^2 - r_1'^2r_2^2)}\ln\frac{r_1^2r_2'^2}{r_1'^2r_2^2}. $

(16) In Eq. (13), we employed the notation
$ {{r}}_1' = x_{\bot}-z_{\bot}' $ ,$ {{r}}_2' = y_{\bot}-z_{\bot}' $ , and$ {{r}}_3 = z_{\bot}-z_{\bot}' $ to denote the transverse size of dipoles.From Eq. (14), we can see there is a double logarithmic term
$ \ln\dfrac{r_1^2}{r^2}\ln\dfrac{r_2^2}{r^2} $ in the evolution kernel, which renders the full NLO BK equation unstable [40]. The solution can turn to a negative value for some region due to the double logarithmic term. Thus, one needs to make a resummation of these double logarithms under the double logarithmic approximation (DLA), as it has done by Iancu et al. in Ref. [41]. When this resummation is applied to the full NLO BK equation, the double logarithmic term is removed from kernel$ K_1 $ , and the resummation will modify kernel$ K_1 $ by multiplying it with kernel$ K^{{\rm{DLA}}} = \frac{J_1\bigg(2\sqrt{ \bar{\alpha}_s \rho^2}\bigg)}{\sqrt{ \bar{\alpha}_s\rho^2}}\simeq 1 - \frac{ \bar{\alpha}_s\rho^2}{2} + {\cal{O}}( \bar{\alpha}_s^2), $

(17) with
$\rho = \sqrt{\ln\dfrac{r_1^2}{r^2}\ln\dfrac{r_2^2}{r^2}}$ .In addition to the double logarithmic term, the single transverse logarithms (STL) will also generate large logarithmic corrections to the evolution equation, as shown in Ref. [36]. The effect of the single transverse logarithm resummation will also modify kernel
$ K_1 $ by multiplying it with kernel$ K^{{\rm{STL}}} = \exp\bigg\{- \bar{\alpha}_s A_1\bigg|\ln\frac{r^2}{{\rm{min}}\{r_1^2, r_2^2\}}\bigg|\bigg\}. $

(18) with anomalous dimension
$ A_1 = \dfrac{11}{12} $ .By resumming the large single and double transverse logarithms as in Ref. [36], the collinearly-improved version of BK evolution equation reads
$ \begin{split} \frac{\partial N(r, Y)}{\partial Y} =& \frac{\bar{\alpha}_s}{2\pi}\int {\rm d}^2r_1K_1^{{\rm{CI}}}[ N(r_1,Y) + N(r_2,Y)-N(r,Y)\\&- N(r_1,Y)N(r_2,Y) ] + \frac{\bar{\alpha}_s^2}{8\pi^2}\int {\rm d}^2r_1{\rm d}^2r_2'K_2 \\ & \times [ N(r_3,Y) + N(r_2',Y) + N(r_1,Y) N(r_2,Y) \\&+ N(r_1,Y)N(r_3,Y)N(r_2',Y)-N(r_2,Y)\\ & - N(r_1,Y)N(r_3,Y)- N(r_1,Y)N(r_2',Y) \\&- N(r_3,Y)N(r_2',Y)] + \frac{\bar{\alpha}_s^2N_f}{8\pi^2N_c}\int {\rm d}^2r_1{\rm d}^2r_2' K_3 \\ & \times [ N(r_1',Y) + N(r_1,Y)N(r_2,Y) \\&- N(r_1,Y) - N(r_1',Y)N(r_2,Y) ], \end{split} $

(19) where the collinearly improved kernel in the first integration term becomes
$ \begin{split} K_1^{{\rm{CI}}} = & K^{{\rm{DLA}}}K^{{\rm{STL}}}\bigg[\frac{r^2}{r_1^2r_2^2} + \frac{1}{r_1^2}\bigg(\frac{\alpha_s(r_1^2)}{\alpha_s(r_2^2)}-1\bigg)+\frac{1}{r_2^2}\bigg(\frac{\alpha_s(r_2^2)}{\alpha_s(r_1^2)}-1\bigg)\bigg]\\ & - \frac{r^2}{r_1^2r_2^2}\bigg(- \bar{\alpha}_s A_1\bigg|\ln\frac{r^2}{{\rm{min}}\{r_1^2, r_2^2\}}\bigg|\bigg) \\&+\frac{ \bar{\alpha}_s(r^2)r^2}{r_1^2r_2^2}\bigg(\frac{67}{36} - \frac{\pi^2}{12} - \frac{5N_f}{18N_c}\bigg). \end{split} $

(20) Notably, Eqs. (9), (11), and (19) shall be numerically solved, and their solutions shall be used as dipole amplitudes to calculate the elastic and differential cross-sections in the following section.
-
Another ingredient to compute the differential cross-section for vector meson production is the overlap function
$ (\Psi_{V}^{*}\Psi)_{T,L} $ , which depends on the quark momentum fraction z, the dipole transverse size$ {{r}} $ , and the photon virtuality$ Q^{2} $ . The overlap function has various prescriptions, such as the boosted Gaussian, Gauss-LC, and DGKP [18]. Ref. [33] showed that for an identified meson, not all overlap functions provide an equally good description of the experimental data, and a meson has its own favorite wavefunction. We focus on studying the higher order effects for vector meson production in this study. Thus, we shall use an unified formalism of the wavefunction for different mesons to gain a better insight into the higher order effects. The overlap function between the photon and the vector meson has transverse and longitudinal components and can be written as [18]$ \begin{split} (\Psi_V^*\Psi)_{T} =& \hat{e}_f e \frac{N_c}{\pi z(1-z)}\Big\{m_f^2 K_0(\epsilon r)\phi_T(r,z)\\& - [z^2+(1-z)^2]\epsilon K_1(\epsilon r) \partial_r \phi_T(r,z)\Big\},\end{split} $

(21) $ \begin{split} (\Psi_V^*\Psi)_{L} =& \hat{e}_f e \frac{N_c}{\pi}2Qz(1-z)K_0(\epsilon r) \Big[M_V\phi_L(r,z)\\&+ \delta\frac{m_f^2 - \nabla_r^2}{M_Vz(1-z)} \phi_L(r,z)\Big].\end{split} $

(22) In Eqs. (21) and (22),
$ \phi(r,z) $ is the scalar function. In our study, the boosted Gaussian scalar functions are employed, since they works well for both light and heavy mesons [58]. In the boosted Gaussian formalism, the scalar functions are given by$ \phi_{T}(r,z) = {\cal{N}}_{T} z(1-z)\exp\Bigg(-\frac{m_f^2 {\cal{R}}_{T}^2}{8z(1-z)} - \frac{2z(1-z)r^2}{{\cal{R}}_{T}^2} + \frac{m_f^2{\cal{R}}_{T}^2}{2}\Bigg), $

(23) $ \phi_{L}(r,z) = {\cal{N}}_{L} z(1-z)\exp\Bigg(-\frac{m_f^2 {\cal{R}}_{L}^2}{8z(1-z)} - \frac{2z(1-z)r^2}{{\cal{R}}_{L}^2} + \frac{m_f^2{\cal{R}}_{L}^2}{2}\Bigg). $

(24) The variable
$ \epsilon $ in the Bessel functions in Eqs. (21) and (22) is$ \epsilon^{2} = z(1-z)Q^{2}+m_f^2 $ . The values of the parameters$ M_V $ ,$ m_f $ ,$ N_{T,L} $ , and$ R_{T,L} $ in the above equations are given in Table 1. It is worth noting that the longitudinal component is ignored in most studies due to its small contribution [54, 59], which is safe in a very small photon virtuality regime, like quasi-real photoproduction. However, the longitudinal component can provide a significant contribution in a large photon virtuality region, as we discussed in Ref. [60]. Thus, the longitudinal component is included in this study, as we compare with the data at various photon virtualities.meson $M_V/{\rm{GeV}}$ 

$m_f/{\rm{GeV}}$ 

$N_{T}$ 

$N_{L}$ 

$R_{T}/{\rm{GeV}}^{-2}$ 

$R_{L}/{\rm{GeV}}^{-2}$ 

$J/\psi$ 

3.097 1.4 0.578 0.575 2.3 2.3 $\phi$ 

1.019 0.14 0.919 0.825 11.2 11.2 Table 1. Parameters of boosted Gaussian formalism for
$J/\psi$ and$\phi$ [18]. -
In this section, we use the dipole amplitudes, which originate from the numerical solutions to the LO, rc, and ci BK evolution equations, to calculate the vector meson productions. First, we provide a brief description on the numerical method to solve differential equations and experimental data sets used in our fit. Then, we show our theoretical calculations of
$ J/\psi $ and$ \phi $ productions and compare them with the experimental data from HERA. Finally, we extend the formalism to LHC energies and make predictions for the rapidity distributions of$ J/\psi $ and$ \phi $ productions in pp collisions at 7 TeV and 13 TeV. -
The LO, rc and ci BK evolution equations are integral-differential equations. To obtain their numerical solutions, we can solve them on a lattice. In this study, we discretize the variable r into 256 points (
$ r_{\rm min} = 2.06 \times 10^{-9} $ and$ r_{\rm max} = 54.6 $ ). Throughout this numerical study, the unit of dipole size r is$ {\rm{GeV}}^{-1} $ . For the rapidity, the number of points are set to 100 with the step size$ \triangle Y = 0.2 $ . This setup can ensure that the grid is sufficiently small for this purpose. To perform the numerical simulations, we employ the GNU scientific library (GSL). The main GSL subroutines we have used are Runge-Kutta for solving ordinary differential equations, the adaptive integration for numerical integrals, and the cubic spline interpolation for interpolating data points.To solve these integro-differential equations, initial conditions are required. There are several kinds of initial conditions in the literature, such as GBW [30] and MV [61] models. Refs. [44] and [45] use both of these models as initial conditions for the rcBK equation in the fit of the reduced cross-sections, they showed that the MV initial condition is significantly more favorable by the experimental data than the GBW model. Thus, we adopt the MV model as initial condition in this study [61],
$ {N}(r,Y\! = \!0) = 1-\exp{\left[-\left(\frac{r^2Q_{s0}^{2}}{4}\right)^{\gamma} \log{\left(\frac{1}{r\,\Lambda_{\rm QCD}}+e\right)}\right]}, $

(25) with
$ \gamma = 1.13 $ ,$ Q^2_{s0} = 0.15\, {\rm{GeV^2}} $ , and$ \Lambda_{\rm QCD} = 0.241\, {\rm{GeV}} $ .In our analysis, we use Eq. (3) to fit the differential cross-section and the elastic cross-section for
$ J/\psi $ and$ \phi $ productions. The experimental data are taken from the ZEUS Collaboration ($ J/\psi $ [24],$ \phi $ [23]) and H1 Collaboration ($ J/\psi $ [26],$ \phi $ [25]). Notably, our studies are within the framework of the CGC, which is valid in the range$ x \leq x_{0} $ with$ x_0 = 10^{-2} $ . Therefore, the data points with x larger than$ x_{0} $ are automatically excluded in the data set. Further, we exclude the data with large error bars at large photon virtuality. After selection, the total number amounts to 177 data points, which are used for the fit. For the details, the elastic cross-section data of$ J/\psi $ and$ \phi $ productions are 58 and 61 points, and the differential cross-section data of$ J/\psi $ and$ \phi $ productions are 24 and 34 points, respectively. -
To demonstrate the significance of high order corrections in the description of the HERA data, one needs to compute the vector meson productions with the LO and NLO dipole amplitudes and compare these calculations. We concentrate on the study of the higher order effects for the vector meson production in this study. Therefore, there are only two free parameters B and R, as indicated by Eq. (8). The other parameters, such as
$ \gamma $ ,$ Q_{s0}^2 $ in the initial condition in Eq. (25), are directly taken from Ref. [44], since it has been shown in Ref. [57] that the initial condition effects are eventually washed-out as the evolution developing with rapidity, so the solutions of the LO and NLO BK equations are insensitive to the choice of the initial condition at high rapidities. Tables 2 and 3 show these two parameters, and$ \chi^{2}/d.o.f $ results from our fit. From the values of the$ \chi^{2}/d.o.f $ in the last columns of Tables 2 and 3, the NLO descriptions of the vector meson productions are better than the LO case, which indicate that the NLO corrections play an important role in the diffractive process. In particular, the$ \chi^{2}/d.o.f $ resulting from the fit to the elastic cross-section,$ \sigma $ , there is a large improvement as compared to the LO description once the NLO corrections are included. By global analysis, the values of$ \chi^{2}/d.o.f $ calculated from the rc and ci dipole amplitudes are closer to unity than those calculated from the LO amplitude.${\cal{N}}(r,x)$ 

$B/{\rm{GeV}}^{-2}$ 

$R/{\rm{GeV}}^{-1}$ 

$\chi^{2}/d.o.f$ 

LO 2.500 3.800 2.159 rc 1.954 3.791 1.097 ci 2.060 3.737 0.932 Table 2. Parameters and
$\chi^{2}/d.o.f$ results for elastic cross-section with different dipole amplitudes.${\cal{N}}(r,x)$ 

$B/{\rm{GeV}}^{-2}$ 

$R/{\rm{GeV}}^{-1}$ 

$\chi^{2}/d.o.f$ 

LO 2.253 3.223 2.056 rc 2.200 3.480 1.449 ci 2.175 3.349 1.357 Table 3. Parameters and
$\chi^{2}/d.o.f$ results for differential cross-section with different dipole amplitudes.Figure 2 shows the elastic cross-sections
$ \sigma $ for$ J/\psi $ and$ \phi $ productions as a function of the photon virtuality$ Q^{2} $ . The dotted blue, dashed red, and solid black lines represent the results calculatied using the LO, rc, and ci dipole amplitudes, respectively (similarly hereinafter). For each meson, we consider the experimental data both from H1 and ZEUS collaborations. For$ J/\psi $ , one can see that the higher order dipole amplitudes are in good agreement with the experimental measurement. For$ \phi $ production, it seems that all dipole amplitudes provide a similarly good description of the data in moderate$ Q^{2} $ , however only the rc and ci amplitudes can provide a precise description of the data in low$ Q^{2} $ . From Fig. 2, it is almost clear that the NLO amplitudes are more favored by the experimental data.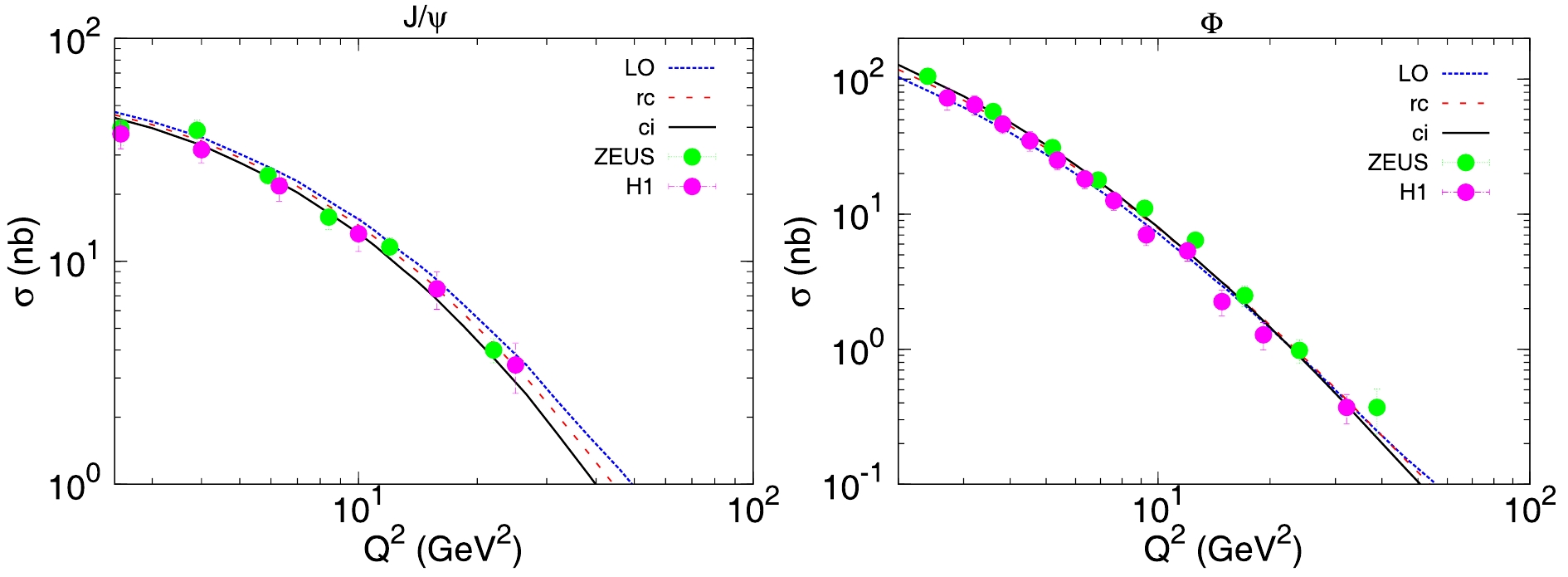
Figure 2. (color online) Elastic cross-section
$\sigma$ for$J/\psi$ and$\phi$ as a function of$Q^{2}$ .The elastic cross-section
$ \sigma $ for$ J/\psi $ and$ \phi $ productions as a function of photon-hadron center of mass energies$ W_{\gamma p} $ at different photon virtuality$ Q^{2} $ are shown in Fig. 3. The left panels of Fig. 3 show that the theoretical calculations from the NLO amplitudes are more consistent with the$ J/\psi $ data. From the right panels of Fig. 3, one can see that the LO calculations have a rather poor description of the experimental data, while the NLO computations provide a relatively good description of the data although the quality is not as good as the$ J/\psi $ case, since the experimental data for the$ \phi $ meson have large uncertainties. From Fig. 3 shows that the NLO calculations have a better agreement with experimental data than the LO BK equation for both$ J/\psi $ and$ \phi $ .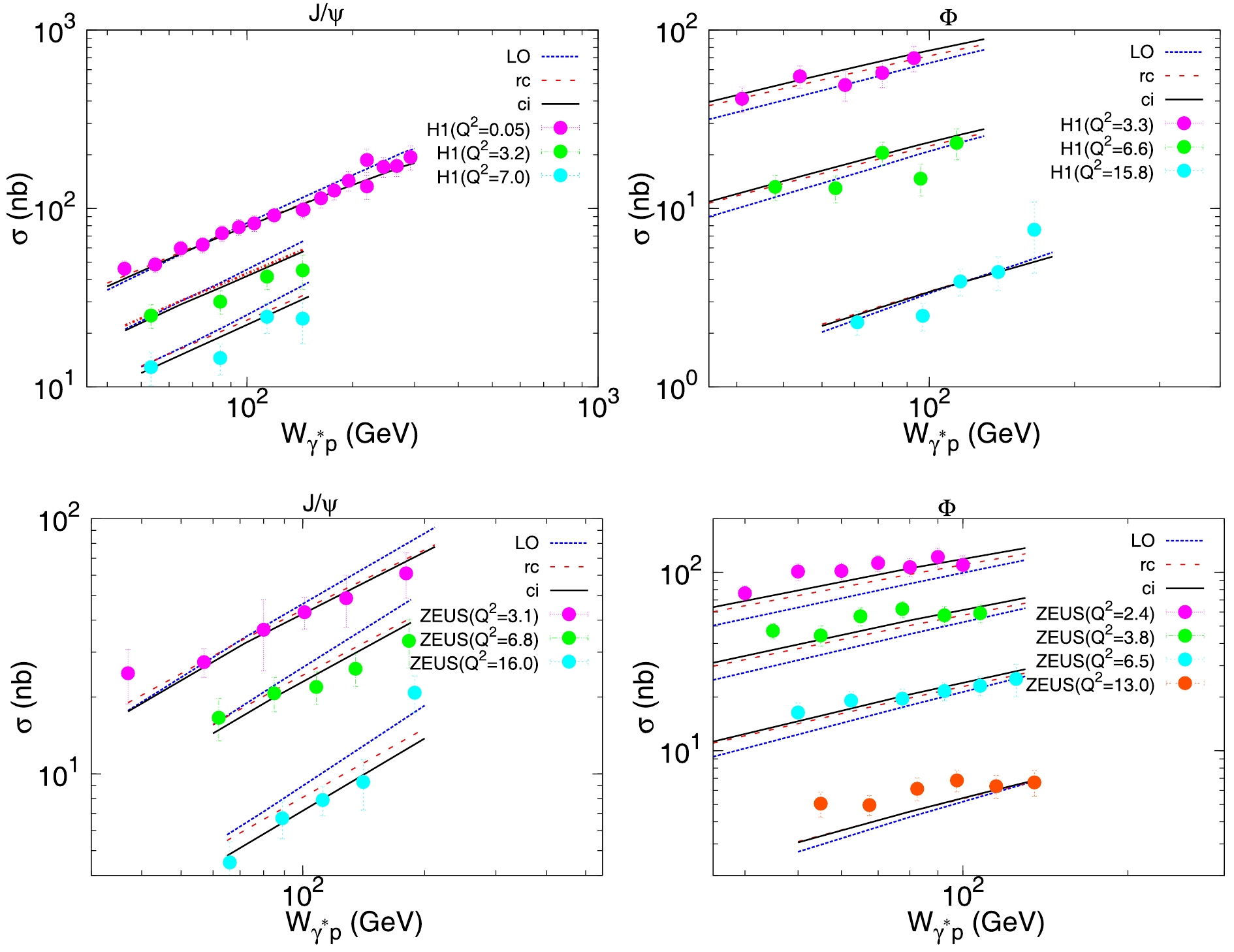
Figure 3. (color online) Elastic cross-section
$\sigma$ for$J/\psi$ and$\phi$ as a function of$W_\gamma p$ at different$Q^{2}$ .The differential cross-section
$ {\rm d}\sigma/{\rm d}t $ for$ J/\psi $ and$ \phi $ as a function of the squared momentum transfer t at different photon virtuality$ Q^{2} $ are shown in Fig. 4. From Fig. 4, it seems that the LO and NLO calculations provide a similar quality description of the experimental data. This is due to the small dataset with large error bars. However, one can clearly see from the last column in Table 3 that the$ \chi^{2}/d.o.f $ computed from the NLO dipole amplitudes are significantly smaller than the ones from LO cases, which indicate that the NLO corrections take an effective role in the diffractive vector meson productions.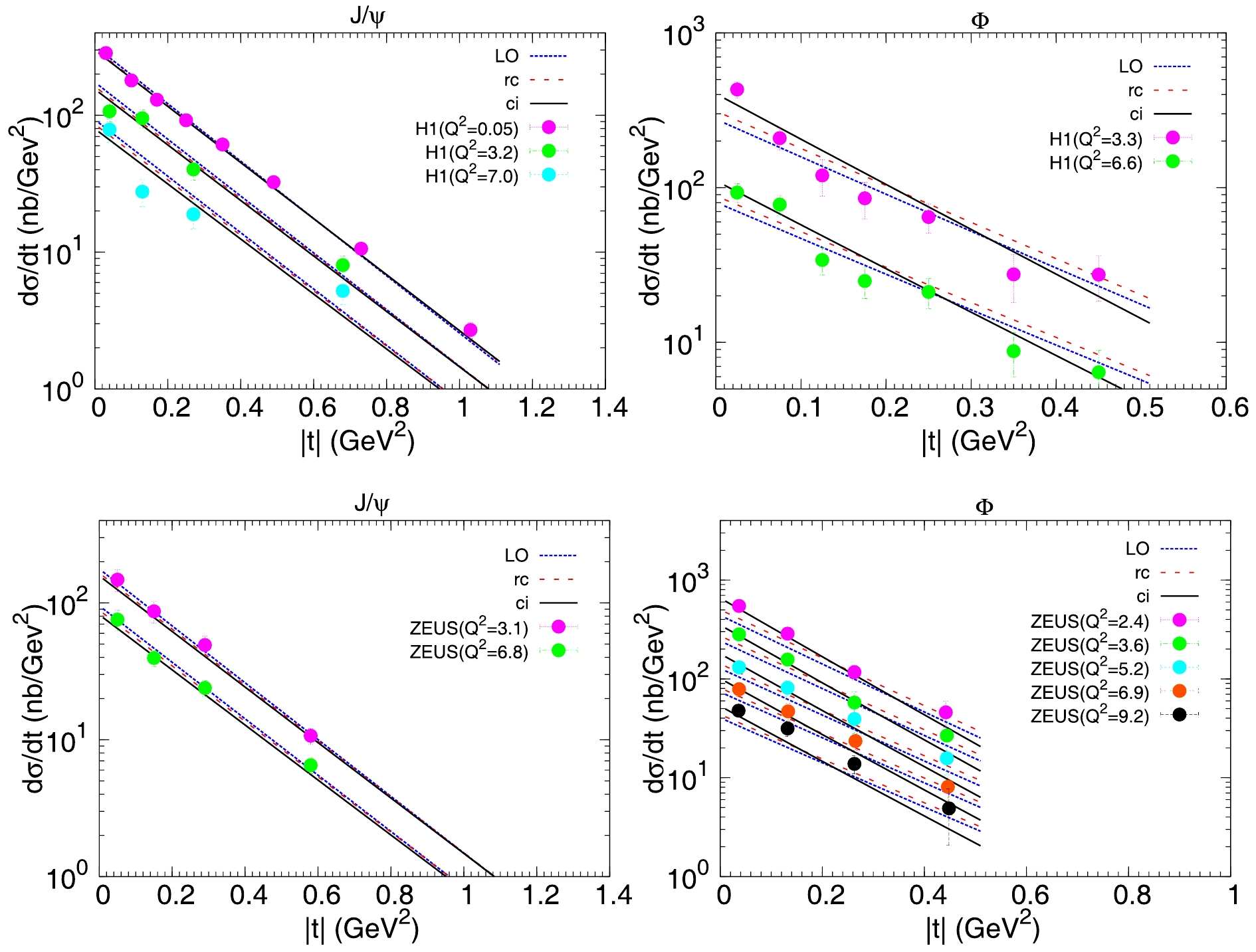
Figure 4. (color online) Differential cross-section
${\rm d}\sigma/{\rm d}t$ for$J/\psi$ and$\phi$ as a function of$t$ at different$Q^{2}$ .Furthermore, it should be noted that there is no significant difference between the description of the experimental data from the rcBK and ci BK calculations. To better interpret the underlying reasons, we have plotted the dipole amplitude,
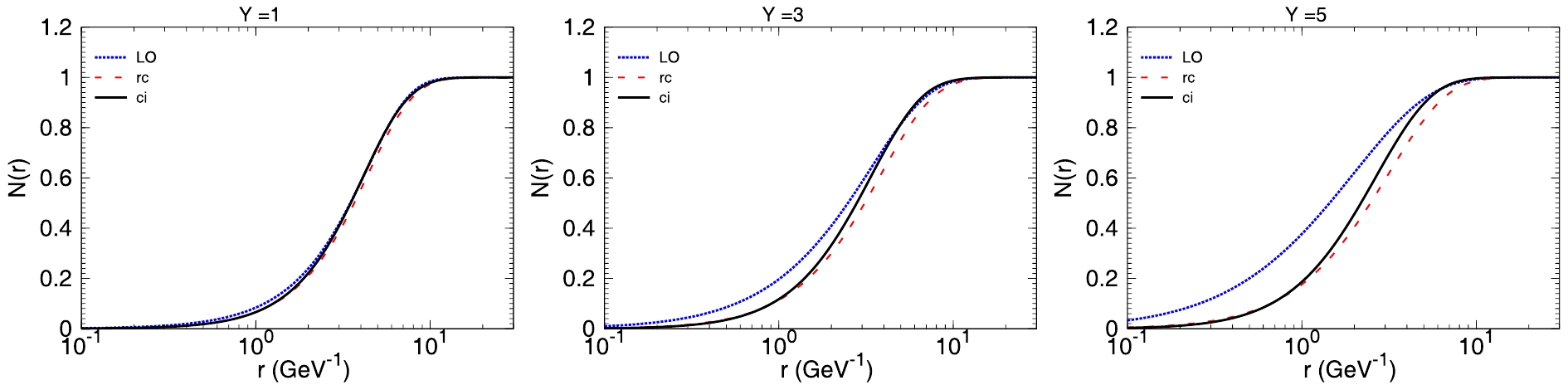
$ {\cal{N}}(r,x) $ , as a function of the dipole size, r, for three different rapidities in Fig. 5. From Fig. 5, we find that the difference between the LO and the NLO (rcBK and ci BK) dipole amplitudes is evident. However, the difference between the amplitudes from rcBK and ci BK equations is miniscule up to large rapidities, i.e.,$ Y = 5 $ . The largest available rapidity at HERA is approximately$ Y = 5 $ ; therefore, it is almost impossible to discriminate the NLO running coupling effect from collinear resummations with current HERA data. This is the reason why we cannot see a remarkable difference between$ \chi^{2}/d.o.f $ resulting from running coupling and resummation improved dipole amplitudes. -
The experimental data from LHC offer a peculiar way to test the hadronic structure, as the higher energy collision will touch even the small-x region. Fig. 5 shows the difference between the dipole amplitudes from rc and ci BK equations at larger rapidities,
$ Y>5 $ (smaller-x region). Thus, the predictions for the LHC energies are meaningful as higher precision and rapidity data will be released by the LHCb collaboration.In the high energy proton-proton collisions, there are events involving interactions at large impact parameters, where the electromagnetic interaction is dominant. In these photon-induced processes, the two protons are kept intact after the interaction. For the total cross-section, this can be written in terms of a convolution of the equivalent photon flux and the photon-proton production cross-section. Therefore, the rapidity distribution for the exclusive vector meson production is given by
$ \begin{split} \frac{{\rm d}\sigma[p_1 + p_2 \rightarrow p_1 \otimes V \otimes p_2]}{{\rm d}y} = \Big[\omega \frac{{\rm d}N_{\gamma/p_1}(\omega)}{{\rm d}\omega}\sigma_{\gamma p_2 \rightarrow V p_2}(\omega )\Big]_{\omega_{\rm L}} +\Big[\omega \frac{{\rm d}N_{\gamma/p_2}(\omega)}{{\rm d}\omega}\sigma_{\gamma p_1 \rightarrow V p_1}(\omega )\Big]_{\omega_{\rm R}}, \end{split}$

(26) where y is the rapidity of the produced vector meson,
$ \sigma_{\gamma p \rightarrow V p} $ is the total photon-proton cross section, and$ \omega $ is the photon energy ($ \omega_{\rm L} = \dfrac{M_{V}}{2} \exp(-y) $ and$ \omega_{\rm R} = \dfrac{M_{V}}{2} \exp(y) $ ). Note that there are two terms on the right hand side of the rapidity distribution equation. This is because the photon can be emitted either from the left or the right proton.In Eq. (26),
$ \displaystyle\frac{{\rm d}N}{{\rm d}\omega} $ is the equivalent photon spectrum of the relativistic proton. In the Weisz$ \ddot{a} $ cker-Williams approximation, this can be written as$ \frac{{\rm d}N}{{\rm d}\omega} = \frac{\alpha_{{\rm{em}}}}{2\pi\omega}\Big[1 + (1 -\frac{2\omega}{\sqrt{s}})^2\Big] \times\Big( \ln{\xi} - \frac{11}{6} + \frac{3}{\xi} - \frac{3}{2\xi^2} + \frac{1}{3 \xi^3}\Big), $

(27) where
$ \xi = 1 + [\,(0.71 \,{\rm{GeV}}^2)/Q_{{\rm{min}}}^2\,] $ with$ Q_{{\rm{min}}}^2 \approx (\omega/\gamma_L)^2 $ at the high energy limit,$ \sqrt{s} $ is the proton-proton center of mass energy, and$ \gamma_L $ is the Lorentz factor.Moreover, the total photon-proton cross-section
$ \sigma_{\gamma p \rightarrow V p} $ can be integrated from the differential cross-section in Eq. (3). The integral over t can be rewritten as follows$ \sigma_{\gamma p \rightarrow V p} = \int_{-\infty}^{0}\frac{{\rm d}\sigma^{\gamma p\rightarrow Vp}}{{\rm d}t}{\rm d}t. $

(28) Using the above formalism and the parameters obtained from fitting the HERA data, we can predict the rapidity distributions for diffractive
$ J/\psi $ and$ \phi $ productions in proton-proton collisions at LHC energies. Figures 6 and 7 show our predictions for the rapidity distributions of exclusive$ J/\psi $ and$ \phi $ in proton-proton collisions at 7 TeV and 13 TeV, respectively. For the LHC kinematics region, there are possible rapidities whose corresponding Bjorken-x can be larger than$ x_0 $ for one of the protons, but still smaller than$ x_0 $ for the other proton. To obtain a smooth curve, we make a linear extrapolation for the dipole amplitudes when$ x > 0.01 $ . We consider three kinds of dipole amplitudes (LO, rc, ci amplitudes) to calculate the rapidity distributions for exclusive vector meson productions and compare with the released data from LHCb [27, 28]. The numerical results in Figs. 6 and 7 show that the NLO dipole amplitudes provide better agrement with experimental data points, as expected. For completeness, we present our predictions of the total cross-section with different kinds of dipole amplitudes in Tables 4 and 5. From the tables, one can see that the production rates of the vector mesons ($ J/\psi $ and$ \phi $ ) are suppressed by the NLO effect, which satisfy theoretical expectations.LO/nb rc/nb ci/nb 7 TeV 37.181 23.204 24.229 13 TeV 61.217 31.016 37.608 Table 4. J/ψ total cross-section with different dipole evolution equations in pp collisions.
LO/nb rc/nb ci/nb 7 TeV 331.567 301.806 317.551 13 TeV 419.120 374.290 398.908 Table 5. ϕ total cross section with different dipole evolution equations in pp collisions.

Figure 6. (color online) Predictions for rapidity distributions of
$J/\psi$ and$\phi$ mesons in pp collisions at 7 TeV as a function of y.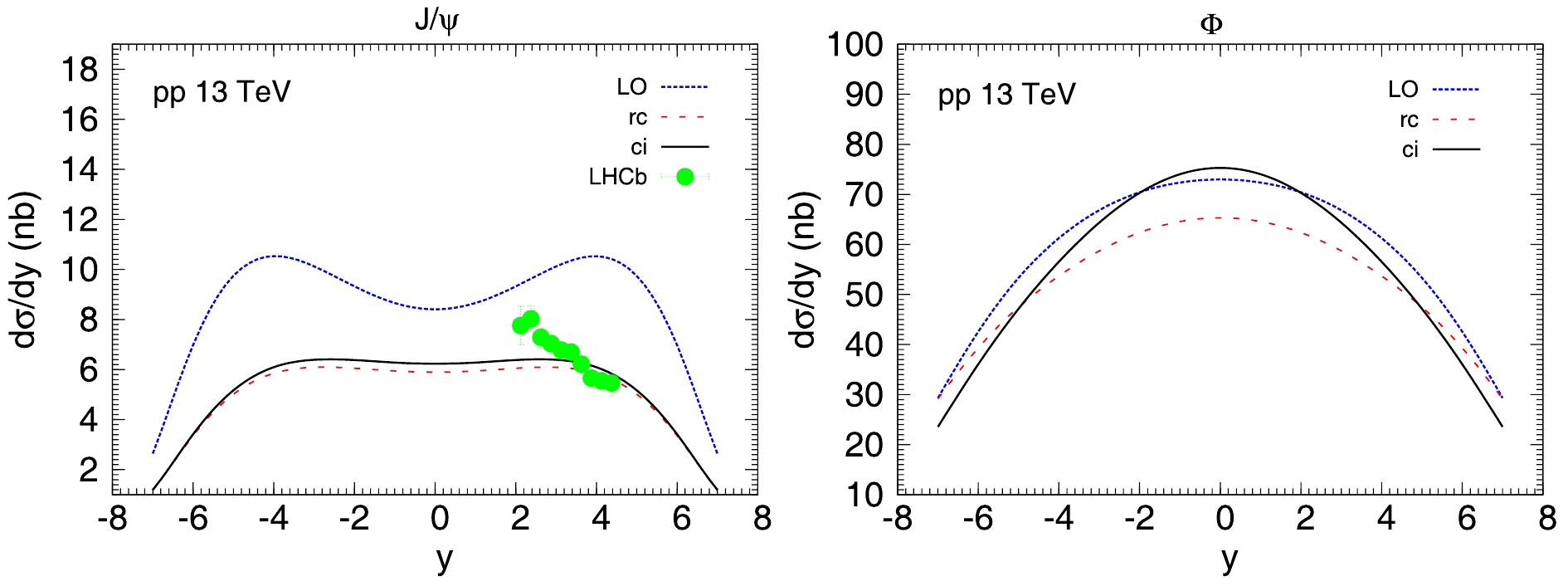
Figure 7. (color online) Predictions for rapidity distributions of
$J/\psi$ and$\phi$ mesons in pp collisions at 13 TeV as a function of y.In summary, we investigated the exclusive vector meson photoproduction for
$ J/\psi $ and$ \phi $ at HERA in the framework of color glass condensate. By comparing the results from the rcBK and ci BK equations with those from the LO BK equation, we find that the results from NLO equations are more consistent with experimental data than the LO BK equation. We also present our predictions for the rapidity distributions in pp collisions by using parameters obtained from fitting the HERA data. These results indicate that the NLO effects are significant in the calculation of the vector meson production at LHC energies. Furthermore, the higher order corrections considered in this work are part of the NLO corrections to the BK evolution equation. As we have studied in Ref. [42], the rare fluctuations also require large corrections to the evolution equation once the gluon loop contributions are included into the rcBK equation. Therefore, the exclusive vector meson production with a rare fluctuation corrections is worth exploring in a future study.
Exclusive photoproduction of vector meson at next-to-leading order from color glass condensate
- Received Date: 2020-03-03
- Available Online: 2020-07-01
Abstract: The exclusive photoproduction of vector mesons (






 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF



















 DownLoad:
DownLoad: