-
Quantum chromodynamics (QCD) at finite isospin chemical potential
$ \mu_I $ has attracted an increasing amount of attention in the study of chiral symmetry breaking ($ \chi $ SB), as well as the color confinement mechanism of strong interaction [1]. In the heavy-ion collision, it is still unclear how the medium evolves through the QCD phase transition with the finite baryon chemical potential$ \mu_B $ and isospin chemical potential$ \mu_I $ at finite temperature [2]. In astrophysics, the neutron star possesses large imbalance between the density of neutrons and protons at very low temperature, which also attracts the researchers' attention on QCD at finite$ \mu_I $ [3].Several theoretical methods are available to study QCD phase transitions at finite
$ \mu_I $ , including the chiral perturbation theory ($ \chi $ PT) [4-12], Nambu-Jona-Lasinio (NJL) models [13-21], quark-meson models [22-25], linear sigma models [26, 27], random matrix models [28, 29], and the perturbation QCD (pQCD) [30, 31]. These theoretical methods provide us with comparable results of the meson condensed phase with non-zero$ \mu_I $ . Lattice QCD (LQCD) is usually considered as one of the most powerful first-principle calculations to explore non-perturbative QCD at finite temperature. However, the notorious negative sign problem of fermion determinant makes it very difficult to study the system at finite baryon chemical potential$ \mu_B $ [32, 33]. Fortunately, there is no such sign problem at finite$ \mu_I $ [34], and the LQCD is extensively used in non-zero isospin systems [35-43]. These studies provide numerical evidence for the proposed meson condensation phase at finite$ \mu_I $ . The$ \mu_I $ axis can roughly be divided into two parts by the point$ 2 m_{0} $ , with$ m_0 $ the vacuum pion mass. In the region of$ 0<\mu_I<2 m_{0} $ , the lattice results are consistent with other theoretical analysis and model calculations. For example, it is shown that the location of zero temperature critical isospin chemical potential is$ \mu_I^c = m_0 $ , and it is a second order transition from the normal phase to pion condensation at low temperature. At the large$ \mu_I $ region, LQCD is difficult to control due to the lattice saturation effects [38]. However, we notice that both in the LQCD study [38] and NJL study [17], the large$ \mu_I $ transition line in$ T-\mu_I $ plane would bend towards the$ \mu_I $ axis, which is completely different from others that show tendencies to increase or saturate. For a review on meson condensation with finite$ \mu_I $ , please refer to Ref. [44].The experimental data and theoretical predictions suggest that the QGP is probably strong coupled [45-51]. To handle the tough strong coupling problems, the holography method [52-55] has been widely applied in many fields, such as nuclear physics [56-58] and condensed matter physics [59, 60]. To mimic QCD physics, in the bottom-up framework, the hard-wall AdS/QCD model Ref. [61] and soft-wall AdS/QCD model Ref. [62] have been constructed. In the hard-wall model, the chiral symmetry breaking can be well described. However, the linear Regge behavior of the hadron spectrum is not depicted in the model. The original soft-wall model can describe the correct Regge behavior of the meson spectrum by introducing an infrared (IR) suppressed dilaton term. Also, it is also quite natural to introduce chemical potential through the 5D gauge field, which is dual to the 4D conserved current. Thus, it provides a good starting point to study physics related to linear confinement and chiral symmetry breaking, both at finite temperature and at finite densities. We also note a series of studies [63-71], where holographic QCD was constructed with more stringy ingredients. The properties of QCD thermodynamics and chiral phase transition in the Veneziano limit have been investigated in detail.
In this study, we attempt to investigate the QCD phase diagram, more concretely, the properties of the pion condensation and chiral condensation, at finite
$ \mu_I $ and T in the framework of the soft wall model. The relevant issues have been studied in the well-known Sakai-Sugimoto model in the probe approximation with an external magnetic field [72, 73]. Actually, in the hard-wall AdS/QCD model, the pion condensation has been studied by introducing a baryonic charge in the IR boundary at zero temperature [74-76]. It has been shown that the phase transition, between the normal phase and pion condensation phase, is of second-order with mean-field critical exponents and occurs at$ \mu_I^c = m_0 $ . Efforts have also been made in the soft-wall framework at finite temperature [77]. This shows that the phase transition is of first-order with two both left and right critical$ \mu_I $ at a particular temperature, which are quite different from the hard wall results. This modified soft wall model is constrained from the chiral phase transition, and the meson spectrum of this model is still unclear. Therefore, it remains interesting to investigate the phase transition in a model describing the experimental meson spectrum. We note that an IR-improved soft-wall AdS/QCD model, proposed in Ref. [78], can generate both the chiral spontaneous breaking and the linear Regge behavior of the hadron spectrum. In particular, the vacuum pion mass$ m_0 = 139.6 $ MeV is well described. Thus, we adopt such an IR-improved soft-wall AdS/QCD model in this study, and we compare our results with the results of the LQCD and analytical theories or models.This paper is organized as follows. In Section 2, we review the IR-improved soft-wall model and introduce
$ \mu_I $ to this model, then derive the effective Lagrangian. In Section 3, we obtain the equations of motion of scalar, pseudo-scalar and axial-vector fields, then study the chiral transition and pion condensation at finite$ \mu_I $ and T. In Section 4, we provide a complete phase diagram of chiral condensation and pion condensation in the$ \mu_I-T $ plane. At last, we present a conclusion and discussion in Section 5. -
The IR-improved soft-wall AdS/QCD model [78] is constructed in the bottom up framework [61, 62] with a quartic term of bulk scalar and a modified 5D conformal mass of the bulk scalar field. The background spacetime of this soft-wall model is the following
$ \rm{AdS}_5 $ spacetime metric,$ {\rm d} s^2 = {\rm e}^{2 A(z)}(\eta_{\mu\nu} {\rm d} x^\mu {\rm d}x^\nu - {\rm d} z^2) , $

(1) where
$ \eta^{\mu\nu} = {\rm{diag}}\{+1,-1,-1,-1\} $ , z is the holographic radial coordinate and$ A(z) = -{\rm{ln}}(z/L) $ with L the AdS curvature radius, which will be set to unity for simplicity in the following calculation.On top of this background geometry, the soft-wall AdS/QCD model with
$ {\cal{N}}_f = 2 $ is constructed with$ SU(2)_L\times SU(2)_R $ gauge symmetry. The meson sector of the 5D action can be written as$ \begin{split} S_M =& \int {\rm d}^5 x \sqrt{g} {\rm e}^{-\Phi (z)} {\rm{Tr}} \{ |D X|^2-m_5^2(z)|X|^2-\lambda|X|^4\\ &-\frac{1}{4g_5^2}(F_L^2+F_R^2)\}, \end{split} $

(2) where g is the determinant of the metric
$ g_{MN} $ ,$ \Phi(z) = \mu_g^2 z^2 $ is the dilaton profile with$ \; \mu_g $ , a constant mass scale necessary for the Regge behavior of the meson spectrum [62].$ |X|^2\equiv X^\dagger X, |X|^4\equiv (X^\dagger X)^2 $ .$ g_5 $ is the gauge coupling that can be determined by comparing the large momentum expansion of correlator of vector current$ J_\mu^a = \bar{q}\gamma_\mu t^a q $ in both AdS/QCD and perturbative QCD [61], where$ t^a $ ($ a = 1,2,3 $ ) are the generators of${SU}(2)$ . In general, the field X, which is a complex$ 2\times 2 $ matrix valued bulk scalar field, can be decomposed into the pseudo-scalar meson field$ \pi(x,z) = \pi^a(x,z) t^a $ and the scalar meson field$ S(x,z) = S^a t^a $ in the form of$ X = (\chi t^0+S) {\rm e}^{2{\rm i}\pi+{\rm i}\eta}, $

(3) where
$t^0 = {I}_2/2$ and$ \chi(z) $ is related to the vacuum expectation value (VEV) of the bulk scalar field X by$\langle{X}\rangle = I_2\chi/2 $ with${I}_2$ the$ 2\times 2 $ identity matrix.To obtain a consistent description of both the meson spectrum and chiral symmetry spontaneously breaking, the 5D mass
$ m_5^2(z) $ , which relate to the quark mass anomalous dimension, can be modified by comparing the ultraviolet (UV) boundary and infrared (IR) boundary expression of the equation of motion (EOM) of the VEV of bulk scalar field [78], expressed as$ m_5^2(z) = -3-\mu_c z^2, $

(4) where
$ \mu_c $ is a free parameter fixed by fitting the meson spectra. The leading constant term$ -3 $ can be determined from the AdS/CFT dictionary$ m_5^2(z) = (\Delta-p)(\Delta+p-4) $ by taking$ p = 0 $ and$ \Delta = 3 $ , which is the dimension of the dual operator$ \bar{q}_R q_L $ [61].The covariant derivative
$ D^M $ and chiral gauge field strength$ F_{L/R}^{MN} $ are defined as$\tag{5a} D^M = \partial ^M X-{\rm i} A_L^M X+{\rm i} X A_R^M,\quad\quad\quad\quad $

$ \tag{5b} F_{L/R}^{MN}= \partial^MA_{L/R}^N-\partial^NA_{L/R}^M-{\rm i}[A_{L/R}^M,A_{L/R}^N], $

where
$ A_{L/R}^M = A_{L/R}^{a,M}t_{L/R}^a $ , and the chiral gauge fields$ A_{L/R}^M $ are dual to relevant QCD operators at the boundary by the AdS/QCD dictionary [61, 62].For convenience, one can redefine the chiral gauge fields into the vector gauge field and the axial-vector gauge field,
$ V^M = \frac{A_{L}^M+A_R^M}{2},\ \ \ A^M = \frac{A_{L}^M-A_R^M}{2}, $

(6) then one has the covariant derivative and transformed chiral gauge field strength as,
$\tag{7a} D_M X = \partial_M X-{\rm i}[V_M,X]-{\rm i}\{A_M,X\} , \quad\quad\quad\quad\quad $

$\tag{7b} \begin{split} F_A^{MN} =& \frac{1}{2}(F_L^{MN}-F_R^{MN})\\ =& \partial^MA^N-\partial^NA^M-{\rm i}[V^M,A^N]-{\rm i}[A^M,V^N], \end{split} $

$\tag{7c} \begin{split} F_V^{MN} =& \frac{1}{2}(F_L^{MN}+F_R^{MN})\\ =&\partial^MV^N-\partial^NV^M-{\rm i}[V^M,V^N]-{\rm i}[A^M,A^N]. \end{split} $

Taking the temperature and isospin chemical potential effects into account, instead of the pure
$ \rm AdS_5 $ space, the AdS/Reissner-Nordstrom (AdS/RN) black hole should be considered as the bulk background, such that the metric ansatz is$ {\rm d}s^2 = {\rm e}^{2A(z)}\bigg(f(z){\rm d}t^2-{\rm d}x_i {\rm d}x^i-\frac{{\rm d}z^2}{f(z)}\bigg). $

(8) For simplicity, we assume the following metric solution with finite
$ \mu_I $ ,$\tag{9a} A(z) = -{\rm{ln}} (z), \quad\quad\quad\quad\quad\quad\quad\;\;\; $

$\tag{9b} f(z) = 1-(1+\gamma \mu_I^2z_h^2)\frac{z^4}{z_h^4}+\gamma\mu_I^2\frac{z^6}{z_h^4}, $

$\tag{9c} v\equiv V_0^3(z) = \mu_I\bigg (1-\frac{z^2}{z_h^2}\bigg), \quad\quad $

where
$ \gamma $ is related to the coupling of$ V_0^3 $ with gravity, which can be taken as a free parameter, and we set$ \gamma = 1 $ . In contrast to Refs. [74, 75], we will take$ V_0^3 $ as a background field other than a dynamical field in the following discussion. The temperature can be introduced if there is a horizon$ z = z_h $ , where$ f(z) = 0 $ . The temperature is related to$ z_h $ by the formula$ T = \frac{1}{4\pi}\bigg|\frac{{\rm d}f(z)}{{\rm d}z}\bigg|_{z = z_h} = \frac{2-\gamma \mu_I^2 z_h^2}{2\pi z_h}, $

(10) where we employ the solution in Eq. (9). By all these definitions, it is demanded that the outer horizon
$ z_h< \sqrt{2/\gamma \mu_I^2} $ to ensure positive temperature and$ z_h = \sqrt{2/\gamma \mu_I^2} $ at$ T = 0 $ other than$ f\equiv 1 $ .In the case of finite
$ \mu_I $ and T, one can verify that$ S^a $ ,$ \pi^a $ , and$ \eta $ vanish if there are no surplus sources of the corresponding operators. The theory indicates the$ U_I(1) $ symmetry, which is a subgroup of the isospin$ SU_I(2) $ . As discussed in Ref. [74], using this$ U_I(1) $ symmetry,$ V_i = A_i = 0 $ by choosing the special angle with vanishing condensation of the$ \pi^2 $ field and maintaining only the$ \pi^1 $ condensation. Furthermore, the iso-triplet scalars do not condense,$ S^a = 0 $ . We let$ \Pi\equiv\pi^1 $ ,$ V_0^1 = V_0^2 = 0 $ ,$ A_0^3 = \pi^3 = 0 $ ,$ \eta = 0 $ , and$ A_0^0 = 0 $ . Under these assumptions, the effective Lagrangian in the 5D space becomes$ \begin{split} {\cal{L}}_{\rm eff} = & \frac{{\rm e}^{A-\Phi} \left({a_1}'^2+{a_2}'^2\right)}{2 {g_5}^2}-\frac{1}{2} f {\rm e}^{3 A-\Phi}\left(\chi^2 \Pi '^2+\chi '^2\right)\\ &-{\rm e}^{5 A-\Phi} \left(\frac{1}{2} m_5^2 \chi^2+\frac{1}{8} \lambda \chi^4\right)+\frac{\chi^2 {\rm e}^{3 A-\Phi}}{2 f} \bigg({a_1}^2\\&- {a_2} v \sin (2 \Pi) +{a_2}^2 \cos ^2(\Pi)+v^2 \sin ^2(\Pi)\bigg), \end{split} $

(11) where v,
$ a_1 $ , and$ a_2 $ instead of$ V_0^3 $ ,$ A_0^1 $ , and$ A_0^2 $ , respectively, and$ ' $ indicates the derivative with respect to z. -
In this section, we study the phase transitions among the pion condensation phase, normal chiral symmetry breaking phase (
$ \chi $ SB), and normal chiral symmetry restored phase ($ \chi $ SR). First, we derive the equations of motion (EOMs) of the scalar field, pseudo-scalar field, and axial-vector fields ($ \chi(z) $ ,$ \Pi(z) $ , and$ a_{1 (2)}(z) $ ). Second, we numerically solve the EOMs and extract the value of chiral condensate and pion condensate according to the holographic dictionary. Finally, we analyze the properties of phases and phase transitions in detail. -
In the equilibrium state, the system is homogeneous everywhere, therefore it is always sufficient to neglect the fluctuation in the coordinate space. By performing the functional derivative of the action in Eq. (11), the corresponding EOMs of
$ \chi(z) $ ,$ \Pi(z) $ , and$ a_{1 (2)}(z) $ are extracted as$ \tag{12a} \begin{split}& \frac{ \chi}{f^2}\left({a_2}^2 \cos ^2(\Pi)-{a_2}v \sin (2 \Pi)+v^2 \sin ^2(\Pi)-\Pi '^2 f^2\right)\\ &\;\;-\frac{{\rm e}^{2 A} \chi}{f}\left(m_5^2+\frac{\lambda}{2} \chi^2\right)+\chi ' \left(3 A'-\Phi '+\frac{f'}{f} \chi '\right)+\chi '' = 0, \end{split}$

$\tag{12b} \begin{split} &\frac{v^2-{a_2}^2}{2 f^2} \sin (2\Pi )-\frac{{a_2} v \cos (2 \Pi )}{f^2}+\Pi ' \bigg(3 A'-\Phi '+\frac{f'}{f} \\ &\;\;+\frac{2 \chi '}{\chi }\bigg)+\Pi'' = 0, \end{split} $

$\tag{12c} -\frac{{\rm e}^{2 A} {g_5}^2 \chi ^2{a_1}}{f}+{a_1}' \left(A'-\Phi '\right)+{a_1}'' = 0, $

$\tag{12d} \begin{array}{l} \dfrac{\chi ^2 {\rm e}^{2 A} {g_5}^2\left( v \sin (2 \Pi )-2{a_2} \cos ^2(\Pi )\right)}{2f}+{a_2}' \left(A'-\Phi '\right)+ {a_2}'' = 0. \end{array} $

No explicit source exsits for the axial vector current, and
$ a_1(z) $ does not appear in other equations, such that we can simply set$ a_1(z) = 0 $ [77].Equations (12a), (12b), and (12d) are coupled nonlinear second order differential equations with multi-singular points, and they do not have exactly analytical solutions. However, we can numerically solve them. Because z and
$ f(z) $ appear in the denominators in Eqs. (12), there are solutions, diverging at UV or IR. However, a physical solution should be finite. Therefore, we will impose the regularity condition of the fields at both UV and IR. Around the UV boundary ($ z = 0 $ ), we obtain the expansion solutions of$ \chi(z) $ ,$ \Pi(z) $ , and$ a_2(z) $ as$\tag{13a} \begin{split} \chi(z) =& m_q \zeta z+\frac{\sigma z^3}{\zeta }+\frac{1}{2} m_q\zeta \left(-{\mu_c}^2+2 {\mu_g}^2+\frac{\lambda}{2} m_q^2\zeta ^2 \right) \\ &\times z^3 \ln (z)+\frac{1}{16} m_q \zeta \left(\mu_c^2-2 \mu_g^2- \frac{\lambda}{2} m_q^2 \zeta ^2 \right) \\ &\times\left(\mu_c^2-6 \mu_g^2- \frac{3\lambda}{2} m_q^2\zeta ^2\right)z^5 \ln (z)+{\cal{O}}(z^5), \end{split}$

(13a) $\tag{13b} \begin{split} \Pi(z) =& \pi _1 z^2+\frac{1}{2} \pi _1 \left(\mu_c^2-2 \mu_g^2- \frac{\lambda}{2} m_q^2\zeta ^2\right)z^4 \ln (z) \\ &+\frac{1}{8} \bigg [a_{2c} \mu_I+\pi _1 \bigg(-\mu_c^2+6 \mu_g^2-\mu_I^2+\frac{\lambda}{2} m_q^2 \zeta ^2 \\ &-\frac{8 \sigma }{ m_q\zeta ^2}\bigg)\bigg ]z^4+{\cal{O}}(z^5), \end{split} $

(13b) $\tag{13c} \begin{split} a_2(z) =& a_{2c} z^2+\frac{1}{8} \left(a_{2c} g_5^2 m_q^2 \zeta ^2 +4 a_{2c} \mu_g^2- \pi_1 g_5^2 \mu_I m_q^2\zeta ^2 \right)z^4\\ & +{\cal{O}}(z^5), \end{split} $

(13c) where
$ m_q \zeta $ ,$ \sigma/ \zeta $ ,$ \pi_1 $ , and$ a_{2c} $ are integral constants. According to the holographic dictionary, we identify the coefficients$ m_q $ ,$ \sigma $ , and$ \pi_1 $ as the quark mass, chiral condensate, and pion condensate, respectively. The normalization constant$ \zeta = \sqrt{N_c}/2\pi $ is introduced to match the two point function$ \langle \bar{q} q(p), \bar{q} q(0)\rangle $ from holographic calculation and 4D calculation [79]. Notice that the external source is not considered in this work, such that the constant terms of$ \Pi(z) $ and$ a_2(z) $ are equal to zero. On the IR boundary (horizon with$ z = z_h $ ), we obtain expansions solutions as$\tag{14a} \begin{split} \chi(z) =& \chi_0+\frac{\chi_0 \left(\lambda \chi_0^2-2\mu_c^2 z_h^2-6\right)(z-z_h) }{4 z_h \left(\mu_I^2 z_h^2-2\right)} \\ &-\frac{\chi_0(z-z_h)^2 }{16 z_h^2 \left(\mu_I^2 z_h^2-2\right)^2}\bigg\{z_h^2 \big [a_{2d} z_h \cos (\Pi_0) \\ &+2 \mu_I \sin(\Pi_0)\big]^2-\frac{3}{4} \chi_0^4 \lambda ^2+2 \chi_0^2 \lambda \big\{z_h^2 \big[\mu_c^2+4\mu_I^2 \\ &+\mu_g^2 \big(2-\mu_I^2 z_h^2\big)\big ]+1\big\}+4 \mu_c^2 \mu_g^2 \mu_I^2 z_h^6 \\ &-z_h^4 \big[\mu_c^4+8 \mu_c^2 \mu_g^2+12 \mu_I^2 (\mu_c^2-\mu_g^2) \big ] \\ &-6z_h^2\left(\mu_c^2+4 \mu_g^2+8\mu_I^2\right)+15\bigg\}+{\cal{O}}[(z-z_h)^3], \end{split} $

(14a) $\tag{14b}\begin{split} \Pi(z) =& \Pi_0+\frac{ (z-z_h)^2}{32\left(\mu_I^2 z_h^2-2\right)^2 }\bigg\{ \big [a_{2d}^2 z_h^2 -4\mu_I^2 \big] \sin (2 \Pi_0) \\ &-4 a_{2d} \mu_I z_h \cos (2 \Pi_0)\bigg \}+{\cal{O}}[(z-z_h)^3], \end{split} $

(14b) $\tag{14c} \begin{split} a_2(z) =& a_{2d} (z-z_h)+\frac{(z-z_h)^2 }{4 z_h^2 \left(\mu_I^2 z_h^2-2\right)}\bigg \{a_{2d}\big [ g_5^2 \chi_0^2z_h \cos ^2 \\ &\times(\Pi_0)+4 \mu_g^2 \mu_I^2 z_h^5-8 \mu_g^2 z_h^3+2 \mu_I^2 z_h^3-4 z_h\big ] \\ &+g_5^2 \mu_I \chi_0^2 \sin (2 \Pi_0)\bigg \}+{\cal{O}}[(z-z_h)^3], \end{split} $

(14c) where
$ \chi_0 $ ,$ \Pi_0 $ , and$ a_{2d} $ are integral constants. In IR boundary expansions, the factor$ 1/(\mu_I^2z_h^2-2) $ exists in all the terms except for the leading one, which is related to the expression of temperature in Eq. (10). When the temperature approaches zero, it will lead to the divergence of coefficients in IR boundary expansions. Therefore, to obtain reliable results at low temperature, more higher-order terms must be considered, and the numerical steps must be properly chosen.By using the UV and IR boundary expansion solutions, we can numerically solve the EOMs from both sides with the "shooting method". From the numerical solutions, we extract all integral constants
$ \sigma $ ,$ \pi_1 $ ,$ a_{2c} $ ,$ \chi_0 $ ,$ \Pi_0 $ , and$ a_{2d} $ from the solutions according to the holographic dictionary. Through preliminary analysis, we find that the EOMs contain two independent solutions, corresponding to zero pion condensation$ \pi_1 = 0 $ ($ \Pi(z) = 0 $ ) and finite pion condensation$ \pi_1\neq 0 $ ($ \Pi(z)\neq 0 $ ), respectively. Other than that, there is a intermediate temperature region, where it is relatively too high to form pion condensation, but chiral condensation can arise. Hence, it is necessary to separately discuss these two different solutions in the following contents. -
When the pion condensation channel is turned off, in other words
$ \Pi(z) = 0 $ , combining EOMs in Eqs. (12b) and (12d), one has that$ a_2(z) $ must be zero, too. The EOMs will degenerate to a simple EOM of$ \chi(z) $ as$ \chi ''+\left(3 A' -\Phi '-\frac{f'}{f}\right)\chi '-\frac{{\rm e}^{2 A}}{f}\left(-3 \chi-\mu_c^2 z^2 \chi+\frac{\lambda}{2}\chi^3\right) = 0.\\ $

(15) The UV and IR asymptotic forms of the VEV
$ \chi(z) $ near$ z = 0 $ and$ z = z_h $ can be derived as$\tag{16a} \begin{split} \chi(z) =& m_q\zeta z+\frac{\sigma z^3}{\zeta }+\frac{1}{2} m_q \zeta z^3 \ln (z)\bigg(-\mu_c^2+2\mu_g^2 \\ &+\frac{\lambda}{2} m_q^2 \zeta ^2\bigg)+{\cal{O}} (z^4), \end{split}$

$\tag{16b} \chi(z) = \chi_0+\frac{\chi_0 (z-z_h) \left(\chi_0^2 \lambda -2\mu_c^2 z_h^2-6\right)}{4 z_h \left(\mu_I^2 z_h^2-2\right)}+{\cal{O}}[(z-z_h)^3]. $

By using the "shooting method", we can numerically solve Eq. (15) with the boundary conditions given in Eqs. (16a) and (16b) to study the crossover from the
$ \chi $ SB phase to$ \chi $ SR phase in terms of T at fixed$ \mu_{I, f} $ . Then, one can obtain the profiles of scalar VEV$ \chi(z) $ from the numerical solutions.For the IR-improved soft-wall AdS/QCD model proposed in Ref. [78], there are two different sets of parameters, including
$ m_q $ ,$ \mu_g $ ,$ \mu_c $ ,$ \lambda $ , and$ g_5 $ , Case I and Case II, as shown in Table 1. Using the parameters of Case I, the meson spectrum is well reproduced. With regard to Case II, the meson spectrum except for the scalar meson spectrum is well matched, other than that the$ \pi-\rho $ coupling constant and the decay constants of$ \pi $ ,$ \rho $ , and$ a_1 $ are more consistent with experimental data.Parameter $m_q$ /MeV

$\mu_g$ /MeV

$\mu_c$ /MeV

$\lambda$ 

$g_5$ 

Case I 3.366 440 1180 33.6 $2\pi$ 

Case II 3.22 440 1450 80 $2\pi$ 

Table 1. Parameters insure the self consistence of the meson spectra and the relevant decay constants in the IR-improved soft-wall AdS/QCD model. Case I accompanies a strange rising-up in the chiral condensate behavior. Case II is derived without considering the scalar meson spectrum. Parameters are provided by Ref. [78].
For these two cases, we separately study the behaviors of chiral condensation
$ \sigma(\mu_{I,f},T) $ , as shown in Figs. 1(a) and (b). In Fig. 1(a), the curves of$ \sigma(\mu_{I, f},T) $ almost maintain a saturated value in the low temperature region along with small unphysical bumps, and then smoothly decrease while T increases. Notice that the small unphysical bump behaviors also can be found in other holographic models [80]. Because the small bump also exists in the small$ \mu_I $ region, the curves of$ \sigma(\mu_{I, f},T) $ , with a set of different$ \mu_{I,f} $ , cross each other in the low temperature region. The pseudo critical temperature of the chiral crossover transition is identified by the position of the peak of the susceptibility,${\rm d}^2\sigma/{{\rm d} T}^2 = 0$ . The measurement results are$ T_c = 0.079 $ ,$ 0.100 $ , and$ 0.117 $ GeV for$ \mu_{I,f} = 0.400 $ ,$ 0.250 $ , and$ 0.050 $ GeV, respectively. There is a tendency that the higher the pseudo critical temperature, the smaller$ \mu_{I,f} $ , which obeys the mechanism that$ \mu_I $ and T are both in favor of restoring the chiral symmetry.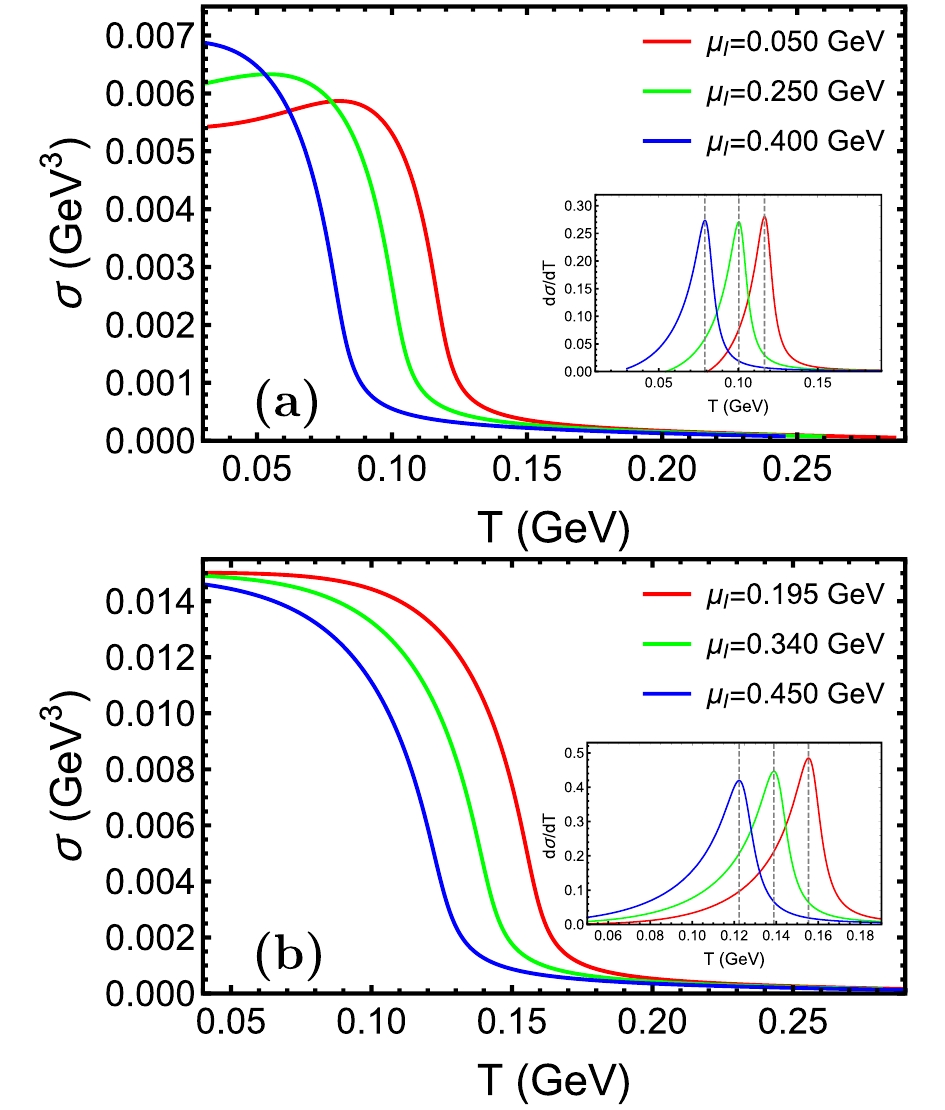
Figure 1. (color online) (a) and (b) dependence of chiral condensation
$\sigma(\mu_{I,f}, T)$ and susceptibility${\rm d}\sigma/{\rm d}T$ (the inside figure) on temperature with the parameters in Case I and Case II, with three different fixed isospin chemical potential$\mu_{I,f}$ , respectively. The pseudo-critical point is determined by the position of the peak of susceptibility,${{\rm d}^2 }\sigma /{{\rm d} T}^2 = 0 $ In Fig. 1(b), the behavior of
$ \sigma({\mu_{I, f}, T}) $ is generally consistent with with Case I, except for the strange rising-up behavior in the low temperature region. The pseudo-critical temperatures are$ T_c = 0.122 $ ,$ 0.139 $ , and$ 0.155 $ GeV for$ \mu_{I, f} = $ 0.195, 0.340, and 0.450 GeV, respectively. However, when$ \mu_{I, f} $ is lower, the peak susceptibility is larger; however, there is no such significant difference in Case I. In addition, when$ \mu_B $ and$ \mu_I $ are both zero, the pseudo critical temperatures are$ T_{c,1} = 0.117 $ GeV in Case I and$ T_{c,2} = 0.164 $ GeV in Case II, where the latter is consistent with results from LQCD simulations [81, 82]. All these behaviors indicate the parameters of Case II more self-consistently. Therefore, we choose parameters in Case II for our following studies presented in this paper. -
When
$ \mu_I $ is large enough, the$ U_I(1) $ symmetry is spontaneously breaking with a massless Goldstone boson [17]. Although symmetry analysis yields a profile of the phase transition, the detailed properties with finite$ \mu_I $ and T are still ambiguous. In this subsection, we study pion condensation and chiral condensation, as well as their interdependent behaviors.In Fig. 2, we numerically solve the complete EOMs of Eqs. (12a), (12b), and (12d) to study the properties of the pion condensation
$ \pi_1(\mu_{I, f}, T) $ and chiral condensation$ \sigma(\mu_{I, f}, T) $ in terms of T with fixed$ \mu_{I,f} $ . The behaviors of$ \pi_1(\mu_{I, f}, T) $ are shown in Fig. 2(b), and along with the increase of T,$ \pi_1(\mu_{I, f}, T) $ continuously decreases all the way down to zero at critical points$ T_{c, \pi_1} $ , where$ T_{c,\pi_1} = 0.096 $ and$ 0.121 $ GeV correspond to$ \mu_{I,f} = 0.202 $ and$ 0.450 $ GeV, respectively. This seems to be a second order phase transition; to verify the universality classes of the pion condensation, we numerically fit out the critical exponent, and the results are$ \beta = 0.499 $ and$ 0.487 $ , corresponding to$ \mu_{I,f} = 0.202 $ and$ 0.450 $ , respectively, as shown in Fig. 2(c). These results are very close to$ 1/2 $ , which indicates that pion condensation in this model belongs to the class of 4D mean field. There are two probable reasons for this. On the one hand, the exact holographic duality is based on the assumption of the large$ N_c $ limit, however$ N_c = 3 $ is just a rough approximation; on the other hand, the back reaction of condensations to the background is also ignored in this AdS/QCD model, and treat the solution of AdS/RN black hole as the bulk background. The curves of$ \sigma(\mu_{I,f}, T) $ are shown in Fig. 2(a), where solid lines and dashed lines represent for the solutions with or without pion condensation, respectively. Compared to$ \pi_1(\mu_{I,f},T) $ in Fig. 2(b), we can divide the T-axis into two regions by$ T_{c,\pi_1} $ . When$ T\geqslant T_{c,\pi_1} $ , these two solutions collapse into one; when$ 0<T<T_{c,\pi_1} $ , these two solutions rise up and drop down, respectively, with the pion condensation channel turned on or off, which means that the chiral condensation is depressed by the pion condensation. Actually, if more of the quarks and anti-quarks form the pion condensation, the numbers of them to form chiral condensation would be lower. This might be the physical explanation of this effect.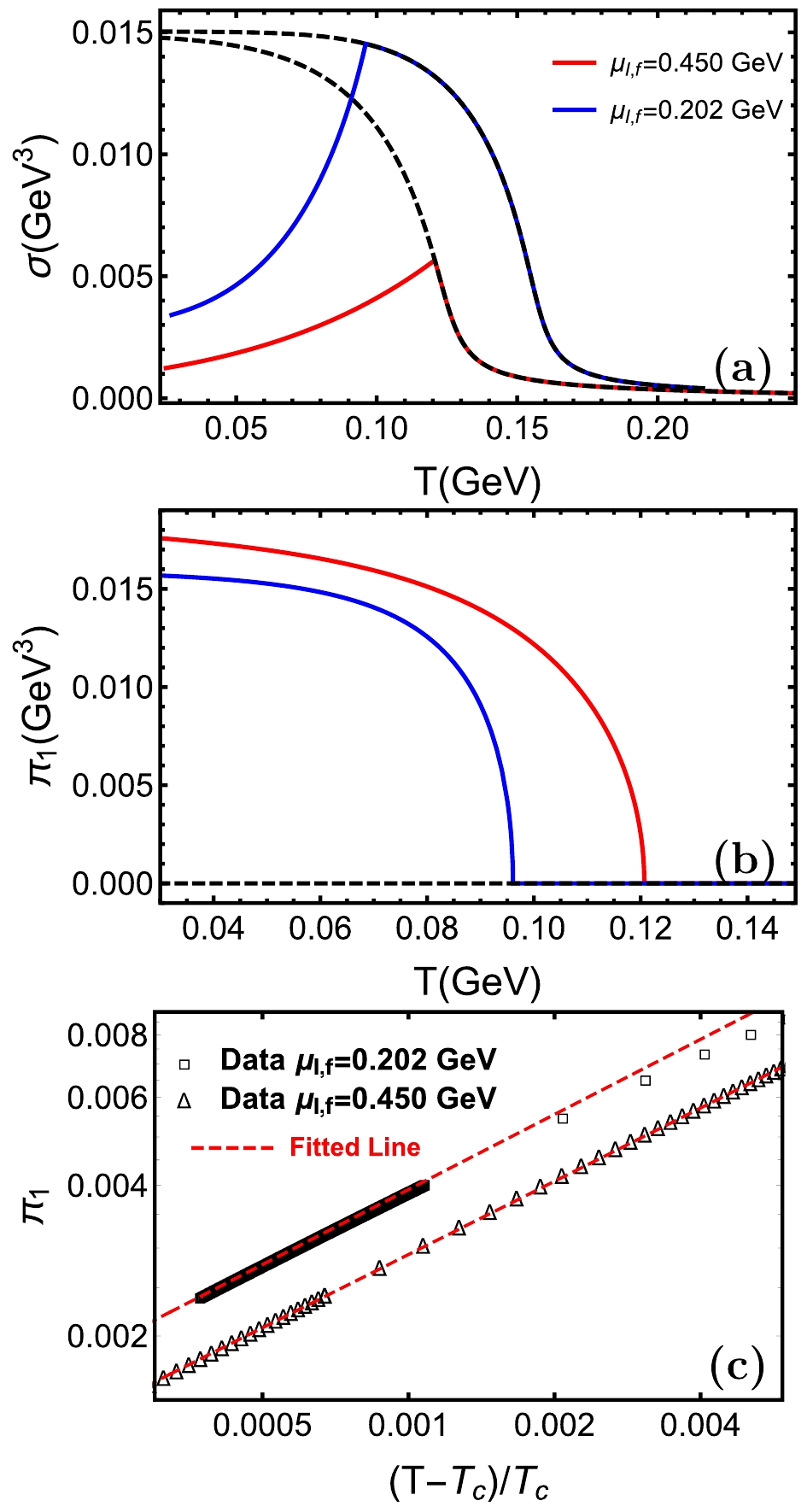
Figure 2. (color online) Chiral condensation (a) and pion condensation (b), with fixed isospin chemical potential
$\mu_{I,f}$ . The dashed and solid lines correspond to$\pi_1 = 0$ and$\pi_1\neq 0$ , respectively. The critical temperatures of pion condensation are$T_{c,\pi_1} = 0.0961$ and$0.121$ GeV for$\mu_{I,f} = 0.202$ and$0.450$ GeV, respectively. (c) Red lines fit the data in the critical region with$\pi_ 1 = 504.704$ $ (0.096 - T)^{0.499}$ and$\pi_ 1 = 343.333 (0.121 - T)^{0.487} $ for$\mu_{I,f} = 0.202$ and 0.450 GeV, respectively.However, pion condensation can also be studied through another perspective, investigating the dependence of
$ \pi_1(\mu_I, T_f) $ on$ \mu_I $ with different fixed temperatures$ T_{f} $ . The numerical results are shown in Fig. 3, where solid and black dashed lines represent turning on and off the pion condensation channel, respectively. In Fig. 3(b), pion condensation possesses two critical points ($ \mu_{I,L}^c $ and$ \mu_{I,R}^c $ ), which divide the figure into three areas, one non-zero pion condensate region ($ \mu_{I,L}^c<\mu_I<\mu_{I,R}^c $ ) in the middle and two zero pion condensate regions ($ 0<\mu_I\leqslant\mu_{I,L}^c $ and$ \mu_I\geqslant\mu_{I,R}^c $ ) on both sides. The critical points are$ \mu_{I, L}^c = 0.170 $ ,$ 0.181 $ , and$ 0.251 $ GeV on the left and$ \mu_{I,R}^c = 0.457 $ ,$ 0.777 $ , and$ 0.891 $ GeV on the right for$ T_{f} = 0.060 $ ,$ 0.075 $ , and$ 0.120 $ GeV, respectively. We find that along with the increasing of$ T_f $ ,$ \mu_{I, L}^c $ and$ \mu_{I, R}^c $ are close to each other, and the pion condensate is gradually decreasing, which indicate that there is a critical temperature at which the pion condensate just disappears in all$ \mu_I $ regions, and the pion condensation phase should possess a raised area in the space of$ \mu_I $ and T. In the corresponding middle region (non-zero pion condensation region) of Fig. 3(a), the chiral condensate is depressed, and the degrees of depression are relatively proportional to the strength of pion condensation. In the regions on both sides,$ \sigma_1(\mu_T, T_f) $ behaves the same as the ordinary chiral crossover without pion condensation. Finally, we note that the behavior that$ \pi_1(\mu_{I}, T_f) $ with both left and right critical points also shows in Ref. [38], calculated by LQCD, and Ref. [77] by a soft-wall AdS/QCD model.
Figure 3. (color online) Chiral condensation (a) and pion condensation (b), with fixed temperature
$T_f$ . The dashed and solid lines correspond to$\pi_1 = 0$ and$\pi_1\neq 0$ , respectively. The left and right critical points of pion condensation are$\mu_{I,L}^c = $ 0.170, 0.181, and 0.251 GeV, and$\mu_{I,R}^c = $ 0.457, 0.777, and 0.891 GeV, corresponding to$T_f = $ 0.060, 0.075, and 0.120 GeV, respectively.The chiral and pion condensations were separately studied in the preceding part of this section. However, there is mutual-interaction between themselves. Therefore, it is necessary to investigate their interdependence relationships. Figure 4 shows the dependency between
$ \sigma(\mu_I,T_f)/\sigma_0 $ and$ \pi_1(\mu_I,T_f)/\sigma_0 $ , where$ \sigma_0 = \sigma(\mu_{I,L}^c,T_f) $ , depicted by the dashed black curve, represents the unit circle$ \widetilde{\sigma}/\sigma_0 = 1 $ , and the absolute chiral condensation is defined as$ \widetilde{\sigma} = \sqrt{\sigma^2+\pi_1^2} $ . With the increase in$ \mu_I $ , the green curve ($ T_f = 0.120 $ GeV) falls into the circle, the red and blue curves ($ T_f = 0.060 $ and$ 0.075 $ GeV) first show the enhancement behavior and then drop sharply to zero when$ \mu_I $ is large enough. These curves indicate a tendency that when the temperature is infinitely close to zero, the dropping line will be infinitely close to the$ \pi_1/\sigma_0 $ -axes, and the enhancement tends to increase infinitely as$ \mu_I $ increases. Moreover, this enhancement only arises when the temperature is low enough. From the expression of action and dilaton, we know that when temperature tends to zero, the dilaton term will approach one as$ z_h $ approaches infinity, the soft wall boundary will back to the hard wall cut, therefore the zero temperature asymptotic behaviors qualitatively coincide with the hard wall results in Ref. [74].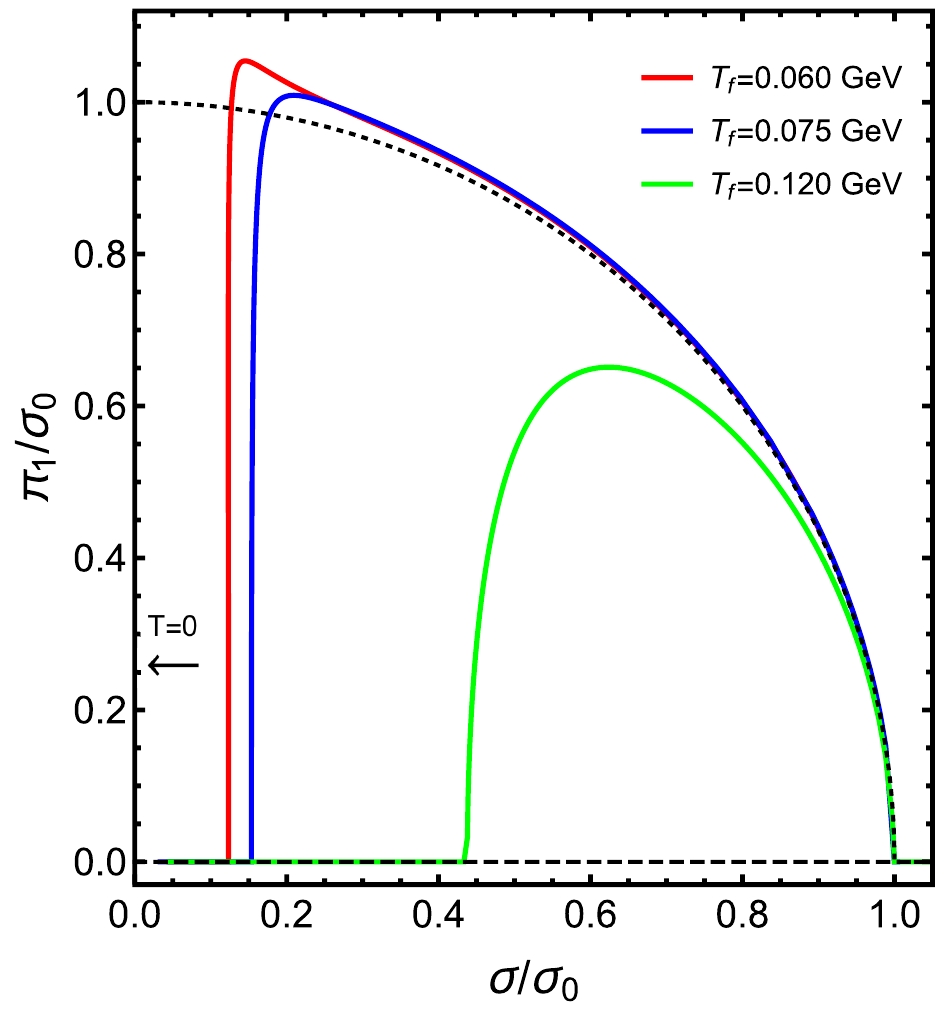
Figure 4. (color online) Interdependence relationship between
${\sigma}/{\sigma_0}$ and$\pi_1/\sigma_0$ , where$\sigma_0 = \sigma(\mu_{I,L}^c,T_f)$ . The dashed black curve represents the unit circle$ \widetilde{\sigma}/\sigma_0 = 1$ . The sharp decreasing line infinitely tends to the y-axis as$T\rightarrow 0$ . -
To obtain the complete phase diagram on the
$ \mu_I $ and T plane, we can let the fixed$ T_f $ ergodic the entire T- axis, and case by case solve the EOMs in Eqs. (12) at a fixed$ T_f $ . Then, we can extract the critical point of pion condensation, as well as the pseudo critical point of the chiral condensation from the solutions, as we did in Secs. 3.2 and 3.3.However, if we just want to determine the phase boundaries, case by case solving the full EOMs may be not necessary. Here, we introduce a more direct method. From the EOMs in Eq. (12) and the UV expansions solution in Eq. (13), we know that
$ \Pi(z) $ and$ a_{2}(z) $ are vanishing small when$ \pi_1 $ and$ a_{2c} $ approach zero. In addition, through the research in Sec. 3.3, we know that$ \pi_1 $ and$ a_{2c} $ ① change continuously from zero to non-zero values around the critical point ($ \mu_{I}^c $ ,$ T_c $ ), such that we can expand$ \Pi(z) $ and$ a_{2}(z) $ in the critical region, based on the background of$ \chi(z) $ . Thus, when there is an infinitesimal perturbation near the critical point$ (\delta \mu_I, \delta T) = (\mu_I-\mu_I^c, T-T_c) $ , we expand$ \Pi(z) $ and$ a_2(z) $ and just keep to linear terms, which is good enough to satisfy the EOMs, and then the boundary EOMs are derived as$ \tag{17a} \delta\Pi ''+\delta\Pi ' \left(3 A'+\frac{f'}{f}-\Phi '+\frac{2 \chi '}{\chi }\right)-\frac{v (\delta a_2-\delta\Pi v)}{f^2} = 0, $

$\tag{17b} \delta a_2''+\delta a_2' \left(A'-\Phi '\right)-\frac{g_5^2 {\rm e}^{2 A} \chi ^2 (\delta a_2-\delta\Pi v)}{f} = 0. $

From Eq. (17), we obtain IR-boundary conditions as
$\tag{18a} \begin{split} \delta\Pi(z) =& \Pi_0+\frac{\mu_I (z-z_h)^2 (a_{21} z_h-2 \mu_I \Pi_0)}{8 \left( \mu_I ^2 z_h^2-2\right)^2}z^2 \\ &+{\cal{O}}[(z-z_h)^3], \end{split} $

$\tag{18b}\begin{split} \delta a_2(z) = &a_{21} (z_h-z)-\frac{(z-z_h)^2 }{4 z_h^2 \left(\mu ^2 z_h^2-2\right)}\big\{a_{21} z_h \big[\chi_0^2 g_5^2\\ &+2 \left(\mu_I ^2 z_h^2-2\right) \left(2 \mu_g^2 z_h^2+1\right)\big ]-2 \chi_0^2 g_5^2 \mu_I \Pi_0\big\} \\ &+{\cal{O}}[(z-z_h)^3], \end{split} $

where
$ \Pi_0 $ and$ a_{21} $ are integral constants.The boundary EOMs in Eq. (17) is a set of linear second order differential equations, such that we can set
$ \Pi_0 = 1 $ and numerically solve the boundary EOMs by using the IR-boundary conditions in Eq. (18). Only when$ (\mu_I,T) = (\mu_I^c,T_c) $ , the conditions of$ \delta \Pi(z)|_{z = 0} = 0 $ and$ \delta a_2(z)|_{z = 0} = 0 $ can be simultaneously satisfied. In Fig. 5, we numerically test the dependence of the norm$ N(\epsilon) = \sqrt{\delta \Pi(\epsilon)^2+\delta a_2(\epsilon) ^2} $ on$ \delta\mu_I $ , where$ \epsilon $ is an infinitely small number, and it behaves linearly proportional to$ \delta \mu_I = \left |(\mu_I-\mu_{I, L}^c)/\mu_{I, L}^c\right | $ , where$ \mu_{I, L}^c\approx 0.170 $ and$ 0.181 $ GeV correspond to$ T_f = 0.060 $ and$ 0.075 $ GeV, respectively.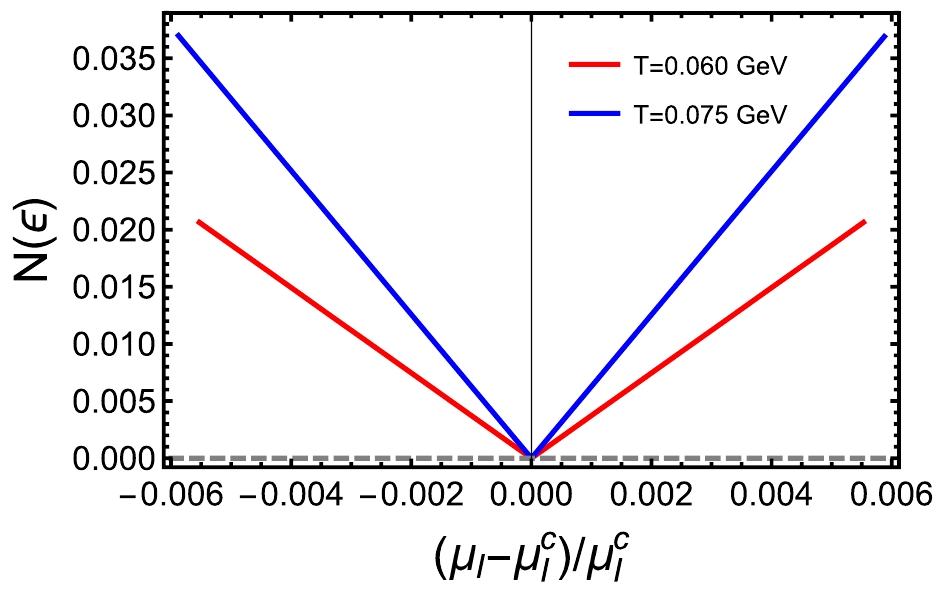
Figure 5. (color online) Norm
$N(\epsilon) = \sqrt{\delta\Pi[\epsilon]+\delta a_2[\epsilon] }$ is linearly proportional to$\delta \mu_I = \left |(\mu_I-\mu_I^c)/\mu_I^c\right |$ , where critical points$\mu_{I,L}^c = $ 0.170 and 0.181 GeV correspond to$T_{f} = $ 0.060 and 0.075 GeV, respectively.In contrast, the
$ U_I(1) $ symmetry is spontaneously broken by pion condensation, which generates a massless Nambu-Goldstone boson. To identify the pion mass on the phase boundary, we can analyze the goldstone mode in the momentum space,$q = (\omega, {{q}})$ . We expand the Lagrange in Eq. (11) to squared terms to deduce the EOMs in the momentum space as$\tag{19a} a_2' \left(A'-\Phi '\right)+a_2''-\frac{ {g5}^2 {\rm e}^{2 A} \chi ^2 \left(a_2+\Pi (\omega -v)\right)}{f} = 0, $

$\tag{19b} \begin{array}{l} \Pi ''+\Pi ' \left(3 A'+\dfrac{f'}{f}-\Phi '+\dfrac{2 \chi '}{\chi }\right)+ \dfrac{(\omega -v) \left [a_2+\Pi (\omega -v)\right ]}{f^2} = 0, \end{array} $

in which we have used the condition that three dimensional momentum
${{q}} = 0$ . The massless goldstone mode is the eigenstate of EOMs in the momentum space [83-85] with$ \omega = m_{\pi_1} = 0 $ and$ \mu_I = \mu_I^c $ . In other words, the pion becomes massless, and pion condensate forms when$ \mu_I $ increase to$ \mu_I^c $ . Under this condition, Eqs. (19) indeed coincide with the boundary EOMs in Eqs. (17). This proves that in the pion condensation phase boundary, the mass of the pion equals to zero,$ m_{\pi_1}(T_c, \mu_I^c) = 0 $ .By solving the boundary EOMs, we obtain the complete phase diagram on the
$ \rm \mu_I $ -$T$ plane, as shown in Fig. 6. The pion condensed phase region is surrounded by the red line and x-axis and is a convex shape with a top point$(\mu_{I,{\rm top}}^c,T_{c,{\rm top}}) = (0.333, 0.129)$ GeV. The black triangle points on the red line are obtained by solving the complete EOMs, and this consistency proves that the two methods give the same results. Despite the divergence problem of the expansion coefficients at zero temperature, we can still infer zero temperature critical point$ \mu_{I, T = 0}^c $ from the low temperature phase boundary trend, and we have$ \mu_{I, T = 0}^c\approx 0.146 $ GeV, which is represented by the end point of the gray dashed line. The zero temperature critical point coincides well with the results of$ \mu_{I, T = 0}^c = m_0 $ in the numerical LQCD [41], analytical chiral perturbation method [4, 12], as well as hard wall AdS/QCD [74]. In the large$ \mu_I $ region, the pion condensation boundary has a tendency of infinitely approaching to zero temperature and infinite$ \mu_I $ , which means pion condensation loses its right side critical point at zero temperature and it is mutual verified with the tendency of enhancement studied in Sec. 3.3. The blue line denotes the boundary of the chiral crossover, and it comes across the pion condensation boundary at a tricritical point, at which three phases (pion condensation phase, normal$ \chi $ SB phase and$ \chi $ SR phase) coexistence terminates,$(\mu_{I,{\rm tri}}^c,T_{c,{\rm tri}} )$ $ = (0.489, 0.116) $ GeV. The part of chiral crossover boundary, which is in the pion condensation region, apart the pion condensation region into left and right areas. The chiral crossover accompanying the chiral symmetry restoration can be seen as a signal in the color deconfinement transition (if one supposes that the two transitions are coincident). This indicates that the left part is a pion condensed phase (BEC). For the right part, we find that the structure is quite similar to the study in Ref. [4], where the right part is a kind of color deconfined Bardeen-Cooper-Schrieffer (BCS) phase, a Fermi liquid with cooper pairing formed as a consequence of an attractive interaction between quarks in the isospin channel. Compared to these studies, it is possible that the right part in Fig. 6 might represent a kind of BCS phase. However, we must verify this in a future study.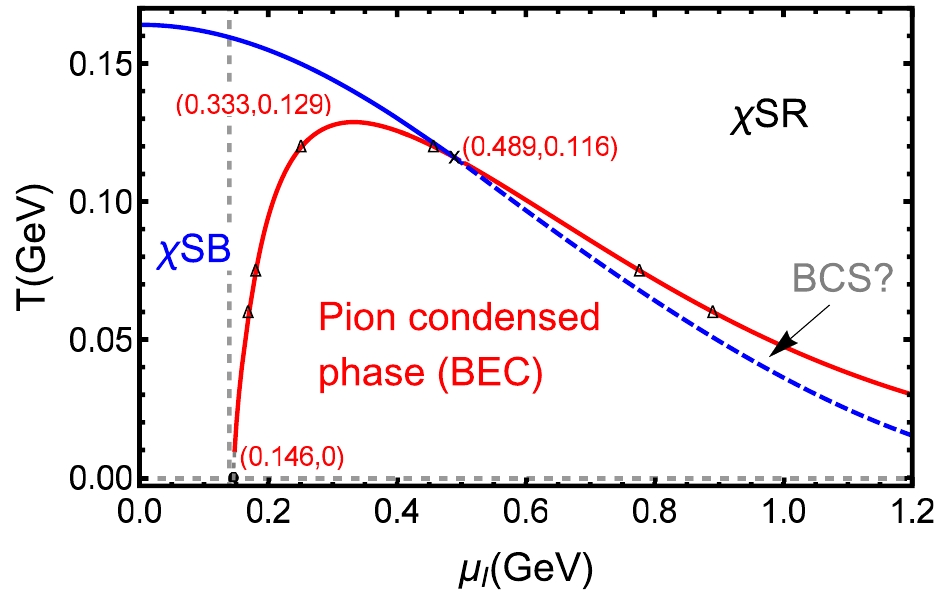
Figure 6. (color online) Phase transition diagram of a chiral crossover and pion condensation in
$\mu_I-T$ plane. The blue curve is the boundary between the normal$\chi$ SB phase and$\chi$ SR phase. The red curve and the$\mu_I$ -axis surround the pion condensed phase. The gray dashed curve depicts the extrapolated pion condensation boundary in the very low temperature region, and the end point is the critical point,$\mu_{I,T = 0}^{c} = 0.146$ GeV, at zero temperature. The chiral crossover boundary and the pion condensation boundary meet at the tricritical point$(\mu_{I,{\rm tri}}^c, T_{c,{\rm tri}}) = $ (0.489, 0.116) GeV. The extreme point of the pion condensation boundary is$(\mu_{I,{\rm top}}^c, T_{c,{\rm top}}) = $ (0.333, 0.129) GeV. We suppose the blue curve below the tricritical point indicates a BEC-BCS crossover. The black triangle points are the critical points of pion condensation, which are obtained by the method in Sec. 3.3. -
In this study, we investigated the pion and chiral condensations with finite
$ \mu_I $ and finite T in the IR improved soft-wall AdS/QCD model. Under a fixed$ T_f $ , we find that pion condensation includes two critical points separately located in the small and large$ \mu_I $ regions, and similar behaviors are exhibited in the LQCD in Ref. [38], the NJL model in Ref. [17], and a solf-wall model in Ref. [77]. The behaviors of the pion condensation continuous changes from zero to non-zero and the measured values of critical exponent$ \beta $ are very close to$ 1/2 $ , which indicates that the pion condensation is of the second order and belongs to the 4D mean field class. To further confirm the order of this phase transition, further studies on the relaxation phenomenon may be helpful. However, to obtain a critical exponent beyond the mean field theory, on one hand, the large-$ N_c $ correction should be taken into consideration [86, 87]. On the other hand, a full back-reaction model including the interaction fo gluodynamics and chiral dynamics should be considered in a more realistic holographic model. The relationship between$ \pi_1 $ and$ \sigma $ indicate that the absolute chiral condensation,$ \widetilde{\sigma} = \sqrt{\sigma^2+\pi_1^2} $ cannot be enhanced by the pion condensation at high temperatures. Instead, it is first enhanced by pion condensation, then steeply decreases to zero along the increasing of$ \mu_I $ at the low temperature region. When the temperature infinitely approaches zero, the enhancement will approach the infinite large pion condensation region, which coincides with the zero temperature holography hard wall results in Ref. [74]. This is because when the temperature tends to zero, the dilaton term will approach one as$ z_h $ approaches zero, such that the soft wall boundary supports the hard wall cut.After studying the condensation in detail, we obtain the QCD phase diagram on the
$ \mu_I-T $ plane. Here, the non-zero pion condensation exhibits a convex shape area; the zero temperature critical point$ \mu_{I, T = 0}^c\approx m_\pi $ is extrapolated from the low temperature tendency, which coincides well with the results in Refs. [41, 62, 74]; the chiral crossover boundary interposes the pion condensation region at the tricritical point, as chiral crossover can be seen as a signal of the color deconfinement transition, and the chiral crossover boundary in the pion condensation region indicates a crossover from BEC to BCS. In addition, the coincidence between the boundary EOMs and the momentum space EOMs at$ \omega = 0 $ and$ \mu_I = \mu_I^c $ , proves the pion mass$ m_{\pi_1}(\mu_I^c,T_c) = 0 $ on the pion condensation phase boundary.From the phase diagram, we know that the maximum pion condensation temperature is
$T_{\rm top} = 0.129$ GeV. However, the LHC data indicate that the chemical freeze-out temperature$ T_{ch} $ is approximately 0.155 GeV [88], which is larger than the maximum pion condensation temperature. This means that no pion condensation forms as the fire ball expands and cools down. Therefore, it seems that the pion condensed phase would not affect heavy-ion collisions at the current stage. However, the thermal freeze-out temperature$ T_{th} $ is estimated at$ 0.1-0.12 $ GeV [89-92], which is smaller than the maximum pion condensation temperature. It means that the pion condensation could form before the thermal freeze-out. As a result of the pion condensation, more low energy spectra of pion would be found in final detection, and the coherent fraction of pions would increase. Also, compared to the zero isospin density situation, the equations of state at finite isospin density would provide certain corrections. It would be more realistic when applying the holographic method to neutron stars. We leave this to a future study.
QCD phase diagram at finite isospin chemical potential and temperature in an IR-improved soft-wall AdS/QCD model
- Received Date: 2020-02-10
- Available Online: 2020-08-01
Abstract: We study the phase transition between the pion condensed phase and normal phase, as well as chiral phase transition in a two flavor (






 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF





















 DownLoad:
DownLoad: