Observational constraints on Rastall gravity from rotation curves of low surface brightness galaxies

One hundred years ago, Einstein proposed the general theory of relativity (GR), thereby describing gravity successfully. One of the important fundamentals of GR is to assume that the covariant derivative of the energy-momentum tensor is zero, and that GR naturally satisfies the equivalence principle. Rastall generalized the covariant conservation of the energy-momentum tensor [1,2] and obtained the conservation equation of the energy-momentum tensor in the form $ T^{\mu\nu}_{;\mu} = \lambda R^{,\nu} $, where $ T^{\mu\nu} $ is the energy momentum tensor, $ R $ is the Ricci curvature (or Ricci scalar) and $ \lambda $ is the parameter of the Rastall gravity. This theory can be reduced to GR in asymptotically flat space-time. However, Rastall gravity is still a controversial gravitational theory. One view is that Rastall gravity is equivalent to GR [3], and the parameter $ \lambda $ represents the re-arrangement of perfect fluid matter. According to this view, we simply need to redefine the energy-momentum tensor so as to satisfy the covariant conservation. The only change is the addition of matter fields with different distributions in space-time. In contrast, Darabi et al. [4] considered that Rastall gravity is not equivalent to GR. Rastall gravity strengthens the role of the Mach principle in gravity theory [5], in which the local structure depends on the distribution of matter across the entire space-time.

Although the nature of Rastall gravity is not clear, we attempt to constrain its properties by using observational events. On the cosmological scale, Batista et al. [6] used the data of type Ia supernovae to analyse the gravity model and achieved some good results. Recently, Li et al. [7] acquired a measured value of the Rastall gravity parameter on the scale of elliptical galaxies and supposed that Rastall gravity can explain the mass distribution of elliptical galaxies. This measured value is consistent with one constrained by the energy condition, but the result of Rastall gravity in accordance with GR on a large scale is a requirement of the theory itself. To test the result, we need the data of galaxies on a smaller scale, such as galaxy nuclei and spiral galaxies. In this study, we will use the data of rotation curves from low surface brightness (LSB) galaxies to constrain Rastall gravity.

The remainder of this paper is organized as follows. In Section 2, we introduce perfect fluid dark matter (PFDM) and Rastall gravity. In Section 3, we constrain the Rastall gravity model based on the rotation curves of LSB spiral galaxies. In Section 4, we discuss our results and compare them with previous results. Finally, in Section 5, we present our conclusions.

Kiselev [8] obtained the black hole solution of perfect fluid matter in GR. They assumed that the equation of state defined by the ratio of pressure to the density of perfect fluid matter $ \omega = p/\rho $ is a constant, where $ p $ and $ \rho $ are the pressure and density of perfect fluid matter, respectively. The expression of the black hole solution is

where $ f(r) $ and $ g(r) $ are written as

$ M $ represents the mass of a black hole, and $ \alpha $ is the intensity parameter of perfect fluid matter around a black hole. If the equation of state is given by $ \omega = -1/3 $, the black hole solution represents a Schwarzschild black hole with a perfect fluid dark matter background [9-12]. In general, perfect fluid dark matter (PFDM) is quintessence matter, because only for this type of matter, the equation of state is possibly equal to -1/3. At the same time, the solution can also be understood as a black hole solution under the PFDM model. In this situation, the flatness of the rotation curves of spiral galaxies at a long distance can be explained naturally. Here, we assume that this property continues to be valid in Rastall gravity.

Heydarzade & Darabi [13] generalized Kiselev's [8] solution from GR to Rastall gravity and obtained a spherically symmetric black hole solution in perfect fluid matter. This solution has the form of

where $ \kappa\lambda $ is a parameter of the Rastall gravity, which determines the distribution of perfect fluid matter. For convenience, we write $ \kappa\lambda $ as $ \beta $ throughout this article, i.e. $ \beta = \kappa\lambda $. For PFDM ($ \omega = -1/3 $), the energy density $ \rho_{DM} $ can be derived from the Einstein equation. Because the motion velocity of a dark matter particle is much smaller than the speed of light, the energy density of PFDM can approximate the mass density. Here, from Kamada et al. [14], the baryon matter can be treated as an index disk, i.e. $\rho_{b} = \Sigma_{0}\exp[-r/r_{d}]\delta(z)$, where $ \Sigma_{0} $ and $ r_{d} $ are the central surface density and scale radius of the disk, respectively. In this space-time metric, using the mass density of the PFDM halo and baryon disk, we can calculate the total mass function, described as $M(r) = 4\pi\int_{0}^{r}\rho_{DM}r^{2}{\rm d}r+ 2\pi\int_{0}^{r}\rho_{b}r{\rm d}r$. We then obtain the rotation velocity of stars on the equatorial plane, written as [15]

Where G is the gravitational constant. Here, we have neglected the contributions of the gas and bulge, because the potentials of gas and bulge are very small compared with those of DM halo and baryonic matter. This is a good approximation for fitting the rotation curves of LSB galaxies (similar reason can be found in [14] on the third page). We will use this equation to fit the rotation curves of LSB galaxies, and determine the $ \beta $ values of the Rastall gravity. The parameter $ r_{d} $ is $ 2 kpc $ [14] in Section 3.

In the theory of gravity, it is extremely difficult to solve the equation of a gravitational field. Through the Einstein field equation, we know that the distribution of the energy-momentum tensor determines the structure of space-time. Due to the complexity of the matter distribution, the energy-momentum tensor cannot be expressed in a specific form. Therefore, certain conditions, i.e. that the energy density is greater than or equal to zero, were used to study the gravitational field equation.

In 1955, Raychaudhuri formally proposed the basic equation of the energy conditions, such as the weak energy condition and strong energy condition. Under these energy conditions, the fundamental properties of gravity are satisfied. In references [13] and [15], they presented a specific study on the energy conditions of Rastall gravity, and found that the constraint of the weak energy condition and strong energy condition on the Rastall parameter $ \beta $ are equal under the assumption of a perfect fluid. They can be given by

If $ \omega = -1/3 $, the perfect fluid matter is described by the PFDM model, and the range of the Rastall parameter $ \beta $ is $ -1/2<\beta<1/4 $. If the $ \beta $ obtained by fitting the observation data is within this range and is a constant on the scale of a spiral galaxy, elliptical galaxy and cosmology, Rastall gravity is supported. If the opposite is true, the model will be excluded.

In this section, we choose LSB galaxies dominated by dark matter to limit the Rastall parameter. Now, according to Eq. (4), we adopt the Bayesian method [16] to fit the rotation curves of 16 LSB spiral galaxies, and obtain good fits overall, with $ \chi^{2}/dof<1 $ for 15 galaxies (F563-1, F568-3, F583-1, F571-8, F579-v1, F583-4, F730-v1, U5750, U11454, U11616, U11648, U11819, ESO0140040, ESO2060140, ESO3020120), and $ \chi^{2}/dof<2 $ for one galaxy (ESO4250180). Here, the predicted velocity $\upsilon_{\rm pre}$ is taken from Eq. (4) as $ \upsilon(r) $, and the observed velocity $\upsilon_{\rm obs}$ is taken from an astronomical website (http://astroweb.case.edu/ssm/data/RCsmooth.0701.dat). For each galaxy, we assume that it has $ i $ data points. Therefore, the likelihood function can be expressed as

where

and $ \delta $ is the intrinsic scatter between $\upsilon_{\rm pre}$ and $\upsilon_{\rm obs}$, which is considered to be a free parameter in our Bayesian analysis (see [16] for a detailed explanation). As it is not a model parameter, it is unrelated to Eq. (4). $\upsilon_{\rm err}$ is the measurement error of $\upsilon_{\rm obs}$. Now, the posterior probability function can be written as

Here, for each LSB galaxy, we choose a flat prior $ p(\alpha, \beta, \Sigma_{0}, \delta) $ and use a Python implementation named Emcee [17] along with four free parameters $ \alpha, \beta, \Sigma_{0}, \delta $ to fit the rotation curves. Our results are shown in Table 1.

Galaxy (1)	$ \beta $ (2)	$ \chi^{2}/dof $ (3)
F563-1	0.053	0.877
F568-3	0.155	0.857
F583-1	0.15	0.893
F571-8	0.143	0.877
F579-v1	0.047	0.125
F583-4	0.141	0.216
F730-v1	0.096	0.53
U5750	0.148	0.821
U11454	0.118	0.823
U11616	0.122	0.778
U11648	0.132	0.361
U11819	0.147	0.951
ESO0140040	0.084	0.778
ESO2060140	0.1	0.813
ESO3020120	0.136	0.405
ESO4250180	0.124	1.756

Table 1.  Best fitting results of the rotation curves for 16 LSB spiral galaxies using Eq. (4). The corresponding rotation curves and the joint constraint plots of the parameters are presented in Figs. 1, 2, 3, 4 in the appendix. Columns (1), (2) and (3) are the name of the galaxy, the fitting values of Rastall parameter $ \beta $ and the $ \chi^{2} $ values, respectively.

In this study, we constrain the parameter $ \beta $ of Rastall gravity by fitting the data of the rotation curves from 16 LSB spiral galaxies. Comparing previous results of type Ia supernovae and elliptical galaxies, we support that Rastall gravity may be equivalent to GR.

On the scale of a spiral galaxy, the values of parameter $ \beta $ we obtained are on the order of $ 10^{-1} $ and within the limits of the strong energy condition in Rastall gravity. On the cosmological scale, Batista et al. [6] used the data of a type Ia supernovae to constrain the parameter $ \beta $ and found that the $ \beta $ value is on the order of $ 10^{-4} $. This is inconsistent with our results within three orders of magnitude. If our analysis is correct, then the value of the Rastall parameter will cause some issues. For example, the value of the parameter $ \beta $ on the scale of the spiral galaxy is not the same as the value on the cosmological scale, which indicates that parameter $ \beta $ is not universally applicable. In contrast, Li et al. [7] recently used the gravitational Lensing data of elliptical galaxies to constrain the Rastall parameter. Their $ \beta $ values obtained by fitting the observed data are consistent with ours, which implies that the parameter values of the Rastall gravity are consistent between elliptical galaxies and spiral galaxies. At the same time, according to the Rastall gravity model, the result of the Rastall gravity being in accordance with GR on a large scale is a requirement of the theory itself, and differences only appear on a smaller scale.

The nature of Rastall gravity is in dispute. What is the explanation of our results for this? If Rastall gravity is equivalent to GR, $ \beta $ only represents the distribution of matter, and different systems will have different values; therefore, it is easy to understand the differences in $ \beta $ between the galactic scale and the cosmological scale. If Rastall gravity is not equivalent to GR, on the basis of assumptions of Rastall gravity, the $ \beta $ values should be same on the galactic scale and the cosmological scale, but this contradicts our analysis results. Therefore, we will conclude that the Rastall parameter $ \beta $ can only be understood as the parameter determining the distribution of matter in space-time. Thus, our results support that Rastall gravity may be equivalent to GR. In contrast, these results may also be considered to be due to some astrophysical modelling bias. These reasons may be related to the DM model of galaxies. In future work, we will examine these possibilities in detail.

In this work, using the rotation curves of 16 LSB spiral galaxies, we obtained the values of parameter $ \beta $ in the Rastall gravity model. These values are approximately 0.1 and satisfy the strong energy condition. After comparing the results of type Ia supernovae and elliptical galaxies, we found that our results support that Rastall gravity may be equivalent to GR, and then, the values of parameter $ \beta $ can only be understood as a re-arrangement of matter in space-time, and the difference between the galactic scale and the cosmological scale can be easily explained.

The authors would like to thank Kuzio de Naray, R., McGaugh, S.S., and de Blok for providing us with the rotation curve data and thank Li Rui for his help in programming. We acknowledge the anonymous referee for their constructive report that has significantly improved this paper.

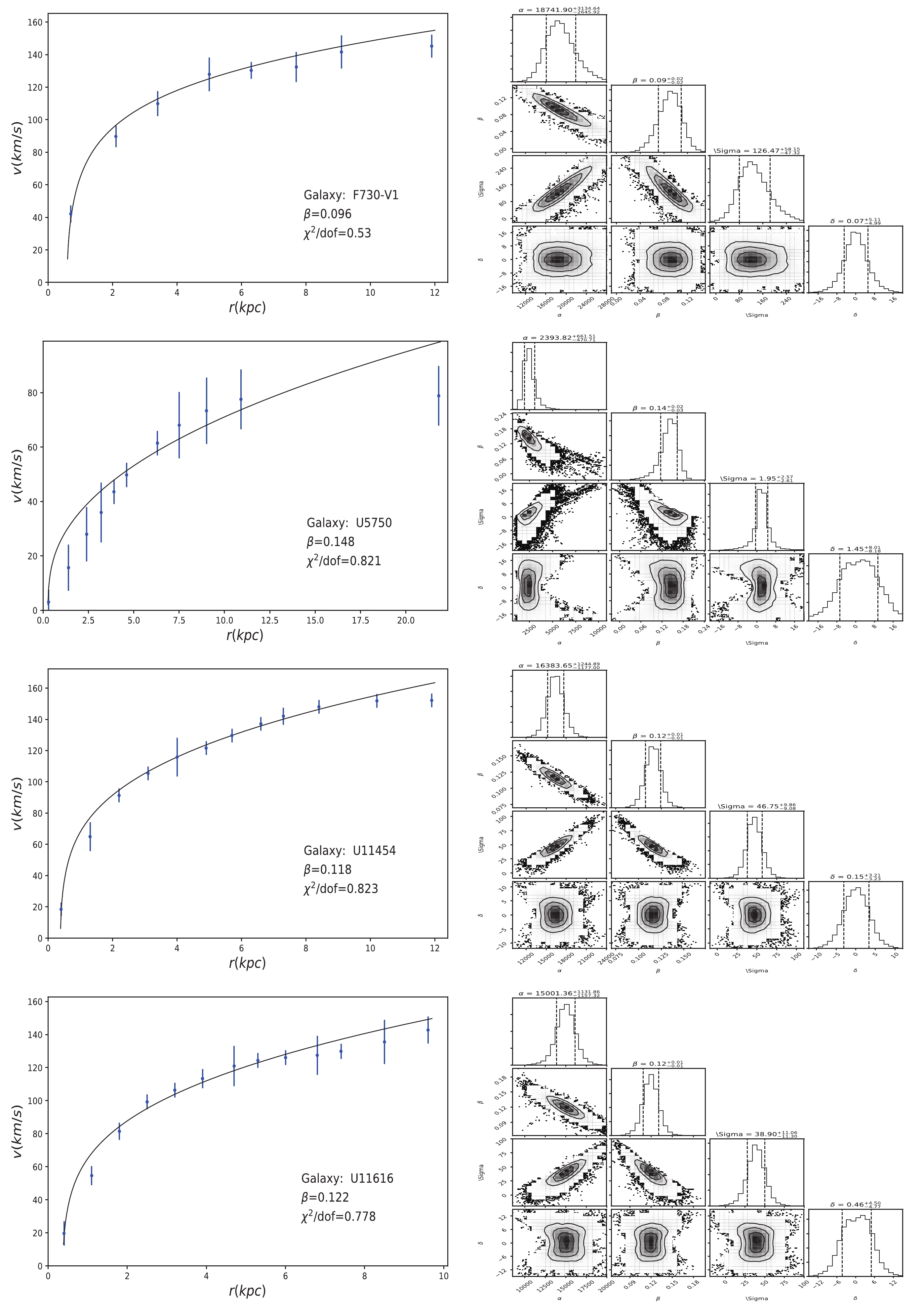
Figure 1.  (color online) The left and right panels show the best fitting results of the rotation curves for F730-v1, U5750, U11454 and U11616 and the joint constraint plots of the parameters, respectively. The black curve is the theoretical prediction obtained from the parametric fit of Eq. (4). The blue dots are the observed data points, for which the vertical lines represent the error bars.

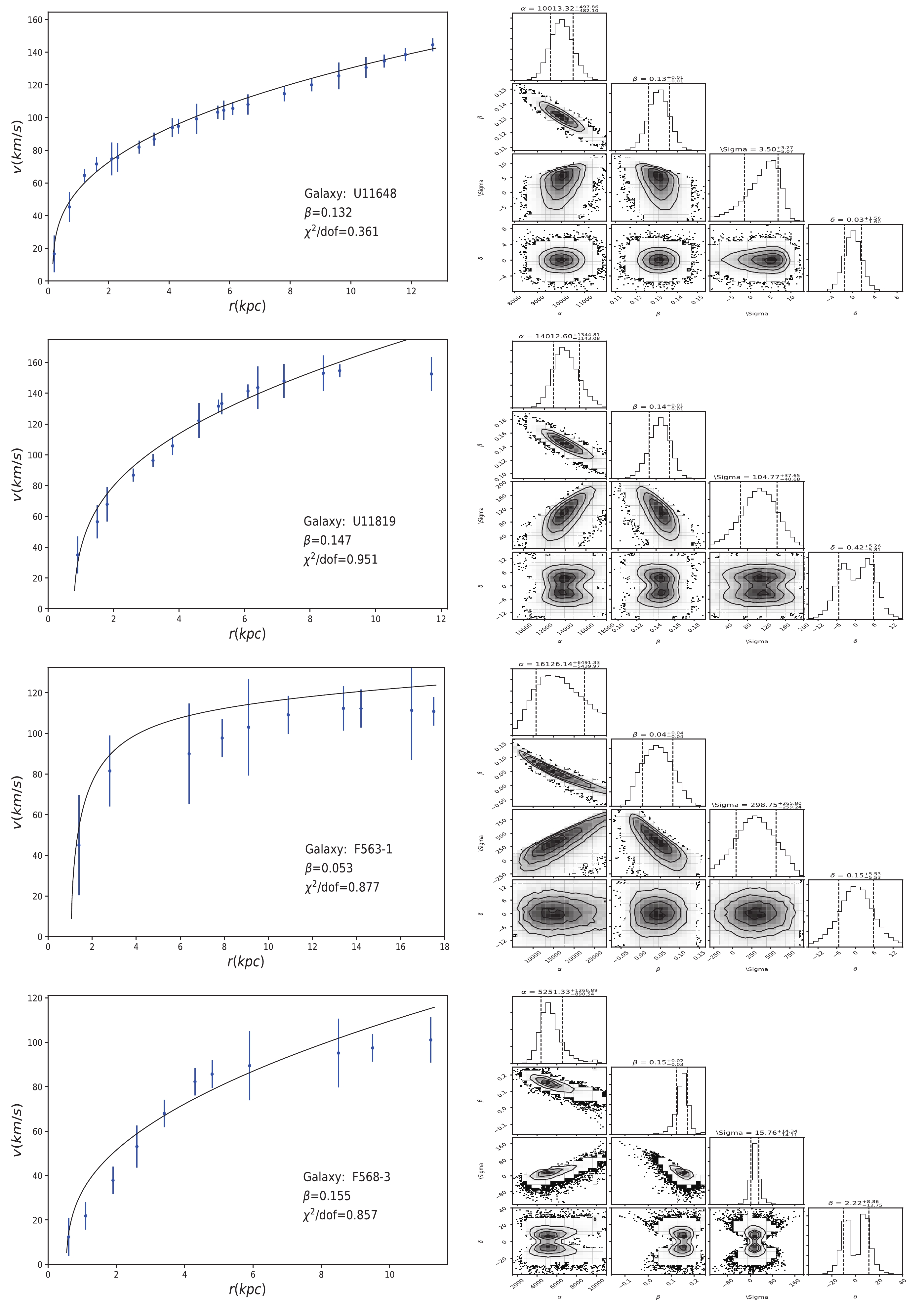
Figure 2.  (color online) The left and right panels show the best fitting results of the rotation curves for U11648, U11819, F563-1 and F568-3 and the joint constraint plots of the parameters, respectively. The black curve is the theoretical prediction obtained from the parametric fit of Eq. (4). The blue dots are the observed data points, for which the vertical lines represent the error bars.

Figure 3.  (color online) The left and right panels show the best fitting results of the rotation curves for F583-1, F571-8, F579-v1 and F583-4 and the joint constraint plots of the parameters, respectively. The black curve is the theoretical prediction obtained from the parametric fit of Eq. (4). The blue dots are the observed data points, for which the vertical lines represent the error bars.

Figure 4.  (color online) The left and right panels show the best fitting results of the rotation curves for ESO0140040, ESO2060140, ESO3020120 and ESO4250180 and the joint constraint plots of the parameters, respectively. The black curve is the theoretical prediction obtained from the parametric fit of Eq. (4). The blue dots are the observed data points, for which the vertical lines represent the error bars.