-
One of the reasons for studying compact stars is to understand the state of strongly interacting matter at extremely high density. It was conjectured long ago that quark and mixed phases appear inside compact quark or hybrid stars [1-3]. Recently, a collaborating group from Advanced LIGO and Advanced VIRGO observed the binary neutron star (BNS) merger event, GW170817 [4], which focused on the constraints on the equation of state of compact stars [5-9]. It appears possible, but not conclusive, that one or both component stars in the merger could be a hybrid star [10-12].
An understanding in terms of quantum chromodynamics (QCD) of how nuclear matter can evolve into deconfined quark matter is unclear at present. The phase transition is assumed to be of the first-order, and a description of the transition depends on knowledge regarding the surface tension
$ \sigma_s $ between the hadron and quark phases [13-15]. In view of uncertainties in the magnitude of$ \sigma_s $ , two extreme cases of a Maxwell construction and a Gibbs construction have been studied. Because it is unclear whether the first-order transition at a finite baryon density is demanded by fundamental considerations, the crossover region of a hadron-quark duality (e.g., quarkyonic matter or interpolated equation of state) has also been recently explored [16-18], and such a continuous crossover in the phase diagram is different from the mixed phase (Gibbs construction).The phase transition from nuclear to quark matter could be a weak transition leading to extremely little difference in mass-radius (M-R) relation between neutron and hybrid stars (called a masquerade) [19, 20], or a strong transition causing observable consequences and providing an indication of the presence of quark matter. If the hybrid stars form a branch of compact stars separated from neutron stars by an instability region, or if they have extremely different M-R relations [21-24], it provides the possibility to address the challenge of constraining a phase diagram of ultra-dense matter. With the operation of NASA's Neutron Star Interior Composition Explorer (NICER) experiment in 2017, the measurements of neutron star radii aim at an accuracy on the order of 5% [25, 26]. With the previously established lower limit on the maximum mass of neutron stars (
$ 1.93M_\odot$ [27, 28] -$2.01M_\odot $ [29]), the measurements of the radii will strengthen existing constraints on the equation of state (EoS) of dense matter.In the main studies on hybrid stars, the stars are composed of a quark core surrounded by a nuclear envelope. The quark-matter core is represented by a single quark phase or a quark-nuclear mixed phase [30, 31]. However, our understanding of the QCD phase diagram has improved over the years, and it has become clear that a quark core may contain layers of distinct phases [32]. High-mass twin stars with and without strangeness in their degrees of freedom were studied [17, 33-37]. Furthermore, twin, and even triplet, hybrid stars with inner cores of nuclear matter, two color-superconducting (2SC) matter, and color-flavor-locked (CFL) matter have been discussed, considering the sequential phase transition from the 2SC to CFL phases [38-42]. In most studies in this area, only a Maxwell construction has been used to describe the phase transition, and different stellar configurations resulting from different phase transition paths have not been discussed in detail.
The main purpose of this study is to interpret the possibilities of hybrid star configurations under different phase transition paths and provide a general description of the conditions and features of different configurations. Both Maxwell and Gibbs constructions based on an assumption of the first-order transition are discussed and the sequential transition from 2flavor quark matter to 3flavor quark matter is considered. In this study, we use a specific model inspired by the non-perturbative features of QCD, i.e., the vector-interaction-enhanced bag model (vBag model) [43] to describe the EoS of the quark matter, and choose different parameters to construct different phase transition paths under Maxwell and Gibbs constructions, providing various possibilities of hybrid star configurations. The rest of this paper is organized as follows: Section 2 describes the nuclear and quark matter equations of state applied and provides a brief review of a Maxwell and Gibbs-type phase transition. Section 3 provides the results for different phase transition paths and the corresponding configurations of the stars, followed by some concluding remarks and a discussion of future research in Section 4.
-
An excellent approximation of the specific energy of neutron-rich matter has been revealed in many different studies,
$ E(n,x) = E\left(n,x = \frac{1}{2}\right)+S(n)(1-2x)^2, $

(1) where x is the proton fraction,
$ E(n,x = \frac{1}{2}) $ is the energy per particle of symmetric nuclear matter, and S(n) is the nuclear symmetry energy.Here, we use the symmetric matter energy
$ E(n,x = \frac{1}{2}) $ and the symmetry energy$ S(n) $ extracted from calculations within the relativistic Dirac-Brueckner-Hartree-Fock (DBHF) approach [44]. Relativistic Brueckner calculations meet the empirical saturation point of nuclear matter with a binding energy of$ -16 \;{\rm MeV} $ at the saturation density. Furthermore, at the saturation density, DBHF provides a symmetry energy of$ 31.5 \;{\rm MeV} $ , which is in good agreement with the empirical models and data from isospin diffusion in heavy-ion collisions. The derivative of the symmetry energy is$ 69.4 \;{\rm MeV} $ and indicates that nuclear matter is relatively soft at saturation density. In addition, DBHF produces a neutron star with a maximum mass of$ M\simeq2.3 M_\odot $ , where$ M_\odot $ is the solar mass. Thus, in an analysis of DBHF EoS and its performance under a neutron star and heavy ion collision constraints, this particular EoS performs extremely well (see [45] for further references). -
Because none of the current quark matter EoSs have been obtained from first-principle QCD-based calculations, a number of quark matter models have been developed, which depend on the QCD key phenomena of a deconfinement and chiral symmetry restoration. We use the vBag model [43] in our study, which is a hybrid approach used to consolidate a number of seemingly discrepancies between the Nambu-Jona-Lasinio (NJL) and Bag model. Assuming bare quark masses and flavor-dependent chiral bag constants to reproduce the proper critical chemical potential for the chiral transition of each flavor, vector interactions are taken into account and analogized into the NJL model, resulting in an expression of the pressure and energy density of a single flavor as follows:
$ P_{{\rm{vBag}},f} = P_{{\rm FG},f}(\mu_f^*)+\frac{K_v}{2}n_{{\rm FG},f}^2(\mu_f^*)-B_{\chi,f}, $

(2) $ \varepsilon_{{\rm{vBag}},f} = \varepsilon_{{\rm FG},f}(\mu_f^*)+\frac{K_v}{2}n_{{\rm F}G,f}^2(\mu_f^*)+B_{\chi,f}, $

(3) where
$ P_{{\rm FG},f}(\mu_f^*) $ and$ \varepsilon_{{\rm FG},f}(\mu_f^*) $ are the pressure and energy given by a Fermi gas expression. The second term originates from the vector interactions at the given coupling constant$ K_v $ . As in the NJL model, the effective flavor chemical potential$ \mu_f^* $ is determined self-consistently at a given bare flavor chemical potential$ \mu_f $ ,$ \mu_f = \mu_f^*+K_v n_{{\rm FG},f}(\mu_f^*). $

(4) $ B_\chi = \sum_f B_{\chi,f} $ will reproduce the bag model bag constant for the activated flavors. Adding a bag constant$ B_{\rm{dc}} $ to the total pressure, the total energy density consequently subtracts$ B_{\rm{dc}} $ to lower the bounded state energy,$\qquad\qquad P_{{\rm{vBag}}} = \sum\limits_f P_{{\rm{vBag}},f}+B_{\rm{dc}},$

(5) $ \qquad\qquad \varepsilon_{{\rm{vBag}}} = \sum\limits_f \varepsilon_{{\rm{vBag}},f}-B_{\rm{dc}}, $

(6) which satisfies the condition in which deconfined quarks are energetically favorable. We further refer to effective two- and three-flavor bag constants to simplify our parameters,
$ \qquad B_{\rm{eff}}^{2f} = B_{\chi,u}+B_{\chi,d}-B_{\rm{dc}}, $

(7) $\qquad B_{\rm{eff}}^{3f} = B_{\chi,u}+B_{\chi,d}+B_{\chi,s}-B_{\rm{dc}}.$

(8) With the parameters of
$ K_v $ and$ B_{\rm eff} $ , the deconfinement quark matter is described using the vBag model. -
The matter in a neutron star is
$ \beta $ -equilibrated and charge neutral. The chemical potentials in nuclear and quark matter satisfy the following:$\qquad\qquad \mu_n = \mu_p+\mu_e, $

(9) $ \qquad\qquad \mu_d = \mu_u+\mu_e, $

(10) $\qquad\qquad \mu_s = \mu_d, $

(11) together with the local charge neutrality conditions in each phase, i.e.,
$ \sum\limits_{i = n,p,e}Q_in_i = 0, \quad \quad \sum\limits_{i = u,d,s,e}Q_in_i = 0. $

(12) To compare both phases, the baryon chemical potential
$ \mu_B $ , which is related to the conserved baryon number, is read as$ \mu_B = \mu_n, $

(13) $ \mu_B = 2\mu_d+\mu_u \;\;\; {\rm{or}}\;\;\; \mu_B = \mu_d+\mu_u+\mu_s, $

(14) respectively. If the phase with the higher pressure minimizes the thermodynamic potential, which is energetically favorable, a phase transition will occur under the condition in which nuclear and quark matter have equal pressure at an equal baryon chemical potential,
$ P^H(\mu_{B,{\rm{dc}}}) = P^Q(\mu_{B,{\rm{dc}}}). $

(15) During the phase transition, the pressure remains constant but the baryon density will show a discontinuity, which is called the Maxwell phase transition.
If the pressure and chemical equilibrium conditions remain valid, the charge neutrality holds over both phases, which is called a Gibbs construction. The total charge conservation is imposed through the following relation:
$ (1-\eta)\sum\limits_{i = n,p,e}Q_in_i+\eta \sum\limits_{i = u,d,s,e}Q_in_i = 0, $

(16) where
$ \eta = V_Q/(V_Q+V_H) $ represents the volume fraction occupied by quark matter. The transition takes place if both phases have the same pressure$ P^H(\mu_{B,{\rm{dc}}}) = P^Q(\mu_{B,{\rm{dc}}}) $ , although the total energy density has a contribution according to the volume fraction,$ \varepsilon = (1-\eta)\varepsilon^H + \eta\varepsilon^Q. $

(17) There is a transition region in which the quark volume fraction grows from zero to 1 and the pressure of the mixed phase increases with an increase in density.
-
Fixing the hadronic EoS as a DBHF model, we choose different vBag model parameter sets of (
$ K_v, B_{\rm eff} $ ). The vector coupling constant$ K_v $ and the bag effective constant$ B_{\rm eff} $ determine the stiffness of the quark matter and the transition density from nuclear matter to quark matter.After extensively varying most parameters and calculating the corresponding M-R relations, we found that, for 2f quark matter,
$ K_v = 2\;{\rm GeV}^{-2} $ is most likely the smallest value that ensures$ M_{\rm max} = \sim2M_\odot $ . When$ K_v $ is increased from zero, the energy density discontinuity becomes progressively smaller. Within the range of$ 0.5\leqslant K_v\leqslant 2.5\; {\rm GeV}^{-2} $ , the M-R curves of stable hybrid stars obtained are continuous, and quarks can appear at$ 1.0\leqslant M_{\rm trans}\leqslant 1.8M_\odot $ ($ M_{\rm trans} $ is the critical mass in which a phase transition occurs in the star center), pertinent to the range of component masses in BNS mergers. For overly large vector couplings, e.g.,$ K_v = 7\;{\rm GeV}^{-2} $ , the onset of the quarks is beyond the central density of the maximum-mass hadronic star, and thus no stable quark cores will be present even if the quark matter is sufficiently stiff. With the vector coupling$ K_v = 2\;{\rm GeV}^{-2} $ , the effective bag constant$ 61\leqslant B_{\rm eff}\leqslant 75\;{\rm MeVfm}^{-3} $ is adjusted such that the transition to quark matter occurs at the transition density$ n_{\rm trans} = 1.5 \sim 3.0 n_{\rm sat}\; (n_{\rm sat} = 0.16\;{\rm fm}^{-3}) $ . For the 3flavor quark matter, within the range of$ 13\leqslant K_v\leqslant 20 \;{\rm GeV}^{-2} $ , the M-R curves of stable hybrid stars are continuous and reach$ M_{\rm max} = \sim2M_\odot $ , and quarks can appear at$ 1.0\leqslant M_{\rm trans}\leqslant 1.8M_\odot $ .The purpose of this study is to interpret the possibilities of hybrid star configurations under different phase transition paths. The sequential transition from 2flavor quark matter to 3flavor quark matter is also considered. Overly soft quark EoSs are not applied because they either violate the
$ M_{\rm max} = \sim2M_\odot $ constraint or cannot establish a valid first-order phase transition, i.e., there is no intersection between the nuclear phase and quark phase in the pressure-baryon chemical potential plane. Furthermore, a sharp transition (as a Maxwell construction) to quark matter with large energy density discontinuity may or may not lead to a stable branch of hybrid stars, which may or may not be connected from the hadronic branch. Thus, we choose a scenario where the EOSs of 2f and 3f quark matter are fairly stiff, with$ K_v = 2\;{\rm GeV}^{-2}, \;B_{\rm eff} = 70\;{\rm MeVfm}^{-3} $ for 2f quark matter and$ K_v = 13\;{\rm GeV}^{-2} $ for 3f, which ensures that all of our mass-radius curves obey the observational lower bound on the maximum mass of a neutron star ($ 1.93(2)M_\odot $ to$ 2.01(4)M_\odot $ ). In particular, the transition from nuclear matter to quark matter occurs at a reasonable density, which guarantees a stable branch of hybrid stars and critical masses within the range of component masses in BNS mergers. An overly large$ K_v $ (correlated with stiffer quark matter) significantly delays the onset for quarks, which yields to no stable hybrid stars. Finally, there remains one parameter,$ B_{\rm eff} $ , of 3f, to fix the different phase transition paths and stellar configurations.Figure 1 shows the phase transition from nuclear to quark matter using the nuclear DBHF model (black line) and quark matter vBag model (the blue line indicates the 2f matter and the red line shows 3f). The phase transition occurs if the nuclear and quark matter have equal pressure at an equal baryon chemical potential
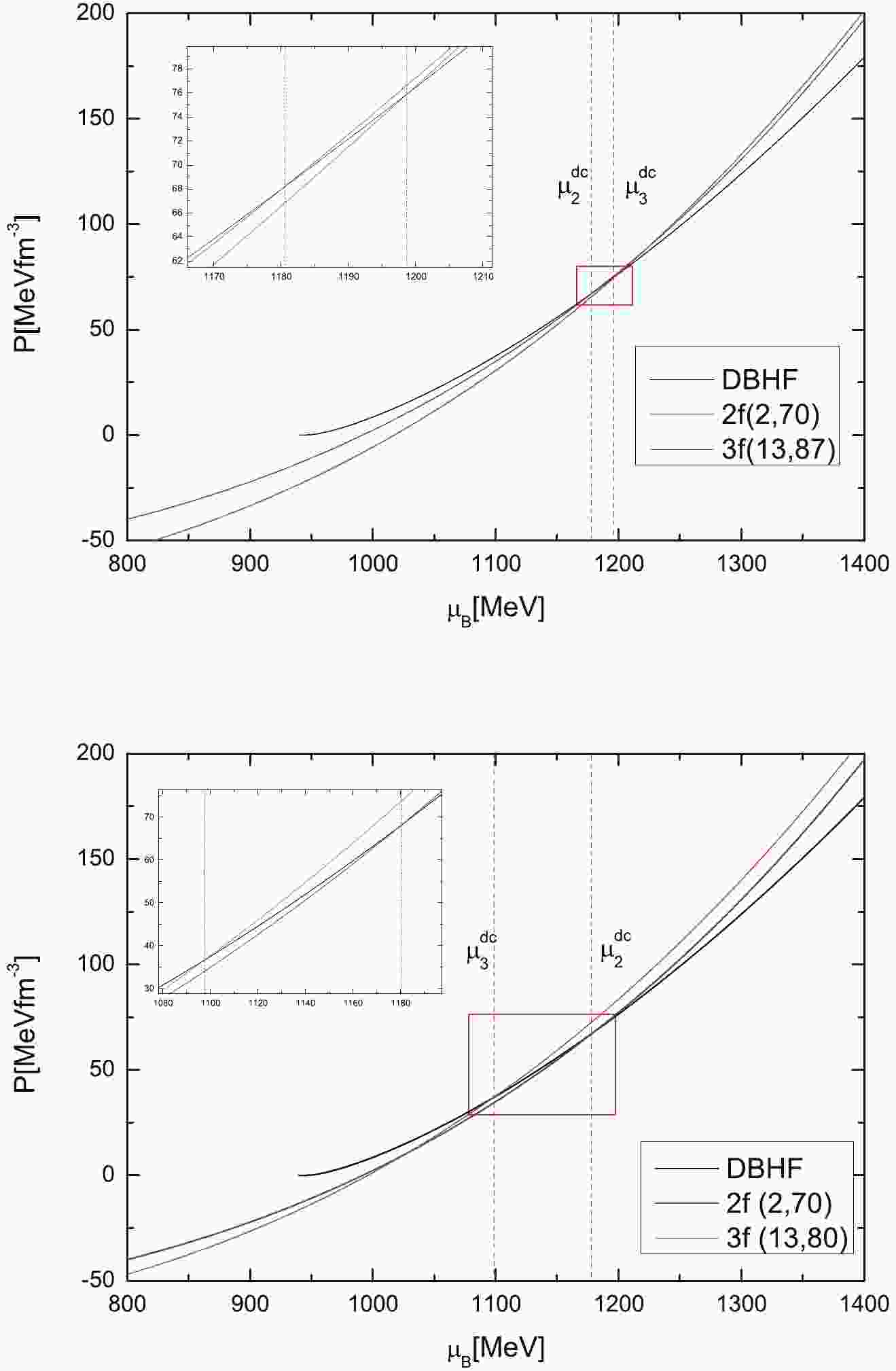
$ \mu^{\rm dc} $ . When$ \mu_2^{\rm dc}<\mu_3^{\rm dc} $ , such as 3f quark matter with$ K_v = 13\;{\rm GeV}^{-2}, \;B_{\rm eff} = 87\;{\rm MeVfm}^{-3} $ , the nuclear matter deconfines to 2f quark matter (top panel). Otherwise, if$ \mu_2^{\rm dc}>\mu_3^{\rm dc} $ , such as 3f quark matter with$ K_v = 13\;{\rm GeV}^{-2},\;B_{\rm eff} = 80\;{\rm MeVfm}^{-3} $ , the nuclear matter directly deconfines to 3f quark matter (bottom panel).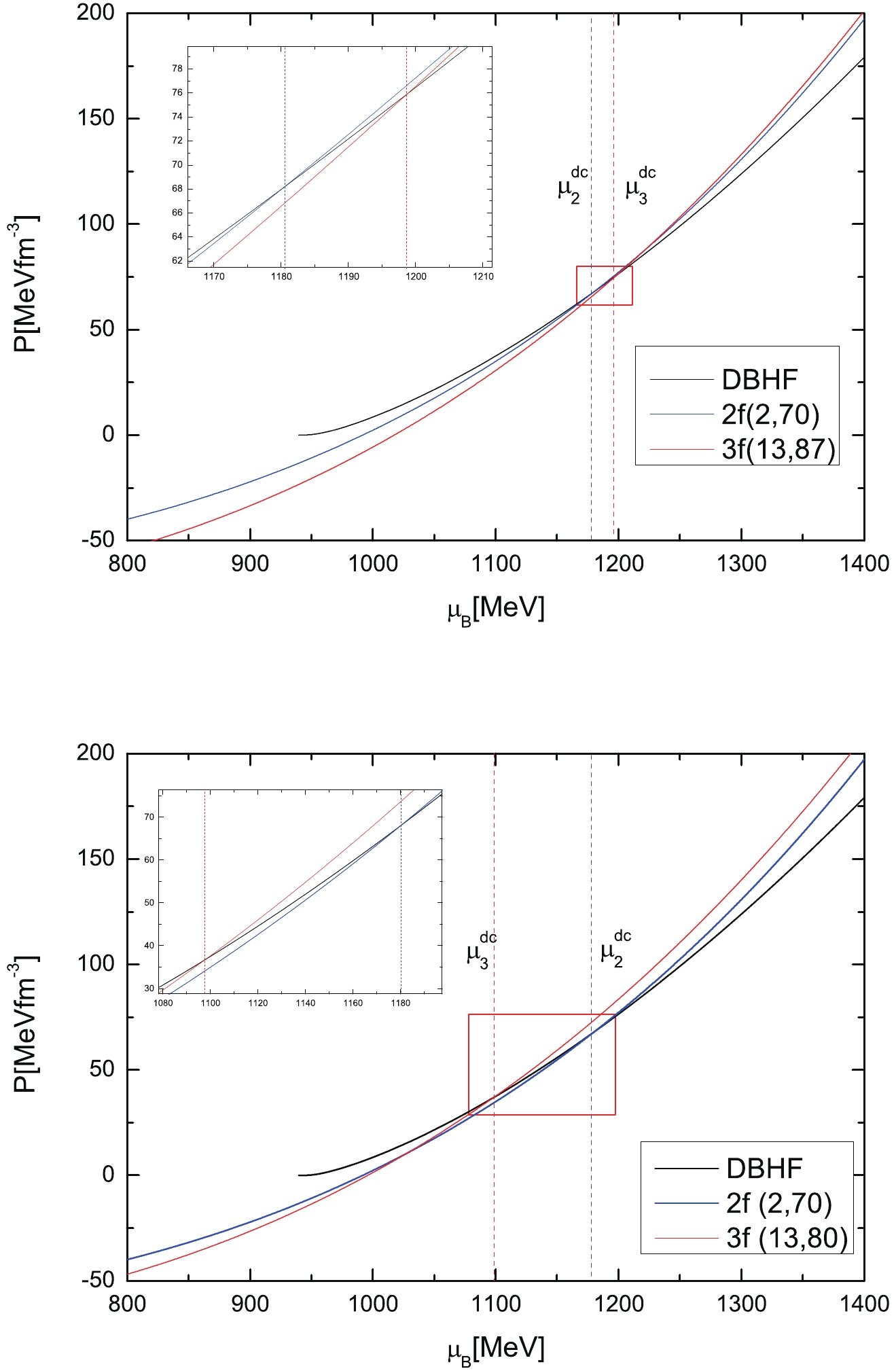
Figure 1. (color online) Phase transition from nuclear to quark matter. The nuclear matter is described using the DBHF model (black line) and the quark matter is described using the vBag model (blue line for 2f quark matter and red line for 3f quark matter). The parameters are shown in the brackets with the units (
$K_v({\rm GeV}^{-2}),\; B_{\rm eff}({\rm MeVfm}^{-3})$ ).Figure 2 shows the EoS relation between the pressure and energy-density of the phase transition from nuclear to 2f quark matter (top panel), and the corresponding M-R relations (bottom panel). Figure 3 shows the transition from nuclear to 3f quark matter. Herein, we use both Maxwell (solid line) and Gibbs (dashed line) constructions. For the transition into 2f quark matter under the Maxwell construction, the onset of quarks is typically reached at
$ n_{\rm trans} = 2.8n_{\rm sat} \;(M_{\rm trans} = 1.612M_\odot) $ , leading to a short stable hybrid branch with$ M_{\rm max} = 1.984M_\odot $ at a central density of$ n_{\rm central} = 5.9n_{\rm sat} $ . For transition into 3f quark matter, the quark matter appears at$ n_{\rm trans} = 2.5n_{\rm sat}\; (M_{\rm trans} = 1.21M_\odot) $ , resulting in a stable hybrid branch with$ M_{\rm max} = 1.964M_\odot $ at a central density of$ n_{\rm central} = 6.65n_{\rm sat} $ . The energy-density jump and transition kink in the M-R curves under the Maxwell construction are smoothed out by the Gibbs construction. In addition, the Gibbs construction advances the onset of the mixed phase to lower the density, whereas it defers the region of the purely quark phase to higher densities. These features are manifested both in the pressure-energy relation and the corresponding M-R curve.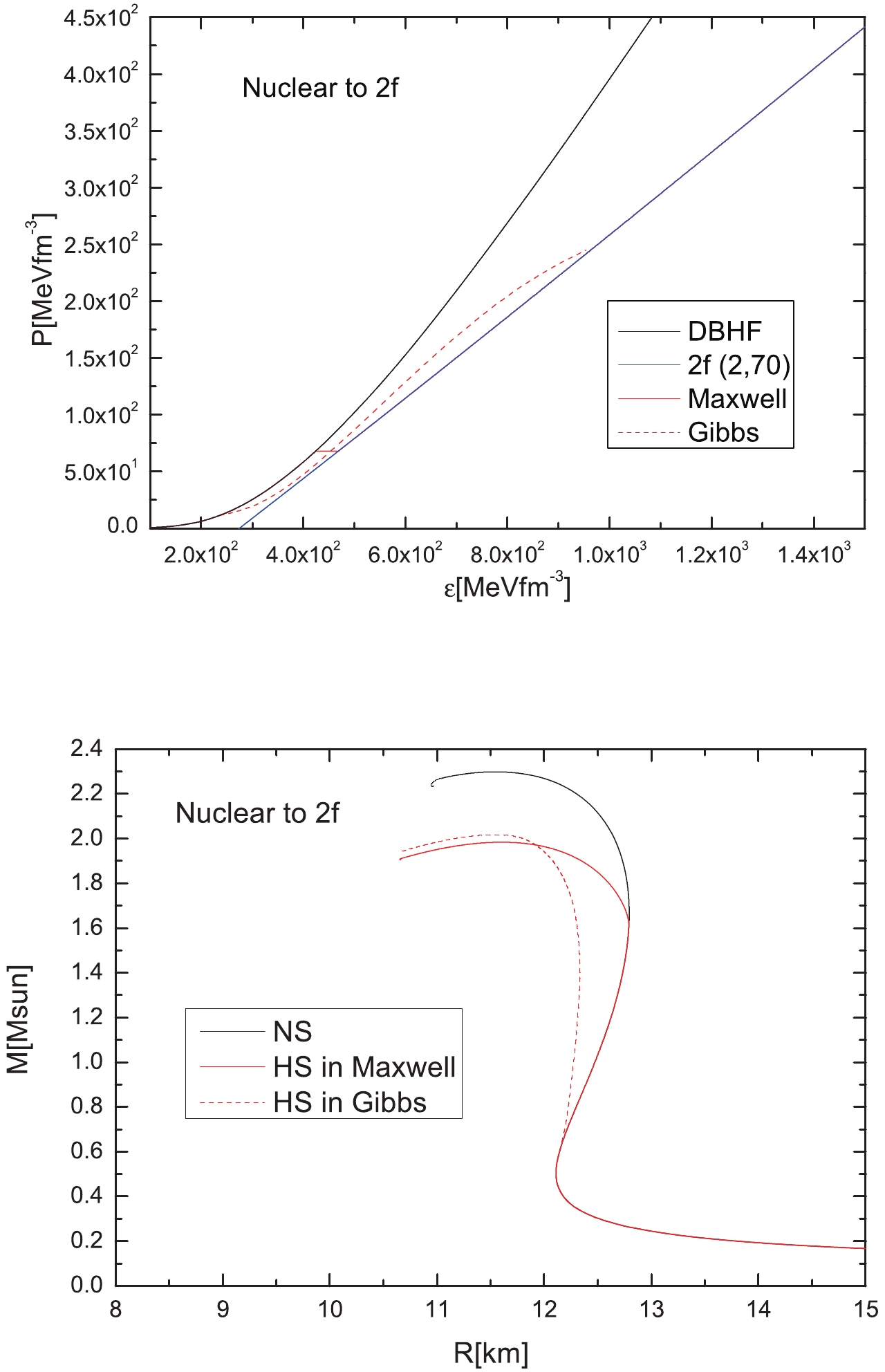
Figure 2. (color online) Equation of state (top) and the corresponding mass-radius relations (bottom) of the phase transition from nuclear to 2f quark matter with the same parameters used in Fig. 1 (top). Both Maxwell and Gibbs constructions are considered.
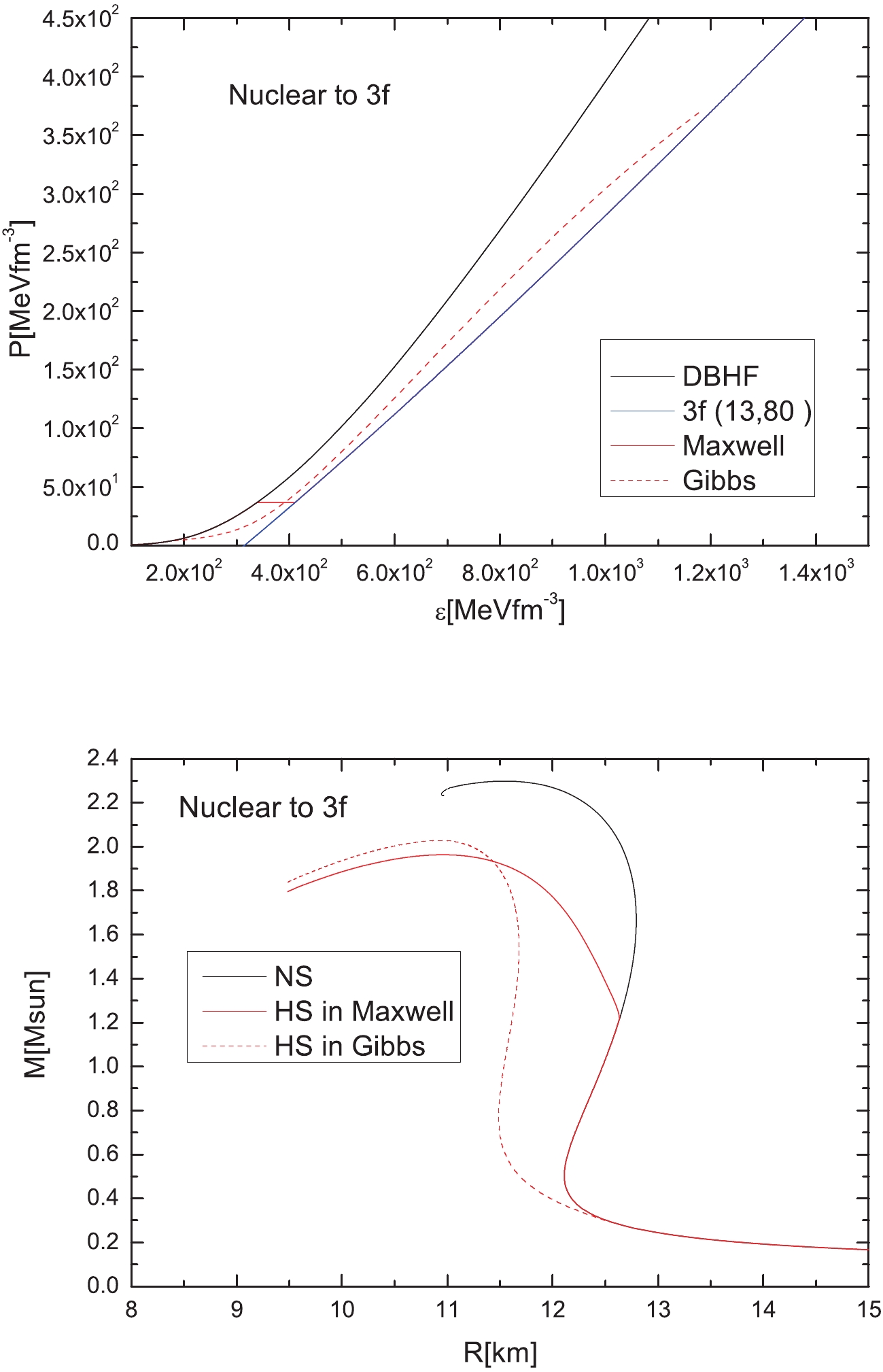
Figure 3. (color online) Equation of state (top) and corresponding mass-radius relations (bottom) of the phase transition from nuclear to 3f quark matter with the same parameters used in Fig. 1 (bottom). Both Maxwell and Gibbs constructions are considered.
In Figs. 4 and 5, we show the pressure profiles of the hybrid stars in Maxwell (top panel) and Gibbs (bottom panel) constructions, all with the maximum mass of the star, that occur for the EoS parameters used in Figs. 2 and 3, respectively. We name the configurations in Fig. 4 as N-2f (Maxwell) and N-2fmix-2f (Gibbs). In addition, the configurations in Fig. 5 are called N-3f (Maxwell) and N-3fmix-3f (Gibbs). For the Maxwell construction (top panel), the pure quark core is covered by the nuclear shell. For the Gibbs construction (bottom panel), the most compact member has a pure quark core and a quark-nuclear mixed outer core surrounded by a nuclear envelope. Most quark matter in the star under a Gibbs construction exist as a mixed phase. When the central density is sufficiently large, the pure quark core appears in the stellar center.
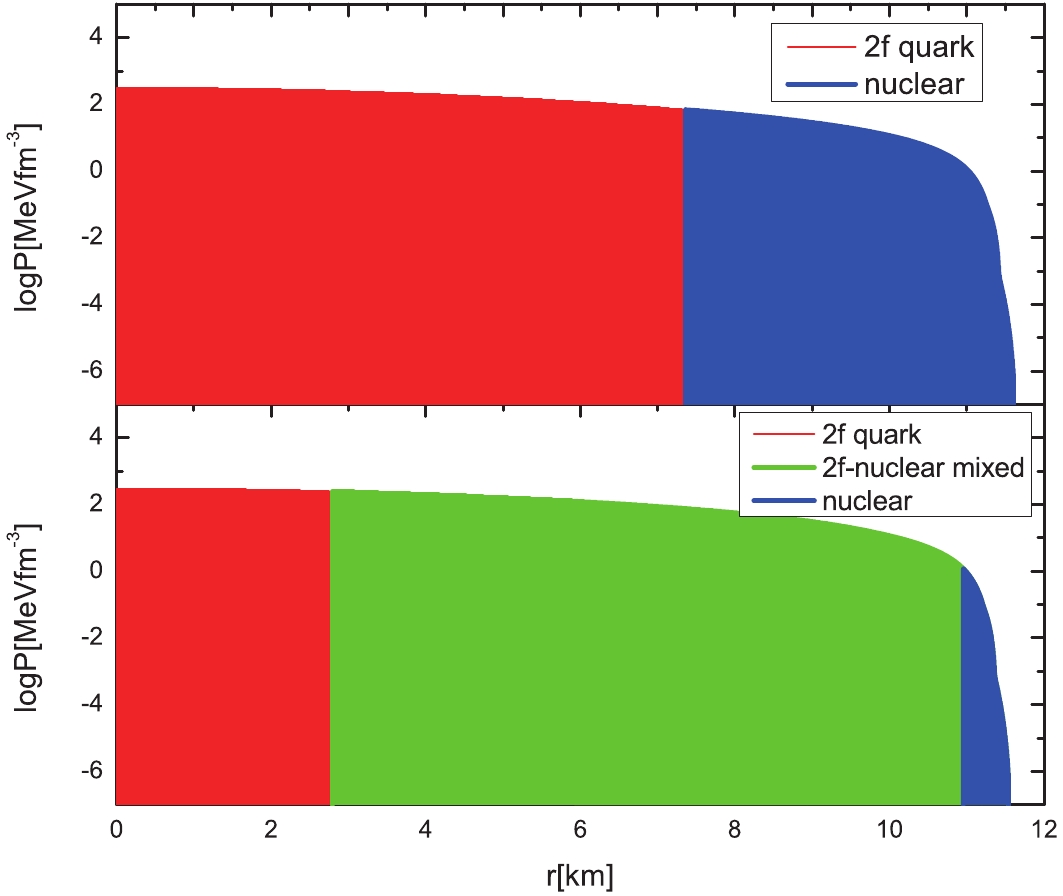
Figure 4. (color online) Pressure profiles of hybrid stars with the maximum mass of the parameters used in Fig. 2. Both Maxwell (top) and Gibbs (bottom) constructions are considered.
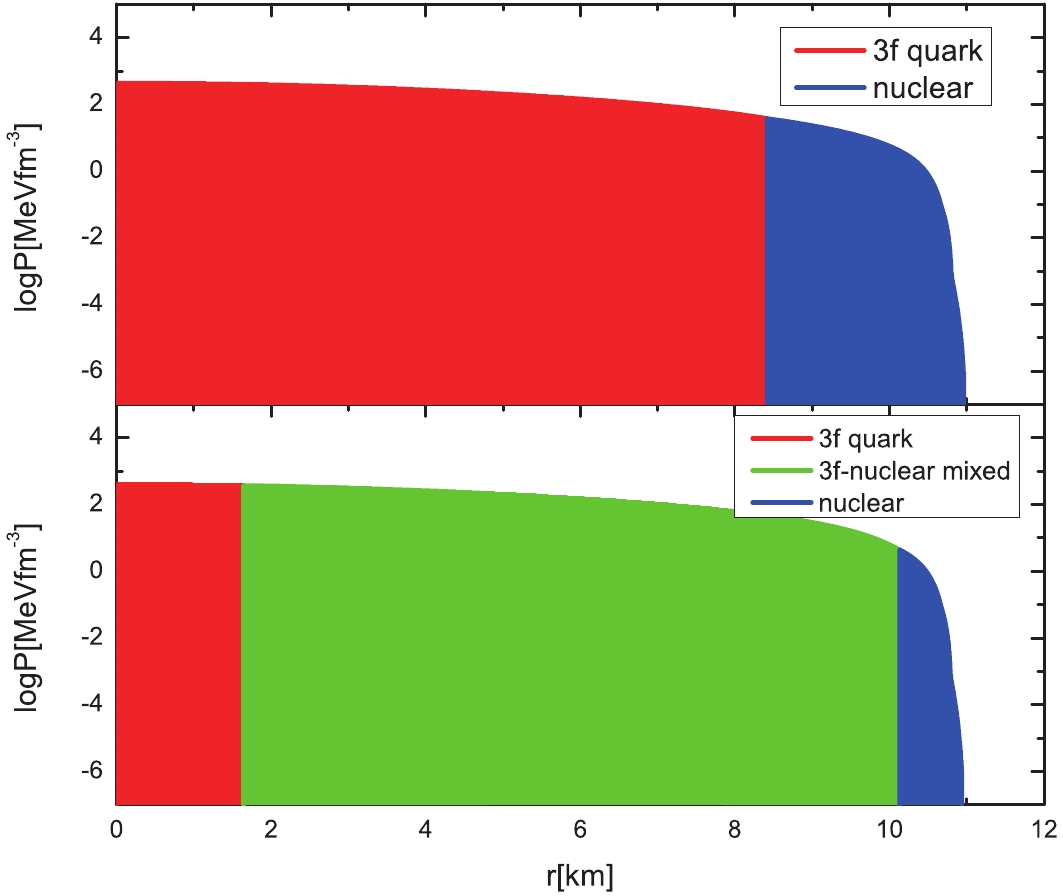
Figure 5. (color online) Pressure profiles of hybrid stars with the maximum mass of the parameters used in Fig. 3. Both Maxwell (top) and Gibbs (bottom) constructions are considered.
-
In the previous cases, we did not assume a sequential appearance of the quark flavors. Because our understanding of the QCD phase diagram has improved over these years, it has become clear that the quark core may contain layers of distinct phases. For a sequential transition, the appearance of a strange quark will always result in a Maxwell-type appearance (owing to a sudden increase in the energy density at a given pressure), regardless of which construction scheme one chooses to model the phase transition. A transition occurs if the pressure of 2f quark matter equals that of 3f quark at an equal baryon chemical potential
$ \mu_{2-3}^{\rm seq} $ .As shown in Fig. 6, when
$ \mu_2^{\rm dc}<\mu_{2-3}^{\rm seq} $ , the nuclear matter deconfines to 2f quark matter first, and 2f quark matter sequentially transforms into 3f. Fig. 7 shows the EoS relation between the pressure and energy-density of the sequential transition (top panel), and the corresponding M-R relations (bottom panel). There are two-fold energy-density jumps in the Maxwell construction. The sequential transition reaches$ n_{\rm trans} = 3.1n_{\rm sat} (M_{\rm trans} = 1.702M_\odot) $ , leading to a short stable hybrid branch with$ M_{\rm max} = 1.971M_\odot $ at a central density of$ n_{\rm central} = 6.3n_{\rm sat} $ , which is within the range of component masses in BNS mergers and obeys the observational lower bound on the maximum mass of a neutron star. Both Maxwell and Gibbs constructions are used. Although the energy-density changes continuously in the Gibbs construction, the curve is clearly bent by the sequential transition from 2f to 3f quark matter. To show the effect of a sequential transition on the M-R relation, we provide the curves of stars only with the transition from nuclear to 2f quark matter for comparison (blue lines in the bottom panel). The sequential transition from 2f to 3f quark matter makes an obvious kink in the M-R curves, but does not dramatically change the mass or radius of the star.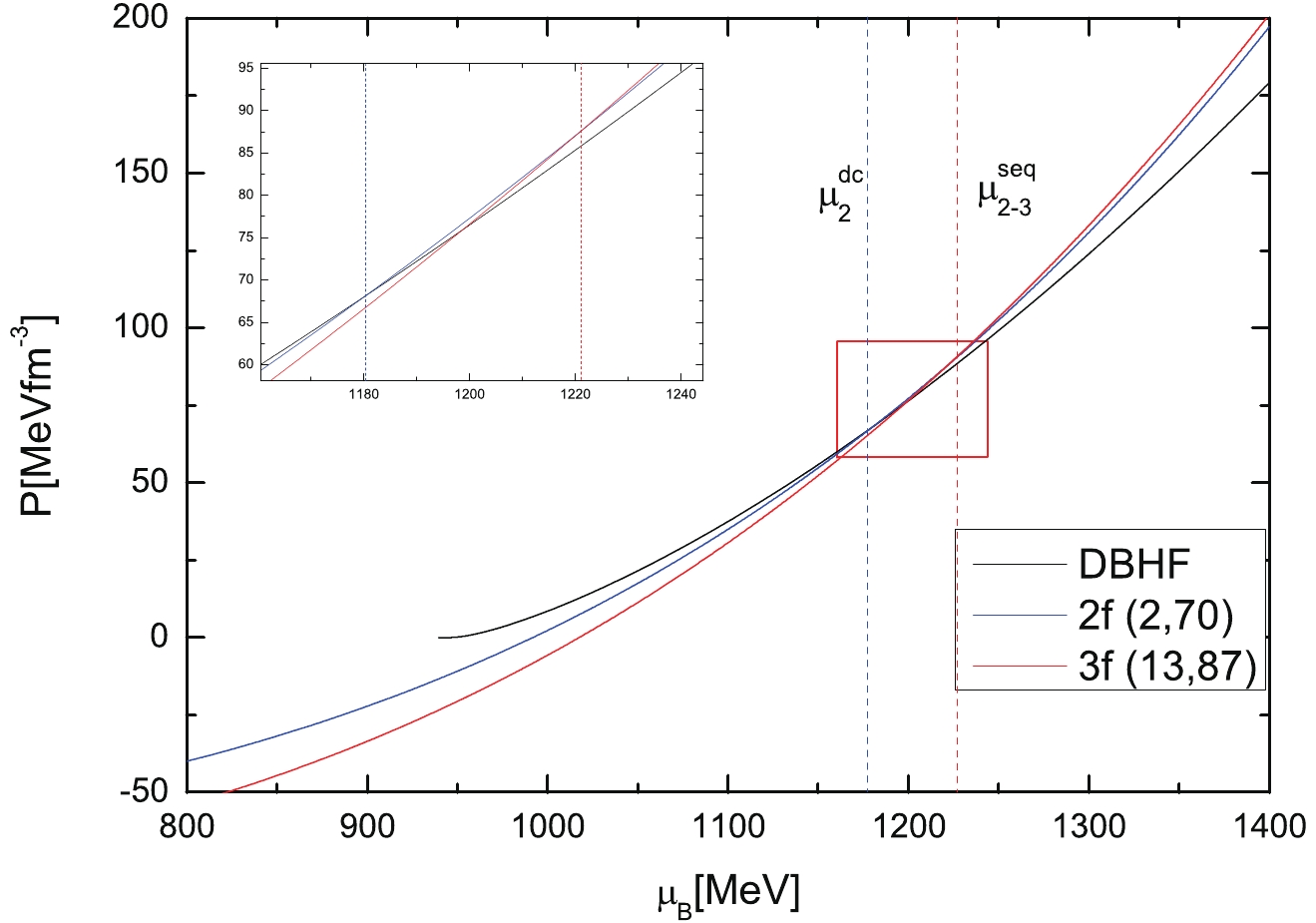
Figure 6. (color online) The sequential phase transition from 2f to 3f quark matter. The first transition is from nuclear to 2f quark matter (at
$\mu_2^{\rm dc}$ ), and from 2f to 3f quark matter sequentially (at$\mu_{2-3}^{\rm seq}$ ). The parameters are shown in the brackets with the units ($K_v({\rm GeV}^{-2}), \;B_{\rm eff}(\rm MeVfm^{-3})$ ).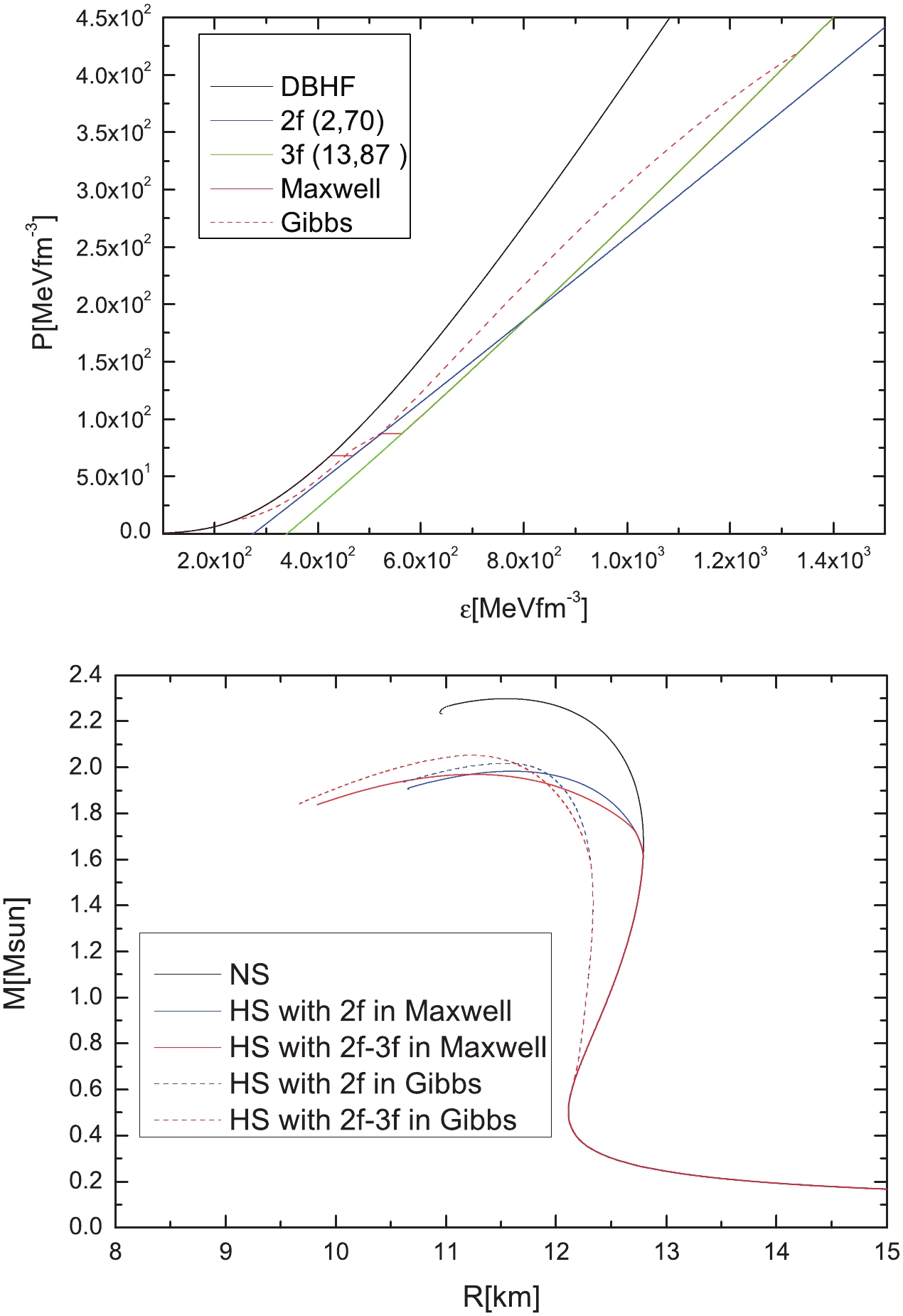
Figure 7. (color online) Equation of state (top) and the corresponding mass-radius relations (bottom) of the sequential phase transition with the same parameters used in Fig. 6. Both Maxwell and Gibbs constructions are considered. The mass-radius relations of the stars with only a phase transition from nuclear to 2f are plotted for comparison.
In Fig. 8, we show the pressure profiles of the hybrid stars with the maximum mass that occurs for the EoS parameters shown in Fig. 6. For the Maxwell construction (top panel), 2f quark matter transforms into 3f quark matter, covered by a nuclear shell, from the center to the surface. For the Gibbs construction (bottom panel), there is no pure quark core at the center, and the 2f-3f-nuclear mixed phase dominates the core of the star, which is surrounded by a nuclear envelope. We call the configurations in Fig. 8 N-2f-3f (Maxwell) and N-2f3fmix (Gibbs).
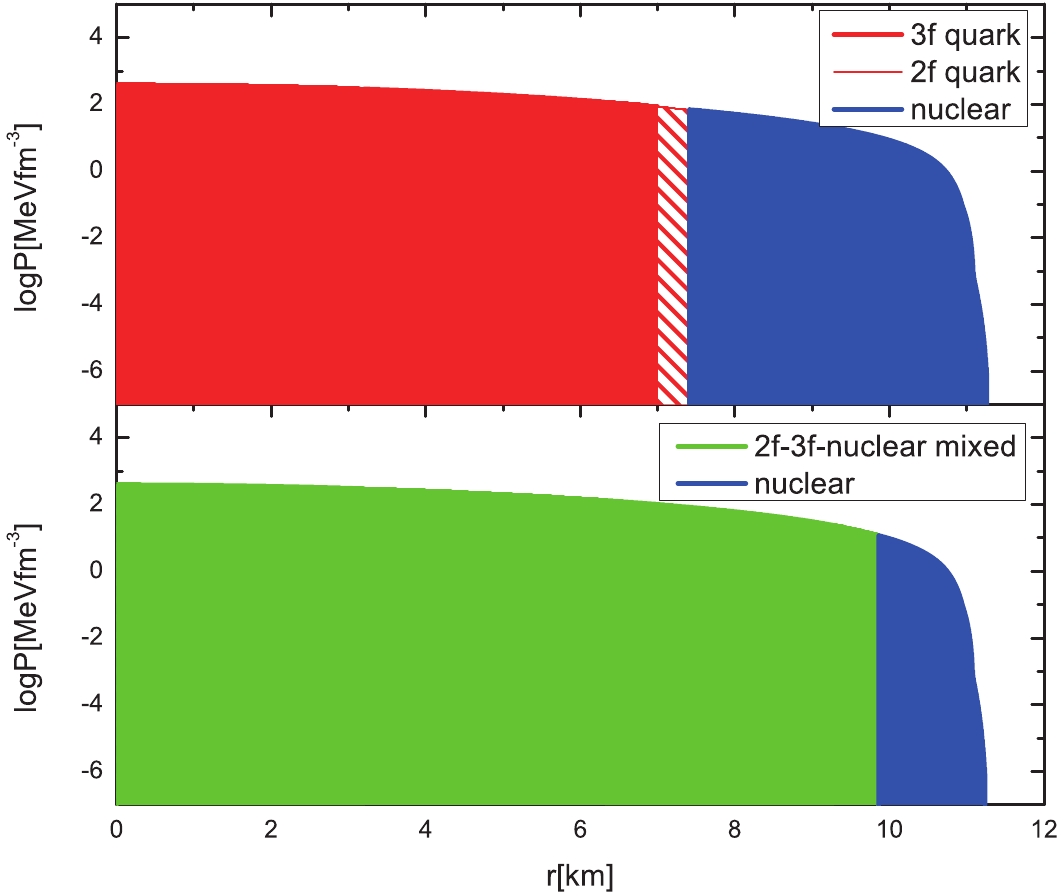
Figure 8. (color online) Pressure profiles of hybrid stars with a sequential phase transition and the maximum mass of the parameters used in Fig. 7. Both Maxwell (top) and Gibbs (bottom) constructions are considered.
In the Gibbs construction, if
$ \mu_{2-3}^{\rm seq} $ is out of the range of the nuclear-2f mixed phase, a 2f-3f-nuclear mixed phase does not appear. For example, the chemical potential range of the 2f-nuclear mixed phase is$ 1013\leqslant \mu_B \leqslant 1460\;{\rm MeV} $ for 2f quark matter$ (K_v = 2\;{\rm GeV}^{-2},\; B_{\rm eff} = 70\;{\rm MeVfm}^{-3}) $ . The sequential transition occurs at$ \mu_{2-3}^{\rm seq} = 1462\;{\rm MeV} $ for 3f quark matter with$ K_v = 13\;{\rm GeV}^{-2}, \; B_{\rm eff} = 91\;{\rm MeVfm}^{-3} $ , which is larger than$ 1460\;{\rm MeV} $ , and thus the sequential phase transition from 2f to 3f does not occur in the nuclear-quark mixed phase. The onset of 3f quark matter occurs at even higher densities above the range of the 2f-nuclear mixed phase, and there is a theoretically pure 2f phase before the pure 3f phase emerges. However, how large the range of the pure 2f phase is depends on the gap between the upper limit of the 2f-nuclear mixed phase and the onset density of the 3f quark phase. As the situation shows in Fig. 9 and Fig. 10, the 2f quark phase is too small to be observed.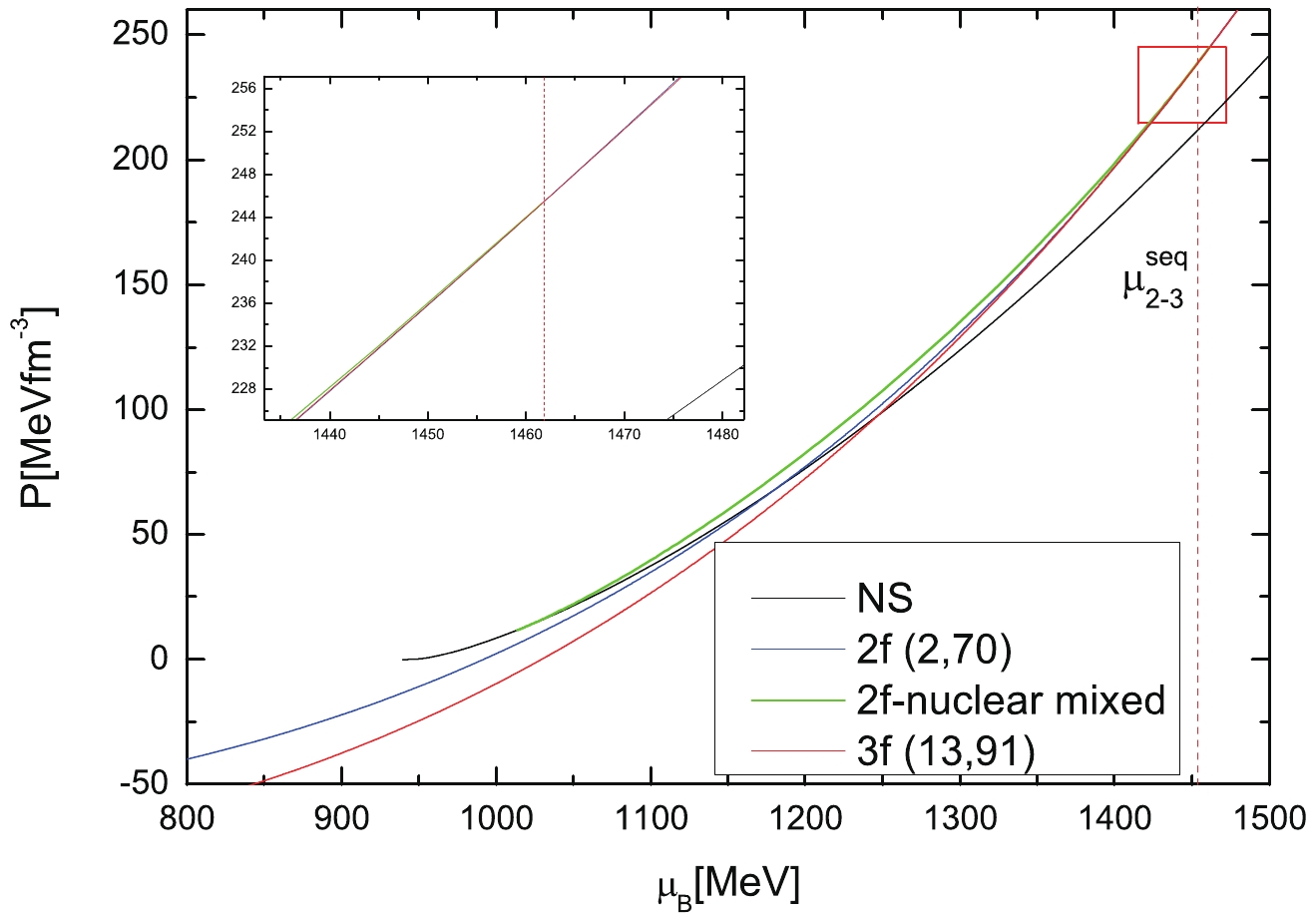
Figure 9. (color online) In the Gibbs construction, the sequential phase transition from 2f to 3f occurs out of the nulcear-2f mixed phase. First, the nuclear matter deconfines to 2f quark matter in the Gibbs construction, and then transforms into 3f sequentially. The parameters are shown in the brackets with the units (
$K_v({\rm GeV}^{-2}), \;B_{\rm eff}(\rm MeVfm^{-3})$ ).
Figure 10. (color online) Equation of state (top) and the corresponding mass-radius relations (bottom) of the sequential phase transition with the same parameters used in Fig. 9. The mass-radius relation of the star with a phase transition from nuclear to 2f only matter in a Gibbs construction is plotted for comparison.
Figure 10 shows the EoS relation between the pressure and energy-density (top panel), as well as the corresponding M-R relations (bottom panel) with the same parameters used in Fig. 9. The energy-density changes continuously in the 2f-nuclear mixed phase, and then jumps to the 3f quark phase during the sequential phase transition (top panel). To show the effect of the sequential transition on the M-R relation, we provide the curve of N-2fmix-2f for comparison (red line on the bottom panel). The sequential transition to 3f quark matter does not change the M-R relation dramatically. We show the pressure profile of the hybrid star with the sequential transition out of the nuclear-2f mixed phase in Fig. 11. There is a 3f pure quark core in the center surrounded by the 2f-nuclear mixed shell because the outside area is the nuclear crust. We call this configuration N-2fmix-3f. Thus, whether the pure quark core is 2f or 3f quark matter depends on the transition path of the matter.
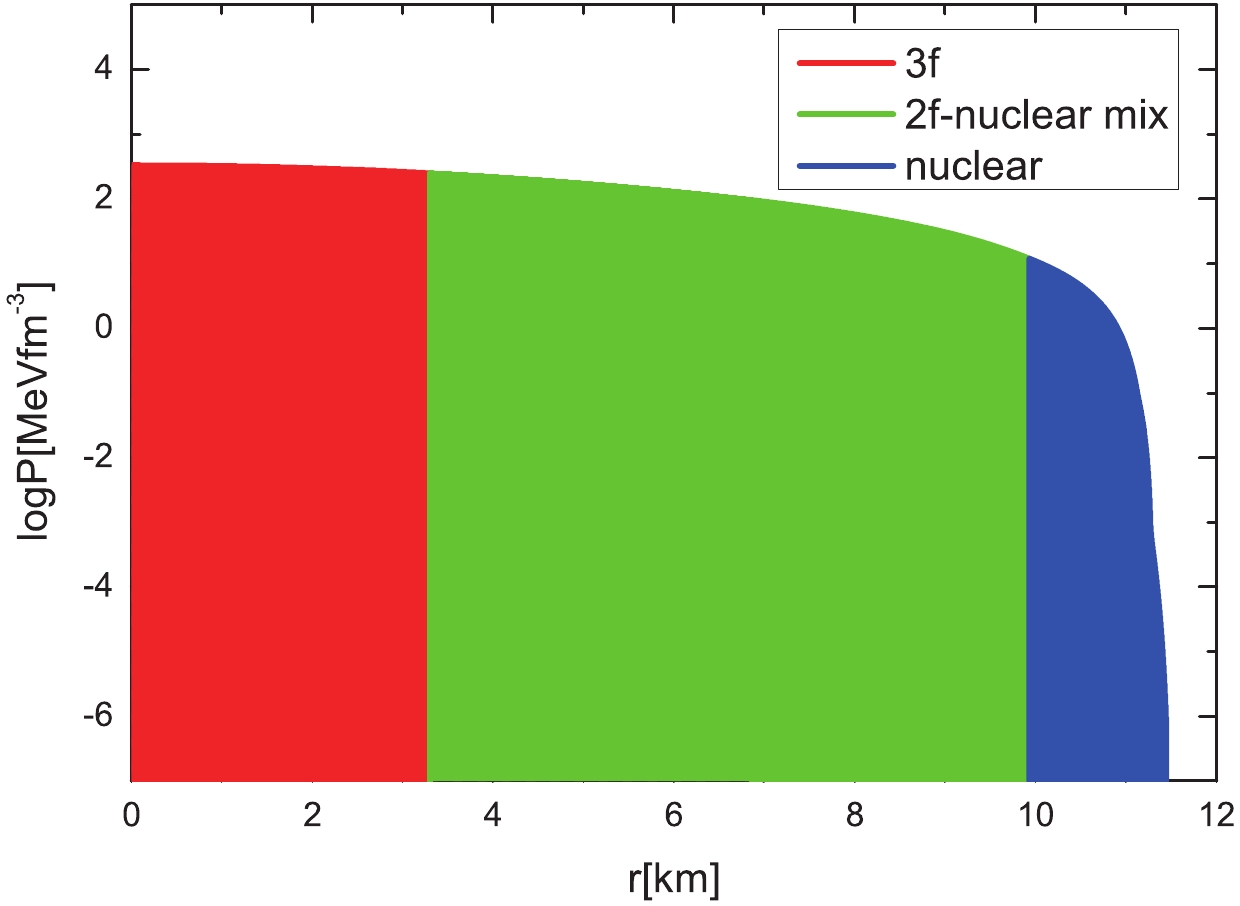
Figure 11. (color online) Pressure profiles of hybrid star with sequential phase transition and the maximum mass of the parameters used in Fig. 10.
-
We studied the possible configurations of neutron stars containing quark matter and provided a general description of the conditions and features of different configurations. We assume that there are two possible phase transition paths: from nuclear phase to 2f quark phase/3f quark phase directly, or first from a nuclear phase to 2f quark phase, and then from that phase to the 3f quark phase sequentially. Using the vBag model to describe the EoS of quark matter and considering two phase transition constructions, i.e., Gibbs and Maxwell, we provide M-R relations of different configurations and discuss their inner pressure profiles. This study focuses on the high-density phase transition, the results of which are applicable to the low-density hadronic part of the EoS when choosing reasonable parameters of the quark matter model.
Choosing a fairly stiff EoS of quark matter with reasonable vBag model parameters, the two possible phase transition paths yield multiple configurations of hybrid stars: N-2f, N-3f, and N-2f-3f for a Maxwell construction, and N-2fmix-2f, N-3fmix-3f, N-2f3fmix, and N-2fmix-3f for a Gibbs construction. Differing from the Maxwell phase transition with a jump in energy-density, the energy changes continuously in the Gibbs transition. In our calculations, we choose parameters with a small energy jump in the Maxwell construction to build stable configurations, although we still noticed that kinks were presented in the M-R relations, which are smoothed out in the Gibbs construction. If the energy jump in the Maxwell phase transition is sufficiently large, the phase transition can induce instabilities, which causes the mass to decrease with the central pressure [46, 47], although the instabilities never appear in the Gibbs construction because of the energy-density continuity.
The appearance of quark matter in a neutron star leads to multi-possibilities of stellar configurations, i.e., a set of stars with the same masses but different central pressures, compositions, and radii. The measurements of neutron star radii in combination with the previously established limit on the maximum mass of neutron stars may provide constraints on the EoS of dense matter, and hints particularly at the presence of quark matter. The M-R relation originated from the weak phase transition is continuous in our models, and hybrid stars are always more massive than neutron stars, which differs from the previously reported twin star scenario [42]. Thus, we compared the radii between an intermediate mass neutron star with
$ 1.4M_\odot $ and different hybrid stars configurations using$ 1.95M_\odot $ for the possible detectable observations, as listed in Table 1. In some configurations, such as N and N-3f (N and N-3fmix-3f), their radii differ by 1km~2km, which is beyond the resolution of the measurements expected from NICER and is potentially detectable. Under certain configurations, however, such as N and N-2f (N and 2fmix-2f), and N-2f and N-3f (N-2fmix-2f and N-3fmix-3f), their radii differ by 0.5km~1km, which is slightly beyond the resolution of the NICER. Furthermore, in other configurations, such as N-2f and N-2f-3f (N-2fmix-2f and N-2f3fmix), and N-2f3fmix and N-2fmix-3f, their radii differ by far smaller than$ 0.5\;{\rm km} $ , which will be difficult to detect by NICER in the near future. From the analysis above, depending solely on the measurements of the stellar radii, it is difficult to probe whether strange quarks in the hybrid star come from the nuclear matter directly or from the 2f quark matter sequentially. Improving the constraints on the various paths of the phase transition will provide motivation for future efforts to make more precise radius measurements.$({{K}}_v,B_{\rm eff})$ 

configurations radii construction $\Lambda_{1.4}$ 

none N 12.727 none 589 (2,70) N-2f 12.112 Maxwell 589 (2,70) N-2fmix-2f 11.9808 Gibbs 443 (13,80) N-3f 11.2941 Maxwell 479 (13,80) N-3fmix-3f 11.3948 Gibbs 307 (13,87) N-2f-3f 11.7352 Maxwell 589 (13,87) N-2f3fmix 11.8652 Gibbs 461 (13,91) N-2fmix-3f 11.9808 Gibbs 443 Table 1. Radii of hybrid stars with
$1.95M_\odot$ in different configurations and neutron star with$1.4M_\odot$ , and the tidal deformability of a star in the Chandrasekhar mass. The parameter pairings in the leftmost column denote the vBag parameters for the quark model. Parameters shown in the brackets are in units of (${\rm GeV}^{-2},\; {\rm MeVfm}^{-3}$ ), the radii values are in units of${\rm km}$ , and$\Lambda_{1.4}$ is dimensionless.Relying only on the possible radii measurements makes it difficult to constrain the EoS of the dense matter in a neutron star. The thermal evolution, oscillation, and spin down, particularly in neutron star mergers, provide astrophysical signatures that can allow us to also infer which forms of matter are present in the interior of the neutron star [48]. In particular, the Advanced LIGO and Advanced VIRGO collaborations observed the BNS merger event GW170817, which opens up a new window into exploring the properties of compact stars. Current bounds for the effective tidal deformability, as reported through the LIGO-VIRGO collaboration [49], have been placed at
$ \widetilde{\Lambda} = 300^{+420}_{-230} $ at a 90% confidence for low-spin priors. Furthermore, the deformability of a star in the Chandrasekhar mass was reported at$ \Lambda_{1.4} $ =$ \Lambda(1.4M_\odot) $ =$ 190^{+390}_{-120} $ under the same conditions. The resulting$ \Lambda_{1.4} $ values presented in Table 1 show that all Gibbs-constructed hybrid models are favored by this tidal constraint. The hybrid model of N-3f under the Maxwell construction is also feasible. The presence of mixed nuclear-quark phases resulting from these types of phase transitions soften the EoS in such a way that these hybrid models are able to adhere to the constraints provided by the multi-messenger observations. However, the neutron star model and the hybrid models of N-2f and N-2f-3f under the Maxwell construction slightly exceed the upper bound of the$ \Lambda_{1.4} $ constraint. With the Maxwell-constructed phase transition from nuclear to 2f quark matter occurring at a relatively higher mass, it becomes extremely apparent as to why these hybrid models fail the$ \Lambda_{1.4} $ constraint. Choosing the parameters of 2f quark matter with larger values of$ B_{\rm eff} $ , N-2f, and N-2f-3f in Maxwell may also agree with the observation constraints. Remarkably, given a particular parameter model, it can still be difficult to determine the nuances of a given configuration using$ \Lambda $ , specifically focusing on the values provided by GW170817. It has been suggested [50-52] that mapping out the radial or non-radial oscillation mode frequencies can provide a clear distinction between neutron and hybrid stars. If non-radial oscillations resonantly excited by tidal forces during an inspiral [53] can be detected either directly by third-generation detectors [54] or indirectly through gravitational wave phasing [55] it could help resolve the masquerade problem. The appearance of strange quarks may influence the non-radial oscillations spectrum of the star and make an imprint in the observations of gravitational waves, providing a new way to probe the quark matter in neutron stars.The independent analyses of the NICER pulse waveform data on PSR J0030+0451 conducted by Miller et al. [56] and Riley et al. [57] are the first to provide a precise and reliable measurement of the mass and radius of a neutron star. The radius and mass estimates given by their analysis are
$ R_e = 13.02^{+1.24}_{-1.06} km $ and$ M = 1.44^{+0.15}_{-0.14}M_\odot $ (68%). These measurements of$ R_e $ and M for PSR J0030+0451 improve the astrophysical constraints on the EoS of dense matter above the nuclear saturation density. Comparing the observations of PSR J0030+0451 with our neutron star model with the EoS of DBHF, the theoretical mass and radius results are in good accord with the observations. For the different hybrid star configurations, most configurations we calculated agree with the observations of PSR J0030+0451 except for N-3f in the Maxwell construction and N-3fmix-3f in the Gibbs construction. These two hybrid star configurations originated from the phase transition from nuclear matter into the three types of flavor quark matter directly, and the evident softening of the EoS causes a dramatic decrease in the radius. Nevertheless, these two configurations cannot be excluded by the observations completely. Choosing parameters of the three flavor quark matter with a larger value of$ K_v $ , these configurations of the N-3f in Maxwell and N-3fmix-3f in Gibbs may also explain the observations.A millisecond pulsar J0740+6620 with mass
$ 2.14_{-0.09}^{+0.10}M_\odot $ (68.3% credibility interval) was recently reported [58], which may hence replace the previously reported heaviest PSR J0348+0432 with mass$ 2.01\pm0.04M_\odot $ and set a new record for the maximum mass of a neutron star. For the neutron star described using the EoS of DBHF model, the theoretical maximum mass of the star can reach$ 2.3M_\odot $ , which is supported by the new observations of PSR J0740+6620. If suitable EoS parameters of quark matter with a vBag model are chosen, the maximum mass of the hybrid stars can reach a mass of$ 2.14_{-0.09}^{+0.10}M_\odot $ as well.In a future study, it would be useful to conduct a more extensive and detailed survey of the parameters. Depending on the precise measurements of the mass and radii of neutron stars, the basic parameter constraints on the quark matter model are worth investigating. Imminent advances in observational techniques, in particular, the Advanced LIGO and VIRGO collaborations and the NICER experiment, are expected to provide further insight into the complex structure of neutron stars and more information regarding their quark matter.
We thank Prashanth Jaikumar, Thomas Klähn, and Xia Zhou for their fruitful discussions.
Multiple configurations of neutron stars containing quark matter
- Received Date: 2019-11-20
- Accepted Date: 2020-03-03
- Available Online: 2020-09-01
Abstract: The main purpose of this study is to interpret the possibilities of hybrid star configurations under different phase transition paths and provide a general description of the conditions and features of the different configurations. We assume that there are two possible phase transition paths, i.e., from a nuclear phase to a 2flavor(2f)/3flavor(3f) quark phase directly, or first from a nuclear phase to a 2f quark phase, and then from that phase to a 3f quark phase sequentially. In addition, we consider Maxwell and Gibbs constructions based on the assumption of a first-order transition, which yields multiple configurations of hybrid stars: N-2f, N-3f, and N-2f-3f for a Maxwell construction, and N-2fmix-2f, N-3fmix-3f, N-2f3fmix, and N-2fmix-3f for a Gibbs construction. From the radii analysis of different hybrid star configurations with the same mass of





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF















 DownLoad:
DownLoad: