Emission time sequence of neutrons and protons as probes of α-clustering structure

High-quality monochromatic photon beams provide a unique way to investigate the behavior of hadrons in nuclear medium [1-5], because photons do not experience the strong interaction and can thus provide useful information about nucleon correlation [6-8]. When the photon energy is beyond the giant dipole resonance region, which is typically around 15–40 MeV, and approaches 140 MeV, the size of the nucleus is larger than the wavelength of the photons, which is close to the size of the deuteron. In this energy domain, a quasi-deuteron [QD, a neutron–proton ($np$) pair inside the nucleus] absorption mechanism has been introduced [9], and thus it could provide a unique tool for the study of $np$ correlation. $np$ correlation can be also studied by the two-nucleon knockout reaction in the QD region [10-12].

Meanwhile the $\alpha$-clustering state is a significant nuclear structure phenomenon especially in light nuclei, which can be observed at excited states or even in the ground state. In the evolution of the Universe and nuclear synthesis, $\alpha$ particles are involved in the synthesis of $^{12} {\rm{C}}$ and $^{16} {\rm{O}}$ nuclei, and $\alpha$-clustering structure could emerge inside such nuclei, which is crucial for understanding the abundance of elements [13-19]. For $^{12} {\rm{C}}$ and $^{16} {\rm{O}}$ nuclei in the present study, $\alpha$-clustering structures have been extensively discussed [15]. $^{12} {\rm{C}}$ is of great interest in nuclear astrophysics due to its three-$\alpha$ clustering structure with the Hoyle state [20-29]. $^{16} {\rm{O}}$ has more $\alpha$-clustering configurations, such as 4-$\alpha$-clustering chain [30], tetrahedral [31], kite, and square configurations [32-39]. Of course, many of these configurations are believed to only emerge in excited states. Some probes have been presented to investigate such clustering structures. For instance, giant resonance photons display corresponding characteristic spectra for different configurations [40-44]. Moreover, other collective observables show sensitivity to various $\alpha$-clustering structures during heavy-ion collisions; see e.g. Refs. [45-52]. However, these probes are still limited and more probes should be expected. In this context, herein we use the neutron–proton momentum correlation function, especially from different velocity-gated correlation functions, to investigate the correspondence due to different initial nuclear structures.

In the present work, we applied an extended quantum molecular dynamics (EQMD) model [53] to simulate photonuclear reactions of $^{12} {\rm{C}}$ and $^{16} {\rm{O}}$ in the QD regime and present a new probe of $\alpha$-clustering structure by the velocity-gated neutron–proton momentum correlation function. Using the Lednicky and Lyuboshitz (LL) method [54], a neutron–proton momentum correlation function ($C_{np}$) can be well constructed through the final-state three-body decay channel from photodisintegration reactions, and the emission time sequence of neutrons and protons can be indicated from the ratio of velocity-gated $C_{np}$, to which we found that they are sensitive regardless of whether the nuclear configuration is $\alpha$-clustered.

The rest of the paper is arranged as follows: in Sec. 2, approaches for calculations are introduced, which include brief introductions to the EQMD model, the process of QD absorption, and the LL analytical method for momentum correlation. In Sec. 3, the results and discussion are presented. It contains a model reliability check by the missing energy and recoil momentum, $np$ emission time difference, $np$ momentum correlation function for different $\alpha$-clustering structures of $^{12} {\rm{C}}$ and $^{16} {\rm{O}}$, and the deduced source sizes with 100 MeV incident photons. Furthermore, the emission time sequence of neutrons and protons is deduced from the ratio of $np$ correlation functions with different velocity gates between neutrons and protons, which demonstrates the sensitivity to whether the nucleus is $\alpha$-clustered or not. Finally, we summarize the present work in Sec. 4.

The quantum molecular dynamics (QMD) model [55, 56] was very successful in dealing with fragmentation in intermediate-energy heavy-ion collisions [57-59], and the EQMD model is one of the extended versions of the QMD model. In this model, the description of the ground state of the nuclear system has been significantly improved by obtaining the lowest point of energy of the nuclei [53] by the cooling process, which cancels the zero-point energy caused by the wave packet broadening in the standard QMD. Meanwhile, the Pauli potential is phenomenologically considered for treating repulsion between identical nucleons [60]. As a result, the saturation property and $\alpha$-cluster structures can be well obtained after energy cooling in the EQMD model [40, 53]. In contrast to the traditional QMD model [55, 56], the width of each wave packet in the EQMD model is taken as a dynamical variable [61]. Details can be found in the original paper of Maruyama et al. [53]. Using the above model, we can obtain different $\alpha$-clustering structures for $^{12} {\rm{C}}$ and $^{16} {\rm{O}}$ [40], which are taken as target nuclei for photonuclear reactions to perform a detailed study of neutron–proton momentum correlation functions in the present work.

The photon absorption mechanism plays a dominant role, as the incident photons are 70–140 MeV and a QD (a $np$ pair inside a nucleus) photodisintegration reaction is considered in a process according to Levinger's QD model [62]. The impulse approximation method is applied, in which the residue nucleons act as spectators beside the correlated $np$ pair after absorbing incident photon energy, and then the nucleus becomes excited and experiences a transport process to the final state, finally leading to particles' ejection. In this article, the three-body decay channel with n + p+ core is our only focus; other decay channels are not discussed here. The phase space information and emission time of protons and neutrons are taken as the input for our correlation calculations using the LL method, which will be briefly introduced later.

In the calculation, for the targets composed of N-$\alpha$ clusters, we assume that the incoming photons are randomly distributed in the $xy$-plane, and then we choose this event if the incoming photon is inside the region of the QD total cross-section. Obviously, the absorption process will take place in one of the $\alpha$-clusters inside the target by ($\gamma$,$^{4} {\rm{He}}$) for each event. For the process of ($\gamma$,$^{4} {\rm{He}}$), we assume the remaining two nucleons besides the absorbed QD inside this $\alpha$-cluster and other clusters in the nucleus to be spectators, because the spatial separation between the $\alpha$-clusters is much larger than the pair of QDs in the EQMD frame. The kinetic process in our calculation is that the photon energy transfers to a chosen $np$ pair, and its process is replaced by the reaction of $^{2} {\rm{H}}$($\gamma$, $np$). Whether the process occurs or not depends on the total cross-section of $^{2} {\rm{H}}$($\gamma$, $np$) in each event by Monte Carlo sampling. Details can be found in Ref. [11]. After the initial part of the process of $(\gamma,$ np $)$ has been completed, the nucleons can be emitted from the excited nucleus through final-state interactions (FSI).

Before demonstrating our results, we provide a brief description of the momentum correlation calculation using the LL method [54]. Momentum correlation is also known as the Hanbury Brown and Twiss (HBT) method [63], which has been extensively applied to studies of heavy-ion collision dynamics [64-70]. The LL method can treat particle–particle correlation functions at small relative momenta that are controlled by particles' quantum-statistical symmetry effects as well as final-state interactions [71, 72]. Through the square of the symmetrized Bethe–Salpeter amplitude averaged over the emission particles' four coordinates and the total spin of the two-particle system, the correlation function can then be obtained. In addition, the FSI of the particle pairs is assumed to be independent in the production process. The particle–particle correlation function can be written as

where ${ r}^*$ (= ${ x}_{1}-{ x}_{2}$) and ${ k}^*$ are the relative distance and half of the relative momentum of two particles at kinetic freeze-out, respectively.

In this work, we present the calculation of neutron–proton correlation functions for photodisintegration from different initial geometric configurations of $^{12} {\rm{C}}$ and $^{16} {\rm{O}}$, which are obtained by a cooling process in the EQMD model. Considering the possible ground-state configurations, with the exception of the non-clustering Woods–Saxon (WS) spherical structure, a triangular three-$\alpha$ structure for $^{12} {\rm{C}}$ and tetrahedral four-$\alpha$ structure for $^{16} {\rm{O}}$ are the most possible. Of course, from a systematic calculation viewpoint, the chain three-$\alpha$ structure for $^{12} {\rm{C}}$ and the chain, kite, and square four-$\alpha$ structures for $^{16} {\rm{O}}$ can also be available in our model. Even though it is very unlikely for the above $\alpha$-clustering structures as candidates to be ground-state configurations, we can still make a complete comparison for observables among all possible configurations in the present calculation. The root-mean-square (RMS) radii and binding energies for different initial nuclei are listed in the first and second columns of Table 1 and Table 2 for $^{12} {\rm{C}}$ and $^{16} {\rm{O}}$, respectively. It is seen that the chain structure, which is extremely deformed, has the largest RMS radius, while the RMS radius and binding energy for the $^{12} {\rm{C}}$ triangular or $^{16} {\rm{O}}$ tetrahedral structure are not significantly different from those of the spherical WS distributed nuclei, as all these configurations are spatially symmetric. In addition, for $^{16} {\rm{O}}$, the RMS radius of the kite structure is larger than that of the square structure. For the binding energies, they display an overall contrasting trend between different initial configurations in comparison with the RMS radius cases, which illustrates that a higher binding energy makes the nucleus more compact.

configuration	$r_{\rm RMS}$/fm	($E_{\rm bind}/A$)/MeV	$\langle \Delta t_{np} \rangle$/(fm/c)	$| \Delta t_{np} |$/(fm/c)	$R_{pp}$/fm	$B.R._{pp}$	$R_{np}$/fm	$B.R._{np}$
chain	2.71	7.17	1.90	10.13	1.85	0.45%	1.60	92.7%
triangle	2.35	7.12	1.84	10.85	1.55	0.75%	1.35	90.5%
sphere	2.23	7.60	0.14	11.32	1.25	5.05%	1.25	52.0%
exp. data	2.4702(22)	7.68

Table 1.  RMS radius ($r_{\rm RMS}$) of the initial configuration, binding energy per nucleon ($E_{\rm bind}/A$) of the initial configuration, average emission time difference between neutrons and protons ($\langle \Delta t_{np} \rangle$) and absolute emission time difference between neutrons and protons ($|\Delta t_{np}|$) from three-body photodisintegration, HBT radius ($R_{pp}$) extracted from the proton–proton momentum correlation function with 100 MeV photon energy for different $^{12} {\rm{C}}$ configurations [73], two-proton emission branching ratios ($B.R._{2p}$), HBT radius ($R_{np}$) extracted from the neutron–proton momentum correlation function with 100 MeV photon energy for different $^{12} {\rm{C}}$ configurations, and neutron–proton emission branching ratios ($B.R._{np}$). The experimental data for RMS radius and $E_{\rm bind}/A$ are also shown for the $^{12} {\rm{C}}$ ground state.

configuration	$r_{\rm RMS}$/fm	($E_{\rm bind}/A$)/MeV	$\langle \Delta t_{np} \rangle$/(fm/c)	$| \Delta t_{np} |$/(fm/c)	$R_{pp}$/fm	$B.R._{pp}$	$R_{np}$/fm	$B.R._{np}$
chain	3.78	7.26	2.21	11.85	2.40	0.40%	1.80	89.9%
kite	3.25	7.22	2.01	12.16	1.75	0.70%	1.60	90.0%
square	2.91	7.29	2.22	12.94	1.60	0.85%	1.55	89.5%
tetrahedron	2.76	7.79	2.32	13.10	1.50	1.30%	1.40	89.9%
sphere	2.60	8.15	0.58	11.23	1.40	5.13%	1.45	60.7%
exp. data	2.6991(52)	7.976

Table 2.  As in Table 1 but for $^{16} {\rm{O}}$ configurations.

In the whole photonuclear reaction simulation in the QD region, there are many different photodisintegration channels, such as two-body, three-body, and four-body channels, and even more channels with very low production probabilities. For three-body channels, we have $^{12} {\rm{C}}$($\gamma$, np)$^{10} {\rm{B}}$, $^{12} {\rm{C}}$($\gamma$, pp)$^{10} {\rm{Be}}$, and $^{12} {\rm{C}}$($\gamma$, nn)$^{10} {\rm{C}}$ for $^{12} {\rm{C}}$, and $^{16} {\rm{O}}$($\gamma$, np)$^{14} {\rm{N}}$, $^{16} {\rm{O}}$($\gamma$, pp)$^{14} {\rm{C}}$, $^{16} {\rm{O}}$($\gamma$, nn)$^{14} {\rm{O}}$ for $^{16} {\rm{O}}$. Out of all the above three-body channels, the $np$ channel dominates. In Tables 1 and 2, we list the branching ratios of the three-body $np$ ($B.R._{np}$) and $pp$ ($B.R._{pp}$) channels from our EQMD calculations. For $^{12} {\rm{C}}$, the $B.R._{np}$ is 92.7%, 90.5%, and 52.0% for the chain, triangle, and sphere configurations, respectively. These are significantly larger than the 0.45%, 0.75%, and 5.05% $B.R._{pp}$ for the same $^{12} {\rm{C}}$ configurations. For $^{16} {\rm{O}}$, the $B.R._{np}$ is 89.9%, 90.0%, 89.5%, 89.9%, and 60.7% for the chain, kite, square, tetrahedron, and sphere configurations, respectively. These are significantly larger than the 0.40%, 0.70%, 0.85%, 1.30%, and 5.13% $B.R._{pp}$ for the same $^{16} {\rm{O}}$ configurations. In comparison with the non-clustering spherical configuration, the $np$ emission channel probabilities are larger for $\alpha$-clustering structures, which is originated from a favorable QD break-up on the $\alpha$-clustering nucleus. As mentioned before, in this work we only focus on the three-body channel in the final state with core + n + p, which is a dominant photodisintegration process. The final-state phase space information of the emitted nucleons is taken as the inputs of the LL model to construct the neutron–proton momentum correlation function.

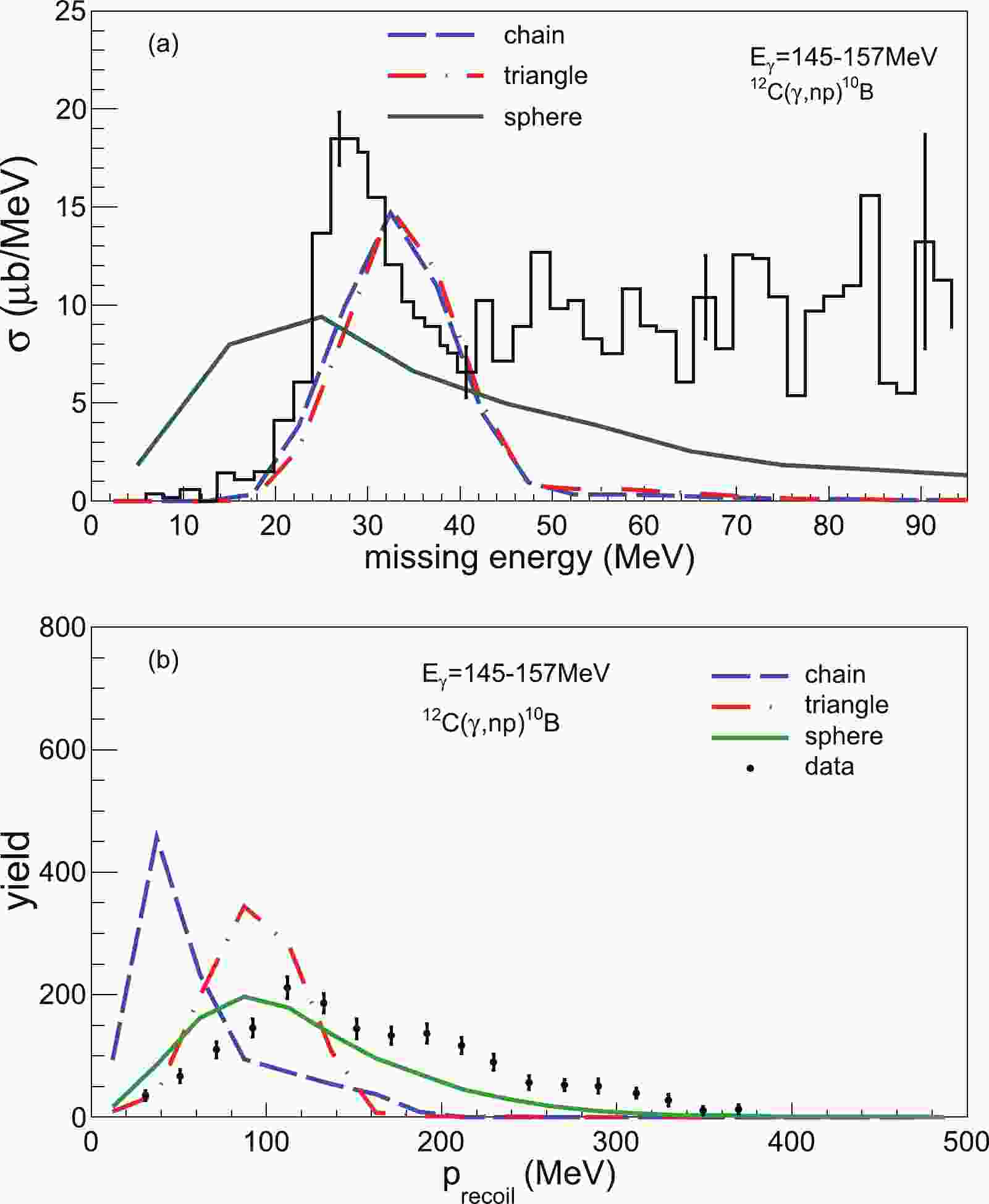
For such a three-body channel, quantitative comparison with the available experimental data is useful to verify the model's reliability. Here, the missing energy spectrum (Fig. 1(a)) and recoil momentum spectrum of $^{12} {\rm{C}}$($\gamma$, $np$)$^{10} {\rm{B}}$ at E$_\gamma$ = 145–157 MeV under the missing energy (Emiss) cut less than 40 MeV (Fig. 1(b)) are presented for comparison. By using the distribution of bremsstrahlung with a weight of 1/$E_{\gamma}$, we can obtain the recoil momentum $\vec{p}_{\rm recoil} = \vec{p}_{\gamma} - \vec{p}_{n} - \vec{p}_{p}$ event by event, where $\vec{p}_{\gamma}$ is the momentum of incident photons, and $\vec{p}_{n}$ and $\vec{p}_{p}$ are the momentum of emitted protons and neutrons, respectively. $E_{\rm miss}$ can be calculated by $E_{\gamma} - T_{n} - T_{p} - T_{\rm recoil}$, where $T_{n}$, $T_{p}$ and $T_{\rm recoil}$ are defined as the kinetic energy of a neutron, a proton, and the recoiled core, respectively. $T_{\rm recoil}$ was obtained from the recoil momentum. To compare with the experimental data directly, we scale the count to nearly the altitude of the data. From fits to the data, both the chain and triangular three-$\alpha$-clustering structures give similar missing energy distribution with a slightly higher peak position than the experimental main peak, whereas the spherical structure gives a broad $E_{\rm miss}$ distribution with a lower peak position. For the $P_{\rm recoil}$ distribution, the chain configuration gives the wrong peak position, while the triangular and spherical structures have similar peak positions close to that of the experimental data. Combined with the above $E_{\rm miss}$ and $P_{\rm recoil}$ observables, the triangular $\alpha$-clustering structure appears to have an overall good agreement with the data, which indicates that it is a very possible ground-state configuration for $^{12} {\rm{C}}$.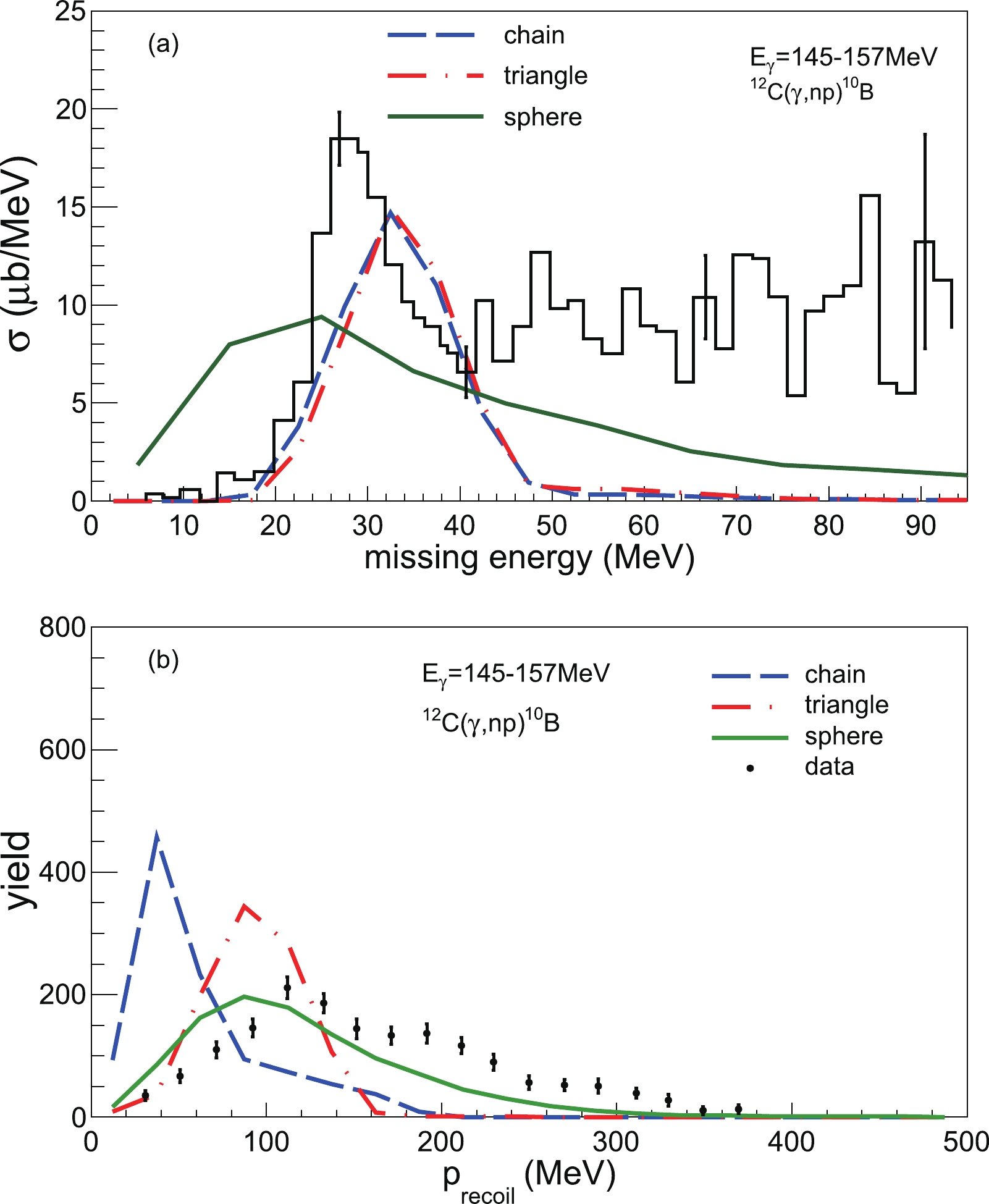

Figure 1.  (color online) Comparison of experimental spectra of missing energy (a) and recoil momentum (b) with our model calculations for $^{12}$C($\gamma,np)$ at E$_\gamma$ = 145–157 MeV. Here, the same cut of $E_{\rm miss}$ $<$40 MeV as the data [8] is applied for the calculated $P_{\rm recoil}$. Different initial geometric configurations of $^{12}$C are indicated in the insert.

After the above reliability check of the model, we could further investigate other observables, such as the emission time, correlation function, and emission time sequence of neutrons and protons, and attempt to find a sensitive probe for $\alpha$-clustering structures, which is the main aim of the present work. As an example, we choose 100 MeV photon-induced three-body disintegration from $^{12} {\rm{C}}$ and $^{16} {\rm{O}}$ targets in the following calculations.

The difference between emission times of neutrons and protons is important for constructing the theoretical HBT correlation, especially in a few-body system. The emission time starts from the beginning of photoabsorption. When a deuteron-like pair inside the target undergo photon absorption, they obtain additional kinetic energy and then interact with other nucleons. By using a method of coalescence at each time step, the process can be roughly described as that where the remaining target nucleons remain an entire core after a proton and a neutron are emitted. The emitted proton and neutron can be tracked and the emission time can be obtained, and then the current emission time and phase space information can be used as the inputs for the calculation of correlation functions.

Figures 2(a) and (b) show the difference in emission time between neutrons and protons for different initial $^{12} {\rm{C}}$ and $^{16} {\rm{O}}$ configurations, respectively. We can see from Fig. 2(a) that the chain structure with the blue dashed line has a sharp peak, while the triangular structure shows a slightly broader distribution, but both have a higher tail in contrast with the spherical one, which is almost symmetrical in shape. The quantitative time differences ($\langle \Delta t_{np} \rangle$ = $\langle t_n - t_p\rangle$) are listed in Table 1. From the chain, triangular, and spherical structures, $\Delta t_{np}$ corresponds to 1.90, 1.84, and 0.14 fm/c, respectively, which indicates that on average a proton is emitted earlier than a neutron for the photodisintegration from the $\alpha$-clustering structures, but the sphere case has roughly the same emission time sequence between the neutron and proton. Here, $\langle \Delta t_{np} \rangle$ is the average over events in which the proton is faster than the neutron (i.e., $\langle \Delta t_{np} \rangle> 0$) and events in which the proton is slower than the neutron (i.e., $\langle \Delta t_{np} \rangle< 0$). A positive value of $\langle \Delta t_{np} \rangle$ indicates that the proton is preferentially emitted earlier than the neutron on average. In addition, another quantity is the absolute value $|\Delta t_{np}|$, which is also listed in Table 1. This value indicates that on average there is around 10–11 fm/c time difference between the proton and neutron for $^{12} {\rm{C}}$ photodisintegration without considering which is faster or slower, i.e., there are about half of the events in which the proton is preferentially emitted around 10–11 fm/c earlier than neutron, and about another half of the events in which the neutron is preferentially emitted around 10–11 fm/c earlier than the proton.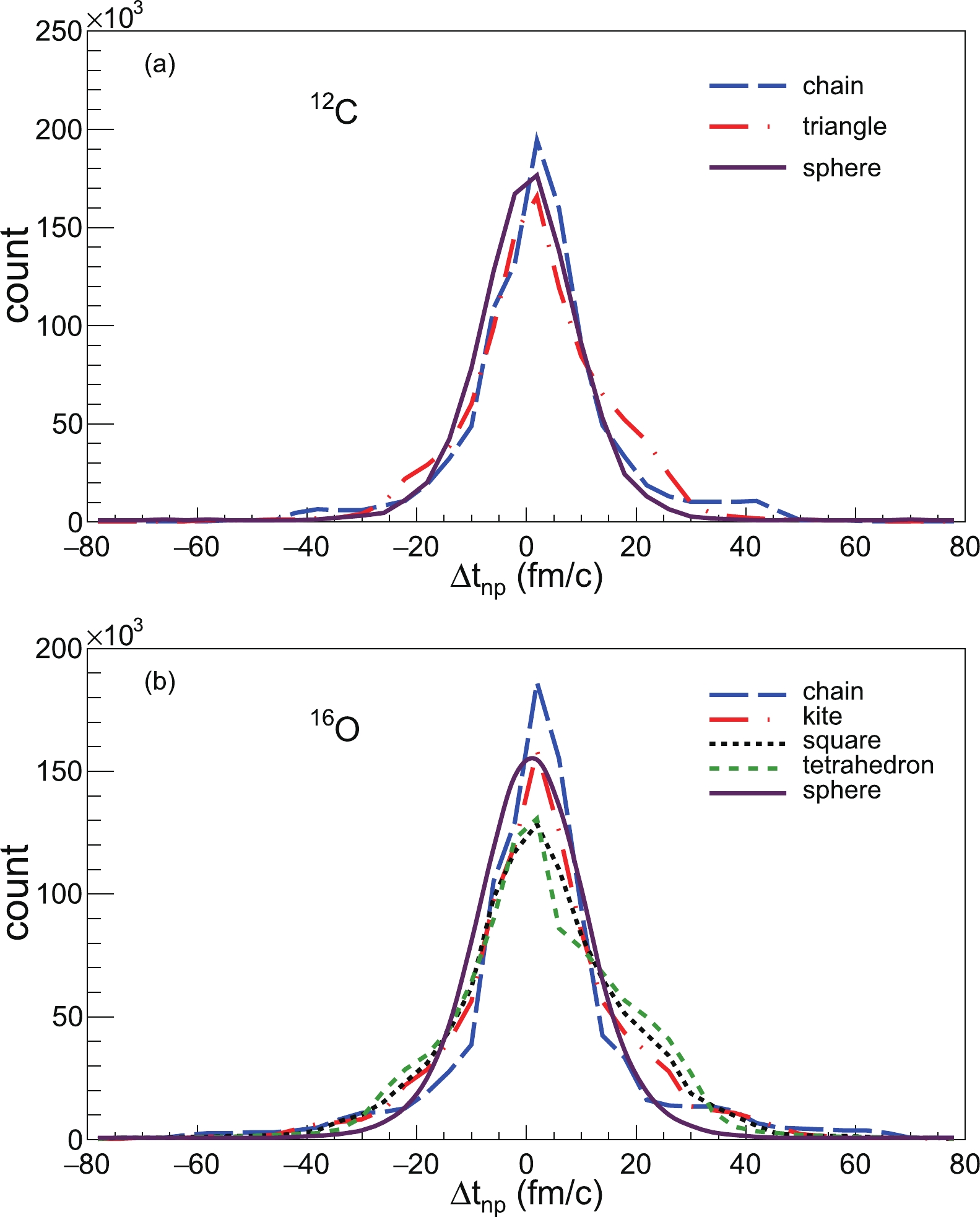

Figure 2.  (color online) Difference in emission time between neutrons and protons for $^{12} {\rm{C}}$ (a) and $^{16} {\rm{O}}$ (b) with different initial geometric configurations at $E_\gamma$ = 100 MeV.

Similarly, Fig. 2(b) shows the $^{16} {\rm{O}}$ cases with four different $\alpha$-clustering configurations together with the spherical case, in which a similar situation to $^{12} {\rm{C}}$ is observed. We see the sharpest peak is given by the chain structure, other $\alpha$-clustering structures are in between, and the most symmetrical shape is again from the spherical structure. If we check the values of $\langle \Delta t_{np} \rangle$ as listed in Table. 2, they are 2.21, 2.01, 2.22, 2.32, and 0.58 fm/c for the chain, kite, square, tetrahedral, and spherical structures, respectively. Therefore, roughly speaking, all $\alpha$-clustering configurations cause protons to be preferentially emitted earlier, but the spherical structure has the same emission time sequence between protons and neutrons. The $|\Delta t_{np}|$ values for each configuration are around 11–13 fm/c, which is the average time difference between protons and neutrons for $^{16} {\rm{O}}$ cases without considering whether either the proton or neutron is faster or slower.

From the above discussion, it seems clear that all $\alpha$-clustering structures favor earlier proton emission on average but the non-clustering spherical structure does not. However, we should keep in mind that the above emission time sequence and time difference are just taken from the calculation and are not available directly from the experimental measurement. A possible way to access such information experimentally is using the velocity-gated $np$ momentum correlation function. In the following parts, we will focus on this.

The neutron–proton momentum correlation function can be constructed with the LL model as mentioned above and is presented in Figs. 3(a) and (b) for the photodisintegration channels of $^{12} {\rm{C}}$($\gamma$, np)$^{10} {\rm{B}}$ and $^{16} {\rm{O}}$($\gamma$, np)$^{14} {\rm{N}}$, respectively. Unlike the proton–proton correlation function, there is no Coulomb dip at low relative momentum for the neutron–proton correlation function. The order of the correlation strength at a certain small $\delta q$, e.g., at 5 MeV/c, follows an increasing trend from the chain, triangular to spherical structure for $^{12} {\rm{C}}$, while it has a similar increasing trend from the chain, kite, square, to tetrahedral or spherical structure for $^{16} {\rm{O}}$. The explanation of Fig. 3 can be mainly attributed to the sizes of different $\alpha$-clustering configurations, which will be quantitatively extracted in the following text. Because the chain structure has the largest RMS size, it is then obvious that the correlation function for the chain structure is the weakest. The triangular structure of $^{12} {\rm{C}}$ and tetrahedral structure of $^{16} {\rm{O}}$ have relatively stronger correlation strength that is closer to the spherical case, which indicates that the emission sources are compact and close to the spherical case.

Figure 3.  (color online) $np$ momentum correlation functions constructed from three-body decay of $^{12}{\rm{C}}$ (a) and $^{16}{\rm{O}}$ (b) at $E_\gamma$ = 100 MeV. Different initial geometric structures are indicated in the inset.

From the above momentum correlation strength, we saw significant differences between various configurations, and interpretation with respect to the source size has been mentioned. To support the above viewpoint, the emission source size was quantitatively determined from the correlation function. As usual, a Gaussian source is assumed for the quantitative estimate of source size from the fits to the HBT correlation results. To do this, the emission time difference between neutrons and protons is considered. The space–time-dependent Gaussian emission source is written as $\exp\left(-\dfrac{r^{2}}{2r^{2}_{0}} - \dfrac{t}{t_{0}}\right)$, where $t_{0}$ is the emission lifetime of the second nucleon under the assumption that the first nucleon is emitted at t = 0. $t_{0}$ can be given by fitting between t and $t^{'}$, where t is the distribution of emission times of the second nucleon and $t^{'}$ is sampled from an expression of $\exp\left(-\dfrac{t^{'}}{t_{0}}\right)$. Through the fit to the $np$ correlation functions, the best-fitted source size can be extracted by looking for a minimum of $\chi^{2}$.

The $\chi^{2}$ fits to the $np$ correlation functions of different configured $^{12} {\rm{C}}$ (a) and $^{16} {\rm{O}}$ (b) are displayed in Fig. 4. The locations of minimum $\chi^{2}$ illustrate that the largest source size among the different $\alpha$-clustering structures is from the chain structure, and the minimum source size is from the triangular structure. The kite and square structures are in the middle for $^{16} {\rm{O}}$. In contrast with the clustering structures, the source size for the spherical configuration is the most compact. The order of $R_{np}$ with different configurations is consistent with the initial RMS radii ($r_{\rm RMS}$) as shown in Tables 1 and 2, from which we note that the bigger the space occupancy, the larger the emission source size.

Figure 4.  (color online) $\chi^2$ fits to $C_{np}$ of Fig. 3. The minimum points represent the best-fitted values of the deduced source sizes, which are listed in Tables 1 and 2 as $R_{np}$.

In Tables 1 and 2, we also show the HBT radius $R_{pp}$, which was recently extracted from the proton–proton correlation function in the same photonuclear reaction [73]. From a quantitative point of view, $R_{pp}$ shows a slightly larger value in comparison with $R_{np}$ for $\alpha$-clustering configurations. The reason for this is that the neutron–proton pair comes from the same $\alpha$-cluster, whereas the proton–proton pair does not. However, the most important point is that the order of source size $R_{pp}$ versus configurations is exactly the same as that of $R_{np}$.

In contrast with the identical particle correlation, the velocity-gated correlation functions for non-identical particles can give the emission chronology information of the particles [74-78]. As we are treating neutrons and protons, the emission time sequence can be deduced from the velocity-gated momentum correlation functions.

Figure 5 shows the ratio between $C_n$ and $C_p$ for different configurations of $^{12} {\rm{C}}$ and $^{16} {\rm{O}}$, where the correlation function $C_{n}$ represents $C_{np}$ gated on the velocity cuts with $v_{n}$$>$$v_{p}$, i.e., the velocity of an emitted neutron is faster than that of a proton, whereas $C_{p}$ represents $C_{np}$ under the cut of $v_{n}$$<$$v_{p}$, i.e., an emitted neutron is slower than an emitted proton. The ratio is defined by comparing the above velocity-gated correlation functions, i.e., $C_n/C_p$. By investigating $C_n/C_p$, we can obtain the emission time sequence in nuclear collisions by a basic ideal as follows: if one particle has lower velocity and is emitted earlier, it will travel a shorter distance before another particle is emitted, and vice versa.

Figure 5.  (color online) Ratio of correlation functions between $C_{n}$ and $C_{p}$ where $C_{n}$ represents $C_{np}$ gated with $v_{n}$$>$$v_{p}$ and $C_{p}$ represents $C_{np}$ gated with $v_{n}$$<$$v_{p}$ for 100 MeV induced three-body photodisintegration of $^{12} {\rm{C}}$ (a) and $^{16} {\rm{O}}$ (b). Different initial geometric configurations are indicated in the insert.

If a proton is on average emitted earlier than a neutron, the ratio $C_{n}/C_{p}$ will show a dip in the region of stronger correlation, otherwise there is a corresponding peak [74]. Interestingly, dips in $\Delta q$ $\approx$ 20 MeV/c, which is the region of $np$ strong interaction, are observed for all $\alpha$-clustering configurations of $^{12} {\rm{C}}$ and $^{16} {\rm{O}}$. This means that a proton is emitted earlier than a neutron on average for photodisintegration from $\alpha$-clustering nuclei, which is consistent with the scenario depicted in Fig. 2, i.e., $\Delta_{np}>0$. For different $\alpha$-clustering configurations, we observe that the triangle case has a slightly deeper and narrower dip than the chain case for $^{12} {\rm{C}}$, which is consistent with a slightly larger $\Delta t_{np}$ value for the chain structure. In great contrast to the $\alpha$-clustering cases, $C_{n}/C_{p}$ for the spherical structure is almost flat, which indicates nearly the same emission sequence for protons and neutrons on average, which is consistent with the negligible $\Delta t_{np}$ values in Table 1.

For $^{16} {\rm{O}}$ cases, the width and depth of $C_{n}/C_{p}$ for the tetrahedron and square cases are almost the same, and both are deeper than the chain and kite cases, which indicates that in all $\alpha$-clustering cases the emitted proton is on average faster than the emitted neutron, and the proton is slightly faster for the square and tetrahedron cases in contrast with the chain and kite cases, which is also represented by the largest values of $\Delta t_{np}$. For the spherical case, an almost flat $C_{n}/C_{p}$ distribution reflects that neither protons nor neutrons have priority emission order, which is consistent with the smallest $\Delta t_{np}$ value listed in Table 2.

Based on the above $C_{n}/C_{p}$ as a function of $\Delta$q and deduced emission time sequence, we found that the $\alpha$-clustering structures, regardless of the ground-state or excited-state configuration candidates of $^{12} {\rm{C}}$ and $^{16} {\rm{O}}$, could be well distinguished from the non-clustering spherical WS structure. This is a very interesting and important conclusion. From an experimental point of view, such measurement is feasible in the near future. Therefore, it is proposed that the velocity-gated $np$ correlation function can be taken as a good probe of $\alpha$-clustering structures. The reason for the above-mentioned different $np$ emission time sequences between the $\alpha$-clustering structures and the non-clustering spherical WS structure might be understood by the stronger Coulomb repulsion for protons inside $\alpha$-clusters than those inside spherical non-clustered nuclei, which causes the former protons to accelerate easily.

The process of QD photoabsorption around 100 MeV photon energy is investigated in the framework of an EQMD model, and $np$ momentum correlation functions are investigated from three-body photodisintegration channels of $^{12} {\rm{C}}$ and $^{16} {\rm{O}}$ systems that are considered by different $\alpha$-clustering structures or non-clustering WS structures. The $np$ momentum correlation function and deduced source size show dependence on the initial structures to some extent. However, a more interesting finding is that the ratio of the $np$ correlation functions gated by $v_{n}$$>$$v_{p}$ and $v_n$$<$$v_p$ reveal the sensitivity to $\alpha$-clustering structures, i.e., broad dips around $\Delta q \simeq$ 20 MeV/c are demonstrated for all $\alpha$-clustering structures but not for spherical WS nucleon distributions. This indicates that the neutron is on average emitted later than the proton in photodisintegration from $\alpha$-clustering nuclei, but neither the proton nor neutron has priority in the average emission time sequence for a non-clustering spherical structure. This is an interesting probe for $\alpha$-clustering structures regardless of ground-state or excited-state $\alpha$-clustering candidates of $^{12} {\rm{C}}$ and $^{16} {\rm{O}}$ from the present systematic calculation. Even though no experimental data are available for such a three-body photodisintegration channel so far, it is expected to perform such photonuclear reactions in near-future photon factories, and then velocity-gated $np$ momentum correlation functions can be measured, which will shed light on nuclear clustering structure information.

The present EQMD model might be further improved by introducing high-momentum tails of neutrons and protons stemming from short-range correlation (SRC) [79], which then may lead to observable effects on the momentum correlations of $np$, $nn$, and $pp$ pairs. Careful comparisons of different nucleon–nucleon pairs with and without SRC, especially from different $\alpha$-clustering structures, could highlight information of SRC specifically for $\alpha$-conjugate nuclei.