-
It is believed that the high energy heavy-ion collisions at both the Relativistic Heavy Ion Collider (RHIC) and the Large Hadron Collider (LHC) have produced a new type of matter, named quark gluon plasma (QGP) [1-3]. One of the key characteristics of QGP is jet quenching: when high energy partons go through the thermal medium, they will interact with the medium and lose their energy via collisional and radiative processes. This phenomenon is usually characterized by the jet quenching parameter
$ \hat{q} $ , defined as the averaged transverse momentum broadening squared per unit mean free path [4, 5]. For the study of$ \hat{q} $ in perturbative QCD, see [6, 7]. However, numerous experiments indicate that QGP is a strongly coupled medium. Thus, it is of interest to study the jet quenching in strongly coupled settings.AdS/CFT [8-10], a conjectured duality between a type IIB string theory in
$ AdS_5\times S^5 $ and$ {\cal{N}} = 4 $ Super Yang-Mills (SYM) in (3+1)-dimensions, provides a powerful tool to describe strongly coupled gauge theories. Over the past two decades, this duality has yielded many important insights for studying various aspects of QGP (see [11, 12] for recent reviews with many phenomenological applications). Using AdS/CFT, H. Liu et al., proposed a nonpeturbative definition of$ \hat q $ , based on the computation of light-like adjoint Wilson loops, and then, applied it to calculate the jet quenching parameter for$ {\cal{N}} = 4 $ SYM plasma at finite temperature [13, 14]. Since, this idea has been extended to various holographic models. For instance, the finite 't Hooft coupling corrections on$ \hat{q} $ are studied in [15-18]. The effect of the chemical potential on$ \hat{q} $ is discussed in [19, 20]. The effect of the electric or magnetic field on$ \hat{q} $ was reported in [21-23]. Further, this quantity has been investigated in some nonconformal settings [24-26]. Other interesting results can be found in [27-35].In this study, we reexamine the jet quenching parameter in a soft wall AdS/QCD model, motivated by the soft wall model of [36]. In particular, we adopt the SW
$ _{T,\mu} $ model by P. Colangelo et al. [37], which was applied to investigate the free energy of a heavy quark-antiquark pair and the QCD phase diagram. This model provides a good phenomenological description of the quark-antiquark interaction. Moreover, the resulting deconfinement line in the$ \mu - T $ plane (with$ \mu $ as the chemical potential and T as the temperature) is similar to that obtained by the lattice and effective models of QCD. Subsequently, the authors of Ref. [38] studied the imaginary part of the heavy quark potential in the SW$ _{T,\mu} $ model and found that the inclusion of nonconformality reduces the quarkonia dissociation, in contrast to the effect of the chemical potential. More recently, the drag force [39] has been discussed in the same model, and the results show that the presence of nonconformality and chemical potential enhance it. For further studies of models of this type, see [40-44]. Drawing inspiration from these findings, we study the jet quenching parameter in the SW$ _{T,\mu} $ model. Specifically, we strive to understand how nonconformality and chemical potential modify this parameter. Further, we compare our results with those of [39] and determine whether nonconformality and chemical potential have the same effect on the energy loss of heavy quarks (related to the drag force) as with light quarks (associated with the jet quenching parameter). This summarizes the purpose of the present work.The paper is organized as follows. In section 2, we briefly review the SW
$ _{T,\mu} $ model given in [37]. In section 3, we analyze the effect of the chemical potential and nonconformality on the jet quenching parameter for this model. The last section presents the summary and discussion. -
The SW
$ _{T,\mu} $ model is defined by the AdS-Reissner Nordstrom black-hole (AdS-RN) multiplied by a warp factor, given by [37]$ {\rm d}s^2 = \frac{r^2h(r)}{R^2}(-f{\rm d}t^2+{\rm d}\vec{x}^2)+\frac{R^2h(r)}{r^2f}{\rm d}r^2, $

(1) with
$ f = 1-(1+Q^2)\left(\frac{r_h}{r}\right)^4+Q^2\left(\frac{r_h}{r}\right)^6,\qquad h(r) = {\rm e}^{\frac{c^2R^4}{r^2}}, $

(2) where R is the radius of AdS. Q represents the black hole charge, constrained in
$ 0\leqslant Q\leqslant\sqrt{2} $ . r denotes the fifth coordinate with$ r = \infty $ as the boundary and$ r = r_h $ the event horizon. The$ h(r) $ term, characterizing the soft wall model, distorts the background metric and yields the mass scale c (or nonconformality), where c is also called the deformation parameter. Note that here, we will not focus on a specific model with fixed c, but rather study the behavior of$ \hat{q} $ in a class of models parametrized by c. Therefore, we make c dimensionless by normalizing it to fixed T and set$ 0\leqslant c/T\leqslant 2.5 $ , which is believed to be most relevant for a comparison with QCD [45].Moreover, the chemical potential reads
$ \mu = \frac{\sqrt{3}Qr_h}{R^2}. $

(3) The temperature reads
$ T = \frac{r_h}{\pi R^2}\left(1-\frac{Q^2}{2}\right). $

(4) -
Now, we follow the argument in [13] to investigate the behavior of the jet quenching parameter for the background metric (1). In the gravity dual description,
$ \hat{q} $ can be computed from light-like adjoint Wilson loops. Specifically, one considers a null-like rectangular Wilson loop C formed by a quark-antiquark pair with separation L travelling along light-cone time duration$ L_- $ . Under the dipole approximation, which is valid for small L and$ LT<<1 $ ,$ \hat{q} $ can be extracted from the Wilson loop expectation value,$ <W^A[{\cal{C}}]> \approx \exp \left[-\frac{1}{4\sqrt{2}}\hat{q}L_-L^2\right], $

(5) where superscript A represents the adjoint representation.
Using the formulas
$ <W^A[{\cal{C}}]>\approx <W^F[{\cal{C}}]>^2 $ and$ <W^F[{\cal{C}}]>\approx\exp[-S_I] $ , one gets$ \hat{q} = 8\sqrt{2}\frac{S_I}{L_-L^2}, $

(6) with
$ S_I = S-S_0 $ , where S is the total energy of the quark anti-quark pair.$ S_0 $ denotes the inertial mass of two single quarks.$ S_I $ represents the regulated finite on-shell string worldsheet action.To carry out the calculation, one needs to rotate the coordinate to light-cone, e.g.,
$ {\rm d}t = \frac{{\rm d}x^++{\rm d}x^-}{\sqrt{2}},\qquad {\rm d}x_1 = \frac{{\rm d}x^+-{\rm d}x^-}{\sqrt{2}}, $

(7) then metric (1) becomes
$\begin{split} {\rm d}s^2 =& -\frac{r^2h(r)}{R^2}(1+f){\rm d}x^+{\rm d}x^-+\frac{r^2h(r)}{R^2}({\rm d}x_2^2+{\rm d}x_3^2)\\&+\frac{r^2h(r)}{2R^2}(1-f)[({\rm d}x^+)^2+({\rm d}x^-)^2])+\frac{R^2h(r)}{r^2f}{\rm d}r^2. \end{split} $

(8) Considering that the Wilson loop stretches across, e.g.,
$ x_2 $ and lies at$ x^+ = constant,x_3 = constant $ , one may choose the following static gauge$ x^- = \tau, \qquad x_2 = \sigma, $

(9) and assume a profile of
$ r = r(\sigma) $ ; then (8) reduces to$ {\rm d}s^2 = h(r)\left[\frac{1}{2}\left(\frac{r^2}{R^2}-f_1\right){\rm d}\tau^2+\left(\frac{r^2}{R^2}+\frac{\dot{r}^2}{f_1}\right){\rm d}\sigma^2\right], $

(10) with
$ \dot{r} = \dfrac{{\rm d}r}{{\rm d}\sigma} $ ,$ f_1\equiv\dfrac{r^2}{R^2}f $ .Given that, the induced metric reads
$\begin{split} g_{00} =& \frac{h(r)}{2}\left(\frac{r^2}{R^2}-f_1\right), \qquad g_{01} = g_{10} = 0, \\ g_{11} =& h(r)\left(\frac{r^2}{R^2}+\frac{\dot{r}^2}{f_1}\right). \end{split}$

(11) The string is governed by the Nambu-Goto action, given by
$ S = -\frac{1}{2\pi\alpha^\prime}\int {\rm d}\tau {\rm d}\sigma\sqrt{-{\rm det}g_{\alpha\beta}}, $

(12) with
$ g_{\alpha\beta} = G_{\mu\nu}\frac{\partial X^\mu}{\partial\sigma^\alpha} \frac{\partial X^\nu}{\partial\sigma^\beta}, $

(13) where
$ X^\mu $ and$ G_{\mu\nu} $ are the target space coordinates and metric, respectively.Plugging (11) into (12), one has
$ S = \frac{\sqrt{2}L_-}{2\pi\alpha^\prime}\int_0^{\frac{L}{2}}{\rm d}\sigma\sqrt{h^2(r)\left(\frac{r^2}{R^2}-f_1\right)\left(\frac{r^2}{R^2}+\frac{\dot{r}^2}{f_1}\right)}, $

(14) where the boundary condition is
$ r(\pm\dfrac{L}{2}) = \infty $ .As action (14) does not depend explicitly on
$ \sigma $ , one obtains a conserved quantity$ \frac{\partial{\cal{L}}}{\partial\dot{r}}\dot{r}-{\cal{L}} = \frac{-h^2(r)\left(\dfrac{r^2}{R^2}-f_1\right)\dfrac{r^2}{R^2}}{\sqrt{h^2(r)\left(\dfrac{r^2}{R^2}-f_1\right)\left(\dfrac{r^2}{R^2}+\frac{\dot{r}^2}{f_1}\right)}} = C, $

(15) resulting in
$ \dot{r}^2 = \frac{f_1r^2}{R^2C^2}\Bigg[\frac{h^2(r) r^2\left(\dfrac{r^2}{R^2}-f_1\right)}{R^2}-C^2\Bigg]. $

(16) The above equation involves determining the zeros. Further, the turning point occurs at
$ f_1 = 0 $ , indicating$ \dot{r} = 0 $ at$ r = r_h $ [13].For convenience, we write
$ B\equiv1/C^2 $ . For$ C\rightarrow0 $ (the low energy limit), one can integrate (16) to the leading order in$ 1/B $ , yielding$ L = 2R^2\int_{r_t}^\infty {\rm d}r \sqrt{\frac{1}{\left(\dfrac{r^2}{R^2}-f_1\right)Bf_1r^4h^2(r)}}. $

(17) Substituting (16) into (14), one obtains
$\begin{split} S =& \frac{\sqrt{2}L_-}{2\pi\alpha^\prime}\int_{r_h}^\infty {\rm d}r \sqrt{\frac{h^4(r)\left(\dfrac{r^2}{R^2}-f_1\right)^2r^2}{f_1\left[h^2(r) r^2\left(\dfrac{r^2}{R^2}-f_1\right)-R^2C^2\right]}}\\ =& \frac{\sqrt{2}L_-\sqrt{B}}{2\pi\alpha^\prime}\int_{r_h}^\infty {\rm d}r\dfrac{h^2(r)\left(\dfrac{r^2}{R^2}-f_1\right)r}{\sqrt{h^2(r)\left(\dfrac{r^2}{R^2}-f_1\right)Bf_1r^2-f_1R^2}}. \end{split} $

(18) Similarly, one expands (18) to the leading order in
$ 1/B $ as,$\begin{split} S =& \frac{\sqrt{2}L_-}{2\pi\alpha^\prime}\int_{r_h}^\infty {\rm d}r\left[1+\frac{R^2}{2h^2(r)\left(\dfrac{r^2}{R^2}-f_1\right)Br^2}\right]\\&\times \sqrt{\frac{1}{f_1}h^2(r)\left(\frac{r^2}{R^2}-f_1\right)}.\end{split} $

(19) However, action (19) is divergent. To eliminate the divergence, it should be subtracted by the inertial mass of two single quarks, given by
$ \begin{split} S_0 =& \frac{2L_-}{2\pi\alpha^\prime}\int_{r_h}^\infty {\rm d}r\sqrt{g_{–}g_{rr}}\\ =& \frac{\sqrt{2}L_-}{2\pi\alpha^\prime}\int_{r_h}^\infty {\rm d}r \sqrt{\dfrac{1}{f_1}h^2(r)\left(\dfrac{r^2}{R^2}-f_1\right)}. \end{split} $

(20) Then, the regulated finite on-shell action is given by
$ S_I = S-S_0 = \frac{\sqrt{2}L_-R^2}{4\pi\alpha^\prime B}\int_{r_h}^\infty {\rm d}r\sqrt{\frac{1}{\left(\dfrac{r^2}{R^2}-f_1\right)f_1r^4h^2(r)}}. $

(21) Substituting (17) and (21) into (6), one acquires the jet quenching parameter in the SW
$ _{T,\mu} $ model$ \hat{q} = \frac{I(q)^{-1}}{\pi\alpha^\prime}, $

(22) with
$ I(q) = R^2\int_{r_h}^\infty {\rm d}r\sqrt{\frac{1}{\left(\dfrac{r^2}{R^2}-f_1\right)f_1r^4h^2(r)}}. $

(23) Note that by setting
$ c = \mu = 0 $ in (22), the jet quenching parameter of SYM [13] is reproduced, that is$ \hat{q}_{\rm SYM} = \frac{\pi^{3/2}\Gamma\left(\dfrac{3}{4}\right)}{\Gamma\left(\dfrac{5}{4}\right)}\sqrt{\lambda}T^3, $

(24) where one has used the relations
$ r_h = \pi R^2T $ and$ \dfrac{R^2}{\alpha^\prime} = \sqrt{\lambda} $ .Let us discuss the results. First, we analyze how
$ \mu $ and c modify$ \hat{q} $ . For this purpose, we plot$ \hat{q}/\hat{q}_{\rm SYM} $ as a function of$ \mu/T $ with fixed$ c/T $ for two different temperatures in Fig. 1, where the left panel denotes the$ T = 170 \;{\rm MeV} $ case, and the right panel denotes the$ T = 500 \;{\rm MeV} $ case. From both panels, one sees that at fixed$ c/T $ , increasing$ \mu/T $ leads to increasing$ \hat{q}/\hat{q}_{\rm SYM} $ , indicating that the inclusion of the chemical potential increases the jet quenching parameter, in accordance with [19, 20]. Likewise, one can see from Fig. 2 that at fixed$ \mu/T $ ,$ \hat{q}/\hat{q}_{\rm SYM} $ increases as$ c/T $ increases, implying that the inclusion of nonconformality increases the jet quenching parameter, similar to [35]. Thus, one concludes that the inclusion of chemical potential and nonconformality both increase the jet quenching parameter, thus enhancing the energy loss, consistently with the findings of the drag force [39].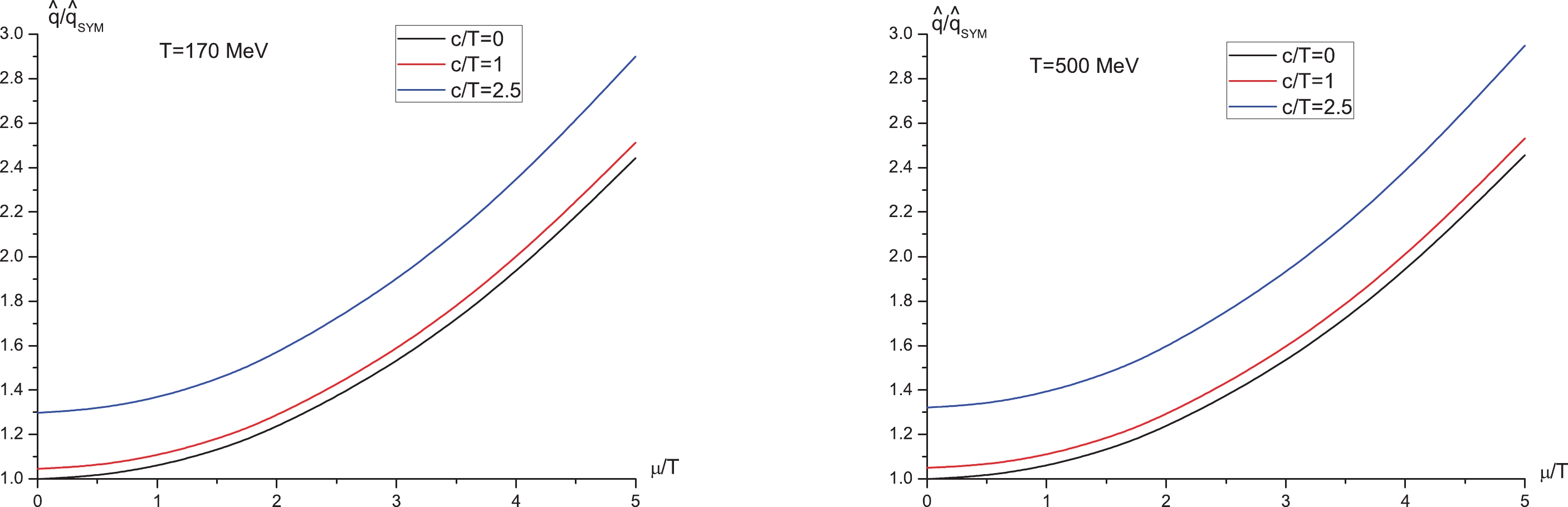
Figure 1. (color online)
$ \hat{q}/\hat{q}_{\rm SYM} $ versus$ \mu/T $ with fixed$ c/T $ . Left:$ T = 170 \;{\rm MeV} $ . Right:$ T = 500 \;{\rm MeV} $ . In both panels from top to bottom,$ c/T = 2.5, 1, 0 $ , respectively.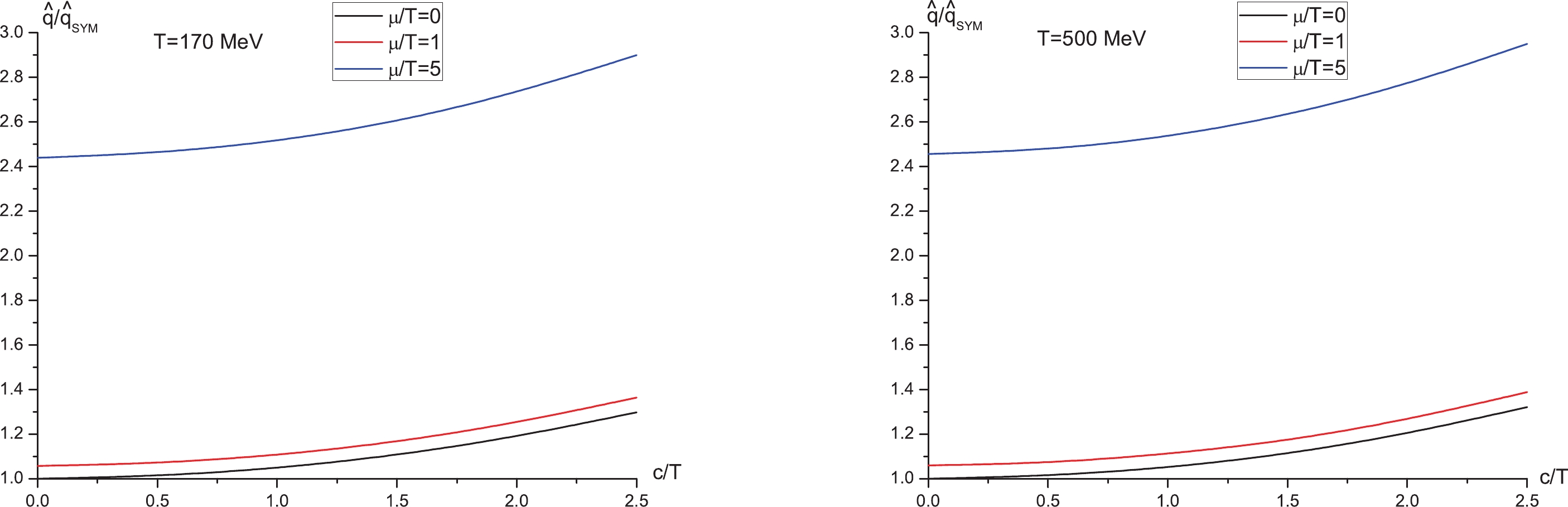
Figure 2. (color online)
$ \hat{q}/\hat{q}_{\rm SYM} $ versus$ c/T $ with fixed$ \mu/T $ . Left:$ T = 170 \;{\rm MeV} $ . Right:$ T = 500 \;{\rm MeV} $ . In both panels from top to bottom,$ \mu/T = 5, 1, 0 $ , respectively.Further, we strive to understand the T dependence of
$ \hat{q} $ for this model. To this end, we plot$ \hat{q}/\hat{q}_a $ , with$ \hat{q}_a|_{c = \mu = 0,\; T = 170\; {\rm MeV}} $ , versus T in Fig. 3, where the left panel presents the$ \mu = 0 $ case, while the right one presents the case of$ \mu = 100 \;{\rm MeV} $ . From these figures, one finds that with fixed$ c/T $ ,$ \hat{q}/\hat{q}_a $ increases with T , as expected.
Figure 3. (color online)
$ \hat{q}/\hat{q}_a $ versus T with fixed$ c/T $ . Left:$ \mu = 0 $ . Right:$ \mu = 100 \;{\rm MeV} $ . In both panels from top to bottom,$ c/T = 2.5, 1, 0 $ , respectively.Finally, we would like to make a comparison to implications of experimental data. In Table 1, we present some typical values of
$ \hat{q} $ , where we have taken$ N_c = 3 $ and$ \alpha_{\rm SYM} = 0.5 $ (reasonable for temperatures not far above QCD phase transition), and$ \lambda = 6\pi $ [13]. Most of the values are consistent with the extracted values from RHIC data ($ 5\sim25 \;{\rm GeV ^2/fm} $ ) [46, 47]. In contrast, because the presence of$ \mu $ and c both enhance the jet quenching parameter, one may infer that increases in$ \mu $ and c may lower the possible allowed domain of T for the computed$ \hat{q} $ to ensure agreement with the experimental data.$ T\setminus(\mu, c) $ 

(0, 0) (0, 0.3) (0, 0.7) (0.1, 0) (0.1, 0.3) (0.1, 0.7) (0.3, 0) (0.3, 0.3) (0.3, 0.7) $ 0.3 $ 

4.50 4.71 5.70 4.53 4.74 5.73 4.76 4.98 6.0 $ 0.4 $ 

10.61 10.89 12.19 10.64 10.93 12.23 10.94 11.23 12.56 $ 0.5 $ 

20.69 21.02 22.65 20.70 21.06 22.70 21.08 21.45 23.10 Table 1. Typical values of
$ \hat{q} $ in$ {\rm GeV ^2/fm} $ ; the first line presents$ (\mu, c) $ , and the first column presents T. Here,$ T,\mu,c $ are all expressed in units of${\rm GeV} $ . -
In this study, we investigate the jet quenching parameter in a soft wall model with finite temperature and chemical potential. The dual space geometry is the AdS-RN black hole (describing finite temperature and density in the boundary theory) multiplied by a background warp factor (generating confinement). Our motivation originates from earlier studies on free energy [37], imaginary potential [38], and drag force [39] in such a model. The inclusion of chemical potential and nonconformality both increase the jet quenching parameter, thus enhancing the energy loss, in agreement with the findings of the drag force [39]. Additionally, we attempted to make a comparison of the implications of the experimental data and found the theoretical estimates agree well with experimental results. Finally, our results suggest that an increase in
$ \mu $ and c may lower the possible allowed domain of T for the computed$ \hat{q} $ to agree with the experimental data.Nevertheless, the SW
$ _{T,\mu} $ model has some drawbacks. The primary disadvantage is that it is not a consistent model, as it does not solve the Einstein equations. Studying the jet quenching parameter in some consistent models, e.g., [48-51] would be informative (however, note that the metrics of those models are only known numerically, as the calculations are very complex). Moreover, the SW$ _{T,\mu} $ model may miss one part regarding the phase transition [52-54] and the effect of the non-trivial dilaton field [55-57]). Considering these effects would likewise be instructive, they should be studied further.
Jet quenching parameter from a soft wall AdS/QCD model
- Received Date: 2020-03-21
- Accepted Date: 2020-06-02
- Available Online: 2020-10-01
Abstract: We study the effect of chemical potential and nonconformality on the jet quenching parameter in a holographic QCD model with conformal invariance broken by background dilaton. The presence of chemical potential and nonconformality both increase the jet quenching parameter, thus enhancing the energy loss, consistently with the findings of the drag force.





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF













 DownLoad:
DownLoad: