-
The
$ \Lambda\Lambda-\Xi N $ system in a pure S wave configuration has quantum numbers$ (i,j^p) = (0,0^+) $ , such that by adding one more nucleon, the$ \Lambda\Lambda N-\Xi NN $ system necessarily has quantum numbers$ (I,J^P) = (1/2,1/2^+) $ . In a series of works based on the chiral constituent quark model [1-3], this system was studied under the assumption that the H dibaryon [4] has the lower limit mass determined by the E373 experiment at KEK [5] from the observation of a$ ^6_{\Lambda\Lambda} $ He double hypernucleus. Despite significant experimental and theoretical efforts, the existence of the H dibaryon remains inconclusive, see Ref. [6] for a recent update. The experimental evidence disfavors large binding energies [7], as predicted in Ref. [4], and the high statistics study of$ \Upsilon $ decays at Belle [8] found no indication of an H dibaryon with a mass near the$ \Lambda\Lambda $ threshold. Recently, the HAL QCD Collaboration [9] has published a$ N_f = 2 + 1 $ study of coupled channel ($ \Lambda\Lambda $ and$ \Xi N $ ) baryon-baryon interactions with near-physical quark masses, namely$ m_\pi = 146 $ MeV, concluding that the H dibaryon could be a$ \Lambda\Lambda $ resonance just below or above the$ \Xi N $ threshold. Similar results were obtained in a low-energy effective field theory study of the H dibaryon in$ \Lambda\Lambda $ scattering [10].The HAL QCD results are being used as input for the study of strangeness - 2 baryon-baryon interactions, as recently done in relativistic chiral effective field theory studies [11]. The HAL QCD
$ \Xi N $ interactions have also recently been used to study the possible existence of$ \Xi NN $ bound states, see Ref. [12], with negative results for the$ (I,J^P) = (1/2,1/2^+) $ channel. For the$ NN $ interaction, they used the AV8 potential [13]. As the coupling between$ \Lambda\Lambda $ and$ \Xi N $ was found to be weak in Ref. [9], they used an effective single-channel$ \Xi N $ potential, in which the coupling to$ \Lambda\Lambda $ in$ ^{11}S_0 $ was renormalized into a single Gaussian form chosen to reproduce the$ \Xi N $ phase shift obtained with channel coupling. The three-body$ \Xi NN $ problem is solved in the real axis by means of a variational method with Gaussian bases, the Gaussian Expansion Method [14,15]. The full coupling between the$ \Xi NN $ and$ \Lambda\Lambda N $ channels was not explicitly considered. A similar calculation based on the Nijmegen ESC08c potentials [16-18] was presented in Ref. [19], also with negative results for the$ (I,J^P) = (1/2,1/2^+) $ channel, see Fig. 2(a) of Ref. [19].Unlike the calculation in Ref. [12], we developed a model in Ref. [20] of the
$ \Lambda\Lambda N - \Xi NN $ three-body system, which allowed us to look for possible three-body resonances. Using separable two-body interactions fitted to the low-energy data of the Nijmegen S wave baryon-baryon amplitudes [16-18], we found a resonance just below the$ \Xi d $ threshold with a very small width of only 0.09 MeV. (It is worth to note that the results for the$ \Xi NN $ system with maximal isospin have been independently reproduced within the integral Faddeev equation formalism [21] in agreement with high accuracy.) Qualitatively similar results have been obtained and are described in Ref. [12]; although as stressed in this manuscript, they are numerically different due to a different$ NN $ potential and a different treatment of the ESC08c Nijmegen S wave baryon-baryon interactions. Such dependencies on the models and parametrizations of the two-body interactions result in this three-body system being ideally suited for testing different models for two-body interactions.However, contrary to the recent results of the HAL QCD Collaboration, the Nijmegen baryon-baryon interactions gave no indication of either a bound state or a resonance in the
$ \Lambda\Lambda - \Xi N $ $ (0,0^+) $ two-body channel, the H-dibaryon channel. It is thus interesting to see if the existence of a resonance just below or above the$ \Xi N $ threshold, as it has been found by the HAL QCD Collaboration [9] and low-energy effective field theory studies [10], may affect the position of the three-body S wave$ (1/2,1/2^+) $ $ \Lambda\Lambda N - \Xi NN $ resonance found in Ref. [20]. For this purpose, we have now constructed separable potential models of the$ \Lambda\Lambda $ ,$ \Xi N $ , and$ \Lambda\Lambda-\Xi N $ amplitudes reproducing the behavior of the HAL QCD collaboration results [9]. We have also performed a full-fledged coupled-channel study of the$ \Lambda\Lambda N - \Xi NN $ three-body system.We use rank-one separable potentials for all uncoupled two-body channels, that is, for all channels except the
$ \Lambda\Lambda-\Xi N $ $ (0,0^+) $ interaction. They are as follows,$ \begin{array}{l} V_i^\rho = g_i^\rho\rangle \lambda\langle g_i^\rho \, , \end{array} $

(1) such that the two-body t-matrices are
$ \begin{array}{l} t_i^\rho = g_i^\rho\rangle \tau_i^\rho\langle g_i^\rho \, , \end{array} $

(2) with
$ \tau_i^\rho = \frac{\lambda}{1- \lambda\langle g_i^\rho|G_0(i)|g_i^\rho\rangle} \, , $

(3) where
$ G_0(i) = 1/(E-K_i+i\epsilon) $ and$ K_i $ is the kinetic energy operator of channel i. We use Yamaguchi form factors [22] for the separable potentials of Eq. (1), i.e.,$ g_i^\rho(p) = \frac{1}{\alpha^2+p^2}. $

(4) For the case of the coupled
$ (0,0^+) $ $ \Lambda\Lambda-\Xi N $ channel, we use a rank-two separable potential of the form [23]$ \begin{array}{l} V_{ij}^{\rho\sigma} = g_i^\rho\rangle \lambda_{ij}\langle g_j^\sigma \, , \end{array} $

(5) such that
$ \begin{array}{l} t_{ij}^{\rho-\sigma} = g_1^\rho\rangle \tau_{ij}^{\rho-\sigma}\langle g_j^\sigma \, , \end{array} $

(6) with
$ \begin{split} \tau_{11}^{\Lambda\Lambda-\Lambda\Lambda} = & \frac{-\lambda_{13}^2G^{\Xi N} -\lambda_{11}(1-\lambda_{33}G^{\Xi N})} {\lambda_{13}^2G^{\Lambda\Lambda}G^{\Xi N} -(1-\lambda_{11}G^{\Lambda\Lambda}) (1-\lambda_{33}G^{\Xi N})} \, , \\ \tau_{33}^{\Xi N - \Xi N} =& \frac{-\lambda_{13}^2G^{\Lambda\Lambda} -\lambda_{33}(1-\lambda_{11}G^{\Lambda\Lambda})} {\lambda_{13}^2G^{\Lambda\Lambda}G^{\Xi N} -(1-\lambda_{11}G^{\Lambda\Lambda}) (1-\lambda_{33}G^{\Xi N})} \, , \\ \tau_{13}^{\Lambda\Lambda-\Xi N} =& \tau_{31}^{\Xi N-\Lambda\Lambda} \!=\! \frac{-{\lambda_{13}}} {\lambda_{13}^2G^{\Lambda\Lambda}G^{\Xi N} \!-\!(1\!-\!\lambda_{11}G^{\Lambda\Lambda}) (1\!-\!\lambda_{33}G^{\Xi N})} , \end{split} $

(7) and
$ \begin{split} G^{\Lambda\Lambda} = & \langle g_1^{\Lambda\Lambda}|G_0(1)|g_1^{\Lambda\Lambda}\rangle \, , \\ G^{\Xi N} = & \langle g_3^{\Xi N}|G_0(3)|g_3^{\Xi N}\rangle \,. \end{split} $

(8) In this case, we also use Yamaguchi-type form factors as
$ \begin{split} g_1^{\Lambda\Lambda}(p) =& \frac{1}{\alpha^2+p^2} \, , \\ g_3^{\Xi N}(p) =& \frac{1}{\beta^2+p^2} \, . \end{split} $

(9) The parameters of the
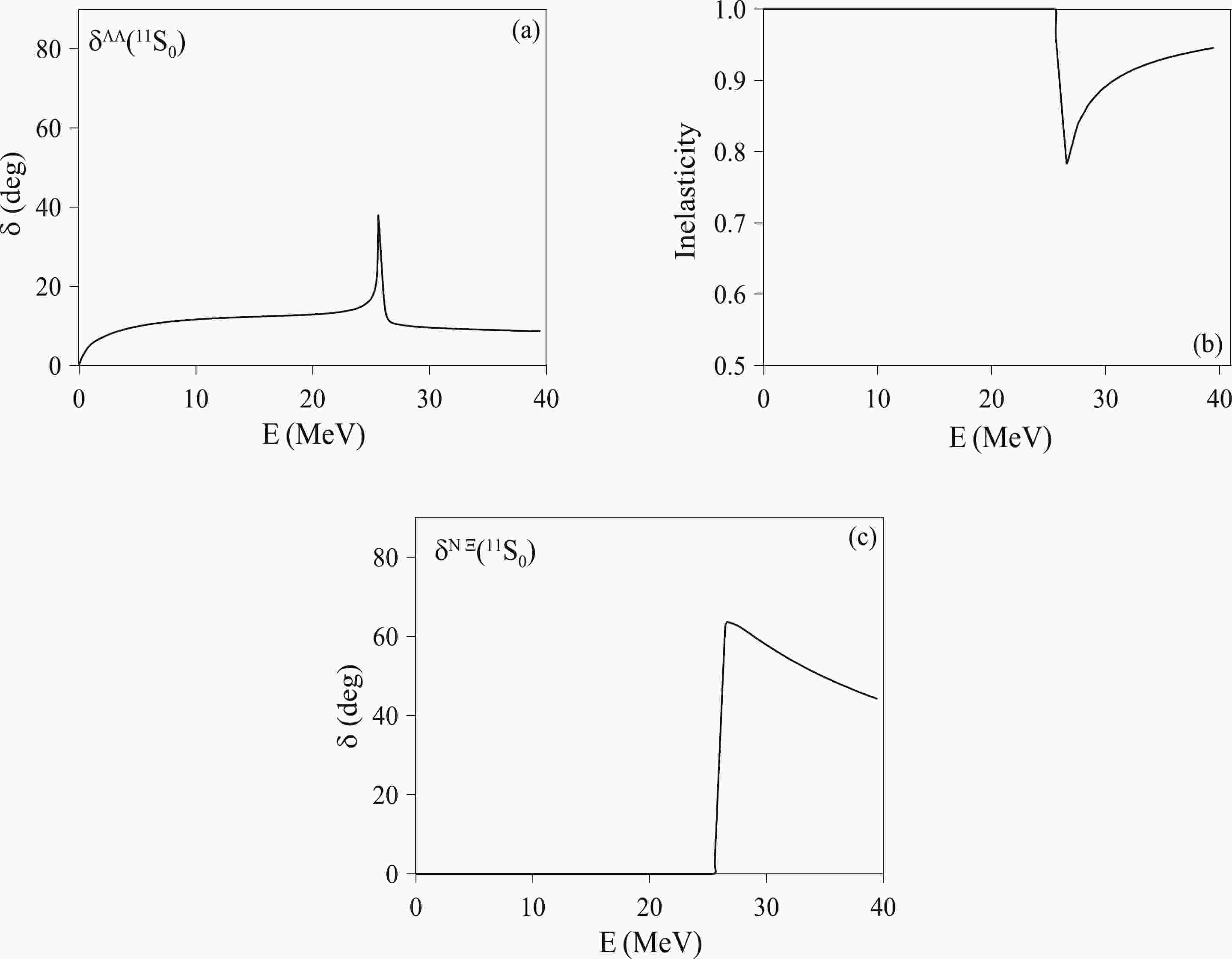
$ \Lambda\Lambda - \Xi N $ model based on the latest HAL QCD potentials are given in Table 1. In Figs. 1(a), (b), and (c) we show the predictions for the$ \Lambda\Lambda $ and$ \Xi N $ phase shifts as well as the inelasticity, which are rather similar to those of model$ t/a = 12 $ of the HAL QCD Collaboration presented in Fig. 4 of Ref. [9]. The corresponding parameters of the uncoupled$ \Xi N $ models are given in Table 2. Note that our results have been obtained by taking the nucleon mass to be the average of the proton and neutron masses and the$ \Xi $ mass as the average of the$ \Xi^0 $ and$ \Xi^- $ masses. Thus, the$ \Xi N $ and$ \Xi NN $ thresholds are 25.6 MeV above the$ \Lambda\Lambda $ and$ \Lambda\Lambda N $ thresholds, respectively. However, this threshold is 32 MeV for the HAL QCD results [9], as they use the values obtained from their lattice QCD study for the baryon masses. Therefore, to compare our phase shifts with those of Ref. [9], one should keep in mind that the energy scale of Ref. [9] corresponds to those of Fig. 1 multiplied by 1.25. The models of the$ NN $ and$ \Lambda N $ subsystems are the same as in Ref. [20].$ \alpha $ 

$ \beta $ 

$ \lambda_{11} $ 

$ \lambda_{33} $ 

$ \lambda_{13} $ 

1.3465 1.1460 $ - $ 0.1390

$ - $ 0.3171

0.0977 Table 1. Parameters
$ \alpha $ and$ \beta $ (in fm$ ^{-1} $ ),$ \lambda_{11} $ ,$ \lambda_{33} $ , and$ \lambda_{13} $ (in fm$ ^{-2} $ ) of the separable-potential model of the coupled$ (i,j^p) = (0,0^+) $ $ \Lambda\Lambda -\Xi N $ two-body system.
Figure 1. (a)
$\Lambda\Lambda$ scattering phase shifts, (b)$\Lambda\Lambda$ inelasticity, and (c)$N \Xi$ scattering phase shifts in the$(i,j^p)=(0,0^+)$ channel.Channel $ \alpha $ 

$ \lambda $ 

$ (0,1^+) $ 

1.41 -0.117 $ (1,0^+) $ 

7.333 22.97 $ (1,1^+) $ 

0.803 -0.016 Table 2. Parameters
$ \alpha $ (in fm$ ^{-1} $ ) and$ \lambda $ (in fm$ ^{-2} $ ) of the separable-potential model of the uncoupled$ (i,j^p) $ $ \Xi N $ two-body channels.The coupled
$ \Lambda\Lambda N - \Xi NN $ three-body system presents the special characteristic that each three-body component consists of two identical fermions and a third one that is different. The homogeneous integral equations of this system appropriate for the search of bound and resonant states were derived in Ref. [3] using a graphical method. Using the new separable models presented in Tables 1 and 2 based on the HAL QCD interactions, we do not find any bound state below the$ \Xi d $ threshold, which is in agreement with the results of Ref. [12]. Therefore, we investigate the possible existence of a resonance above the$ \Xi d $ threshold by calculating the$ \Xi d $ scattering amplitude.We adopt the same convention as in Refs. [3,20], i.e., particles
$ 2 $ and$ 3 $ are identical and particle$ 1 $ is different in each three-body component. After the reduction for identical particles, the inhomogeneous integral equations appropriate for$ \Xi d $ elastic scattering take the following form$ \begin{split} \langle 1|T_1|\phi_0\rangle = & 2\langle 1|t_1^{\Lambda\Lambda}|1\rangle \langle 1|3\rangle G_0(3)\langle 3|T_3|\phi_0\rangle \\&+ \langle 1|t_{13}^{\Lambda\Lambda-N\Xi}|3\rangle \langle 3|1\rangle G_0(1) \langle 1|U_1|\phi_0\rangle \\& -\langle 1|t_{13}^{\Lambda\Lambda-N\Xi}|3\rangle \langle 2|3\rangle G_0(3) \langle 3|U_3|\phi_0\rangle,\\ \langle 3|T_3|\phi_0\rangle = &-\langle 3|t_3^{N\Lambda}|3\rangle \langle 2|3\rangle G_0(3) \langle 3|T_3|\phi_0\rangle \\&+\langle 3|t_3^{N\Lambda}|3\rangle \langle 3|1\rangle G_0(1) \langle 1|T_1|\phi_0\rangle, \end{split} $

$ \begin{split} \\ \langle 1|U_1|\phi_0\rangle =& 2\langle 1|t_1^{NN}|1\rangle \langle 1|3\rangle G_0(3) \langle 3|U_3|\phi_0\rangle, \\ \langle 3|U_3|\phi_0\rangle =& 2\langle 3|t_3^{N\Xi}|\phi_0\rangle \\& - \langle 3|t_3^{N\Xi}|3\rangle \langle 2|3\rangle G_0(3) \langle 3|U_3|\phi_0\rangle \\&+\langle 3|t_3^{N\Xi}|3\rangle \langle 3|1\rangle G_0(1) \langle 1|U_1|\phi_0\rangle \\& +2\langle 3|t_{31}^{N\Xi-\Lambda\Lambda}|1\rangle \langle 1|3\rangle G_0(3) \langle 3|T_3|\phi_0\rangle, \end{split} $

(10) where
$ |\phi_0\rangle $ is the initial state consisting of the deuteron wave function times a$ \Xi $ plane wave.Substituting Eqs. (2) and (6) into the integral Eq. (10) and introducing the transformations
$ \langle i|T_i|\phi_0\rangle $ =$ \langle i|g_i^{\alpha_i}\rangle \langle i|X_i|\phi_0\rangle $ and$ \langle i|U_i|\phi_0\rangle = \langle i|g_i^{\beta_i}\rangle \langle i|Y_i|\phi_0\rangle $ , one obtains the inhomogeneous one-dimensional integral equations$ \begin{split} \langle 1|X_1|\phi_0\rangle = & 2\tau_1^{\Lambda\Lambda}\langle g_1^{\Lambda\Lambda}|1\rangle \langle 1|3\rangle G_0(3)\langle 3|g_3^{N\Lambda}\rangle \langle 3|X_3|\phi_0\rangle \\& + \tau_{13}^{\Lambda\Lambda-N\Xi}\langle g_3^{N\Xi}|3\rangle \langle 3|1\rangle G_0(1) \langle 1|g_1^{NN}\rangle \langle 1|Y_1|\phi_0\rangle \\& - \tau_{13}^{\Lambda\Lambda-N\Xi}\langle g_3^{N\Xi}|3\rangle \langle 2|3\rangle G_0(3) \langle 3|g_3^{N\Xi}\rangle \langle 3|Y_3|\phi_0\rangle, \\ \langle 3|X_3|\phi_0\rangle = & -\tau_3^{N\Lambda} \langle g_3^{N\Lambda}|3\rangle\langle 2|3\rangle G_0(3) \langle 3|g_3^{N\Lambda}\rangle \langle 3|X_3|\phi_0\rangle \\& + \tau_3^{N\Lambda}\langle g_3^{N\Lambda}|3\rangle \langle 3|1\rangle G_0(1) \langle 1|g_1^{\Lambda\Lambda}\rangle \langle 1|X_1|\phi_0\rangle, \\ \langle 1|Y_1|\phi_0\rangle =& 2\tau_1^{NN}\langle g_1^{NN}|1\rangle \langle 1|3\rangle G_0(3) \langle 3|g_3^{N\Xi}\rangle \langle 3|Y_3|\phi_0\rangle, \end{split} $

$ \begin{split} \langle 3|Y_3|\phi_0\rangle = & 2\tau_3^{N\Xi}\langle g_3^{N\Xi}|\phi_0\rangle \\& -\tau_3^{N\Xi}\langle g_3^{N\Xi}|3\rangle \langle 2|3\rangle G_0(3) \langle 3|g_3^{N\Xi}\rangle \langle 3|Y_3|\phi_0\rangle \\& + \tau_3^{N\Xi}\langle g_3^{N\Xi}|3\rangle \langle 3|1\rangle G_0(1) \langle 1|g_1^{NN}\rangle \langle|Y_1|\phi_0\rangle \\& +2\tau_{31}^{N\Xi-\Lambda\Lambda}\langle g_1^{\Lambda\Lambda}|1\rangle \langle 1|3\rangle G_0(3) \langle 3|g_3^{N\Lambda}\rangle\langle 3|X_3|\phi_0\rangle. \end{split} $

(11) If one neglects the inhomogeneous terms in Eqs. (10) and (11), they become identical to Eqs. (14) and (15) of Ref. [20]. The
$ \Xi d $ scattering amplitude normalized as in the Argand diagram is given by$ \begin{array}{l} F = -\pi q_0\nu\langle \phi_0|U_3|\phi_0\rangle, \end{array} $

(12) where
$ q_0 $ and$ \nu $ , respectively, are the$ \Xi d $ on-shell momentum and the reduced mass. We solve the integral Eqs. (11) using the standard method [24], where the momentum variables are rotated into the complex plane as$ q_i\to q_i {\rm e}^{-{\rm i}\phi} $ and the results are checked to be independent of the rotation angle$ \phi $ . If the resonance lies below the$ \Xi d $ threshold, as it was the case in Ref. [20], the contour rotation method allows to simultaneously consider both the momentum variables and the energy variable as complex, such that one can determine the position of the pole in the complex plane. However, if the resonance lies above the$ \Xi d $ threshold, as in the present case, the contour rotation method works only if one takes the momentum variables as complex but leaves the energy variable real, such that one cannot determine the position of the pole in the complex plane.We show, in Fig. 2, the Argand diagram of the
$ \Xi d $ system between 0 and 10 MeV above the$ \Xi d $ threshold, where one sees the typical counterclockwise behavior of a resonant amplitude. If one neglects the$ (i,j^p) = (0,0^+) $ channel, the counterclockwise behavior disappears, which shows that the H-dibaryon channel$ (i,j^p) = (0,0^+) $ is basic for the existence of the three-body$ \Lambda\Lambda N - \Xi NN $ S wave resonance.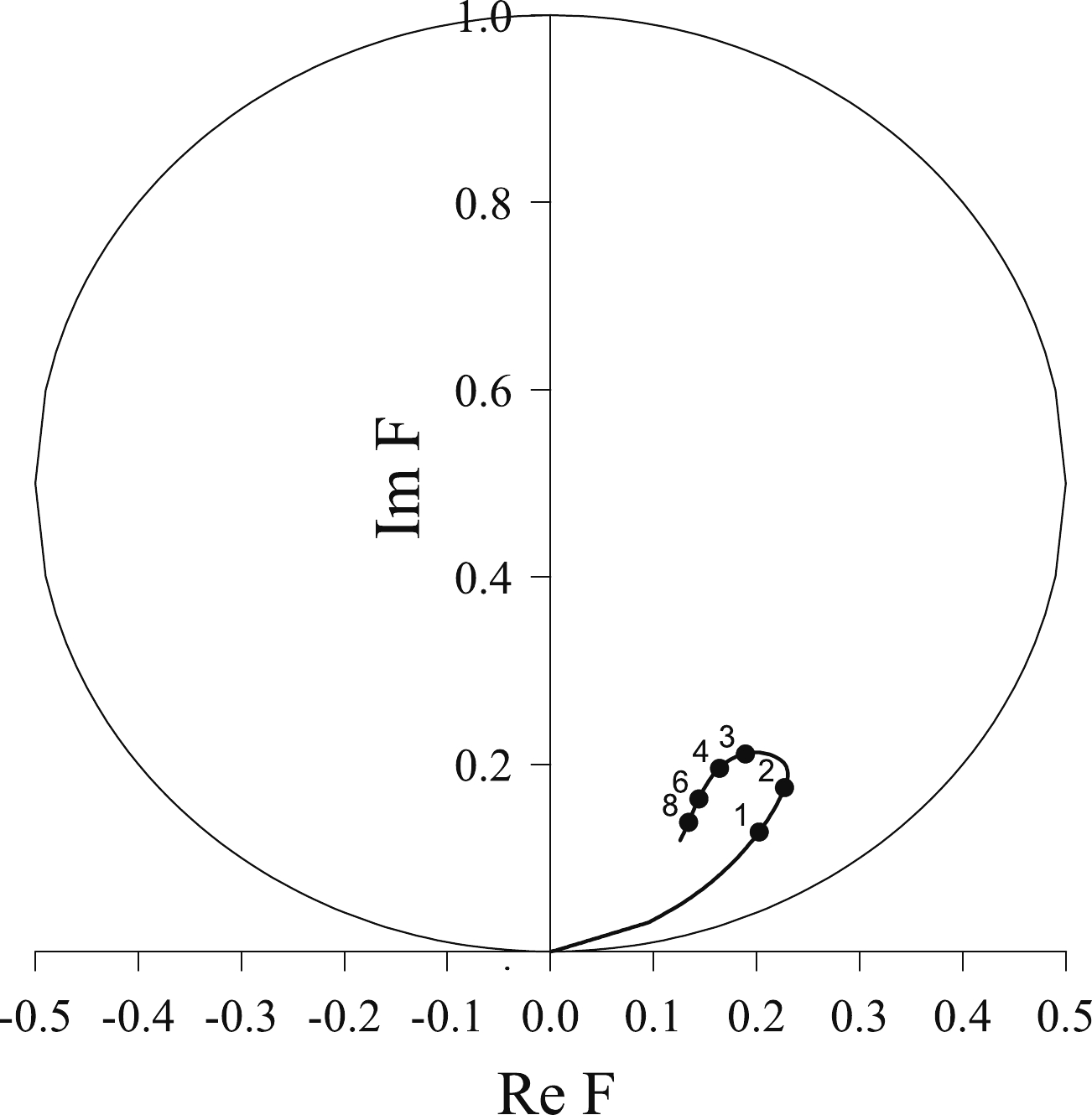
Figure 2. Argand diagram of the
$ \Xi d $ system between 0 and 10 MeV above the$ \Xi d $ threshold. Several relevant energies, in MeV, are indicated.As already mentioned in the introduction, the HAL QCD
$ \Xi N $ interactions have recently been used to study the possible existence of$ \Xi NN $ bound states in Ref. [12] with negative results for the$ (I,J^P) = (1/2,1/2^+) $ channel, which is in agreement with our findings despite using a different$ NN $ interaction and method.We have finally evaluated the
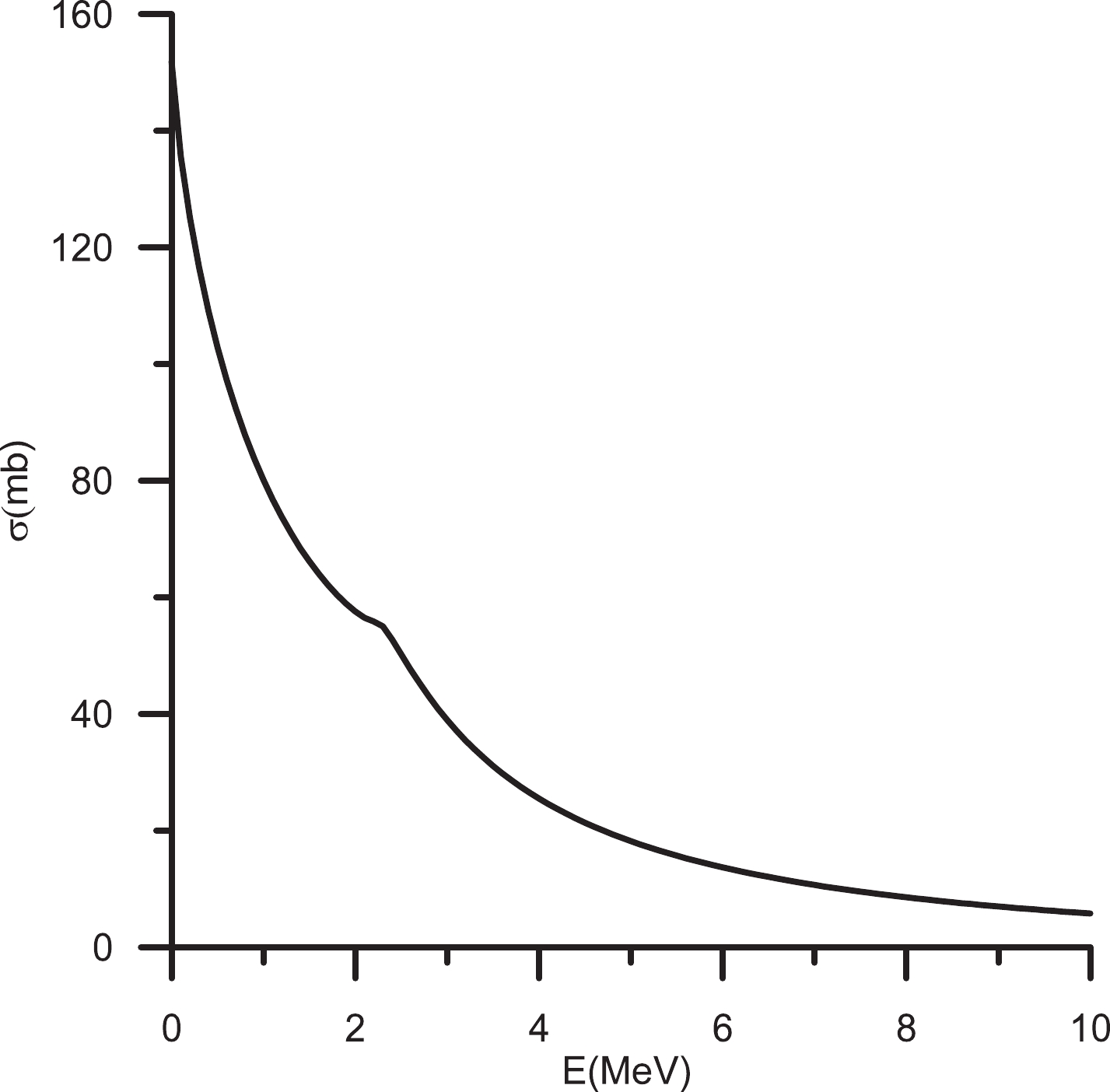
$ \Xi d $ elastic cross-section as a function of energy, where we have included not only the$ (I,J^P) = (1/2,1/2^+) $ $ \Xi d $ amplitude but also the$ (1/2,3/2^+) $ amplitude, which is very small. The result is shown in Fig. 3. As one can see, the resonance shows up as a change of slope of the cross section at an energy around 2.3 MeV, i.e., close to the$ \Xi d $ breakup threshold$ \sqrt{S} = 2m_N+m_\Xi $ . The bump in the cross section would become larger for a stronger$ (i,j^p) = (0,0^+) $ transition potential, and as noted above, it would disappear if the$ (i,j^p) = (0,0^+) $ channel is not considered or the two-body resonance in the H-dibaryon channel does not exist. The$ \Xi d $ cross section would allow for discrimination among the different models for the strangeness$ - $ 2 two-baryon interactions. It could be studied through the quasifree$ \Xi^- $ production in the$ (K^-,K^+) $ reaction on a deuteron target [25,26].Let us finally note that if one drops the coupling to the
$ \Lambda\Lambda N $ channel, Fig. 2 changes by about 10 % while maintaining its shape and rotating slightly to the right; similarly, in Fig. 3 the cross-section at$ E = 2.3 $ MeV changes from 55 mb to 58 mb.It is interesting to compare this resonance with the nucleon-nucleon
$ ^1D_2 $ Hoshizaki resonance [27], which has a mass close to$ \sqrt{S} = m_N+m_\Delta $ , since it arises due to the process,$ NN\to\pi NN $ , which is driven by the pion-nucleon$ \Delta $ resonance [28]. The resonance we are studying here is driven by the$ \Lambda\Lambda- \Xi N $ H-dibaryon resonance, which appears either just below or above the$ N\Xi $ threshold [9], such that it has a mass,$ m_H = m_N+m_\Xi $ . Following the comparison with the Hoshizaki state, one expects that the$ \Lambda\Lambda N - \Xi NN $ resonance will have a mass close to$ \sqrt{S} = m_N +m_H = 2m_N+m_\Xi $ , which is precisely the$ \Xi d $ threshold and in agreement with Figs. 2 and 3.In brief, we have shown that the possible existence of a
$ \Lambda\Lambda N - \Xi NN $ resonance would be highly sensitive to the$ \Lambda\Lambda - \Xi N $ interaction. In particular, by using a separable potential based on the most recent results of the HAL QCD Collaboration, characterized by the existence of a resonance just below or above the$ \Xi N $ threshold in the H-dibaryon channel,$ (i,j^p) = (0,0^+) $ , a three-body resonance appears at 2.3 MeV above the$ \Xi d $ threshold. A theoretical and experimental effort to constrain the$ \Lambda\Lambda - \Xi N $ interaction is the basic requirement for progress in our investigation of the strangeness$ - $ 2 sector.
$ {{ \Lambda}{ \Lambda}{ N} { -} { \Xi} { N}{ N}} $ S wave resonance
- Received Date: 2020-06-11
- Available Online: 2020-10-01
Abstract: We use an existing model of the






 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF






















 DownLoad:
DownLoad: