-
To probe the properties of the quark-gluon plasma (QGP) in heavy-ion collisions (HICs), the modification of the medium of energetic partons, which are produced by initial hard scattering and later propagate through the fireball, has been extensively investigated. This is referred to as the jet quenching phenomenon, and an enormous effort has been devoted to exploring its effect on various observables, from the suppression of high-
$ p_{\rm T} $ hadron production to inclusive reconstructed full jets, and even less inclusive jets such as dijets and tagged jets as well as a variety of jet substructures [1-32]. Among these, the transverse momentum imbalance of the inclusive dijets is one of the early and fundamental observables. The jet quenching effect accords a net imbalance to the$ p_{\rm T} $ distributions of the back-to-back jets, which can exceed the imbalance caused by the QCD correction. This additional imbalance is attributed to the energy losses that these two jets suffer when they are propagated through the QGP medium. The dependence of the parton on flavor, which initiates the jets, is quite essential to the underlying dynamics of the in-medium evolution and energy loss of the jet. It is difficult for experimentalists to determine such dependence in inclusive jet and dijet events. However, the pair production of heavy quark$ b\bar{b} $ jets that are azimuthally back-to-back provides a possibility to isolate the type of partons that initiate the jets. This is because the produced jets can be restricted to be$ b(\bar{b}) $ quark initiated. It is of significant interest to compare the possible modification effects of the$ b\bar{b} $ dijets with those of inclusive dijets for various media, as jets in inclusive dijet events are predominantly initiated by light quarks and gluons.The ATLAS [33] and CMS [34] collaborations reported their measurements of the production of
$ b\bar{b} $ dijets in the p + p collision at the LHC when compared with several next-to-leading order (NLO) and LO QCD Monte Carlo simulations, but a theoretical prediction of the medium modification of$ b\bar{b} $ dijets in Pb + Pb collisions is required to compare with the available CMS data [34].Multiple mechanisms can be employed for the production of
$ b\bar{b} $ dijets in p + p collisions; these not only enhance the production in the desired scenario but also precisely determine the production using other mechanisms, so that we can quantitatively compare the calculations with the experimental data. Another challenge in the study of the production of these dijets in A + A collisions is that simultaneous description is required to consider the in-medium evolution of heavy and light quarks. The manuscript is organized as follows: We first introduce the production mechanisms of the$ b\bar{b} $ pair as well as the p + p baseline of$ b\bar{b} $ dijets: both the simulation setup and event selection. Thereafter, we introduce the framework of the simultaneous description of the in-medium evolution of heavy and light quarks. Subsequently, we present the theoretical results of the transverse momentum imbalance distribution of the$ b\bar{b} $ dijets as a function of$ p_{\rm T} $ to compare with the CMS data in the A + A collisions. We also analyze the difference between$ b\bar{b} $ dijets and inclusive dijets with respect to the transverse momentum imbalance. Finally, we predict the distribution of the normalized azimuthal angle of the$ b\bar{b} $ dijet in the Pb + Pb collisions at$ 5.02 $ TeV and compare it with the p + p reference. -
By definition, a
$ b(\bar{b}) $ jet is a full jet with at least one b or$ \bar{b} $ quark inside the jet cone with a jet radius parameter R. The production mechanism of a$ b\bar{b} $ pair can be categorized into three types, which can be used to understand the$ b\bar{b} $ dijet system [35-38]. The flavor creation (FCR) describes the production of both b and$ \bar{b} $ jets that originated from the b and$ \bar{b} $ quarks produced back-to-back azimuthally from the initial hard scattering. Therefore, these jets are expected to be the most difficult to produce in the event. This process is perfect for isolating the type of parton (b quark) that initiates a jet. The gluon splitting (GSP) mechanism allows a pair of$ b(\bar{b}) $ jets to initiate from the b and$ \bar{b} $ quarks created in the gluon splitting process$ g \to b \bar{b} $ . This pair of jets is expected to propagate in the same direction. However, the flavor excitation (FEX) mechanism is more complex and the produced$ b(\bar{b}) $ jet pair is more likely to be neither back-to-back nor on the same side. The NLO calculation without further kinetic constraints indicates that there are large fractions of contribution from all three mechanisms in the$ p_{\rm T} $ region investigated [39]. Therefore, a suitable kinetic constraint should be imposed to select the desired mechanism. For instance, to consider pairs of$ b(\bar{b}) $ jets that are constrained back-to-back in the azimuth experimentally, one may largely reduce the contribution from GSP and mainly focus on the FCR process by imposing energetic$ p_{\rm T} $ triggers as well as restricting the intersection angle between the two$ b\bar{b} $ jets. This configuration is essential for providing a less ambiguous observable.It has been demonstrated in both the ATLAS [33] and CMS [34] reports that the NLO effects are essential for the modeling of such observables, as the NLO QCD calculation with POWHEG provides a better description than that provided by PYTHIA 6 alone. It is also noted that the configurations are slightly different in these two experimental reports.
In our simulation, we employ the NLO + parton shower (PS) event generator SHERPA 2.2.4 [40] to produce inclusive jets as well as inclusive dijet events in p + p collisions. We select single b-jet and
$ b\bar{b} $ dijet events from these inclusive events as our p + p baseline. In the SHERPA generator, we set the tree-level matrix elements as calculated using Amegic [41] and Comix [42], whereas the one-loop matrix elements are calculated using BlackHat [43]. The parton shower is implemented based on the Catani-Seymour subtraction method [44]. The NLO QCD matrix elements are matched with the parton shower using the MC@NLO method [45]. The NLO PDF sets in NNPDF3.0 [46] with five flavors have been chosen in our simulation. FASTJET [47] with an anti-$ k_{\rm T} $ algorithm is used for event selection and final-state jet reconstruction. The jets are defined in a cone with the jet radius parameter$ \Delta R = \sqrt{(\Delta \phi)^2+(\Delta \eta)^2} $ , where$ \phi $ and$ \eta $ are the azimuthal angle and the rapidity of particles, respectively. The corresponding configuration has been set up to be in line with each p + p measurement in CMS [48, 49] and ATLAS [33].To test the setup used to generate the b-jet events in SHERPA, in the upper plots of Fig. 1, we present a comparison of the results of the theoretical simulation of the production of inclusive b-jets in a p + p collision at
$ \sqrt{s_{ NN}} = 2.76 $ TeV with the CMS data. A good agreement was found. We further select the$ b\bar{b} $ dijet events from the SHERPA-generated inclusive dijet events, which naturally include all three production mechanisms of the$ b\bar{b} $ dijets. Thereafter, we reproduce the differential cross section of the$ b\bar{b} $ dijets as a function of the azimuthal angle between the two b-jets. An accurate description of the ATLAS data is presented in the bottom plots of Fig. 1. The figure illustrates that the azimuthal angle distribution of the two b-jets at a certain value of$ p_{\rm T} $ triggers the$ b\bar{b} $ events. It is noted that there is a same-side peak in the small azimuthal angle region, which is unusual for the double inclusive observables that we investigated earlier. The fairly accurate description of the experimental data indicates that the higher-order correction and its matched PS provided by SHERPA are essential for a solid p + p baseline. We also find that this type of double peak distribution is sensitive to the imposed kinetic cut. It requires a leading b-jet,$ p_{\rm T}>270 $ GeV, and the lower threshold of the$ p_{\rm T} $ cut of the b-jet is relatively small,$ p_{{\rm T}, b_{\rm{jet}}}>20 $ GeV, in the ATLAS publication. By increasing the minimum requirement of the b-jet$ p_{\rm T} $ to$ 40 $ GeV, we find that the same-side peak begins to vanish. From this observation, we can conclude that the double-peak structure is primarily caused by the contribution of the GSP process. Moreover, to focus on the FCR process to ensure that a greater proportion of the b-jets are b-quark-initiated, a relatively higher$ p_{\rm T} $ cut of the lower threshold of the b-jet$ p_{{\rm T}, b_{\rm{jet}}} $ will facilitate it. With this basic knowledge on the production of$ b\bar{b} $ dijets and the accurate performance of the SHERPA simulation, we have a strong platform to investigate the in-medium modification of the$ b\bar{b} $ dijets.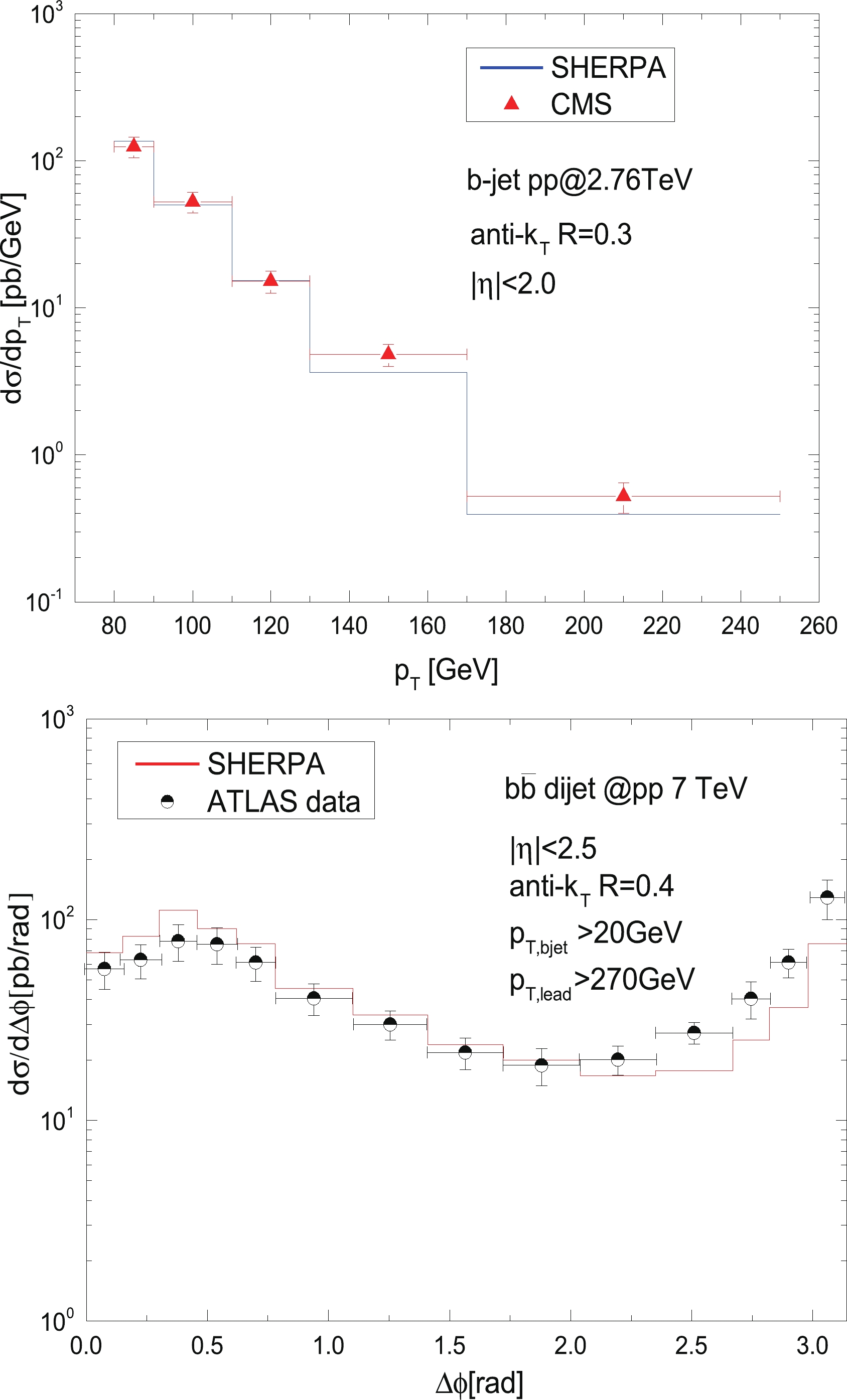
Figure 1. (color online) Upper: NLO + PS result of b-jet production in p + p collisions at
$ \sqrt{s_{{ NN}}} = 2.76 $ TeV calculated in SHERPA (indicated by vertical line) is compared with CMS data (indicated by red points with error bars) [49]. Bottom: NLO + PS differential cross section of$ b\bar{b} $ dijet production in p + p collision at$ \sqrt{s_{{ NN}}} = 7 $ TeV as a function of the azimuthal angle between two b-jets,$ \Delta \phi $ , calculated using SHERPA is compared with ATLAS data [33].Presently, the exact mechanism of the in-medium interaction between heavy quarks and the QCD medium is still an open question, which has been extensively investigated using both perturbative and nonperturbative approaches [50, 51]. Transport models such as the Langevin and Boltzmann approaches incorporated with the evolution profile of the bulk medium have been employed earlier for the description of the in-medium evolution of the heavy quark [44, 50, 52-60]. In a framework in which the in-medium evolution and energy loss of heavy and light quarks can be considered simultaneously, we employ a modified Langevin transport equation with an additional radiation term to include the radiative energy loss to describe the transport and energy loss (elastic and inelastic) of heavy quarks in hot and dense medium [54, 61, 62] as follows:
$\vec{x}(t+\Delta t) = \vec{x}(t)+\frac{\vec{p}(t)}{E}\Delta t,$

(1) $\vec{p}(t+\Delta t) = \vec{p}(t)-\Gamma\vec{p} \Delta t+\vec{\xi}(t)-\vec{p}_g, $

(2) where
$ \Delta t $ is the evolution time step defined in the simulation;$ \Gamma $ is the drag coefficient that can control the strength of the elastic energy loss, and$ \vec{\xi}(t) $ is the stochastic term representing the random kicks by quasiparticles in such a thermal medium and obeys$ \left \langle \xi^i(t)\xi^j(t') \right \rangle = \kappa \delta^{ij}\delta(t-t') $ , where$ \kappa $ is the diffusion coefficient. The classic fluctuation-dissipation relation [63] between$ \Gamma $ and$ \kappa $ has been employed:$ \kappa = 2\Gamma ET = \frac{2T^2}{D_s}, $

(3) where
$ D_s $ is the spatial diffusion coefficient. Over the years,$ D_s $ has been used as a parameter to represent the strength of the elastic interaction between heavy quarks and the thermal medium, and it has been calculated using several theoretical models [64-67]. We note that lattice calculations allow the prediction of a range of values of$ D_s $ :$ 2\pi TD_s\sim 3.7-7.0 $ [51, 68]. The inclusion of the last term$ \vec{p}_g $ in the momentum update equation is an effective treatment; it is assumed that the radiative energy loss of the heavy quark is carried away by the radiative gluon. The calculation of such a term is based on the higher-twist scheme [69-72], which can provide the radiative gluon spectrum:$ \frac{{\rm d}N}{{\rm d}x{\rm d}k^{2}_{\perp}{\rm d}t} = \frac{2\alpha_{s}C_sP(x)\hat{q}}{\pi k^{4}_{\perp}}\sin^2\left(\frac{t-t_i}{2\tau_f}\right)\left(\frac{k^2_{\perp}}{k^2_{\perp}+x^2M^2}\right)^4, $

(4) where x and
$ k_\perp $ are the energy fraction and the transverse momentum of the radiated gluon, respectively, and M is the mass of the parent parton. In addition,$ C_s $ is the quadratic Casimir in color representation,$ P(x) $ is the splitting function in vacuum [73],$ \tau_f = 2Ex(1-x)/(k^2_\perp+x^2M^2) $ is the time required for the gluon to form, and$ \hat{q} $ is the jet transport parameter proportional to the local parton density in the medium when the jet is probed. The time-space evolution of the QCD medium can thus be considered by altering the value of$ \hat{q} $ relative to its initial value$ \hat{q}_0 $ in the exact center of the overlap region at the initial time when the QGP is formed [74]. Therefore,$ \hat{q}_0 $ is the other parameter used for controlling the strength of the bremsstrahlung jet-medium interaction.In the simulation, the particles listed in the p + p events with the full vacuum parton shower produced by SHERPA, with their initial positions sampled from the Glauber model, serve as the input for the in-medium evolution. A heavy quark evolves in the QCD medium with the modified Langevin formalism, described above, in a fixed evolving time step when the position and momentum of a light quark update simultaneously. A Poisson probability distribution is implemented to compare with uniform random numbers to determine whether radiative energy loss occurs in a given Langevin evolution time step for both heavy and light quarks. It is expressed as
$ P_{\rm rad}(t,\Delta t) = 1-{\rm e}^{-\left\langle N(t,\Delta t)\right\rangle}, $

(5) where
$ \left\langle N(t,\Delta t)\right\rangle $ is the averaged radiative gluon number in the fixed update time step$ \Delta t $ at a certain evolution time t and can be derived by integrating Eq. (4). If radiation occurs, the number of radiated gluons can then be sampled by this distribution [Eq. (5)]. x and$ k_\perp $ can be sampled according to the radiative gluon spectrum expressed in Eq. (4) to obtain the momentum of the radiated gluon. Therefore, the$ \vec{p}_g $ term of Eq. (2) in each time interval is determined. Note that the four-momentum of the heavy quark will first be boosted into the local rest frame, then will be updated according to Eq. (2), and will be boosted back into the laboratory frame at every evolution time step, so that it can update its position.The smooth iEBE-VISHNU hydro model [75] has been used to provide the evolution information in a hot and dense medium. During the in-medium simulation, each parton propagates in the expanding medium until the probed temperature of the local medium is under
$ T_c = 165 $ MeV. In this manuscript, we directly set the free parameter$ \hat{q}_0 = 1.2 $ GeV2/fm, which is the best value taken from the global extraction of the identified hadron production in Pb + Pb collisions at$ 2.76 $ TeV in our previous work [76], as the properties of the QGP medium are also described by the smooth iEBE-VISHNU hydro model therein.It is noted that the treatment of including radiative energy loss in the Langevin equation [Eq. (2)] is an effective approach to simulate the in-medium evolution of heavy quarks, as it is difficult to include radiative energy loss without disturbing the fluctuation-dissipation relation. A lower energy cut to the radiative gluon is imposed to ensure that the heavy quark can reach thermal equilibrium in the low-
$ p_{\rm T} $ regime, as it can naturally be dominated by elastic energy loss in such a regime [54, 77]. There are actually two free parameters in this framework:$ \kappa $ , which controls the elastic energy loss of the heavy quark, and$ \hat{q}_{0} $ , which controls the strength of the medium-induced radiative energy loss from both the light and heavy quarks. In addition, we neglect the energy loss caused by the collision of the light quark and the gluon, owing to their small contributions to the total energy loss of the light quark at a higher value of$ p_{\rm T} $ [78]. Recently, this framework was extended to the study of the medium modifications of the radial distributions of$ D^0 $ meson inside jets in Pb + Pb collisions relative to those in the p + p collisions at the LHC, and a decent agreement was observed between the model calculations and the experimental measurement [62]. -
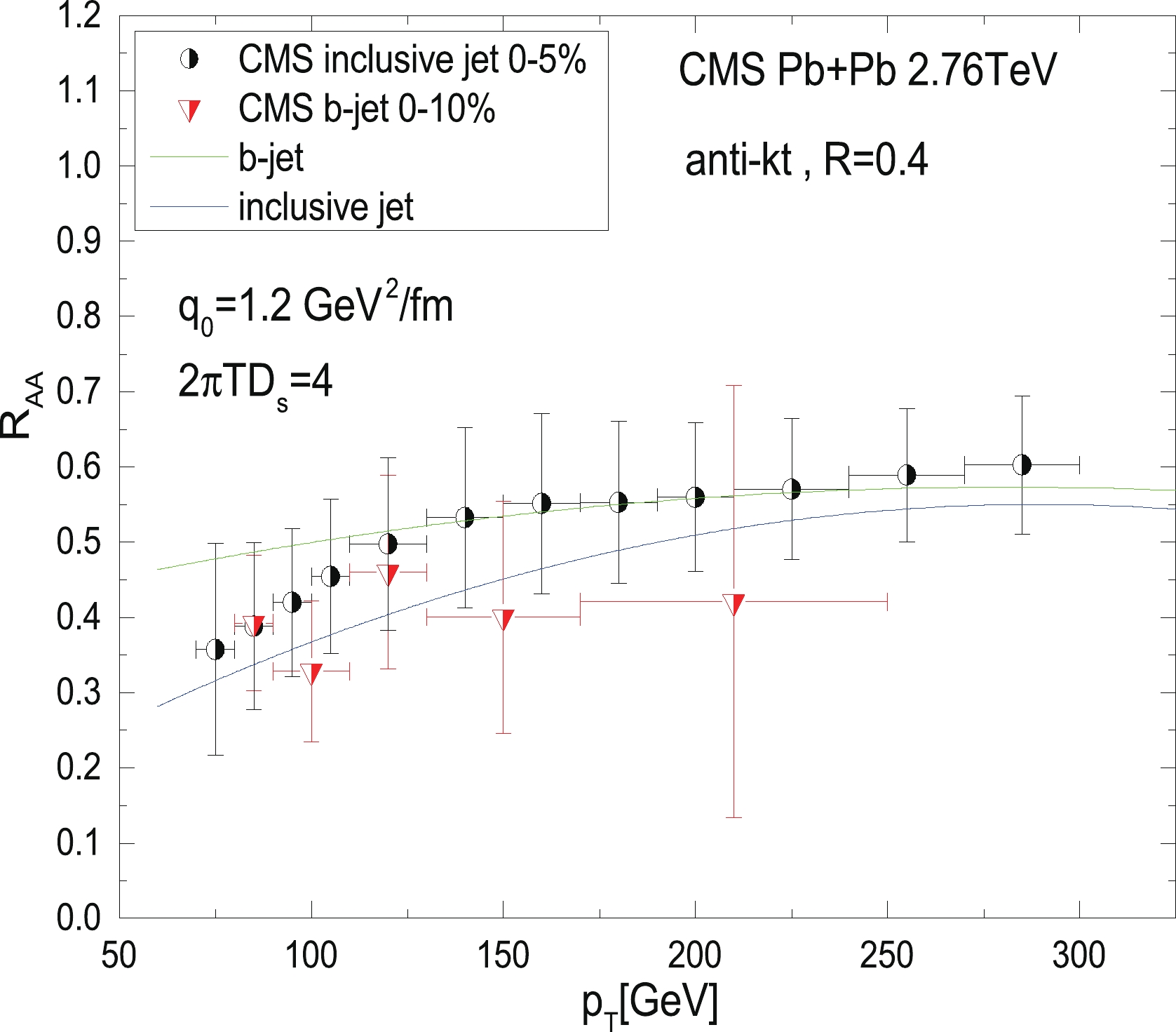
After the SHERPA generates the p + p events evolved in the above framework, we obtain the final-state partons, which include the partons produced, jet shower, and radiated gluon after their in-medium modification. Implementing the jet reconstruction as well as jet selection through FASTJET [47] on these final-state partons, we could derive the jet production in the Pb + Pb collisions at the LHC. Comparing this production with that in their p + p counterparts, we can study the medium modification of jet observables. To test the validation of this framework as well as to verify its performance, we first calculate the nuclear modification factor with respect to the jet
$ p_{\rm T} $ of both inclusive jets and inclusive b-jets in the Pb + Pb collisions at the LHC,$ \sqrt{s} = 2.76 $ TeV, to compare with the experimental data [48, 49]. We extracted the spatial diffusion factor$ D_s $ from the lattice that satisfies$ 2\pi TD_s = 4.0 $ and the jet transport parameter from the hadron suppression study, which is$ \hat{q}_0 = 1.2 $ GeV2/fm, as mentioned in the preceding section. We found that our simultaneous simulation for both inclusive jets and inclusive b-jets$ R_{\rm{AA}} $ can describe the CMS data [49] fairly well within the margin of error; only the simulation for inclusive b-jet$ R_{\rm{AA}} $ slightly overestimates the CMS data presented in Fig. 2, which is similar to the calculation presented in Refs. [27, 28]. With the parameters chosen as mentioned above, our prediction indicates that, in the lower-$ p_{\rm T} $ region, the heavy quark jets suffer less energy loss than the light ones. However, the mass effect of the jet quenching tends to disappear when it reaches the higher-$ p_{\rm T} $ regime, where the$ R_{\rm{AA}} $ values of the inclusive b-jets coincide with those of the inclusive jets. The establishment of such an evolution framework allows us to investigate the modification of the medium of the$ b\bar{b} $ dijet production in the A + A collisions.The momentum balance of the
$ b\bar{b} $ dijets is defined as the ratio of the$ p_{\rm T} $ of the sub-leading jet to that of the leading jet:$ x_{\rm J} = p_{\rm T,2}/p_{\rm T,1} $ . These two leading jets are required to be b-jets. We demonstrate the simulation results of the normalized distributions of$ x_{\rm J} $ in p + p and Pb + Pb collisions for$ b\bar{b} $ dijets to compare with experimental data. As for the same selection with the CMS experiment, we set the minimum$ p_{\rm T} $ cut of the leading and the sub-leading jets to be$ 100 $ and$ 40 $ GeV, respectively. Further, the selection of$ \vert \Delta \phi \vert > 2\pi/3 $ was also applied to ensure that the opening angles of the two jets are back-to-back in azimuth, both in the p + p and A + A collisions. A similar smearing treatment suggested by CMS was performed to compare with the CMS data, as presented in Fig. 3. Note that the p + p reference in the experiment is obtained from each jet$ p_{\rm T} $ data smeared by resolution parametrization at a given centrality, and our results are consistent with both the p + p and Pb + Pb experimental measurements at$ 5.02 $ TeV. The energy loss effect will suppress the distribution in the larger-$ x_{\rm J} $ region and enhance it at lower$ x_{\rm J} $ . It, therefore, leads to a lower shift in the overall$ x_{\rm J} $ distribution. We note that the shift in the A + A$ x_{\rm J} $ distribution relative to the p + p reference is quite visible in the central collisions depicted in the left plots. A much smaller shift is observed at the 10%-30% Pb + Pb collisions depicted in the bottom panel of Fig. 3, suggesting lower energy loss suffered in more peripheral collisions, which is consistent with the case in dijets [34].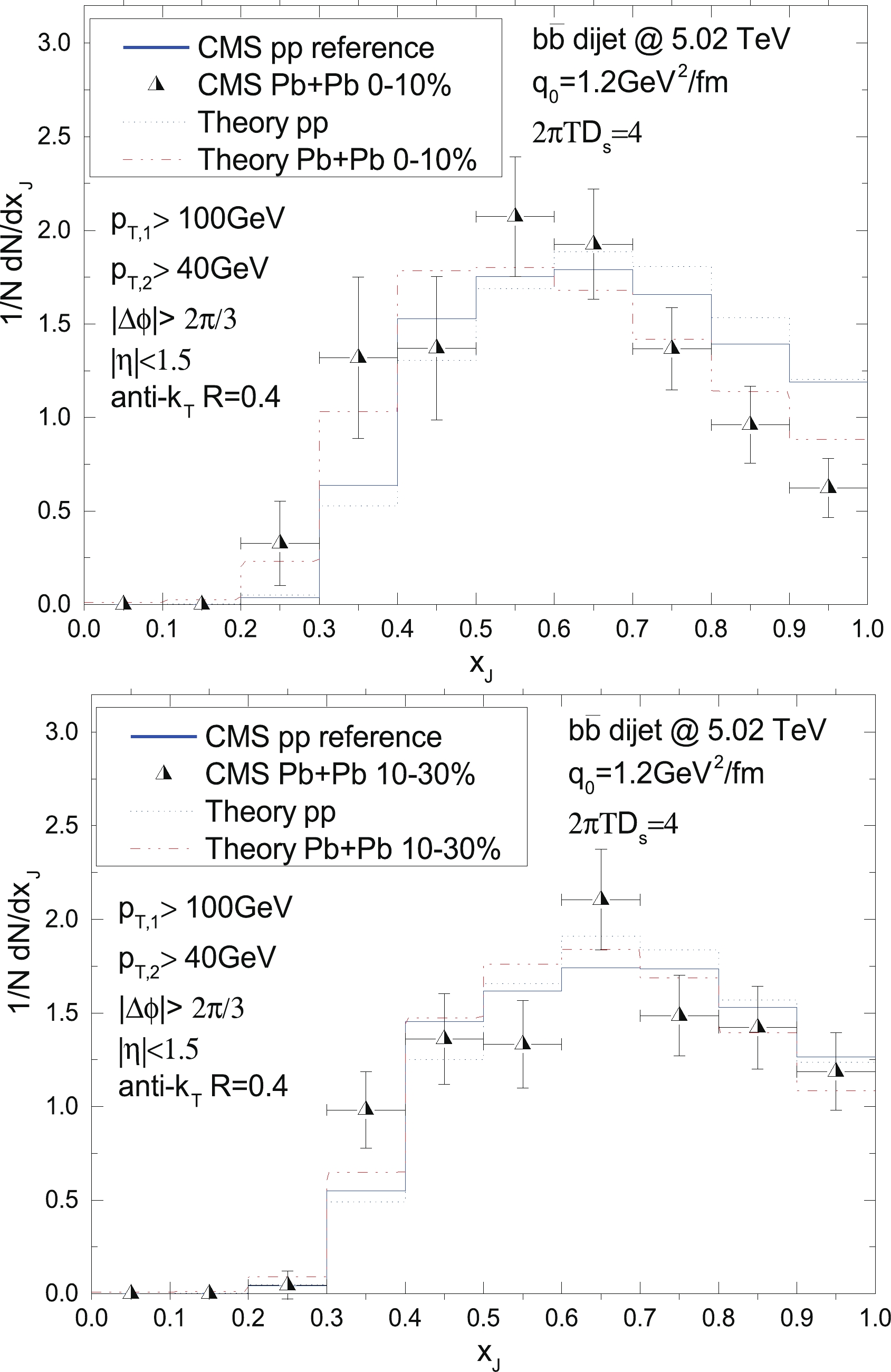
Figure 3. (color online) Upper: Calculated normalized
$ x_{\rm J} $ distribution of$ b\bar{b} $ dijets in p + p and 0%-10% Pb + Pb collisions at$ 5.02 $ TeV compared with the smeared p + p baseline and experimental data in A + A collisions. Bottom: Calculated normalized$ x_{\rm J} $ distribution of$ b\bar{b} $ dijets in p + p and 10%-30% Pb + Pb collisions at$ 5.02 $ TeV compared with the smeared p + p baseline and experimental data in A + A collisions.To further demonstrate the centrality dependence of the jet quenching effects on the momentum balance of the
$ b\bar{b} $ dijets, we calculate the averaged$ x_{\rm J} $ values as functions of the number of participants obtained in the Pb + Pb collisions and the smeared p + p reference. A comparison of the values in systems with different centralities and the corresponding CMS data is presented in the bottom plots in Fig. 4. A good agreement is observed between the theoretical calculations and experimental data. We find that the imbalance increases with the increasing centrality, and even the averaged$ x_{\rm J} $ of the p + p reference shifts to a smaller value with the increasing centrality, which is attributed to the resolution effects introduced by the experiment. More significantly, the shift in the averaged$ x_{\rm J} $ value owing to the jet quenching effect is well visible in the central collision. However, the imbalance in larger centrality, such as in a 30%-100% Pb + Pb collision, is compatible with their p + p reference, which is unlike the case of the dijets depicted in the upper plots in Fig. 4, indicating a lower energy loss than inclusive dijets in a smaller centrality system.
Figure 4. (color online) Upper: Averaged
$ x_{\rm J} $ in inclusive dijet production as a function of the number of participants calculated in p + p and Pb + Pb collisions at different centralities compared with experimental p + p references and A + A data, respectively. Bottom: Averaged$ x_{\rm J} $ in$ b\bar{b} $ dijet production as a function of number of participants calculated in p + p and Pb + Pb collisions at different centralities compared with experimental p + p references and A + A data, respectively.As the three production mechanisms can be experimentally separated by three event categories in the azimuthal angle plane, it is essential to investigate the azimuthal angle distribution of the
$ b\bar{b} $ productions in the p + p collisions and its modification in the A + A collisions. We find that its structure is quite sensitive to the selection of the jet event. When ATLAS defines the dijet system such that the minimum transverse momentum of the two highest-$ p_{\rm T} $ b-jets in an event should be$ p_{\rm T} > 20 $ GeV and also$ \vert \eta \vert < 2.5 $ GeV, requiring that their distance should be at least$ \Delta R = 0.4 $ and the$ p_{\rm T} $ of the trigger jet should be greater than$ 270 $ GeV [33]. Our simulation on the production for$ b\bar{b} $ dijets normalized by the number of events in the p + p collisions provided by SHERPA can describe the experimental data quite well (as seen in the upper plots of Fig. 1), particularly at the same-side peak ($ \Delta \phi \to 0 $ ), which can be attributed to domination by the GSP process. Similar to the case of inclusive dijets, the angular correlation of the$ b\bar{b} $ dijet would also be modified by the hot and dense medium. We present the prediction of the medium modification for the angular correlation of$ b\bar{b} $ dijets and inclusive dijets in Pb + Pb collisions at$ \sqrt{s} = 5.02 $ TeV with a centrality of 0%-10% using the CMS configuration in the upper panel of Fig. 5. The same-side peaks of the$ b\bar{b} $ dijets disappear even in the p + p collisions as compared to the ATLAS measurement reported above. The energy loss effect will suppress the distribution at small$ \Delta \phi $ and enhance the distribution at large$ \Delta \phi $ , both for the$ b\bar{b} $ and inclusive dijets. In such selected b-jets, the b quark poses 80%$ \to $ 95% energy of the jets in the p + p collision. However, if we implement the configuration of ATLAS in the Pb + Pb collisions at$ 5.02 $ TeV, the minimum transverse momentum of the two highest-$ p_{\rm T} $ b-jets (or jets) in an event should be set at$ p_{\rm T} > 15 $ GeV and the leading jet$ p_{\rm T}>100 $ GeV, as shown in the bottom panel of Fig. 5. We find that the energy loss effect on the inclusive dijet production is similar to that in the upper plots, and this effect on the$ b\bar{b} $ dijet production would suppress and broaden the same-side (small$ \Delta \phi $ ) peak as well as enhance and sharpen the far-side (near$ \Delta \phi = \pi $ ) peak. However, an overall suppression is found, which means that it suffers a stronger suppression in the small-angle region when compared with the large-angle region. Because the$ b\bar{b} $ dijets produced at the small opening angle are dominated by the GSP processes, these b-jets are relatively "softer'' than those produced by FCR. The energy loss effect would cause the$ p_{\rm T} $ of the low-energy b jet to fall below the threshold of the event selection of the$ b\bar{b} $ dijet observables.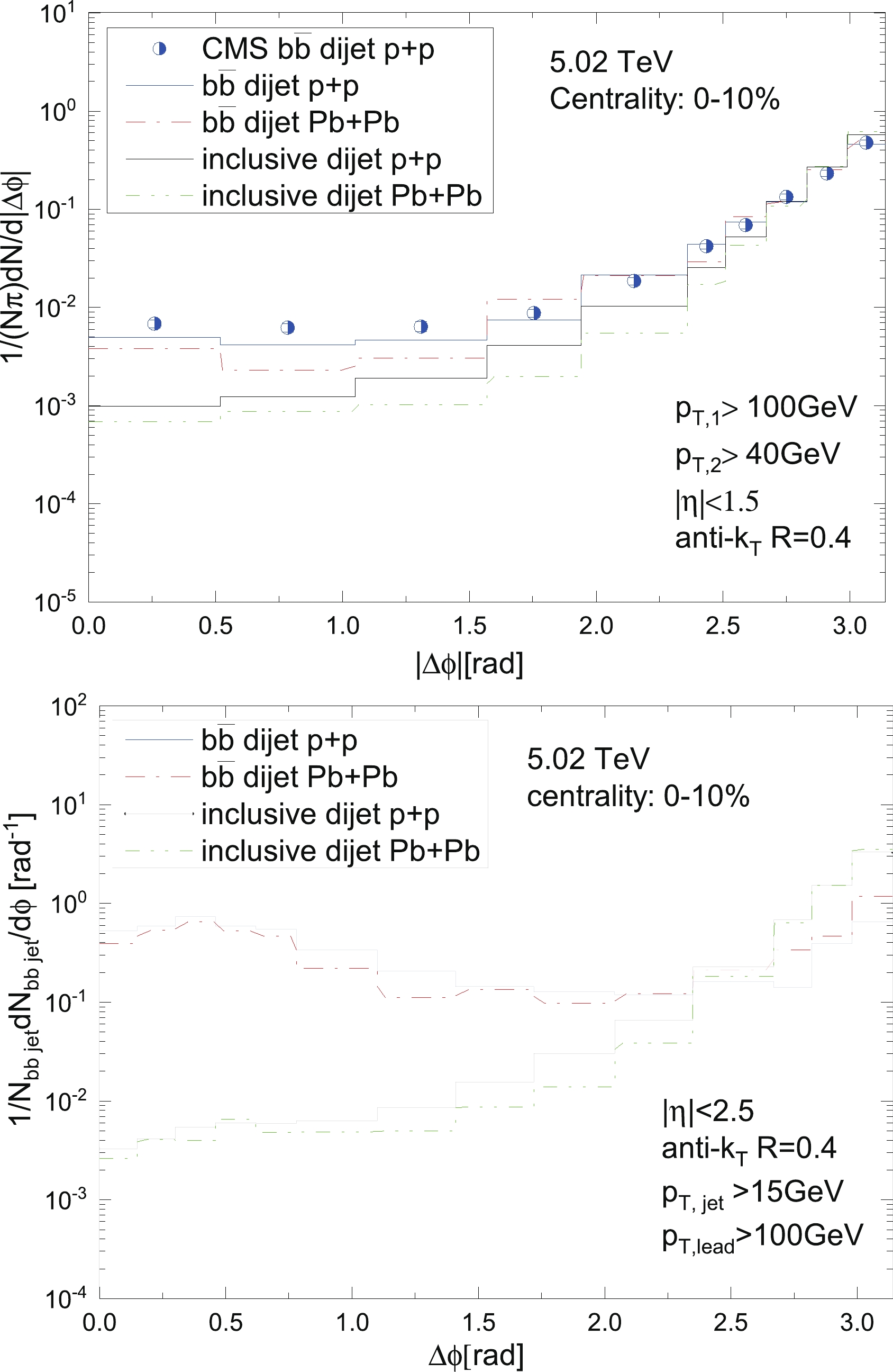
Figure 5. (color online) Upper: Production of
$ b\bar{b} $ dijets and inclusive dijets normalized by number of events as functions of$ \Delta \phi $ in p + p and Pb + Pb collisions at$ 5.02 $ TeV using CMS configuration [34] as compared to$ b\bar{b} $ dijets p + p data. Bottom: Production of$ b\bar{b} $ dijets and inclusive dijets normalized by number of events as functions of$ \Delta \phi $ in p + p and Pb + Pb collisions at$ 5.02 $ TeV using the lower minimum requirement of jets,$ p_{\rm T} = 15 $ GeV. -
In summary, using the NLO + PS event generator SHERPA, we implement a Monte Carlo simulation to consider the collisional and radiative energy loss of heavy and light quarks simultaneously in a hot and dense medium. For the first time, we present the theoretical calculation of the transverse momentum balance
$ x_{\rm J} = p_{\rm T,2}/p_{\rm T,1} $ of the$ b\bar{b} $ dijet in Pb + Pb collisions at$ 5.02 $ TeV and compare it with the recent CMS measurement. We find that, in$ b\bar{b} $ dijets, the$ x_{\rm J} $ -distribution shifts to a lower value owing to the in-medium jet interaction, similar to that observed in inclusive dijets. Furthermore, a comparison between the deviations in$ \left\langle x_{\rm J} \right\rangle_{\rm pp}- \left\langle x_{\rm J} \right\rangle_{\rm PbPb} $ of inclusive dijets and$ b\bar{b} $ dijets at different centralities indicates lower energy loss in$ b\bar{b} $ dijets than in inclusive dijets with increasing centralities. Finally, we find that the energy loss effect will suppress the same-side peak and enhance the far-side peak of the normalized$ \Delta \phi $ distribution in the central Pb + Pb collisions at$ 5.02 $ TeV. This can be attributed to the fact that the near-side peak distribution is dominated by the contribution of the GSP processes, and most of them are low-energy$ b\bar{b} $ dijets; the$ p_{\rm T} $ of the$ b\bar{b} $ dijets can easily be reduced to fall below the kinetic cut.The authors would like to thank D. Naplettano for a helpful discussion on SHERPA as well as P. Zhuang, K. Zhou , Z. Xu, and S. Chen for helpful discussions on heavy-flavor transport.
Transverse momentum balance and angular distribution of ${{b\bar{b}}}$ dijets in Pb + Pb collisions
- Received Date: 2020-05-12
- Available Online: 2020-10-01
Abstract: In this study, the production of inclusive b-jet and






 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF






















 DownLoad:
DownLoad: