-
Dark Matter (DM) with mass of a few hundred GeVs, which is known as the weakly interacting massive particle (WIMP), is one of the leading motivations for weak-scale new physics beyond the standard model (SM). Any such new physics, if it exists, should play an important role at the LHC. If WIMP-like DM can be detected via DM direct-detection experiments, the LHC can serve as a useful tool for verification. More interestingly, if WIMP-like DM cannot be detected via DM direct detection, the LHC serves as an alternative discovery platform. This paper is devoted to addressing the following question: What is the potential of high-luminosity (HL) [1-3] LHC probes of general WIMP-like DM.
WIMP-like DM can be hosted in a variety of weak-scale new physics. For instance, it can be identified as the neutral fermion in the fourth-generation lepton model [4, 5], where there are mixing effects between the new leptons and SM leptons, the lightest neutralino in the minimal supersymmetric standard model (MSSM) [6], in the next-to-minimal supersymmetric standard model (NMSSM) [7], or the lightest neutral fermion in singlet-doublet (SD) [8-10] and vector-like (VL) lepton model [11-14], where there is no direct mixing with SM leptons. In the various aforementioned contexts, there are diverse interactions and model parameters. As a result, it seems difficult to work on universal predictions, such as WIMP-like DM. To address this question, the first task is to determine a framework viable for the most sophisticated WIMP-like DM models.
This paper is organized as follows. In Sec. 2, we employ a framework that can describe the three above-mentioned benchmark WIMP-like DM models, where we introduce model parameters. In Sec. 3, we uncover the DM parameter space, which satisfies the DM relic density and survives in the latest DM direction-detection limits. Sec. 4 is devoted to explore the exclusion as well as discovery potentials on the DM mass ranges in light of LHC probes of lepton pairs in the Z- and W-associated electroweak processes such as
$pp \to \ell^\pm \ell^\mp+ E_T^{\rm{miss}}$ ,$ pp \to \ell^\pm \ell^\mp jj + E_T^{\rm{miss}} $ , and$ pp \to \ell^\pm \ell^\mp \ell^\pm + E_T^{\rm{miss}} $ at the HL-LHC, where$ \ell $ , j, and$ E_T^{\rm{miss}} $ refer to lepton, jet, and missing energy, respectively. The samples used for event simulations are directly extracted from the parameter space of electroweak DM. Finally, we conclude this paper in Sec. 5. -
In various contexts of weak-scale new physics, the SM electroweak sector is extended by a couple of electroweak doublets
$ E^{\pm} $ $ E^{+} = \left( \begin{array}{c} \eta^{+} \\ \eta^{0}\\ \end{array} \right), \; \; E^{-} = \left( \begin{array}{c} \tilde{\eta}^{0} \\ \eta^{-}\\ \end{array} \right), $

(1) for which the effective Lagrangian at the weak scale can be described as
$ {\cal{L}}\supset \frac{{\rm i}}{2}\overline{E^{+}}{\not\!\!{D}}E^{+} + \frac{\rm i}{2}\overline{E^{-}}{\not\!\!{D}}E^{-}-m_{E}E^{+}E^{-}, $

(2) with
$ m_E $ being a vectorlike (VL) mass. If there are no other mass sources for the doublets, the charged fermion$ \chi^{\pm} $ composed of$ (\eta^{+},\overline{\eta^{-}}) $ and the neutral fermion$ \chi^{0} $ composed of$ (\eta^{0},\tilde{\eta}^{0}) $ will have nearly degenerate masses$ m_{\chi^{\pm}}\simeq m_{\chi^{0}} $ up to a small radiative correction [5]. This mass degeneracy kinematically suppresses the decay$\chi^{\pm}\rightarrow \chi^{0}W^{\pm}$ , and reduces the signal of the lepton pair$ \chi^{+}\chi^{-} $ .The mass degeneracy disappears whenever there are moderate or large mixing effects. The mixing effects can be classified into two different types. In the first type,
$ E^{\pm} $ directly mixes with SM leptons as in the fourth-generation lepton models. In the second type,$ E^{\pm} $ mixes with some new fermion singlets N as in the MSSM, NMSSM, SD, and VL lepton models, which gives rise to sufficient splitting between the charged and neutral fermion masses. The scope of this paper is restricted to the large mass splitting driven by the electroweak singlet fermion.In this case, the Lagrangian
$ {\cal{L}} $ in Eq. (2) is modified by$ \delta{\cal{L}}\supset \frac{{\rm i}}{2} N{\not\!\!{\partial}}N-\frac{m_{N}}{2}N^{2}-(y_{1}N\overline{E^{+}}+y_{2}NE^{-})H+{\rm{h.c}},\\ $

(3) where
$ m_N $ is the singlet mass and H refers to the SM Higgs doublet with a vacuum expectation value (vev)$ \upsilon = 174 $ GeV. Note that some parity should be imposed in Eq. (2) and Eq. (3) in order to keep the electroweak DM stable. With the new Yukawa interactions in Eq. (3), the neutral fermions are now composed of$ (N,\eta^{0}, \tilde{\eta}^{0}) $ , whose mass matrix$ M_{\chi^{0}} $ is given by$ {\cal{M}}_{\chi^{0}} = \left( \begin{array}{ccc} m_{N} & y_{1}\upsilon & y_{2}\upsilon \\ * & 0 & m_{E} \\ * &* & 0\\ \end{array} \right). $

(4) The mixing effects in Eq. (4) are responsible for the mass splitting between the three neutral fermion mass
$ m_{\chi^{0}_{i}} $ ($ i = 1-3 $ ) and charged fermion mass$ m_{\chi^{\pm}} $ .Under the basis of mass eigenvalues, the Lagrangian is rewritten as
$ \begin{split} {\cal{L}}\supset-& h\overline{\chi^{0}_{i}}\left(c_{h,ij}P_{L}+c^{*}_{h,ij}P_{R}\right)\chi^{0}_{j}\\ &-Z_{\mu}\overline{\chi^{0}_{i}}\gamma^{\mu}\left(c_{Z,ij}P_{L}-c^{*}_{Z,ij}P_{R}\right)\chi^{0}_{j}\\ -&\left[\frac{g}{\sqrt{2}}W_{\mu}^{-}\overline{\chi^{0}_{i}}\gamma^{\mu}(N_{i3}P_{L}-N_{i2}P_{R})\chi^{+}+{\rm{h.c}}\right] \end{split} $

(5) with
$ \begin{split} c_{Z,ij} =& \frac{g}{4c_{W}} \left(U_{i3}U^{*}_{j3}-U_{i2}U^{*}_{j2}\right),\\ c_{h,ij} =& \frac{1}{\sqrt{2}}\left(y_{2}U_{i3}U^{*}_{j1}+y_{1}U_{i2}U^{*}_{j1}\right), \end{split} $

(6) where
$ c_W $ and g denote the weak mixing angle and weak gauge coupling constant, respectively, and the unitary matrix U is introduced to diagonalize$ {\cal{M}}_{\chi^{0}} $ . We have written fermions in the 4-component notation, with$ \chi^{+} = (\eta^{+}, \overline{\eta^{-}}) $ and$ \chi^{0}_{i} = (\chi^{0}_{i}, \overline{\chi^{0}_{i}}) $ . In this setting, the lepton pair is a couple of$ \chi^{\pm} $ and$ \chi^{0}_{i} $ ($ i = 2,3 $ ), with their couplings to the SM sector given in Eq. (5). -
With the lightest neutral state
$ \chi^{0}_{1} $ identified as the thermal electroweak DM, we can determine the parameter space of DM relic density from Eq. (4) and Eq. (5). In the framework above, there are four parameters,$ y_1 $ ,$ y_2 $ ,$ m_N $ , and$ m_E $ . Since electroweak DM favors the coupling$ y = \sqrt{y^{2}_{1}+y^{2}_{2}} $ of the order of weak interactions$ \sim 0.3-1.0 $ and DM mass of the order of a weak scale,$ \sim 100-1000 $ GeV, we consider the following parameter regions,$ \begin{split} &{0.3 \leqslant y \leqslant 1.2,}\\ &{100\;{\rm{GeV}} \leqslant {m_E} \leqslant 1500\;{\rm{GeV}},}\\ &{100\;{\rm{GeV}} \leqslant {m_N} \leqslant 1500\;{\rm{GeV}},} \end{split}$

(7) over which we perform random scans, with
${\rm{sign}}({{y}}_{2}/{{y}}_{1})$ either being positive or negative.We employed the code micrOMEGAs [15] to calculate the relic density of the lightest neutral fermion
$ \chi^{0}_{1} $ , and recorded the spin-independent (SI) and spin-dependent (SD)$ \chi^{0}_{1} $ -nucleon scattering cross sections. Shown in Fig. 1 are the parameter spaces of the electroweak DM with$ {\rm{sign}}(y_{2}/y_{1})<0 $ (left panel) and$ {\rm{sign}}(y_{2}/y_{1})>0 $ (right panel), respectively. The two types of plots therein clearly indicate that the DM relic density is sensitive to both the magnitude of y and${\rm{sign}}({y}_{2}/{y}_{1})$ . We direct the reader's attention to Table 1 regarding${\rm{sign}}({{y}}_{2}/{{y}}_{1})$ in the benchmark electroweak DM models.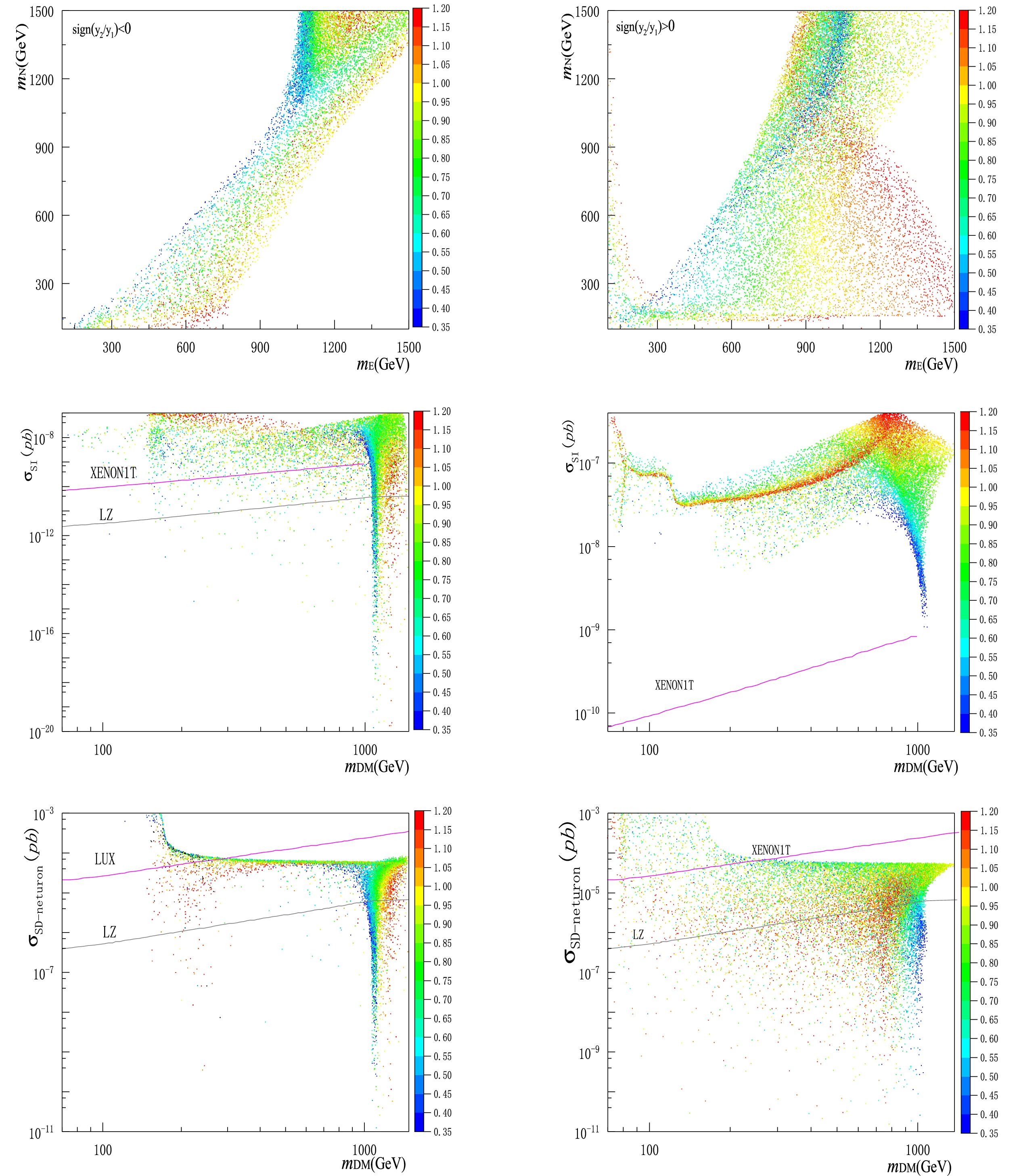
Figure 1. (color online) Plots in the left and right panels correspond to
$ {\rm{sign}}(y_{1}/y_{2})<0 $ and$ {\rm{sign}}(y_{1}/y_{2})>0 $ , respectively, where we show the parameter space of DM relic density$ \Omega{\rm{h}}^{2} = 0.12\pm 0.005 $ ($ {\rm{top}} $ ), the SI$ \chi^{0}_{1} $ -nucleon scattering cross section ($ {\rm{middle}} $ ), and the SD$ \chi^{0}_{1} $ -neutron scattering cross section ($ {\rm{bottom}} $ ) as functions of DM mass$ m_{\rm{DM}} $ and coupling y, with the Xenon1T [16], LUX [17], and the future LZ [18] limits shown for comparison.${\rm{model}}$ 

${\rm{fields}}$ 

y ${\rm{sign} }({{y} }_{2}/{{y} }_{1})$ 

${\rm{MSSM}}$ 

$\tilde{B}^{0}$ ,

$\tilde{h}_{u}^{0}$ ,

$\tilde{h}_{d}^{0}$ 

$0.35$ 

$-$ 

$\tilde{W}^{0}$ ,

$\tilde{h}_{u}^{0}$ ,

$\tilde{h}_{d}^{0}$ 

$0.63$ 

$-$ 

${\rm{SD}}$ 

N, $E^{0}$ ,

$\tilde{E}^{0}$ 

$0.7-1.0$ 

$\pm$ 

${\rm{VL}}$ 

N, $E^{0}$ ,

$\tilde{E}^{0}$ 

$1.0-1.2$ 

$\pm$ 

Table 1. Matter content, the magnitude of y, and
${\rm{sign}}({{y}}_{2}/{{y}}_{1})$ in various benchmark WIMP-like DM models. We focus on the parameter regions in the SD model which differ from the MSSM, and those in the VL model which are favored by the SM Higgs mass constraint.A few comments are in order regarding the parameter space of electroweak DM. Firstly, the left plots with
${\rm{sign}}({{y}}_{2}/{{y}}_{1}) < 0$ correspond to the simplified MSSM [19-23], SD [24, 25], and VL [14] models.● For the simplified MSSM, the coupling
$ y = e/\cos\theta_{W} $ and$ y = e/\sin\theta_{W} $ for simplified bino-higgsino and wino-higgsino systems, respectively, with$ \theta_{W} $ being the weak mixing angle. In both simplified models,$ y_{2}/y_{1}\rightarrow -\tan\beta $ , where$ \tan\beta $ is the ratio of two vacuum expectation values (vevs) of the Higgs doublets. The left middle and bottom plots show that portions of samples with$ y = 0.35 $ [23] or$ y = 0.63 $ [22] survive.● For either the SD or VL model, the parameter space with coupling
$ y>1 $ is nearly excluded for DM mass beneath$ 1 $ TeV if not entirely, in light of the Xenon1T limit, as shown in the left middle plot. This plot suggests that both the SD and VL models tend to survive in the small y region, which is consistent with the previous observations on the SD model in [24, 25] and the VL model in [14], respectively.Secondly, the plots in the right panel with
${\rm{sign}}({{y}}_{2}/{{y}}_{1}) > 0$ correspond to the SD [24, 25] and VL [14] models.● Comparing the two middle plots in Fig. 1 shows that the Xenon1T limit is more stringent in the situation with
${\rm{sign}}({{y}}_{2}/{{y}}_{1}) > 0$ , although the number of samples is relatively large in this case. It turns out that the DM mass between$ 1 $ TeV is almost excluded by the Xenon1T limit in this case, which strengthens the earlier results in Ref. [25].● The importance of
${\rm{sign}}({{y}}_{2}/{{y}}_{1})$ on the SI or SD cross section can be understood from the earlier analysis on blind spots in Ref. [19], under which either the SI or SD cross section is dramatically suppressed. From our setup in Eq. (7), the condition of blind spots for the SI cross section favors a negative${\rm{sign}}({{y}}_{2}/{{y}}_{1})$ .Finally, we would like to mention that our analysis not only reproduces, but also expands the parameter space beyond the three benchmark electroweak DM models, as shown in Table 1. Some of the new parameter regions may be useful for other models of new physics around the weak scale. Moreover, one observes that portions of samples are even below the sensitivity of the future LZ experiment. However, they may be within the reach of the LHC in the future, which is the subject of our ensuing discussion.
-
According to the effective Lagrangian in Eqs. (2)-(3), the production of new lepton pairs at the LHC, shown in Table 2, for which the Feynman diagrams can be found in Fig. 2, mainly depends on electroweak interactions with SM gauge bosons and Higgs scalar.
${\rm{lepton\;pair}}$ 

${\rm{SM\;background}}$ 

${\rm{Refs.} }$ 

$\chi^{+}\chi^{-}$ 

$pp \to \ell_{\alpha/\beta}^\pm \ell_{\alpha/\beta}^\mp+ E_T^{\rm{miss}}$ 

[26, 29, 30] $\chi^{\pm}\chi^{0}_{2}$ 

$pp \to \ell_{\alpha/\beta}^\pm \ell_{\alpha/\beta}^\mp jj' + E_T^{\rm{miss}}$ 

[26-28] $pp \to \ell_\alpha^\pm \ell_\alpha^\mp \ell_{\alpha/\beta}^\pm jj+ E_T^{\rm{miss}}$ 

[26-28] $\chi^{\pm}\chi^{0}_{2}$ 

$pp \to \ell_\alpha^\pm \ell_\alpha^\mp \ell_{\alpha/\beta}^\pm+ E_T^{\rm{miss}}$ 

[27, 28] Table 2. SM backgrounds for the electroweak production of lepton pairs
$\chi^{+}\chi^{-}$ and$\chi^{\pm}\chi^{0}_{2}$ , with subsequent electroweak decay to$\chi^{0}_{1}$ , where$j, j'$ and$\alpha,\, \beta$ refer to jets and charged leptons$\ell=\{e,\mu\}$ . For example, in the first case, the two leptons can have either the same or different flavors with opposite signs.
Figure 2. (color online) Feynman diagrams for the signal channels of new lepton pairs in Table 2.
Here, we focus on the electroweak production of lepton pairs, which subsequently decay into on-shell Z and/or W. The combination of DM direct detection experiments and LHC probes of lepton pairs makes our analysis intuitive, which differs from either
$ i) $ the experimental analysis [26-30] on the electroweakinos reported by the ATLAS and CMS collaborations, where the samples were not extracted from the electroweak DM parameter space, or$ ii) $ the DM direct-detection predictions on the electroweak DM as above, where the collider probes are unclear. Since we focus on the parameter space of electroweak DM as shown in Fig. 3, where the final lepton states are standard rather than soft due to the large mass splitting between the charged/heavier neutral states and DM, our analysis is also different from$ iii) $ the studies on the electroweak DM in the parameter space with small mass splitting, such as the disappearing tracks [31-34], mono-jets [34-38], and soft lepton final states [39-42].
Figure 3. (color online) An illustration of samples extracted from the parameter space of electroweak DM in the plots in the left panel of Fig. 1 in this work.
Shown in Table 2 are the SM backgrounds, by referring to the electroweak productions of lepton pairs
$ \chi^{+}\chi^{-} $ and$ \chi^{\pm}\chi^{0}_{2} $ at the LHC.● The electroweak production of lepton pair
$ \chi^{+}\chi^{-} $ is dominated by$ pp\rightarrow Z^{*} \rightarrow \chi^{+}\chi^{-} $ , which decays as$ \chi^{\pm}\rightarrow W^{\pm}\chi^{0}_{1} $ , with$ W\rightarrow \ell\nu $ . The SM background for this process is composed of two charged leptons with missing energy$ E_T^{\rm{miss}} $ .● The electroweak production of lepton pair
$ \chi^{\pm}\chi^{0}_{2} $ is similar to that of$ \chi^{+}\chi^{-} $ , which decays as$\chi^{\pm}\rightarrow W^{\pm}\chi^{0}_{1}\rightarrow jj\chi^{0}_{1}$ or$ \chi^{\pm}\rightarrow W^{\pm}\chi^{0}_{1}\rightarrow \ell \nu\chi^{0}_{1} $ and$ \chi^{0}_{2}\rightarrow Z\chi^{0}_{1}\rightarrow \ell\ell \chi^{0}_{1} $ , respectively. The SM backgrounds are composed of either two leptons and two jets with$ E_T^{\rm{miss}} $ or three leptons with$ E_T^{\rm{miss}} $ .For numerical calculation, we firstly use the package FeynRules [43] to prepare the model files for MadGraph5 [44], which contains the package Pythia 8 [45] for parton showering and hadronization, and the package Delphes 3 [46] for fast detector simulation. Then, we use Madgraph5 to generate
$ 2000 $ events for each sample that is directly extracted from the parameter space of electroweak DM. The total number of samples in the plots in the left panel in Fig. 1 is about$ \sim 3660 $ , some of which can yield the on-shell decays$ \chi^{\pm}\rightarrow \chi^{0}_{1}W^{\pm} $ and/or$ \chi^{0}_{2}\rightarrow \chi^{0}_{1}Z $ , and finally reveal both the exclusion and discovery limits at the 14 TeV LHC with the integrated luminosities 300 fb$ ^{-1} $ and 3000 fb$ ^{-1} $ , respectively.For selections of events, we use the 13-TeV cuts reported by the ATLAS collaboration in Ref. [27] and Ref. [30] for lepton pair
$ \chi^{\pm}\chi^{0}_{2} $ with SM backgrounds$ pp \to \ell_\alpha^\pm \ell_\beta^\pm jj + E_T^{\rm{miss}} $ or$ pp \to \ell_\alpha^\pm \ell_\beta^\pm \ell_\gamma^\pm+ E_T^{\rm{miss}} $ and lepton pair$ \chi^{+}\chi^{-} $ with SM background$ pp \to \ell_\alpha^\pm \ell_\beta^\pm + E_T^{\rm{miss}} $ , respectively. The effects on the event numbers due to deviation from the 14-TeV cuts are expected to be in percent level.We summarized the details regarding the cuts in Table 3, where
$ {p_{T}}^{l_{1(2)}} $ is the transverse momentum of the first (second) leading lepton$ \ell = \{e,\mu\} $ ,$ \eta_{e(\mu)} $ is the pseudo-rapidity of e($ \mu $ ), and$ m_{l_{1}l_{2}} $ is the invariant mass of the two leptons with same (or different) flavor for the lepton pair$ \chi^{+}\chi^{-} $ or the shell mass of the same lepton flavor for the lepton pair$ \chi^{\pm}\chi^{0}_{2} $ . In this table, the transverse mass is defined as$m_ {\rm{T}} = \sqrt{2\times|{{p}}_{\rm{T,1}}|\times|{{p}}_{\rm{T,2}}|\times(1-{\rm{cos}}(\Delta\phi))}$ , where$ \Delta\phi $ is the difference in azimuthal angles between the particles with transverse momenta${{p}}_{\rm{T,1}}$ and${{p}}_{\rm{T,2}}$ ,$n_{ {b}}$ is the number of b-tagging jets, variable$n_{{\rm non}-b}$ refers to the number of jets with$ p_{T}>30 $ GeV that do not satisfy the b-tagging criteria,$ m_{jj} $ is the invariant mass of the two leading jets, and the significance of missing energy$ E_{T, s}^{\rm{miss}} $ is linked to$ E_T^{\rm{miss}} $ by$ E_T^{\rm{miss}}/\sqrt{H} $ , with H being the transverse momenta of all final states.$\chi^{+}\chi^{-}$ 

$\chi^{\pm}\chi^{0}_{2}$ (2

$\ell$ 2j)

$\chi^{\pm}\chi^{0}_{2}$ (3

$\ell$ )

$p_{T}^{l_{1(2)}}$ 

$> 25$ 

$> 25$ 

$> 25$ 

$\eta_{e(\mu)}$ 

$> 2.47(2.7)$ 

$> 2.47(2.7)$ 

$> 2.47(2.7)$ 

$m_{l_{1}l_{2}}$ 

$> 100(121.2) $ 

81-101 81.2-101.2 $E_T^{\rm{miss}}$ 

$> 110$ 

$> 100$ 

$> 170$ 

$m_{T}$ 

$> 100$ 

− $> 110$ 

$n_{{\rm non}-b}$ 

0 2 0 $n_{{b} }$ 

0 0 0 $m_{jj}$ 

− 70-90 − $E_{T,s}^{\rm{miss}}$ 

$> 10$ 

− − Table 3. Main cuts used for event selections of both signals and backgrounds as shown in Table 2, where mass parameters have the unit of GeV. See text for definitions and explanations about these cuts.
For
$ pp \to \ell_\alpha^\pm \ell_\beta^\pm jj + E_T^{\rm{miss}} $ in the second column in Table 3, we need additional cuts as follows:$\Delta\phi_{(p_{T}^{\rm miss} ,Z)} < 0.8$ ,$\Delta\phi_{(p_{T}^{\rm miss} ,W)} > 1.5$ ,$ 0.6<E_T^{\rm{miss}}/p^{Z}_{\rm{T}}<1.6 $ , and$ E_T^{\rm{miss}}/p^{W}_{\rm{T}}<0.8 $ , in which the symbols W and Z correspond to the reconstructed W and Z bosons in the final state, because the Z boson is always reconstructed from the two leptons, whereas the W boson is reconstructed from the two jets. Here,$ p^{Z}_{\rm{T}} $ and$ p^{W}_{\rm{T}} $ are the transverse momenta of dileptons and dijets respectively, with$\Delta\phi_{(p_{T}^{\rm miss} ,Z)}$ or$\Delta\phi_{(p_{T}^{\rm miss} ,W)}$ referring to the azimuthal angle between the dilepton or dijets transverse momentum and$p_{T}^{\rm miss}$ .In terms of the cuts above, we can analyze the signal significances. We firstly show in Table 4 the simulations of events of the SM backgrounds. Then, we show in Fig. 4 and Fig. 5 both the 2
$ \sigma $ exclusion (left panel) and 5$ \sigma $ discovery limits (right panel) at the 14 TeV LHC with the integrated luminosity$ L = 300 $ fb$ ^{-1} $ and$ 3000 $ fb$ ^{-1} $ , respectively. In these figures, the top, middle and bottom plots refer to lepton pairs$ \chi^{+}\chi^{-} $ and$ \chi^{\pm}\chi^{0}_{2} $ , respectively, where the efficiencies among the three channels are comparable. The combination of the individual results yields our final observations:channel $\sigma_{\rm{LO} }/{\rm{fb} }$ 

$N_{\rm{tot}} $ 

$N_{\rm{re}}$ 

$pp \to W^{+}W^{-} \to 2l + E_T^{\rm{miss}}$ 

$3300$ 

$1\times 10^{5}$ 

$51$ 

$pp \to WZjj \to 3l +2j+ E_T^{\rm{miss}}$ 

$540$ 

$1\times 10^{5}$ 

$7$ 

$pp \to ZZjj \to 2l +2j+ E_T^{\rm{miss}}$ 

$100$ 

$1\times 10^{5}$ 

$12$ 

$pp \to WZ \to 3l+ E_T^{\rm{miss}}$ 

$800$ 

$1\times 10^{6}$ 

$10$ 

Table 4. Raw data of the simulations of SM backgrounds in Table 2, where
$\sigma_{\rm{LO}}$ is the leading-order (LO) cross section, and the efficiencies on the SM backgrounds after cuts imposed are given by$\epsilon=N_{\rm{re}}/N_{\rm{tot}}$ , with$N_{\rm{tot}}$ and$N_{\rm{re}}$ referring to the numbers of events before and after cuts imposed, respectively.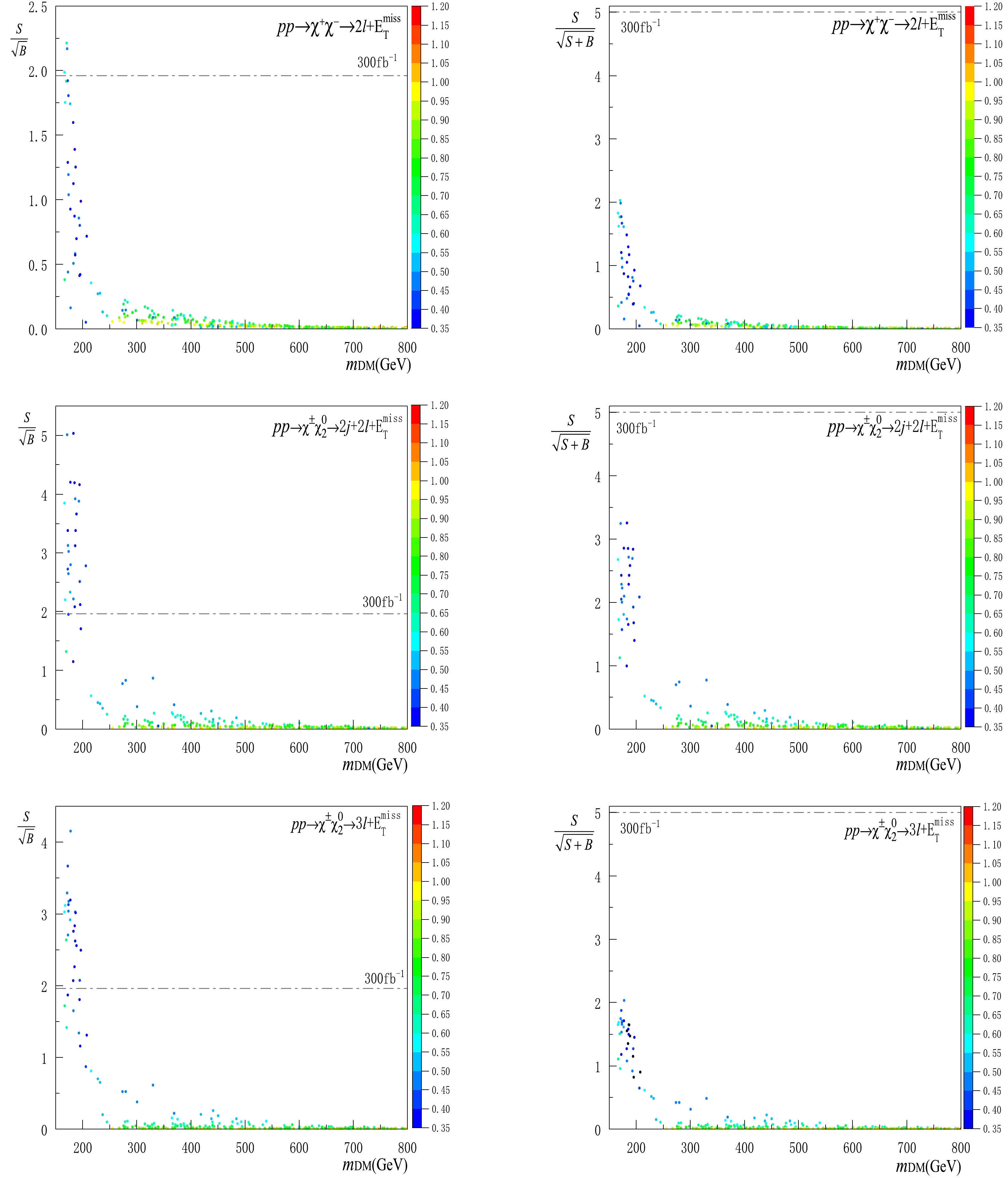
Figure 4. (color online) Plots in the left and right panels refer to 2
$ \sigma $ exclusion and 5$ \sigma $ discovery, respectively, at the 14 TeV LHC with the integrated luminosity$ L = 300 $ fb$ ^{-1} $ , where the lepton pairs$ \chi^{+}\chi^{-} $ and$ \chi^{\pm}\chi^{0}_{2} $ are shown in the top as well as middle and bottom plots, respectively. All the samples used for event simulations are extracted from the DM parameter space of the plots in the left panel in Fig. 1, which satisfy the DM relic density and survive in the DM direct detections simultaneously.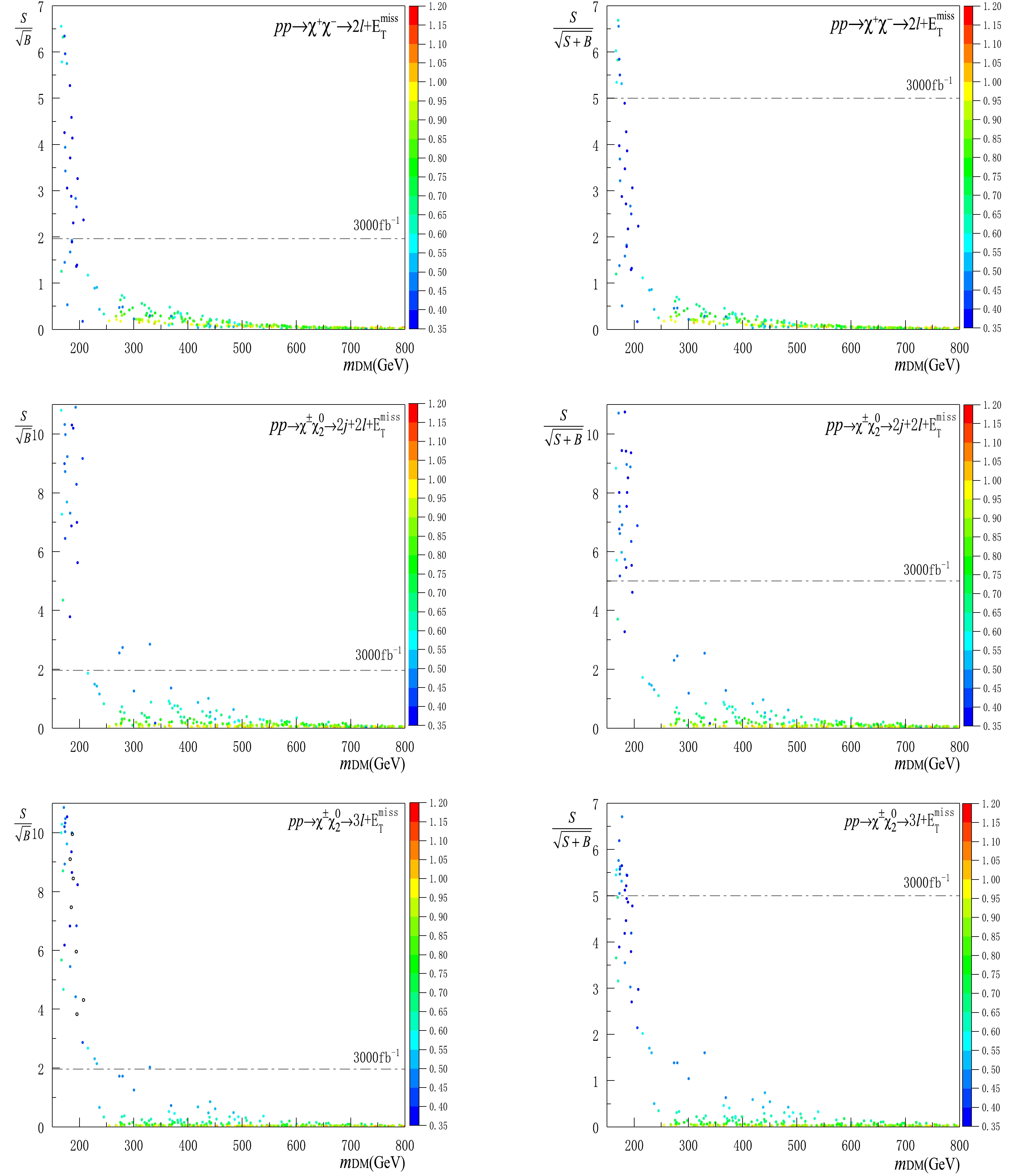
Figure 5. (color online) Same plots as those in Fig. 4 with
$ L = 3000 $ fb$ ^{-1} $ instead.● In the coupling range
$ y\sim 0.35-0.5 $ represented by the dark blue points, which is viable for the bino-higgsino system, the DM mass range of$ \sim 170-210 $ GeV can be excluded at the 2$ \sigma $ level with$ L = 300 $ fb$ ^{-1} $ , and the DM mass range of$ \sim 175-205 $ GeV can be discovered at 5$ \sigma $ level with$ L = 3000 $ fb$ ^{-1} $ . These limits are comparable with those [41] of soft lepton final states, where the exclusion and discovery limits are$ \sim 200-280 $ GeV and$ \sim 130 $ GeV, respectively. For previous discussions regarding simplified MSSM at the LHC, see Refs. [47-49].● In the coupling range
$ y\sim 0.5-0.65 $ illustrated by the blue points, which can be applied to the wino-higgsino system, the DM mass range of$ \sim 172-210 $ GeV can be excluded at the 2$ \sigma $ level with$ L = 300 $ fb$ ^{-1} $ , and the DM mass range of$ \sim 180-200 $ GeV can be discovered at the 5$ \sigma $ level with$ L = 3000 $ fb$ ^{-1} $ .● In the coupling range
$ y\sim 0.65-1.0 $ represented by the green and orange points, which is viable for the SD and VL models, all samples with DM mass above$ \sim 250 $ GeV give rise to very small significances. Thus, they are beyond the detection scope of the LHC. For a previous discussion on this point, see Ref. [50].Our analysis presented above is subject to both the Monte Carlo (MC) based uncertainties and the systematic uncertainties. For the MC uncertainties, the LO cross sections for both the signals and their SM backgrounds can be enhanced by the higher-order QCD effects [51, 52]. The K-factors
$ k_{b} $ with respect to the WW and WZ channels in Table 4 are of the order of$ \sim1.67 $ and$ \sim1.85 $ , respectively, implying that for the inferred K-factor$ k_{s} $ of the order of$ \sim 1.2-1.3 $ for the signals, the significances plotted in Fig. 4 and Fig. 5 are corrected by a factor of$ \sim6 $ % and$ \sim9 $ %, respectively. For the systematic uncertainties, even though those in the lepton reconstruction efficiency and the b-tagging efficiency, etc., are small [27], the uncertainties related to the jet energy scale and the resolution are not negligible [53]. -
In this work, we have revisited general electroweak DM considering combined search via DM direct detection experiments and LHC probes of new lepton pairs which appear together with DM in the new weak scale physics. Compared to the earlier works, this analysis is more intuitive. Moreover, we have utilized a general framework that can effectively describe three well-known extensions on the electroweak sector that contains both DM and new lepton pairs simultaneously.
The outcomes are two-fold. First, instead of two separate studies, either for DM direct detection or LHC probes, the combination of the two direct detections allowed us to explore the real status of the electroweak DM. Second, the general description enabled us to uncover a bigger parameter region that was yet to be explored. Utilizing three Z- and W-associated electroweak processes at the 14 TeV LHC, we have illustrated that in the parameter space with the lepton pairs decaying to on-shell Z or W:
$ i) $ for$ y\sim 0.35-0.5 $ , DM mass up to$ \sim 170-210 $ GeV can be excluded at the$ 2\sigma $ level with$ L = 300 $ fb$ ^{-1} $ and up to$ \sim 175-205 $ GeV can be discovered at the$ 5\sigma $ level with$ L = 3000 $ fb$ ^{-1} $ ;$ ii) $ for$ y\sim 0.5-0.65 $ , DM mass up to$ \sim 172-210 $ GeV can be excluded at the$ 2\sigma $ level with$ L = 300 $ fb$ ^{-1} $ and up to$ \sim 180-200 $ GeV can be discovered at the$ 5\sigma $ level with$ L = 3000 $ fb$ ^{-1} $ ;$ iii) $ for$ y\sim 0.65-1.0 $ , DM mass above$ 250 $ GeV is totally beyond the detection scope of LHC.The low reach for the electroweak DM mass in the situation with large mass splitting, together with similar trends in the small mass splitting, suggests that new search strategies are needed in order to examine higher electroweak DM mass ranges. Few directions for improvement in the future are as follows. Firstly, the ability of detection of the electroweak DM may be improved in other channels that are rarely considered. Moreover, compared to the sophisticated data analysis adopted here, novel methods such as machine learning may provide alternative views, see, e.g. Refs. [54, 55]. Finally, setting aside the colliders, one may carefully consider astrophysical probes of the electroweak DM, which may be stringent under certain circumstances.
The authors would like to thank Lorenzo Calibbi, Huayong Han, Yang Zhang, and Pengxuan Zhu for the helpful discussions.
Probing electroweak dark matter at 14 TeV LHC
- Received Date: 2020-04-16
- Accepted Date: 2020-06-29
- Available Online: 2020-11-01
Abstract: Well-motivated electroweak dark matter is often hosted by an extended electroweak sector that also contains new lepton pairs with masses near the weak scale. In this study, we explore such electroweak dark matter by combining dark matter direct detection experiments and high-luminosity LHC probes of new lepton pairs. Using Z- and W-associated electroweak processes with two or three lepton final states, we show that depending on the overall coupling constant, dark matter masses of up to






 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF



















 DownLoad:
DownLoad: