Mesonic condensation in isospin matter under rotation

Recently, interest in understanding the properties and phase structures of matter under extreme fields like magnetic field or global rotation has been growing rapidly [1, 2]. Examples of such physical systems arise from a variety of areas, such as the hot quark-gluon plasma in peripheral heavy-ion collisions [3–11], dense nuclear matter in rapidly spinning neutron stars [12–14], lattice gauge theory in rotating frame [15], cold atomic gases [16–18], as well as certain condensed matter materials [19, 20].

Rotation provides a new and interesting type of macroscopic control parameter, in addition to conventional temperature and density, for a many-body system. In particular, it nontrivially interacts with microscopic spin degrees of freedom through the effect of rotational polarization and frequently induces novel phenomena. For example, there are highly nontrivial anomalous transport effects such as the chiral vortical effect and chiral vortical waves in rotating fluids with chiral fermions [21–27]. Furthermore, if the underlying materials contain fermions that may form a condensate via pairing, their phase structures can be significantly influenced by the presence of global rotation [28–41]. A generic effect is the rotational suppression of fermion pairing in the zero angular momentum state that has been demonstrated, e.g., for chiral phase transition and color superconductivity in a strong interaction system [28]. Given the suppression of scalar pairing states in these systems, it is reasonable to speculate on what may happen to pairing states with nonzero angular momenta, e.g., a spin-1 condensate of fermionic pairs. Generally, one would expect them to be enhanced by rotation that prefers states with finite angular momenta and tends to polarize the angular momentum along the rotational axis. It is of great interest to examine this in concrete physical systems.

In this paper, we perform the first analysis of the influence of rotation on the phase structure of isospin matter—the Quantum Chromodynamics (QCD) matter at finite isospin density (or, equivalently, isospin chemical potential) that implies an imbalance between the u-flavor and d-flavor of quarks in the system [42, 43]. Such isospin matter is relevant for understanding the properties of neutron star materials that have a significant mismatch between the number of neutrons and protons and thus between u-quarks and d-quarks. In addition, the dense matter created in low-energy heavy-ion collisions bears significant isospin density that arises from the initial beam nuclei being stopped. It is also possible to simulate such isospin matter with two-component cold fermionic gases. This paper focuses on a theoretical understanding with a brief outline of the potential experimental application that will be the topic of a future detailed study.

One particularly interesting phenomenon in isospin matter is pion condensation [44–57]: while the system contains a chiral $ \sigma $ condensate at low isospin density (from quark-anti-quark pairing in the scalar channel), this becomes a pion condensate (from quark-anti-quark pairing in the pseudo-scalar channel) at high isospin density. Because both pairing states have zero angular momenta, one would expect a rotational suppression effect on both. Furthermore, rotation may induce condensation in other mesonic channels arising from quark-anti-quark pairing in states with nonzero angular momenta, such as the $ \rho $-channel. We will perform the first systematic study of all these possible mesonic condensation pairing states simultaneously in isospin matter under global rotation. We will show that there is indeed the suppression of scalar pairing and the enhancement of vector pairing due to fluid rotation, with the emergence of the rho condensation phase at high isospin density under rapid rotation. Such analysis will further allow us to envision and map a new phase diagram on the rotation-isospin parameter plane with highly nontrivial phase structures. Note the system considered here consists of rotating normal components and irrotational condensates. The formation of condensate vortices is an interesting opportunity for further study.

To investigate the mesonic condensation of isospin matter, we will adopt a widely used effective model, namely the two-flavor Nambu-Jona-Lasinio (NJL) model with four-fermion interactions in various channels at finite isospin chemical potential $ \mu_I $:

In the above, the $ m_0 = 5\;{\rm{MeV}} $ is the light quark mass parameter while $ G_s = G_v = 5.03\ {{\rm{GeV}}^{-2}} $ are the scalar and vector channel coupling constants, respectively. The NJL-type effective model also requires a momentum cut-off parameter $ \Lambda = 650\ {\;{\rm{MeV}}} $.These choices are quite standard, leading to the correct pion mass and decay constant in the vacuum as well as the vacuum expectation value (VEV) of the$ \sigma $ field to be $ \sigma_0 = 2\times(250\;{\rm{MeV}})^3 $. The NJL model is dissimilar to the QCD but effectively captures its low energy chiral dynamics.

In the most general case, we consider three possible mesonic condensation scenarios these being the condensation of the $ \sigma $, $ \pi $ or $ \rho $ fields. Following the standard mean-field method, we introduce the corresponding condensates:

At the first assessment of the operator level, the operator in the $ \rho $ condensate is nothing but the isospin density operator; however, the rho-meson condensate itself is determined by the gap equations, whereas the isospin density is determined by the derivative of the system's pressure with respect to the isospin chemical potential $ n_i = \dfrac {\partial P} {\partial \mu_i} $. They are two different physics quantities. We will show thatonly when the rotation is strong enough the real ground state is in $ \rho $ condensate dominated phase.

Note that a possible extension of the present analysis is to include an axial-vector channel coupling term into the Lagrangian Eq. (1). This may allow a new axial-vector mean-field condensate in competition with those above that directly couples the baryon density and acts as a shift of the baryon chemical potential. Here, we focus on the interplay of rotation and isospin chemical potential and leave it as an interesting possibility for further study.

Furthermore, this system is being considered under global rotation around the $ \hat{z} $-axis with an angular velocity of $ \vec{\omega} = \omega \hat{z} $. To do this, one can study the system in the rotating frame and rewrite the spinor theory with the curved metric associated with the rotating frame [28]. In such a description, the main new effect is a global polarization term in the Lagrangian density:

where $ \vec{S}_{4\times 4} = \dfrac{1}{2} {\rm Diag}\left(\vec{\sigma} , \vec{\sigma} \right) $ is the spin operator with $ \vec{\sigma} $ being the $ 2\times 2 $ Pauli matrices. Physically, this term polarizes both the orbital and spin angular momenta to be aligned with the global rotation axis, and its effect is identical for particles and antiparticles.

Within the mean-field approximation and assuming $ \omega\ r \ll 1 $, one obtains the NJL model's thermodynamic potential for isospin matter under rotation as follows:

where $ J_n $ are n-th Bessel functions of the first kind and the quasiparticle dispersion relations are given by

with $ \widetilde{\mu_I} = \dfrac{\mu_I}{2}+G_v\, \rho $. At a given temperature T and isospin chemical potential $ \mu_I $, one then determines the mean-field condensates by solving the gap equations:

These equations can be solved numerically. When there are multiple solutions, the true physical state should be determined from the absolute minimum of the thermodynamic potential. Note that also under rotation, the system is no longer homogeneous, with the thermodynamic quantities varying according to radial coordinate r. For the numerical results presented later, we use a value $ r = 0.1\ {{\rm{GeV}}}^{-1} $. This is a rather modest value that ensures $ \omega\, r \ll 1 $ in all our calculations and renders negligible the finite boundary effect. Only when r is very large, will the boundary effects influence the results. When r has a realistic size, the boundary effects are negligible. The qualitative features of our findings do not depend on this particular choice and the rotational effect generally increases with larger r values. For other relevant discussions, see e.g. [29].

We first demonstrate the rotational suppression of scalar pairing channels, i.e., mesonic condensates arising from quark-anti-quark pairing in the zero total angular momentum $ J = 0 $ states. While such rotational suppression was previously proposed as a generic phenomenon in fermion pairing transitions and demonstrated, e.g., for chiral condensate or color superconductivity [28], it has never been examined for mesonic condensation in isospin matter. In our case, the scalar pairing channels include the condensates of both the $ \sigma $ (scalar) and $ \pi $ (pseudo-scalar) fields. To show this effect clearly, we will temporarily "turn-off" the vector channel in the present section by setting $ G_v $ and $ \rho $ to zero in Eq. (6).

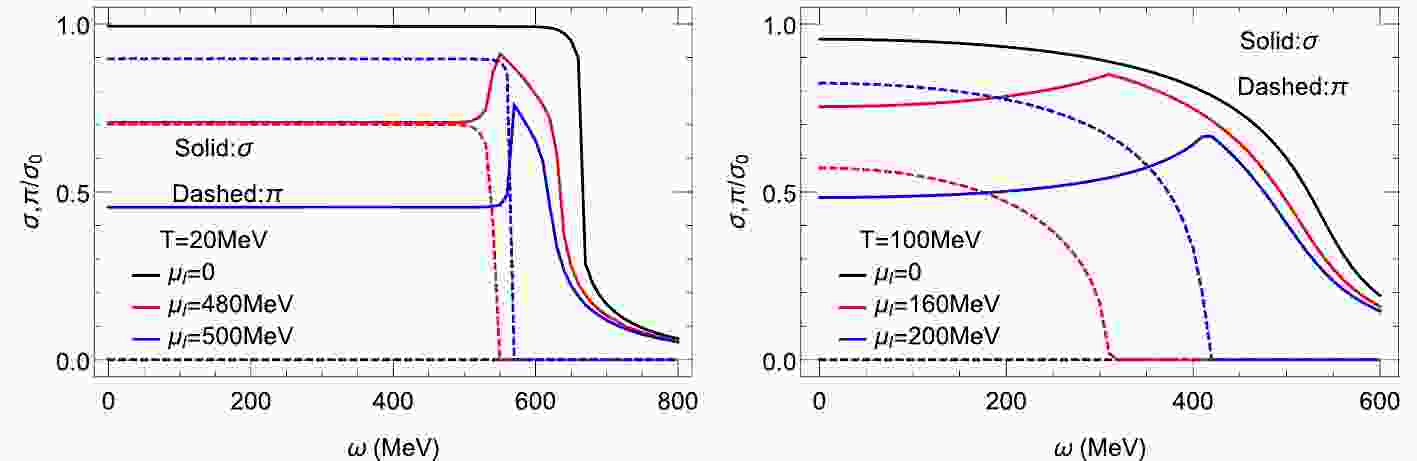
In the case without rotation, this system has been very well studied. At low isospin density, the system is vacuum-like with only a nonzero $ \sigma $ condensate, which will decrease as density increases. At a certain adequately high isospin density, the $ \pi $ condensate starts to form via a second-order phase transition—a phenomenon called pion condensation [46, 47, 54–56]. Here, we focus on the influence of rotation on this phenomenon.

In Fig. 1, we show the sigma and pion condensates $ \sigma $ and $ \pi $ (scaled by $ \sigma_0 $) as a function of $ \omega $ at $ T = 20\;{\rm{MeV}} $ (left) and $ T = 100\;{\rm{MeV}} $ (right) for several different values of $ \mu_I $. As one can see, there is indeed a generic suppression in both the $ \sigma $ and $ \pi $ condensates, due to the presence of global rotation always "preferring" states with nonzero angular momenta and thus disfavors these $ J = 0 $ mesonic pairing channels. What is most interesting is the case at high isospin density when a system is in the pion condensation phase of a nonzero pion condensate without rotation. However, with rotation being increased, this condensate eventually approaches zero via either a first-order (at low T) or second-order (at high T) transition. Thus, the spontaneously broken isospin symmetry in the pion condensation phase can be restored under rapid rotation, which is a new effect.

Figure 1.  (color online) The sigma and pion condensates $\sigma$ and $\pi$ (scaled by $\sigma_0$) as a function of $\omega$ at $T=20\;{\rm{MeV}}$ (left) and $T=100\;{\rm{MeV}}$ (right) for several different values of $\mu_I$.

Suppression of the scalar pairing suggests an opportunity for enhanced pairing of states with nonzero angular momenta, such as the $ \rho $ condensate. Indeed, the $ \rho $ state has $ J = 1 $ and should be favored by the presence of global rotation. While the emergence of the $ \rho $ condensate at a high isospin density has been studied previously [57], the interplay between the rho condensate and rotation and its implication for the phase structure of isospin matter is discussed for the first time here. To do this, we now consider the full thermodynamic potential in Eq. (6) and consistently solve the coupled gap equations of all three possible condensates in Eq. (8). In Fig. 2, we compare the results for the sigma, pi, and rho condensates $ \sigma,\ \pi,\ \rho $ (scaled by the vacuum chiral condensate $ \sigma_0 $) as a function of isospin chemical potential, for $ \omega = 0 $, $ \omega = 30\;{\rm{MeV}} $ and $ \omega = 80\;{\rm{MeV}} $, respectively. The temperature for this calculation is $ T = 10\;{\rm{MeV}} $ and the quark chemical potential is 250 MeV .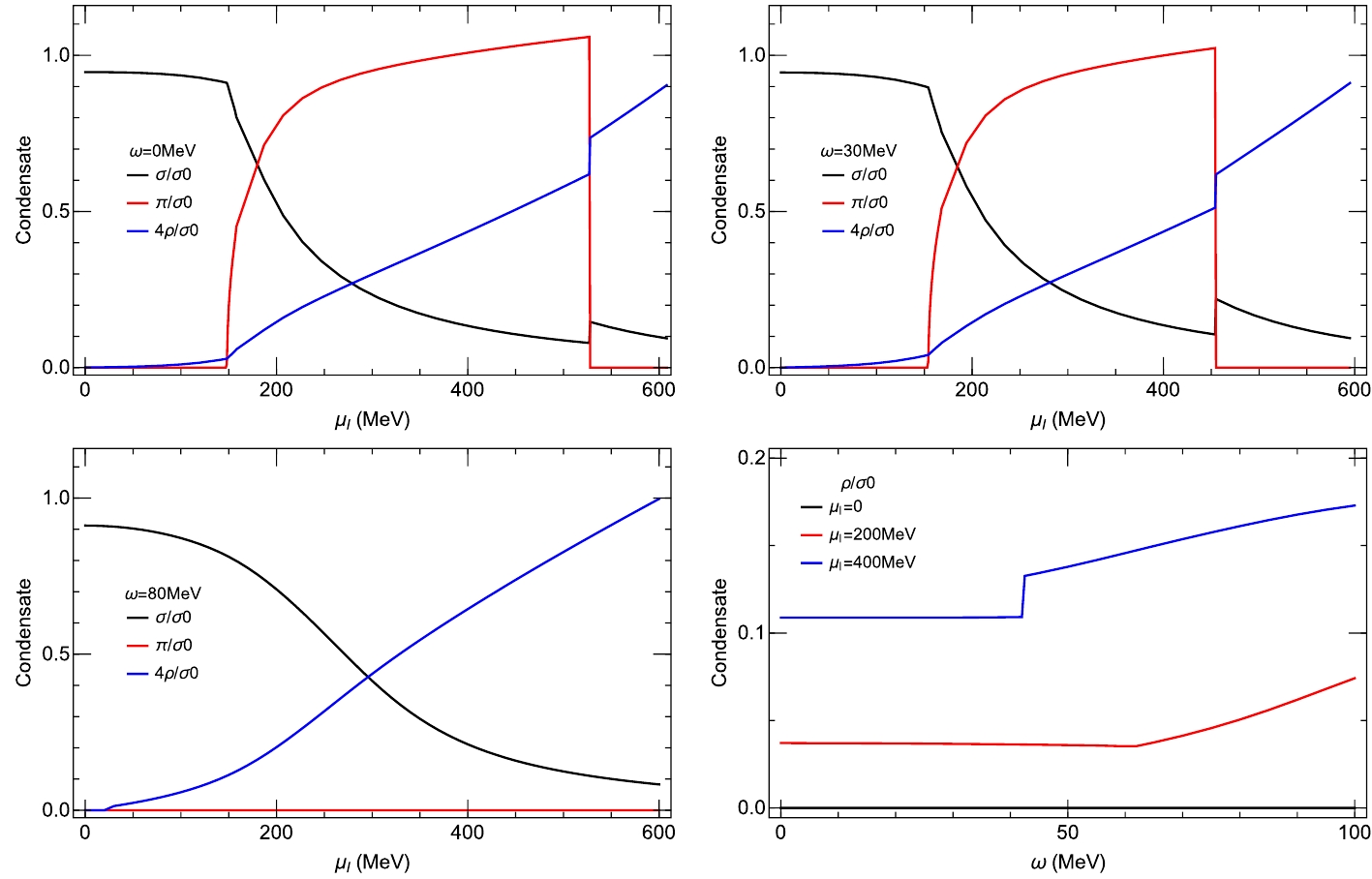

Figure 2.  (color online) The sigma, pi and rho condensates $ \sigma,\ \pi,\ \rho $ (scaled by the vacuum chiral condensate $ \sigma_0 $) as a function of isospin chemical potential, for $ \omega = 0 $, $ \omega = 30\;{\rm{MeV}} $ and $ \omega = 80\;{\rm{MeV}} $, respectively; The scaled $ \rho $ condensate as a function of $ \omega $ for different $ \mu_I $ (lower right). The temperature is $ T = 10\;{\rm{MeV}} $ and quark chemical potential is $ \mu = 250\;{\rm{MeV}} $.

In the case without rotation (Fig. 2 top left panel), the chiral condensate decreases with increasing $ \mu_I $ while both pion and rho condensates start to grow for $ \mu_I $ greater than the critical value at about $ 140\;{\rm{MeV}} $ for a second-order phase transition. The pion condensate dominates the system at a larger isospin chemical potential.

In the case with strong rotation, $ \omega = 30\;{\rm{MeV}} $ (Fig. 2 top right panel), the situation changes. Both pion and rho condensates still start to grow for $ \mu_I $ greater than the critical value. However, at an even higher isospin density, a new first-order transition occurs and the pion condensate drops to zero. In this new region, the rho condensate becomes dominant.

At the even stronger rotation, $ \omega = 80 \;{\rm{MeV}} $ (Fig. 2 lower left panel), the pion condensate disappears altogether. By increasing the isospin chemical potential $ \mu_I $, there is a smooth crossover from a $ \sigma $-dominated phase at a low isospin density to a $ \rho $-dominated phase at a very high isospin density. In Fig. 2 (lower right panel), it is shown more explicitly that the condensate ρ increases with the rotation.

These results clearly demonstrate the influence of rotation on mesonic condensation in isospin matter and envision a new phase diagram on the $ \omega-\mu_I $ plane, as shown in Fig. 3. This new phase structure is characterized by three distinctive regions: a vacuum-like, sigma-dominated phase in the low isospin density, and slow-rotation region; a pion-condensation phase in the mid-to-high isospin density with moderate rotation; and a rho-condensation phase in the high-isospin and rapid-rotation region. A second-order transition line separates the sigma-dominant and pion-dominant regions while a first-order line separates the pion-dominant and rho-dominant regions, with a tri-critical point connecting them. A similar phase structure has been found at various temperatures and quark chemical potentials and is a robust feature that arises from the interplay between rotation and isospin.

Figure 3.  (color online) A new phase diagram on the $\omega-\mu_I$ plane for mesonic condensation in isospin matter under rotation, upper panel for $\mu=0$, lower for $\mu=250\;{\rm{MeV}}$. The solid line indicates the first-order phase transition and the dashed line, the second-order transition, while the dotted line is for crossover, with the star symbol denoting a tri-critical point (TCP) at ($\mu_I^c=165{\;{\rm{MeV}}},\omega^c=548{\;{\rm{MeV}}}$ for upper) ($\mu_I^c=300{\;{\rm{MeV}}}, \omega^c=57{\;{\rm{MeV}}}$ for lower). The temperature is $T=10\;{\rm{MeV}}$.

In this paper, we have investigated the mesonic condensation in isospin matter under rotation. Using the two-flavor NJL effective model in the presence of global rotation, we have demonstrated two important effects of the rotation on the phase structure: the rotational suppression of the scalar-channel condensates, in particular, the pion condensation region; and the rotational enhancement of the rho condensation region with vector-channel condensate. A new phase diagram for isospin matter under rotation has been mapped on the $ \omega-\mu_I $ plane where three distinctive phases, corresponding to the $ \sigma $, $ \pi $, $ \rho $ dominated regions, respectively, are separated by a second-order line at low isospin chemical potential and a first-order line at high rotation which are joined at a tri-critical point. While the quantitative details may depend on the model, we expect such three-region phase structures to be generic.

As in other NJL-model studies, the cutoff and coupling constants here are chosen to reproduce the vacuum quark condensate and pion-decay constant to be physical value [58, 59]. The cut off artifacts should be considered near the cutoff momentum [29, 59]. However, in our phase diagram Fig. 3, the transition region is distant from the cutoff. By increasing the cutoff, we also checked that the qualitative feature does not change, although the phase boundary shifts a little.

In this study, we have not considered the finite-size effect on the phase structure [29]. The finite-size correction may further reduce the region of pion condensation, but the qualitative feature of the phase structure is expected to remain. Our calculation of the thermodynamic potential with rotation is under mean-field approximation, and the inclusion of fluctuations beyond this approximation may change the precise locations of the tri-critical point or phase-transition lines. Even so, the influence of rotation on mesonic condensation revealed in this paper should remain the same.

The novel phase structure found here may be useful and relevant for understanding properties and phenomena in isospin-asymmetric nuclear matter in various physical systems. For peripheral heavy-ion collisions at relatively low beam energies, such as experiments at the RHIC Beam Energy Scan or at the future FAIR and NICA facilities [60], the created matter has a significant rotation as well as high isospin density due to the stopping effect and the asymmetry between protons and neutrons in the initial nuclei. Studies on the phase structure of asymmetric dense cold nuclear matter with rotation at finite baryon density and low temperature will be useful for studying the structures and properties of rotating compact stars. Furthermore, by including finite baryon chemical potential at low temperature, one could study the phase structure of asymmetric dense cold nuclear matter with rotation. This would be useful for studying the structures and properties of rotating compact stars. Additional rich phases, such as vortex lattice or inhomogeneous FFLO states [61], in such environments are also interesting possibilities for further study. Based on the theoretical study in the present paper, a detailed investigation of relevant real-world systems is underway and will be reported elsewhere in the future.

The authors thank Yin Jiang and Shuzhe Shi for the useful discussions and communications.