-
The existence of dark matter (DM) has been well established by numerous astrophysical and cosmological observations, especially by very precise measurements of the cosmic microwave background (CMB) [1, 2]. The most prevailing and convincing DM candidates are the so-called weakly interacting massive particles (WIMPs). Assuming the standard thermal cosmological history, the WIMPs produced in the early universe through thermal freeze-out naturally afford the observed DM relic density (“WIMP miracle”) [3]. Because of their weak interactions with the Standard Model (SM) particles, WIMPs with a mass of approximately
$ 100\; {\rm{GeV}} $ would create significant signals in direct and indirect detection experiments, and they could also be produced copiously at high-energy colliders. In the last two decades the precision of DM direct detection experiments has been improved significantly, and it is approaching the “neutrino floor” that is the intrinsic background for DM direct detection [4-8]. However, till now, null results have been reported for every type of dark matter search experiment, and this challenges the WIMP assumptions for DM. As demonstrated in Ref. [9], if the DM candidate couples directly to quarks, the parameter regions to provide the correct relic density are not consistent with the null results of either direct detection, indirect detection, or collider searches. This motivates us to consider the possibility that the DM candidate interacts with electroweak gauge bosons [10-28] or leptons in the SM [29-39].Rather than focusing on specific DM models, we use an effective-field theory (EFT) approach to parametrize the interactions of the DM candidate and the SM particles at a new physics scale
$ \Lambda $ . More specifically, the interactions with gauge bosons are described by dimension-7 operators, while those with leptons are described by dimension-6 operators. The DM candidate is considered to be the only new particle in the energy region relevant for current experiments, and those high-dimensional effective operators are presumably generated by new heavy particles in the dark sector that are substantially heavier than the DM candidate. Even though the DM candidate does not interact directly with quarks in the SM, the quantum effects can induce such interactions and yield a direct detection signal. Hence, an important question in DM direct detection experiments is whether on reaching the neutrino floor one can use other experiments to explore the properties of DM.An important feature is that energy scales in different experiments vary. For instance, the momentum exchange involved in DM-nucleus recoil is
$ {\cal{O}}(100)\; {\rm{MeV}} $ , while it is$ {\cal{O}}(100)\; {\rm{GeV}} $ in the LHC searches. Different phenomena are created by operators generated at different energy scales. These operators are related by renormalization group equations (RGE). These loop effects or RGE effects have been widely studied while assuming that DM interacts with gauge bosons [40-43] and leptons [44-47] and that DM interacts with quarks where spin-independent interaction vanishes at tree level [48-51].In this work, we evolve the RGE from the scale
$ \Lambda $ down to the direct detection scale$ \mu_D $ . Theoretical observations, performed at a corresponding energy scale, are compared with experimental observations. We show that the collider searches can explore some regions under the neutrino floor.The rest of the paper is organized as follows. In Sec. 2 we give a brief description of DM interactions with electroweak gauge bosons, identify the parameter regions that could overclose the universe, and that could be explored by DM direct detection experiments and LHC searches. In Sec. 3, we repeat the calculations, but for DM interacts with leptons, in that case we also identify parameter regions that could be explored by future electron-positron colliders and DM indirect detection experiments. Finally, we conclude in Sec. 4.
-
We start with the case that the DM candidate is a Dirac fermion (
$ \chi $ ) and it interacts only with the electroweak gauge bosons in the SM. We first analyze the effective operators that could contribute to the direct detection of DM when gradually evolving from the new physics (NP) scale$ \Lambda $ down to the scale$ \mu_D $ that is the characteristic energy scale for directly detecting DM. -
At the level of dimension-5, there are only two operators
$ \bar{\chi} \gamma^{\mu\nu}\chi B_{\mu\nu},\; \; \; \; \; \; \; \; \; \; \bar{\chi} \gamma^{\mu\nu}\chi \tilde{B}_{\mu\nu}, $

(1) where
$ \gamma^{\mu\nu}\equiv [\gamma^\mu,\gamma^\nu]/4 $ and$ B_{\mu\nu}\equiv\partial_\mu B_\nu-\partial_\nu B_\mu $ are the field strength tensors of the$ U(1)_{\rm Y} $ gauge group. These correspond to the weak magnetic and electric dipoles of DM, respectively, and induce unsuppressed cross sections correspoding to the annihilation of DM into the$ \gamma\gamma $ and$ \gamma Z $ modes, yielding a significant line spectrum of cosmic gamma-rays, and thus are tightly constrained by current indirect detection experiments [52]. At the level of dimension-7, there are four scalar-type operators built from$ \bar{\chi}\chi $ or$ \bar{\chi} \gamma^5 \chi $ as follows:$ \begin{split} &{\bar \chi \chi {B_{\mu \nu }}{B^{\mu \nu }},}\quad\quad{\bar \chi \chi W_{\mu \nu }^i{W^{i\mu \nu }},}\\ &{\bar \chi {\gamma ^5}\chi {B_{\mu \nu }}{{\tilde B}^{\mu \nu }},}\quad\quad{\bar \chi {\gamma ^5}\chi W_{\mu \nu }^i{{\tilde W}^{i\mu \nu }},} \end{split}$

(2) and six tensor operators constructed from
$ \bar{\chi}\gamma^{\mu\nu}\chi $ , which are$ \bar{\chi}\gamma^{\mu\nu}\chi B_{\alpha\mu} \tilde{B}^{\alpha\nu},\; \; \; \; \; \bar{\chi}\gamma^{\mu\nu}\chi W_{\alpha\mu}^i \tilde{W}^{i\alpha\nu}, $

(3) and
$ \begin{split} &{\bar \chi {\gamma ^{\mu \nu }}\chi {B_{\mu \nu }}|\Phi {|^2},}\quad\quad{\bar \chi {\gamma ^{\mu \nu }}\chi {{\tilde B}_{\mu \nu }}|\Phi {|^2},}\\ &{\bar \chi {\gamma ^{\mu \nu }}\chi {W_{i\mu \nu }}{\Phi ^\dagger }{\tau ^i}\Phi ,}\quad\quad{\bar \chi {\gamma ^{\mu \nu }}\chi {{\tilde W}_{i\mu \nu }}{\Phi ^\dagger }{\tau ^i}\Phi .} \end{split}$

(4) Here,
$ W^i_{\mu\nu}\equiv \partial_\mu W_\nu^i-\partial_\nu W_\mu^i+g_2\epsilon^{ijk}W_\mu^jW_\nu^k $ is the field-strength tensor of the$ SU(2)_{\rm L} $ gauge group and$ \tilde{W}^{i\mu\nu} $ is the corresponding dual tensor. The last two operators in Eq. (2) and the two operators in Eq. (3) lead to unsuppressed$ \gamma\gamma $ and$ \gamma Z $ signals, and the four operators in Eq. (4) induce unsuppressed$ \gamma h $ signals, therefore, they are highly constrained and are ignored hereafter. For further discussions and phenomena related to these operators, please refer to Refs. [41, 42, 53]. Finally, we have only the first two operators in Eq. (2), and the Lagrangian can be expressed as$ {\cal{L}}_{\rm eff} = \frac{C_B}{\Lambda^3} \bar{\chi}\chi B_{\mu\nu}B^{\mu\nu} + \frac{C_W}{\Lambda^3} \bar{\chi}\chi W_{\mu\nu}^iW^{i\mu\nu} .$

(5) They yield velocity-suppressed annihilation cross sections and, therefore, are free from the tight constraint of the gamma ray line spectrum observations [52].
$ C_{B,W} $ denotes the Wilson coefficient of the corresponding operator.We assume that only these two operators are generated at the scale
$ \Lambda $ when other new-physics resonances much heavier than$ \Lambda $ are all decoupled. Even though the DM candidate$ \chi $ and the SM quarks are not directly coupled at the NP scale$ \Lambda $ , they are linked by quantum effects at a lower scale through the RGE running. For example, as shown in Ref. [42], two extra operators that couple the DM candidate to quarks, i.e.$ {\cal{O}}_y = y_q\bar{\chi}\chi\bar{q}\phi q, \; \; \; \; \; \; {\cal{O}}_{\phi} = \bar{\chi}\chi(\phi^\dagger\phi)^2, $

(6) are generated when evolving from
$ \Lambda $ down to the weak scale. Here,$ y_q = \sqrt{2}m_q/v $ is the Yukawa coupling and v is the vacuum expectation value (VEV) of the SM Higgs doublet$ \phi $ . It is straightforward to show that, to the leading logarithmic (LL) order, the Wilson coefficients of the$ {\cal{O}}_{y,\phi} $ and$ {\cal{O}}_{B,W} $ operators are related as follows:$ C_y^q({\mu}) \simeq \frac{3 Y_{qL} Y_{qR} \alpha_1}{\pi} {\rm{ln}}\left(\frac{\mu^2}{\Lambda^2}\right) C_B(\Lambda), $

(7) $ C_\phi({\mu} ) \simeq - \frac{9 \alpha_1^2}{2} {\rm{ln}}\left(\frac{\mu^2}{\Lambda^2}\right) C_W(\Lambda), $

(8) where
$ Y_{qL} $ ($ Y_{qR} $ ) are the hypercharges of the left-handed (right-handed) quarks assigned as$ Y_{uL} = Y_{dL} = 1/6 $ ,$ Y_{uR} = 2/3 $ , and$ Y_{dR} = -1/3 $ .$ \alpha_1 $ and$ \alpha_2 $ are the gauge coupling constants of the$ U(1)_{\rm Y} $ and$ SU(2)_{\rm L} $ gauge group, respectively. At the weak scale$ \mu_Z(\equiv m_Z) $ ,$ \alpha_1(\mu_Z) \simeq 1/98 $ , and$ \alpha_2(\mu_Z) \simeq 1/29 $ .After electroweak symmetry-breaking (EWSB),
$ B_\mu $ and$ W_\mu^3 $ mix into the photon field$ A_\mu $ and massive gauge field$ Z_\mu $ . The effect of$ Z_\mu $ decouples at the lower scale, below$ \mu_Z $ , and the relevant operator bases become$ {\cal{O}}_A = \bar{\chi}\chi F_{\mu\nu}F^{\mu\nu}, $

and
$ {\cal{O}}_q = m_q \bar{\chi}\chi \bar{q} q. $

(9) The matching conditions between these two operator bases are
$ \begin{split} & C_A(\mu_Z) = c_{ W}^2 C_B(\mu_Z) + s_{ W}^2 C_{W}(\mu_Z), \\ & C_q(\mu_Z) = C_y^q(\mu_Z) - \dfrac{v^2}{m_h^2} C_\phi(\mu_Z), \end{split}$

(10) where
$ c_{ W} \equiv {\rm{cos}}\theta_{ W} $ and$ s_{ W} \equiv {\rm{sin}}\theta_{W} $ are related to the Weinberg angle$ \theta_{W} $ .Next, we further evolve RGEs from
$ \mu_Z $ down to the hadronic scale$ \mu_{D} \sim 1\; {\rm{GeV}} $ at which the DM candidate interacts with the nucleons.$ {\cal{O}}_q $ will receive contributions from$ {\cal{O}}_A $ through the exchanging of virtual photons [41]. To LL accuracy,$ C_q(\mu) \simeq C_q(\mu_Z) + \frac{3 Q_q^2 \alpha}{\pi} {\rm{ln}}\Bigg(\frac{\mu^2}{\mu_Z^2}\Bigg) C_A(\mu_Z) $

(11) for
$ m_q < \mu < \mu_Z $ , where$ Q_q $ is the electric charge of quarks. During the evolution of RGEs, heavy quarks in the SM are integrated out, yielding an operator$ {\cal{O}}_G = \alpha_s \bar{\chi}\chi G_{\mu\nu}^a G^{a,\mu\nu}, $

(12) where
$ G_{\mu\nu}^a $ denotes the field strength of a gluon. The matching condition is given by the simple replacement [54]$ C_t m_t \bar{\chi}\chi \bar{t} t \to C_G \alpha_s \bar{\chi}\chi G_{\mu\nu}^a G^{a,\mu\nu}, $

(13) with
$ C_G $ given at the leading order by$ C_G(m_t) = -\frac{1}{12\pi} C_t (m_t). $

(14) Finally, we have the operator basis consisting of
$ {\cal{O}}_q $ ,$ {\cal{O}}_A $ , and$ {\cal{O}}_G $ . The mixing of$ {\cal{O}}_G $ with$ {\cal{O}}_q $ and$ {\cal{O}}_A $ is subdominant and can be safely ignored. Taking into account the threshold effects at$ m_b $ and$ m_c $ that contribute to$ {\cal{O}}_G $ , we obtain the final expressions for the Wilson coefficients as follows:$ \begin{split} C_q(\mu)\simeq & \bigg(\frac{3Y_{qL}Y_{qR}\alpha_1}{\pi}C_B(\Lambda)+\frac{9\alpha_2^2}{2}\frac{v^2}{m_h^2}C_W(\Lambda)\bigg){\rm{ln}}\bigg(\frac{m_Z^2}{\Lambda^2}\bigg) \\ & +\frac{3Q_q^2\alpha}{\pi}C_A(\mu_Z){\rm{ln}}\bigg(\frac{\mu_D^2}{m_Z^2}\bigg),\\ C_G(\mu)\simeq &-\frac{1}{12\pi}\bigg\{\bigg(\frac{\alpha_1}{2\pi}C_B(\Lambda)+\frac{27\alpha_2^2}{2}\frac{v^2}{m_h^2}C_W(\Lambda)\bigg){\rm{ln}}\bigg(\frac{m_Z^2}{\Lambda^2}\bigg)\\ & +\frac{\alpha}{3\pi}C_A(\mu_Z)\bigg[{\rm{ln}}\bigg(\frac{m_b^2}{m_Z^2}\bigg)+4{\rm{ln}}\bigg(\frac{m_c^2}{m_Z^2}\bigg)\bigg]\bigg\}. \end{split}$

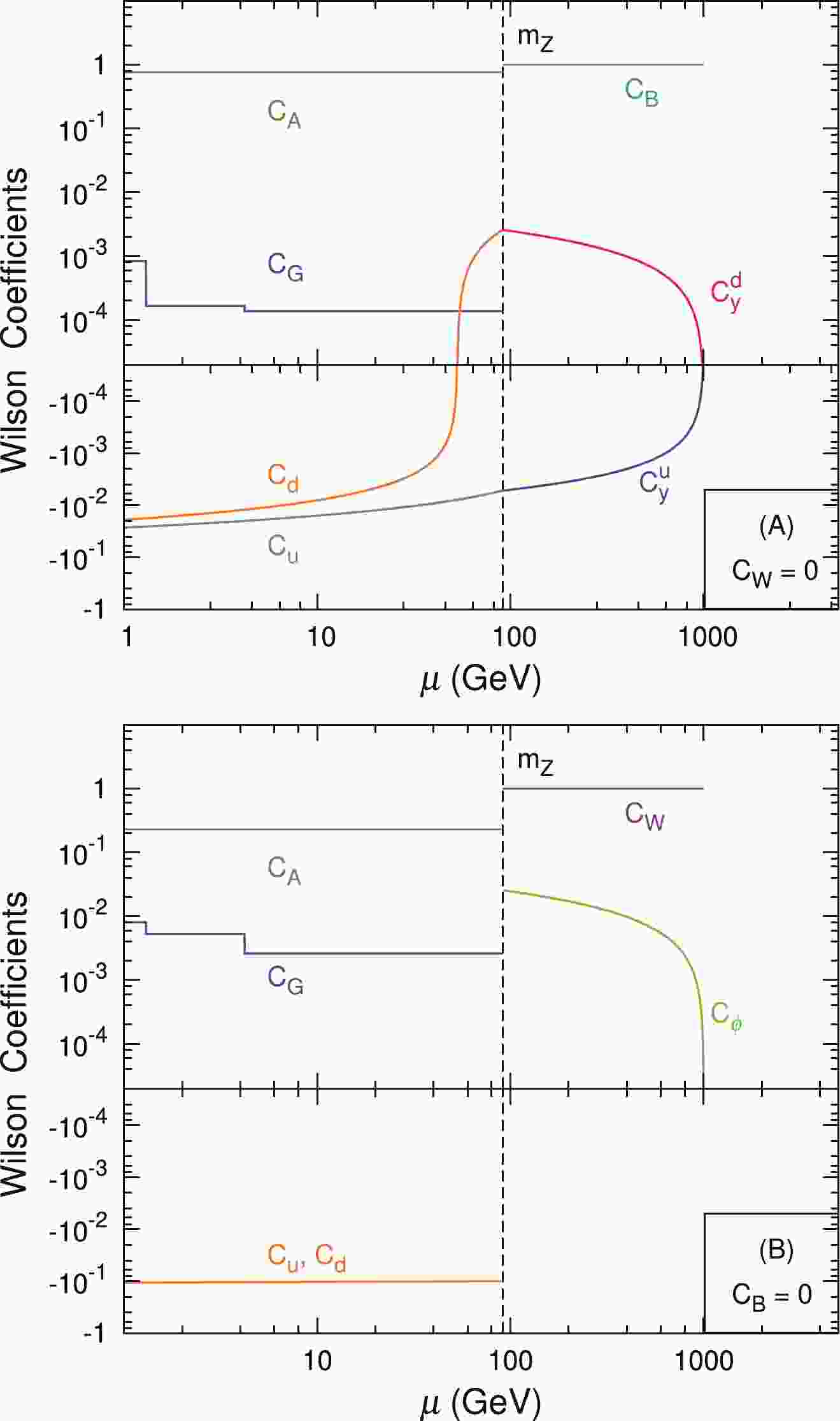
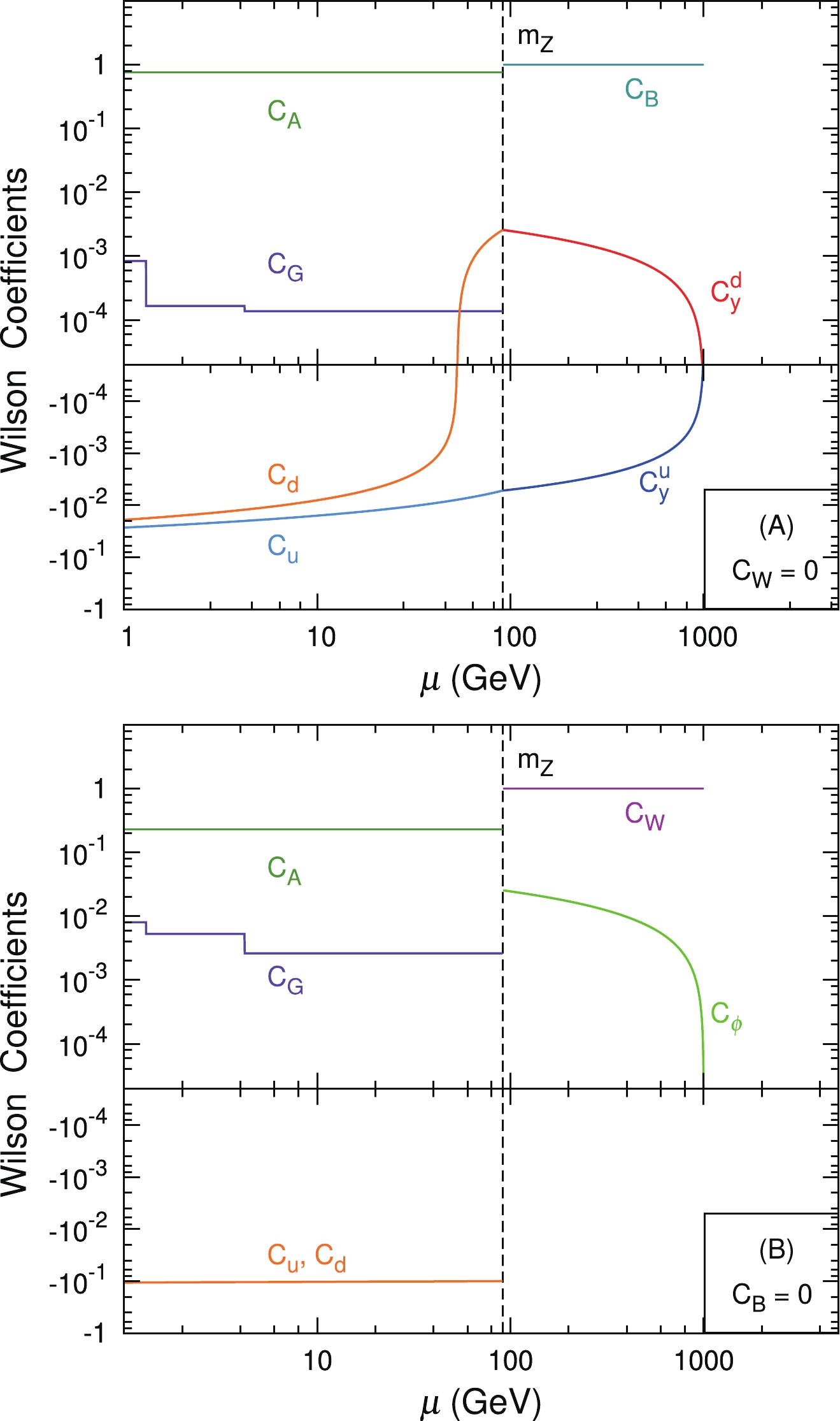
(15) Figure 1 displays the RGE running of the Wilson coefficients. For simplicity, we consider the operators individually i.e., either
$ C_W = 0 $ (a) or$ C_B = 0 $ (b) and fix the cut-off scale$ \Lambda $ to be$ 1000\ {\rm{GeV}} $ . In the case of$ C_W = 0 $ , the Wilson coefficients involving the up-type quark ($ C_y^u $ ) and down-type quark ($ C_y^d $ ) exhibit opposite signs as the hypercharges of the up-type and down-type quarks are different; see the red and blue curves in the top figure. The sign difference remains unchanged even after the EWSB and matching. However, running from the weak scale$ \mu_Z $ down to the hadronic scale$ \mu_D $ , the correction of$ C_A $ to$ C_d $ is significant and changes the sign of$ C_d $ from positive to negative. Conversely, in the case of$ C_B = 0 $ , both the$ C_u $ and$ C_d $ coefficients receive identical contributions from$ C_\phi $ while the contributions from$ C_A $ can be ignored safely; see the bottom figure. -
As an important approach to probe the DM candidate, the direct detection experiments search for the recoil signals of target nuclei scattered off by incident DM particles. Even though the DM candidate in our model does not interact with quarks directly at the scale
$ \Lambda $ , the direct detection signal could be induced at the hadron scale. For example, quantum loop effects induce the interactions of the DM candidate with quarks and gluons, e.g.,$ {\cal{O}}_q $ and$ {\cal{O}}_G $ in Eqs. (9) and (12) that result in the interaction between the DM candidate and nucleon. In addition, the exchange of two virtual photons will induce an interaction with the entire nucleus, with the interaction strength being proportional to the total electric charge$ Ze $ of the nucleus [40].The contributions of these operators are coherent, leading to the spin-independent (SI) cross section for DM scattering with nuclei [40-42],
$ \sigma_N^{\rm{SI}}\simeq\frac{m_{\rm{red}}^2m_N^2}{\pi\Lambda^6}\bigg|\frac{\alpha Z^2}{A}f_F^N C_A(\mu_D) +\frac{Z}{A} f_p +\frac{A-Z}{A} f_n \bigg|^2, $

(16) where
$ m_{\rm{red}} $ is the label of the reduced mass of DM-nuclei system,$ m_N $ is the nucleon mass,$ f_F^N $ is the form factor for photons, which equals$ 0.08 $ (0.12) for the Xenon (Argon) target. The form factor$ f_N $ ($ N = p, n $ ) describes the interactions between the DM candidate and nucleon that are related to the interactions with quarks through$ f_N = \sum\limits_{q = u,d,s}f_q^N C_q(\mu_D)-\frac{8\pi}{9}f_G^N C_G(\mu_D), $

(17) where the nucleon form factors
$ f_q^N $ are given by [55]$ \begin{split} & {f_d^p = 0.0191,}\quad\quad{f_u^p = 0.0153,}\quad\quad{f_d^n = 0.0273,}\\ & {f_u^n = 0.0110,}\quad\quad{f_s^p = f_s^n = 0.0447,}\quad\quad{} \end{split} $

(18) and
$ f_G^N = 1- \sum\limits_{q = u,d,s} f_q^N. $

(19) The contributions of the proton and neutron are separated in Eq. (16) as the DM candidate couples differently to them.
Figure 2 displays the constraints on the Wilson coefficients as a function of
$ m_\chi $ at the 90% confidence level (C.L.) using PandaX-II [59], XENON1T [58], and DEAP-3600 [60]. For illustration, we fix the cutoff scale as$ \Lambda = 1\; {\rm{TeV}} $ and$ C_W = 0 $ ($ C_B = 0 $ ) in the top (bottom) of Fig. 2, respectively. Both the PandaX-II and XENON1T experiments use the Xenon target; therefore, the contributions of$ C_A $ are enhanced by a relatively large$ Z^2 $ , and they dominate the contributions of$ f_p $ and$ f_n $ . Conversely, the contributions of$ f_p $ and$ f_n $ dominate in the DEAP-3600 experiment that uses an Argon target. For illustration, we plot the contours of the correct relic abundance,$ \Omega_\chi h^2 = 0.1186\pm 0.0020 $ [2]; see the Appendix for detailed calculations.
Figure 2. (color online) Constraints in the
$m_\chi$ -$C_B$ plane (a) and$m_\chi$ -$C_W$ plane (b) with$\Lambda=1\;{\rm{TeV}}$ . Brown and green solid lines denote the exclusion limits from the mono-photon [56] and mono-jet [57] searches at the 95% confidence level at the 13 TeV LHC. For the SI DM-nucleon scattering, recent bounds from XENON1T [58], PandaX-II [59], and DEAP-3600 [60] are shown. The gray shaded region denotes the parameter space where the EFT is invalid, and it is estimated as$m_\chi > \Lambda/2$ . For illustration, the contours of the relic abundance,$\Omega_\chi h^2=0.1186$ , are also plotted; see the dark dashed curves.The yellow regions in Fig. 2 denote the so-called neutrino floor that represents the WIMP-discovery limit obtained by assuming an exposure of 1000
$ ^8{\rm{B}} $ neutrinos that are detected on a Xenon target [8]. Recently, a few new methods have been proposed to improve the sensitivity of DM detection beneath the neutrino floor, e.g., using the annual modulation signal [4], directional detection methods [5, 6], or looking for a possible complementarity between different target nuclei [8]. However, the effectiveness of these methods is still limited. It is important to study whether the collider search can probe the DM candidate below the neutrino floor.The typical energy of a collider process is
$ {\cal{O}}(100)\; {\rm{GeV}} $ ; thus, after EWSB and matching to mass eigenstates, we obtain interactions between quarks and DM that are adopted to calculate the collider observables directly. The processes in the colliders of interest to us are$ q\bar{q} \to \chi\bar{\chi}+j $ and$ q\bar{q} \to \chi\bar{\chi}+\gamma $ , where j denotes a light-flavor jet. The DM candidate often appears as an invisible object in the colliders and yields the signature of missing transverse momentum (${\not\!\!{E}}_{\rm{T}}$ ). The event topology of the two signal processes consists of a large${\not\!\!{E}}_{\rm{T}}$ with either a hard jet or a hard photon. The former signature is often termed a “mono-jet” while the latter is termed a “mono-photon.” For the model considered in this section, operator$ {\cal{O}}_A $ will induce a${\rm{mono-photon}}+{\not\!\!{E}}_{\rm{T}}$ signal and operator$ {\cal{O}}_q $ will induce a${\rm{mono-jet}}+{\not\!\!{E}}_{\rm{T}}$ signal. To attain the sensitivities of LHC searches, we perform collider simulations of the mono-jet and mono-photon channels. The parton-level events are generated by$ \texttt{MadGraph 5}$ [61], and$\texttt{PYTHIA 6}$ [62] is used to deal with parton showers and hadronization. We adopt$\texttt{Delphes 3}$ [63] to carry out a fast detector simulation with a parameter setup for the ATLAS detector.We follow the procedure of the ATLAS group of the
${\rm{mono-photon}}+{\not\!\!{E}}_{\rm{T}}$ [56] and${\rm{mono-jet}}+{\not\!\!{E}}_{\rm{T}}$ [57] analysis with an integrated luminosity of$ 36.1\; {\rm{fb}}^{-1} $ at the$ \sqrt{s} = 13\; {\rm{TeV}} $ LHC. Figure 2 presents the exclusion limits derived from the mono-photon search (brown) and the mono-jet search (green) at the LHC. It is difficult to probe directly a DM candidate heavier than about$ 2\; {\rm{TeV}} $ at the LHC as it is limited by the colliding energy. Conversely, when the DM is light, e.g.$ m_\chi \lesssim 100\; {\rm{GeV}} $ , the limits are independent of the DM mass as the production cross sections are mainly determined by the effective couplings. Obviously, the collider search has a higher sensitivity than direct detection experiments in regimes where the EFTs are valid, e.g.$ m_\chi \lesssim 2\; {\rm{TeV}} $ . We emphasize that the collider searches can probe a light DM ($ m_\chi \lesssim 10\; {\rm{GeV}} $ ) below the neutrino floor.In the case of
$ C_W = 0 $ , the sensitivity of the mono-photon channel is much higher than that of the mono-jet channel, cf. Fig. 2(a). This can be understood as follows. First, the mono-photon signal event can be generated by the$ {\cal{O}}_A $ and$ {\cal{O}}_q $ , while the mono-jet signal event can be generated only by the$ {\cal{O}}_q $ . Note that$ {\cal{O}}_A $ is directly linked with$ {\cal{O}}_B $ , while$ {\cal{O}}_q $ is generated through loop effects and is much smaller than$ {\cal{O}}_A $ ; see Fig. 1(a). Second, the SM background of the mono-photon channel is much cleaner than that of the mono-jet channel, and it yields higher sensitivity to the DM searches at colliders. As a result, the mono-photon channel can cover the entire parameter space of the neutrino floor.In the case of
$ C_B = 0 $ ,$ {\cal{O}}_A $ is suppressed by the weak mixing angle after EWSB. Conversely,$ O_q $ is slightly enhanced after matching at the weak scale. As a result, the mono-photon and mono-jet channels yield comparable sensitivities to the DM searches; see Fig. 2(b). Even though both channels are better than the DM direct detection experiments, they cannot reach the neutrino floor for$ m_\chi \gtrsim 10\; {\rm{GeV}} $ . -
In this section, we study the scenario of a fermionic DM (
$ \chi $ ) interacting only with leptons at the NP scale$ \Lambda $ , termed lepton-philic DM. We assume that the DM candidate$ \chi $ interacts universally with all the leptons in the SM through$ {\cal{L}}_{\rm eff}^l = \frac{C_l}{\Lambda^2} \sum\limits_i \bar{\chi} \gamma_{\mu} \chi \Bigg(\overline{l_L^i}\gamma_\mu l_L^i + \overline{e_R^i}\gamma_\mu e_R^i\Bigg), $

(20) where the summation over the three generations of leptons in the SM is understood. Again, even though the DM candidate does not directly couple to the SM quarks at scale
$ \Lambda $ , the RGE running effects would induce non-zero interactions between the DM candidate and the quarks as follows:$ \begin{split} & {\cal{O}}_q^i = \bar\chi\gamma^\mu\chi\overline{q_L^i}\gamma_\mu q_L^i, \\ &{\cal{O}}_u^i = \bar\chi\gamma^\mu\chi\overline{u_R^i}\gamma_\mu u_R^i, \\ &{\cal{O}}_d^i = \bar\chi\gamma^\mu\chi\overline{d_R^i}\gamma_\mu d_R^i. \end{split} $

(21) Initially, the DM candidate only sees the leptons but is blind to the quarks; however, the connection between the DM candidate and the SM quarks is built through the operator
$ \bar\chi\Gamma^\mu\chi \phi^\dagger i\overleftrightarrow{D}_\mu \phi $ [46, 47].The strategy of calculating the RGE running effects is similar to that described in the previous section. After matching, the interactions of interest to us are
$ {\cal{L}} \subset \frac{C_u^V}{\Lambda^2} \bar\chi\gamma^\mu\chi \bar{u} \gamma_\mu u + \frac{C_d^V}{\Lambda^2} \bar\chi\gamma^\mu\chi \bar{d} \gamma_\mu d + \frac{C_e^V}{\Lambda^2} \bar\chi\gamma^\mu\chi \bar{e} \gamma_\mu e. $

(22) In principle, both the Yukawa and gauge interactions would influence the running of RGEs. However, in the case when the DM candidate interacts equally with left-handed and right-handed leptons, the contributions of the Yukawa interactions cancel themselves in each generation [46]. As a result, the induced interactions in Eq. (22) are independent of the quarks' masses and yield identical Wilson coefficients for the three generations. For the sake of simplicity, hereafter, we ignore the index of generation.
We follow Refs. [46, 47] and adopt the package
$ \texttt{runDM}$ [64] to perform a complete RGE running from the NP scale down to the scale of DM direct detection. Figure 3 displays the Wilson coefficients for different operators. The up-quarks and down-quarks obtain opposite signs with a strength differing by a factor of$ 2 $ as the electromagnetic interaction plays the leading role in the RGE running [46].
Figure 3. (color online) RGE running of Wilson coefficients of the effective couplings of
$\chi$ to the SM fermions.Equipped with the effective couplings of the DM candidate to the SM quarks, we can discuss the detection of the lepton-philic DM. First, one must consider the direct detection experiment. Owing to the conservation of vector current, the sea quarks and gluons inside nuclei do not contribute. The contributions of all the valence quarks aggregate coherently, leading to the WIMP-nucleus scattering cross sections, as follows:
$ \sigma_N^{\rm{SI}} = \frac{m_{\rm{red}}^2}{\pi\Lambda^4} \bigg| \frac{Z}{A} C_{p}^V+ \frac{A-Z}{A} C_{n}^V \bigg|^2. $

(23) Here,
$ C_{p}^V $ and$ C_{n}^V $ denote the interactions of the DM candidate$ \chi $ with a proton and neutron, respectively. They are related to the effective couplings of$ \chi $ to the u quark and d quark as follows:$ C_{p}^V = 2 C_u^V + C_d^V,\qquad C_{n}^V = C_u^V + 2 C_d^V, $

(24) where
$ C_u^V $ and$ C_d^V $ can be approximated as [46]$ C_u^V \simeq \frac{4\alpha}{3\pi} C_l, \qquad C_d^V \simeq - \frac{2\alpha}{3\pi} C_l . $

(25) Therefore, the interaction between
$ \chi $ and the neutron can be safely ignored.Figure 4 shows the bounds on the Wilson coefficient
$ C_l $ , at the 90% confidence level, obtained from various direct detection experiments. The yellow shaded region denotes the parameter space below the neutrino floor. Similarly to the case when the DM candidate interacts only with electroweak gauge bosons, the direct detection of the lepton-philic DM cannot touch the neutrino floor. Another method to search for the DM candidate is to examine high-energy cosmic rays, gamma rays, and neutrinos induced by DM decay or annihilation in galactic and extragalactic objects. In the lepton-philic model, the DM candidates predominantly annihilate into a pair of leptons. The constraint on$ C_l $ from the indirect search of DM through the cosmic gamma-ray observation by the Fermi-LAT collaboration [65] is plotted in Fig. 4; see the brown dashed curve. Even though the DM will annihilate into all the three-generation leptons, the$ \tau^+\tau^- $ channel dominates in the gamma-ray observations as more photons are produced from the$ \tau $ -lepton decay. Unfortunately, the indirect search experiment also cannot reach the neutrino floor .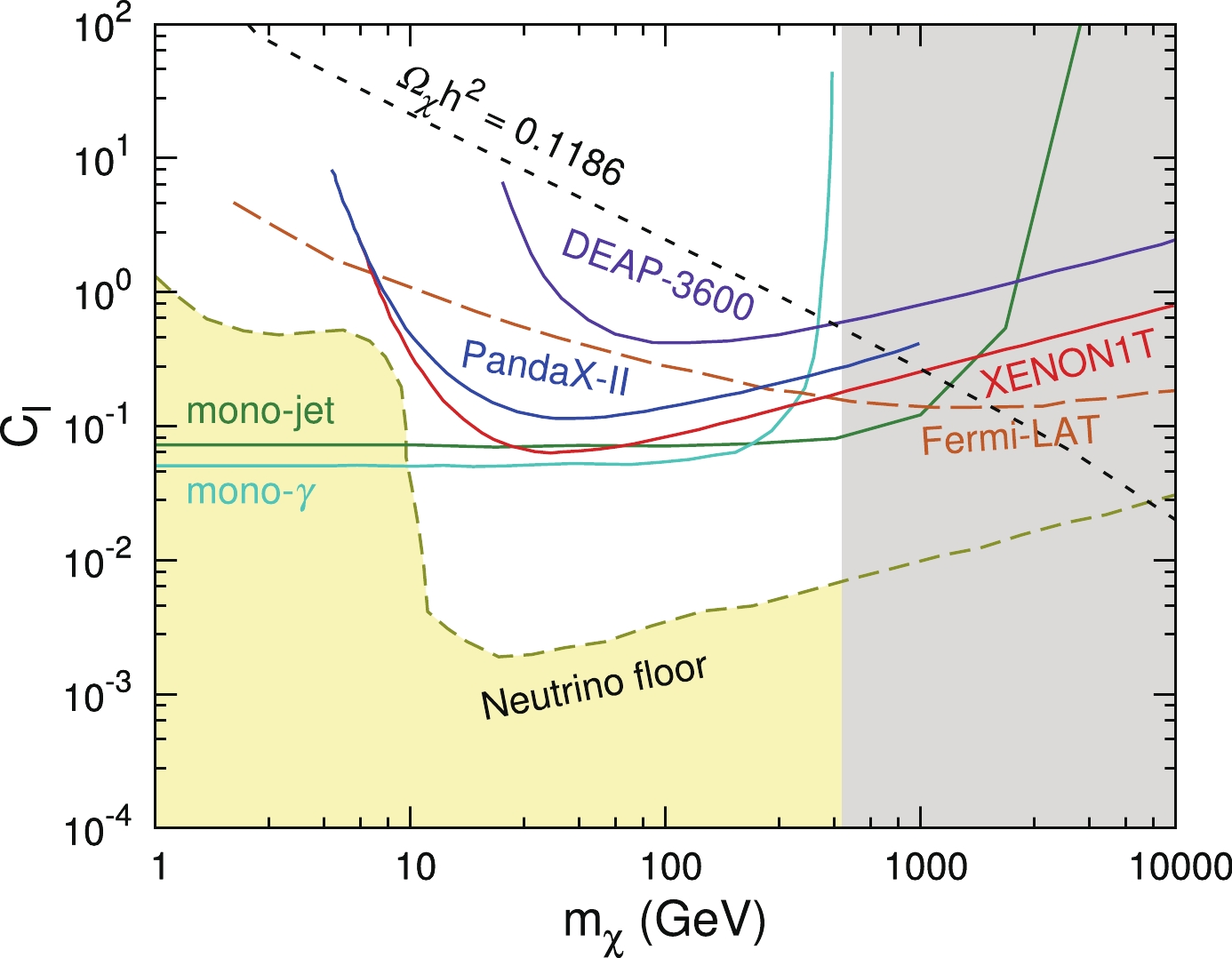
Figure 4. (color online) The bounds in the
$m_{\chi}$ -$C_l$ plane with$\Lambda=1\;{\rm{TeV}}$ . The brown dashed curve denotes the recent limit from the Fermi-LAT gamma-ray observations of the dwarf galaxies [65], and the cyan solid curve represents the projected sensitivity of the mono-$\gamma$ channel at the ILC.The effective couplings of
$ \chi $ to the SM quarks given in Eq. (21) give rise to the mono-jet signal at the LHC; therefore, it yields a strong bound on$ C_l $ . See the green curve in Fig. 4. Obviously the LHC will constrain the DM$ \chi $ with a mass up to about 2 TeV. For$ m_\chi \lesssim 10\; {\rm{GeV}} $ , the LHC can probe the parameter space below the neutrino floor.The lepton-philic DM can be better probed at future electron-positron colliders, e.g. CEPC [66] and ILC [67]. In this work, we explore the potential of the ILC with
$ \sqrt{s} = 1\; {\rm{TeV}} $ and an integrated luminosity of$ 1\; {\rm{ab}}^{-1} $ . To identify the mono-$ \gamma $ signal, we require that the signal event contains one energetic photon with energy$ E_\gamma > 10\; {\rm{GeV}} $ and$ 10^\circ < \theta_\gamma < 170^\circ $ , where$ \theta_\gamma $ is the polar angle between the hard photon and the beam axis. We also require missing mass$ m_{\mathrm{miss}} > 200{\rm GeV} $ , where the missing mass$ m_\mathrm{miss} $ is defined as$ m_\mathrm{miss} = \sqrt{(p_{e^+}+ p_{e^-} -p_{\gamma})^2} $ with$ p_{e^+} $ ($ p_{e^-} $ ) is the 4-momentum of the initial positron (electron) and$ p_\gamma $ is the 4-momentum of final photon [68]. Note that another searching strategy has been developed recently in Ref. [69] which imposes cuts on$ \theta_{\gamma}-E_\gamma $ plane directly. The cyan solid line in Fig. 4 represents the projected sensitivity of the ILC experiment on$ C_l $ . The ILC has a higher sensitivity than the LHC for the DM candidate in the mass regions of interest to us, e.g.$ m_\chi \lesssim 200\; {\rm{GeV}} $ ; unfortunately, the collider searches cannot reach the neutrino floor for$ m_\chi\gtrsim 10\; {\rm{GeV}} $ . -
With increasing exposures the sensitivity of direct detection of the dark matter (DM) candidate approaches the so-called neutrino floor, below which it is difficult to distinguish the signal induced either by a DM candidate or by a neutrino. In this study, we consider a worst-case scenario that all the direct detection experiments report null results even though the detection sensitivity reaches the neutrino floor. We demonstrate that the collider searches can probe the parameter space under the neutrino floor.
For illustration, we adopt two simplified models in which the DM candidate only couples to electroweak gauge bosons or leptons. Rather than focusing on a specific theoretical model, we use an effective Lagrangian approach to parametrize the interactions of DM with the gauge bosons or the leptons in the SM at a new physics scale
$ \Lambda $ and assume that all other heavy resonances in the UV complete model decouple at the scale$ \Lambda $ . Specifically, we consider two effective Lagrangians as follows:$\begin{split} &{\cal{L}}^{V}_{\rm{eff}} = \frac{C_B}{\Lambda^3} \bar{\chi}\chi B_{\mu\nu}B^{\mu\nu} + \frac{C_W}{\Lambda^3} \bar{\chi}\chi W_{\mu\nu}^iW^{i\mu\nu},\nonumber\\ &{\cal{L}}_{\rm{eff}}^L = \frac{C_l}{\Lambda^2} \sum\limits_i \bar{\chi} \gamma_{\mu} \chi (\overline{l_L^i}\gamma_\mu l_L^i + \overline{e_R^i}\gamma_\mu e_R^i). \end{split} $

Even though the DM candidate does not couple to the SM quarks directly at the scale
$ \Lambda $ , it can interact with the quarks and gluons in the SM through the RGE running effects. In this work, we evolve the RGE from high scale$ \Lambda $ to the EWSB scale, match to the basis of mass eigenstates, and then further evolve the RGE down to the direct detection energy scale. For simplicity, we consider the parameters individually and set the other two coefficients to be zero.We investigate relevant constraints from the direct/indirect detection and collider searches and find that the collider search has higher sensitivity than the direct and indirect detection experiments in the regime where the EFT is valid, e.g.
$ m_\chi \lesssim 2\; {\rm{TeV}} $ . In all the three simplified models, the collider searches can probe a light DM ($ m_\chi \lesssim 10\; {\rm{GeV}} $ ) below the neutrino floor. More interestingly, in the case of$ C_B \neq 0 $ and$ C_W = 0 $ , the current data of the mono-photon channel at the 13 TeV LHC has already covered the entire parameter space of the neutrino floor. -
The relic abundance predicted by this model should be smaller than the observed quantity reported by the Planck collaboration,
$ \Omega_\chi h^2 = 0.1186\pm 0.0020 $ [2]. Assuming that DM particles were thermally produced in the early universe, the relic abundance was determined by their thermally averaged annihilation cross sections during the decoupling epoch. If the annihilation cross sections are too small, DM would be overproduced, thereby contradicting the observation.The evaluation of DM density is performed using the Boltzmann equations. Assuming the standard thermal history of the universe, the DM relic abundance can be parameterized as [3, 70]
$ \Omega_\chi h^2 \simeq \frac{1.04\times 10^9 \; {\rm{GeV}}^{-1} (T_0/2.725\; {\rm{K}})^3 x_f}{M_{\rm{pl}}\sqrt{g_\star (x_f)}(a+ 3b/x_f)}, \tag{A1}$

where
$ x_f \equiv m_\chi /T_f $ ; here,$ T_f $ denotes the DM freeze-out temperature.$ g_\star (x_f) $ represents the effectively relativistic degrees of freedom at the time of the DM freeze-out.$ M_{\rm{pl}} $ is the Planck mass and$ T_0 $ is the present CMB temperature. a and b are the coefficients of the velocity expansion of the annihilation cross section$ \sigma_{\rm{ann}} v = $ $ a+ b v^2 + {\cal{O}}(v^4) $ . If DM can annihilate into more than one channel, a and b are the total coefficients of all open channels. To calculate the relic density for DM in this work, we should first calculate the a and b coefficients in various annihilation channels.In this scenario, DM interacts with electroweak gauge bosons and can annihilate to
$ \gamma\gamma $ ,$ ZZ $ ,$ \gamma Z $ , and$ W^+W^- $ . After EWSB,$ B_\mu $ , and$ W_\mu^3 $ mix into the photon field$ A_\mu $ and massive gauge field$ Z_\mu $ . The effective interactions in terms of physical fields$ A^\mu $ and$ Z^\mu $ are$\begin{split} & {\cal{L}} \supset \frac{C_A}{\Lambda^3} \bar{\chi} \chi F_{\mu\nu}F^{\mu\nu} + \frac{C_{\gamma Z}}{\Lambda^3} \bar{\chi} \chi F_{\mu\nu}Z^{\mu\nu}\\ & + \frac{C_{ZZ}}{\Lambda^3} \bar{\chi} \chi Z_{\mu\nu}Z^{\mu\nu} + \frac{C_{W^+W^-}}{\Lambda^3} \bar{\chi} \chi W_{\mu\nu}W^{\mu\nu} \end{split}\tag{A2}$

with
$ F_{\mu\nu} = \partial_\mu A_\nu - \partial_\nu A_\mu $ ,$ Z_{\mu\nu} = \partial_\mu Z_\nu - \partial_\nu Z_\mu $ , and$ W_{\mu\nu} = \partial_\mu W_\nu^+ - \partial_\nu W_\mu^- $ . The matching conditions for interactions involving neutral gauge bosons are$ \begin{split} & C_A = C_B c_W^2 + C_W s_W^2, \\ & C_{\gamma Z} = 2 s_W c_W (C_W-C_B), \\ &C_{ZZ} = C_B s_W^2 + C_W c_W^2. \end{split} \tag{A3} $

The interaction with W bosons only originates from
$ C_W \bar{\chi}\chi W_{\mu\nu}^i W^{i \mu\nu} $ , leading to$ C_{W^+W^-} = C_W $ .Coefficient a vanishes in each channel and the leading contribution to
$ \left<\sigma_{\rm{ann}} v\right> $ is from the p-wave. The coefficients bs for the annihilation channels of$ \chi \chi \to \gamma \gamma $ ,$ \chi \chi \to ZZ $ ,$ \chi \chi \to \gamma Z $ , and$ \chi \chi \to {W^ + }{W^ - } $ are$ \begin{split} & b_{\chi\chi\to \gamma\gamma} = \frac{{C_{{\rm{A}}}^2m_\chi ^4}}{{\pi {\Lambda ^6}}},\\ & b_{\chi\chi\to ZZ} = \frac{{C_{{\rm{ZZ}}}^2{\rho _Z} m_\chi ^4 (8 - 8 x_Z + 3 x_Z^2)}}{{8\pi {\Lambda ^6}}}, \end{split} $

$ \begin{split} & b_{\chi\chi\to \gamma Z} = \frac{C_{\rm{\gamma Z}}^2 \rho_{\gamma Z}^2 (4-x_Z)^2 }{{32\pi {\Lambda ^6}}}, \\ & b_{\chi \chi \to {W^ + }{W^ - }} = \frac{{C_{W^+W^-}^2{\rho _W}m_\chi ^4 (8 - 8 x_W + 3x_W^2)}}{{4\pi {\Lambda ^6}}}, \end{split} \tag{A4}$

where
$ x_{Z/W}\equiv m_{Z/W}^2/m_\chi^2 $ ,$ {\rho _{Z/W}} \equiv \sqrt {1 - m_{Z/W}^2/m_\chi ^2} $ , and$ \rho_{\gamma Z} \equiv \sqrt{1- m_Z^2/4m_\chi^2} $ .Summing over all the annihilation channels and writing the coefficients bs in terms of
$ C_B $ and$ C_W $ , we obtain$ \begin{split} & b_B = \frac{1}{\pi }\frac{{m_\chi ^4}}{{{\Lambda ^6}}}\left( {c_w^4 + s_w^4\frac{{{\rho _Z}(8 - 8{x_Z} + 3x_Z^2)}}{8} + \frac{{c_w^2s_w^2\beta _{\gamma Z}^2{{(4 - {x_Z})}^2}}}{8}} \right) C_B^2, \\ & b_W = \frac{1}{\pi }\frac{{m_\chi ^4}}{{{\Lambda ^6}}}\left( {s_w^4 + c_w^4\frac{{{\rho _Z}(8 - 8{x_Z} + 3x_Z^2)}}{8} + \frac{{c_w^2s_w^2\beta _{\gamma Z}^2{{(4 - {x_Z})}^2}}}{8} + \frac{{{\rho _W}(8 - 8{x_Z} + 3x_Z^2)}}{4}} \right)C_W^2,\\ & b_{BW} = \frac{1}{\pi }\frac{{m_\chi ^4c_w^2s_w^2}}{{{\Lambda ^6}}}\left( {1 + \frac{{{\rho _Z}(8 - 8{x_Z} + 3x_Z^2)}}{4} - \frac{{\beta _{\gamma Z}^2{{(4 - {x_Z})}^2}}}{4}} \right) C_B C_W. \end{split} \tag{A5}$

Loop-induced annihilation of quarks and gluons is subdominant and can be safely ignored. It is known that when
$ C_W = 0 $ , the annihilation channel of$ \gamma \gamma $ always dominates and the constraint on$ C_B $ is roughly proportional to the inverse of$ m_\chi^2 $ . In contrast, in the case$ C_B = 0 $ , the annihilation channel of$ \gamma Z $ or$ W^+W^- $ will dominate once the channel opens, explaining the behavior of the relic density curve with$ m_\chi $ around$ 80\; {\rm{GeV}} $ in Fig. 2(b).In the case when the DM candidate interacts with leptons, DM decays to leptons directly with a and b coefficients given by
$ a = \frac{1}{2\pi \Lambda^4} \sum\limits_l C_l^2 \rho_l (2 m_\chi^2 + m_l^2) , \tag{A6}$

$ b = \frac{1}{2\pi \Lambda^4} \sum\limits_l C_l^2 \rho_l (2 m_\chi^2 + m_l^2) \frac{-4 + 2 m_f^2/m_\chi^2 + 11 m_f^4/m_\chi^4}{24(1-m_f^2/m_\chi^2)(2+m_f^2/m_\chi^2)}.\tag{A7}$

Here, the summing is performed for all lepton flavors.
Dark matter search at colliders and neutrino floor
- Received Date: 2020-06-30
- Available Online: 2020-11-01
Abstract: The sensitivity of the direct detection of dark matter (DM) approaches the so-called neutrino floor, below which it is difficult to disentangle the DM candidate from the neutrino background. In this work, we consider the scenario that no DM signals are reported in various DM direct detection experiments and explore whether collider searches could probe DM below the neutrino floor. We adopt several simplified models in which the DM candidate couples to electroweak gauge bosons or leptons in the standard model only through high-dimensional operators. After including the RGE running effect, we investigate the constraints of direct detection, indirect detection, and collider searches. The collider search can probe light DM below the neutrino floor. Particularly, for the effective interaction of






 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF














 DownLoad:
DownLoad: