-
The study of the modification of the hadronic properties (masses and widths) of light non-strange vector mesons,
$ \rho $ ,$ \omega $ ,$ \phi $ ; light strange pseudoscalar mesons K and$ {\bar K} $ ; pseudoscalar mesons,$ \eta $ ,$ \eta^{\prime} $ ; as well as open and hidden charm mesons D and$ J/\psi $ in a strongly interacting environment has received considerable interest in recent years owing to the expectation to observe a partial restoration of chiral symmetry in a nuclear medium (see, for example, [1-13]). The in-medium properties of hyperons at finite density have also been a matter of intense theoretical investigations in the last two decades [14-24]. Another interesting case of medium renormalization of hadrons is that of the strange vector$ K^*(892) $ and axial-vector$ K_1(1270) $ mesons with the same charge states (or with the same quark structure$ q{\bar s} $ or$ {\bar q}s $ with$ q = u,d $ ); for these mesons, the in-medium mass difference, as is expected [25-27], is sensitive to the chiral order parameter, giving rise to the possibility to identify unambiguously the effect of the breaking of chiral symmetry in a nuclear medium. The$ K^*(892) $ and$ K_1(1270) $ mesons in the quark model are kaonic excitations with angular momenta of 1 and with opposite parities. Namely, their isospins, spins–parities are$ I(J^P) = \frac{1}{2}(1^-) $ for$ K^*(892) $ and$ I(J^P) = \frac{1}{2}(1^+) $ for$ K_1(1270) $ . They are chiral partners and have relatively large vacuum decay widths of 50 and 90 MeV, respectively, corresponding to mean lifetimes of 4 and 2.2 fm/c.On the theoretical side, in the literature there are several publications devoted to the study of the in-medium properties of hadronic resonances
$ K^*(892) $ and$ K_1(1270) $ . Thus, the properties of$ {\bar K}^*(892) $ and$ K^*(892) $ mesons in cold nuclear matter have been investigated in Refs. [28-30] and [30, 31], respectively, on the basis of a chirally motivated model of the meson self-energies. In particular, it was shown that the$ {\bar K}^*(892) $ in-medium width is enlarged beyond 200 MeV at normal nuclear matter density$ \rho_0 $ , whereas that of$ K^*(892) $ is barely influenced by nuclear matter. The model also predicts, for the$ {\bar K}^*(892) $ and$ K^*(892) $ mesons, moderately attractive and repulsive real low-energy nuclear potentials (or their in-medium mass shifts) of about -50 and +40 MeV, respectively, at density$ \rho_0 $ . These are similar to those for light strange mesons$ {\bar K} $ and K. In contrast, a negative mass shift of about -20 MeV has been predicted for the$ K^*(892)^+ $ meson, with the same quark composition$ u{\bar s} $ as that of the$ K^+ $ one, at rest and for saturation density$ \rho_0 $ within the quark-meson coupling model [32]. Mass shifts of the$ K^*(892) $ and$ K_1(1270) $ mesons of about -40 and -150 MeV at density$ \rho_0 $ were obtained in more recent calculations in the framework of the three-flavor extended linear sigma model [33]. Other recent calculations performed in Ref. [26] using the QCD sum rule show that the upper limits of the mass shifts of$ K_1^- $ and$ K_1^+ $ mesons in nuclear matter are -249 and -35 MeV, respectively.Concerning the experimental situation, up to now only scarce data on
$ K^* $ production in heavy-ion and proton–proton collisions have been collected in the experiments performed in the SPS [34], RHIC [35], and LHC [36] energy domains. At SIS energies, the subthreshold and deep subthreshold production of$ K^*(892)^0 $ mesons in Al+Al and Ar+KCl collisions at beam kinetic energies of 1.9 and 1.76 A GeV, respectively, have been reported by the FOPI [37] and HADES [38] collaborations. While the$ K^*(892)^0 $ /$ K^0 $ yield ratio deduced in the FOPI experiment is found to be in good agreement with the corresponding prediction of the UrQMD transport model, this ratio extracted in the HADES experiment is overestimated by the model by a factor of about two. Less discrepancy would probably appear here if in-medium modifications of kaon properties were implemented into this transport model. The medium modification of the$ K_1(1270) $ meson could be probed at J-PARC through the$ K^- $ reaction on various nuclear targets [26]. Such measurement together with that of$ K^*(892) $ will shed light on the partial restoration of chiral symmetry in nuclear matter [26].As guidance for such future dedicated experiments, and as a first step in the implementation of this program, herein we give predictions for the absolute differential and total cross sections for near-threshold production of
$ K^*(892)^+ $ mesons in$ {\pi^-}^{12}C \to {K^*(892)^+}X $ and${\pi^-}^{184}W \to $ $ {K^*(892)^+}X $ reactions, at laboratory angles of 0°–45°, by incident pions with momenta below 2.0 GeV/c; in addition, we give predictions for their relative yields from these reactions under different scenarios for the$ K^*(892)^+ $ in-medium mass shift. These nuclear targets were employed in recent measurements [39] of$ \phi $ meson production in$ {\pi^-}A $ reactions at the GSI pion beam facility using the HADES spectrometer and, therefore, can be adopted in studying the$ {\pi^-}A \to {K^*(892)^+}X $ interactions here. The calculations are based on a first-collision model using an eikonal approximation, developed in Refs. [9, 10, 21] for the description of the inclusive$ \phi $ and$ \eta^{\prime} $ mesons as well as$ \Lambda(1520) $ hyperon production and extended to account for different scenarios of the$ K^*(892)^+ $ in-medium mass shift. This model is based on the quasiparticle picture; therefore, it is more appropriate for consideration of the$ K^* $ meson production in nuclei than for the study of$ {\bar K}^* $ meson creation here because, contrary to the$ {\bar K}^* $ meson, the$ K^* $ meson behaves in the medium as a quasiparticle with a single-peak spectral function and a modified effective mass [30, 31]. Our calculations can be used as an important tool for possible extraction of valuable information on the$ K^*(892)^+ $ in-medium mass shift from data that could be obtained via a dedicated experiment at the GSI pion beam facility. -
As we are interested in near-threshold incident pion beam momenta below 2.0 GeV/c, we have accounted for the following direct elementary
$ K^*(892)^+ $ production process, which has the lowest free production threshold momentum (1.84 GeV/c):$ \pi^-+p \to K^*(892)^++\Sigma^-. $

(1) We can ignore in the momentum domain of interest the contribution to the
$ K^*(892)^+ $ yield from the processes$ \pi^-p \to {K^*(892)^+}\Lambda{\pi^-} $ and$\pi^-N \to {K^*(892)^+}\Sigma{\pi} $ due to larger their production thresholds ($ \approx 1.97 $ and 2.15 GeV/c, respectively) in${\pi^-}p $ and$ \pi^-N $ collisions. Moreover, taking into consideration the results of the study [9] of pion-induced$\phi $ meson production on 12C and 184W nuclei at beam momentum of 1.7 GeV/c, we neglect in this domain by analogy with [9] the secondary pion–nucleon${\pi}N \to {K^*(892)^+}\Lambda $ and$ {\pi}N \to {K^*(892)^+}\Sigma $ production processes. For numerical simplicity, in our calculations we will account for the medium modification of the final$ K^*(892)^+$ meson participating in production process (1) by adopting its average in-medium mass$<m_{K^*}^*> $ instead of its local effective mass$ m_{K^*}^*(|{{r}}|) $ in the in-medium cross section of this process, with$ <m_{K^*}^*> $ defined according to Refs. [9, 10] as$ <m^*_{K^*}> = m_{K^*}+V_0\frac{<{\rho_N}>}{{\rho_0}}. $

(2) Here,
$ m_{K^*} $ is the$ K^*(892)^+ $ free space mass,$ V_0 $ is the$ K^*(892)^+ $ effective scalar nuclear potential (or its in-medium mass shift) at normal nuclear matter density$ {\rho_0} $ , and$ <{\rho_N}> $ is the average nucleon density. For target nuclei$ ^{12} $ C and$ ^{184} $ W, the ratio$ <{\rho_N}>/{\rho_0} $ was chosen as 0.55 and 0.76, respectively, in the present work. With regard to the quantity$ V_0 $ , in line with the above-mentioned, we will adopt the five following options: i)$ V_0 = -40 $ MeV, ii)$ V_0 = -20 $ MeV, iii)$ V_0 = 0 $ MeV, iv)$ V_0 = +20 $ MeV, and v)$ V_0 = +40 $ MeV throughout the study. Following the predictions of the chiral effective field theory approach [18, 40] and the SU(6) quark model [41, 42] for the fate of hyperons in nuclear matter and phenomenological information deduced from hypernuclear data [6, 43], i.e., that the$ \Sigma $ hyperon experiences only a moderately repulsive nuclear potential of about 10–40 MeV at central nuclear densities and finite momenta as well as a weakly attractive potential at the surface of the nucleus, we will ignore the modification of the mass of the$ \Sigma^- $ hyperons, produced together with the$ K^*(892)^+ $ mesons in process (1), in the nuclear medium. The in-medium threshold energy①$ \sqrt{s^*_{\rm{th}}} = <m_{K^*}^*>+m_{\Sigma^-} $ of process (1) resembles that for the final charged particles, also influenced by the respective Coulomb potentials, due to the cancellation of these potentials, we will also neglect their impact on these particles here.The total energy
$ E^{\prime}_{K^*} $ of the$ K^*(892)^+ $ meson in nuclear matter is expressed via its average effective mass$ <m^*_{K^*}> $ and its in-medium momentum$ {{p}}^{\prime}_{K^*} $ by the expression [9, 10]:$ E^{\prime}_{K^*} = \sqrt{\left({{p}}^{\prime}_{K^*}\right)^2+\left(< m^*_{K^*}>\right)^2}. $

(3) The momentum
$ {{p}}^{\prime}_{K^*} $ is related to the vacuum$ K^*(892)^+ $ momentum$ {{p}}_{K^*} $ as follows [9, 10]:$ E^{\prime}_{K^*} = \sqrt{\left({{p}}^{\prime}_{K^*}\right)^2+\left(<m^*_{K^*}>\right)^2} = \sqrt{{{p}}^2_{K^*}+m^2_{K^*}} = E_{K^*}, $

(4) where
$ E_{K^*} $ is the$ K^*(892)^+ $ total energy in a vacuum.As the
$ K^*(892)^+ $ –nucleon total cross section is expected to be small [44], we will neglect both inelastic and quasielastic$ {K^*(892)^+}N $ interactions in the present study. Then, accounting for the distortion of the incident pion in nuclear matter and the attenuation of the flux of the$ K^*(892)^+ $ mesons in the nucleus due to their decays here② as well as using the results given in [9, 10, 21], we represent the inclusive differential cross section for the production of$ K^*(892)^+ $ mesons with vacuum momentum$ {{p}}_{K^*} $ in nuclei in the direct process (1) as follows:$\begin{split} \frac{{\rm d}\sigma_{{\pi^-}A \to {K^*(892)^+}X}^{({\rm{prim}})} ({{p}}_{\pi^-},{{p}}_{K^*})} {{\rm d}{{p}}_{K^*}} = I_{V}[A,\theta_{K^*}] \left(\frac{Z}{A}\right) \left<\frac{{\rm d}\sigma_{{\pi^-}p\to K^*(892)^+{{\Sigma^-}}}\left({{p}}_{\pi^-}, {{p}}^{\prime}_{{K^*}}\right)}{{\rm d}{{p}}^{\prime}_{{K^*}}}\right>_A\frac{{\rm d}{{p}}^{\prime}_{{K^*}}} {{\rm d}{{p}}_{{K^*}}}, \end{split}$

(5) where
$ \begin{split} I_{V}[A,\theta_{{K^*}}] =& A\int\limits_{0}^{R}r_{\bot}{\rm d}r_{\bot} \int\limits_{-\sqrt{R^2-r_{\bot}^2}}^{\sqrt{R^2-r_{\bot}^2}}{\rm d}z \rho\left(\sqrt{r_{\bot}^2+z^2}\right)\exp {\left[-\sigma_{{\pi^-}N}^{\rm{tot}}A\int\limits_{-\sqrt{R^2-r_{\bot}^2}}^{z} \rho\left(\sqrt{r_{\bot}^2+x^2}\right){\rm d}x\right]}\\& \times \int\limits_{0}^{2\pi}{\rm d}{\varphi}\exp {\left[- \int\limits_{0}^{l(\theta_{{K^*}},\varphi)}\frac{{\rm d}x} {\lambda_{K^*}\left(\sqrt{x^2+2a(\theta_{{K^*}},\varphi)x+b+R^2}\right)}\right]}, \end{split}$

(6) $ a(\theta_{K^*},\varphi) = z\cos{\theta_{K^*}}+ r_{\bot}\sin{\theta_{K^*}}\cos{\varphi},\ b = r_{\bot}^2+z^2-R^2, $

(7) $ l(\theta_{K^*},\varphi) = \sqrt{a^2(\theta_{K^*},\varphi)-b}- a(\theta_{K^*},\varphi), $

(8) $ \lambda_{K^*}(|{{r}}|) = \dfrac{p^{\prime}_{K^*}}{m^*_{K^*}(|{{r}}|)\Gamma_{K^*}},\,\,\,\;\; m^*_{K^*}(|{{r}}|) = m_{K^*}+V_0\dfrac{{\rho_N}(|{{r}}|)}{{\rho_0}} $

(9) and
$ \begin{array}{l} \left<\dfrac{{\rm d}\sigma_{{\pi^-}p\to K^*(892)^+{\Sigma^-}}\left({{p}}_{\pi^-},{{p}}^{\prime}_{K^*}\right)} {{\rm d}{{p}}^{\prime}_{K^*}}\right>_A = \int\int P_A\left({{p}}_t,E\right){\rm d}{{p}}_t{\rm d}E \times \left\{\dfrac{{\rm d}\sigma_{{\pi^-}p\to K^*(892)^+{\Sigma^-}}[\sqrt{s},<m_{K^*}^*>, m_{\Sigma^-},{{p}}^{\prime}_{K^*}]} {{\rm d}{{p}}^{\prime}_{K^*}}\right\}, \end{array}$

(10) $ s = (E_{\pi^-}+E_t)^2-({{p}}_{\pi^-}+{{p}}_t)^2, $

(11) $ E_t = M_A-\sqrt{(-{{p}}_t)^2+(M_{A}-m_{N}+E)^{2}}. $

(12) Here,
$ {\rm d}\sigma_{{\pi^-}p\to {K^*(892)^+}{\Sigma^-}}[\sqrt{s},<m_{K^*}^*>,m_{\Sigma^-},{{p}}^{\prime}_{K^*}] /{\rm d}{{p}}^{\prime}_{K^*} $ is the off-shell inclusive differential cross section for the production of the$ {K^*(892)^+} $ meson and$ \Sigma^- $ hyperon with modified mass$ <m_{K^*}^*> $ and free mass$ m_{\Sigma^-} $ , respectively. The$ K^*(892)^+ $ meson is produced with in-medium momentum$ {{p}}^{\prime}_{{K^*}} $ in process (1) at the$ {\pi^-}p $ center-of-mass energy$ \sqrt{s} $ .$ E_{\pi^-} $ and$ {{p}}_{\pi^-} $ are the total energy and momentum of the incident pion ($ E_{\pi^-} = \sqrt{m^2_{\pi}+{{p}}^2_{\pi^-}} $ ;$ m_{\pi} $ is the free-space pion mass);$ \rho({{r}}) $ and$ P_A({{p}}_t,E) $ are the local nucleon density and the spectral function of the target nucleus A normalized to unity (the concrete information about these quantities, used in the subsequent calculations, is given in Refs. [9, 45-47]);$ {{p}}_t $ and E are the internal momentum and removal energy of the struck target proton involved in the collision process (1);$ \sigma_{{\pi^-}N}^{\rm{tot}} $ is the total cross section of the free$ {\pi^-}N $ interaction (we use in our calculations the value of$ \sigma_{{\pi^-}N}^{\rm{tot}} = 35 $ mb for initial pion momenta of interest); Z and A are the numbers of protons and nucleons in the target nucleus, and$ M_{A} $ and R are its mass and radius;$ m_N $ is the free-space nucleon mass; and$ \theta_{K^*} $ is the polar angle of vacuum momentum$ {{p}}_{{K^*}} $ in the laboratory system with the z-axis directed along the momentum$ {{p}}_{{\pi^-}} $ of the incident pion beam.In line with [9], we assume that the off-shell differential cross section
$ {\rm d}\sigma_{{\pi^-}p \to {K^*(892)^+}{\Sigma^-}}[\sqrt{s},<m_{K^*}^*>,m_{\Sigma^-}, {{p}}^{\prime}_{K^*}] /$ $ {\rm d}{{p}}^{\prime}_{K^*} $ for$ K^*(892)^+ $ production in channel (1) is equivalent to the respective on-shell cross section calculated for the off-shell kinematics of this channel as well as for the final$ K^*(892)^+ $ and hyperon in-medium mass$ <m_{K^*}^*> $ and free mass$ m_{\Sigma^-} $ , respectively. Accounting for the two-body kinematics of process (1), we obtain the following expression for the differential cross section$ {\rm d}\sigma_{{\pi^-}p \to {K^*(892)^+}{\Sigma^-}} $ $[\sqrt{s},<m_{K^*}^*>,m_{\Sigma^-},{{p}}^{\prime}_{K^*}] /{\rm d}{{p}}^{\prime}_{K^*} $ :$ \begin{split} \dfrac{{\rm d}\sigma_{\pi^{-}p \to {K^*(892)^+}{\Sigma^-}}[\sqrt{s},<m_{K^*}^*>,m_{\Sigma^-},{{p}}^{\prime}_{K^*}]} {{\rm d}{{p}}^{\prime}_{K^*}} = & \dfrac{\pi}{I_2[s,<m_{K^*}^*>,m_{\Sigma^-}]E^{\prime}_{K^*}} \dfrac{{\rm d}\sigma_{{\pi^{-}}p \to {K^*(892)^+}{\Sigma^-}}\left(\sqrt{s},<m_{K^*}^*>,m_{\Sigma^-},\theta^*_{K^*}\right)} {{\rm d}{{\Omega}}^*_{K^*}} \\& \times \dfrac{1}{\left(\omega+E_t\right)}\delta\left[\omega+E_t-\sqrt{m_{\Sigma^-}^2+\left({{Q}}+{{p}}_t\right)^2}\right], \begin{array}{l} \end{array} \end{split} $

(13) where
$ I_2[s,<m_{K^*}^*>,m_{\Sigma^-}] = \frac{\pi}{2} \frac{\lambda[s,\left(<m_{K^*}^*>\right)^{2},m_{\Sigma^-}^{2}]}{s}, $

(14) $ \lambda\left(x,y,z\right) = \sqrt{{\left[x-\left({\sqrt{y}}+{\sqrt{z}}\right)^2\right]}{\left[x- \left({\sqrt{y}}-{\sqrt{z}}\right)^2\right]}}, $

(15) $ \omega = E_{\pi^-}-E^{\prime}_{K^*}, \,\,\,\,\;\;{{Q}} = {{p}}_{\pi^-}-{{p}}^{\prime}_{K^*}. $

(16) Here,
$ {\rm d}\sigma_{{\pi^{-}}p \to {K^*(892)^+}{\Sigma^-}}(\sqrt{s},<m_{K^*}^*>,m_{\Sigma^-},\theta^*_{K^*}) /{\rm d}{{\Omega}}^*_{K^*} $ is the off-shell differential cross section for the production of$ K^*(892)^+ $ mesons in process (1) under the polar angle$ \theta^*_{K^*} $ in the$ {\pi^-}p $ c.m.s. It is assumed to be isotropic in our calculations of$ K^*(892)^+ $ meson production in$ {\pi^-}A $ reactions:$ \frac{{\rm d}\sigma_{{\pi^{-}}p \to {K^*(892)^+}{\Sigma^-}}(\sqrt{s},<m_{K^*}^*>,m_{\Sigma^-},\theta^*_{K^*})} {{\rm d}{\bf{\Omega}}^*_{K^*}} = \frac{\sigma_{{\pi^{-}}p \to {K^*(892)^+}{\Sigma^-}}(\sqrt{s},\sqrt{s^*_{\rm{th}}})}{4\pi}. $

(17) Here,
$ \sigma_{{\pi^{-}}p \to {K^*(892)^+}{\Sigma^-}}(\sqrt{s},\sqrt{s^*_{\rm{th}}}) $ is the "in-medium" total cross section of channel (1) with the threshold energy$ \sqrt{s^*_{\rm{th}}} $ defined above. According to the above-mentioned, it is equivalent to the vacuum cross section$ \sigma_{{\pi^{-}}p \to {K^*(892)^+}{\Sigma^-}}(\sqrt{s},\sqrt{s_{\rm{th}}}) $ , in which the vacuum threshold energy$ \sqrt{s_{\rm{th}}} = m_{K^*}+m_{\Sigma^-} = 2.089 $ GeV is replaced by the in-medium one,$ \sqrt{s^*_{\rm{th}}} $ , and the free collision energy$ s = (E_{\pi^-}+m_N)^2-{{p}}_{\pi^-}^2 $ by the in-medium expression (11). For the free total cross section$ \sigma_{{\pi^{-}}p \to {K^*(892)^+}{\Sigma^-}}(\sqrt{s},\sqrt{s_{\rm{th}}}) $ we have adopted the following parametrization of the available scarce experimental data [48]:$ \begin{split}\sigma_{{\pi}^-p \to {K^*(892)^+}{\Sigma^-}}(\sqrt{s},\sqrt{s_{\rm{th}}}) = \left\{ \begin{array}{l} 67.30\left(\sqrt{s}-\sqrt{s_{\rm{th}}}\right)^{0.287}\; [{\text µ}{\rm{b}}] \rm{for $0 < \sqrt{s}-\sqrt{s_{\rm{th}}} \leqslant 0.355\; {\rm{GeV}}$}, \\ 5.66/\left(\sqrt{s}-\sqrt{s_{\rm{th}}}\right)^{2.103}\; [{\text µ}{\rm{b}}] \rm{for $\sqrt{s}-\sqrt{s_{\rm{th}}} > 0.355\; {\rm{GeV}}$}. \end{array} \right. \end{split}$

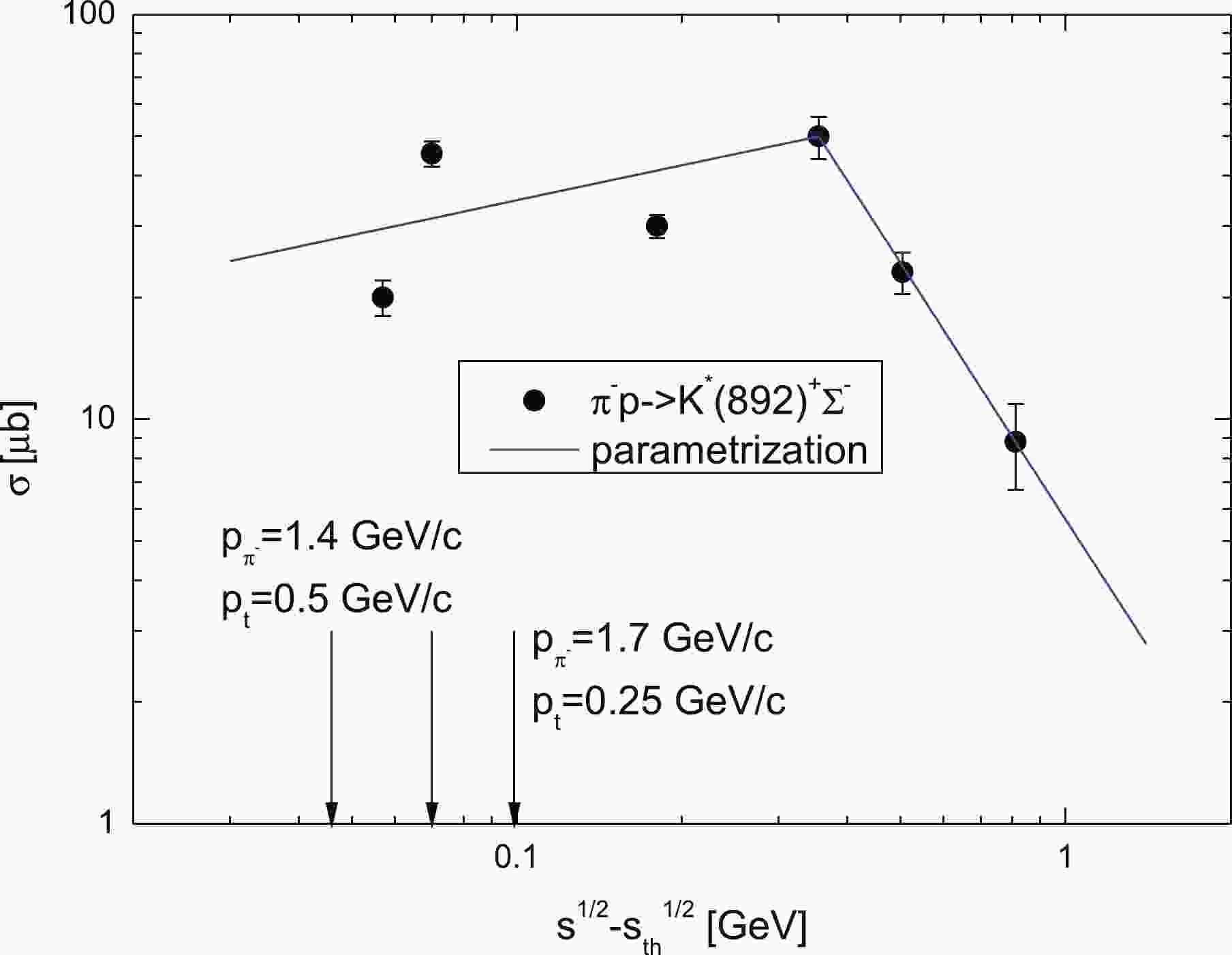
(18) As can be seen from Fig. 1, the parametrization (18) (solid line) fits the data [48] (full circles)③ for the
$ {\pi^-}p \to {K^*(892)^+}{\Sigma^-} $ reaction reasonably well. One can also see that the on-shell cross section$\sigma_{{\pi}^-p \to {K^*(892)^+}{\Sigma^-}} $ amounts to approximately 31 μb for the initial pion momentum of 2.0 GeV/c and a free target proton at rest. The off-shell cross sections$ \sigma_{{\pi}^-p \to {K^*(892)^+}{\Sigma^-}}$ , calculated in line with Eqs. (11), (12), and (18) for pion momenta of 1.4 and 1.7 GeV/c, a target proton bound in$ ^{12} $ C by 16 MeV, and with relevant internal momenta of 500 and 250 MeV/c, are about 28 and 35 μb, respectively④. This opens up the possibility of measuring the$ K^*(892)^+ $ yield in$ \pi^-A $ reactions both at the near-threshold and far-below-threshold beam momenta at the GSI pion beam facility with a sizable strength. It should be pointed out that the use in the calculations for the in-medium$K^*(892)^+ $ angular distribution of the same anisotropic form as was adopted in Ref. [45] for the$ {\pi^-}p \to K^+\Sigma^- $ reaction, namely:${\rm d}\sigma_{{\pi^{-}}p \to {K^*(892)^+}{\Sigma^-}}$ $(\sqrt{s}, <m_{K^*}^*>, m_{\Sigma^-}, \theta^*_{K^*})/ {\rm d}{\bf{\Omega}}^*_{K^*} = \left[1+|\cos{\theta^*_{K^*}}|\right] $ $ \sigma_{{\pi^{-}}p \to {K^*(892)^+}{\Sigma^-}}(\sqrt{s}, \sqrt{s^*_{\rm{th}}})/6\pi $ instead of isotropic one (17) leads to only insignificant corrections to the absolute$ K^*(892)^+ $ momentum differential cross sections presented in Figs. 2, 3 and 4. They are about 5%–10% for subthreshold pion momenta of 1.4 and 1.7 GeV/c (at which these cross sections possess a high sensitivity to changes in the in-medium shift$V_0 $ of the$ K^*(892)^+ $ mass) as well as ~15%–20% for incident pion momentum of 2.0 GeV/c, as our calculations showed. The corrections to the predicted in the paper on the basis of Eq. (17) enhancement factors (see below) are even smaller. They are about 3%–5% at beam momenta of interest. In view of numerical results given below, this means that employing of the isotropic distribution (17) in calculations of the near-threshold$ K^*(892)^+ $ production in${\pi^-}A $ reactions with the aim of studying of a possibility of distinguishing between considered options for the$ K^*(892)^+$ in-medium mass shift is very well justified. In Eqs. (6)–(8) we assume that the direction of the$K^*(892)^+ $ three-momentum is not changed during the propagation from its production point inside the nucleus in the relatively weak nuclear field, considered in the work, to the vacuum far away from the nucleus. As a consequence, the quantities$ \left<{\rm d}\sigma_{{\pi^-}p\to K^*(892)^+{{\Sigma^-}}} ({{p}}_{\pi^-}, {{p}}^{\prime}_{{K^*}})/{\rm d}{{p}}^{\prime}_{{K^*}}\right>_A $ and$ {\rm d}{{p}}^{\prime}_{{K^*}}/{\rm d}{{p}}_{{K^*}} $ , entered into Eq. (5), can be put in the simple forms$ \left<{\rm d}\sigma_{{\pi^-}p\to K^*(892)^+{{\Sigma^-}}}(p_{\pi^-}, p^{\prime}_{{K^*}}, \theta_{K^*})/ p^{\prime2}_{K^*}{\rm d}p^{\prime}_{{K^*}}{\rm d}{{\Omega}}_{K^*}\right>_A $ and$ p^{\prime}_{{K^*}}/p_{{K^*}} $ , where$ {\bf{\Omega}}_{K^*}(\theta_{K^*},\varphi_{K^*}) = {{p}}_{{K^*}}/p_{{K^*}} $ . Here,$ \varphi_{K^*} $ is the azimuthal angle of the$ K^*(892)^+ $ momentum$ {{p}}_{K^*} $ in the laboratory system. Accounting for the HADES spectrometer acceptance as well as the fact that in the considered energy region$ K^*(892)^+ $ mesons are mainly emitted, due to the kinematics in the forward directions⑤, we will calculate the$ K^*(892)^+ $ momentum differential and total production cross sections on$ ^{12} $ C and$ ^{184} $ W target nuclei for laboratory solid angle$ {\Delta}{\bf{\Omega}}_{K^*} $ =$ 0^{\circ} \leqslant \theta_{K^*} \leqslant 45^{\circ} $ and$ 0 \leqslant \varphi_{K^*} \leqslant 2{\pi} $ . Upon integrating the full inclusive differential cross section (5) over this angular domain, we can represent the differential cross section for$ K^*(892)^+ $ meson production in$ {\pi^-}A $ collisions from the direct process (1), corresponding to the HADES acceptance window, in the following form: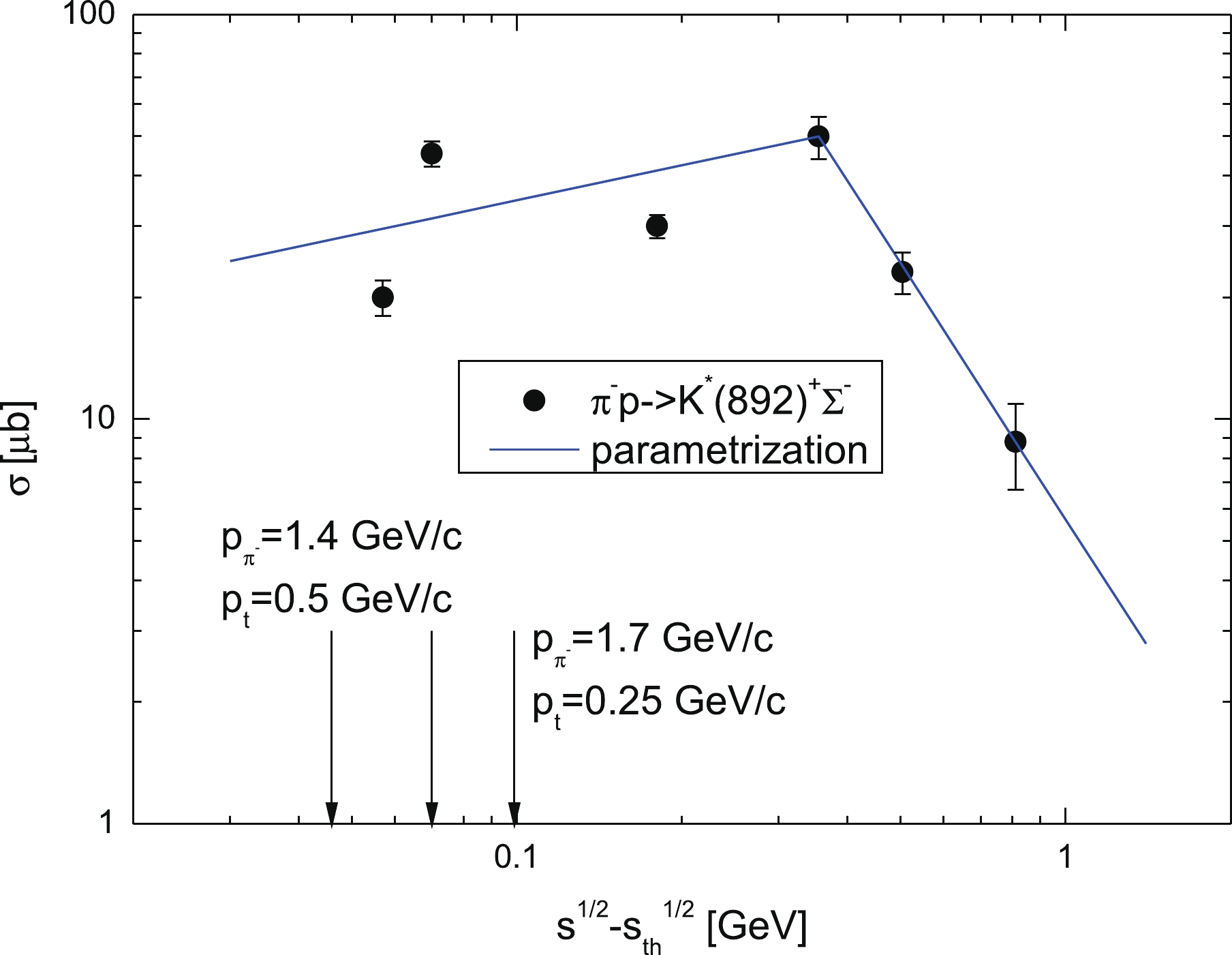
Figure 1. (color online) Total cross section for the reaction
$ \pi^-p \to {K^*(892)^+}{\Sigma^-} $ as a function of the excess energy$ \sqrt{s}-\sqrt{s_{\rm{th}}} $ . The left and right arrows indicate the excess energies$ \sqrt{s}-\sqrt{s_{\rm{th}}} $ = 46 MeV and$ \sqrt{s}-\sqrt{s_{\rm{th}}} $ = 99 MeV corresponding to the incident pion momenta of 1.4 and 1.7 GeV/c and a target proton bound in$ ^{12} $ C by 16 MeV and with momenta of 500 and 250 MeV/c, respectively. The latter ones are directed opposite to the incoming pion beam. The middle arrow indicates the excess energy$ \sqrt{s}-\sqrt{s_{\rm{th}}} $ = 70 MeV corresponding to the initial pion momentum of 2.0 GeV/c and a free target proton at rest. For the rest of the notation see the text.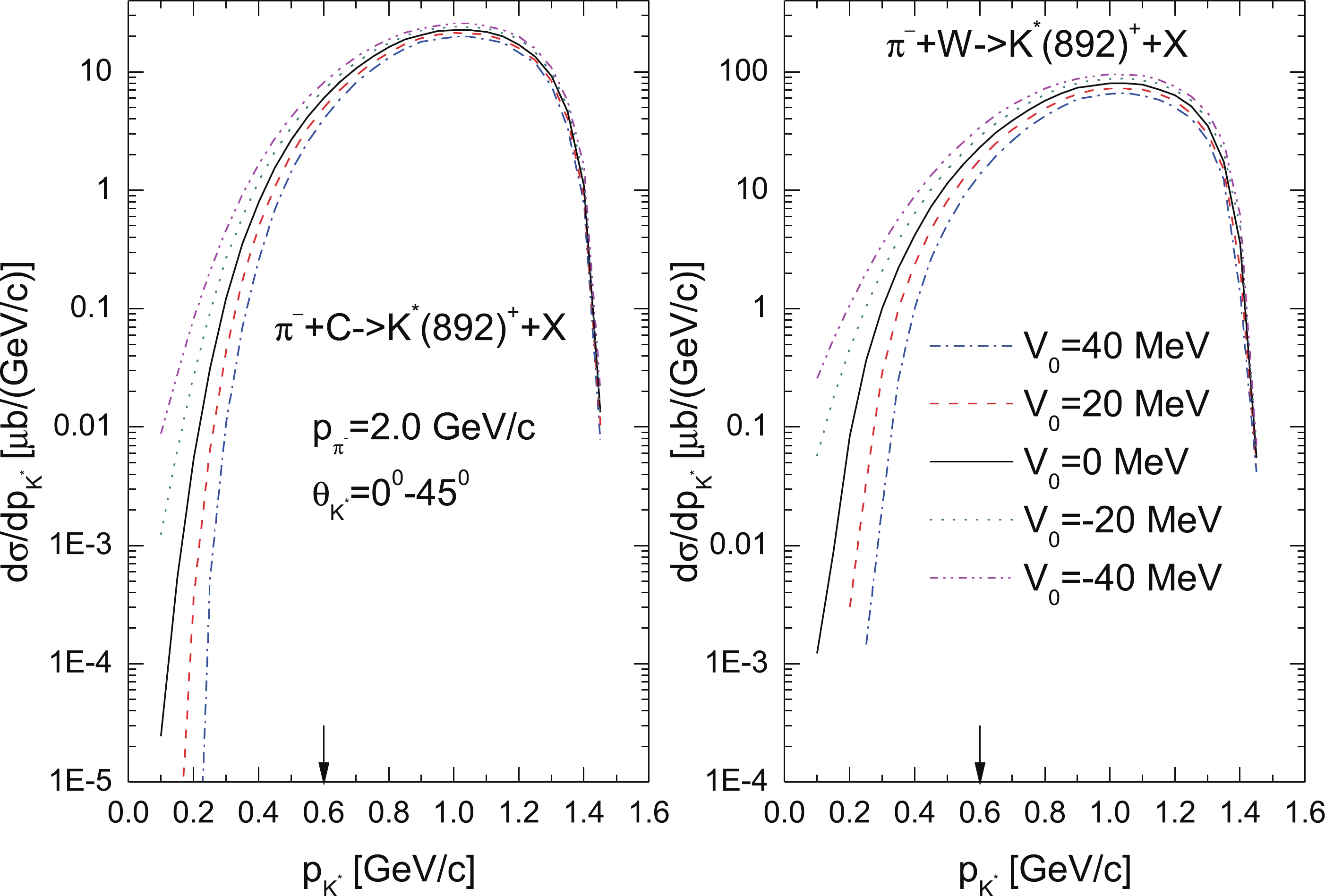
Figure 2. (color online) Momentum differential cross sections for the production of
$ K^*(892)^+ $ mesons from the primary$ {\pi^-}p \to {K^*(892)^+}{\Sigma^-} $ channel in the laboratory polar angular range of 0°–45° in the interaction of$ \pi^- $ mesons of momentum 2.0 GeV/c with$ ^{12} $ C (left) and$ ^{184} $ W (right) nuclei, calculated for different values of the$ K^*(892^+) $ meson effective scalar potential$ V_0 $ at density$ \rho_0 $ indicated in the inset. The arrows indicate the boundary between the low-momentum and high-momentum regions of the$ K^*(892)^+ $ spectra.
Figure 3. (color online) As in Fig. 2, but for the incident pion beam momentum of 1.7 GeV/c.
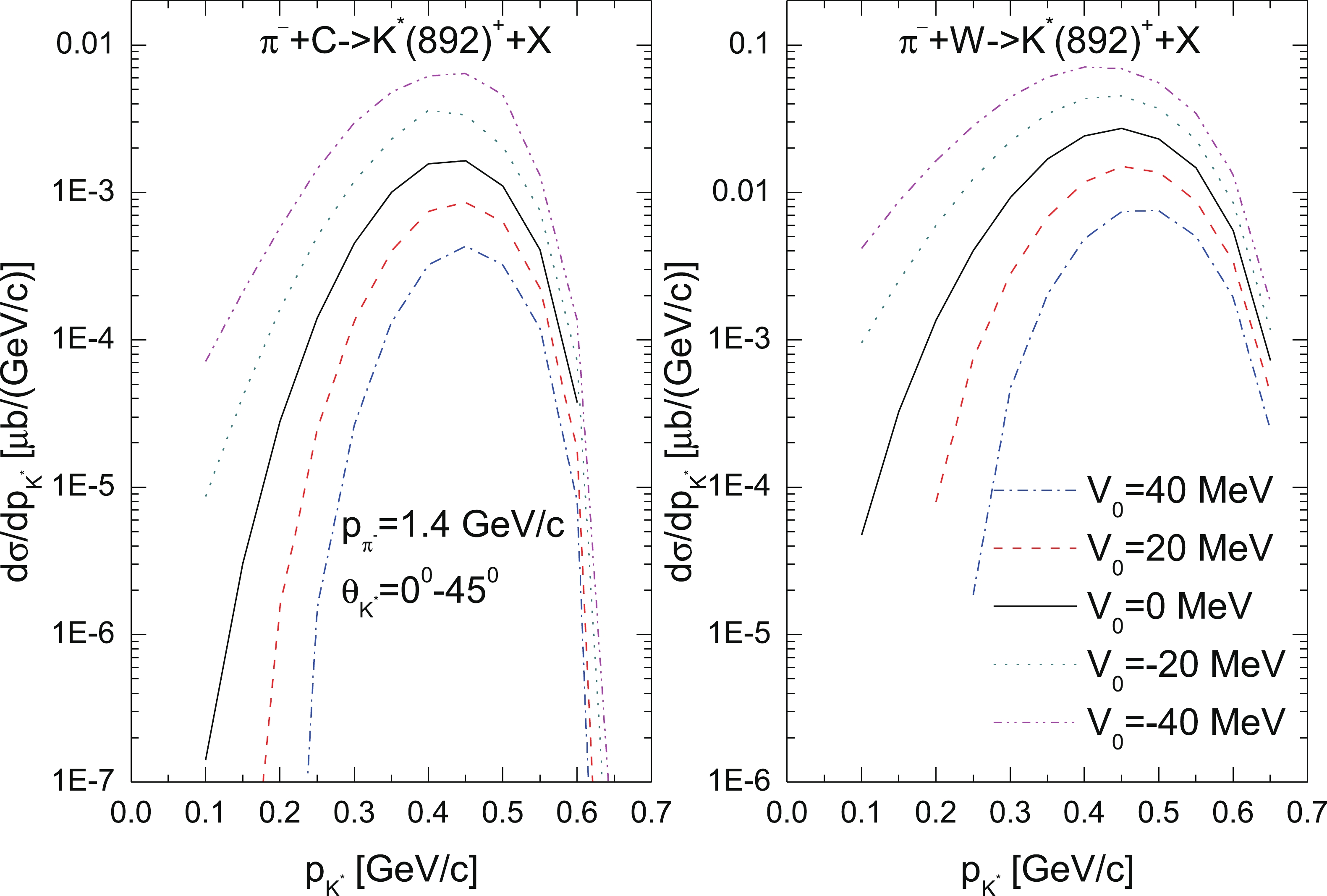
Figure 4. (color online) As in Fig. 2, but for the incident pion beam momentum of 1.4 GeV/c.
$ \begin{split} \frac{{\rm d}\sigma_{{\pi^-}A\to {K^*(892)^+}X}^{({\rm{prim}})} (p_{\pi^-},p_{K^*})}{{\rm d}p_{K^*}} =& \int\limits_{{\Delta}{\bf{\Omega}}_{K^*}}^{}{\rm d}{\bf{\Omega}}_{K^*} \frac{{\rm d}\sigma_{{\pi^-}A\to {K^*(892)^+}X}^{({\rm{prim}})} ({{p}}_{\pi^-},{{p}}_{K^*})}{d{{p}}_{K^*}}p_{K^*}^2 \\ =& 2{\pi}\left(\frac{Z}{A}\right)\left(\frac{p_{K^*}}{p^{\prime}_{K^*}}\right) \int\limits_{\cos45^{\circ}}^{1}{\rm d}\cos{{\theta_{K^*}}}I_{V}[A,\theta_{K^*}] \left<\frac{{\rm d}\sigma_{{\pi^-}p\to {K^*(892)^+}{\Sigma^-}}(p_{\pi^-}, p^{\prime}_{K^*},\theta_{K^*})}{{\rm d}p^{\prime}_{K^*}{\rm d}{\bf{\Omega}}_{K^*}}\right>_A. \end{split} $

(19) At HADES the
$ K^*(892)^+$ mesons could be identified via the hadronic decays$ K^*(892)^+ \to K^0{\pi^+} $ with a branching ratio of 2/3 or via their radiative decays$ K^*(892)^+ \to$ $ K^+{\gamma} $ with sizable branching ratio of 10−3 [49]. -
In the beginning, we consider the absolute
$ K^*(892)^+ $ momentum differential cross sections from the direct$ K^*(892)^+ $ production mechanism in$ \pi^- $ $ ^{12} $ C and$ \pi^- $ $ ^{184} $ W collisions. These cross sections were calculated according to Eq. (19) in five considered scenarios for the$ K^*(892)^+ $ in-medium mass shift at density$ \rho_0 $ at laboratory angles of 0°–45° and for incident pion momenta of 2.0, 1.7, and 1.4 GeV/c. They are presented, respectively, in Figs. 2, 3, and 4. It is seen that the$ K^*(892)^+ $ meson momentum distributions are notably sensitive to its in-medium mass shift, mainly in the low-momentum region of 0.1–0.6 GeV/c, for both target nuclei and for all considered beam momenta. Here, there are sizeable and experimentally accessible differences between the results obtained by employing the different$ K^*(892)^+ $ in-medium mass shifts under consideration, which for each target nucleus are practically similar to each other at these initial pion momenta. Thus, for example, for incident pion and outgoing$ K^*(892)^+ $ meson momenta of 2.0 and 0.3 GeV/c, respectively, in the case of a$ ^{12} $ C nucleus, the$ K^*(892)^+ $ yield is enhanced at mass shift$ V_0 = +20 $ MeV by a factor of approximately 4.1 compared to that obtained for the shift$ V_0 = +40 $ MeV. When going from$ V_0 = +20 $ MeV to$ V_0 = 0 $ MeV, from$ V_0 = 0 $ MeV to$ V_0 = -20 $ MeV, and from$ V_0 = -20 $ MeV to$ V_0 = -40 $ MeV, the enhancement factors are about 2.8, 2.2, and 1.8, respectively. In the case of a$ ^{184} $ W target nucleus, these enhancement factors are about 14.0, 3.5, 2.1, and 1.7, respectively. At an initial beam momentum of 1.4 GeV/c and the same outgoing kaon momentum of 0.3 GeV/c, the corresponding enhancement factors are similar: they are about 5.0, 3.3, 2.6, and 2.5 and 6.0, 3.3, 2.4, and 2.0 in the cases of$ ^{12} $ C and$ ^{184} $ W target nuclei, respectively. However, the$ K^*(892)^+ $ low-momentum production differential cross sections at a beam momentum of 1.4 GeV/c are very small (in the range of$ \sim $ 0.0001–0.1 μb/(GeV/c)) and they are less than those at pion momenta of 1.7 and 2.0 GeV/c by about two to three orders of magnitude. Therefore, the measurements of the$ K^*(892)^+ $ differential cross sections in$ {\pi^-}A $ reactions in the near-threshold incident pion momentum region (at 1.7–2.0 GeV/c) with the aim of distinguishing between considered options for the$ K^*(892)^+ $ mass shift in nuclear matter look promising.The sensitivity of the low-momentum parts of the
$ K^*(892)^+ $ meson production differential cross sections to the related in-medium mass shift$ V_0 $ , shown in Figs. 2, 3, and 4, can also be studied from such integral measurements as the measurements of the total cross sections for$ K^*(892)^+ $ production in$ {\pi^-}^{12} $ C and$ {\pi^-}^{184} $ W reactions by 1.4, 1.7, and 2.0 GeV/c pions at laboratory angles of 0°–45° in the low-momentum region (0.1–0.6 GeV/c) and in the full-momentum region allowed for a given beam momentum. These cross sections, calculated by integrating Eq. (19) over the$ K^*(892)^+ $ momentum$ p_{K^*} $ in these regions, are shown in Fig. 5 as functions of the mass shift (or effective scalar potential)$ V_0 $ . It can be seen from this figure that again the low-momentum range of 0.1–0.6 GeV/c shows the highest sensitivity to this potential. Thus, for instance, the ratios between the total cross sections of$ K^*(892)^+ $ production by 1.4, 1.7, and 2.0 GeV/c pions on$ ^{12} $ C and$ ^{184} $ W target nuclei in this momentum range, calculated with the potential$ V_0 = -40 $ MeV, and the same cross sections as those obtained in the scenario$ V_0 = +40 $ MeV, are about 21.0, 5.0, and 3.0 and 14.0, 10.0, and 4.0, respectively. These ratios in the full-momentum regions are about 21.0, 3.0, and 1.4 for$ ^{12} $ C and 14.0, 4.0, and 1.7 for$ ^{184} $ W, respectively. In the low-momentum region of interest the highest sensitivity of the$ K^*(892)^+ $ production total cross sections to the potential$ V_0 $ is observed, as is expected, at the initial pion momentum of 1.4 GeV/c. However, these cross sections are small and they are less than those at beam momenta of 1.7 and 2.0 GeV/c by several orders of magnitude. As the latter ones have a measurable strength$ \sim $ 0.1–5 μb, the low-momentum total cross section measurements of$ K^*(892)^+ $ meson production in nuclei in the near-threshold incident pion momentum region$ \sim $ 1.7–2.0 GeV/c, with regard to the aim of distinguishing between adopted options for its mass shift in nuclear matter, look promising as well.
Figure 5. (color online) Total cross sections for the production of
$ K^*(892)^+ $ mesons from the primary$ {\pi^-}p \to {K^*(892)^+}{\Sigma^-} $ channel in C and W target nuclei with momenta of 0.1–0.6 GeV/c (upper two panels) and with all allowed momenta$ \ge $ 0.1 GeV/c at a given beam momentum (lower two panels) in the laboratory polar angular range of 0°–45° by 1.4, 1.7, and 2.0 GeV/c$ \pi^- $ mesons as functions of the effective scalar$ K^*(892)^+ $ potential$ V_0 $ at normal nuclear density. The lines are visual guides.The fact that the low-momentum range of 0.1–0.6 GeV/c shows the highest sensitivity to the
$ K^*(892)^+ $ in-medium mass shift$ V_0 $ at the central density$ \rho_0 $ is also clearly supported by the results given in Fig. 6. Here, the ratios R of the$ K^*(892)^+ $ meson production total cross sections, calculated for the mass shift$ V_0 $ and presented in Fig. 5 to the analogous cross sections determined at$ V_0 = 0 $ MeV are shown as functions of this mass shift. It is worth noting that an analysis of these ratios has the advantage of no dependence on the absolute normalization of the calculated and measured cross sections. As seen from this figure, the highest sensitivity of the ratios in both considered kinematic ranges to the quantity$ V_0 $ is indeed observed at a pion momentum of 1.4 GeV/c. For example, at this momentum and for these ranges the cross-section ratios R for$ V_0 = -40 $ MeV are about 4.5 and 3.2 for$ ^{12} $ C and$ ^{184} $ W, respectively. As the pion-beam momentum increases to 1.7 and 2.0 GeV/c, the sensitivity of the cross-section ratios to variations in the mass shift$ V_0 $ decreases. Thus, in the case where$ K^*(892)^+ $ mesons of momenta of 0.1–0.6 GeV/c are produced by 1.7 and 2.0 GeV/c pions incident on$ ^{12} $ C and$ ^{184} $ W targets, the ratios being considered for$ V_0 = -40 $ MeV take smaller yet sizeable values of 2.1 and 1.6, and 2.6 and 1.8, respectively. The analogous ratios for the production of$ K^*(892)^+ $ mesons in the full-momentum regions by 1.7 and 2.0 GeV/c pions in$ ^{12} $ C and$ ^{184} $ W nuclei are even smaller at about 1.6 and 1.2, and 1.9 and 1.3, respectively.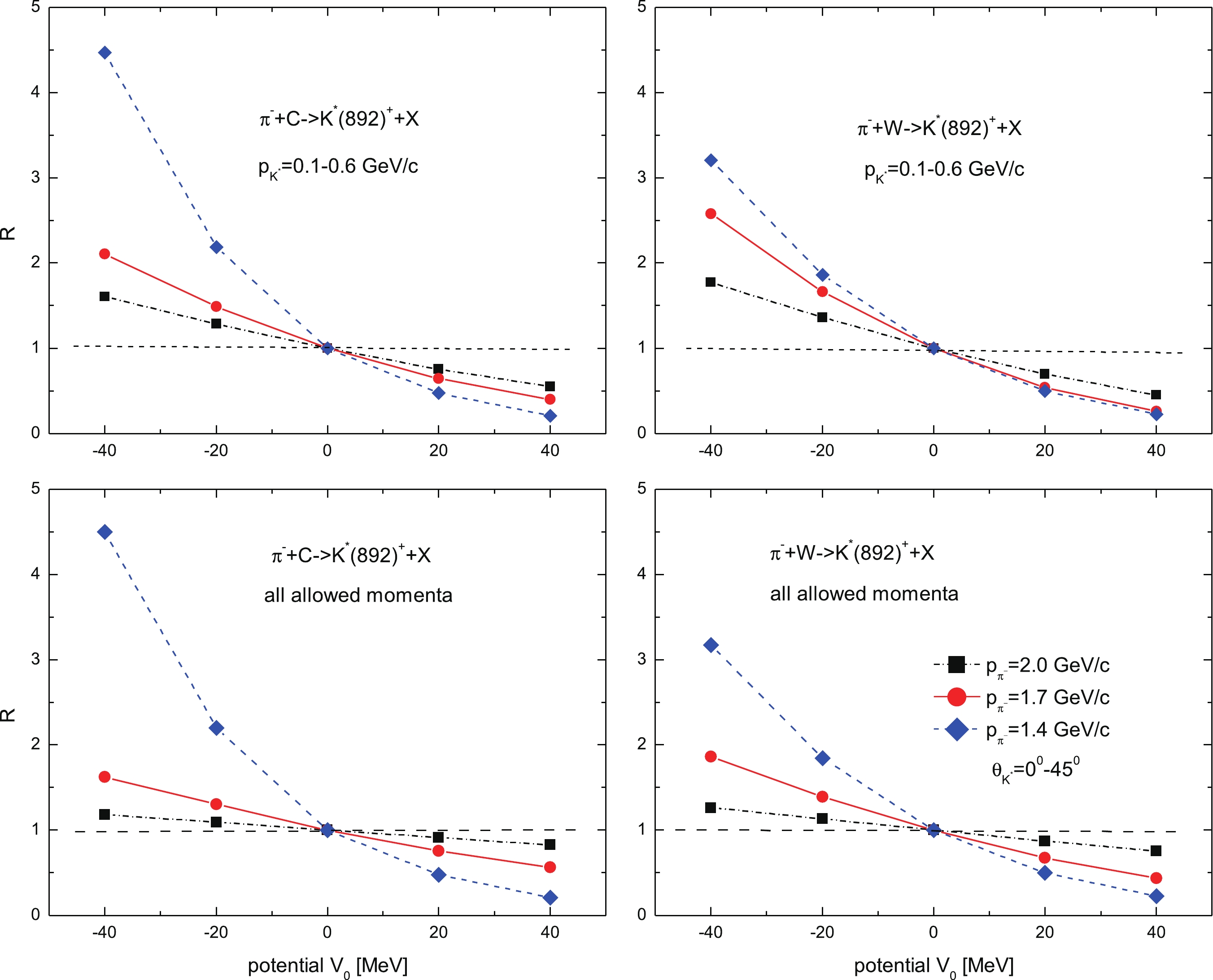
Figure 6. (color online) Ratio between the total cross sections for the production of
$ K^*(892)^+ $ mesons from the primary$ {\pi^-}p \to {K^*(892)^+}{\Sigma^-} $ channel on$ ^{12} $ C and$ ^{184} $ W target nuclei at laboratory angles of 0°–45° with momenta of 0.1–0.6 GeV/c (upper two panels) and with all allowed momenta$ \geqslant $ 0.1 GeV/c at a given beam momentum (lower two panels) by 1.4, 1.7, and 2.0 GeV/c$ \pi^- $ mesons, calculated with and without the$ K^*(892)^+ $ in-medium mass shift$ V_0 $ at normal nuclear density, as a function of this shift. The lines are visual guides.Therefore, we conclude that a comparison of the low-momentum "integral" results shown in Figs. 5 and 6 with the respective near-threshold experimental data, which could be obtained in future experiments using
$ \pi^- $ beams at the GSI pion beam facility or at J-PARC [50], will also allow the study of the in-medium properties of the$ K^*(892)^+ $ mesons.These properties can be also investigated [5] from other integral measurements such as the measurements of the excitation functions for
$ K^*(892)^+ $ production in$ {\pi^-}^{12} $ C and$ {\pi^-}^{184} $ W reactions at laboratory angles of 0°–45° in the low-momentum (0.1–0.6 GeV/c) and full-momentum regions. They were calculated for five adopted scenarios for the$ K^*(892)^+ $ in-medium mass shift and are given in Fig. 7. One can see that the absolute values of the excitation functions show a wider variation for the mass shift range of$ V_0 = -40 $ to +40 MeV in the low-momentum region for all considered beam momenta. In this momentum region and at beam momenta not far below the threshold (at$ p_{\pi^-} $ $ \sim $ 1.6–1.84 GeV/c), there are well separated and experimentally distinguishable differences ($ \sim $ 25%–45% for$ ^{12} $ C and$ \sim $ 30%–60% for$ ^{184} $ W) between all calculations corresponding to different options for the$ K^*(892)^+ $ in-medium mass shift. Here, the total$ K^*(892)^+ $ production cross sections have a measurable strength$ \sim $ 30–3000 nb. At above-threshold pion momenta of 1.84–2.0 GeV/c, the impact of the$ K^*(892)^+ $ meson mass shift on its yield decreases. Here, the respective differences are$ \sim $ 20%–30% for$ ^{12} $ C and$ \sim $ 25%–35% for$ ^{184} $ W, but one might expect these to also be measured in future experiments at the GSI pion beam facility. Since, as one may hope, the precision of these experiments can reach the same value$ \sim $ 15% as was achieved in recent measurements here [39] of$ \pi^-$ meson-induced K+ meson production in$ {\pi^-}^{12}C \to K^+X $ and$ {\pi^-}^{184}W \to K^+X$ reactions at 1.7 GeV/c beam momentum.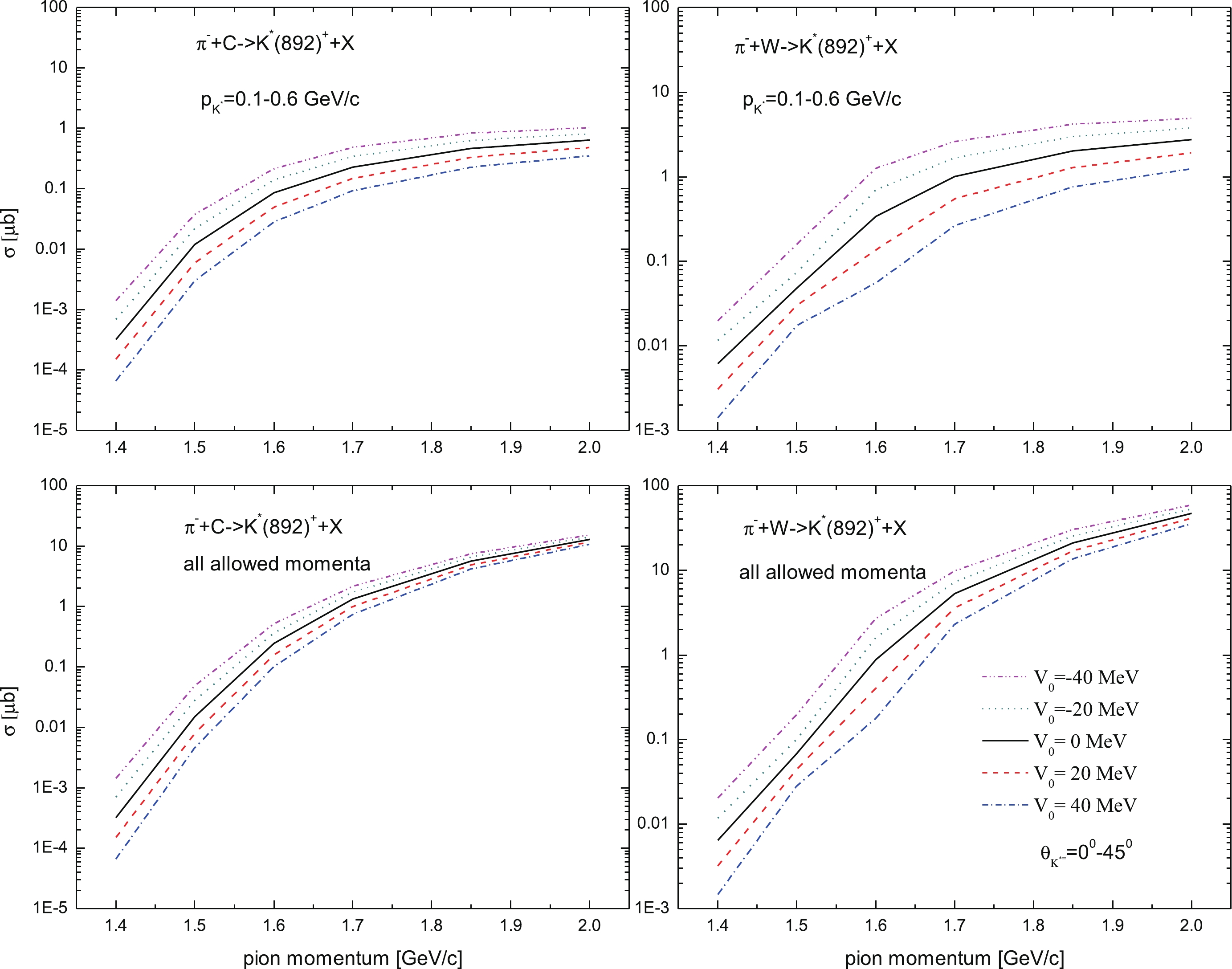
Figure 7. (color online) Total cross sections for the production of
$ K^*(892)^+ $ mesons from the primary$ {\pi^-}p \to {K^*(892)^+}{\Sigma^-} $ channel on$ ^{12} $ C and$ ^{184} $ W target nuclei at laboratory angles of 0°–45° with momenta of 0.1–0.6 GeV/c (upper two panels) and with all allowed momenta$ \geqslant $ 0.1 GeV/c at a given beam momentum (lower two panels), calculated with the$ K^*(892)^+ $ in-medium mass shift$ V_0 $ at normal nuclear density depicted in the inset, as functions of the incident pion momentum.Considering the above, one can conclude that the near-threshold
$ K^*(892)^+ $ differential and total cross section measurements at$ K^*(892)^+ $ momenta of 0.1–0.6 GeV/c in$ {\pi^-}A $ interactions will allow us to shed light on the possible$ K^*(892)^+ $ in-medium mass shift at these momenta. -
In this paper, we elucidate inclusive strange vector meson
$ K^*(892)^+ $ production in$ {\pi^-}A $ reactions at near-threshold laboratory incident pion momenta of 1.4–2.0 GeV/c via a nuclear spectral function approach. The approach accounts for incoherent primary$ \pi^- $ meson–proton$ {\pi^-}p \to {K^*(892)^+}\Sigma^- $ production processes as well as the influence of the scalar$ K^*(892)^+ $ nucleus potential (or the$ K^*(892)^+ $ in-medium mass shift) on these processes. We calculate the absolute differential and total cross sections for the production of$ K^*(892)^+ $ mesons in carbon and tungsten target nuclei at laboratory angles of 0°–45° and at the aforenoted initial pion momenta within five scenarios for the above shift. We show that the$ K^*(892)^+ $ momentum distributions and their excitation functions (absolute and relative) possess a high sensitivity to changes in the in-medium$ K^*(892)^+ $ mass shift in the low-momentum region of 0.1–0.6 GeV/c. Therefore, the measurement of such observables in a dedicated experiment at the GSI pion beam facility in the near-threshold momentum domain will allow us to get valuable information on the$ K^*(892)^+ $ in-medium properties.
Near-threshold K*(892)+ meson production in the interaction of π− mesons with nuclei
- Received Date: 2020-06-16
- Available Online: 2020-11-01
Abstract: We study the inclusive production of strange vector





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF





















 DownLoad:
DownLoad: