-
The standard model (SM) of particle physics has been completed by the Higgs discovery [1, 2]. It is, however, still unsatisfactory that the dynamics of electroweak symmetry breaking (EWSB) are not yet understood in detail: in the SM, the sign of the Higgs mass is necessarily assumed to be negative to realize EWSB; so in that sense, the SM only provides an incomplete answer to the origin of EWSB as well as the origin of mass. This issue would be related to the gauge hierarchy problem or fine tuning problem involving the physics bridging the EW and Planck scales through the unique dimensional parameter. Motivated by this longstanding problem, people have to date extensively worked on a possible new dynamics and/or mechanism that could be dormant behind the Higgs sector.
Scale symmetry could be one of the clues to penetrate this issue and is currently significant in the Higgs physics domain, as a possible solution to the gauge hierarchy problem, à la Bardeen [3]: Quadratic divergent corrections to the Higgs mass term, a critical part of the hierarchy problem, are assumed not to provide a physical scaling; hence, they should be removed, such that the Higgs mass term only undergoes logarithmic corrections that are proportional to the bare Higgs mass or SM particle masses coupled to the Higgs. In that case, no massive cancellation or instability of the radiative power corrections associated with the Planck scale is required for the Higgs mass term since no gauge hierarchy problem is present. If the Higgs mass parameter can be turned off at some scale in the renormalization evolution, possibly at the Planck scale, the Higgs mass will not develop up to the logarithmic corrections. This can be done by assuming the realization of scale symmetry at the Planck scale, and the physical Higgs mass then may arise by entering only the logarithmic corrections as the quantum scale anomaly effect.
Nature might have in fact supported the presence of an approximate scale ( or conformal) invariance and an orientation nearly along a conformal theory: the observed SM-like Higgs is thought to be lying in a nearly conformal direction in the EW broken phase at the vacuum expectation value (VEV) of
$ v \simeq 246 $ GeV, and it acquires mass due to the small quartic coupling breaking the scale symmetry (at the tree-level).$ \lambda_H = (m_h^2/2v^2) \simeq 1/8 \ll 1 $ . Thus, a flat (conformal) direction can be seen in the SM by taking the limit$ \lambda_H \to 0 $ , where the Higgs potential in the EW broken phase becomes completely flat.Generically, flat (conformal) directions are observed as stationary hyper-surfaces spanned by aligned scalar VEVs:
$ v_i = n_i v $ , where i runs the number of scalars and v is the average magnitude of the VEVs spontaneously breaking the scale symmetry [4]. Along the flat (conformal) direction, one finds the flat curvature, hence expects the presence of a massless scalar associated with the scale (conformal) symmetry broken by the VEVs, i.e., a “dilaton.” The conformal limit in the SM ($ \lambda_H \to 0 $ ) can be understood as the simplest case for a generic flat direction argument [5], where the zero determinant of the quartic coupling matrix, reflected as the constraint on the$ n_i $ vector, is given as a necessary condition for a flat direction, which is trivially realized by$ \lambda_H = 0 $ in the SM. In that sense, the SM can indeed be termed a nearly (classically) conformal theory (the nearly conformal SM), and the 125 GeV Higgs can be regarded as a light “pseudo-dilaton” associated with the approximate conformal direction (with a small curvature).This observation, which is still perturbatively operative even when including quantum corrections that will, however, directly be linked to the instability of the EW vacuum in the SM when
$ \lambda_H $ is reduced, even approaches, or goes negative because of the sizable top loop correction [6-35]. Thus, the nearly conformal SM has to be remedied by new dynamics that remains in a conformal direction that includes the SM for low-energy description, maintaining the approximate scale invariance (without power corrections to the Higgs mass term) at the quantum level up to the Planck scale.The realization of scale invariance at the quantum level (quantum scale-invariance) has been developed from Bardeen's initial proposal, as described above, that is currently not simply an ad hoc assumption, but rather involves two nontrivial dynamical issues: One is to dynamically achieve the initial renormalization condition at the Planck scale
$ (\Lambda_{\rm pl}) $ as the Higgs mass parameter$ m_H(\Lambda_{\rm pl}) = 0 $ , while the other is to eliminate the threshold corrections to$ m_H $ from the running of other couplings to realize the nontrivial ultraviolet (UV) fixed points. The former can be realized by a dynamical cancellation at$ \Lambda_{\rm pl} $ over the Planckian contribution, as has been argued in [36-40]. The latter is subject to some UV completion for the conformal SM embedded in a nontrivial-UV safety theory (called asymptotic safety), which has recently been explored extensively [41-58]. With these dynamical conditions at hand, no corrections to the Higgs mass term can be generated at any loop order, which indeed gives rise to the quantum-scale invariant SM at the infrared EW scale; thus, no fine-tuning or unnatural Higgs mass parameter will arise.The key point here is to note that this kind of conformally extended SM (embedded in the asymptotic safety) necessarily includes one SM-singlet scalar, S, which couples to the Higgs doublet via biquadratic forms with a real scalar [59], an extra
$ U(1) $ -charged scalar [60], or a generic complex scalar with or without$ CP $ violation [61-63], such as$ |H|^2 S^2 $ , known as the Higgs portal scenario. Then, the renormalization group evolution of$ \lambda_H $ necessarily receives positive contributions from such portal couplings and allows the$ \lambda_H $ bounded from zero to attain a stable EW vacuum. In this case, the EW scale can be generated dynamically from the scale-symmetry breaking at the quantum level in the following two ways:● perturbative-type – Coleman-Weinberg (CW) mechanism [4, 64] for weakly coupled massless scalars ([59-63] and also see, e.g., related references that have cited those papers);
● nonperturbative-type – dimensional transmutation of a nonperturbatively created scale by a strongly coupled hidden sector [65-73].
Any scenario of this class can therefore be called a Higgs-portal scalegenesis.
A common feature that all perturbative-type Higgs-portal scalegenesis mechanisms share is the presence of a flat direction in the tree-level scalar potential. It is necessarily present if the determinant of the scalar quartic-coupling matrix vanishes [5]. It ensures that all scalars acquire their VEVs simultaneously by quantum corrections, i.e. the CW mechanism, and thus, an inevitably light dilaton-like scalar state emerges as a pseudo-Nambu-Goldstone (NG) boson associated with the anomalous scale symmetry [64] (also called the scalon in the original Gildener-Weinberg approach [4]).
Even in the nonperturbative-type Higgs-portal scenarios, similar flat directions can be observed in terms of low-energy effective scalar potential, where the Higgs portal interactions are established between the SM-like Higgs and composite scalars generated by the underlying strong dynamics. Nevertheless, the scale-symmetry breaking that is nonperturbatively generated appears built-in at the tree-level in low-energy effective scalar theory.
Note that Higgs portal scalegenesis posseses universal experimental evidences: the predicted dilaton, arising as a singlet scalar fluctuation mode from the portal field S, will couple to SM particles due to mixing with the SM-like Higgs boson h through the Higgs portal interaction
$ |H|^2 |S|^2 = v_S v \, hs + \cdots $ with the vacuum expectation values of S and H,$ v_S $ and v. The size of the dilaton coupling to the SM particles as well as the 125 GeV Higgs couplings to them are then universally controlled by the mixing angle$ \theta $ , respectively, in which the latter has been constrained severely by the Higgs coupling measurement experiments as$ |\sin \theta| \lesssim 0.3 $ [74]. When the dilaton mass is of the order of the EW scale, or higher, it is mainly produced by a gluon fusion process and decays to the EW-dibosons$ WW $ and$ ZZ $ at hadron collider, like the LHC. The possible excess events, which are$ \propto \sin^2 \theta \times $ SM-like Higgs events at the invariant mass around the EW scale in those diboson channels will thus be a generic prediction of the Higgs portal scenario.In addition to the diboson signatures, the Higgs potential structure, including the higher order terms in the h field, such as the cubic
$ h^3 $ term, will be modified by the SM prediction that is parametrized by functions of$ \theta $ , with the ratio of$ v_s/v $ , and will be subject to the light dilaton resonance coupled to the diHiggs in the trilinear Higgs amplitude through the h-s conversion process, such as$ h^{(*)} \to s^{(*)} \to hh $ . Note also that the dilaton resonance is generically narrow due to the small coupling strength to SM particles set by the phenomenologically small$ \sin \theta $ . Thus, the diHiggs signatures will also be a characteristic indicator of this scenario, as has been discussed by means of a specific Higgs portal scalegenesis [73].Those signals can be predicted no matter what kind of method is applied to realize the EWSB via Higgs portal interactions with a sufficiently light and narrow scalar (at some decoupling limit for heavier particles, if any); hence, they are universal predictions expected in an energy range that is within the reach of collider experiments [73]. Without having been analyzed, it is obvious that other models regarded as the Higgs portal scalegenesis [4, 5, 59-72] can generically predict similar collider signatures.
Thus, this kind of conformal extension of the SM, namely, the Higgs-portal scalegenesis, is thought to form a universality class, in the universal low-energy effective theory and related phenomenological sense.
Even in such a Higgs-portal scalegenesis, actually, the main focus on the realization of the EWSB is simply going to be moved from the origin of the Higgs mass itself to the origin of the portal coupling because the latter has to be “negative.” Even working in the CW mechanism [64], one requires the portal coupling to be “negative” by hand; otherwise, none of the models can realize the EWSB (see, e.g., [75], [76, 77]① and references therein): The CW mechanism cannot simply be applied to generate the EW scale since the required parameters will not be compatible with the observed values.
This implies the requirement for a dynamical origin for the generation of both the scale and Higgs portal couplings, including the negative sign to propose the origin of mass for scenario completion. Furthermore, it should offer a definite phenomenological consequence distinguishable in the sense of a unified category for the Higgs-portal scalegenesis.
In this paper, we demonstrate a universal interpretation of models that lead to the Higgs-portal scalegenesis as a low-energy effective theory, which arises along a conformal/flat direction, with an EWSB structure similar to that encoded by the SM. This constructs the universality class in the (nearly) conformal/flat direction including the SM, without loss of generality as will be seen below. We then present a discriminator for the universality class, which must be closely related to the very origin of the negative Higgs mass term/origin of mass: A dynamical origin of the Higgs portal.
-
First, we demonstrate that a conventional scale-invariant Higgs portal scenario emerges in a decoupling limit for the scale-invariant realization of two-Higgs-doublet models with a light dilaton introduced. In addition, we observe that in this class of models, a softly broken
$ Z_2 $ /$ U(1)_A $ for the Higgs sector plays a crucial role to realize the negative Higgs-portal coupling between the SM-like Higgs and the light dilaton.Having in mind a scale-invariant realization of a two-Higgs-doublet model with a light dilaton
$ (\chi) $ , one finds potential terms such as$ V \ni \chi^2 \left[ c_0 |H_1|^2 + c_1 (H_1^\dagger H_2 + {\rm{H.c.}}) + c_2 |H_2|^2 \right] \,,$

(1) where
$ c_{0,1,2} $ are arbitrary dimensionless coefficients and$ H_{1,2} $ are the Higgs doublets. Manifestly, to perceive a symmetry structure of interest, one may introduce a two-by-two Higgs matrix form,$ \Sigma = (H_1, H_2^c) $ (with$ H_2^c $ being the charge conjugated field of$ H_2 $ ), to rewrite the terms as$V \ni \chi^2 \Bigg[ \left( \frac{c_0 + c_2}{2}\right) {\rm tr} \left[ \Sigma^\dagger \Sigma \right] + c_1 ({\rm{det}} \Sigma + {\rm{H.c.}}) + \left( \frac{c_0 - c_2}{2} \right) {\rm tr} \left[ \Sigma^\dagger \Sigma \sigma^3 \right] \Bigg] \,, $

(2) where
$ \sigma^3 $ is the third Pauli matrix. It is facile to see that the potential is structured on a global chiral$ U(2)_L \times U(2)_R $ symmetry for the two Higgs flavors, where the$ SU(2)_R $ component is in part explicitly broken down (to the subgroup corresponding to the third component of$ SU(2) $ ) by the third term and the$ U(1)_A $ component (that is usually called a soft-$ Z_2 $ breaking term in the context of two-Higgs-doublet models) is broken by the second$ c_1 $ term. The same chiral two-Higgs sector structure (without the scale invariance) has been discussed in [78, 79].At this point, the dimensionless couplings
$ c_{0,1,2} $ are simply assumed to be real and positive for them to have a conformal/flat direction. In that case the conformal/flat direction for both the scale and EW breaking VEVs can be achieved, where the direction for the EW scale is somewhat deformed due to the mass mixing by$ c_1 $ as$ \tilde{v}_2 \equiv v_2 + (c_1/c_2) v_1 = 0 \,. $

(3) Note that this deformation is nothing but a base transformation:
$ v_{1,2} \to \tilde{v}_1( = v_1), \tilde{v}_2 $ and can generally and smoothly be connected to the SM limit with$ v_1 $ only.Now, assume the maximal isospin breaking for the two-Higgs doublets, where
$ c_0/c_2 \to 0 $ , and the soft-enough$ U(1)_A $ /$ Z_2 $ is broken, by taking$ c_1/c_2 \ll 1 $ . Then, one may integrate the heavy Higgs doublet$ H_2 $ to get the solution for the equation of motion,$ H_2 \approx - (c_1/c_2) H_1 $ ②. Plugging this solution back into the potential, one finds$V \approx - \left(\frac{c_1^2}{c_2} \right) \chi^2 |H_1|^2 \,, $

(4) which is nothing but a desired Higgs portal model, where the portal coupling
$ \lambda_{H \chi} = - c_1^2/c_2 $ has been dynamically induced including the minus sign without any assumptions and is reflected by the attractive interaction of the scalar-exchange induced potential in the quantum mechanical sense. One should also realize that the small portal coupling can actually be rephrased by the small size of the soft-$ Z_2 $ /$ U(1)_A $ breaking for the underlying two-Higgs doublet model. Note also that the conformal/flat direction oriented in the original two-Higgs doublet model is smoothly reduced back to that in the Higgs portal model, as it should be.This generation mechanism is nothing less than the bosonic seesaw [80-90], which one can readily check if the scalar mass matrix assumes the seesaw form, namely, its determinant is negative under the aforesaid assumption. Note also that the original conformal/flat direction
$ \tilde{v}_2 \equiv v_2 + (c_1/c_2) v_1 = 0 $ can also be rephrased in terms of the bosonic seesaw relation: when the mixing is reduced (i.e.$ c_1/c_2 \ll 1 $ ), the heavy Higgs partner arises via the bosonic seesaw as approximately$ \tilde{H}_2 \simeq H_2 + (c_1/c_2) H_1 $ , so the conformal/flat direction has been realized due to the presence of an approximate inert$ H_2 $ . Thus, the bosonic seesaw provides the essential source for the Higgs-portal scalegenesis to predict the universal low-energy new-physics signatures such as significant deviations for Higgs cubic-coupling measurements compared with the SM prediction, and for the light dilaton signatures in diHiggs, diEW bosons, as aforementioned. -
One can further observe that a hidden strong gauge dynamics – often called hidden QCD (hQCD) or hypercolor [85-87, 90] – provides the dynamical origin for the softly-broken
$ Z_2 $ or$ U(1)_A $ symmetry and alignment to the flat direction that are supplied as ad hoc assumptions in the framework of the scale-invariant realization of the two-Higgs doublet model, as executed immediately above. Indeed, a class of the hQCD as explored in [85-87, 90] can dynamically generate a composite dilaton (arising generically as an admixture of fluctuating modes for the hQCD fermion bilinear, like conventional sigma mesons in QCD and gluon condensates such as glueballs. Even in a naive scale-up version of QCD with the small number of flavors as applied in the literature [86, 87, 90], it has recently been argued [91] that there might exist an infrared conformality, supporting the QCD dilaton to be light enough, compared to the dynamical intrinsic scale. Even if it is not the case, the hQCD flavor structure can straightforwardly be extended from the three flavor to many flavors, say, eight's [92, 93], with keeping the bosonic seesaw mechanism, so that a manifest light composite dilaton can be generated by the nearly conformal dynamics, as has recently been discussed [94]).Consider an hQCD with three colors and three flavors, as a minimal model to realize the bosonic seesaw as discussed in [85-87], where the hQCD fermions form the
$ SU(3) $ -flavor triplets,$ F_{L,R} = (\Psi_i, \psi)^T_{L,R} $ , having vectorlike charges with respect to the SM gauges like$ \Psi_{i(i = 1,2)} \sim (N, 1, 2, 1/2) $ and$ \psi \sim (N, 1, 1, 0) $ for the hQCD color group$ SU(N = 3) $ and$ SU(3)_c \times SU(2)_W \times U(1)_Y $ . Thus, this hQCD possesses the (approximate) “chiral”$ U(3)_{F_L} \times U(3)_{F_R} $ symmetry as well as classical-scale invariance, of which the former is explicitly broken by the vectorlike SM gauges. Besides, we shall introduce the following terms, which are SM gauge-invariant but explicitly break the chiral symmetry:$ {\cal L}_{y_H} \!=\! - y_H \, \bar{F}_L \cdot\left(\!\! \begin{array}{cc} 0_{2\times 2} & H \\ H^\dagger & 0 \end{array}\!\!\right) \cdot F_R + {\rm{H.c.}} $ . Note that in addition to this$ y_H $ -Yukawa term, the$ U(1)_{F_A} $ symmetry is explicitly broken also by the anomaly coupled to hQCD gluons that can, however, be transferred to this$ y_H $ -Yukawa term by the$ U(1)_{F_A} $ rotation, so that it fully controls the size of the$ U(1)_{F_A} $ symmetry breaking.The remaining (approximate) chiral
$ SU(3)_{F_L} \times SU(3)_{F_R} (\times U(1)_{F_V}) $ symmetry is broken down by the chiral condensate invariant under the SM gauge symmetry,$ \langle \bar{F}F \rangle = \langle \bar{\Psi}_i \Psi_i \rangle = \langle \bar{\psi} \psi \rangle \neq 0 $ , down to the diagonal subgroup$ SU(3)_{F_V} (\times U(1)_{F_V}) $ at the scale$ \Lambda_{\rm{hQCD}} $ , similar to the ordinary QCD. This spontaneous chiral breaking thus leads to the low-energy spectrum with the eight NG bosons.The low-energy description for
$ {\cal L}_{y_H} $ , below the scale$ \Lambda_{\rm{hQCD}} $ , can be as follows:$ \chi^2 \left[ c_1 (H_1^\dagger \Theta + {\rm{H.c.}}) + c_2 |\Theta|^2 \right] = \chi^2 \left\{ c_1 ({\rm{det}} \Sigma + {\rm{H.c.}}) + c_2 {\rm tr}\left[\Sigma^\dagger \Sigma \left(\frac{1-\sigma^3}{2} \right)\right] \right\} \,, $

(5) where
$ \Sigma = (H, \Theta^c) $ with$ \Theta \sim \bar{\psi}_R \Psi_L $ is a composite Higgs doublet (Note that when one works on hQCD theory with hQCD fermions in higher dimensional representations, like a real or a pseudo-real representation, the seesaw partner$ \Theta $ would be a composite Nambu-Goldstone Higgs-doublet, as employed in [89]③);$ c_1 \simeq y_H $ up to some renormalization effect scales down to$ \Lambda_{\rm{hQCD}} $ ; and$ c_2 $ has been generated by the chiral condensate$ \langle \bar{F}F \rangle $ scaled by the VEV of the composite hQCD dilaton$ \chi $ . This is nothing but the form of a scale-invariant two-Higgs doublet model as discussed above, so the bosonic seesaw should work, to bring the theory back to the Higgs portal model as the low-energy description. It is important to note also that the approximate inertness of the second Higgs doublet that is necessary for the conformal/flat direction is now manifest because of the robust Vafa-Witten theorem [95].This ensures the zero VEV for the non-vectorlike condensates such as
$ \Theta \sim \bar{\psi}_R \Psi_L $ , in this vectorlike hQCD and the positiveness of the$ c_2 $ (i.e. the positive mass square of the$ \Theta $ ), as long as the chiral manifold describing the low-energy hQCD is stable. -
One may identify
$ U(1)_{F_A} $ in the hQCD as$ U(1)_A $ for the previous two-Higgs sector. Then one can say that the ad hoc assumption (the soft-$ Z_2 $ /$ U(1)_A $ broken by taking$ c_1/c_2 \ll 1 $ and maximal isospin breaking for the Higgs sector:$ c_0 = 0 $ ) is naturally realized by the hQCD in which the bosonic seesaw mechanism is built and where the smallness of$ c_1 $ can be understood by the presence of light hQCD pions. Although the$ y_H $ gives a tachyonic mass to the lightest neutral hQCD pion, one can resolve it by introducing extra singlet pseudoscalar as discussed in [86, 87, 90] without conflicting any discussions in the present paper. Thus, the origin of the EWSB derived from the negative portal coupling is tied to the explicit-hidden chiral symmetry-breaking (and/or$ U(1)_A $ breaking) in the hQCD sector.The small
$ y_H $ coupling can lead to custodial symmetry breaking, and oblique corrections, such as the T-parameter constraint, must be discussed due to the corrections from the EW-charged hQCD pions. Such EW charged pions also significantly contribute to the 125 GeV Higgs decaying to diphotons in addition to overall suppression by the mixing angle and the light dilaton that is universally present in Higgs-portal scalegenesis. We have confirmed that parameter spaces are sufficiently allowed under those constraints and this will be reported in detail in another publication. For instance, when we take$ \Lambda_{\rm{hQCD}} = 1(2) $ TeV, the EW-charged hQCD pion mass is bound to be$ \gtrsim 450(700) $ GeV for the Higgs-dilaton mixing strength$ \sin^2\theta = 0.1 $ , and$ \gtrsim 400(600) $ GeV for$ \sin^2\theta = 0.05 $ , along with the soft-$ Z_2/U(1)_A $ breaking coupling$ y_H \lesssim 0.1 $ , which yields the Higgs portal coupling$ \lambda_{H\chi} \lesssim 0.1 $ , and the hQCD dilaton having the mass around 300 GeV as in [73]. Such light pions can be produced at the LHC by EW interactions (vector boson fusions) via the chiral anomaly in the hQCD for the predicted production cross sections to be quite small (roughly at most$ \sim 10^{-1} $ fb at 13 TeV) due to the loop factor suppression that is compared with the currently stringent upper bound$ \sim 10^2 $ fb at the corresponding mass range [96], and it may be hard to detect directly, even in the high-luminosity epoch (for similar EW-charged pion signals, e.g., see [97]). Note even in that case that the presently proposed hQCD can be probed by correlated deviations for the 125 GeV Higgs to decay to diphotons by hQCD pion loops and the diboson channels including diHiggs and di-EW bosons, as discussed in [73], that are definitely characteristic of the universality class of the Higgs-portal scalegenesis.Thus, the light hQCD pions will be definite discriminators for the universality class of the Higgs portal scalegenesis. If both a light dilaton and hQCD pions (the masses of which are expected to be around/below TeV scale) are detected at forthcoming collider experiments it would be the hQCD that indicates the very origin of the Higgs portal coupling, and hence the very origin of the Higgs mass term. In addition, the
$ y_H $ term which breaks chiral symmetry explicitly potentially induces a significant deviation of the T parameter [98, 99]. Thus, the EW precision data also provide some hints to explore the models of this universality class. -
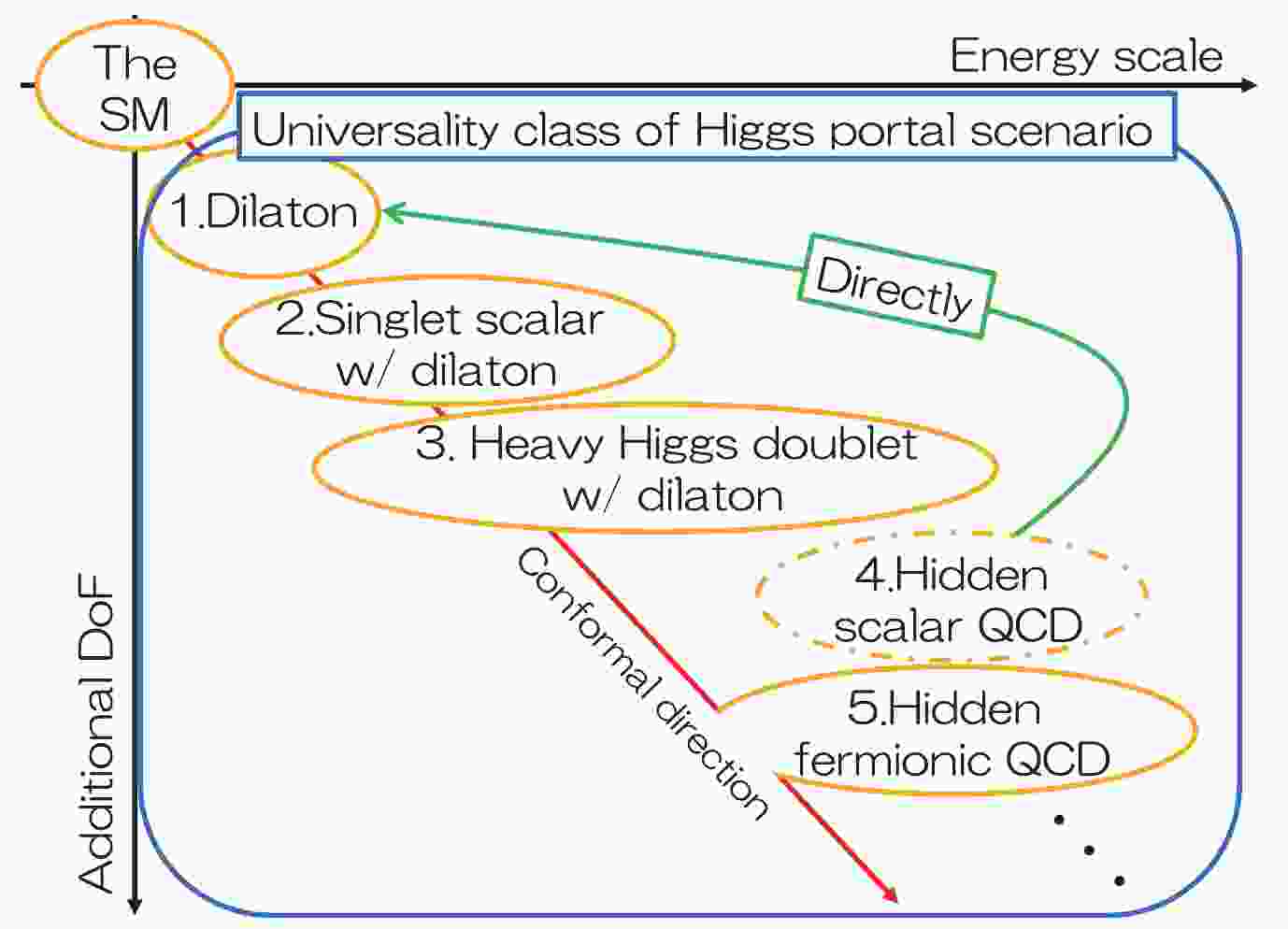
In conclusion, the universality class that is presently proposed can be depicted as in Fig. 1. The universality class and its disentangled dynamical origin would provide a novel guideline along the conformal extension of the SM and possibly lead to resolving the longstanding inquiry into the gauge hierarchy (fine tuning) problem. This would also provide a clear understanding of the hidden new physics in the search for the dynamical origin of the Higgs sector and hence the origin of mass that can be tested in upcoming collider experiments.

Figure 1. (color online) A schematic picture of the universality class for Higgs portal scenarios. All the extensions correspond to 1). [4, 64], 2). [59-63], 3). [78, 79, 84], 4). [65, 67, 70-73], and 5). [66, 82, 83, 85-90], respectively. All categorized models predict the same low-energy phenomenology related to the Higgs physics, as do those noted in the main text. A dynamical origin for this universality class can be encoded in a type of fermionic hQCD (#5 in the figure) with distinct light pion signatures as well as the universal Higgs-related ones.
More detailed studies regarding distinct collider signatures for the two-Higgs-doublet model type and hQCD type are worth performing and will be pursued elsewhere. In addition, the thermal histories as well as possible gravitational wave signals for this universality class could be discriminated, which is a worthy future research direction.
We are grateful to Kristjan Kannike and Jiang-Hao Yu for the fruitful discussions.
Unified interpretation of scalegenesis in conformally extended standard models: a dynamical origin of Higgs portal
- Received Date: 2020-06-18
- Available Online: 2020-11-01
Abstract: We present a universal interpretation of a class of conformal extended standard models that include Higgs portal interactions as realized in low-energy effective theories. The scale generation mechanism in this class (scalegenesis) arises along the (nearly) conformal/flat direction for breaking scale symmetry, where the electroweak symmetry-breaking structure arises similarly as in the standard model. A dynamical origin for the Higgs portal coupling can provide the discriminator for the low-energy “universality class,” to be probed in forthcoming collider experiments.





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF














 DownLoad:
DownLoad: