${{X(2239)}}$ and ${{\eta(2225)}}$ as hidden-strange molecular states from ${{\Lambda}}{\bar{\Lambda}}$ interaction

After the observation of $ X(3872) $ at Belle, increasing numbers of $ XYZ $ particles have been reported at different experimental facilities, attracting great theoretical interest [1]. Many $ XYZ $ particles are suggested to be candidate exotic hadrons beyond the conventional $ q\bar{q}/qqq $ picture. One of the popular interpretations of the $ XYZ $ particles is the molecular state, which is a loosely bound state composed of two hadrons. The possible molecular states have been widely discussed theoretically and applied to explain the observed exotic hadrons. The molecular states from the interaction of charmed/bottomed and anticharmed/antibottomed mesons are often related to $ XYZ $ particles, such as $ Z_c(3900) $, $ Z_b(4020) $, $ Z_b(10610) $, and $ Z_c(10650) $ [2-8]. The recently observed $ P_c $ states near the $ \Sigma_c^{(*)}\bar{D}^{(*)} $ threshold provide more confidence in the molecular state picture [9-20]. In the light sector, $ \Lambda(1405) $ has also been proposed to be generated from the $ \bar{K}N $ interaction [21-24]. However, the study of a molecular state composed of a baryon and an antibaryon is scarce in the literature, and experimental hints regarding such a state have also rarely been reported. In the charmed sector, $ Y(4630) $ has been explained as a bound sate from the $ \Lambda_c\bar{\Lambda}_c $ interaction [25]. Theoretically, the interaction between two baryons is analogous to that between two mesons. Moreover, generally speaking, it is not difficult to produce a baryon-antibaryon pair experimentally. Hence, it is interesting to study the molecular state composed of a baryon and an antibaryon.

In fact, even before the proposition of the quark model, the possibility of interpreting the $ \pi $ meson as an $ N\bar{N} $ bound state was discussed by Fermi and Yang [26]. However, this interpretation was found to be incorrect, based on later studies, and it was soon abandoned. $ X(1835) $ has also been connected to an $ N\bar{N} $ bound state [27-29]. Recently, the BESIII collaboration reported a resonance structure by analyzing the cross-section of the process $ e^{+}e^{-} \rightarrow K^{+}K^{-} $ at center-of-mass energies ranging from $ 2 $ to $ 3.08 $ GeV. The structure is denoted as $ X(2239) $, which has a mass of $ 2239\pm7.1\pm11.3 $ MeV and a width of $ 139.8\pm 12.3\pm20.6 $ MeV [30]. Some investigations have been performed to interpret $ X(2239) $ [31, 32]. From Ref. [32], based on the mass estimated in a relativized quark model, $ X(2239) $ can be explained as a candidate for the P-wave $ ss\bar{s}\bar{s} $ tetraquark state. An important observation about $ X(2239) $ is that it is almost at the threshold of the $ \Lambda\bar{\Lambda} $ interaction, after considering the experimental uncertainty of the mass. If we recall that $ X(2239) $ has spin parity $ J^{P} = 1^{-} $ and has been observed in the hidden-strange $ K^+K^- $ channel, it is a good candidate for a hidden-strange molecular state composed of a baryon $ \Lambda $ and an antibaryon $ \bar{\Lambda} $.

Before the observation of $ X(2239) $, another state with the same quantum number, $ Y(2175) $, also denoted as $ \phi(2170) $ in the literature, was observed by the Babar Collaboration in the initial-state-radiation process $ e^{+}e^{-}\rightarrow \gamma_{ISR}\phi(1020)f_{0}(980) $ with a mass of approximately $ 2175 $ MeV [33]. Since $ Y(2175) $ was observed, it has been investigated in many theoretical frameworks, including the $ qqg $ hybrid [34, 35], $ ss\bar{s}\bar{s} $ tetraquark state [36-38], excited $1^{--}s\bar{s}$ state [39], resonance state of $ \varphi K\bar{K} $ [40, 41], and some other interesting speculations [42-44]. It is also possible that $ X(2239) $ and $ X(2175) $ are the same state [1, 45]. However, a $1^{--}$ state with a mass of $ 2135\pm8\pm9 $ MeV and a width of $ 104\pm24\pm12 $ MeV has also been observed in the $ \phi f_0(980) $ channel at BESIII [46]. It is more appropriate to consider these states as two separate states if we accept the large mass gap between these two states as observed experimentally. In addition, a state with a mass of approximately $ 2220 $ MeV was observed by the DM2 Collaboration and confirmed at MARK-III in the radiative decays $ J/\psi\rightarrow\gamma\phi\phi $ [47, 48]. Later, the BES and BESIII Collaborations also confirmed the existence of $ \eta(2225) $ [49, 50]. There are also a few theoretical interpretations of $ \eta(2225) $, such as a $ 4^{1}S_{0} $ $ s\bar{s} $ state [51, 52].

As indicated in Ref. [53], which was reported before the observation of $ X(2239) $ at BESIII, $ Y(2175) $ and $ \eta(2225) $ can be interpreted as the $ \Lambda\bar{\Lambda}(^{3}S_{1}) $ and $ \Lambda\bar{\Lambda}(^{1}S_{0}) $ molecular states, respectively; this is the first attempt to discuss a possible molecular state from the $ \Lambda\bar{\Lambda} $ interaction. However, it should be noted that the $ \Lambda\bar{\Lambda} $ threshold is approximately 2231.3 MeV, while the mass of $ Y(2175) $ is approximately $ 60 $ MeV lower than the $ \Lambda\bar{\Lambda} $ threshold, making it too deep to be a molecular state. Moreover, a recent measurement at BESIII indicates that the mass of $ Y(2175) $ is approximately 2135 MeV [46], which is approximately 100 MeV below the $ \Lambda \bar{\Lambda} $ threshold. Regarding the newly observed $ X(2239) $, its mass seems to be closer to the $ \Lambda\bar{\Lambda} $ threshold. Hence, it is interesting to study the possibility of assignment of $ X(2239) $, rather than $ Y(2175) $, as a candidate for the $ \Lambda\bar{\Lambda}(1^{-}) $ molecular state. There are also theoretical studies of the molecular state from the $ \Lambda{\Lambda} $ interaction [54-56]. It has been reported that in a lattice calculation, the $ \Lambda{\Lambda} $ interaction is attractive, but it is too weak to form a molecular state [54].

From the results in Ref. [53], the mass gap between $ Y(2175) $ and $ \eta(2235) $ was reproduced from a calculation with S-wave $ \Lambda\bar{\Lambda} $ interaction in the one-boson-exchange model by solving the non-relativistic Schrödinger equation. The $ 1^- $ state has a larger binding energy than does the $ 0^- $ state, and the D-wave interaction only involves the $ 1^- $ state, which suggests that inclusion of the relativistic effect and S-D mixing may change the mass gap between the two states. In the quasipotential Bethe-Salpeter (qBSE) approach, such effects can be included naturally. It is thus interesting to make calculations in such an approach to see the variation in the mass gap. This approach provides the possibility of obtaining two bound states both close to the threshold, which is consistent with the molecular state as a loosely bound state of two hadrons. Additionally, for the $ N\bar{N} $ interaction, the annihilation effect has been found to be important [57-60] and may affect the $ \Lambda\bar{\Lambda} $ interaction. The theoretical values of the mass will deviate from the that within the one-boson-exchange model, and the bound state will acquire a width after the annihilation effect is included.

In the current work, we adopt the qBSE approach to study the $ \Lambda\bar{\Lambda} $ interaction. With the help of effective Lagrangians, the one-boson-exchange model with pseudoscalar, scalar, and vector exchanges is applied to construct the interaction. The annihilation effect is introduced by the coupled-channel effect plus an imaginary optical potential. By inserting the potential into the qBSE, the molecular states with quantum numbers $ I^G(J^{PC}) = 0^+(0^{-+}) $ and $0^-(1^{--})$ can be investigated.

The paper is organized as follows. After the introduction, we present relevant Lagrangians to construct the meson exchange potential. The qBSE approach is also briefly introduced in Section 2. The numerical results of bound states produced from the $ \Lambda\bar{\Lambda} $ interaction within the one-boson-exchange model are presented in Subsection 3.1. We discuss the annihilation effect on the $ \Lambda\bar{\Lambda} $ interaction, and the results with this effect are given in Subsection 3.2. The paper ends with discussion and summary.

First, we describe the $ \Lambda\bar{\Lambda} $ interaction within the one-boson-exchange model. As in Ref. [53], to construct the potential, the Lagrangians for the couplings between the $ \Lambda $ baryon and exchanged mesons can be written as

where $ \psi_{\Lambda} $, $ \eta $, $ \eta' $, $ \sigma $, $ \omega $, and $ \phi $ are the fields of the $ \Lambda $ baryon and $ \eta $, $ \eta' $, $ \sigma $, $ \omega $, and $ \phi $ mesons, respectively. The coupling constant $ g_{\alpha\Lambda\Lambda} $ can be derived from the SU(3) symmetry and considering the mixings between octet and singlet states [53], and the masses of exchanged mesons $ m_e $ are cited from the Review of Particle Physics (PDG) [1]; the explicit values are listed below:

The mass of the $ \sigma $ meson has a large uncertainty of $ 400-550 $ MeV [1]. Here, we choose a value of 500 MeV, and the uncertainty will be discussed latter.

In the current work, we consider the $ \Lambda\bar{\Lambda} $ interaction instead of the $ \Lambda\Lambda $ interaction. Hence, the couplings between the light mesons and the antibaryon $ \bar{\Lambda} $ are also required. As in the nucleon-antinucleon interaction, we adopt the well-known G-parity rule to write the $ \Lambda\bar{\Lambda} $ interaction from the $ \Lambda\Lambda $ interaction. By inserting the $ G^{-1}G $ operator into the potential, the G-parity rule can be obtained easily as [57, 61]

The G parity of the exchanged meson is left as a $ \zeta_{i} $ factor for the i meson. Because $ \omega $ and $ \phi $ mesons carry odd G parity, $ \zeta_{\omega} $ and $ \zeta_{\phi} $ should be $ -1 $, and the others are still $ 1 $. Finally, we obtain the following relation:

Now, we only need the potential of the $ \Lambda{\Lambda} $ interaction. With the Lagrangians and the coupling constants given above, we can write the relevant meson exchange potentials with the standard Feynman rule as

where $ u_\Lambda $ is the spinor of the $ \Lambda $ baryon. q, $ m_{\mathbb P} $, $ m_{\mathbb V} $, and $ m_\sigma $ are the exchanged momentum and the masses of exchanged pseudoscalar $ {\mathbb P} $ ($ \eta $ and $ \eta' $), vector $ {\mathbb V} $ ($ \omega $ and $ \phi $), and scalar $ \sigma $ mesons, respectively.

Usually, a form factor needs to be introduced at the vertices because the exchanged mesons are not point particles and have internal structures. Such form factors are also used to ensure the convergence of the integral (the qBSE is an integral equation and will be given later). There are many types of form factors in the literature. Because of the absence of experimental data regarding the $ \Lambda\Lambda $ interaction, we cannot determine which type is more realistic. In the current work, we adopt three types of form factors, as in Ref. [62]:

We parameterize the cutoff in the form of $ \Lambda_{e} = m_{e}+ \alpha_{e}\; 0.22 $ GeV, where $ m_e $ is the mass of an exchanged meson [16, 62-66]. Such cutoff parameterization can introduce the effect of the mass of an exchanged meson, which is more reasonable than the adoption of the same cutoff for different mesons. $ \alpha_{e} $ is taken as a free parameter close to 1. Considering the explicit forms of form factors, the $ \alpha $ for $ f_1 $ should be larger than 0 to avoid an unphysical suppression near $ \Lambda_e = m_e $. For the other two types of form factors, a value of approximately zero can be chosen. The aforementioned form factors satisfy the requirement that $ f(m^2) = 1 $. The radius of the $ \Lambda $ baryon can be estimated with the relation $r^2 = 6/f(0)\; {\rm d}f(q^2)/ {\rm d}q^2|_{q^2\to0}$, which leads to a reasonable value, approximately 0.5 fm, for three choices of form factors. Hence, the three types of form factors satisfy the basic requirements, and we will further check whether our conclusion is sensitive to different choices.

Different from Ref. [53], we will adopt the qBSE to explore possible bound states from the $ \Lambda\bar{\Lambda} $ interaction. The potential kernel obtained above will be inserted into the Bethe-Salpeter equation to obtain the scattering amplitude, the poles of which correspond to bound states. The Bethe-Salpeter equation is a 4-dimensional integral equation in Minkowski space. Considering the complexity and difficulty of directly solving such an integral equation, we adopt a quasipotential approximation approach to reduce the 4-dimensional Bethe-Saltpeter equation to a 3-dimensional integral equation [67-69]. Then, using partial-wave decomposition, the 3-dimensional equation is further reduced to a 1-dimensional equation with fixed spin parity $ J^P $ as follows [5, 70],

where the sum extends only over nonnegative helicity $ \lambda'' $. In the current case, we will consider spin parities $ J^P = 0^- $ and $ 1^- $, which can couple to baryons $ \Lambda $ and $ \bar{\Lambda} $ in the S wave, and are called S-wave states in the non-relativistic calculation [53]. Since we make a decomposition on spin parity $ J^P $ directly, contributions from all possible orbital angular momenta L are included naturally. Hence, in the qBSE approach, no special treatment is needed to include the D-wave contribution.

The reduced propagator with the spectator approximation can be written down in the center-of-mass frame with $ P = (W,{ 0}) $ as

where $ \delta^+(p''^{\; 2}_2-m_2^{2}) $ is the Dirac delta function, but with only $p''^{0}_2 = +E_2({{p}}'')$. Here, as required by the spectator approximation, we place one of the particles, 2 here, on the shell, which satisfies $p''^0_2 = E_{2}({{p}}'') = \sqrt{ m_{2}^{\; 2}+{{p}}''^2}$. In the above equations, the definition ${{p}} = |{ p}|$ is adopted.

The partial-wave potential is defined with the potential of the $ \Lambda\bar{\Lambda} $ interaction obtained above as

where $ \eta = PP_1P_2(-1)^{J-J_1-J_2} $, with P and J being the parity and spin for the system, $ \Lambda $, or $ \bar{\Lambda} $ baryon. The initial and final relative momenta are chosen as $ { p} = (0,0,{\rm{p}}) $ and ${ p}' = ({{p}}'\sin\theta,0,{{p}}'\cos\theta)$. $ d^J_{\lambda\lambda'}(\theta) $ is the Wigner d-matrix. Since particle 1 is off-shell in the qBSE approach, a form factor should also be introduced to reflect its internal structure. Here, we adopt an exponential regularization by introducing a form factor into the propagator as $G_{0}(p)\rightarrow G_{0}(p)[{\rm e}^{-(k^{2}_{1}-m^{2}_{1})^{2}/\Lambda^{4}_{r}}]^{2}$, where $ k_{1} $ and $ m_{1} $ are the momentum and mass of the off-shell particle, respectively. With such regularization, the convergence of the integral equation is guaranteed, even without the form factor for the exchanged meson. The cutoff $ \Lambda_{r} $ is parameterized as in the $ \Lambda_{e} $ case, that is, $ \Lambda_{r} = m_{e}+\alpha_{r}\; 0.22 $ GeV, where $ m_{e} $ is the mass of the exchanged meson and $ \alpha_{r} $ serves the same function as the parameter $ \alpha_{e} $.

With the Gauss discretization of momentum, the 1-dimensional integral equation in Eq. (12) is transformed into the matrix equation $ M = V+VG_0M $ [24]. The molecular states correspond to the poles of the scattering amplitude $ M $ in the complex energy plane at $ |1-V(z)G(z)| = 0 $, where $z = W+{\rm i}\Gamma/2$ is the system energy W at the real axis [5].

We first consider the case without the annihilation effect included. Since only one channel is considered in this work, the bound state pole is located at the real axis. The parameters in the qBSE approach are the cutoffs $ \Lambda_{e,r} $ which have been parameterized into $ \alpha_{e,r} $. In the calculation, we choose $ \alpha_e $ equivalent to $ \alpha_r $, and rename them as a parameter $ \alpha $, for simplification. We consider the two spin parities $ 0^- $ and $ 1^- $, which can be obtained from S-wave coupling.

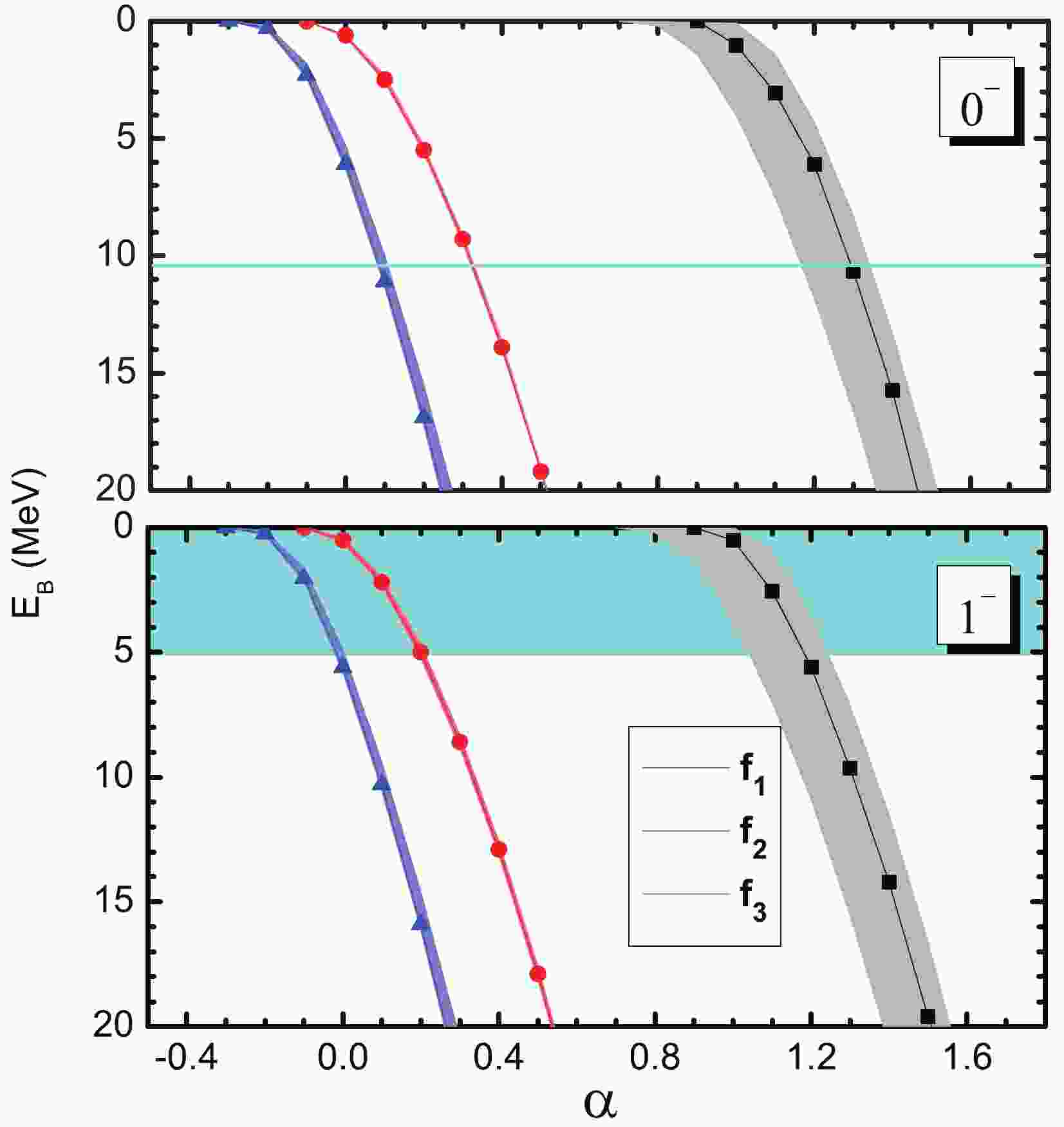
In Fig. 1, the binding energy $ E_B = m_{th}-W $, where $ m_{th} $ and W are the threshold and the position, respectively, of the pole obtained with different types of form factors. The bound state from the $ \Lambda\bar{\Lambda} $ interaction with quantum numbers $ I^G(J^{PC}) = 0^+(0^{-+}) $ is presented in the upper panel of Fig. 1. The bound state can be produced from the interaction with reasonable $ \alpha $. For the monopole type of the form factors $ f_1(a^2) $, the bound state appears at an $ \alpha $ of approximately 1, which is a standard value of $ \alpha $. In Fig. 1, the suggested value of the mass of $ \eta(2225) $ in the PDG [1] is also shown as a cyan line, which can be reproduced at an $ \alpha $ of approximately 1.2. Since the uncertainty of the mass of $ \eta(2225) $ is approximately 10 MeV, which just fills the region we considered, we do not show the uncertainty in the figure. The uncertainty corresponds to $ \alpha $ values ranging from 0.8 to 1.5. For the other two types of form factors, the bound state is produced at an $ \alpha $ of approximately zero, which corresponds to a standard cutoff of approximately 1 GeV. The shapes of the three curves for the different form factors are analogous to each other. Considering that $ \alpha $ is a free parameter in a reasonable range, it is clear that the different choices of form factors do not affect the conclusion. Hence, comparing the theoretical results with experimental ones, the $ 0^- $ state from the $ \Lambda\bar{\Lambda} $ interaction can be related to $ \eta(2225) $.

Figure 1.  (color online) Binding energy $ E_{B} $ with variation of $ \alpha $. The upper and lower panels are for bound states with spin parities $ 0^- $ and $ 1^- $, respectively. The black square, red circle, and blue triangle denote the results with different types of form factors $ f_{i}(q^2) $ with $ i = 1,2,3 $ in Eqs. (9)-(11), respectively. The bands denote the uncertainties from the uncertainties of mass of the $ \sigma $ meson, $ 400\sim550 $ MeV [1]. The cyan line in the upper panel is the suggested value of the mass of $ \eta(2225) $ in the PDG [1]. The cyan band in the lower panel denotes the experimental mass of $ X(2239) $ with uncertainties, where only the part below the threshold is presented [30]. More explanation is given in the text.

Now, we turn to the $0^-(1^{--})$ case, which is shown in the lower panel of Fig. 1. Contrary to the results in [53], the binding energies of the $ 1^- $ state are similar to those of the $ 0^- $ state with the same parameter. For the monopole form factor $ f_1(q^2) $, the bound state appears at an $ \alpha $ of approximately 0.9, increases with increasing $ \alpha $, and reaches a binding energy of approximately 20 MeV at an $ \alpha $ of approximately 1.5. For the other two types of form factors, the bound state is produced at an $ \alpha $ of approximately zero. The experimental mass of $ X(2239) $ reported by the BESIII Collaboration is $ 2239\pm7.1\pm11.3 $ MeV. The central value is slightly higher than the $ \Lambda\bar{\Lambda} $ threshold. After considering the uncertainty, $ X(2239) $ is just on the threshold. In Fig. 1, we also present the uncertainty of the mass of $ X(2239) $ below the $ \Lambda\bar{\Lambda} $ threshold as a cyan band. The experimental uncertainty of $ X(2239) $ corresponds to $ \alpha $ values ranging from 0.8 to 1.2.

From the above results, it is clear that the mass gap between the $ 0^- $ and $ 1^- $ states in our model is quite small. The two states appear almost at the same cutoff, and the mass gap at a certain $ \alpha $ is only several MeV in the region considered in Fig. 1. This is quite different from the results in Ref. [53]. In that work, with reasonable cutoffs, they obtained a loosely bound state of $ 0^- $ with a binding energy of approximately $ 7\sim13 $ MeV, while the $ 1^- $ state had a larger binding energy of approximately $ 50\sim82 $ MeV. The mass gap is approximately 50 MeV, which is much larger the one in the current work. Because the Lagrangians and coupling constants adopted in the two works are the same, the difference should arise from the different treatments, such as the different solution method, the relativistic effect, and S-D mixing. We also present the bands from the uncertainties of the mass of the $ \sigma $ meson. The results are found to be insensitive to this uncertainty.

In our model, five exchanges, including $ \eta $, $ \eta' $, $ \phi $, $ \omega $, and $ \sigma $ exchanges, are considered to construct the interaction potential. Usually, these exchanges play different roles in producing bound states. In the qBSE approach, the potential cannot be shown as a function of the range r as in the non-relativistic calculation [53]. We check their roles by turning on and off one or more exchanges and vary the parameter $ \alpha $ from -1 to 3 to search for bound states. If we only keep one of five exchanges, no bound state can be produced from $ \eta $, $ \eta' $, or $ \phi $ exchanges while the interaction with only the $ \omega $ or only $ \sigma $ exchange is still strong enough to produce a bound state with a larger $ \alpha $. This result suggests that the $ \omega $ and $ \sigma $ exchanges play the most important role in producing the bound states. We provide more explicit results in Fig. 2 to show the role of exchanges.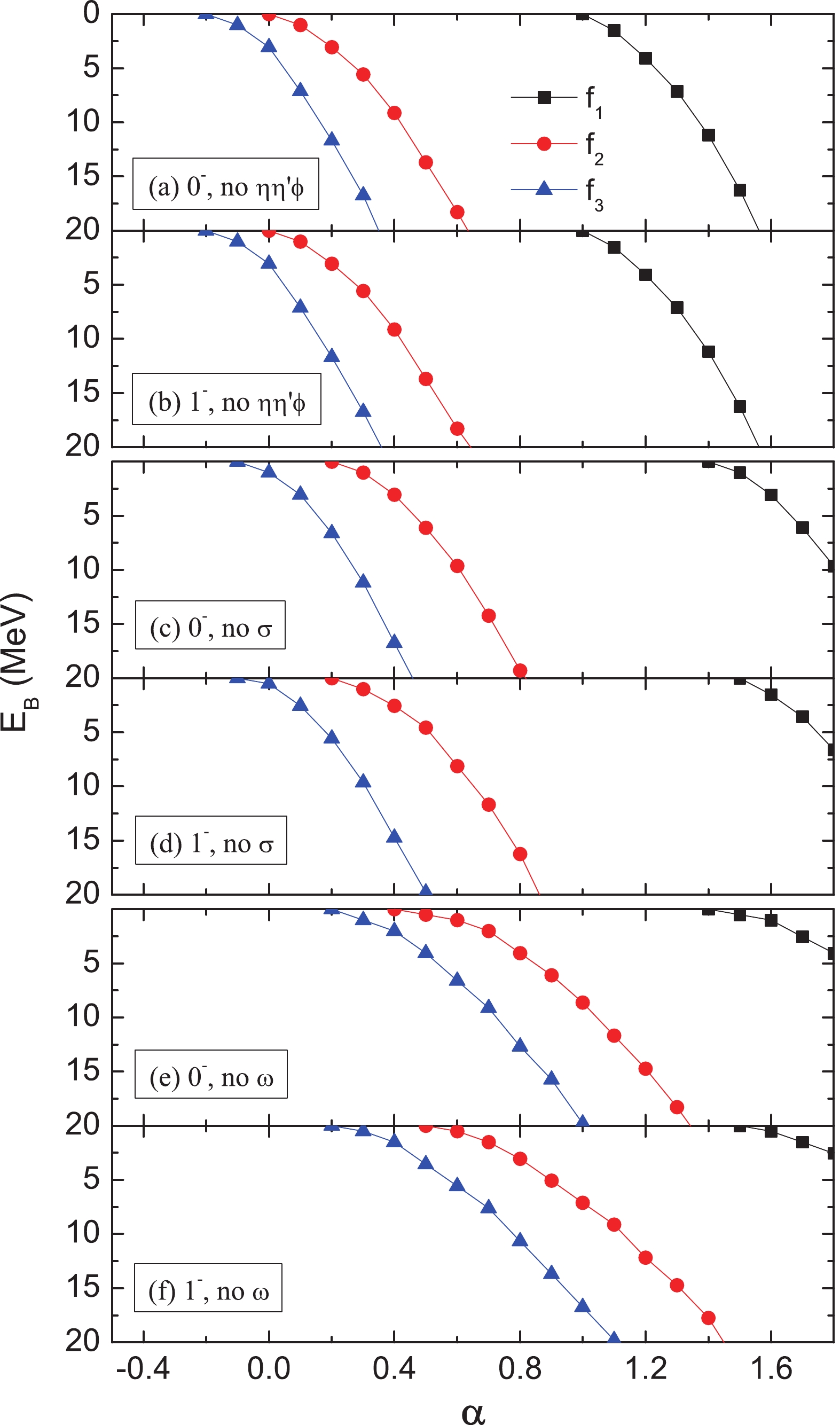

Figure 2.  (color online) Binding energy $ E_{B} $ without the $ \eta,\eta' $, and $ \phi $ exchanges (a and b), without the $ \sigma $ exchange (c and d), and without the $ \omega $ exchange (e and f). Other conventions are the same as in Fig. 1.

We present the results after turning off the $ \eta $, $ \eta' $ and $ \phi $ exchanges and only keeping the $ \omega $ and $ \sigma $ exchanges in panels (a) and (b) of Fig. 2. As shown in the figure, the bound states with $ 0^- $ and $ 1^- $ can be produced from the $ \omega $ and $ \sigma $ exchanges with a slight increase in the parameter $ \alpha $ for all three types of form factors. We also check the case after removing both $ \omega $ and $ \sigma $ exchanges but keeping $ \eta $, $ \eta' $, and $ \phi $ exchanges. No bound state can be found with a reasonable parameter. This result suggests that the $ \omega $ and $ \sigma $ exchanges are essential to produce the bound state with $ 0^- $ and $ 1^- $. In panels (c) and (d), the results after removing the $ \sigma $ exchange are presented. Larger values of $ \alpha $ are required for the three types of form factors than in the previous case. The largest effect comes from the $ \omega $ exchange, as shown in panels (e) and (f). To reproduce the binding energy in the full model, the parameter $ \alpha $ should be increased by 0.5 or more.

In the above calculation, we do not consider the effect of the annihilation of baryon $ \Lambda $ and antibaryon $ \bar{\Lambda} $. The annihilation effect was found to be important in the study of the $ N\bar{N} $ interaction [58-60]. This contribution is often considered as the multipion intermediation in the s channel, which is usually replaced by annihilation into two mesons, plus an optical potential [71-74]. The annihilation effect induces an imaginary potential, which leads to a width and variation of the mass of the bound state [75, 76]. In the $ \Lambda\bar{\Lambda} $ interaction, such annihilation can also occur, which will affect the experimental observables [77, 78].

In the literature, the two-meson intermediation part of the annihilation effect was included by introducing a box diagram or coupled-channel effect [75, 76, 79-81]. In the current work, we will adopt the latter treatment, i.e., a coupled-channel calculation in our qBSE approach, which was developed in Ref. [62]. Explicitly, we follow the method in Ref. [81], which has been successfully applied to the $ N\bar{N} $ interaction and is more consistent with our qBSE approach.

In Ref. [81], the annihilation effect was introduced by the two-meson intermediation and an imaginary phenomenological optical potential. Regarding the former, we still adopt the two-meson intermediation picture here, as in the $ N\bar{N} $ case. As in the aforenoted calculation, only the pseudoscalar mesons $ {\mathbb P} $ ($ \pi $, $ \eta $ and $ \eta' $), vector mesons $ {\mathbb V} $ ($ \omega $ and $ \phi $), and scalar meson $ \sigma $ will be considered to avoid more uncertainties arising from the incorporation of more Lagrangians and coupling constants. In the current work, we focus on states with quantum numbers $ I^G(J^{PC}) = 0^+(0^{-+}) $ and $ 0^-(1^{–}) $. For the former state, the possible intermediated two-meson channels include $ {\mathbb V}{\mathbb V} $ and $ {\mathbb P}\sigma $, which leads to an eight-channel calculation. For the latter state, the $ {\mathbb P}{\mathbb V} $ and $ {\mathbb V}\sigma $ channels are involved in the calculation, which includes twelve channels. Additionally, the $ K\bar{K} $ channel will be considered for the $ 0^-(1^{–}) $ state, which is forbidden for the $ 0^+(0^{-+}) $ state. We introduce the $ \Lambda\bar{\Lambda}-m_1m_2 $ interaction, where $ m_1m_2 $ are two of the mesons considered. Following the treatment in the $ N\bar{N} $ case [74], all interactions between two mesons and couplings between different meson channels are ignored in the calculation.

As in Ref. [81], we consider a two-channel interaction to provide a simple explanation about the relation of the standard coupled-channel approach to the well-known forms in the study of the the annihilation $ N\bar{N} $ interaction from the box diagram in Ref. [75]. The coupled-channel Bethe-Salpeter equation in matrix form is written as

where B and m refer to $ \Lambda\bar{\Lambda} $ and $ m_1m_2 $ channels, respectively, and $ V_{el} $ is the potential given in Eq. (7). Here, we choose $ V^{mm} = 0 $, that is, the interaction between two mesons is not considered. Then, we can obtain the following equations

By inserting Eq. (17) into Eq. (16), we obtain

where we define $ V^{BB} = V_{el}+V^{Bm}G^{mm}V^{mB} $ as in Ref. [81]. Here, the second term is the annihilation term from the box diagram. Hence, we need the transition potential, which can be obtained from the Lagrangians in Eqs. (1)-(5) as

where $ g_{m_{1,2}\Lambda\Lambda} $ is the coupling constant given in the previous section, and $ u_\Lambda $ and $ v_{\bar{\Lambda}} $ are the spinors for the $ \Lambda $ and $ \bar{\Lambda} $ baryons, respectively. The $ \Gamma_{1,2} $ has a vertex of $ 1 $, $ \gamma_5 $, or $ \epsilon\!\!\!/ $ for scalar, pseudoscalar and vector mesons, respectively. Here, we need an additional coupling constant $ g_{NK\Lambda} = 13.926 $ for the $0^-(1^{--})$ state [82]. q and $ m_\Lambda $ are the momentum and mass of the exchanged $ \Lambda $ baryon, respectively. $ f_i(q^2) $ is the form factor introduced in the previous section. $ \zeta $ has a sign that reflects the difference between a baryon and antibaryon following the G-parity rule. It does not affect the result because the aforementioned interaction always appears in a pair.

Obviously, the above treatment is not enough to include all annihilation effects. A phenomenological treatment is often introduced in the literature [73, 78, 81, 83-87]. In the current work, we introduce an additional imaginary optical potential into $ V_{el} $ with the following parameterization in coordinate space, as in Ref. [81]:

To insert this optical potential into our qBSE approach, we need to transform it into momentum space using the Fourier transformation,

where q is the four-momentum, as for the exchanged mesons. Because of a lack of experimental data for the $ \Lambda\bar{\Lambda} $ interaction, the parameters are not as well determined as for the $ N\bar{N} $ interaction. In Ref. [78], the $ p\bar{p}\to\Lambda\bar{\Lambda} $ process was studied, and the parameters were determined to be $ W\approx-1 $ GeV and $ r_0\approx0.3 $ fm, which will be adopted in the current calculation. These values are similar to those in the nucleon-nucleon interaction as adopted in Ref. [81], $ W = -1 $ GeV and $ r_0 = 0.4 $ fm, which are also similar to the values adopted in Ref. [87].

The positions of the poles of the bound states with different $ \alpha $ values are listed in Table 1. The real part of $ M_{th}-z $ presented in the table is the binding energy of the $ \Lambda\bar{\Lambda} $ molecular states. After including the annihilation effect, the poles appear at $ \alpha $ valules of approximately 1.9, 0.8, and 0.4 for the respective form factors. Compared with the results in Fig. 1, a larger $ \alpha $ is required to produce molecular states from the interaction. This result suggests that the attraction of the interaction becomes weaker and requires a larger $ \alpha $ to compensate. However, the changes in the mass gap between the $ 0^- $ and $ 1^- $ states are slight. For most cases, the mass of the $ 1^- $ state becomes even larger than that of the $ 0^- $ state, with mass gaps of approximately 11, 8, and 5 MeV for the three respective form factors, which is more consistent with the assignment of the two states as $ X(2235) $ and $ \eta(2225) $. In Table 1, we also present the results without the coupled-channel effect, that is, with only the imaginary optical potential. The result suggests that the coupled-channel effect on the mass is obvious. The mass decreases by approximately 5 and 10 MeV for the $ 0^- $ and $ 1^- $ states, respectively, after including the coupled-channel effect.

$J^P$	$f_1$			$f_2$			$f_3$
	$\alpha$	$M_{th}-z$		$\alpha$	$M_{th}-z$		$\alpha$	$M_{th}-z$
$0^-$	1.9	$11.9+84i$		0.8	$8.42+38i$		0.4	$6.21+25i$
		$6.35+84i$			$3.41+37i$			$3.17+22i$
	2.0	$22.8+89i$		0.9	$16.8+43i$		0.5	$13.2+30i$
		$17.2+91i$			$10.3+41i$			$9.58+27i$
	2.1	$34.4+94i$		1.0	$25.9+48i$		0.6	$21.7+34i$
		$28.6+96i$			$18.6+46i$			$16.2+31i$
$1^-$	2.0	$14.5+85i$		0.9	$14.6+41i$		0.5	$12.2+27i$
		−			−			−
		$6.67+97i$			$2.41+46i$			$4.26+29i$
	2.1	$25.5+ 90i$		1.0	$22.2+44i$		0.6	$19.3+32i$
		$3.6+114i$			$1.21+55i$			$0.67+38i$
		$17.4+104i$			$9.02+50i$			$9.62+35i$
	2.2	$37.5+ 95i$		1.1	$37.7+48i$		0.7	$27.6+36i$
		$8.3+132i$			$12.5+65i$			$3.1+47i$
		$22.8+113i$			$26.4+58i$			$15.3+41i$

Table 1.  Position of the poles of $ 0^- $ and $ 1^- $ states with different $ \alpha $. $ M_{th}-z $ denotes the mass of the $ \Lambda\bar{\Lambda} $ threshold $ M_{th} $ minus the position of the pole z, in units of MeV. $ f_i $ refers to the results with different types of form factors. The first and second lines for every $ \alpha $ are the results without and with the coupled-channel effect. For the $ 1^- $ state, the results with the coupled-channel effect, except for the $ K\bar{K} $ channel, are listed in the third line.

Another obvious variation after including the annihilation effect is that the poles leave the real axis and the states acquire widths. The imaginary part of $ M_{th}-z $ corresponds to half of the width of the states. The current result suggests large widths for both $ 0^- $ and $ 1^- $ states, approximately 200, 100, and 60 MeV for the three form factors, respectively. This is consistent with the experimental observation that $ X(2239) $ and $ \eta(2225) $ have widths of $ 139.8\pm12.3\pm20.6 $ MeV [30] and $ 185^{+40}_{-20} $ MeV [1], respectively. Here, we also consider the results without the coupled-channel effect. It is clear that the variations of the widths for the two states and different form factors range from several to approximately 10 MeV. Considering that the widths are several dozens of MeV, the variations of width caused by the coupled-channel effect considered here are relatively small. The widths are primarily from the imaginary potential. For the $ 1^- $ state, we present the results with and without the $ K\bar{K} $ channel; the result suggests that the $ K\bar{K} $ channel provides a width comparable with all the contributions from other channels.

The molecular state composed of a baryon and an antibaryon is an interesting topic in the study of exotic mesons. In the present work, we study the possibility to assign the newly observed $ X(2239) $ as a $ \Lambda\bar{\Lambda} $ molecular state in the qBSE approach. The potential kernel of the $ \Lambda\bar{\Lambda} $ interaction is constructed within the one-boson-exchange model with the help of the Feynman rule, and the annihilation effect is introduced by introducing the coupled-channel effect and optical potential. After decomposition on spin parity, the bound state can be found by studying the pole of the scattering amplitude.

Two bound states with spin parities $ J^P = 0^- $ and $ 1^- $ are produced from the $ \Lambda\bar{\Lambda} $ interaction. Our results suggest that these two bound states are both close to the $ \Lambda\bar{\Lambda} $ threshold. Before the observation of $ X(2239) $, there existed only one possible state, $ Y(2175) $, near the $ \Lambda\bar{\Lambda} $ interaction, so it is often assigned as the $ 1^- $ molecular state. However, a binding energy larger than 50 MeV is required for this assignment. Here, $ X(2239) $ was observed in the $ K^+K^- $ channel, and it is just on the $ \Lambda\bar{\Lambda} $ threshold if the experimental uncertainty is considered. In addition, in Ref. [82], the study of the strong decay of the $ \Lambda\bar{\Lambda} $ bound state was performed, and it was found that the dominant decay channel of the $ 1^- $ state is the $ K\bar{K} $ channel, which is the observation channel of $ X(2239) $ at BESIII. In the current work, the $ K\bar{K} $ channel was also found to provide the width in all channels considered. Hence, it is more suitable to assign these two states with spin parities $ 1^- $ and $ 0^- $ from the $ \Lambda\bar{\Lambda} $ interaction to $ X(2239) $ and $ \eta(2225) $, respectively.

We now discuss the effect of each exchange on producing the bound state. Among the five exchanges, including the $ \eta $, $ \eta' $, $ \phi $, $ \omega $, and $ \sigma $ exchanges, the $ \omega $ and $ \sigma $ exchanges, especially the former, play the most important role in producing two bound states. This conclusion is consistent with the previous studies in Refs. [25, 53]. We also determined the effect of different choices of form factors on the conclusion. The behaviors of the results with three types of form factors are analogous to each other. If we recall that the cutoff is a free parameter, the result suggests that the same conclusion can be reached with different choices of form factors.

In the $ N\bar{N} $ interaction, annihilation is an important topic [58-60]. In the current work, we include the annihilation effect by following the procedure in Ref. [81]. The coupled-channel effect from the two-meson intermediation and an imaginary optical potential are introduced and inserted into our qBSE approach. However, unlike the $ N\bar{N} $ interaction, experimental information about the $ \Lambda\bar{\Lambda} $ interaction is scarce. Hence, we choose the parameters from fitting the data of the $ p\bar{p}\to\Lambda\bar{\Lambda} $ process [78]. The calculation suggests that the variations of the poles are very large. The cutoff should be increased to give the molecular states. A large width of approximately 100 MeV is also produced from the annihilation, especially the optical potential. However, our conclusion from the single-channel calculation with one-boson exchange is unchanged qualitatively after the annihilation effect is considered. More exact determination of this effect requires more experimental data and theoretical analysis.

In the current work, we propose that the observation of $ X(2239) $ at BESIII provides a more suitable candidate for the $ \Lambda\bar{\Lambda} $ molecular state with spin parity $ 1^- $. In the charmed sector, the $ \Lambda_c\bar{\Lambda}_c $ molecular state has also been studied theoretically, and it was assigned as $ Y(4630) $ by some authors [25]. As in the hidden-strange sector, many states have been observed near the $ \Lambda_c\bar{\Lambda}_c $ threshold, including $ Y(4630) $, $ Y(4660) $, and a structure at 4625 MeV observed very recently at Belle [88], which has attracted the attention of many theorists [89, 90]. More comprehensive investigation of the $ \Lambda_{(c)}\bar{\Lambda}_{(c)} $ interaction in both theory and experiment is important for understanding these structures.

The conclusion of the current work is based on the assumption that $ X(2239) $ is below the $ \Lambda\bar{\Lambda} $ threshold. Although the experimental mass with uncertainties can reach the region below the threshold, the nominal value is above the threshold. If this is still true with smaller uncertainties, $ X(2239) $ cannot be considered as a molecular state from the $ \Lambda\bar{\Lambda} $ interaction, as suggested in the current work. In addition, the current work is based on the experimental results regarding $ X(2239) $ released by the BESIII Collaboration [30]. More experimental data and careful analysis are necessary to confirm whether $ X(2239) $ and $ Y(2175) $ are different states. In Ref. [45], a fitting of the experimental data points for the process $ e^+e^-\to K^+K^- $ at BESIII suggests that the structure can be reproduced with interference between the states near 2200 MeV, which is also much larger than the usual mass of $ Y(2175) $, and the background without a real state near 2.24 GeV. However, the current experimental data are not sufficient to give a confirmative conclusion. Hence, a more precise measurement of the mass of $ X(2239) $ is necessary to confirm such an assignment [91].