-
The emission of
$ \alpha $ clusters represents the favored decay mode for most unstable medium mass nuclei, heavy nuclei, and super-heavy nuclei. Since its first experimental observation by Rutherford [1, 2], it naturally became one of the standard tools for the study of nuclear structures and reactions and the exclusive way for the identification of new super-heavy nuclei. Moreover, the theoretical interpretation of$ \alpha $ decay as a quantum tunneling effect through a nuclear Coulomb barrier [3] represented a real breakthrough for quantum physics in general, by validating its hypotheses experimentally. The basic experimental observables related to this phenomenon are the$ \alpha $ decay energy$ Q_{\alpha} $ and the associated half-lives$ T_ {\frac {1}{2}} $ . The first notable success of treating$ \alpha $ decay as a semiclassical one-dimensional quantum tunneling process lead to simple but extremely precise correlations relating half-lives,$ Q_{\alpha} $ values, and nucleon numbers through a WKB estimation of the barrier penetration probability. The first correlation of this type was proposed by Geiger and Nuttall [4], which became the basis for various continuously improved empirical formulas for$ \log_{10}T_{\frac {1}{2}} $ [5-7]. Alternatively,$ \alpha $ decay constitutes a convenient test-ground for nuclear structure models used to describe predominantly the cluster preformation and formation stages of the process, such as for example the super-asymmetric fission model [8], the density-dependent cluster model [9, 10], the generalized liquid drop model [11], the unified fission model [12], the relativistic mean field theory [13], the double-folded potential approach [14], and the coupled channel formalism [15]. Nuclear structure effects are usually incorporated in the inner part of a phenomenological potential barrier. Such phenomenological potential models vary basically in the theoretical treatment of the short-range nuclear interaction.The external part of a potential barrier represented by electrostatic repulsion is usually considered to be well understood and appropriately accounted for by a Coulomb potential. In this paper, one aims to investigate in what measure deviations from this idealized picture of the electrostatic interaction influence the half-lives of the
$ \alpha $ decay process. To do this, one considers here a Hulthen potential [16, 17] for the electrostatic interaction, which is a generalization of the Coulomb potential by means of a screening effect. The idea of a screened electrostatic barrier defined through a Hulthen potential was first proposed for nuclear decays in Ref. [18], where it was successfully used to describe proton emission half-lives. It was later also employed for the$ \alpha $ decay process [19], with similar success. We propose here a new analytical model for the determination of$ \alpha $ decay half-lives, based on a WKB approximation applied to a barrier composed of a Hulthen potential matched with an inner barrier part associated with the nuclear interaction and simulated by an infinite square well. The model is applied to describe the half-lives for 209 favored and 70 unfavored$ \alpha $ decays of nuclei with$ Z\geqslant 84 $ . The dependence of the proposed formalism mainly on the screening measure is used to ascertain the validity of the Coulomb potential for the considered experimental data. Additionally, model interpolations are used for 6$ \alpha $ decays with uncertain data. -
The half-life of a parent nucleus decaying by the emission of an
$ \alpha $ cluster can be defined as$ T_{1/2} = \frac{\ln2}{\nu P}10^{h}, $

(2.1) where P is the probability of the
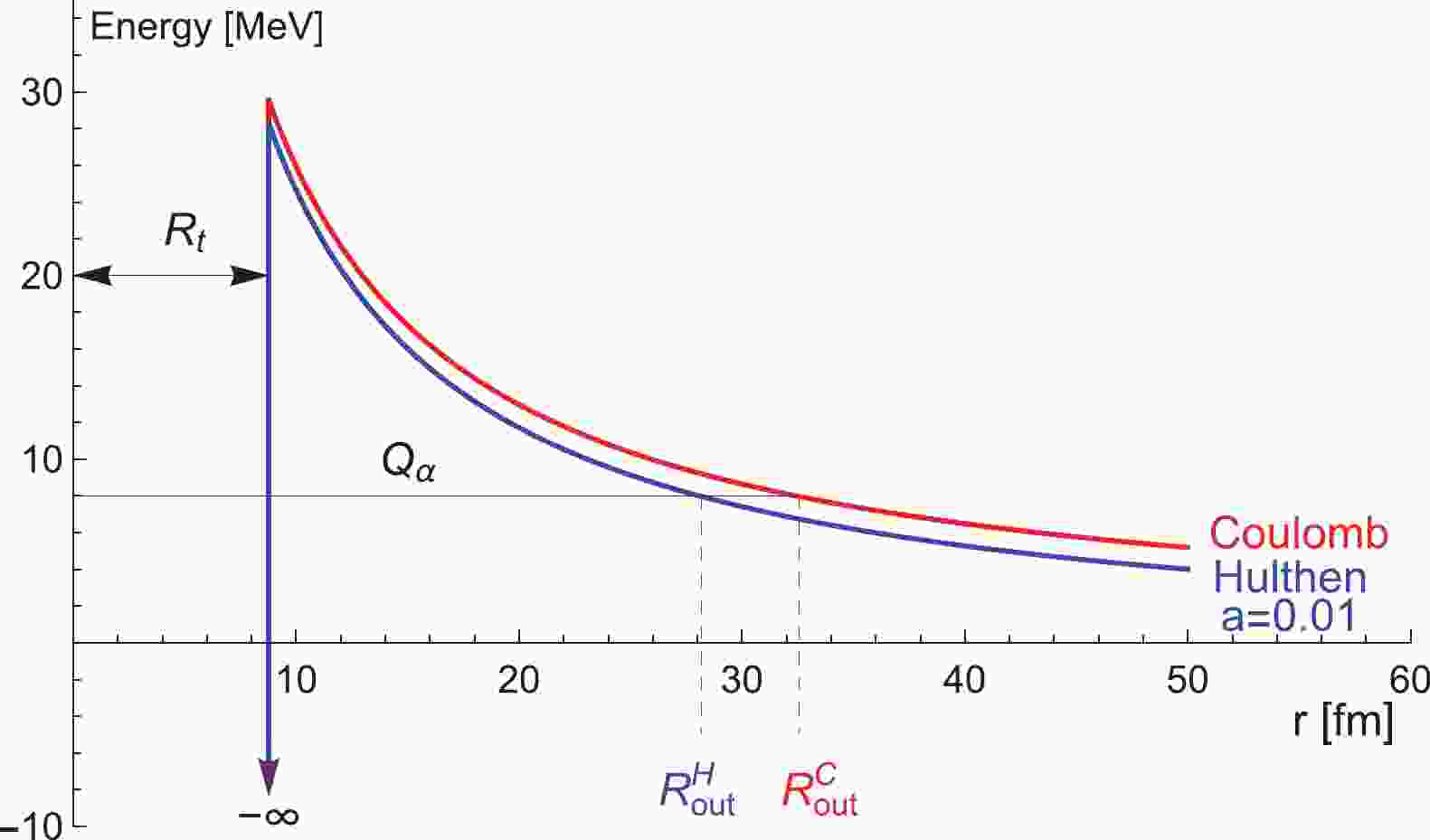
$ \alpha $ particle penetrating a phenomenological potential barrier,$ \nu $ is its assault frequency on the barrier, and h is a hindrance term accounting for some structural characteristics of the parent nucleus.As can be seen from Fig. 1, the barrier starts at the distance associated with the touching configuration
$ R_{t} = R_{1}+R_{\alpha} $ , where$ R_{1} $ and$ R_{\alpha} $ are the radii of the daughter nucleus and of the$ \alpha $ cluster, respectively. Hard nuclear radii are defined by [20]
Figure 1. (color online) Schematic representation of the total potential for
$ ^{212}_{90} $ Th as a function of the distance between the centers of the decaying nuclei, with screened and bare electrostatic interactions. For simplicity, the centrifugal contribution is omitted.$ R = 1.28A^{1/3}-0.76+0.8A^{-1/3}, $

(2.2) where A is the corresponding mass number. Beyond the touching radius, the potential is defined as the sum of a centrifugal contribution from the kinetic energy and an electrostatic repulsion potential. For a reduced mass
$ \mu = 4mA_{1}/(A_{1}+4) $ of the decaying nuclear system, with m being the nucleon mass, and an orbital momentum l of the emitted$ \alpha $ particle, the centrifugal energy contribution is$ V_{l}(r) = \frac{\hbar^{2}\left(l+\frac{1}{2}\right)^{2}}{2\mu r^{2}}. $

(2.3) This is modified with the Krammers-Langer transformation, which is necessary when considering the first order WKB approximation [21]. The orbital momentum l must satisfy the angular momentum and parity conservation laws concerning the initial and final nuclear states.
The electrostatic interaction is modeled here by a Hulthen [16, 17] type potential,
$ V_{H}(r) = \frac{2a e_{p}^{2}Z_{1}}{e^{ar}-1}, $

(2.4) where
$ Z_{1} $ is the charge number of the daughter nucleus,$ e_{p} $ is the proton charge, and parameter a defines the screening effect on the usual Coulomb potential. Thus, in limit$ a\rightarrow0 $ , the above potential acquires a Coulomb interaction form. Here, screening is understood as the combined contribution of various deviations from point-like electrostatic approximation, such as finite size effects, nuclear interactions, superposition of involved electric charges, inhomogeneous charge distributions, electrodynamic effects, diffuseness, deformations, and fluctuations of nuclear surfaces. The introduction of screening shortens the range of the electrostatic interaction. The modifications with respect to the simple Coulomb case are shown in Fig. 1, in which the case of$ ^{212}_{90} $ Th is shown with an omitted centrifugal contribution and overstated screening for better understanding. Basically, the Hulthen potential acts as a Coulomb interaction at small distances; however, it decays more rapidly due to its exponential short-range character. The consequences on the potential barrier consist of the lowering of its peak and more importantly, of the shortening of the exit radius.The barrier penetrability is calculated by means of the WKB approximation:
$ P = {\rm Exp}\left\{-\frac{2}{\hbar}\int_{R_{t}}^{R_{\rm out}}\sqrt{2\mu\left[V(r)-Q_{\alpha}\right]}{\rm d}r\right\}, $

(2.5) where
$ V(R_{\rm out}) = Q_{\alpha} $ with$ V(r) = V_{H}(r)+V_{l}(r) $ . The integral in the exponent can be calculated numerically, but an analytical expression is always more desirable. To obtain such an expression, one must first approximate the centrifugal term as [22]:$ \frac{1}{r^{2}}\approx\frac{a^{2}}{\left(e^{ar}-1\right)^2}. $

(2.6) As the values of parameter a are expected to be small, the radius of validity for such an approximation is well beyond the exit radius corresponding to the total potential barrier. Within this approximation, the barrier exit radius can be analytically expressed as
$ R_{\rm out} = \frac{1}{a}\ln{\left[\frac{2V_{1}}{\sqrt{V_{0}^{2}+4V_{1}Q_{\alpha}}-V_{0}}+1\right]}, $

(2.7) where
$ V_{0} = 2ae^{2}_{p}Z_{1},\;\;\,\,\;\;V_{1} = \frac{a^{2}\hbar^{2}\left(l+\frac{1}{2}\right)^{2}}{2\mu}. $

(2.8) The integral
$ I = -\hbar\ln{P}/(2\sqrt{2\mu}) $ in the same approximation is analytically given by [18]:$ I = \frac{1}{a}\left[I_{1}(r)+I_{2}(r)\right]\Big|_{R_{t}}^{R_{\rm out}}. $

(2.9) The two terms have the following expressions:
$\begin{split} {I_1}(r) =& - \sqrt {{V_1}{x^2} + {V_0}x - {Q_{\alpha}}} \\ &+\sqrt {{Q_{\alpha}}} \arcsin \left[ {\frac{{x{V_0} - 2{Q_{\alpha}}}}{{x\sqrt {4{Q_{\alpha}}{V_1} + V_0^2} }}} \right] \\ &-\frac{{{V_0}}}{{2\sqrt {{V_1}} }}\ln \left[ {2\sqrt {{V_1}\left( {{V_1}{x^2} + {V_0}x - {Q_{\alpha}}} \right)} + {V_0} + 2{V_1}x} \right], \end{split}$

(2.10) $\begin{split} {I_2}(r) =& \sqrt {{V_1}{y^2} + {U_0}y - {U_1}} \\ &-\sqrt {{U_1}} \arctan \left[ {\frac{{y{U_0} - 2{U_1}}}{{2\sqrt {{U_1}\left( {{V_1}{y^2} + {U_0}y - {U_1}} \right)} }}} \right] \\ &+\frac{{{U_0}}}{{2\sqrt {{V_1}} }}\ln \left[ {2\sqrt {{V_1}\left( {{V_1}{y^2} + {U_0}y - {U_1}} \right)} + {U_0} + 2{V_1}y} \right], \end{split}$

(2.11) where the following notations are used:
$\begin{split} &x = {({e^{ar}} - 1)^{ - 1}},\;\;\;\;\;{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} y = 1 + {({e^{ar}} - 1)^{ - 1}},\\ &{U_0} = {V_0} - 2{V_1},\;\;\;\;\;{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {U_1} = {Q_{\alpha}} + {V_0} - {V_1}. \end{split}$

(2.12) The assault frequency of the
$ \alpha $ particle on the potential barrier is defined as$ \nu = v/2R_{t} $ , where the speed is$ v = \sqrt{2E/\mu} $ . Here, one will consider only the decay of nuclei from ground state to ground state. Therefore, the kinetic energy of the$ \alpha $ particle is just the ground state energy for an infinite square-well potential, which is$ E = \hbar^{2}x_{l}^{2}/(2\mu R_{t}^{2}) $ , where$ x_{l} $ is the first zero of the spherical Bessel function$ j_{l}(x) $ [23] associated with the solution for a spherical infinite square well. Combining all these definitions, one obtains the following simple expression for the assault frequency:$ \nu = \frac{x_{l}\hbar}{2\mu R_{t}^{2}}. $

(2.13) In this way, the angular momentum becomes involved in both sides of the touching configuration [24]. When
$ l = 0 $ ,$ x_{0} = \pi $ and one recovers the formula for the assault frequency from Ref. [25]. -
The model contains only two free parameters by construction: the screening measure a and the hindrance term h. Their values are determined by fitting the experimental data [26], which are limited here to only the half-lives of ground state to ground state
$ \alpha $ decays of nuclei with$ Z\geqslant 84 $ , for which the branching ratios, decay partial percentages, and the spins of the involved ground states are well established. In the first stage, fits were performed on distinct parities of proton and neutron numbers, and separately for favored and unfavored decays. The latter are decays with non-zero angular momentum transfer. The transferred angular momentum is determined as being the minimal value among the allowed ones. The initial results showed that the hindrance term h has a negligible effect on the rms deviation,$ \sigma = \sqrt{\frac{1}{n}\sum_{i = 1}^{n}\left[\log_{10}\left(\frac{T_{\rm th}^{i}}{T_{\rm exp}^{i}}\right)\right]^{2}}, $

(2.14) in the case of favored decays, where n is the number of considered data points. Therefore, the screening parameter actually accounts effectively for the additional odd neutron or proton. Finally, for favored decays, one considered
$ h = 0 $ and fitted the experimental data only against variations of the screening parameter a. The fitting results are listed in Table 1, where one compared them with fits on the same data with the Universal Decay Law (UDL) [27-29]:parity Z-N n $ \sigma_{H} $ 

a/fm $ ^{-1} $ 

$ \Delta\sigma $ 

$ \sigma_{\rm UDL} $ 

A B C e-e 113 0.395 6.38939695708103 $ \cdot10^{-4} $ 

0.135 0.392 0.398 −0.422 −20.383 e-o 33 0.314 2.46665033427710 $ \cdot10^{-4} $ 

0.021 0.246 0.418 −0.478 −18.724 o-e 44 0.377 2.61840144529958 $ \cdot10^{-9} $ 

0.085 0.365 0.432 −0.493 −19.396 o-o 19 0.211 3.44650362496230 $ \cdot10^{-9} $ 

0.086 0.139 0.431 −0.557 −14.659 Table 1. Parameters a, A, B, and C resulting from fitting
$ (Z-N) $ parity differentiated data sets of favored ground state to ground state$ \alpha $ decay half lives with the present model and with UDL formula (16) are listed together with the corresponding rms values$ \sigma $ , number of considered data points, and the present model rms gain$ \Delta\sigma $ with respect to the$ a = 0 $ case.$ \log_{10}{T_{1/2}} = A\chi'+B\rho'+C, $

(2.15) where
$ A,B $ , and C are free parameters and$ \chi' = 4Z_{1}\sqrt{\frac{A_{1}}{(A_{1}+4)Q_{\alpha}}},\;\;\;\,\,\rho' = \sqrt{\frac{8A_{1}Z_{1}(A_{1}^{1/3}+4^{1/3})}{A_{1}+4}}. $

(2.16) This formula combines the most common dependencies, and due to its high success in reproducing the experimental data, it is currently considered as a reference empirical formula for cluster radioactivity in general and even for the proton emission process [30]. It must be mentioned here that due to the exponential dependence on a, the sum of residuals in this fitting procedure has a highly oscillatory behavior. The numerical search for the best a value is then performed with different starting values, and the final result is expressed in a high precision format.
The present model fits are in very good agreement with the experiment. This is an impressive result, when one takes into account that the proposed formalism uses a single adjustable parameter in comparison to the UDL formula, in which three free parameters are used. The rms values for even-even and odd-even emitters are essentially the same as those obtained with the UDL formula. UDL fares significantly better only for the remaining data sets. Its newly determined parameters are very similar to those obtained originally in Ref. [28]. The effect of screening can be judged by the gain in rms value with respect to the usual Coulomb electrostatic interaction with
$ a = 0 $ . Surprisingly, the results for even-even nuclei are improved the most, even though these nuclei constitute the largest data set (113 nuclei). This is because the fitted value of the screening parameter a for these nuclei is the largest one. As a matter of fact, the whole relationship$ a_{\rm ee}>a_{\rm eo}>a_{\rm oe}>a_{\rm oo} $ is counterintuitive, because one would expect that an odd proton would generate greater, not lower screening. The origin of this feature comes from the even-odd staggering of the charge radii [31], which is leveled here by the hard radius formula (2). This averaging effect tends to overestimate the effective radius of the electric charge in odd-Z nuclei, such that its influence on the screening of the electrostatic interaction is subdued.The theoretical description and systematization of unfavored
$ \alpha $ decay half lives is notoriously deficient with regards to overall agreement with experimental data. The particularity of these decays resides in the fact that the$ \alpha $ cluster has a non-zero orbital momentum l, and its preformation probability is very sensitive to the nuclear structure of the emitting nucleus, such as neutron and proton shell filling or deformations. Due to the fact that all these effects have various contributions, the$ \alpha $ cluster preformation probability has a very erratic evolution with decay data. Attempts to model its evolution from nucleus to nucleus by means of the simple algebraic functions of deformation, orbital momentum, proton-neutron asymmetry, and mass number were made in Refs. [32, 33]. However, such parametrizations exhibit only a moderate improvement in terms of agreement with experiments, at the cost of considerably raising the number of adjustable parameters. Here, one will approach this issue by averaging the inhibition of the$ l\neq0 $ $ \alpha $ cluster preformation probability into the hindrance parameter h, while the influence of the resulting orbital momentum of the$ \alpha $ cluster is taken into consideration with the assault frequency. The collected data sets of unfavored$ \alpha $ decays are then used to fit a and h for specific$ N-Z $ parities. The fit details are given in Table 2, where one also listed the fits performed with the UDL formula amended with a centrifugal termparity Z-N n $ \sigma_{H} $ 

a/fm $ ^{-1} $ 

h $ \sigma_{\rm UDL} $ 

A B C D e-o 40 0.987 1.78941575339607 $ \cdot10^{-8} $ 

1.998 0.567 0.446 −0.269 −35.882 2.302 o-e 19 0.886 2.80959277085025 $ \cdot10^{-9} $ 

2.133 0.675 0.434 −0.128 −45.325 −1.3947 o-o 11 0.740 1.96239498909705 $ \cdot10^{-8} $ 

1.779 0.650 0.415 −0.182 −37.998 2.532 Table 2. Parameters a, h, A, B, C and D resulting from fitting
$ (Z-N) $ parity differentiated data sets of unfavored ground state to ground state$ \alpha $ decay half lives with the present model and with the modified UDL formula (18) are listed together with the corresponding rms values$ \sigma $ and the number of considered data points.$ \log_{10}{T_{1/2}} = A\chi'+B\rho'+D\frac{l(l+1)}{\rho'}+C. $

(2.17) The above formula was shown to be extremely successful in the description of proton emission half lives, for which the transferred orbital momentum is of major importance. A similar term added to the Ni-Ren-Dong-Xu formula [27], which is an approximated UDL with constant touching radius
$ R_{t} $ , was shown to provide very good results for$ \alpha $ decay [34]. Nevertheless, this extension of the UDL formula has not yet been fully exploited, even though, as can be seen from Table 2, it provides a very good description of the experimental data for unfavored decays. The fits with the proposed formula have once again an rms value very close to that of the modified UDL formula. The hindrance factor h has almost the same value, around 2, while the a values keep their relationship$ a_{\rm eo}>a_{\rm oe}>a_{\rm oo} $ also for unfavored decays. The fitted parameter a for unfavored decays from odd-even and odd-odd nuclei has a similar order as for favored decays, while for even-odd nuclei its value is significantly lower in the unfavored case. Regarding the modified UDL fits, the corresponding parameters suffer obvious changes from the simple UDL formula parameters determined from fitting favored decay data. Only parameter A remains roughly similar. A distinct negative value of the additional parameter D is obtained for the fit of the odd-even unfavored decay data set. It is related to the predominance of small l values in this particular set.The logarithms of
$ \alpha $ decay half-lives calculated with the present formalism and using the parameters listed in Tables 1 and 2 are compared with the corresponding measured data for the most extended eight isotopic chains in Fig. 2. Agreement with the experiment is overall good. The enhancement of experimental half-lives for unfavored decays is theoretically reproduced. Although the favored decay data is described better, there are singular nuclei, for which sizable differences are encountered, especially with undervalued theoretical results. One such example is the lightest$ ^{194} $ Rn isotope. Furthermore, the low Z isotopic chains have some undervalued calculations for isotopes right below the$ N = 126 $ shell closure.
Figure 2. (color online) Comparison between experimental data and theoretical values for
$ \log_{10}T_{1/2} $ obtained with the fitted values of a and h for the isotopic chains of Po, At, Rn, Fr, Ra, Ac, Th, and U.Having fewer model parameters and a better description is not just a mathematical goal: it has some physical advantages. For example, one can judge more precisely the validity of the theoretical formalism and methods to improve it by studying the evolution of the involved parameters with decay data. This method is especially suited for the present model description of favored
$ \alpha $ decay half-lives, for which just a single parameter was used, namely the screening a. Equating the theoretical and experimental half-lives, one determines the value of a for each nucleus in part. For mere completeness, one applies the same procedure to the unfavored decay data, by keeping the hindrance term h fixed to the value found from the fittings. Obviously, there are cases where the aforementioned equation does not have a physical solution. In this situation, one considers the value of a, which minimizes the absolute difference between the theoretical and experimental half-lives. The evolution of the screening a with neutron and proton numbers is schematically depicted in Fig. 3, where the shell effects are clearly observable. Considering only the favored decay data in the first stage, one can see that the determined values of a have a well-defined discontinuity at the neutron magic number$ N = 126 $ . The$ N\leqslant 126 $ a values decrease up to$ N = 126 $ , and then, suddenly jump to higher values. The phenomenology behind this sudden transition is related to the fact that a nucleus with a closed shell is naturally more compact, whereas adding nucleons to such nuclei significantly extends their effective radius. There is also a small gradient of a with Z, in the$ N\leqslant 126 $ region, which is a consequence of the low-lying$ Z = 82 $ proton shell closure. The small screening found before the intersection of both proton and neutron closed shells seems to reoccur at higher mass, just below the supposedly deformed$ N = 162 $ neutron and$ Z = 108 $ proton closed shells [35, 36]. The predominance of low a values actually starts close to another deformed neutron shell closure at$ N = 152 $ . As its effect is known to be smaller than that of$ N = 162 $ , at least for the$ \alpha $ decay half lives [8], there is no discontinuity observed similar to the case of the spherical shell closure$ N = 126 $ . The a values for unfavored decays also follow the same trends listed above, but more loosely.
Figure 3. (color online) Z-N chart of values of screening parameter a determined from experimental data. For unfavored decays, the hindrance term is fixed to the fitted value reported in Table 2.
Deformed shell closures are highly localized at relatively large quadrupole deformations
$ \beta_{2} $ [37]. Therefore, a corresponding deformation dependence of the screening parameter is expected. This is confirmed by the plot in Fig. 4, in which few available values of$ \beta_{2} $ extracted from measured quadrupole transition probabilities are correlated with parameter a determined for each corresponding nucleus from its measured$ \alpha $ decay data. As can be seen, there is a parabolic-like evolution of a with$ \beta_{2} $ . The screening is heightened for moderate deformations where the shell structure is essentially destroyed, and it is minimal for spherical nuclear shapes and considerably suppressed at very high deformations, where deformed single-particle energy gaps are generated.
Figure 4. Dependence of a values determined from experimental data on the quadrupole deformation
$ \beta_{2} $ deduced from experimental$ B(E2) $ transition rates [38].The strong effect of the
$ N = 126 $ shell closure can be better seen from the evolution along the isotopic chains of the a values reproducing the experimental data, shown in Figs. 5 and 6. The shell closure is reflected in a sharp minimum of a near$ N = 124,126 $ for even N nuclei. Although not always obvious, a similar minimum is found for odd N nuclei, which is shifted down to around$ N = 123 $ in even Z data. The minima in the isotopic curves of a are extended over more nuclei in the case of$ Z = 84-87 $ isotopic chains, which speaks for the influence of the proton magic number$ Z = 82 $ . The evolution of the odd N data points is in general more erratic, with staggering sequences of alternating favored and unfavored decay processes. This staggering increases with Z, such that for$ Z = 84, 85 $ chains the odd N data have a completely smooth evolution that closely mirrors the even N data. With increasing Z, staggering appears and a alternates between values similar to the even N curve and much lower ones. At higher Z chains, the staggering once again disappears from the evolution of the odd N data points, which favors now the lower values (Cm and Cf plots of Fig. 5).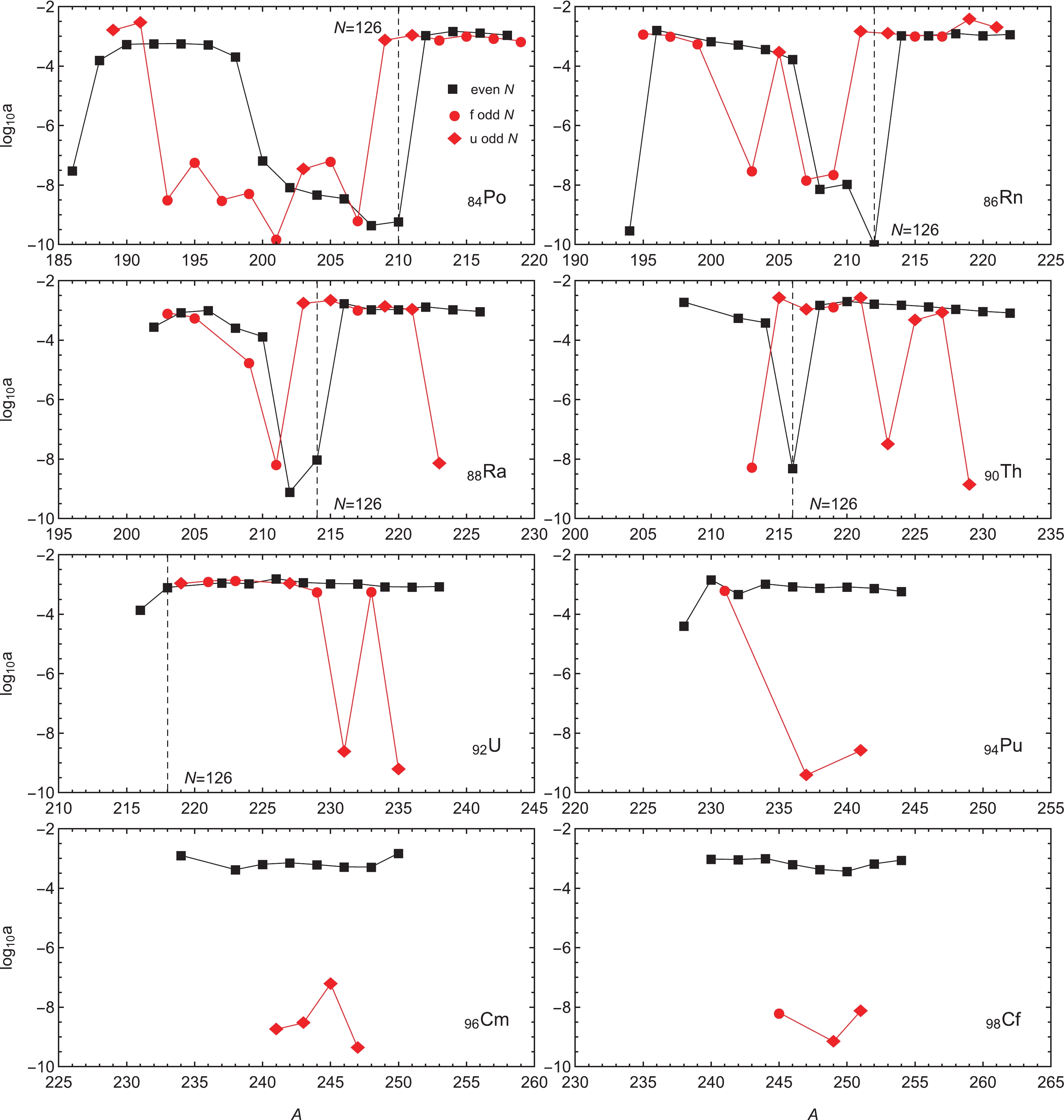
Figure 5. (color online) Evolution of a values determined from experimental data along selected even Z isotopic chains. For unfavored decays, the hindrance term is fixed to the fitted value reported in Table 2.
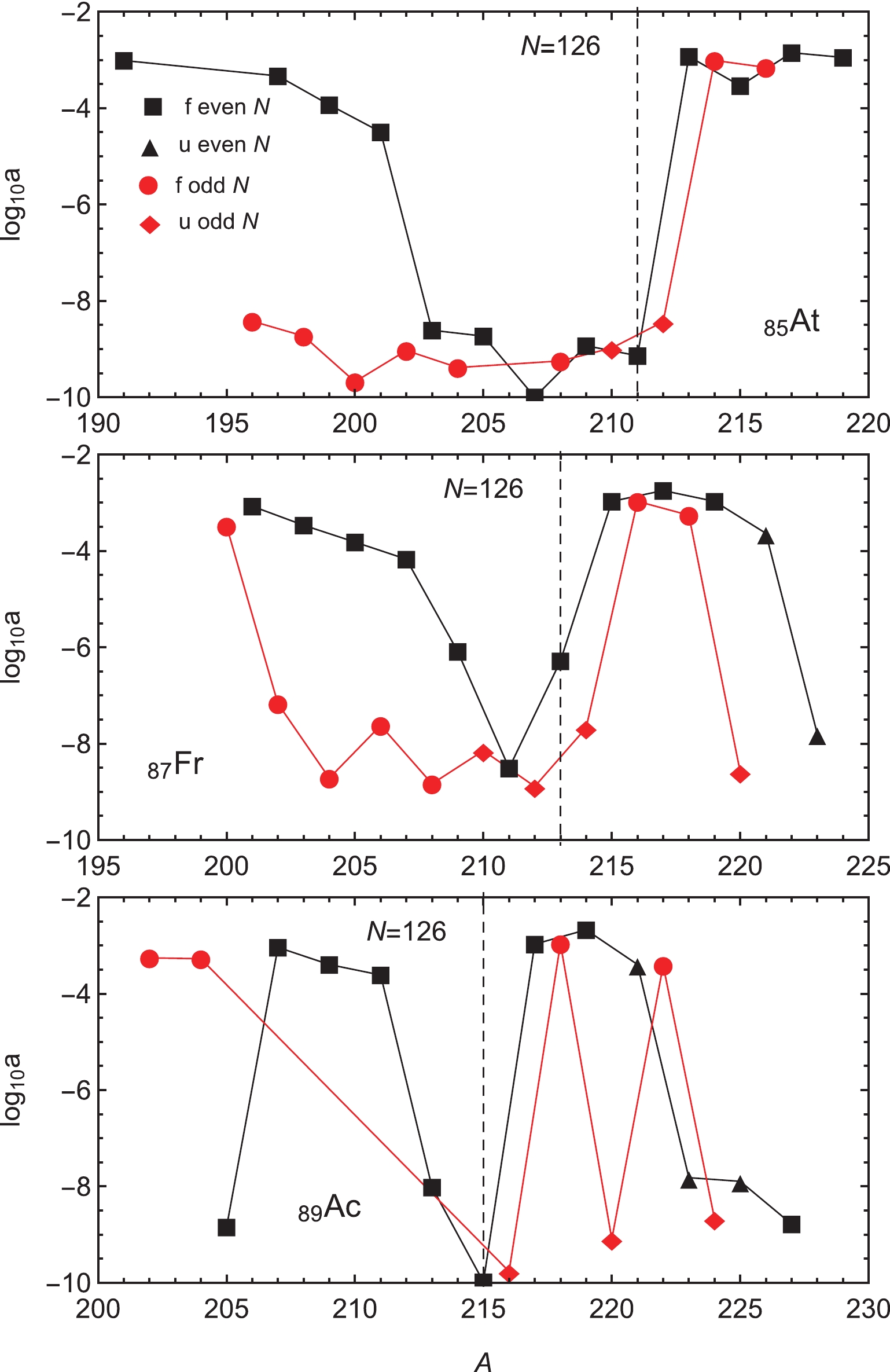
Figure 6. (color online) Evolution of a values determined from experimental data along selected odd Z isotopic chains. For unfavored decays, the hindrance term is fixed to the fitted value reported in Table 2.
Despite the occasional staggering, the evolution of a with odd or even N is predictably smooth in extended regions of the nuclei. This fact is used here to make some predictions for nuclei for which only uncertain or incomplete decay data is available. Taking into account the distinct characteristics of nuclei with even or odd numbers of protons and neutrons, one linearly interpolates the immediate neighboring a values from an isotopic chain, which also has the same neutron number parity as the nucleus considered in the predictions. Given this specific rule, there are only few cases to be calculated, which are listed in Table 3. For completeness, one also listed the predictions of the present formalism with fitted a and h values, as well as with the UDL formula and the newly determined parameters. One source of uncertainty in the data corresponding to these
$ \alpha $ decays is the angular momentum assignment to the ground states of the parent and daughter nuclei, which establishes the orbital momentum l of the emitted$ \alpha $ cluster. This is the case for the$ ^{206}_{85} $ At emitter, whose ground state is considered to be the same as that of its daughter nucleus, i.e.$ 5^{+} $ . Other experiments do not exclude$ 5^{-} $ and$ 6^{-} $ ground states for the same emitter, which is the preferred case according to the predictions of all three methods. The interpolation approach, however, gives the best result. The$ ^{225}_{\; 92} $ U nucleus is in a similar situation, whereas its ground state is not even known. All calculations suggest however that it undergoes most likely a favored$ \alpha $ decay, which is better described with fitted a and h parameters. The other source of uncertainty in the decay data comes from the interplay with other decay channels, such as proton and cluster emission, spontaneous fission, and$ \alpha $ decay to excited states. When the exact branching ratios are not known, the measured half-live represents the lower bound of the considered decay. This type of situation is found for ground state to ground state$ \alpha $ decays from$ ^{198}_{86} $ Rn and$ ^{207}_{88} $ Ra nuclei. The predictions for these two nuclei with interpolated values of screening are one of the closest to the boundary value, whereas, the$ \alpha $ decay from the ground state of$ ^{239}_{94} $ Pu to the ground state of its daughter nucleus has not yet been experimentally observed. However, it is theoretically allowed with a small probability from systematic considerations. Its$ \alpha $ decay half-live is better reproduced by the UDL formula. Finally, the half-live of$ ^{236}_{96} $ Cm has not yet been measured and the considered theoretical calculations predict around 49, 63, and 70 min, respectively. It is worth mentioning that in all other cases considered in Table 3, the present model predictions with interpolated or fitted screening are very close to the measured half-lives. This is a supporting feature for the prediction power of the proposed formalism.nucleus $ Q_{\alpha} $ /MeV

l a/fm $ ^{-1} $ 

$ \log_{10}{T_{1/2}} $ Exp.

$ \log_{10}{T_{1/2}} $ Th1.

$ \log_{10}{T_{1/2}} $ Th2.

$ \log_{10}{T_{1/2}} $ UDL

$ ^{206}_{85} $ At

5.8884 (0) 4.900 $ \times 10^{-10} $ 

7.355 4.558 4.590 4.969 (1) 6.418 6.335 5.605 $ ^{198}_{86} $ Rn

7.3490 0 1.143 $ \times 10^{-3} $ 

$ \geqslant $ −1.184

−1.113 −0.913 −0.879 $ ^{207}_{88} $ Ra

7.2700 0 2.991 $ \times 10^{-4} $ 

$ \geqslant $ 0.130

0.148 0.171 0.147 $ ^{225}_{92} $ U

8.0150 (0)? 1.242 $ \times 10^{-3} $ 

−1.080 −1.411 −1.015 −1.185 $ ^{239}_{94} $ Pu

5.2445 3 1.494 $ \times 10^{-9} $ 

15.404 $ ^{*} $ 

14.525 14.329 15.378 $ ^{236}_{96} $ Cm

7.0670 0 8.475 $ \times 10^{-4} $ 

? 3.466 3.577 3.621 * Ground state to ground state decay not observed. The associated branching ratio is deduced from systematics. Table 3. Predictions for
$ \alpha $ emitters with uncertain or incomplete experimental data, calculated with interpolated values of the screening parameter a and fixed hindrance h to the value from Table 2 (Th1.), with both a and h fitted to data (Th2.) and with the UDL formula, whose parameters are updated. Uncertain data are written in round parentheses, while missing information is indicated by "?". -
A simple analytical model based on the WKB approximation is proposed for the calculation of
$ \alpha $ decay half-lives. The WKB formalism was used to calculate the penetrability of a phenomenological barrier defined by the centrifugal contribution and a screened electrostatic interaction described by a Hulthen potential. The additional preformation probability is accounted for by considering an infinite square well for the nuclear interaction part of the phenomenological barrier. For favored decays, the model depends solely on the screening parameter defining the Hulthen potential, while for unfavored ones, an additional hindrance term is introduced. The parameters are fixed by fitting 279 data points divided in separate sets for favored/unfavored decays and N-Z parity. Although the model uses one or two parameters, agreement with the experiment is very good and comparable with the results of the universal decay law employing two more parameters. The highest screening is found for even-even$ \alpha $ emitters, while the lowest is reported for odd-odd parent nuclei.Using the fact that the barrier penetration probability depends only on the screening parameter, one determined the optimal screening for each nucleus by matching the theoretical model to each experimental data point. The systematics of the obtained values for the screening parameter showed its dependence on the proton as well as the neutron shells filling. A specific discontinuity in the screening is observed at the neutron magic number
$ N = 126 $ , marking a sudden transition from low to high values. The dependence of the screening on the neutron and proton numbers acknowledges in a similar way also the deformed shell closures. This is supported by an enhancement of the screening at moderate deformations, for which the shell structure disappears. The evolution of the screening with the neutron number was found to be smooth within isotopic chains close to closed proton shells. This aspect is used to make some interpolated predictions for nuclei with uncertainties in the decay data.In conclusion, the generalization of the electrostatic interaction by a mean screening effect can account efficiently for missing secondary ingredients affecting the
$ \alpha $ decay, and provides a good description of the particularities of the experimental data. Moreover, the dependence of the optimal screening effect for each$ \alpha $ emitter on the degree of shell filling demonstrates the deficiency of the Coulomb potential in modeling the outer potential barrier.The authors acknowledge the financial support received from the Romanian Ministry of Education and Research, through Project PN-19-06-01-01/2019-2022.
Alpha decay of heavy and super heavy nuclei with a generalized electrostatic potential
- Received Date: 2020-06-30
- Available Online: 2020-12-01
Abstract: Half-lives of α decay for Z≥ 84 nuclei are calculated based on the WKB theory applied for a phenomenological potential barrier composed of a centrifugal contribution and a screened electrostatic interaction represented by a Hulthen potential. For favored decays, the model has a single adjustable parameter associated with the screening of the electrostatic potential. The description of half lives for unfavored decays requires an additional hindrance term. A good agreement with experimental data is obtained in all considered cases. The evolution of the screening parameter for each nucleus revealed its dependence on shell filling. The model is also used for theoretical predictions on a few nuclei with uncertain or incomplete decay information.





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF













 DownLoad:
DownLoad: