-
Many pieces of cosmological evidence point towards the existence of dark matter (DM), such as rotation curves in galaxies, the masses of clusters of galaxies, and the gravitational lensing of galaxies [1, 2]. However, there is no candidate for DM in the Stand Model (SM). In collider physics, the Higgs boson might be the portal connecting the new physics, such as DM and the fourth generation neutrino, and the SM [3-5]. In this case, the DM particles, which interact weakly with ordinary matter and are completely invisible to detectors, can be observed indirectly by studying the Higgs decays. In the SM, the Higgs boson can only decay invisibly via
$ H\rightarrow ZZ^\ast \rightarrow \nu\overline{\nu}\nu\overline{\nu} $ , as shown in Fig. 1, and its branching ratio (BR) is 1.06$ \times10^{-3} $ [6]. Therefore, any evidence of invisible Higgs decays that exceed this BR will indicate a phenomenon that is beyond the SM (BSM).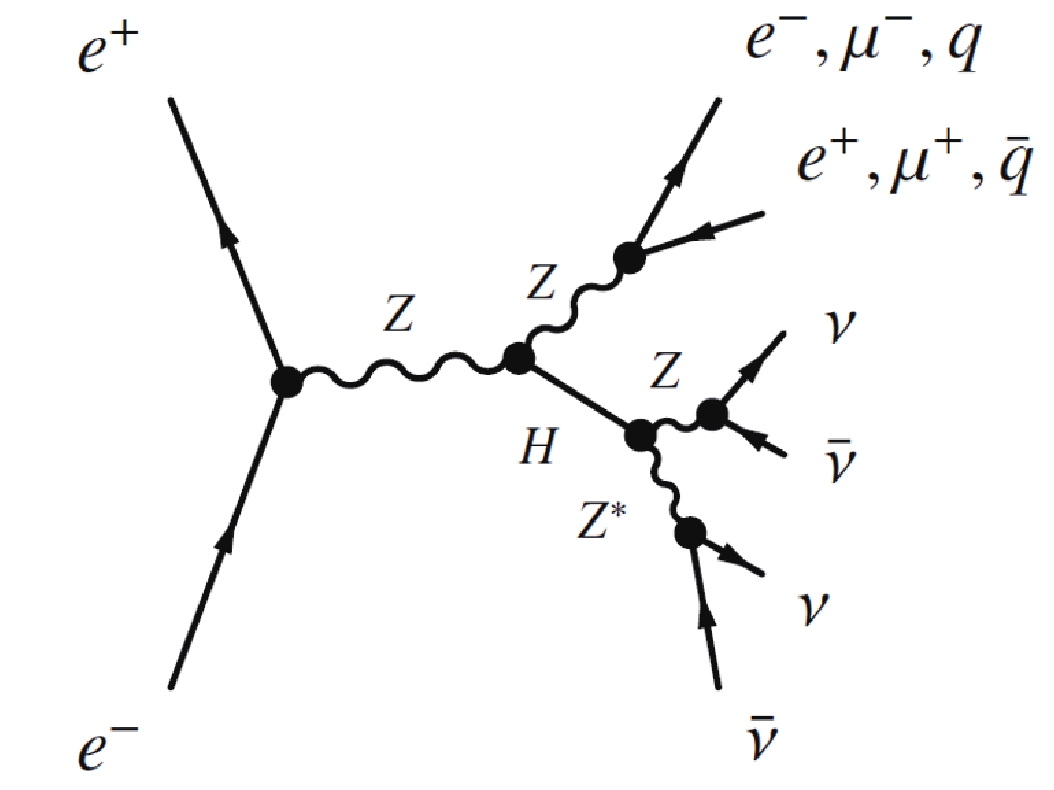
Figure 1. Feynman diagrams of the Higgs boson's invisible decays at an electron-positron collider such as the CEPC. In the process
$e^+e^- \rightarrow ZH$ , the invisible decays of the Higgs boson are via$H\rightarrow ZZ^\ast \rightarrow \nu\overline{\nu}\nu\overline{\nu}$ .The search for the invisible decays of the Higgs boson has been performed at the Large Hadron Collider (LHC). The signature for the invisible Higgs decays at the LHC is a large missing transverse momentum recoiling against a visible system. ATLAS and CMS yielded the 95% confidence level (CL) upper limits of 26% [7] and 19% [8], respectively, for the Higgs boson invisible branching ratio (BR(
$ H \rightarrow $ inv)). These results were obtained by the ATLAS and CMS detectors, respectively, using combined 4.7 fb−1, 20.3 fb−1, 36.1 fb−1 and combined 4.9 fb−1, 19.7 fb−1, 38.2 fb−1 of proton-proton collisions at the center-of-mass energy of 7 TeV, 8 TeV, and 13 TeV at the LHC. Compared with the results reported by the LHC, Higgs boson candidates can be identified using a technique known as the recoil mass method without using its decays at the Circular Electron Positron Collider (CEPC) [6]. An example of the recoil mass method is as follows: in the$ e^{+}e^{-} $ $ \rightarrow $ $ ZH(Z \rightarrow f\bar{f} $ ,$ H \rightarrow $ inv) channel, fermions (f) can be identified, and their momentum can be measured. By selecting the fermion pair from the Z boson decay, the mass of the system recoiling against the fermion pair, commonly known as the recoil mass$ M_{\rm{recoil}} $ , can be calculated as$ M_{\rm{recoil}} = \sqrt{(\sqrt{s} - E_{f\bar{f}})^{2} - P_{f\bar{f}}^{2}} \ , $

(1) where
$ E_{f\bar{f}} $ and$ P_{f\bar{f}} $ are the total energy and the momentum of the two fermions, respectively, and$ \sqrt{s} $ is the center-of-mass energy. The$ M_{\rm{recoil}} $ distribution is expected to exhibit a peak at the Higgs boson mass around 125 GeV for the$ f\bar{f} $ $ \rightarrow ZH $ process. In this way, the properties of the Higgs boson can be measured precisely without reconstructing the Higgs boson from its decay products. Therefore, the Higgs boson production can be disentangled from its decay in a model-independent way. Moreover, the$ e^+e^- $ collisions have a much lower hadronic background (Higgs boson channels form the signal) contamination compared with hadron collisions, which allows better exclusive measurements of the Higgs boson decay channels. The electron-positron Higgs factory is an essential machine for understanding the nature of the Higgs boson.CEPC is a Higgs factory proposed by the Chinese high energy physics community. CEPC is designed for delivering a combined integrated luminosity of 5.6 ab−1 to two detectors in 7 years. CEPC will operate at a center-of-mass energy
$ \sqrt{s} $ $ \sim $ 240-250 GeV, and over one million Higgs boson events will be produced during this period. Owing to the large statistics, the good beam energy spread of approximately 0.16% [9], and a novel particle flow algorithm [10], the mass and width of the Higgs boson are expected to be measured with high precision. With the SM$ ZH $ production rate, the upper limit of BR($ H \rightarrow $ inv) could reach 0.26% at the 95% CL, which is an expected improvement of two orders of magnitude over the results of ATLAS and CMS.In a previous study on CEPC, the upper limit of BR(
$ H \rightarrow $ inv) was 0.41% [6]. The previous study used the CEPC-v1 detector, whereas the CEPC-v4 detector is used in this study. The main change from CEPC-v1 to CEPC-v4 is the reduction of the solenoidal field intensity from 3.5 Tesla to 3.0 Tesla and changing the$ \sqrt{s} $ of the collider from 250 GeV to 240 GeV. Moreover, the reconstruction algorithm is different in both studies. Therefore, this study does not involve the comparison of the two results.This study performs three independent analyses corresponding to
$ \mu\mu H $ ,$ eeH $ , and$ qqH $ channels, for estimating the upper limit on the BR($ H \rightarrow $ inv) measurement at the CEPC. This paper is organized as follows. Section 2 presents a brief introduction to the CEPC detector and Monte Carlo simulations. Section 3 presents an introduction to the event selection of the three channels. A method for determining the upper limit, along with dependence of the Boson Mass Resolution (BMR), is discussed in Section 4. Section 5 lists our conclusions. -
One of the physics programs at the CEPC is precision measurement of the Higgs boson properties. The CEPC detector is expected to reconstruct and identify all key physical objects, including charged leptons, photons, jets, missing energy, and missing momentum.
The CEPC-v4 [6] detector was designed using the International Large Detector (ILD) [11, 12] as a reference. The detector of CEPC-v4 is simulated using MokkaC [13] and Geant4 [14]. It is composed of a tracking system, Time-Projection-Chamber tracker (TPC), high granularity calorimeter system, solenoid that generates a 3 Tesla magnetic field, and muon detector embedded in a magnetic field return yoke. The tracking system consists of silicon vertexing and tracking detectors. The calorimetry system consists of an electromagnetic calorimeter (ECAL) and an iron scintillator for a hadronic calorimeter (HCAL).
The analysis is performed on Monte Carlo (MC) samples simulated at the CEPC-v4 detector. The Higgs boson signal and SM backgrounds at the center-of-mass energy of 240 GeV, corresponding to the overall luminosity of 5.6 ab−1, are generated with WHIZARD1.95 [15]. The generated events are then processed with MokkaC, and an attempt is made to reconstruct every visible particle with ARBOR [10]. The cross sections of the major SM processes of the
$ e^{+}e^{-} $ collisions as functions of the center-of-mass energy$ \sqrt{s} $ are used in the simulations, including the Higgs boson production as well as the major backgrounds, where the initial-state radiation (ISR) effect has been taken into account. The Higgs boson signal and backgrounds are processed using Geant4 based full detector simulations and reconstruction. Limited by finite computational resources, approximately 20% of the two fermion backgrounds are used in full simulations.All samples are grouped into signal and backgrounds, and the backgrounds are classified according to their final states. For the signal, this paper mainly focuses on the process
$ e^{+}e^{-}\rightarrow ZH $ , which is called the “$ ZH $ ” process. Then, Z bosons decay into leptons or hadrons, and the Higgs particle decays into two Z bosons, which eventually decay into four neutrinos. For the backgrounds, the major SM backgrounds are divided into 2-fermion processes and 4-fermion processes, according to the final states. The 2-fermion backgrounds are$ e^{+}e^{-} $ $ \rightarrow $ $ f\bar{f} $ , where f refers to all lepton and quark pairs, except$ t\overline{t} $ . The 4-fermion backgrounds are divided into 6 types: “single_z,” “single_w,” “szorsw,” “zz,” “ww,” and “zzorww,” which are shown in Table 1. The processes whose four final states are a pair of electrons and two other fermions, or a pair of electron neutrinos and two other fermions, are named “single_z”. The “single_w” processes include one electron, one electron neutrino, and two other fermions. If a final state includes a pair of electrons and a pair of electron neutrinos simultaneously, the corresponding processes are named “szorsw”. In addition to the above-mentioned backgrounds, the same four fermions in the final state can be combined into different two intermediate bosons. If the two intermediate bosons can be two Z bosons, the processes are named “zz”. The “ww” process is the one in which two intermediate bosons can become two W bosons. If two intermediate bosons can become two Z bosons or two W bosons, the corresponding process is “zzorww”.Type Four final states single_z Two electrons, two other fermions or two electron neutrinos, and two other fermions single_w One electron, one electron neutrino, and two other fermions szorsw A pair of electrons and a pair of electron neutrinos Type Two intermediate bosons zz Two Z bosons ww Two W bosons zzorww Two Z bosons or two W bosons Table 1. Six types of 4-fermion backgrounds.
-
The signal in this analysis consists of three different channels, namely
$ ZH(Z \rightarrow qq, H \rightarrow $ inv),$ ZH(Z \rightarrow \mu\mu, H \rightarrow $ inv), and$ ZH(Z \rightarrow ee, H \rightarrow $ inv). Table 2 lists detailed information about the Higgs boson decay channels. The observed upper limit on BR($ H \rightarrow $ inv) at 95% CL at the CMS is 19%, and the CEPC is expected to yield more accurate results. In the event selection part, this analysis uses BR($ H \rightarrow $ inv) = 10%, and the event selection is based on the distribution of the signal and backgrounds. Event selection for each channel is detailed below.Process Cross sections /fb Expected $ffH$ 

203.66 1140496 $e^{+}e^{-} H$ 

7.04 39424 ${\mu^+}{\mu^-} H$ 

6.77 37912 $q\bar{q} H$ 

136.81 766136 Table 2. Cross sections of the Higgs boson production at
$\sqrt{s}$ = 240 GeV and number of events expected in 5.6 ab−1. -
In the
$ ZH(Z \rightarrow qq, H \rightarrow $ inv) process, owing to the presence of quarks, many final states are expected. The event selection uses the information about all visible particles, and the distributions of the signal and backgrounds are shown in Fig. 2. The comprehensive event selections are as follows. In the$ e^+e^- \rightarrow ZH(Z \rightarrow qq, H \rightarrow $ inv) process, the mass of the system recoiling against all visible particles from the Z boson is$ M_{\rm{recoil}}^{\rm{visible}} $ , which can be calculated using Eq. (1) by replacing$ E_{f\bar{f}} $ ,$ P_{f\bar{f}} $ with$ E_{\rm{visible}} $ ,$ P_{\rm{visible}} $ .$ E_{\rm{visible}} $ and$ P_{\rm{visible}} $ is the total energy and momentum of all visible particles. The peak of the$ M_{\rm{recoil}}^{\rm{visible}} $ distribution is close to the Higgs boson mass. Considering the resolution of the detector,$ M_{\rm{recoil}}^{\rm{visible}} $ is limited to (100,150) GeV, as shown in Fig. 2(a). To suppress 2-fermion backgrounds, the transverse momentum of all visible particles is required to satisfy$ P_{\rm{T}}^{\rm{visible}}> $ 18 GeV, as shown in Fig. 2(b), and the difference between the azimuthal angles of the two jets should be below 175°. Two jets are reconstructed from Z boson decay particles.$ E_{\rm{visible}} $ is the energy of all visible particles, which can be described as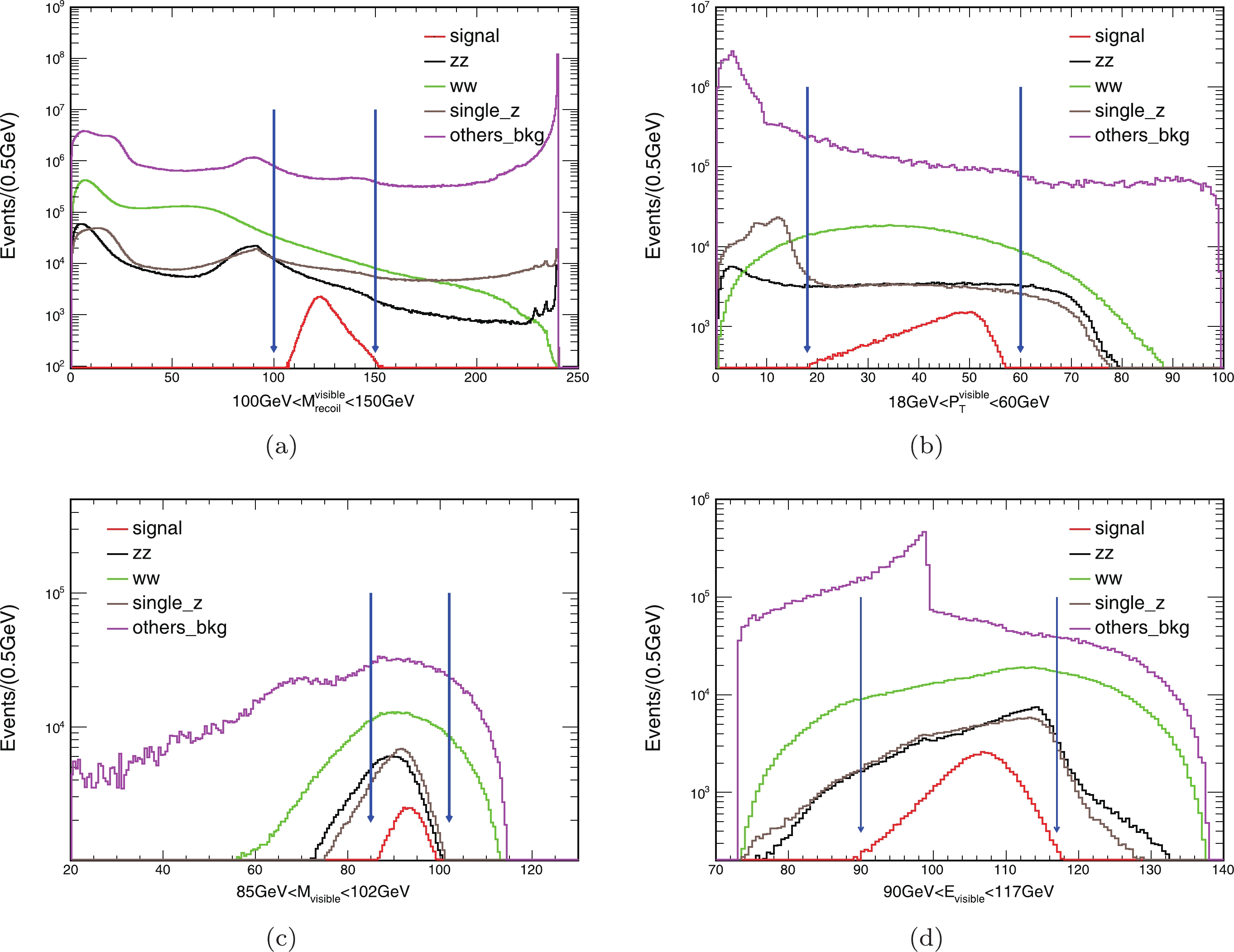
Figure 2. (color online) The distributions of
$M_{\rm{recoil}}^{\rm{visible}}$ ,$P_{\rm{T}}^{\rm{visible}}$ ,$E_{\rm{visible}}$ , and$M_{\rm{visible}}$ for signal and backgrounds in the$ZH(Z \rightarrow qq, H \rightarrow$ inv) process with BR($H \rightarrow$ inv) = 10% are plotted with all cuts except the ones shown already applied in the figure and the subsequent cuts (based on Table 3). The blue arrows mark the cut ranges.$ E_{\rm{visible}} = \frac{s+M_{\rm{visible}}^{2}-(M_{\rm{recoil}}^{\rm{visible}})^{2}}{2\sqrt{s}} , $

(2) where
$ M_{\rm{recoil}}^{\rm{visible}} $ is approximately 125 GeV,$ \sqrt{s} = 240 $ GeV, and the invariant mass of the visible system ($ M_{\rm{visible}} $ ) is equal to the Z boson mass, which is 91.2 GeV.$ M_{\rm{visible}} $ should be limited to (85,102) GeV, as shown in Fig. 2(c). Using the values of the parameters in Eq. (2),$ E_{\rm{visible}} $ should be near 105 GeV, as shown in Fig. 2(d). According to the equation$ P_{\rm{visible}}^2 = E_{\rm{visible}}^2 - M_{\rm{visible}}^2 $ ,$ P_{\rm{visible}} $ should be near 52 GeV. Owing to the presence of quarks, the final states may include many charged particles. It is necessary to limit the number of charged particles ($ N_{\rm{charged}} $ ) with energy greater than 1 GeV to be larger than 5. To suppress the backgrounds from tau particles, a dedicated tau-finding algorithm TAURUS has been developed [16]. Since the$ ZH(Z \rightarrow qq, H\rightarrow $ inv) process may include tau particles, the mass of all tau particles ($ M_{\tau} $ ) should be less than 95 GeV, for suppressing the backgrounds containing tau and quarks.Table 3 lists the yields of signal (
$ qqH $ _inv) and its backgrounds of the cut chain. The value of the significance [17] is used to judge the effect of the cuts. After the event selection, the signal selection efficiency is 60.81%, and the total background rejection efficiency is 99.97%. The backgrounds, which contain neutrinos and two quarks, account for 95% of the total remaining backgrounds. The compositions of these backgrounds are similar to the signal channel and are difficult to suppress further.Process $qqH$ _inv

2f single_w single_z szorsw zz ww zzorww ZH_visible total_bkg Significance Total generated 76614 801152072 19517400 9072952 1397088 6389432 50826216 20440840 1140496 909936496 2.54 100 GeV $<M_{\rm{recoil}}^{\rm{visible}}<$ 150 GeV

73800 47294924 1388875 822729 229217 507567 1752827 658204 97387 52751730 10.16 18 GeV $<P_{\rm{T}}^{\rm{visible}}<$ 60 GeV

67115 9165311 1000762 269328 152273 282630 1294265 462029 79965 12706563 18.81 90 GeV $<E_{\rm{visible}}<$ 117 GeV

63912 5748712 595697 223049 92958 231058 785392 272518 33705 7983089 22.59 85 GeV $<M_{\rm{visible}}<$ 102 GeV

53786 605791 238191 148850 39280 135641 392277 113043 18284 1691357 41.14 $\Delta\phi_{\rm{dijet}}<175^ \circ $ 

51911 390077 230273 141494 38359 129135 379931 109735 17395 1436399 43.06 30 GeV $<P_{\rm{visible}}<$ 58 GeV

48572 241510 148607 69457 24393 46807 226883 74781 13466 845904 52.32 $N_{\rm{charged}}>5,E_{\rm{charged}}>1$ GeV

47772 7986 18399 62990 6 43728 121365 4110 11699 270283 89.36 $M_{\tau}<$ 95 GeV

46589 7111 11044 59815 1 41180 104784 3126 11111 238172 92.58 Efficiency 60.81% 0.00% 0.06% 0.66% 0.00% 0.64% 0.21% 0.02% 0.97% 0.03% Table 3. Yields for backgrounds and
$ ZH(Z \rightarrow qq, H \rightarrow $ inv) signal at the CEPC, with$ \sqrt{s} $ = 240 GeV, BR($ H \rightarrow $ inv) = 10%, and integrated luminosity of 5.6 ab−1. -
The
$ ZH(Z \rightarrow \mu^+\mu^-, H \rightarrow $ inv) process and the$ ZH(Z \rightarrow e^+e^-, H \rightarrow $ inv) process are similar, and the two processes will be introduced together. Firstly, it is natural that only a pair of oppositely charged muons or electrons is required in the visible final states. By selecting two muons or two electrons, many related parameters can be used for background suppression. The event selections are as follows. The recoil masses of two muons ($ M_{\rm{recoil}}^{\mu^{+}\mu^{-}} $ ) and two electrons ($ M_{\rm{recoil}}^{e^{+}e^{-}} $ ) can be calculated using Eq. (1). The peak of$ M_{\rm{recoil}}^{\mu^{+}\mu^{-}} $ and$ M_{\rm{recoil}}^{e^{+}e^{-}} $ distribution should be around the Higgs boson mass 125 GeV. Considering the resolutions of muons and electrons and the distributions of signal and backgrounds as shown in Fig. 3 and Fig. 4, the recoil mass should satisfy 120 GeV$ <M_{\rm{recoil}}^{\mu^{+}\mu^{-}}< $ 150 GeV or 120 GeV$ <M_{\rm{recoil}}^{e^{+}e^{-}}< $ 170 GeV, and the invariant mass of two muons ($ M_{\mu^{+}\mu^{-}} $ ) or two electrons ($ M_{e^{+}e^{-}} $ ) is closer to the Z boson mass. To suppress the 2-fermion backgrounds, the transverse momenta of the muon pair ($ P_{\rm{T}}^{\mu^+\mu^-} $ ) and the electron pair ($ P_{\rm{T}}^{e^{+}e^{-}} $ ) are required to be more than 12 GeV, as shown in Fig. 3(c) and Fig. 4(c). Moreover, the angle between the two muons ($ \Delta\phi_{\mu^+\mu^-} $ ) should be under 175° or that between the two electrons ($ \Delta\phi_{e^+e^-} $ ) should be under 176° to suppress the 2-fermion backgrounds. The visible energy ($ E_{\rm{visible}} $ ), which is described in Eq. (2), is mainly the energy of two muons ($ E_{\mu^{+}\mu^{-}} $ ) or two electrons ($ E_{e^{+}e^{-}} $ ) from the Z boson decays; the value of$ E_{\rm{visible}} $ is approximately 105 GeV, as shown in Fig. 3(d) and Fig. 4(d). Using the approximate values of$ M_{\mu^{+}\mu^{-}} $ and$ E_{\mu^{+}\mu^{-}} $ in the relativistic energy-momentum relation$ M_{\mu^{+}\mu^{-}}^2 = E_{\mu^{+}\mu^{-}}^2- P_{\mu^{+}\mu^{-}}^2 $ , the value of$ {E_{\mu^{+}\mu^{-}}}\big/{P_{\mu^{+}\mu^{-}}} $ is close to 2, similar to that of$ {E_{e^+e^-}}\big/{P_{e^+e^-}} $ .
Figure 3. (color online) The distributions of
$M_{\rm{recoil}}^{\mu^{+}\mu^{-}}$ ,$P_{\rm{T}}^{\mu^+\mu^-}$ ,$E_{\rm{visible}}$ , and$M_{\mu^+\mu^-}$ for signal and backgrounds in the$ZH(Z \rightarrow \mu^+\mu^-, H \rightarrow$ inv) process with BR($H \rightarrow$ inv) = 10% are plotted with all cuts except the ones shown already applied in the figure and the subsequent cuts (based on Table 4). The blue arrows mark the cut ranges.
Figure 4. (color online) The distributions of
$M_{\rm{recoil}}^{e^+e^-}$ ,$P_{\rm{T}}^{e^+e^-}$ ,$E_{\rm{visible}}$ , and$M_{e^+e^-}$ for signal and backgrounds in the$ZH(Z \rightarrow e^+e^-, H \rightarrow$ inv) process with BR($H \rightarrow$ inv) = 10% are plotted with all cuts except the ones shown already applied in the figure and the subsequent cuts (based on Table 5). The blue arrows mark the cut ranges.Table 4 lists the yields for the
$ \mu\mu H $ _inv signal and its backgrounds. The remaining backgrounds containing two muons and two neutrinos account for 61% of the total backgrounds. These backgrounds have similar topology as the signal which is difficult to suppress further. The remaining backgrounds containing the muon, tau, and two neutrinos account for 38% of the total backgrounds. The algorithm TAURUS does not increase the significance of the$ \mu\mu H $ _inv signal.Process $\mu\mu H$ _inv

2f single_w single_z szorsw zz ww zzorww ZH total_bkg Significance Total generated 3791 801152072 19517400 9072952 1397088 6389432 50826216 20440840 1140496 909936496 0.13 $N_{\mu^{+}}=1,N_{\mu^{-}}=1$ 

3370 22737312 36123 723402 0 702045 1255617 1223596 59978 26738073 0.65 120 GeV $<M_{\rm{recoil}}^{\mu^{+}\mu^{-}}<$ 150 GeV

3286 652655 24 100435 0 62463 250819 112143 5708 1184247 3.02 85 GeV $<M_{\mu^{+}\mu^{-}}<$ 97 GeV

2791 381056 0 10739 0 20857 16720 24419 4493 458284 4.12 12 GeV $<P_{\rm{T}}^{\mu^{+}\mu^{-}}$ 

2705 92200 0 9483 0 18257 15906 21063 4331 161240 6.72 $\Delta\phi_{\mu^{+}\mu^{-}}<175^ \circ $ 

2598 72197 0 8894 0 17029 14769 20231 4142 137262 6.99 102 GeV $<E_{\rm{visible}}<$ 107 GeV

2273 62 0 1456 0 484 4379 5435 10 11826 20.28 $\frac{E_{\mu^{+}\mu^{-}}}{P_{\mu^{+}\mu^{-}}}<2.4$ 

2243 27 0 1344 0 440 3502 4090 6 9409 22.29 Efficiency 59.17% 0.00% 0.00% 0.01% 0.00% 0.01% 0.01% 0.02% 0.00% 0.00% Table 4. Yields for backgrounds and
$ ZH(Z \rightarrow \mu^+\mu^-, H \rightarrow $ inv) signal at the CEPC, with$ \sqrt{s} $ = 240 GeV, BR($ H \rightarrow $ inv) = 10% and integrated luminosity of 5.6 ab−1.Table 5 lists the yields for the
$ eeH $ _inv signal and its backgrounds at the CEPC. The cut Vertex$ _{\tau}< $ 0.0011, which is the position of the decay vertex, changes the value of significance from 10.91 to 13.79. Since the signal channel does not contain tau, the Vertex$ _{\tau} $ of the signal channel is much smaller than the backgrounds from tau. The final states of the remaining backgrounds, which are composed of two electrons and two neutrinos, account for 70% of the total background. These backgrounds are the same as the final particles of the signal channel. The final particles of the remaining backgrounds containing tau, electron, and two neutrinos account for 23% of the total background, and the information about tau particles cannot further suppress these backgrounds. In conclusion, the tau-finding algorithm TAURUS can improve the significance of the Higgs invisible decays to a certain extent, but it cannot completely suppress the backgrounds containing tau.Process $eeH$ _inv

2f single_w single_z szorsw zz ww zzorww ZH total_bkg Significance Total generated 3942 801152072 19517400 9072952 1397088 6389432 50826216 20440840 1140496 909936496 0.13 $N_{e^{+}}=1,N_{e^{-}}=1$ 

3472 120476492 1286971 1945217 1161098 134637 796860 292694 117024 126210993 0.31 120 GeV $<M_{\rm{recoil}}^{e^{+}e^{-}}<$ 170 GeV

3179 6469896 515411 226357 288321 4901 12836 34015 12443 7564180 1.16 71 GeV $<M_{e^{+}e^{-}}<99$ GeV

2617 2415241 98434 69803 105255 453 926 10853 9153 2710118 1.59 12 GeV $<P_{\rm{T}}^{e^{+}e^{-}}<$ 55 GeV

2511 1351168 87124 45901 91180 352 788 9396 8774 1594683 1.99 $\Delta\phi_{e^{+}e^{-}}<176^ \circ $ 

2397 462573 81317 37220 87409 208 712 8613 8456 686508 2.89 101 GeV $<E_{\rm{visible}}<$ 107 GeV

1614 6555 15198 2820 17583 12 54 1175 47 43444 7.70 $1.8<\frac{E_{e^+e^-}}{P_{e^+e^-}}<2.4$ 

1455 1423 6634 1127 7685 4 17 393 23 17306 10.91 ${\rm{Vertex}}_{\tau}$ 

$<$ 0.0011

1393 323 2436 926 5967 1 7 86 9 9755 13.79 Efficiency 35.34% 0.00% 0.01% 0.01% 0.43% 0.00% 0.00% 0.00% 0.00% 0.00% Table 5. Yields for backgrounds and
$ ZH(Z \rightarrow e^+e^-, H \rightarrow $ inv) signal at the CEPC, with$ \sqrt{s} $ = 240 GeV, BR($ H \rightarrow $ inv) = 10%, and integrated luminosity of 5.6 ab-1. -
After the event selections, the 95% CL upper limit of BR(
$ H \rightarrow $ inv) is computed within the CL$ _{s} $ formalism, using the profile likelihood ratio as a test statistic [18], in which systematic uncertainties are ignored. The likelihood ratio method uses$ \mu $ S+B, where$ \mu $ is the signal strength, S is the signal, and B is the background. First, the signal and background samples are fitted to obtain their distribution functions, which are used for generating Asimov data. The Asimov data provide a simple method for obtaining the median experiment sensitivity of the measurement as well as fluctuations around this expectation. Then, the test statistic distribution generated for signal+background and background-only hypotheses is constructed assuming the signal strength$ \mu $ , and each$ \mu $ corresponds to the CL$ _{s} $ value calculated by the ratio of the two hypothesis probabilities [19]. When the CL$ _{s} $ value is 0.05, the$ \mu $ value is its 95% CL upper limit. The corresponding negative logarithmic profile likelihood ratio$-\Delta$ log(L) as a function of$ \mu $ is shown in Fig. 5. The horizontal axis corresponding to$-\Delta$ log(L) = 2 on the y-axis is approximately 95% CL interval of$ \mu $ .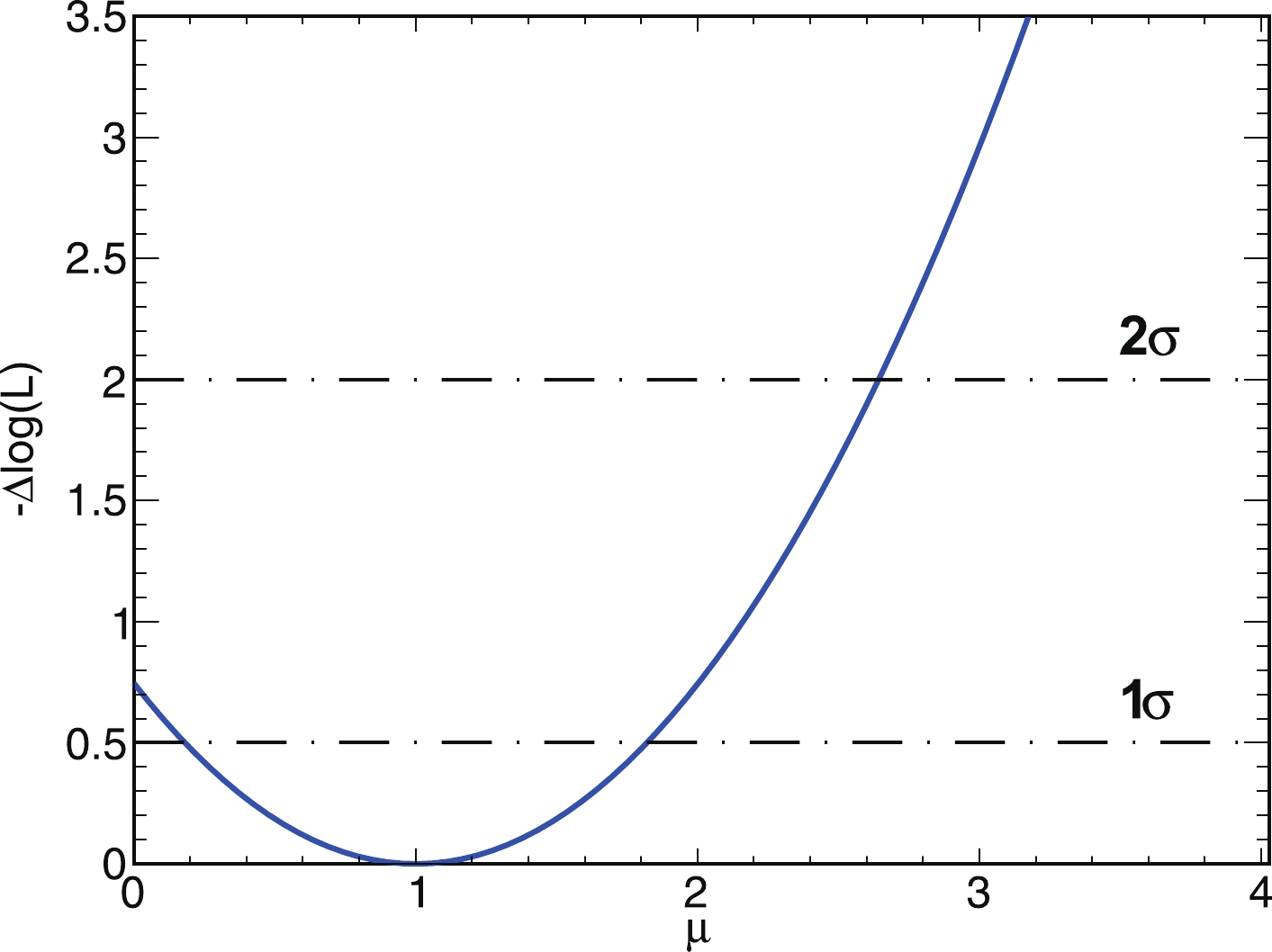
Figure 5. (color online) The
$\mu$ distribution from the likelihood profile, where the horizontal dash-dotted lines indicate the location of the approximately 68%, 95% CL interval, which corresponds to$-\Delta$ log(L) = 0.5, 2 on the y-axis.Table 6 summarizes the expected precision of the measurement of BR(
$ H \rightarrow $ inv) and the 95% CL upper limit on BR($ H \rightarrow $ inv), for the dataset of 5.6 ab-1. The estimated combined 95% CL upper limit of three channels is 0.26%. Any evidence of invisible Higgs decays that exceeds this value will indicate the BSM phenomenon.$ZH$ final

statesPrecision of
BR($H \rightarrow$ inv)

$\times$ 100 (%)

Upper limit on
BR($H \rightarrow$ inv) (%)

$Z \rightarrow e^+e^-$ ,

$H \rightarrow$ inv

45.37 1.08 $Z \rightarrow \mu^+\mu^-$ ,

$H \rightarrow$ inv

23.57 0.55 $Z \rightarrow q\overline{q}$ ,

$H \rightarrow$ inv

9.54 0.27 Combination 8.68 0.26 Table 6. Expected precision of the measurement of BR(
$H \rightarrow$ inv) and the 95% CL upper limit on BR($H \rightarrow$ inv) for the dataset 5.6 ab−1.The precision of the upper limit is affected by various systematic uncertainties [20], such as the luminosity, beam energy, efficiency of the object reconstruction, and acceptance of the detector. The precision of luminosity can be 0.1%, and the beam energy is expected to be better than 1 MeV, which can be ignored in experimental recoil mass measurements. For tracks within the detector acceptance and transverse momenta larger than 1 GeV, the track finding efficiency is better than 99%. These systematic uncertainties are expected to be small and will be ignored in this study.
The precision of the upper limit of BR(
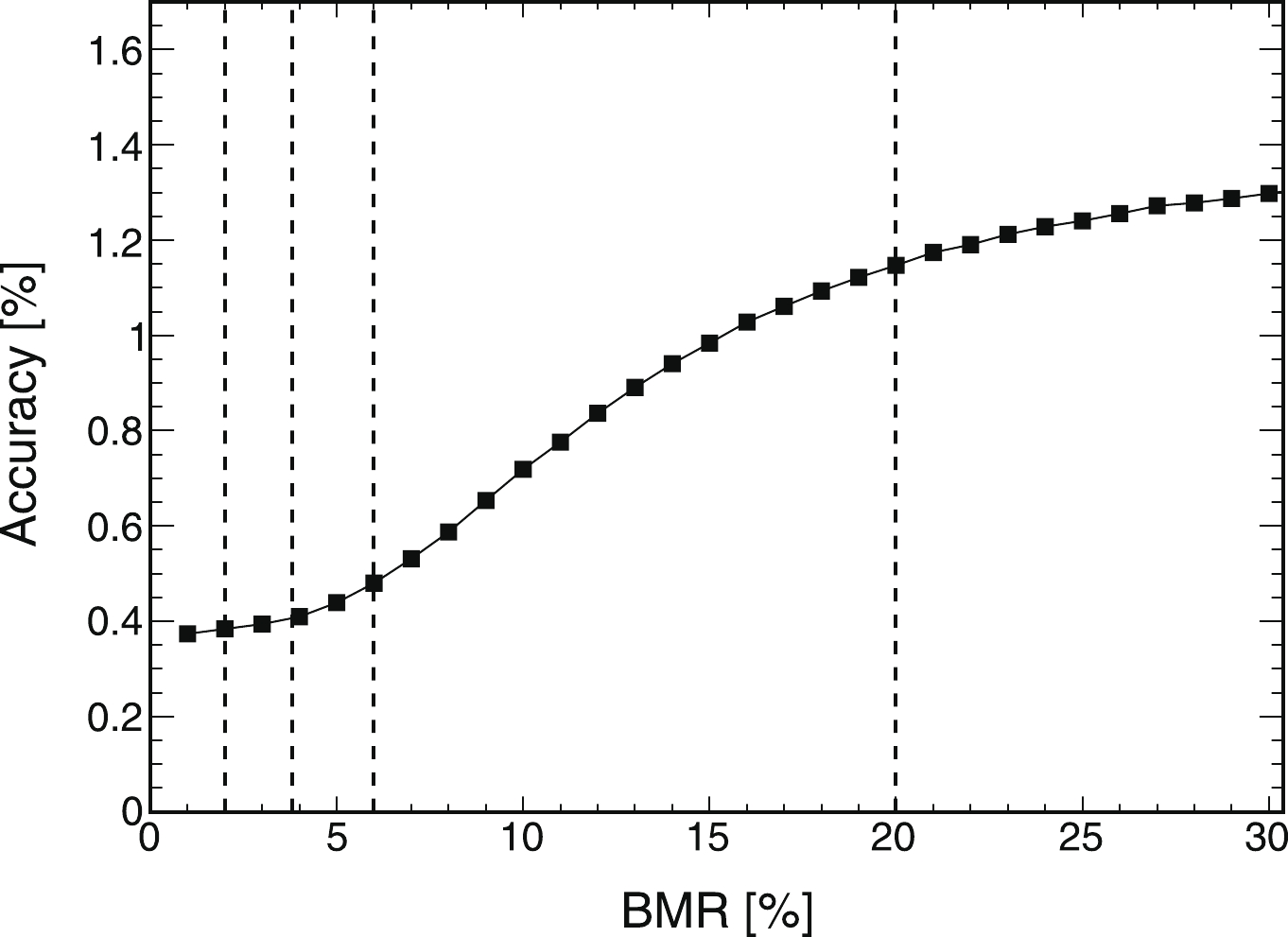
$ H \rightarrow $ inv) in$ ZH(Z \rightarrow qq, H \rightarrow $ inv) channel strongly relies on the invariant mass reconstruction of the Z boson. The boson mass resolution (BMR) is defined as the visible invariant mass resolution of the$ ZH(Z \rightarrow qq, H \rightarrow $ inv) event for quantifying the invariant mass reconstruction of the Z boson.The BMR of the CEPC detector can reach 3.8% using the ARBOR reconstruction algorithm [10, 21]. A fast simulation was performed for quantifying this dependence. The fast simulation took into account the signal of
$ ZH(Z \rightarrow qq, $ $H \rightarrow $ inv) and the main background of$ ZZ (Z \rightarrow qq, Z \rightarrow $ inv) after the event selection. Fig. 6 shows the accuracy [16] of$ ZH(Z \rightarrow qq, H \rightarrow $ inv) for different BMR values. For BMR values between 4% and 20%, the accuracy degrades rapidly with increasing BMR, while for BMR values below 4%, the change in the accuracy is below 0.06%. Based on the fast simulation, it can be concluded that BMR is vital and will affect the measurement precision of the$ ZH(Z \rightarrow qq, H \rightarrow $ inv) channel. Therefore, the BMR value of 4% can be used as an essential reference upper bound for detector design and optimization. -
This paper studied the measurement of the Higgs invisible decays at the CEPC. The upper limit on the Higgs invisible decays was measured using three independent channels
$ ZH(Z \rightarrow qq, H \rightarrow $ inv),$ ZH(Z \rightarrow \mu^+\mu^-, H \rightarrow $ inv), and$ ZH(Z \rightarrow e^+e^-, H \rightarrow $ inv). The combined result for the 95% CL upper limit of BR($ H \rightarrow $ inv) was 0.26% for the three channels. Compared with the LHC results (26% for ATLAS and 19% for CMS), the result obtained at the CEPC is better by two orders of magnitude. Compared with the High-Luminosity LHC (HL-LHC) result for 14 TeV, which is expected to be 2.5% [22], the result obtained at the CEPC is better by one order of magnitude. The accuracy of the upper limit for the CEPC is significantly better than those for hadron colliders, because the reconstructed Higgs recoil mass spectrum at the electron-positron Higgs factories gives a very clear and distinct signature of the Higgs boson, as well as the high productivity of the Higgs bosons at the CEPC.The CEPC result is consistent with the results for other electron-positron colliders, such as the International Linear Collider (ILC) and the Future Circular Collider (FCC-ee), for which the 95% CL upper limits on BR(
$ H \rightarrow $ inv) were 0.26% for ILC [23] and 0.22% for FCC-ee (5 ab-1 at 240 GeV and 0.19% by combining 365 GeV) [24]. Among these three signal channels, the$ qqH $ channel yielded the best result owing to its largest number of events. The precision of the upper limit on the$ qqH $ channel strongly relies on the invariant mass of the visible hadronic decay system, and BMR better than 4% provides a clear separation between the Higgs signal and the$ ZZ $ background, which shall be pursued as one of the key physics requirements for designing future CEPC detectors.The authors would like to thank Chengdong FU and Xianghu ZHAO for providing the simulation tools and samples. We also thank Patrick Janot for a helpful discussion about FCC results.
Search for invisible decays of the Higgs boson produced at the CEPC
- Received Date: 2020-02-04
- Accepted Date: 2020-08-21
- Available Online: 2020-12-01
Abstract: The Circular Electron Positron Collider (CEPC), proposed as a future Higgs boson factory, will operate at a center-of-mass energy of 240 GeV and will accumulate 5.6 ab−1 of integrated luminosity in 7 years. In this study, we estimate the upper limit of BR(






 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF

















 DownLoad:
DownLoad: