-
Symmetry energy plays an important role in understanding the isospin asymmetric subject, e.g., in neutron stars [1, 2] and neutron rich heavy ion collisions [3-5]. However, the density dependence of symmetry energy, especially at high density, is still largely unknown. In addition to the efforts on the constraints of the symmetry energy at suprasaturation density by analyzing the neutron star merging events [2, 6-15], constraints related to heavy ion collisions are also needed. The ratio of multiplicity of
$ \pi^- $ to$ \pi^+ $ , known as$ \pi^-/\pi^+ $ ratios, in heavy ion collisions with neutron rich beam and target at the$ \pi $ production threshold energy was supposed to be a sensitive observable to probe the density dependence of the symmetry energy at suprasaturation density [16].The pion data of Au+Au at beam energy ranging from 0.4 A GeV to 1.2 A GeV [17] were used for extracting the information of the symmetry energy. However, contradictory conclusions on the symmetry energy were obtained when comparing data to calculations with different transport models [18-23]. In addition to the model uncertainties, which arise from the philosophy of solving the high dimensionality transport equation, another important reason is that the sensitivity of
$ \pi^-/\pi^+ $ ratios may not be strong enough to clearly distinguish the stiffness of symmetry energy at higher beam energy, where the nucleon-nucleon collisions play a dominant role instead of the mean field. This stimulated the remeasurement of pion multiplicities and$ \pi^-/\pi^+ $ ratios near the$ \Delta $ threshold energy by using neutron rich reaction systems.Recently, the MSU group measured the charged pion multiplicities for
$ ^{132,112,108} $ Sn+$ ^{124,112} $ Sn by using the S$ \pi $ RIT Time Projection Chamer at 0.27 A GeV, which is subthreshold energy [24]. The energy spectra of single$ \pi^-/\pi^+ $ ratios, i.e.,$R(\pi^-/\pi^+) = \dfrac{{\rm d}M_{\pi^-}}{{\rm d}E_k}/\dfrac{{\rm d}M_{\pi^+}}{{\rm d}E_k}$ , and double ratios$ DR(\pi^-/\pi^+) = R_{\mathrm{A}}(\pi^-/\pi^+)/R_{\mathrm{B}}(\pi^-/\pi^+) $ (A is$ ^{132} $ Sn+$ ^{124} $ Sn, B is$ ^{108} $ Sn+$ ^{112} $ Sn ) are provided, and they may have a more exclusive sensitivity to the density dependence of the symmetry energy than the total multiplicity of pions [21, 25].In addition, the behavior of the pion energy spectral or pion flow could also be sensitive to the pion potential [26-30]. The reason is that, for beam energy below 0.3 A GeV, the pions are mainly produced through the low mass
$ \Delta $ s. The produced pions via low mass$ \Delta $ s decay have smaller momentum ($ |\mathbf{k}|<0.119 $ GeV$ < m_\pi $ ), so they have longer mean-free-path given that the cross sections of$ \pi+N $ near the threshold energies are relative small [31]. Consequently, one can expect that the in-medium effects on pion propagation and collision gradually become more important, and the on-shell transport seems reasonably accurate. The relativistic Vlasov-Uehling-Uhlenbeck (RVUU) model calculations showed that the$ \pi^-/\pi^+ $ ratio is reduced by approximately 10% by considering the in-medium pion dispersion relation, and a large effect is also observed in isospin-dependent Boltzmann-Uehling-Uhlenbeck (IBUU) [28] calculations at subthreshold energy. There exists model dependence on the in-medium effects on the pion production mechanism in the transport model simulations partly due to the separate treatments on pion potential, the$ \pi N\to \Delta $ cross sections, and$ \Delta \to \pi N $ decay widths. Thus, providing a theoretical description of the pion potential,$ \pi N\to \Delta $ cross sections, and$ \Delta \to \pi N $ decay widths in isospin asymmetric nuclear matter from the same Lagrange is very useful to achieve a deep understanding of the pion production mechanism and reduce the model uncertainties related to the medium corrections separately for pion potential and$ N\pi\to \Delta / \Delta\to N\pi $ .Generally, the pion potential can be obtained from the phenomenological pion potential [23, 27-30], or from effective methods, such as the closed-time path green functions method [32] or the chiral perturbation theory [33, 34]. Dmitriev et al. studied the in-medium pion dispersion relation by the pion self-energy via meson exchange interaction [35] for symmetric nuclear matter. Then, a study by Guangjun Mao also discussed the pion dispersion relation with the relativistic form of pion self-energy in symmetric nuclear matter and its effect on the
$ N\pi\to \Delta $ cross section and$ \Delta\to N\pi $ decay width [32, 36].This increasing interest on the study of isospin asymmetric nuclear matter led Kaiser et al. to study the pion s-wave self-energy in isospin asymmetric nuclear matter based on the chiral perturbation theory up to the two-loop approximation [33]. With the s-wave pion self-energy reported in Ref. [33], Zhen Zhang et al. also added p-wave pion potential for the estimation of the in-medium
$ N\pi\to \Delta $ cross sections and$ \Delta \to \pi N $ decay widths by including N and$ \Delta $ masses in free space [37]. Qingfeng Li et al. discussed the$ N\pi\to \Delta $ cross sections and$ \Delta \to \pi N $ decay widths in asymmetric nuclear matter based on the closed-time path green function method [36], but the pion dispersion relation they used was still in symmetric nuclear matter [32]. In these calculations, the energy conservation is an important issue and should be carefully considered in isospin asymmetric nuclear matter for$ NN\to N\Delta $ [38].In this study, we investigated the pion self-energy, the in-medium
$ N\pi\to \Delta $ cross section, and the$ \Delta\to N\pi $ decay width in asymmetric nuclear matter with the consideration of energy conservation and effective mass splitting effects based on relativistic form interaction. Given that we focused on the pion self-energy, the medium effects of pion absorption cross section, and$ \Delta $ decay width, we did not include the$ \Delta $ width in the$ \Delta $ propagator for calculating the pion self-energy and other related results with an approximation. The paper is organized as follows. In Sec. II, we introduce the theoretical model on the pion self-energy,$ N\pi\to \Delta $ cross section, and$ \Delta $ decay width. Then, the in-medium pion dispersion relation,$ N\pi\to \Delta $ cross section, and$ \Delta \to \pi N $ decay width are presented and discussed in Sec. III. Finally, a summary and conclusions are provided in Sec. IV. -
Based on the particle-hole and
$ \Delta $ -hole with relativistic form interaction, we studied the in-medium pion dispersion relation and calculated the$ \pi N\to \Delta $ cross sections and$ \Delta \to \pi N $ decay widths in an asymmetric medium. The Lagrangian density we adopted is as follows [38-42]:$ \mathcal{L} = \mathcal{L}_F+\mathcal{L}_I , $

(1) where
$ \mathcal{L}_F $ is the free Lagrangian for the nucleon and$ \Delta $ [38, 42]. The interaction part of the Lagrangian is$ \begin{aligned}[b] \mathcal{L}_I =& \frac{g_{\pi NN}}{m_{\pi}}\bar{\Psi}\gamma_{\mu}\gamma_{5}{{\tau}} \cdot\Psi\partial^{\mu}{{\pi}}\\&+\frac{g_{\pi N\Delta}}{m_{\pi}}\bar{\Delta}_{\mu}{{\mathcal{T}}}\cdot \Psi\partial^{\mu}{{\pi}}+ {\rm h.c.} \end{aligned}$

(2) Here,
$ {{\tau}} $ is the isospin matrices of the nucleon [39], and$ {{\mathcal{T}}} $ is the isospin transition matrix between the isospin 1/2 and 3/2 fields [41].The pion dispersion relation in a nuclear medium is
$ \omega_{\pi^i}^2 = m_{\pi^i}^2+\mathbf{k}^2+\Pi(k), $

(3) where
$ \pi^i $ denotes different isospin states of the pion, i.e.,$ \pi^+ $ ,$ \pi^0 $ , and$ \pi^- $ . Here,$ \Pi(k) $ is the pion self-energy; it includes the particle-hole ($ \Pi_N(k) $ ) and$ \Delta $ -hole parts ($ \Pi_\Delta(k) $ ), i.e.,$ \Pi(k) = \Pi_N(k)+\Pi_\Delta(k). $

(4) For the on-shell pion dispersion relation in Eq. (3), the
$ \Pi(k) $ should be the real part ($ \mathrm{Re}\Pi(k) $ ). For convenience, all the Re notions in the$ \Pi(k) $ are ignored in this study. The lowest order$ \pi $ self-energies in nuclear matter are$ \begin{aligned}[b] \Pi_{N} =& (-{\rm i}) \left(\frac{g_{\pi NN}}{m_{\pi}}\right)^2 \langle t^\prime |\tau^{\lambda} | t \rangle\langle t |\tau^{\dagger\lambda^{\prime}} | t^\prime \rangle \delta_{\lambda\lambda^{\prime}}\\& \times\int\frac{{\rm d}^4 q}{(2\pi)^4} \mathbf{Tr}[k/\gamma_{5} G_{N}(q+k)k/\gamma_{5}G_{N}(q)], \end{aligned} $

(5) $ \begin{aligned}[b] \Pi_{\Delta} =& (-{\rm i})\left(\frac{g_{\pi N\Delta}}{m_{\pi}}\right)^2 \langle t^\prime |\mathcal{T}^{\lambda} | t \rangle\langle t |\mathcal{T}^{\dagger\lambda^{\prime}} | t^\prime \rangle \delta_{\lambda \lambda^{\prime}}\\ &\times\int\frac{{\rm d}^4q}{(2\pi)^4} \mathbf{Tr}[k_{\mu}k_{\nu}G^{\mu\nu}_{\Delta}(q+k)G_{N}(q)], \end{aligned} $

(6) where isospin matrix
$ \tau^{\lambda} $ can be$ \tau^{+} $ ,$ \tau^{0} $ , and$ \tau^{-} $ , as in Ref. [43]. Here, we take the isospin factors$ \langle t^\prime |\tau^{\lambda} | t \rangle = I_{NN} $ , and$ \langle t^\prime |\mathcal{T}^{\lambda} | t \rangle = I_{N\Delta} $ , which can be found in Table A1-A2 in Appendix A.$NN\pi$ 

$I_{NN}$ 

$pp\pi^0$ 

1 $nn\pi^0$ 

−1 $pn\pi^+$ 

− $\sqrt{2}$ 

$np\pi^-$ 

$\sqrt{2}$ 

Table A1. Isospin factors
$I_{NN}$ .Channel $I_{N\Delta}$ 

$\Delta^{++}\to \pi^{+}p$ 

1 $\Delta^{+}\to \pi^{+} n$ 

$\sqrt{\dfrac{1}{3} }$ 

$\Delta^{+}\to \pi^{0} p$ 

$\sqrt{\dfrac{2}{3} }$ 

$\Delta^{0}\to \pi^{0} n$ 

$\sqrt{\dfrac{2}{3} }$ 

$\Delta^{0}\to \pi^{-} p$ 

$\sqrt{\dfrac{1}{3} }$ 

$\Delta^{-}\to \pi^{-}n$ 

1 Table A2. Isospin factors
$I_{N\Delta}$ .The nucleon and
$ \Delta $ propagators in a nuclear medium can be expressed using the above Lagrangian as follows:$ \begin{aligned}[b] G_{N}(q_0, \mathbf{q}) =& \frac{q/+m_{N}}{q^2_0-E^2_{N}(q)+{\rm i}\epsilon}\\& +{\rm i}2\pi\frac{q/+m_{N}}{2E_{N}(q)}n(|\mathbf{q}|)\delta(q_0-E_{N}(q)), \end{aligned} $

(7) $ \begin{aligned}[b] G^{\mu\nu}_{\Delta}(q_0, \mathbf{q}) =& \frac{\mathcal{P}^{\mu\nu}}{q^2_0-E^2_{\Delta}(q)+{\rm i}\epsilon} \\& +{\rm i}2\pi\frac{q/+m_{0,\Delta}}{2E_{\Delta}(q)}n(|\mathbf{q}|)\delta(q_0-E_{\Delta}(q)), \end{aligned} $

(8) where
$ \mathcal{P}^{\mu\nu} $ is$ \mathcal{P}^{\mu\nu} = -(q/+m_{0,\Delta})\left[g^{\mu\nu}-\frac{1}{3}\gamma^{\mu}\gamma^{\nu}-\frac{2q^{\mu}q^{\nu}}{3m^{2}_{0,\Delta}}+\frac{q^{\mu}\gamma^{\nu}-q^{\nu}\gamma^{\mu}}{3m_{0,\Delta}}\right]. $

(9) Here,
$ q/ = q^{\mu}\gamma_{\mu} $ and$ m_{0,\Delta} $ is the pole mass of$ \Delta $ . The first parts of Eqs. (7) - (8) are the vacuum propagators, and$ n(|\mathbf{q}|) $ denotes the occupation number in the medium. Note that we made an approximation on the$ \Delta $ propagator, i.e., we replaced the imaginary part${\rm i}\sqrt{p^2}\Gamma_\Delta(p^2)$ from Eq. (8) in Ref. [44] with${\rm i}\epsilon$ in Eq. (8) . This is because we wanted to focus on the in-medium effect on pion self-energy, absorption, and production cross sections at a beam energy$ < $ 0.4 A GeV. If we do not consider the Fermi motion, the estimated maximum$ \Delta $ mass is approximately less than 1.13 GeV, and the momentum of pion is less than 0.119 GeV/c in$ \Delta $ 's rest frame. Correspondingly, the decay width of$ \Delta $ is also small, below 0.03 GeV. Thus, in the following discussion, we mainly discuss the results of pion self-energy,$ N \pi\to \Delta $ cross sections, and$ \Delta $ decay width within$ s^{1/2}_{N\pi}<1.15 $ GeV. Concerning the medium effects on pion related issues at a beam energy around and above 1 A GeV for heavy ion collisions,${\rm i} \sqrt{p^2}\Gamma_\Delta(p^2)$ should be adopted in the$ \Delta $ propagator for the calculations of pion self-energy, cross section, and decay width, as in Refs. [26, 32, 37, 45, 46].The pion self-energies can also be expressed in terms of an analog of the susceptibility
$ \chi $ ,$ \Pi_N = k^2\chi_N $

(10) $ \Pi_\Delta = k^2\chi_\Delta $

(11) and the short range correlations is incorporated into
$ \chi $ as follows:$ \begin{aligned}[b] &\chi_{N}\to \frac{1+(g^{\prime}_{N\Delta}-g^{\prime}_{\Delta\Delta})\chi_{\Delta}}{(1-g^{\prime}_{\Delta\Delta}\chi_{\Delta})(1-g^{\prime}_{NN}\chi_{N})-g^{\prime}_{N\Delta}\chi_{\Delta}g^{\prime}_{N\Delta}\chi_{N}} \chi_{N},\\& \chi_{\Delta}\to \frac{1+(g^{\prime}_{N\Delta}-g^{\prime}_{NN})\chi_{N}}{(1-g^{\prime}_{\Delta\Delta}\chi_{\Delta})(1-g^{\prime}_{NN}\chi_{N})-g^{\prime}_{N\Delta}\chi_{\Delta}g^{\prime}_{N\Delta}\chi_{N}} \chi_{\Delta}. \end{aligned} $

The Migdal parameters for the short-range interaction are
$ g^{\prime}_{NN} = 0.9 $ and$ g^{\prime}_{N\Delta} = g^{\prime}_{\Delta\Delta} = 0.6 $ , as in Ref. [47]. The detailed calculation and self-energies of$ \pi^+ $ ,$ \pi^0 $ , and$ \pi^- $ are shown in Appendices B - C.For the calculation of the in-medium
$ \Delta\to N\pi $ decay widths and$ \pi N\to \Delta $ cross sections, we used the quasiparticle approximation [48] by replacing$ m_i \to m^*_i $ and$ p_i \to p^*_i $ ($ i $ could be nucleon or$ \Delta $ ) in their formula. The effective momentum can be written as$ \mathbf{p}_i^* = \mathbf{p}_i $ given that the spatial components of the vector field vanish in the rest nuclear matter, i.e.,$ \mathbf{\Sigma} = 0 $ . Thus, in the mean field approach, the effective energy reads$ p_i^{*0} = p^{0}_{i}-\Sigma^{0}_{i}. $

(12) The Dirac effective mass of nucleon and the effective pole mass of
$ \Delta $ read$ m^{*}_{i} = m_{i}+\Sigma^{S}_{i}. $

(13) Here,
$ i = n $ , p,$ \Delta^{++} $ ,$ \Delta^{+} $ ,$ \Delta^{0} $ , and$ \Delta^{-} $ . The details about$ \Sigma^{0}_{i} $ and$ \Sigma^{S}_{i} $ can be found in Refs. [38, 42]. Likewise, the parameters of the relativistic mean field are NL$ \rho \delta $ , as in Ref. [49].Based on the approximation we adopted,
$ \mathbf{p}_{N}+\mathbf{k} = \mathbf{p}^*_{N}+\mathbf{k}^* $ . The energy conservation is given by the canonical momentum conservation relation, i.e.,$ E_{\Delta} = E_{N}+\omega $ , with$ E_{\Delta} = E^*_{\Delta}+\Sigma^{0}_{\Delta} $ and$ E_{N} = E^*_{N}+\Sigma^{0}_{N} $ ,$ m^*_{\Delta}+\Sigma^{0}_{\Delta} = E^{*}_{N}+\Sigma^{0}_{N}+\omega(\mathbf{k}). $

(14) By using the effective momenta and masses, one can obtain the in-medium
$ \Delta\to N\pi $ decay widths and$ \pi N\to \Delta $ cross sections. In this study, the in-medium decay widths of a given charged state of$ \Delta $ , i.e.,$ \Delta\to N\pi $ are expressed as follows:$ \begin{aligned}[b] \Gamma^* =& \frac{1}{2m^*_{\Delta}}\int \frac{{\rm d}^3\mathbf{p}^*_{N}}{(2\pi)^32E^*_{N}}\frac{{\rm d}^3\mathbf{p}^*_{\pi} {\rm d}\omega}{(2\pi)^3 }\overline{|\mathcal{M}_{\Delta\to N\pi}|^2}\\& \times\delta(\omega^2-\mathbf{p}^{*2}_{\pi}-m^2_{\pi}-\Pi) \\& \times(2\pi)^4\delta^3(\mathbf{p}^*_{N}+\mathbf{p}^*_{\pi})\delta(E^*_{N}+\omega+\Delta\Sigma-m^*_{\Delta})\\ =& Z_B\frac{\mathbf{k}^2}{8\pi m^*_{\Delta} E^*_{N}\omega}\frac{\overline{|\mathcal{M}^*_{\Delta\to N\pi}|^2}}{\bigg|\dfrac{\mathbf{k}}{E^*_{N}}+\dfrac{\mathbf{k}}{\omega}\bigg|}, \end{aligned} $

(15) where
$ \mathbf{p}^*_{\pi} = \mathbf{p}_{\pi} = \mathbf{k} $ in the static nuclear medium, and$ \Delta\Sigma = \Sigma^0_N-\Sigma^0_\Delta $ . The spreading width of$ \Delta $ [50-54] from the$ \Delta $ absorption and the rescattering processes were neglected in this study because the process of$ \Delta N\to NN $ and the multiplicity of pions are relatively scarce. For example, the pion multiplicity is less than 1 per event for Sn+Sn at 0.27 A GeV and less than 6 for Au+Au at 0.4 A GeV [17].$ Z_B $ is the wave function renormalization factor,$ \begin{aligned}[b] Z_B = \frac{1}{1-\dfrac{1}{2\omega}\dfrac{\partial \Pi(\omega,\mathbf{k})}{\partial \omega}\bigg|_{\omega = E_{\pi}^*}}, \end{aligned}$

(16) where
$ E_{\pi}^* = \sqrt{\mathbf{k}^{2}+m^2_{\pi}+\Pi(\omega,\mathbf{k})}. $

(17) Given that we focused on the cross sections used in the heavy ion collisions near the threshold energy where the low mass
$ \Delta $ s dominates, the pion branch plays the main role for$ \Delta $ , and the$ \Delta $ -hole branch is ignored. Thus, we set$ Z_B = 1 $ , as in Ref. [32]The in-medium
$ \pi N\to\Delta $ cross section is expressed as$ \sigma^{*}_{\pi N\to \Delta} = \frac{\pi f^*(m^*_{\Delta})}{4m^*_{\Delta}}\frac{\overline{|\mathcal{M}^*_{\pi N\to \Delta}|^2}}{|\mathbf{k}|(E^*_{N}+\omega )} , $

(18) where
$ \overline{|\mathcal{M}^*_{\pi N\to \Delta}|^2} = 2\overline{|\mathcal{M}^*_{\Delta \to N \pi}|^2} $ . With the effective mass, the mass distribution$ f^* $ is written as$ f^* = \frac{2}{\pi}\frac{m^{*2}_{0,\Delta}\Gamma^*_t}{(m^{*2}_{0,\Delta}-m^{*2}_{\Delta})^2+m^{*2}_{0,\Delta}\Gamma^{*2}_t },$

(19) where
$ \Gamma^{*}_t $ is the total decay width of$ \Delta \to N \pi $ [54]. Note that$ m^*_{\Delta} $ in Eqs. (15), (18), and (19) is the energy of the$ N\pi $ system in medium and is calculated based on the energy conservation relationship in Eq. (14) with given$ \mathbf{k} $ , which corresponds to the center-of-mass of energy as$ \sqrt{s} = m_\Delta = \sqrt{m^2_\pi+\mathbf{k}^2}+\sqrt{m^2_N+\mathbf{k}^2} $ in a$ \Delta $ static frame for free space. With$|\mathbf{k}| = \dfrac{1}{2\sqrt{s}}\sqrt{(s-(m_\pi+m_N)^2)(s-(m_\pi-m_N)^2)}$ , the$ \Delta $ effective mass can be$ m^*_{\Delta}\equiv m^*_{\Delta}(|\mathbf{k}|) = m^*_{\Delta}(\sqrt{s}) $ , with$ f^* = f^*(\sqrt{s}) $ , and the in-medium$ \pi N\to\Delta $ cross section can be written as$ \sigma^{*}_{\pi N\to \Delta} = \frac{2\pi^2f^*(\sqrt{s})\Gamma^*}{\mathbf{k}^2} . $

(20) The
$ \Delta $ effective pole mass$ m^{*}_{0,\Delta} $ above is derived from Eq. (13).The coupling constants we used were determined by fitting the cross section of
$ \pi^{+}p\to\Delta^{++} $ and$ \Delta\to N\pi $ decay width in free space [55]. The decay width of$ \Delta\to N\pi $ in free space is$ \begin{aligned}[b] \Gamma =& \frac{1}{2m_{\Delta}}\int \frac{{\rm d}^3\mathbf{p}_{N}}{(2\pi)^32E_{N}}\frac{{\rm d}^3\mathbf{p}_{\pi} }{(2\pi)^3 2\omega}\overline{|\mathcal{M}_{\Delta\to N\pi}|^2}\\& \times (2\pi)^4\delta^3(\mathbf{p}_{N}+\mathbf{p}_{\pi})\delta(E_{N}+\omega-m_{\Delta})\\ =&\frac{\mathbf{k}^2}{8\pi m_{\Delta} E_{N}\omega}\frac{\overline{|\mathcal{M}_{\Delta\to N\pi}|^2}}{\bigg| \dfrac{\mathbf{k}}{E_{N}}+\dfrac{\mathbf{k}}{\omega} \bigg|} \end{aligned} $

(21) where
$ \mathbf{p}_{\pi} = \mathbf{k} $ . Here,$ \overline{|\mathcal{M}_{\Delta \to N \pi}|^2} $ is calculated as follows:$ \begin{aligned}[b] \overline{|\mathcal{M}_{\Delta \to N \pi}|^2} =& \frac{1}{4}\sum_{s_{\Delta}}|\mathcal{M}_{\Delta \to N \pi}|^2\\ =& \frac{g_{\pi N \Delta}^{2}I^{2}_{N\Delta}}{4m^{2}_{\pi}}\sum_{s}\Psi(p_{N})\bar{\Psi}(p_{N})k^{\mu}\Delta_{\mu}(p_{\Delta})\bar{\Delta}_{\nu}(p_{\Delta})k^{\nu}\\ =& \frac{g_{\pi N \Delta}^{2}I^{2}_{N\Delta}}{4m^{2}_{\pi}}{\rm Tr}[(p/_{N}+m_{N})k^{\mu}\mathcal{P}_{\mu\nu}(p_{\Delta})k^{\nu}]\\ =& \frac{2g_{\pi N \Delta}^{2}I^{2}_{N\Delta}}{3m^{2}_{\pi}} (m_{N}+E_{N})\mathbf{k}^2m_{\Delta} . \end{aligned} $

(22) The expression of the
$ \pi N\to \Delta $ cross section is$ \begin{aligned}[b] \sigma_{\pi N\to \Delta} =& \int {\rm d} m_{\Delta}f(m_{\Delta})\int \frac{{\rm d}^3\mathbf{p}_{\Delta}}{(2\pi)^32E_{\Delta}}\frac{\overline{|\mathcal{M}_{\pi N\to \Delta}|^2}}{4E_{N}\omega|\dfrac{\mathbf{p}_{N}}{E_{N}}-\dfrac{\mathbf{k}}{\omega}|}\\ &\times (2\pi)^4\delta^3(\mathbf{p}_{N}+\mathbf{k}-\mathbf{p}_{\Delta})\delta(E_{N}+\omega-E_{\Delta}). \end{aligned} $

(23) In the
$ \Delta $ rest frame,$ \sigma_{\pi N\to \Delta} $ can be written as$ \sigma_{\pi N\to \Delta} = \frac{\pi f(m_{\Delta})}{4m_{\Delta}E_{N}\omega}\frac{\overline{|\mathcal{M}_{\pi N\to \Delta}|^2}}{\bigg|\dfrac{\mathbf{k}}{E_{N}}+\dfrac{\mathbf{k}}{\omega}\bigg|}. $

(24) Note that
$ f(m_{\Delta}) $ is the mass distribution of$ \Delta $ resonance in free space, which reads$ f(m_{\Delta}) = \frac{2}{\pi}\frac{m^{2}_{0,\Delta}\Gamma_t}{(m^{2}_{0,\Delta}-m^{2}_{\Delta})^2+m^{2}_{0,\Delta}\Gamma^2_t }. $

(25) The coupling constants used in this study, i.e.,
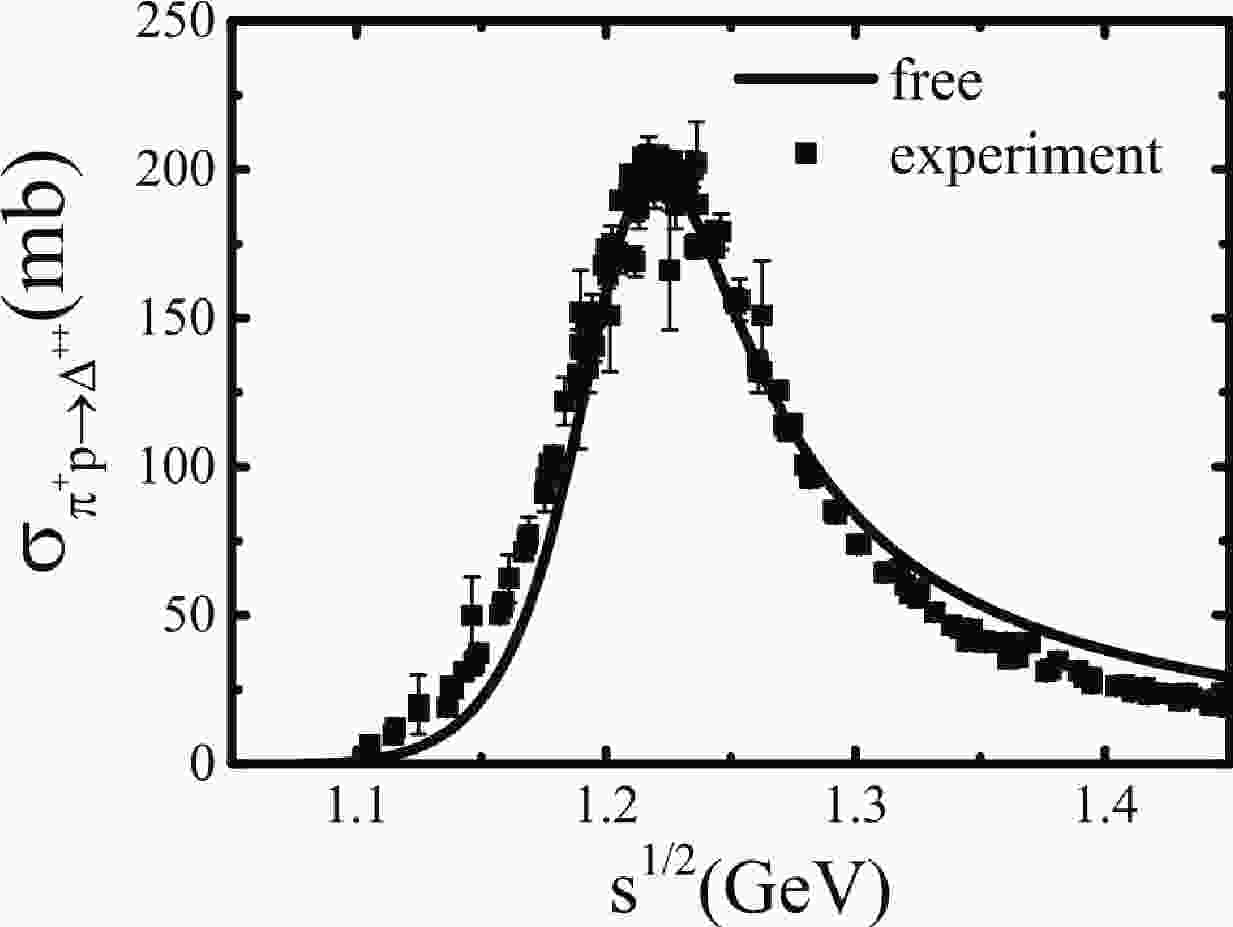
$ g_{\pi NN} = 1.008 $ ,$ g_{\pi N\Delta} = 2.3 $ , and the cut-off$\Lambda^2 = \exp (-2\mathbf{k}^2/b^2)$ with$ b = 7m_{\pi} $ , are obtained by fitting the experimental data of cross section and decay width [55] shown in Fig. 1. The decay width$ \Gamma = 0.120 $ GeV for the pole mass$ m_{\Delta} = 1.232 $ GeV can be calculated from Eq. (21).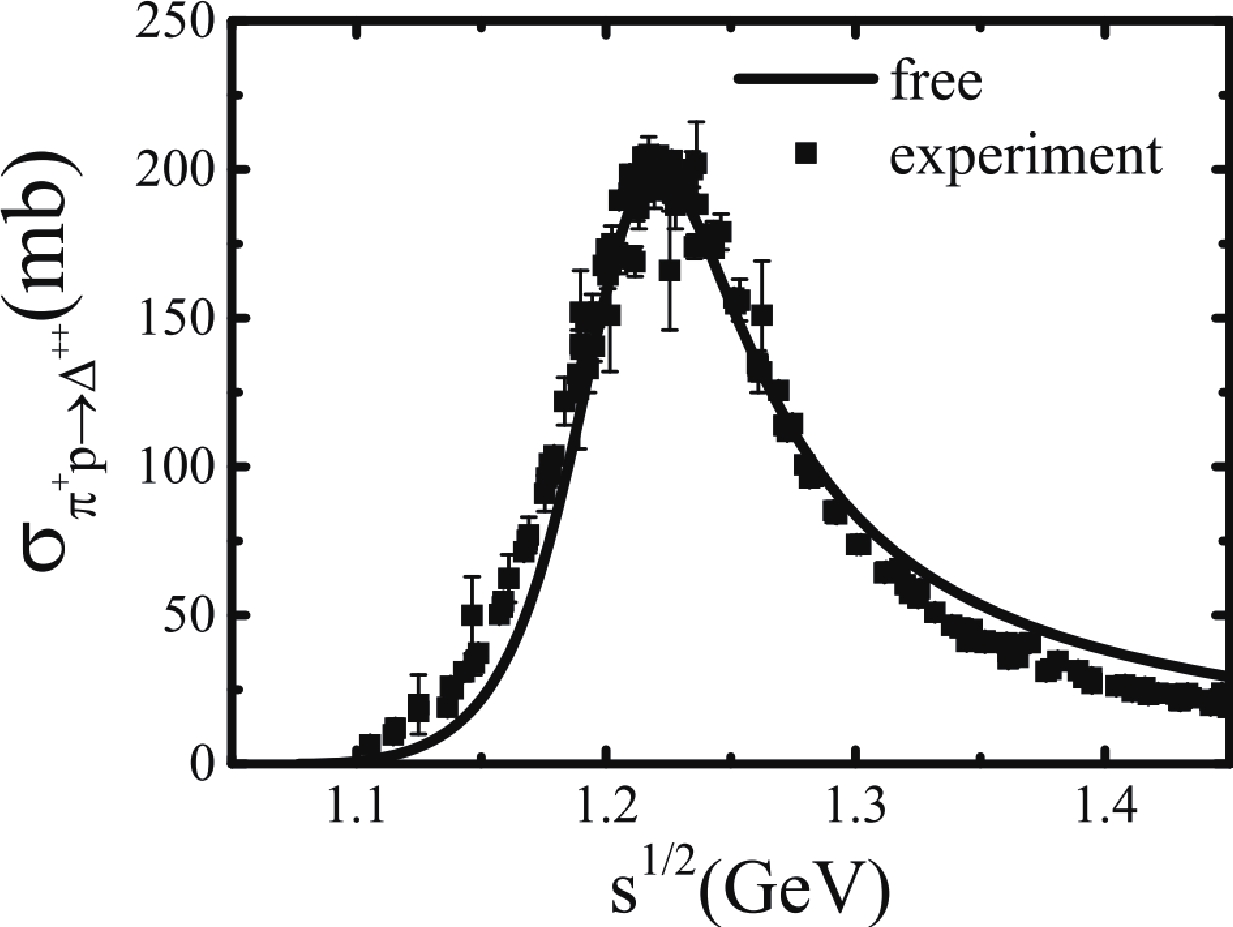
Figure 1.
$\sigma_{\pi^+ p\rightarrow \Delta^{++}}$ as a function of$s^{1/2}$ in free space; the experimental data are extracted from Ref. [55]. -
According to Eq. (3), the pion dispersion relation has two solutions, i.e., the lower one near the free pion energy
$ \omega_{F} = \sqrt{m_{\pi}^2 +\mathbf{k}^2} $ , known as the particle-hole branch, and higher one near$ \omega_{\Delta} = \dfrac{\mathbf{k}^2}{2m_{\Delta}}+m_{\Delta}-m_{N} $ , known as the$ \Delta $ -hole branch [32, 37]. In Ref. [37], it was pointed out that the threshold for the$ \Delta $ resonance to decay into a pion through the$ \Delta $ -hole branch is larger than 1.36 GeV. It implies that the$ \Delta $ decay into pion via$ \Delta $ -hole branch is less important given that we focused on the effects near the$ \pi $ production threshold energy. Thus, we neglected the decay of$ \Delta $ into a pion through the$ \Delta $ -hole branch, as in Ref. [37].In Fig. 2, we present the pion dispersion relation
$ \omega(k) $ and optical potential$ V_\pi(k) $ at different densities in symmetric nuclear matter for$ |\mathbf{k}|< m_{\pi} $ . The black solid, red dashed, green dotted, blue dash-dotted, and magenta dash-dotted lines represent$ \omega $ in free space,$ 0.5\rho_0 $ ,$ \rho_0 $ ,$ 1.5\rho_0 $ , and$ 2\rho_0 $ , respectively. The pion optical potential can be written as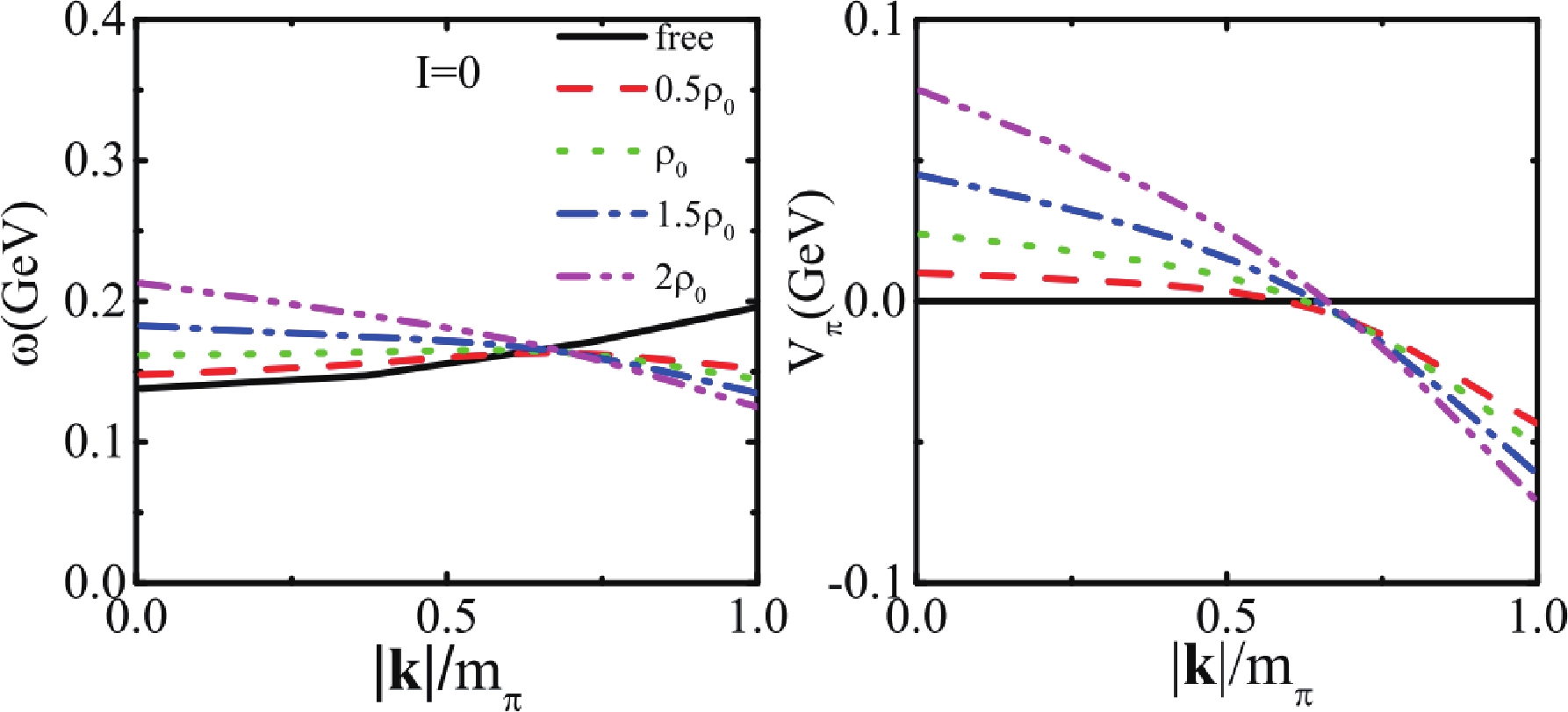
Figure 2. (color online) Left panel: pion dispersion relation at different densities (
$0.5\rho_0$ ,$\rho_0$ ,$1.5\rho_0$ , and$2\rho_0$ ) in symmetric nuclear matter. Right panel: pion optical potential at different densities in symmetric nuclear matter.$ V_{\pi^i} = \omega_{\pi^i}(\mathbf{k})-\sqrt{m^2_{\pi^i}+\mathbf{k}^2}. $

(26) Note from Fig. 2 that both the in-medium pion energy
$ \omega $ and pion optical potential$ V_{\pi} $ do not vanish at$ |\mathbf{k}| = 0 $ . This is because$ k^2 $ and$ (pk)^2-m^2_{N}k^2 $ appear in the relativistic forms of$ \Pi_{N} $ and$ \Pi_{\Delta} $ (see Appendix B). One can also find that the in-medium pion self-energy does not vanish at momentum$ |\mathbf{k}| = 0 $ , i.e., the color lines deviate from the black line at$ |\mathbf{k}| $ = 0, which is different from the results in the nonrelativistic form of pion self-energy reported in Ref. [37]. The in-medium pion energy$ \omega $ increases with density at lower momentum ($ |\mathbf{k}|/m_{\pi}<0.66 $ ) while decreases with density at higher momentum ($ |\mathbf{k}|/m_{\pi}>0.66 $ ). The pion energy in this study is similar to that reported in Refs. [32, 35], and the results are the same as those in Ref. [47] according to nonrelativistic calculations. In the right panel of Fig. 2, we present the pion optical potential for symmetric nuclear matter. The calculation results show that the pions with$ |\mathbf{k}|/m_{\pi}<0.66 $ experience a repulsive force, while the pions with$ |\mathbf{k}|/m_{\pi}>0.66 $ experience an attractive force. Consequently, one can expect that the pion energy obtained in the heavy ion collisions may show their maximum values at a certain kinetic energy compared to the calculations without considering such pion potential. The energy slope of the pion energy spectra may be a probe to investigate the pion optical potential. For the convenient application of the in-medium pion energy in estimation of$ \Delta $ decay width and optical potential in transport models, we provide the parameterization form of$ \omega $ as a function of$ |\mathbf{k}| $ in Table D1-D5 in Appendix D, where$ |\mathbf{k}| $ is expanded to$ m_{\pi} $ .Density x $ a_0 $ 

$ a_1 $ 

$ a_2 $ 

$ a_3 $ 

$ a_4 $ 

$ a_5 $ 

$ a_6 $ 

$ 0.5\rho_0 $ 

$ x\leqslant 1.125 $ 

0.14762 0.00329 0.15947 −1.09393 3.2301 −3.73303 1.42962 $ x>1.125 $ 

−0.08538 −0.99954 3.29955 −3.44383 1.71089 −0.41244 0.03884 $ \rho_0 $ 

$ x\leqslant 1.125 $ 

0.16428 −0.10651 0.5233 −0.72545 0.28734 0 0 $ x>1.125 $ 

0.40054 −0.63405 0.50715 −0.15842 0.0181 0 0 $ 1.5\rho_0 $ 

$ x\leqslant 1.125 $ 

0.18147 0.04198 −0.53115 1.52268 −1.70649 0.62449 0 $ x>1.125 $ 

0.66757 −1.15148 0.83679 −0.25277 0.02837 0 0 $ 2\rho_0 $ 

$ x\leqslant 1.125 $ 

0.21177 −0.0107 −0.35514 0.96565 −1.09207 0.40349 0 $ x>1.125 $ 

0.83163 −1.50549 1.08558 −0.3289 0.03692 0 0 Table D1. The parameters for
$ \omega $ in symmetric nuclear matter.Density x $a_0$ 

$a_1$ 

$a_2$ 

$a_3$ 

$a_4$ 

$a_5$ 

$a_6$ 

$0.5\rho_0 $ 

$x\leqslant 1.125$ 

0.14982 −0.00805 0.29261 −1.79699 4.812 −5.31034 1.9898 $x>1.125$ 

−0.29222 0.68732 −0.38933 0.10963 −0.01166 0 0 $\rho_0 $ 

$x\leqslant 1.125$ 

0.16437 0.09541 −0.77778 2.16077 −2.37432 0.86589 0 $x>1.125$ 

1.24039 −2.78125 2.6344 −1.20503 0.27254 −0.02435 0 $1.5\rho_0 $ 

$x\leqslant 1.125$ 

0.16901 −0.03369 0.38116 −1.92408 4.44758 −4.51472 1.61273 $x>1.125$ 

0.67832 −1.52577 1.60052 −0.79736 0.19558 −0.01883 0 $2\rho_0 $ 

$x\leqslant 1.125$ 

0.22697 0.0085 −0.62447 1.60553 −1.77879 0.66572 0 $x>1.125$ 

1.3686 −3.15732 2.95638 −1.34067 0.30092 −0.02673 0 Table D5. The parameters for
$\omega_{\pi^{-}}$ at isospin asymmetry$I = 0.3$ .In Fig. 3, we present the pion dispersion relation in asymmetric nuclear matter for
$ I = 0.2 $ , where$ I = \dfrac{\rho_n-\rho_p}{\rho_n+\rho_p} $ is the isospin asymmetry. As shown in Fig. 3,$ \omega $ is split for different charged states of pions, and the difference between$ \omega(\pi^-) $ and$ \omega(\pi^+) $ is related to the difference between the densities of the neutron and proton,$ \rho_n-\rho_p $ , in asymmetric nuclear matter. Interestingly, one can say that$ \omega(\pi^-)>\omega(\pi^+) $ at$ |\mathbf{k}|<0.66 m_\pi $ , and it turns over at$ |\mathbf{k}|>0.66 m_\pi $ . This behavior agrees with the prediction from nonrelativisitc calculation in Ref. [37], where s-wave plus p-wave potential was adopted. Meanwhile, the magnitude of the splitting of in-medium energy$ \omega $ , i.e.,$ |\omega^{-}-\omega^+| $ , increases with increasing density in the energy region we discuss.
Figure 3. (color online) Pion dispersion relation at different densities (
$\rho_0$ ,$1.5\rho_0$ and$2\rho_0$ ) in asymmetric nuclear matter with$I = 0.2$ .Fig. 4 clearly depicts that
$ \delta V_{\pi} = V_{\pi^-}-V_{\pi^+} $ depends on the isospin asymmetry, i.e., the amplitude of the charged pion potential splitting increases with increasing isospin asymmetry. -
Energy conservation is an important issue to be carefully addressed in the calculations of
$ N\pi\to \Delta $ and$ \Delta\to N\pi $ in isospin asymmetric nuclear matter as well as for$ NN\to N\Delta $ [38], based on the formulas of the in-medium$ \Delta\to N\pi $ decay widths and$ N\pi\to\Delta $ cross sections, i.e., Eqs. (15) and (18). The$ \Delta $ pole mass$ m^*_{0,\Delta} $ and distribution function$ f^* $ are crucial variables and key parts besides$ \overline{|\mathcal{M}^*_{\pi N\to \Delta}|^2} $ , because$ m^*_{0,\Delta} $ can determine the height and position$ (\sqrt{s}) $ of the peak of$ f^* $ . Thus, we first analyze the values of$ m^*_{0,\Delta} $ under the condition of energy conservation, as in Eq. (14).The peak of
$ f^* $ should be around$ m^*_{0,\Delta} $ , which corresponds to a certain momentum$ |\mathbf{k}|_{0} $ , or energy$ s^{1/2}_0 = \sqrt{m^2_\pi+\mathbf{k}^2_{0}}+\sqrt{m^2_N+\mathbf{k}^2_{0}} $ , and it satisfies the following relationship:$ m^*_{0,\Delta}+\Sigma^{0}_{\Delta} = \sqrt{m^*_N+|\mathbf{k}|^{2}_{0}}+\Sigma^{0}_{N}+\omega(|\mathbf{k}|_{0}) . $

(27) As shown in Fig. 2,
$ \omega(\mathbf k) $ at normal density is reduced by 50 MeV at$ |\mathbf{k}|\sim m_{\pi} $ . Both$ m^*_{0,\Delta} $ and$ m^*_N $ decrease with the increase in density, and$ m^*_{0,\Delta}-m^*_N = m_{0,\Delta}-m_N $ with$ |\Sigma^{0}_{\Delta}-\Sigma^{0}_{N}| = 0 $ in symmetric nuclear matter. In isospin asymmetric nuclear matter with$ I = 0.2 $ ,$ m^*_{0,\Delta}-m^*_N $ and$ |\Sigma^{0}_{\Delta}-\Sigma^{0}_{N}| $ are approximately 40-50 MeV near$ 2\rho_0 $ . It indicates that the values of$ \omega $ are key quantities for determining the solution of$ |\mathbf k|_0 $ from Eq. (27). When the reductions of$ \omega $ is taken into account and the energy conservation relationship is considered, a larger$ |\mathbf{k}|_0 $ is expected. Consequently, the position of the peak of$ f^* $ moves to a higher energy with smaller effective mass. In the left panel of Fig. 5, we present$ s^{1/2}_0 $ as a function of$ m^*_{0,\Delta} $ . It clearly illustrates that the behavior of$ s^{1/2}_0 $ increases with the decrease in effective mass, or equivalently, with the increase in density.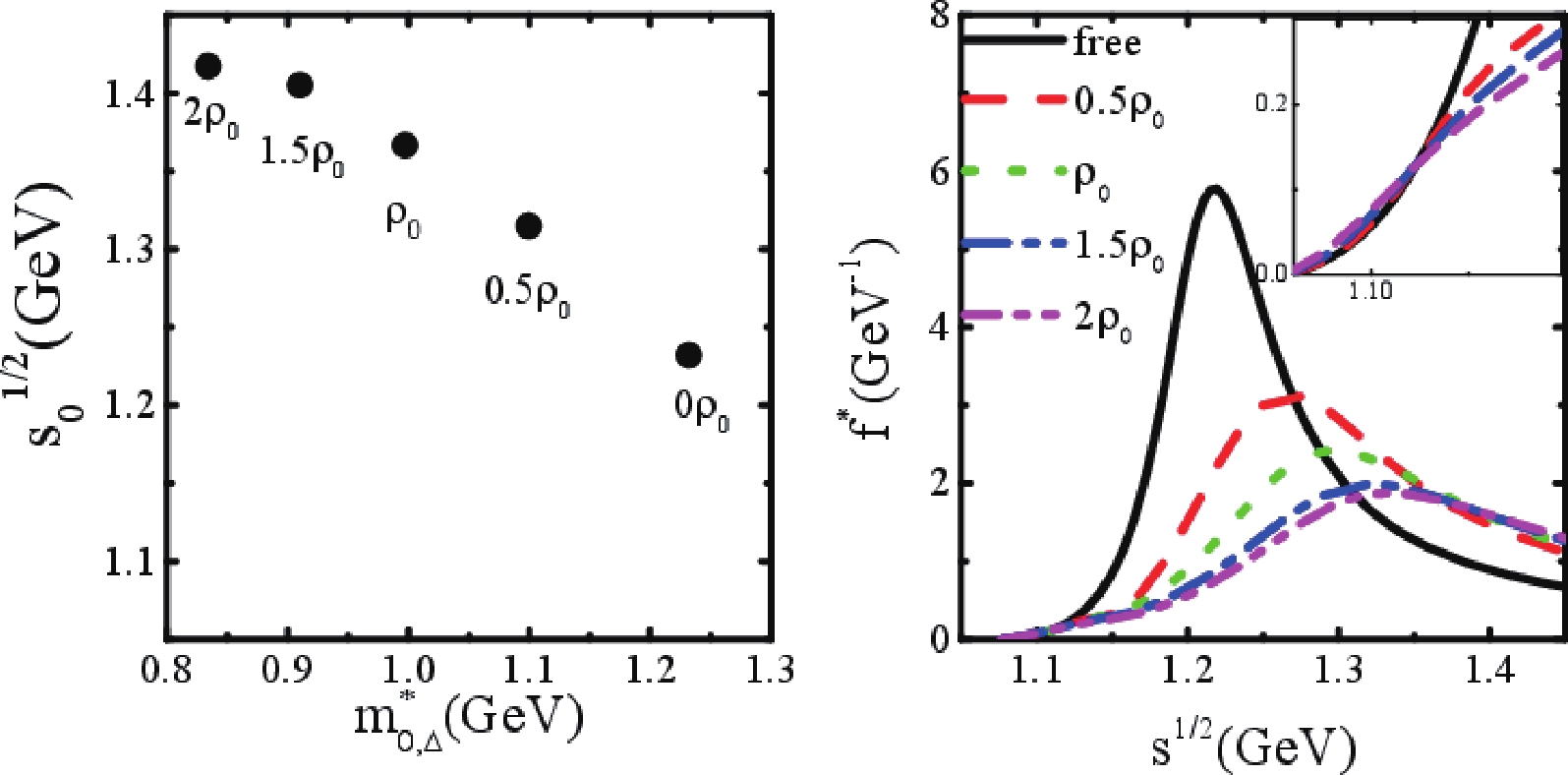
Figure 5. (color online) Left panel:
$s^{1/2}_0$ as a function of$ m^*_{0,\Delta}$ (details about$s_0^{1/2}$ are in the text). Right panel:$f^*$ as a function of$s^{1/2}$ .To obtain a general impression on the aforementioned effects,
$ f^* $ as a function of$ s^{1/2} $ at different densities is presented in symmetric nuclear matter in the right panel of Fig. 5. For a low energy near$ s^{1/2}<1.15 $ GeV, which corresponds to the threshold energy of pion production, our results show that$ f^* $ is enhanced with respect to that in free space at$ s^{1/2}<1.11 $ GeV (as shown in the inserted panel in Fig. 5) and decreases with respect to$ f $ in free space at$ s^{1/2}>1.11 $ GeV. In addition, the peak of$ f^* $ shifts to a higher momentum, which results in the reduction of in-medium$ \pi N \to \Delta $ cross sections at high energies. Note that, at$ s^{1/2}> $ 1.3 GeV, there is an enhancement of$ f^* $ with respect to f in free space. The conclusions about this energy region could change by considering the medium effects on the decay width of$ \Delta $ and on$ \Delta $ propagation.Based on the in-medium pion energy and effective masses of N and
$ \Delta $ , the in-medium$ \Delta \to \pi N $ decay width and cross section of$ \pi^+ p\to \Delta^{++} $ at different densities in symmetric nuclear matter were calculated according to Eqs. (15) and (18); they are presented in Figs. 6(a) and (c). Panels (b) and (d) present the medium correction factors$ R_{\Gamma} = \Gamma^*/\Gamma^{\mathrm{free}} $ and$ R_{\sigma} = \sigma^*/\sigma^{\mathrm{free}} $ , respectively. As shown in panel (b), the in-medium$ \Delta \to \pi N $ decay widths are reduced with respect to that in free space at$ s^{1/2}<1.15 $ GeV. The in-medium effect at the energy region ($ s^{1/2}<1.15 $ GeV) we studied is more evident than that at higher energies ($ s^{1/2}>1.15 $ GeV). Generally speaking, the medium effect on the decay width is weak, because the impacts of$ m^*_{\Delta}(E^*_{N}+\omega ) $ and$ \overline{|\mathcal{M}^*_{\pi N\to \Delta}|^2} $ in Eq. (21) conceal each other at higher energies.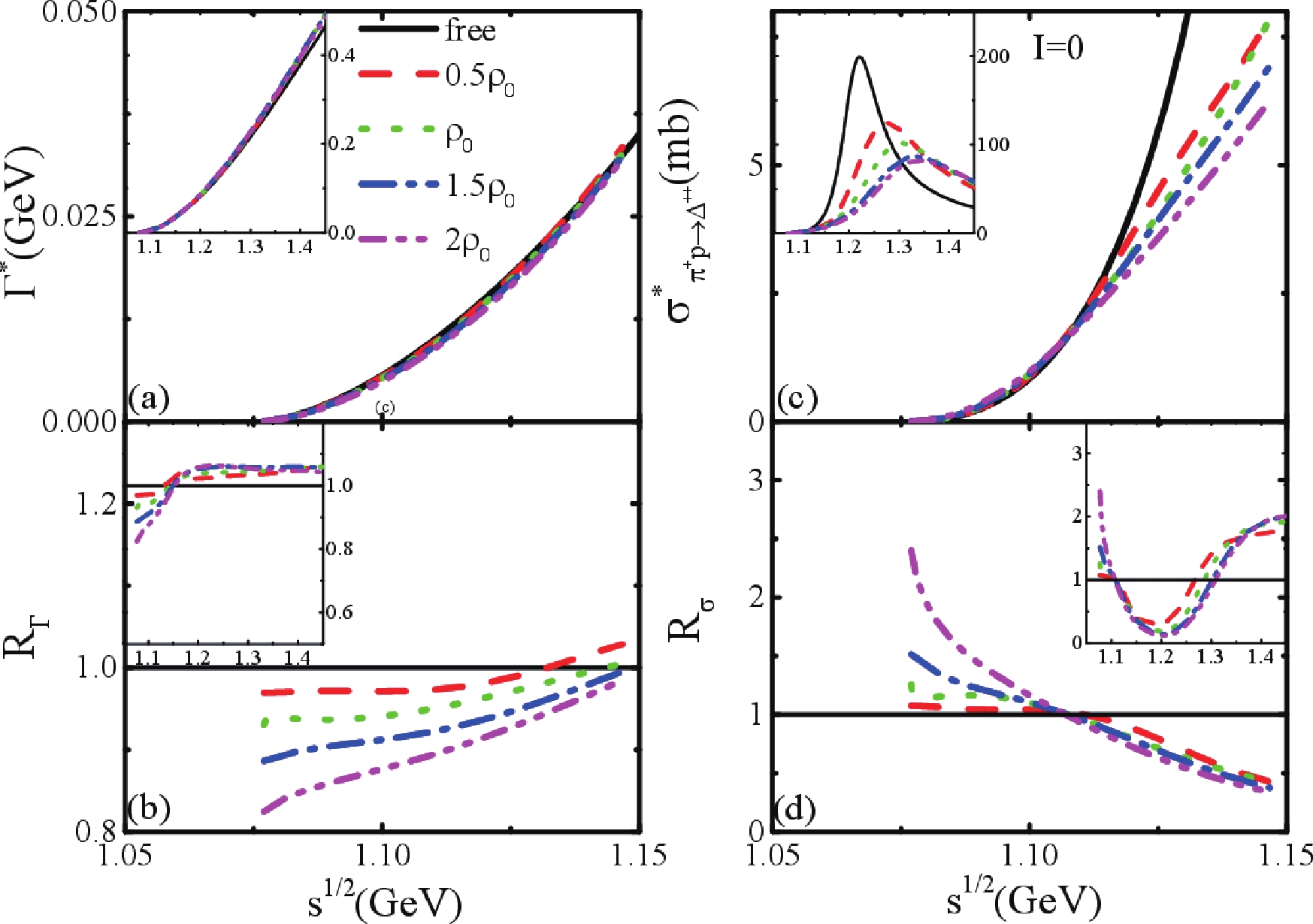
Figure 6. (color online) Left panels: (a) in-medium decay width of
$\Delta \to \pi N$ at different densities in symmetric nuclear matter; (b) medium correction factor$\Gamma^*/\Gamma^{\mathrm{free}}$ . Right panels: (c) in-medium cross sections of$\pi^+ p\to \Delta^{++}$ at different densities in symmetric nuclear matter; (d) medium correction factor$\sigma^*/\sigma^{\mathrm{free}}$ .Concerning the in-medium pion absorption cross sections
$ \pi N\to \Delta $ , as shown in panel (c) of Fig. 6, they are enhanced at$ s^{1/2}<1.11 $ GeV ($ E_{\mathrm{beam}}\sim $ 0.36 A GeV) and then suppressed at approximately$ s^{1/2}>1.11 $ GeV, as presented in panel (d). The enhancement of the in-medium pion absorption cross sections$ \pi N\to \Delta $ near$ s^{1/2}<1.11 $ GeV could lead to the reduction of pions in the HIC near the threshold energy, while the enhancement of pion production may occur at$ s^{1/2}>1.11 $ GeV. At$ s^{1/2}>1.3 $ GeV, the cross sections are enhanced again, but our results were obtained by neglecting the width of$ \Delta $ in the$ \Delta $ propagator in the calculation of the pion self-energy. This should be carefully investigated at high energy. Our predictions on the in-medium effects for the$ \pi N\to \Delta $ cross sections are similar to the conclusions in Ref. [37], in which enhancement of in-medium$ N\pi\to\Delta $ cross sections near the threshold energies was reported. However, the amplitude of the enhancement and the energy region of the results in this study are both smaller than those in Ref. [37] because the effects of effective masses on$ f^* $ were considered in this study but not in Ref. [37]. This suggests that a further experimental study of the pion production in heavy ion collisions will be useful for elucidating the in-medium$ N\pi\to \Delta $ .Given that the nuclear medium correction on the decay width of
$ \Delta \to \pi N $ is weak in the approximation adopted in this study, we next focus on the in-medium cross sections of$ N\pi\to \Delta $ and their correction factor in isospin asymmetric nuclear matter. In Fig. 7, we present the in-medium cross sections and$ R_\sigma = \sigma^*/\sigma^{\mathrm{free}} $ for$ \pi^{+} p\to \Delta^{++} $ ,$ \pi^{-} n\to \Delta^{-} $ ,$ \pi^{0} p\to \Delta^{+} $ ,$ \pi^{0} n\to \Delta^{0} $ ,$ \pi^{+} n\to \Delta^{+} $ , and$ \pi^{-} p\to \Delta^{0} $ channels, respectively, at$ 2\rho_0 $ in asymmetric nuclear matter with$ I = 0.2 $ . If we do not consider the splitting of effective masses, the ratios between the cross sections of different channels are$ \sigma_{\pi^{+} p\to \Delta^{++}} $ ($ \sigma_{\pi^{-} n\to \Delta^{-}} $ ):$ \sigma_{\pi^{0} p\to \Delta^{+}} $ ($ \sigma_{\pi^{0} n\to \Delta^{0}} $ ) :$ \sigma_{\pi^{+} n\to \Delta^{+}} $ ($ \sigma_{\pi^{-} p\to \Delta^{0}} $ )$ = 3:2:1 $ , and the medium correction factors, i.e.,$ R = \sigma^*/\sigma^{\mathrm{free}} $ , are the same for different channels. With the nucleon and$ \Delta $ effective masses splitting as well as pion energies in asymmetric nuclear matter to be considered, the in-medium correction factors$ R $ on the cross sections of$ \pi N\to \Delta $ and$ \Delta \to \pi N $ are different for different channels as$ \omega_{\pi^+}>\omega_{\pi^-} $ at higher energies,$ m^{*}_{\Delta^{++}}>m^{*}_{\Delta^{+}}>m^{*}_{\Delta^{0}}>m^{*}_{\Delta^{-}} $ , and$ m^{*}_{p}>m^{*}_{n} $ . The cross sections of different channels for$ N\pi\to\Delta $ cross sections in asymmetric nuclear matter are shown in the left panels of Fig. 7. It can be more clearly observed in the right panels of Fig. 7, i.e.,$ R_{\pi^{-} n\to \Delta^{-}}>R_{\pi^{+} p\to \Delta^{++}} $ at$ s^{1/2}<1.11 $ GeV while$ R_{\pi^{-} n\to \Delta^{-}}<R_{\pi^{+} p\to \Delta^{++}} $ at$ s^{1/2}>1.11 $ GeV,$ R_{\pi^{0} n\to \Delta^{0}}>R_{\pi^{0} p\to \Delta^{+}} $ , and$ R_{\pi^{+} n\to \Delta^{+}}>R_{\pi^{-} p\to \Delta^{0}} $ at$ s^{1/2}<1.15 $ GeV.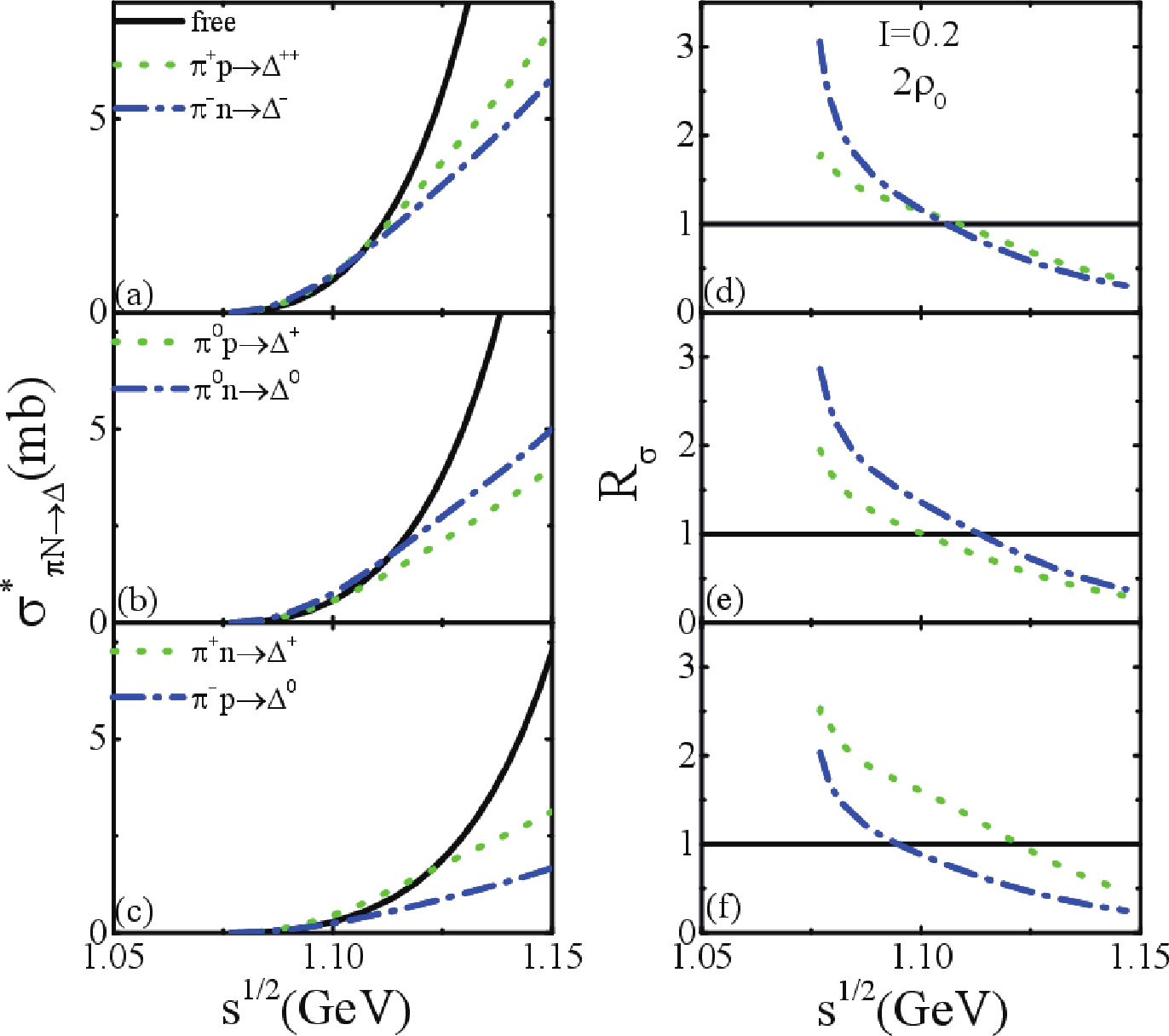
Figure 7. (color online) Left panels: in-medium cross sections of
$\pi N\to\Delta$ ; right panels: in-medium correction factor$R_\sigma$ at$2\rho_0$ in isospin asymmetric nuclear matter with I = 0.2;$\pi^{+} p\to \Delta^{++}$ and$\pi^{-} n\to \Delta^{-}$ (upper panels),$\pi^{0} p\to \Delta^{+}$ and$\pi^{0} n\to \Delta^{0}$ (middle panels), and$\pi^{+} n\to \Delta^{+}$ and$\pi^{-} p\to \Delta^{0}$ (bottom panels).The results are similar to those of the study from Li et al. in Ref. [36], but the magnitude of the in-medium cross section and the splitting among the different channels are more evident than in Ref. [36], where the effect of
$ \omega $ in asymmetric nuclear matter was ignored. Based on above discussions on the in-medium cross section of$ N\pi\to\Delta $ , one can expect that if$ \sigma^*_{N\pi\to\Delta} $ is included in transport model simulations, the production of pion may be modified, with the beam energy decreasing from 0.4 A GeV to 0.3 A GeV. -
In summary, we investigated the pion dispersion relation, in-medium
$ N\pi\to \Delta $ cross section, and$ \Delta \to N \pi $ decay width near the threshold energy of pion production in isospin asymmetric nuclear matter by using the same relativistic interaction within the framework of the one-boson-exchange model. With the consideration of threshold effects (or energy conservation in isospin asymmetric nuclear medium) and in-medium pion energy effects,$ f^* $ is enhanced at$ s^{1/2}<1.11 $ GeV and reduced at$ s^{1/2}>1.11 $ GeV. This results in an enhancement of in-medium$ N\pi\to\Delta $ cross sections near$ s^{1/2}<1.11 $ GeV and then suppression at$ s^{1/2}>1.11 $ GeV, similar to the conclusions in Ref. [37]. Concerning the in-medium decay width of$ \Delta\to N\pi $ , it is reduced at$ s^{1/2}<1.15 $ GeV.By including the pion energy
$ \omega $ and effective mass splitting in asymmetric nuclear matter for the calculation of$ N\pi\to \Delta $ , our results show that the in-medium correction factors on the cross sections of$ \pi N\to \Delta $ are different for different channels, e.g.,$ R_{\pi^{+}p\to\Delta^{++}}<R_{\pi^{-}n\to\Delta^{-}} $ . As a result of the medium correction and isospin splitting of$ \sigma^*_{N\pi\to\Delta} $ in asymmetric nuclear matter, a smaller pion multiplicity and$ \pi^-/\pi^+ $ ratios could be predicted with respect to the calculation utility of$ \sigma^{\mathrm{free}}_{N\pi\to\Delta} $ near the threshold energy if the other parameters in the transport model remain unchanged.However, it should be kept in mind that the simulation of heavy ion collision is much more complicated. Our results suggest that a systematic study of the pion production mechanism near the threshold energy of pion production by using multi-observables, i.e., pion's multiplicity, energy spectra, and flow, is needed. With the increase in beam energy, there are more
$ \pi N\to \Delta $ and$ N\Delta\to NN $ processes taking place. Thus, the width of$ \Delta $ in the$ \Delta $ propagator should be considered in the calculations of pion self energy, in-medium cross section of$ N\pi\to\Delta $ , and decay width of$ \Delta $ . Beam energy scanning, for example, from subthreshold energy to 1.5 A GeV, and system size dependence, from smaller systems to heavier systems, could help us elucidate the medium effects on the cross sections of$ N\pi\to \Delta $ . -
Here, we remove the contributions from virtual particle-particle excitations as in Ref. [32], which is consistent with the mean field approximation. According to the on-shell pion dispersion relation in Eq. (3),
$ \Pi(k) $ means the real part of pion self-energy, ($ \mathrm{Re}\Pi(k) $ ). For convenience, "Re" ahead of$ \Pi(k) $ is ignored in the following discussion.The pion self-energies of
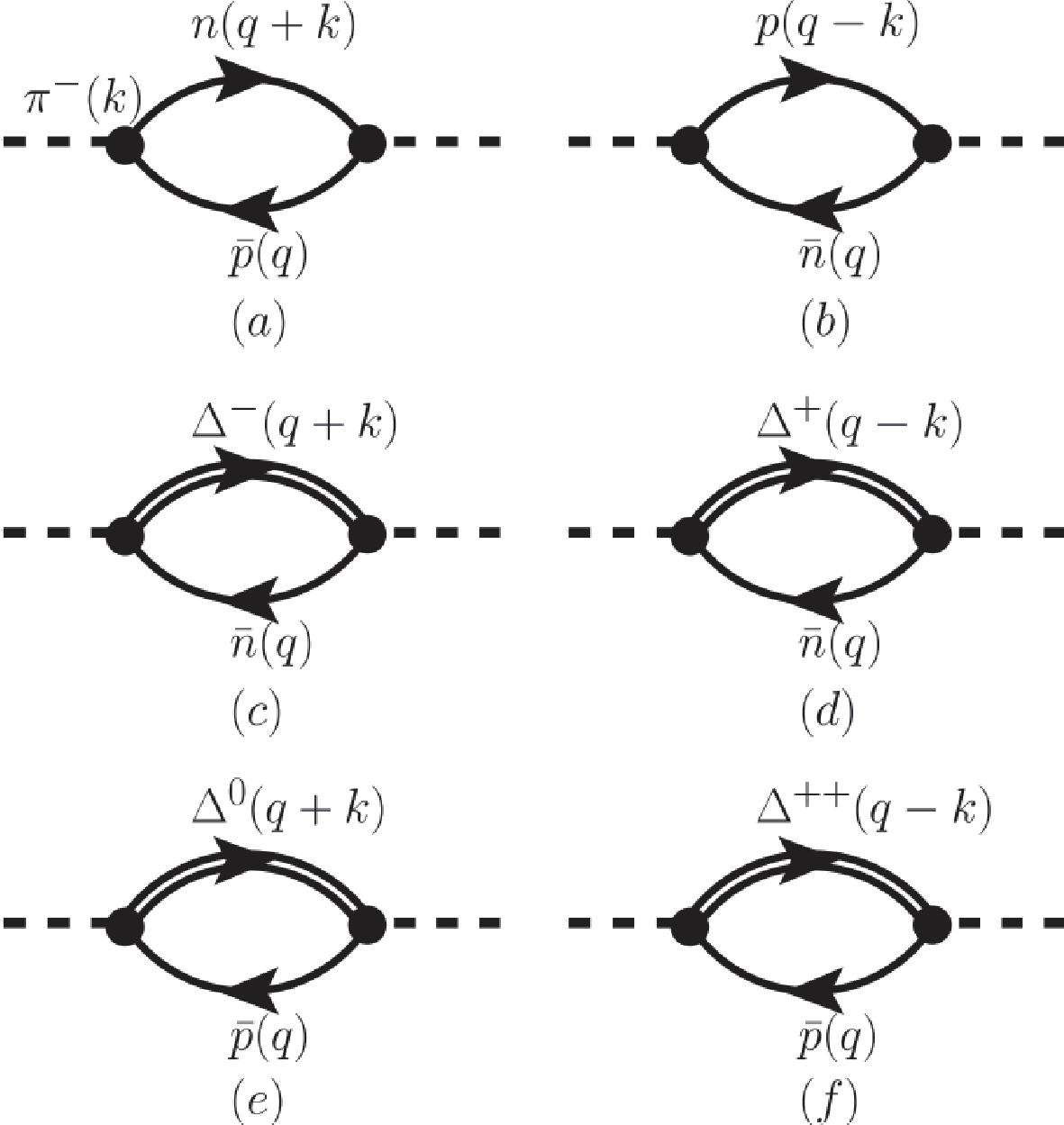
$ \pi^+ $ are given by the graphs shown in Fig. B1. The particle-hole part of the$ \pi^{+} $ self-energy can be written as follows:
Figure B1. Self-energy of
$\pi^{+}(\omega, \mathbf{k})$ ; (a) and (b) constitute the particle-hole part, whereas (c), (d), (e), and (f) constitute the$\Delta$ -hole part.$\tag{B1} \Pi_{N}(\pi^+) = \Pi_{a}(\pi^+)+\Pi_{b}(\pi^+) $

where
$ \Pi_{a}(\pi^{+}) $ is$ \begin{aligned}[b] \Pi_{a}(\pi^+) =& -{\rm i}\left(\frac{-\sqrt{2}g_{\pi NN}}{m_{\pi}}\right)^2 \int\frac{{\rm d}^4 q}{(2\pi)^4} \mathrm{Tr} \Bigg [ k/\gamma_{5} \frac{q/+m_{n}}{2E_{n}(q)} k/\gamma_{5}\\ & \times\frac{q/+k/+m_{p}}{(q_0+k_0)^2-E^{2}_{p}(q+k)} i2\pi\theta(q_{F, n}-|\mathbf{q}|)\delta(q^0-E_{n}(q))\Bigg] \end{aligned} $

$\tag{B2} \begin{aligned}[b] = &\left(\frac{g_{\pi NN}}{m_{\pi}}\right)^2 \int\frac{{\rm d}^4 q}{(2\pi)^3} \theta(q_{F, n}-|\mathbf{q}|)\delta(q^0-E_{n}(q))\\& \times \frac{-4m_{n}m_{p}k^2-4q^2k^2+8(qk)^2+4k^2(q k)}{E_{n}(q)((q_0+k_0)^2-E^{2}_{p}(q+k))}\\ =& \left(\frac{g_{\pi NN}}{m_{\pi}}\right)^2 \int\frac{{\rm d}^3 \mathbf{q}}{(2\pi)^3} \frac{\theta(q_{F, n}-|\mathbf{q}|)}{E_{n}(q)[(E_{n}(q)+\omega)^2-E^{2}_{p}(q+k)]}\\& \times \Big[-4m_{n}m_{p}k^2-4m^{2}_{n}k^2\\& +4(E_{n}(q)\omega-\mathbf{q}\cdot \mathbf{k})(2E_{n}(q)\omega-2\mathbf{q}\cdot \mathbf{k}+k^2)\Big ].\end{aligned} $

Here,
$ k_0 = \omega $ ,$ E_{n}(q) = \sqrt{m^2_n+\mathbf{q}^2} $ , and$ k^2 = k^2_0-\mathbf{k}^2 = \omega^2-\mathbf{k}^2 $ . In addition,$ n(|\mathbf{q}|) = \theta(q_F-|\mathbf{q}|) $ denotes the occupation number in zero temperature nuclear matter in the Fermi momentum$ q_F $ . The isospin factor$ I_{N\Delta} = -\sqrt{2} $ is listed in Table A1. Finally,$ \Pi_{b}(\pi^{+}) $ can also be calculated in the same way:$\tag{B3} \begin{aligned}[b] \Pi_{b}(\pi^+) =& -{\rm i}\left(\frac{\sqrt{2}g_{\pi NN}}{m_{\pi}}\right)^2 \int\frac{{\rm d}^4 q}{(2\pi)^4} \mathrm{Tr} \Bigg [ k/\gamma_{5} \frac{q/+m_{p}}{2E_{p}(q)} \\& \times k/\gamma_{5}\frac{q/-k/+m_{n}}{(q_0-k_0)^2-E^{2}_{n}(q-k)}\\& \times i2\pi\theta(q_{F, p}-|\mathbf{q}|)\delta(q^0-E_{p}(q))\Bigg] \\ =& \left(\frac{g_{\pi NN}}{m_{\pi}}\right)^2 \int\frac{{\rm d}^3 \mathbf{q}}{(2\pi)^3} \frac{\theta(q_{F, p}-|\mathbf{q}|)}{E_{p}(q)[(E_{p}(q)-\omega)^2-E^{2}_{n}(q-k)]} \\&\times\Big[-4m_{n}m_{p}k^2-4m^{2}_{p}k^2\\& +4(-E_{p}(q)\omega+\mathbf{q}\cdot \mathbf{k})(-2E_{p}(q)\omega+2\mathbf{q}\cdot \mathbf{k}+k^2) \Big]. \end{aligned} $

The
$ \Delta $ -hole part of the$ \pi^+ $ self-energy is expressed as$\tag{B4}\Pi_{\Delta}(\pi^+) = \Pi_{c}(\pi^+)+\Pi_{d}(\pi^+)+\Pi_{e}(\pi^+)+\Pi_{f}(\pi^+), $

where
$ \Pi_{c}(\pi^{+}) $ $\tag{B5} \begin{aligned}[b]\Pi_{c}(\pi^+) =& -{\rm i}\left(\frac{g_{\pi N\Delta}}{m_{\pi}}\right)^2\int\frac{{\rm d}^4 q}{(2\pi)^4} \mathrm{Tr}\Bigg [\frac{k_{\mu}k_{\nu}D^{\mu\nu}(q+k)(q/+k/+m_{0,\Delta})}{(q_0+k_0)^2-E^{2}_{\Delta}(q+k)}\\& \times \frac{q/+m_{n}}{2E_{p}(q)}\theta(q_{F, p}-|\mathbf{q}|)(i2\pi\delta(q_0-E_{p}(q)))\Bigg]\\ =& \left(\frac{g_{\pi N\Delta}}{m_{\pi}}\right)^2\int\frac{{\rm d}^3 \mathbf{q}}{(2\pi)^3} \frac{\theta(q_{F, p}-|\mathbf{q}|)}{2E_{p}(q)((E_{p}(q)+k_0)^2-E^{2}_{\Delta}(q+k))}\\& \times 4\left[\frac{2m_{p}(qk)^2}{3m_{0,\Delta^{++}}}+\frac{4m_{p}(qk)k^2}{3m_{0,\Delta^{++}}}+\frac{2m_{p}k^4}{3m_{0,\Delta^{++}}}-\frac{2m_{p}m_{0,\Delta^{++}}k^2}{3}\right.\\ & +\frac{2q^2 k^4}{3m^{2}_{0,\Delta^{++}}}+\frac{2(q k)^3}{3m^{2}_{0,\Delta^{++}}} +\frac{2q^2 (q k)^2}{3m^{2}_{0,\Delta^{++}}}+\frac{4k^2 (q k)^2}{3m^{2}_{0,\Delta^{++}}}\\& \left.+\frac{2k^4 (q k)}{3m^{2}_{0,\Delta^{++}}}+\frac{4q^2k^2 (q k)}{3m^{2}_{0,\Delta^{++}}}-\frac{2q^2k^2 }{3}-\frac{2k^2(pk) }{3}\right]\\ =& \frac{2}{3}\left(\frac{g_{\pi N\Delta}}{m_{\pi}}\right)^2\int\frac{{\rm d}^3 \mathbf{q}}{(2\pi)^3} \frac{\theta(q_{F, p}-|\mathbf{q}|)}{E_{p}(q)}\\ &\times\large \left[\frac{(qk)^2-m^2_{p}k^2}{m^{2}_{0,\Delta^{++}}}+k^2\frac{2m_{p}}{m_{0,\Delta^{++}}}\left(1+\frac{m_{p}}{m_{0,\Delta^{++}}}\right)\right.\\& \left.+\frac{(qk)^2-m^{2}_{p}k^2}{m^{2}_{0,\Delta^{++}}}\frac{(m_{p}+m_{0,\Delta^{++}})^2-k^2}{2qk+k^2-(m^{2}_{0,\Delta^{++}}-m^{2}_{p})}\large\right],\end{aligned} $

where
$ qk = E_{p}(q)\omega-\mathbf{q}\cdot \mathbf{k} $ .$ \Pi_{d}(\pi^{+}) $ ,$ \Pi_{e}(\pi^{+}) $ , and$ \Pi_{f}(\pi^{+}) $ can be obtained in the same way:$\tag{B6} \begin{aligned}[b] \Pi_{d}(\pi^+) =& \frac{2}{9}\left(\frac{g_{\pi N\Delta}}{m_{\pi}}\right)^2\int\frac{{\rm d}^3 \mathbf{q}}{(2\pi)^3} \frac{\theta(q_{F, p}-|\mathbf{q}|)}{E_{p}(q)}\\& \times\large \left[\frac{(qk)^2-m^2_{p}k^2}{m^{2}_{0,\Delta^{0}}}+k^2\frac{2m_{p}}{m_{0,\Delta^{0}}}\left(1+\frac{m_{p}}{m_{0,\Delta^{0}}}\right)\right.\\&\left.+\frac{(qk)^2-m^{2}_{p}k^2}{m^{2}_{0,\Delta^{0}}}\frac{(m_{p}+m_{0,\Delta^{0}})^2-k^2}{-2qk+k^2-(m^{2}_{0,\Delta^{0}}-m^{2}_{p})}\large\right],\end{aligned} $

$\tag{B7} \begin{aligned}[b] \Pi_{e}(\pi^+) = &\frac{2}{9}\left(\frac{g_{\pi N\Delta}}{m_{\pi}}\right)^2\int\frac{{\rm d}^3 \mathbf{q}}{(2\pi)^3} \frac{\theta(q_{F, n}-|\mathbf{q}|)}{E_{n}(q)}\\& \times\large \left[\frac{(qk)^2-m^2_{n}k^2}{m^{2}_{0,\Delta^+}}+k^2\frac{2m_{n}}{m_{0,\Delta^+}}\left(1+\frac{m_{n}}{m_{0,\Delta^+}}\right)\right.\\ &\left.+\frac{(qk)^2-m^{2}_{n}k^2}{m^{2}_{0,\Delta^+}}\frac{(m_{n}+m_{0,\Delta^+})^2-k^2}{2qk+k^2-(m^{2}_{0,\Delta^+}-m^{2}_{n})}\large\right],\end{aligned} $

$\tag{B8} \begin{aligned}[b] \Pi_{f}(\pi^+) =& \frac{2}{3}\left(\frac{g_{\pi N\Delta}}{m_{\pi}}\right)^2\int\frac{{\rm d}^3 \mathbf{q}}{(2\pi)^3} \frac{\theta(q_{F, n}-|\mathbf{q}|)}{E_{n}(q)}\\& \times\large \left[\frac{(qk)^2-m^2_{n}k^2}{m^{2}_{0,\Delta^-}}+k^2\frac{2m_{n}}{m_{0,\Delta^-}}\left(1+\frac{m_{n}}{m_{0,\Delta^-}}\right)\right.\\& \left.+\frac{(qk)^2-m^{2}_{n}k^2}{m^{2}_{0,\Delta^-}}\frac{(m_{n}+m_{0,\Delta^-})^2-k^2}{-2qk+k^2-(m^{2}_{0,\Delta^-}-m^{2}_{n})}\large\right].\end{aligned} $

The particle-hole and
$ \Delta $ -hole of$ \pi^- $ self-energy are shown in Fig. B2. The particle-hole part of the$ \pi^{-} $ self-energy can be written as follows:$\tag{B9} \Pi_{N}(\pi^-) = \Pi_{a}(\pi^-)+\Pi_{b}(\pi^-). $

Here,
$ \Pi_{a}(\pi^{-}) $ and$ \Pi_{b}(\pi^{-}) $ are expressed as follows:$\tag{B10} \begin{aligned}[b] &\Pi_{a}(\pi^-)\\ =& \left(\frac{g_{\pi NN}}{m_{\pi}}\right)^2 \int\frac{{\rm d}^3 \mathbf{q}}{(2\pi)^3} \frac{\theta(q_{F, p}-|\mathbf{q}|)}{E_{p}(q)[(E_{p}(q)+\omega)^2-E^{2}_{n}(q+k)]}\\& \times [-4m_{n}m_{p}k^2-4m^{2}_{p}k^2\\& +4(E_{p}(q)\omega-\mathbf{q}\cdot \mathbf{k})(2E_{p}(q)\omega-2\mathbf{q}\cdot \mathbf{k}+k^2) ]. \end{aligned} $

$\tag{B11} \begin{aligned}[b] &\Pi_{b}(\pi^-) \\ =& \left(\frac{g_{\pi NN}}{m_{\pi}}\right)^2 \int\frac{{\rm d}^3 \mathbf{q}}{(2\pi)^3} \frac{\theta(q_{F, n}-|\mathbf{q}|)}{E_{n}(q)[(E_{n}(q)-\omega)^2-E^{2}_{p}(q-k)]}\\& \times [-4m_{n}m_{p}k^2-4m^{2}_{n}k^2\\& +4(-E_{n}(q)\omega+\mathbf{q}\cdot \mathbf{k})(-2E_{n}(q)\omega+2\mathbf{q}\cdot \mathbf{k}+k^2) ]. \end{aligned} $

The
$ \Delta $ -hole part of the$ \pi^- $ self-energy is$ \tag{B12} \Pi_{\Delta}(\pi^-) = \Pi_{c}(\pi^-)+\Pi_{d}(\pi^-)+\Pi_{e}(\pi^-)+\Pi_{f}(\pi^-) . $

Here,
$ \Pi_{c}(\pi^{-}) $ ,$ \Pi_{d}(\pi^{-}) $ ,$ \Pi_{e}(\pi^{-}) $ , and$ \Pi_{f}(\pi^{-}) $ can be calculated as follows:$\tag{B13} \begin{aligned}[b] \Pi_{c}(\pi^-) =& \frac{2}{3}\left(\frac{g_{\pi N\Delta}}{m_{\pi}}\right)^2\int\frac{{\rm d}^3 \mathbf{q}}{(2\pi)^3} \frac{\theta(q_{F, n}-|\mathbf{q}|)}{E_{n}(q)}\\& \times\large \left[\frac{(qk)^2-m^2_{n}k^2}{m^{2}_{0,\Delta^-}}+k^2\frac{2m_{n}}{m_{0,\Delta^-}}\left(1+\frac{m_{n}}{m_{0,\Delta^-}}\right)\right.\\& \left.+\frac{(qk)^2-m^{2}_{n}k^2}{m^{2}_{0,\Delta^-}}\frac{(m_{n}+m_{0,\Delta^-})^2-k^2}{2qk+k^2-(m^{2}_{0,\Delta^-}-m^{2}_{n})}\large\right], \end{aligned} $

$\tag{B14} \begin{aligned}[b] \Pi_{d}(\pi^-) =& \frac{2}{9}\left(\frac{g_{\pi N\Delta}}{m_{\pi}}\right)^2\int\frac{{\rm d}^3 \mathbf{q}}{(2\pi)^3} \frac{\theta(q_{F, n}-|\mathbf{q}|)}{E_{n}(q)}\\& \times\large \left[\frac{(qk)^2-m^2_{n}k^2}{m^{2}_{0,\Delta^+}}+k^2\frac{2m_{n}}{m_{0,\Delta^+}}\left(1+\frac{m_{n}}{m_{0,\Delta^+}}\right)\right.\\& \left.+\frac{(qk)^2-m^{2}_{n}k^2}{m^{2}_{0,\Delta^+}}\frac{(m_{n}+m_{0,\Delta^+})^2-k^2}{-2qk+k^2-(m^{2}_{0,\Delta^+}-m^{2}_{n})}\large\right],\end{aligned} $

$\tag{B15} \begin{aligned}[b] \Pi_{e}(\pi^-) =& \frac{2}{9}\left(\frac{g_{\pi N\Delta}}{m_{\pi}}\right)^2\int\frac{{\rm d}^3 \mathbf{q}}{(2\pi)^3} \frac{\theta(q_{F, p}-|\mathbf{q}|)}{E_{p}(q)}\\& \times\large \left[\frac{(qk)^2-m^2_{p}k^2}{m^{2}_{0,\Delta^{0}}}+k^2\frac{2m_{p}}{m_{0,\Delta^{0}}}\left(1+\frac{m_{p}}{m_{0,\Delta^{0}}}\right)\right.\\& \left.+\frac{(qk)^2-m^{2}_{p}k^2}{m^{2}_{0,\Delta^{0}}}\frac{(m_{p}+m_{0,\Delta^{0}})^2-k^2}{2qk+k^2-(m^{2}_{0,\Delta^{0}}-m^{2}_{p})}\large\right],\end{aligned} $

$\tag{B16} \begin{aligned}[b] \Pi_{f}(\pi^-) =& \frac{2}{3}\left(\frac{g_{\pi N\Delta}}{m_{\pi}}\right)^2\int\frac{{\rm d}^3 \mathbf{q}}{(2\pi)^3} \frac{\theta(q_{F, p}-|\mathbf{q}|)}{E_{p}(q)}\\& \times\large \left[\frac{(qk)^2-m^2_{p}k^2}{m^{2}_{0,\Delta^{++}}}+k^2\frac{2m_{p}}{m_{0,\Delta^+}}\left(1+\frac{m_{p}}{m_{0,\Delta^{++}}}\right)\right.\\& \left.+\frac{(qk)^2-m^{2}_{p}k^2}{m^{2}_{0,\Delta^{++}}}\frac{(m_{p}+m_{0,\Delta^{++}})^2-k^2}{-2qk+k^2-(m^{2}_{0,\Delta^{++}}-m^{2}_{p})}\large\right].\end{aligned} $

The
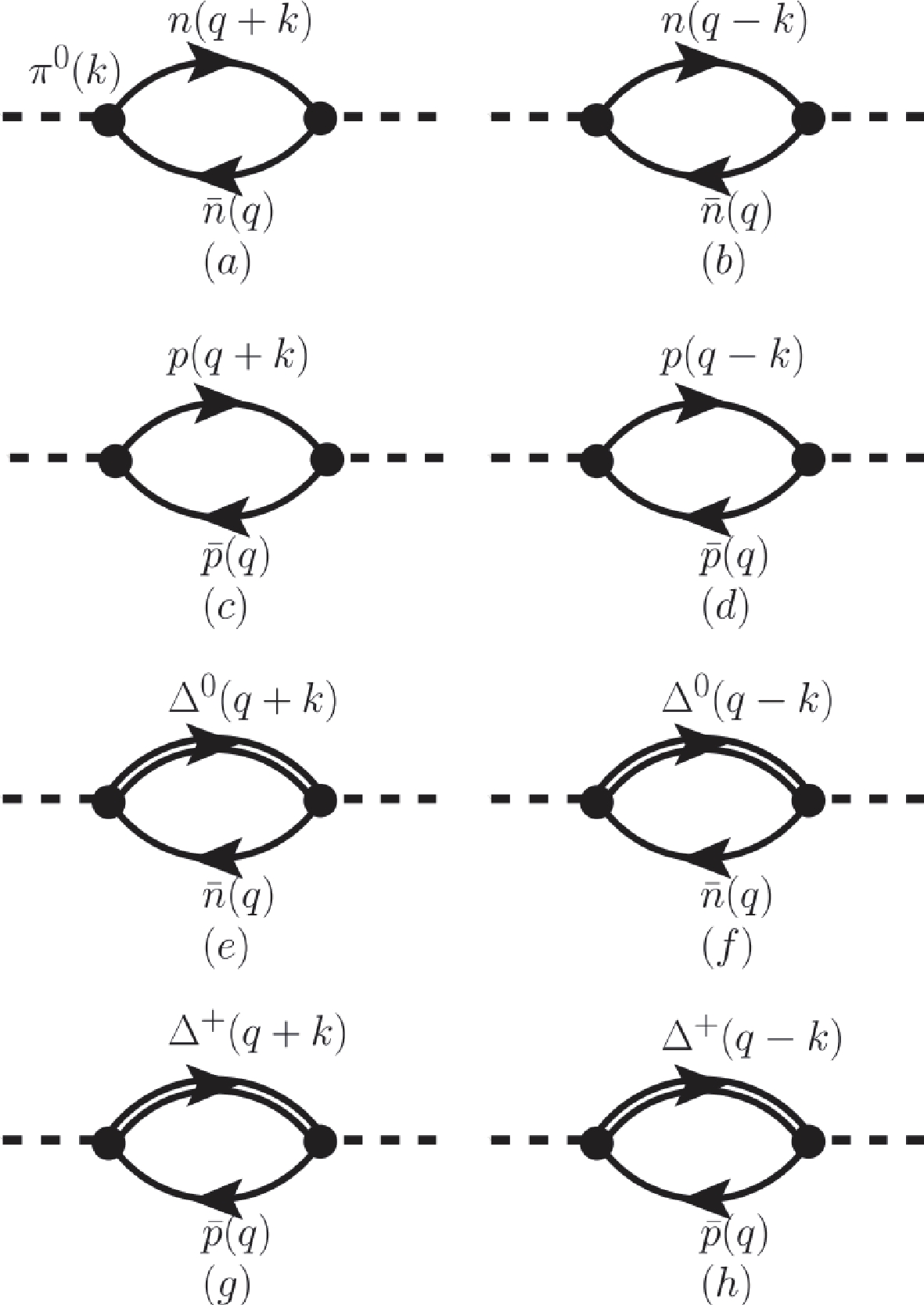
$ \pi^0 $ self-energies are contains the diagrams depicted in Fig. B3. The particle-hole part of the$ \pi^{0} $ self-energy can be written as follows:$ \tag{B17} \Pi_{N}(\pi^{0}) = \Pi_{a}(\pi^{0})+\Pi_{b}(\pi^{0})+\Pi_{c}(\pi^{0})+\Pi_{d}(\pi^{0}). $

Here,
$ \Pi_{a}(\pi^{0}) $ ,$ \Pi_{b}(\pi^{0}) $ ,$ \Pi_{c}(\pi^{0}) $ , and$ \Pi_{d}(\pi^{0}) $ are expressed as follows:$ \tag{B18}\begin{aligned}[b] \Pi_{a}(\pi^0) =& \left(\frac{g_{\pi NN}}{m_{\pi}}\right)^2 \int\frac{{\rm d}^3 \mathbf{q}}{(2\pi)^3}\theta(q_{F, n}-|{{q}}|) \\& \times \left[\frac{-4m^{2}_{n}k^2}{E_{n}(q)(2E_{n}(q)\omega-2\mathbf{q}\cdot \mathbf{k}+\omega^2-\mathbf{k}^2)} +2\omega \right] ,\end{aligned} $

$\tag{B19} \begin{aligned}[b] \Pi_{b}(\pi^0) =& \left(\frac{g_{\pi NN}}{m_{\pi}}\right)^2 \int\frac{{\rm d}^3 \mathbf{q}}{(2\pi)^3}\theta(q_{F, n}-|{{q}}|) \\& \times \left[\frac{-4m^{2}_{n}k^2}{E_{n}(q)(-2E_{n}(q)\omega+2\mathbf{q}\cdot \mathbf{k}+\omega^2-\mathbf{k}^2)} -2\omega \right] ,\end{aligned} $

$\tag{B20} \begin{aligned}[b] \Pi_{c}(\pi^0) =& \left(\frac{g_{\pi NN}}{m_{\pi}}\right)^2 \int\frac{{\rm d}^3 \mathbf{q}}{(2\pi)^3}\theta(q_{F, p}-|{{q}}|) \\& \times \left[\frac{-4m^{2}_{p}k^2}{E_{p}(q)(2E_{p}(q)\omega-2\mathbf{q}\cdot \mathbf{k}+\omega^2-\mathbf{k}^2)} +2\omega \right] ,\end{aligned} $

$ \tag{B21}\begin{aligned}[b] \Pi_{d}(\pi^0) =& \left(\frac{g_{\pi NN}}{m_{\pi}}\right)^2 \int\frac{{\rm d}^3 \mathbf{q}}{(2\pi)^3}\theta(q_{F, p}-|{{q}}|) \\& \times \left[\frac{-4m^{2}_{p}k^2}{E_{p}(q)(-2E_{p}(q)\omega+2\mathbf{q}\cdot \mathbf{k}+\omega^2-\mathbf{k}^2)} -2\omega \right].\end{aligned} $

The
$ \Delta $ -hole part of the$ \pi^- $ self-energy is$ \tag{B22} \Pi_{\Delta}(\pi^{0}) = \Pi_{e}(\pi^{0})+\Pi_{f}(\pi^{0})+\Pi_{g}(\pi^{0})+\Pi_{h}(\pi^{0}). $

Here,
$ \Pi_{e}(\pi^{0}) $ ,$ \Pi_{f}(\pi^{0}) $ ,$ \Pi_{g}(\pi^{0}) $ , and$ \Pi_{h}(\pi^{0}) $ can be calculated as follows:$ \tag{B23}\begin{aligned}[b] \Pi_{e}(\pi^{0}) =& \frac{4}{9}\left(\frac{g_{\pi N\Delta}}{m_{\pi}}\right)^2\int\frac{{\rm d}^3 \mathbf{q}}{(2\pi)^3} \frac{\theta(q_{F, n}-|\mathbf{q}|)}{E_{n}(q)}\\ &\times\large \left[\frac{(qk)^2-m^2_{n}k^2}{m^{2}_{0,\Delta^{0}}}+k^2\frac{2m_{n}}{m_{0,\Delta^{0}}}\left(1+\frac{m_{n}}{m_{0,\Delta^{0}}}\right)\right.\\ &\left.+\frac{(qk)^2-m^{2}_{n}k^2}{m^{2}_{0,\Delta^{0}}}\frac{(m_{n}+m_{0,\Delta^{0}})^2-k^2}{2qk+k^2-(m^{2}_{0,\Delta^{0}}-m^{2}_{n})}\large\right], \end{aligned} $

$\tag{B24} \begin{aligned}[b] \Pi_{f}(\pi^{0}) =& \frac{4}{9}\left(\frac{g_{\pi N\Delta}}{m_{\pi}}\right)^2\int\frac{{\rm d}^3 \mathbf{q}}{(2\pi)^3} \frac{\theta(q_{F, n}-|\mathbf{q}|)}{E_{n}(q)}\\& \times\large \left[\frac{(qk)^2-m^2_{n}k^2}{m^{2}_{0,\Delta^{0}}}+k^2\frac{2m_{n}}{m_{0,\Delta^{0}}}\left(1+\frac{m_{n}}{m_{0,\Delta^{0}}}\right)\right.\\ &\left.+\frac{(qk)^2-m^{2}_{n}k^2}{m^{2}_{0,\Delta^{0}}}\frac{(m_{n}+m_{0,\Delta^{0}})^2-k^2}{-2qk+k^2-(m^{2}_{0,\Delta^{0}}-m^{2}_{n})}\large\right], \end{aligned} $

$\tag{B25} \begin{aligned}[b] \Pi_{g}(\pi^{0}) =& \frac{4}{9}\left(\frac{g_{\pi N\Delta}}{m_{\pi}}\right)^2\int\frac{{\rm d}^3 \mathbf{q}}{(2\pi)^3} \frac{\theta(q_{F, p}-|\mathbf{q}|)}{E_{p}(q)}\\& \times\large \left[\frac{(qk)^2-m^2_{p}k^2}{m^{2}_{0,\Delta^+}}+k^2\frac{2m_{p}}{m_{0,\Delta^+}}\left(1+\frac{m_{p}}{m_{0,\Delta^+}}\right)\right.\\& \left.+\frac{(qk)^2-m^{2}_{p}k^2}{m^{2}_{0,\Delta^+}}\frac{(m_{p}+m_{0,\Delta^+})^2-k^2}{2qk+k^2-(m^{2}_{0,\Delta^+}-m^{2}_{p})}\large\right], \end{aligned} $

$\tag{B26} \begin{aligned}[b] \Pi_{h}(\pi^{0}) =& \frac{4}{9}\left(\frac{g_{\pi N\Delta}}{m_{\pi}}\right)^2\int\frac{{\rm d}^3 \mathbf{q}}{(2\pi)^3} \frac{\theta(q_{F, p}-|\mathbf{q}|)}{E_{p}(q)}\\ &\times\large \left[\frac{(qk)^2-m^2_{p}k^2}{m^{2}_{0,\Delta^+}}+k^2\frac{2m_{p}}{m_{0,\Delta^+}}\left(1+\frac{m_{p}}{m_{0,\Delta^+}}\right)\right.\\& \left.+\frac{(qk)^2-m^{2}_{p}k^2}{m^{2}_{0,\Delta^+}}\frac{(m_{p}+m_{0,\Delta^+})^2-k^2}{-2qk+k^2-(m^{2}_{0,\Delta^+}-m^{2}_{p})}\large\right]. \end{aligned}$

In symmetric nuclear matter, the pion self-energy is
$\tag{B27} \begin{aligned}[b] \Pi_{N} =& -8m^{2}_{N}k^2\left(\frac{g_{\pi NN}}{m_{\pi}}\right)^2 \int\frac{{\rm d}^3 \mathbf{q}}{(2\pi)^3}\frac{\theta(q_{F, N}-|{{q}}|)}{E_{N}(q)} \\& \times \left[\frac{1}{2E_{N}(q)\omega-2\mathbf{q}\cdot \mathbf{k}+\omega^2-\mathbf{k}^2}\right. \\& \left.-\frac{1}{-2E_{N}(q)\omega+2\mathbf{q}\cdot \mathbf{k}+\omega^2-\mathbf{k}^2} \right] ,\end{aligned} $

and
$\tag{B28} \begin{aligned}[b] \Pi_{\Delta} =& \frac{8}{9}\left(\frac{g_{\pi N\Delta}}{m_{\pi}}\right)^2\int\frac{{\rm d}^3 \mathbf{q}}{(2\pi)^3} \frac{\theta(q_{F, N}-|\mathbf{q}|)}{E_{N}(q)}\\& \times\left\{\frac{(qk)^2-m^2_{N}k^2}{m^{2}_{0,\Delta}}+k^2\frac{2m_{N}}{m_{0,\Delta}}\left(1+\frac{m_{N}}{m_{0,\Delta}}\right)\right.\\ &+\frac{(qk)^2-m^{2}_{N}k^2}{m^{2}_{0,\Delta}}\left[\frac{(m_{N}+m_{0,\Delta})^2-k^2}{2qk+k^2-(m^{2}_{0,\Delta}-m^{2}_{N})}\right.\\ & \left.\left.+\frac{(m_{N}+m_{0,\Delta})^2-k^2}{-2qk+k^2-(m^{2}_{0,\Delta}-m^{2}_{N})} \right] \right\}. \end{aligned} $

-
The pion self-energies in Appendix A can be expressed in terms of an analog of the susceptibility
$ \chi $ as follows:$ \tag{C1}\Pi_N = k^2\chi_N $

$\tag{C2} \Pi_\Delta = k^2\chi_\Delta. $

Here, we introduce the effect of nonrelativistic interaction as the nuclear spin-isospin short range correlation, as in Ref. [35]:
$\tag{C3} \begin{aligned}[b] W =& \left(\frac{g_{\pi NN}}{m_{\pi}}\right)^2 g^{\prime}_{NN}{{\sigma}}_1 \cdot {{\sigma}}_2{{\tau}}_1\cdot{{\tau}}_2\\& +\left(\frac{g_{\pi N\Delta}}{m_{\pi}}\right)^2 g^{\prime}_{\Delta\Delta}{{S}}_1^\dagger \cdot {{S}}_2{{\mathcal{T}}}_1^\dagger \cdot{{\mathcal{T}}}_2\\ &+\frac{g_{\pi NN}g_{\pi N\Delta}}{m_{\pi}^2} g^{\prime}_{N\Delta}{{S}}_1^\dagger \cdot {{\sigma}}_2{{\mathcal{T}}}_1^\dagger \cdot{{\tau}}_2+ {\rm h.c.} \end{aligned} $

With the short-range interaction, the pion dispersion relation can be expressed as follows:
$\tag{C4} \omega^2 = m_{\pi}^2+\mathbf{k}^2+\Pi = m_{\pi}^2+\mathbf{k}^2+k^2\chi $


$\tag{C5} \chi = \chi_1 +\chi_2 $


$ \tag{C6} \chi_1 = \chi_{N}^{\prime}\frac{1+g^{\prime}_{N\Delta}\chi_{\Delta}^{\prime}}{1-g^{\prime}_{N\Delta}\chi_{\Delta}^{\prime}g^{\prime}_{N\Delta}\chi_{N}^{\prime}} $


$\tag{C7} \chi_2 = \chi_{\Delta}^{\prime}\frac{1+g^{\prime}_{N\Delta}\chi_{N}^{\prime}}{1-g^{\prime}_{N\Delta}\chi_{N}^{\prime}g^{\prime}_{N\Delta}\chi_{\Delta}^{\prime}}. $


$ \tag{C8} \chi_{N}^{\prime} = \frac{\chi_{N}}{1-g^{\prime}_{NN}\chi_{N}} $


$\tag{C9} \chi_{\Delta}^{\prime} = \frac{\chi_{\Delta}}{1-g^{\prime}_{\Delta\Delta}\chi_{\Delta}} . $

Then, the susceptibility can be written as follows:
$\tag{C10} \begin{aligned}[b] \chi_{N}\to \chi_1 =& \frac{1+(g^{\prime}_{N\Delta}-g^{\prime}_{\Delta\Delta})\chi_{\Delta}}{(1-g^{\prime}_{\Delta\Delta}\chi_{\Delta})(1-g^{\prime}_{NN}\chi_{N})-g^{\prime}_{N\Delta}\chi_{\Delta}g^{\prime}_{N\Delta}\chi_{N}} \chi_{N} ,\\ \chi_{\Delta}\to \chi_2 =& \frac{1+(g^{\prime}_{N\Delta}-g^{\prime}_{NN})\chi_{N}}{(1-g^{\prime}_{\Delta\Delta}\chi_{\Delta})(1-g^{\prime}_{NN}\chi_{N})-g^{\prime}_{N\Delta}\chi_{\Delta}g^{\prime}_{N\Delta}\chi_{N}} \chi_{\Delta} . \end{aligned} $

-
The pion energy
$ \omega $ in the nuclear matter can be written in the following parametrization form:$ \tag{D1} \omega = a_0+a_1 x+a_2 x^2+a_3 x^3+a_4 x^4+a_5 x^5+a_6 x^6 , $

where
$ x = |\mathbf{k}|/m_{\pi} $ , and$ a_0 $ ,$ a_1 $ ,$ a_2 $ ,$ a_3 $ ,$ a_4 $ ,$ a_5 $ , and$ a_6 $ are all expressed in GeV.Here, the parametrization form of
$ \omega(\pi^0) $ at$ I = 0.3 $ and$ I = 0.2 $ is the same as in symmetric nuclear matter.Density x $ a_0 $ 

$ a_1 $ 

$ a_2 $ 

$ a_3 $ 

$ a_4 $ 

$ a_5 $ 

$ a_6 $ 

$ 0.5\rho_0 $ 

$ x\leqslant 1.125 $ 

0.14646 −0.01197 0.3134 −1.66811 4.26204 −4.60666 1.7103 $ x>1.125 $ 

−0.07165 0.26725 −0.0744 0.00899 0 0 0 $ \rho_0 $ 

$ x\leqslant 1.125 $ 

0.15305 0.14062 −1.03791 2.95229 −3.30208 1.23473 0 $ x>1.125 $ 

0.10479 −0.03411 0.08511 −0.02918 0.00353 0 0 $ 1.5\rho_0 $ 

$ x\leqslant 1.125 $ 

0.16982 0.09594 −0.78495 2.17423 −2.39857 0.88103 0 $ x>1.125 $ 

0.36904 −0.54203 0.41088 −0.1227 0.01366 0 0 $ 2\rho_0 $ 

$ x\leqslant 1.125 $ 

0.19358 0.04438 −0.57001 1.53095 −1.67771 0.61064 0 $ x>1.125 $ 

1.36471 −3.0588 2.86344 −1.30201 0.29304 −0.02607 0 Table D2. The parameters for
$ \omega_{\pi^{+}} $ at isospin asymmetry$ I = 0.2 $ .Density x $ a_0 $ 

$ a_1 $ 

$ a_2 $ 

$ a_3 $ 

$ a_4 $ 

$ a_5 $ 

$ a_6 $ 

$ 0.5\rho_0 $ 

$ x\leqslant 1.125 $ 

0.14953 −0.0217 0.40913 −2.12781 5.18789 −5.4529 1.99392 $ x>1.125 $ 

−0.03752 0.2044 −0.04916 0.00566 0 0 0 $ \rho_0 $ 

$ x\leqslant 1.125 $ 

0.16601 −0.01132 0.14963 −0.30154 0.13559 0 0 $ x>1.125 $ 

0.49951 −0.77281 0.55235 −0.15885 0.01696 0 0 $ 1.5\rho_0 $ 

$ x\leqslant 1.125 $ 

0.18891 0.05333 −0.64292 1.713 −1.85345 0.6668 0 $ x>1.125 $ 

0.86713 −1.568 1.12794 −0.34088 0.03816 0 0 $ 2\rho_0 $ 

$ x\leqslant 1.125 $ 

0.2235 −2.27582 −0.53085 1.3709 −1.51562 0.56282 0 $ x>1.125 $ 

1.65668 −3.85346 3.62636 −1.65695 0.37366 −0.03324 0 Table D3. The parameters for
$ \omega_{\pi^{-}} $ at isospin asymmetry$ I = 0.2 $ .Density x $ a_0 $ 

$ a_1 $ 

$ a_2 $ 

$ a_3 $ 

$ a_4 $ 

$ a_5 $ 

$ a_6 $ 

$ 0.5\rho_0 $ 

$ x\leqslant 1.125 $ 

0.14561 −0.01313 0.33908 −1.79495 4.55558 −4.90908 1.822 $ x>1.125 $ 

−0.06849 0.25597 −0.06608 0.00771 0 0 0 $ \rho_0 $ 

$ x\leqslant 1.125 $ 

0.15103 0.13677 −1.00479 2.89048 −3.2475 1.2163 0 $ x>1.125 $ 

0.02613 0.11939 −0.01774 0.00182 0 0 0 $ 1.5\rho_0 $ 

$ x\leqslant 1.125 $ 

0.19645 −0.07531 0.39858 −1.90247 4.05329 −3.87382 1.32371 $ x>1.125 $ 

1.9563 −4.52087 4.22417 −1.92159 0.4317 −0.03829 0 $ 2\rho_0 $ 

$ x\leqslant 1.125 $ 

0.18406 0.07659 −0.71693 1.92654 −2.10031 0.76536 0 $ x>1.125 $ 

0.50864 −0.82079 0.60002 −0.17954 0.02003 0 0 Table D4. The parameters for
$ \omega_{\pi^{+}} $ at isospin asymmetry$ I = 0.3 $ .
In-medium pion dispersion relation and medium correction of ${{N \pi \leftrightarrow \Delta}} $ near the threshold energy of pion production
- Received Date: 2020-12-14
- Available Online: 2021-04-15
Abstract: Transport models cannot simultaneously explain very recent data on pion multiplicities and pion charged ratios from central collision of Sn+Sn at 0.27 A GeV. This stimulates further investigations on the pion dispersion relation, in-medium






 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF



















 DownLoad:
DownLoad: