-
Numerous cosmological observations strongly suggest that the universe is undergoing accelerated expansion in the present epoch [1-6]. The most widely accepted idea is that a mysterious dominant component, dark energy with negative pressure, drives this cosmic acceleration. The most popular dark energy model is quintessence. It is described by a canonical scalar field accompanied by a particular potential that results in the late time acceleration of the universe. However, there has been a growing interest in the study of alternative models characterized by a non-canonical kinetic term, and there has been great progress in this area. This scenario was originally proposed to drive the inflation in the early universe [7, 8]. It was first applied to describe late time cosmic acceleration in Ref. [9]. A more general formalism of the scalar field dark energy model, called k-essence, was proposed in Refs. [10, 11].
As we know, the scalar field dynamical dark energy models suffer from the so-called fine-tuning problem and the coincidence problem. To attack these problems, we can resort to scalar field models which have scaling solutions; see Refs. [12-18] and therein (also see Ref. [19] for a review). As a dynamical attractor, the scaling solution can partly alleviate these two problems. In addition, we can also study the stability conditions of the scalar field dynamical dark energy models, see for example Refs. [20-22].
Lots of dynamical dark energy models, including k-essence, have been studied in depth in the framework of standard cosmology. However, it is expected that in the regime of very high curvature, general relativity (GR) breaks down and the Big Bang singularity emerges. A theory of quantum gravity should provide us a natural scenario to resolve this problem. One of the candidate theories of quantum gravity is loop quantum gravity (LQG), a non-perturbative and background-independent quantum gravity theory [23-26]. Based on LQG, we can construct a symmetry-reduced cosmological model with homogeneous and isotropic spacetimes, known as loop quantum cosmology (LQC) [27-32]. The non-perturbative quantum gravity effects result in a
$ -\rho^2 $ modification to the standard Friedmann dynamics. The Big Bang singularity in the early universe can be resolved in this scenario [27, 28, 31, 33-39]. It is very interesting to notice that even at the semi-classical level, instead of the Big Bang singularity, a Big Bounce emerges [40, 41]. The LQG effect also results in the emergence of the super-inflationary phase [42]. The horizon problem with only a small number of e-foldings can be resolved in this landscape [43]. Further, to search for potential observable prints, the cosmological perturbative theory in LQC is also deeply explored in Refs. [44-51] and the primordial power spectrum is studied in Refs. [43, 52-58]. In addition, the large scale effect of LQG is also found in Ref. [59], which provides us the possibility to study the LQG effect on the dark energy evolution. Many scalar field dark energy models and their dynamics have been widely studied in the framework of LQC; see Refs. [60-65] and therein.In this paper, we study the dynamics of k-essence and its attractor solutions in LQC. Our paper is organized as follows. In Section II, we introduce the k-essence in the LQC framework and derive the equations of motion of the dynamical system. Then, we study the dynamics of k-essence for constant coupling parameters and dynamically changing coupling parameters in Section III and Section IV, respectively. Some discussion and conclusions are briefly presented in Section V.
-
In the quintessence scalar field dark energy model, the potential energy of the scalar field plays a key role in driving the cosmic late-time acceleration. If we introduce a non-canonical kinetic energy term in the Lagrangian, we find that even when the potential vanishes, the cosmic acceleration can still be achieved. This model, characterized by a non-canonical kinetic energy term, is called the k-essence model. The most general Lagrangian of k-essence is a function of the scalar field
$ \phi $ and its kinetic energy term$ X\equiv\dfrac{1}{2}\partial_{\mu}\phi\partial^{\mu}\phi $ , i.e.,$ {\cal{L}} = f(\phi,X) $ . In this paper, we consider a specific form of k-essence [10, 11, 66],$ {\cal{L}} = \alpha(\phi)X+\beta(\phi)X^2-V(\phi)\,, $

(1) where
$ V(\phi) $ is the potential, and the coefficients$ \alpha $ and$ \beta $ are functions of the scalar field. The above Lagrangian is a polynomial of degree$ 2 $ in the kinetic energy X. This type of Lagrangian can emerge from low-energy effective string theory [7, 8].Incorporating the LQG effect, instead of the standard Friedmann equation, we have an effective one [27-32],
$ H^2 = {\frac{\rho_t}{3M_p^2}}\bigg(1-{\frac{\rho_t}{\rho_{c}}}\bigg)\,, $

(2) where
$ H\equiv\dot{a}/a $ is the Hubble parameter and$ \rho_t $ is the total energy density of the cosmological contents.$M_p^2 = \dfrac{1}{8\pi G}$ is the square of the Planck mass. In what follows, we set$ M_p^2 = 1 $ for convenience.$ \rho_{c} = {\sqrt{3}}/(16{\pi}{\gamma}^3G^2{\hbar}) $ is the critical density, where$ \gamma $ is the dimensionless Barbero-Immirzi parameter and$ \hbar $ is the Planck constant. Before proceeding, we would like to point out that there is an alternative version of modified Friedmann equation proposed in [59, 67], which could be derived from full LQG as recently shown by [68].Along with the conservation law
$ \dot{\rho_t}+3H({\rho_t}+p_t) = 0\,, $

(3) the effective Friedmann equation provides a description of the universe incorporating the LQG effect.
$ p_t $ in the above equation is the total pressure. Differentiating the Friedmann equation (2) and using the conservation law (3), one achieves the following effective Raychaudhuri equation:$ \dot{H} = -{\frac{(\rho_t+p_t)}{2}}\bigg(1-{\frac{2\rho_t}{\rho_{c}}}\bigg)\,. $

(4) We assume that the contents of the universe include the k-essence scalar field and the dark matter. So the total energy density and pressure of the contents of the universe are:
$ \begin{aligned}[b] \rho_t = \rho_\phi+\rho_m\,, \quad p_t = p_\phi+p_m\,, \end{aligned} $

(5) where
$ \rho_\phi $ ($ \rho_m $ ) and$ p_\phi $ ($ p_m $ ) are the energy density and pressure of the dark energy (dark matter), respectively. From the Lagrangian of k-essence (1), we can easily derive$ \rho_\phi $ and$ p_\phi $ in a flat Friedmann-Robertson-Walker (FRW) background as [10, 11, 66]$ \rho_\phi = \alpha(\phi) X+3 \beta(\phi) X^2+ V (\phi) \,, $

(6) $ p_\phi = {\alpha(\phi)}X+{\beta(\phi)}X^2-V{(\phi)}\,. $

(7) Since we have assumed that the universe is homogeneous and isotropic, one has
$X = {\dfrac{1}{2}}{\dot{\phi}^2}$ , where the dot denotes the derivative with respect to time. Further, taking the variation of the Lagrangian (1) with respect to the scalar field$ \phi $ , one obtains the Klein-Gordon (KG) equation as:$ \begin{aligned}[b] & \ddot{\phi}[{\alpha(\phi)}+3{\beta(\phi)}\dot{\phi}^2]+\alpha{'}{(\phi)}{\frac{\dot{\phi}^2}{2}}+3{\beta{'}(\phi)}{\frac{\dot{\phi}^4}{4}}\\ &\quad +3H\dot{\phi}[{\alpha(\phi)}+{\beta(\phi)}\dot{\phi}^2]+V{'}{(\phi)} = 0\,. \end{aligned} $

(8) To study the dynamics of the above system, we define the following set of dimensionless variables:
$ \begin{split} x =& {\frac{\alpha(\phi)\dot{\phi}^2 }{6H^2}},\quad y = {\frac{\beta(\phi)\dot{\phi}^4 }{12H^2}}\,, \\ b =& {\frac{V(\phi)}{3H^2}},\quad \lambda = {\frac{1}{\alpha}}{\frac{{\rm d}\alpha}{{\rm d}\phi}}{\frac{\dot{\phi}}{H}}\,, \\ \delta =& {\frac{1}{\beta}}{\frac{{\rm d}\beta}{{\rm d}\phi}}{\frac{\dot{\phi}}{H}},\quad z = {\frac{\rho_t}{\rho_{c}}}\,. \end{split}$

(9) In term of the above dimensionless variables, the effective Friedman equation (2) and Raychaudhuri equation (4) can be rewritten as:
$ \frac{\rho_m}{3H^2} = \frac{1}{1-z}-(x+3y+b)\,, \ $

(10) $ \frac{\dot{H}}{H^2} = -\frac{3}{2}\left[2x+4y+\frac{1-(x+3y+b)(1-z)}{1-z}\right](1-2z)\,. $

(11) Then, we recast the above system into the following autonomous form:
$ x{'} = x{\lambda}+3x{\cal{G}}-2x{\cal{F}}\,, \ $

(12) $ y{'} = y{\delta}+3y{\cal{G}}-4y{\cal{F}}\,, \ $

(13) $ b{'} = {\sigma}b+3b{\cal{G}}\,, \ $

(14) $ \lambda{'} = {\frac{3}{2}}{\lambda}{\cal{G}}-{\lambda}{\cal{F}}-{\lambda}^2(1-{\Gamma})\,, \ $

(15) $ \delta{'} = {\frac{3}{2}}{\delta}{\cal{G}}-{\delta}^2(1-{\tau})-{\delta}{\cal{F}}\,, \ $

(16) $ z{'} = -3z(1+x+y+b(-1+z)-xz-yz)\,, $

(17) where
$ {\cal{F}} = {\frac{3(x+2y)}{x+6y}}+{\frac{x{\lambda}+3{\delta}y+{\sigma}b}{2(x+6y)}}\,, \ $

(18) $ {\cal{G}} = {\frac{(-1+2z)(1+x+y+b(-1+z)-xz-yz)}{-1+z}}\,, $

(19) and
$ \begin{aligned}[b] \Gamma = & {\frac{\alpha\left({\dfrac{{\rm d}^2{\alpha}}{{\rm d}{\phi}^2}}\right)}{\left({\dfrac{{\rm d}{\alpha}}{{\rm d}{\phi}}}\right)^2}}\,,\quad \tau = {\frac{\beta\left({\dfrac{{\rm d}^2{\beta}}{{\rm d}{\phi}^2}}\right)}{\left({\dfrac{{\rm d}{\beta}}{{\rm d}{\phi}}}\right)^2}}\,, \\ \sigma = & {\frac{{\rm d}(\ln\; V)}{{\rm d}N}}\,. \end{aligned}$

(20) Notice that here we have introduced the number of e-folding
$ N\equiv\ln(a/a_0) $ , with$ a_0 $ being the current value of the scale factor and the prime representing the derivative with respect to N in the above equations.Compared with the standard FRW cosmology, an additional dimensionless variable
$ z\equiv\rho_t/\rho_c $ is introduced to describe the system in LQC. The nonzero z represents the LQG effect. Next, we shall treat$ \lambda $ and$ \delta $ as constant coupling parameters and dynamically changing variables respectively, to study the dynamics of the system. -
In this section, we consider
$ \lambda $ and$ \delta $ as constant coupling parameters and so we set$ \lambda = \lambda_0 $ and$ \delta = \delta_0 $ . The dynamic system reduces to a$ 4 $ -dimensional one. A non-trivial$ \lambda $ and$ \delta $ give the following relation:$ \lambda_0(1-{\Gamma}) = \delta_0(1-{\tau})\,. $

(21) From Eqs. (15) and (16), it is easy to derive the following constraints:
$ \lambda_0 = \frac{\dfrac{3}{2}{\cal{G}}-{\cal{F}}}{1-\tau}\,,\; \; \; \; \; \delta_0 = \frac{\dfrac{3}{2}{\cal{G}}-{\cal{F}}}{1-\Gamma}\,. $

(22) -
As was pointed out in the introduction, different from quintessence, the non-canonical kinetic term of k-essence plays a key role in driving the cosmic acceleration. So in this subsection, we first consider the pure k-essence model, i.e.
$ V(\phi) = 0 $ . In this case,$ b = 0 $ and the system reduces to a$ 3 $ -dimensional one.Also, we are interested in the k-essence fractional density parameter
$ \Omega_\phi $ and the effective k-essence equation of state (EoS) parameter$ \gamma_\phi $ , which read:$ \Omega_\phi = \frac{\rho_\phi}{3H^2} = x+3y\,, $

(23) $ \gamma_\phi = 1+\omega_\phi = 1+\frac{p_\phi}{\rho_\phi} = \frac{2x+4y}{x+3y}\,, $

(24) for
$ V(\phi) = 0 $ . We see that$ \Omega_\phi $ and$ \gamma_\phi $ have the same expressions as in standard FRW cosmology [66]. The observations constrain the current values for$ \Omega_\phi $ and$ \gamma_\phi $ as [69]:$ \Omega_\phi\approx0.68\,, \ $

(25) $ \gamma_\phi\approx0.05\,. $

(26) Therefore, we have
$ x_0 = -1.309 $ and$ y_0 = 0.663 $ for the current universe.By setting
$ x' = 0 $ ,$ y' = 0 $ and$ z' = 0 $ , one obtains the fixed points for this system. We can explore the stability of the fixed points by evaluating the corresponding eigenvalues. Following the strategy outlined in Refs. [15, 19, 70], one can work out the eigenvalues. The corresponding$ \Omega_\phi $ and$ \gamma_\phi $ are also worked out. These results are summarized in Table 1.Point x y z Eigenvalues $ \Omega_{\phi} $ 

$ \gamma_{\phi} $ 

Stability Condition A. 0 $ \dfrac{1}{3} $ 

0 −4,1, $ \dfrac{1}{2}(4-\delta+2\lambda) $ 

1 $ \dfrac{4}{3} $ 

Saddle point B. 1 0 0 −6,3, $ -6+\delta-2\lambda $ 

1 2 Saddle point $ {\rm C}.$ 

$ \dfrac{1}{2}(\delta-2\lambda-4) $ 

$ \dfrac{1}{6}(6-\delta+2\lambda) $ 

$ 0$ 

$ -\delta+2\lambda ,\; \delta-2\lambda-3 ,\;\dfrac{(2\lambda-\delta+4)(2\lambda-\delta+6)}{\delta-2(4+\lambda)}$ 

$ 1$ 

$ \dfrac{\delta-2\lambda}{3} $ 

$ 2\lambda<\delta<2\lambda+3 $ 

Table 1. Fixed points for pure k-essence.
From this table, we can see that the fixed point C is stable if
$ 2\lambda<\delta<2\lambda+3\,, $

(27) is satisfied. Comparing with the case of k-essence in standard FRW cosmology in Ref. [66], the LQG effect imposes a lower bound on
$ \delta-2\lambda $ . Given the condition (27), one has$ \gamma_\phi<0 $ , i.e.,$ \omega_\phi>-1 $ , for which the big rip [71] in the later universe is avoided. Notice that to have an accelerated expansion universe at a later stage, we have$ \gamma_\phi<2/3 $ , which further leads to a tighter constraint:$ 2\lambda<\delta<2\lambda+2\,. $

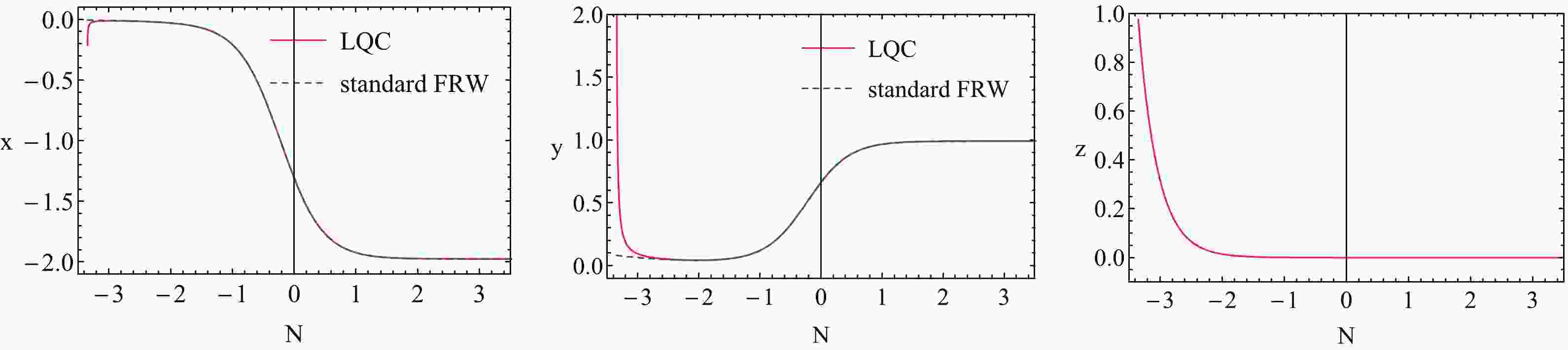
(28) Now, we turn to study the evolution of the system with N. To solve the EOMs of this system, we take the initial conditions to satisfy the current observation constraints, i.e. Eqs. (25) and (26). Besides, we assume that z is small in the current universe. The evolutions of x, y and z as functions of N are shown in Fig. 1. The red curves are for LQC and the blue dashed curves for the standard FRW cosmology. Note that the parameters
$ \lambda $ and$ \delta $ are chosen as$ \lambda = 2 $ and$ \delta = 4.05 $ , which satisfies the stability condition (28).
Figure 1. (color online) Evolutions of the system with N for pure k-essence. The red curves are for LQC and the blue dashed curves for the standard FRW cosmology. Here we have chosen
$ \lambda = 2 $ and$ \delta = 4.05 $ .From this figure, we find that for most of the time of the universe evolution, x and y in LQC are the same as in the standard FRW cosmology. Only in the early epoch of the universe is there a difference, where x rapidly decreases and y increases as time goes back. On the other hand, z almost vanishes for most of the time of the universe evolution, but as time goes back, it rapidly increases in the early epoch of the universe. These phenomena indicate that the LQG effect plays an important role only in the early epoch of the universe. We show the parameter plot of x, y and z in Fig. 2. The universe finally evolves into the stability attractor solution (point C, the red point in Fig. 2).
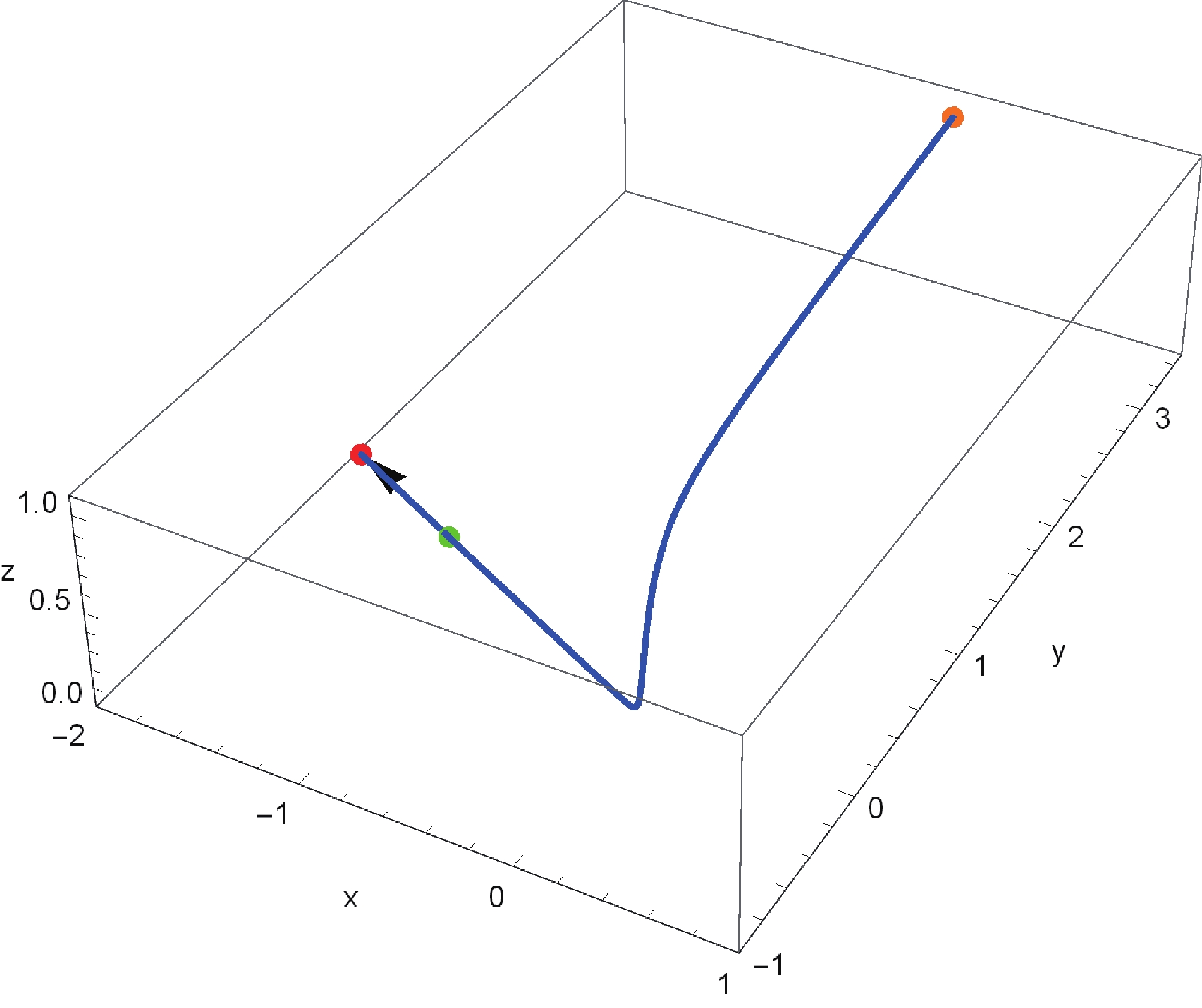
Figure 2. (color online) The parameter plot of x, y and z for pure k-essence. The blue curve exhibits the time evolution from the past (orange point) to the attractor (red point). The green point stands for the present universe. Here we have chosen
$ \lambda = 2 $ and$ \delta = 4.05 $ .Furthermore, we plot the evolutions of the deceleration parameter q with N in Fig. 3. We see that in the early epoch, the universe undergoes a so-called super-inflation stage due to the LQG effect [62, 72-74]. After that, the universe enters into a decelerated phase, which is almost the same as that for the standard FRW cosmology. The universe then changes from this decelerated phase to an accelerated expansion stage where the LQG effect is diluted.
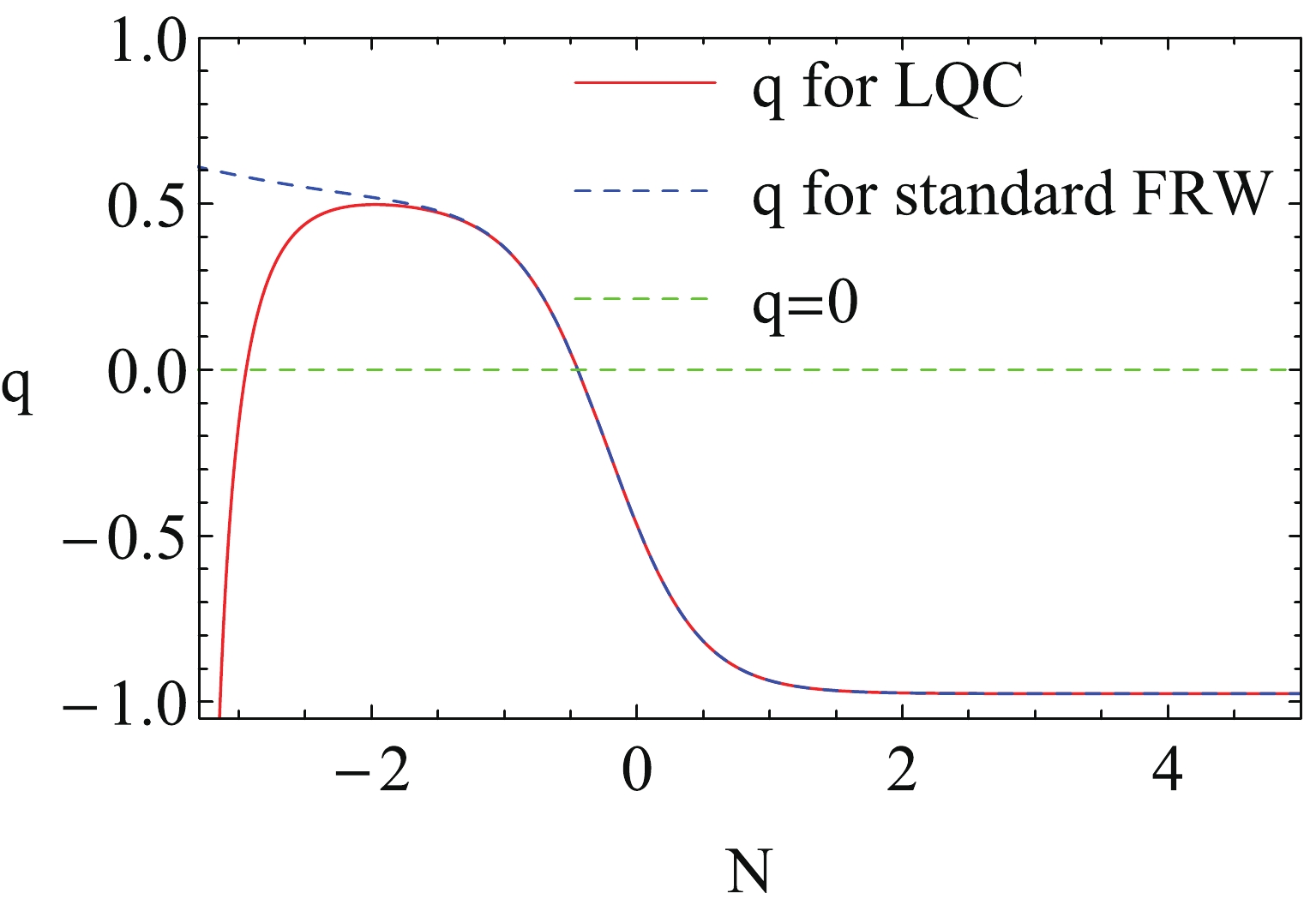
Figure 3. (color online) Evolutions of the deceleration parameter q with N for pure k-essence. The red curve is for LQC and the blue dashed curve for the standard FRW cosmology. Here we have chosen
$ \lambda = 2 $ and$ \delta = 4.05 $ .In Fig. 4, we show the evolution of
$ \gamma_\phi $ and$ \Omega_\phi $ with N in the standard FRW cosmology (left) and LQC (right). Again, the LQC effect plays a key role only in the early universe and is diluted as the time evolves. Finally, the universe evolves into the stable attractor with$ \gamma_\phi = 0 $ and$ \Omega_\phi = 1 $ , which means the universe is dominated by the scalar field.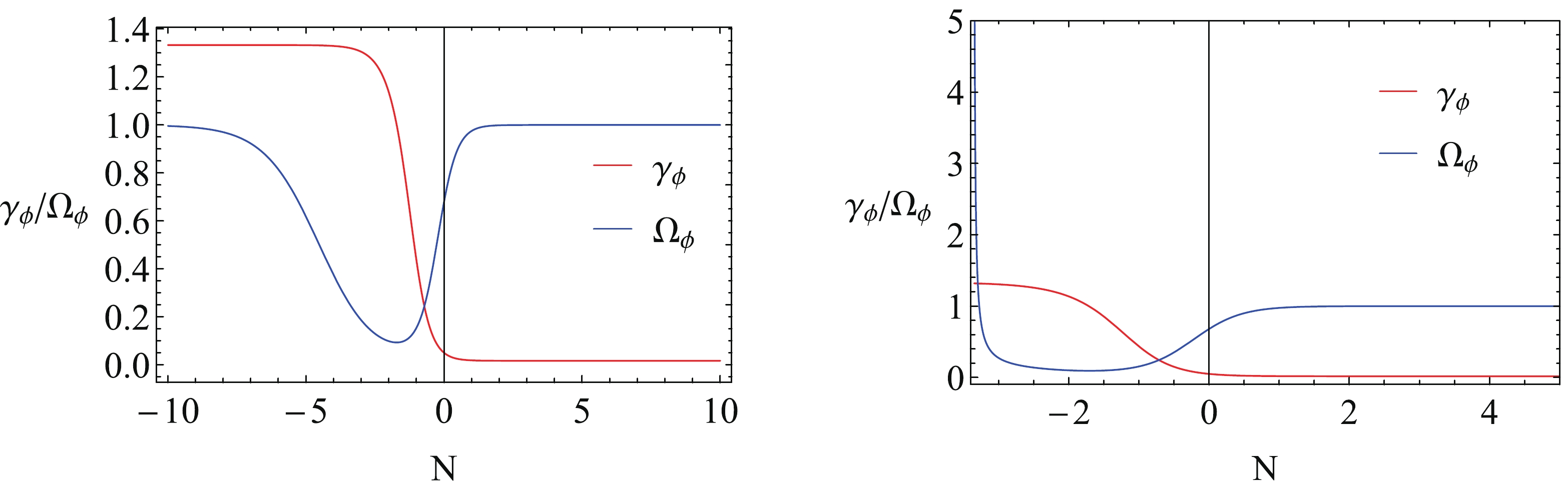
Figure 4. (color online) Evolutions of
$ \gamma_\phi $ and$ \Omega_\phi $ with N for pure k-essence, for (left) standard FRW cosmology and (right) LQC. Here we have chosen$ \lambda = 2 $ and$ \delta = 4.05 $ .Finally, we would like to point out that the fixed points A and B are not stable fixed points but are saddle points, because there is at least one negative eigenvalue for them (see Table 1).
-
In this subsection, we study the dynamics of k-essence with non-zero potential.
$ V(\phi)\neq0 $ leads to$ b\neq 0 $ and so this dynamical system becomes$ 4 $ -dimensional. Then the scalar field fractional energy density$ \Omega_\phi $ and the EOS parameter$ \gamma_\phi $ become:$ \Omega_\phi = x+3y+b\,, \ $

(29) $ \gamma_\phi = \frac{2x+4y}{x+3y+b}\,. $

(30) The values of
$ \Omega_\phi $ and$ \gamma_\phi $ of the current universe (Eqs. (25) and (26)) give the initial condition space as:$ x+3y+b = 0.68\,, \ $

(31) $ 2x+4y = 0.034\,. $

(32) Given the initial conditions, we can determine the evolutions of x, y, z and b with N. Note that the initial condition space is the same as in the standard FRW cosmology. For detailed discussions, please refer to Ref. [66].
Following the same procedure as above, we work out the fixed points and the stability conditions, which are shown in Table 2. From this table, we can see that points D and E are unstable. We do not discuss these unstable points.
Point x y z b Eigenvalues $ \Omega_{\phi} $ 

$ \gamma_{\phi} $ 

Stability condition A 0 $-\dfrac{\sigma}{12}$ 

0 $\dfrac{4+\sigma}{4}$ 

$ \dfrac{1}{2}(-\delta+2\lambda-\sigma) $ ,

$ \sigma $ ,

$ -\sigma-3 $ ,

$ -4-\sigma $ 

1 $ {-\dfrac{\sigma}{3}} $ 

$ 2\lambda<\delta+\sigma $ and

$ \sigma>-3 $ 

B $ -\dfrac{\sigma}{6} $ 

0 0 $ \dfrac{6+\sigma}{6} $ 

$ \sigma $ ,

$ -3-\sigma $ ,

$ -6-\sigma $ ,

$ \delta-2\lambda+\sigma $ 

1 $ {-\dfrac{\sigma}{3}} $ 

$ 2\lambda>\delta+\sigma $ and

$ \sigma>-3 $ 

C $ \dfrac{1}{2}(\delta-2(2+\lambda)) $ 

$ \dfrac{1}{6}(6-\delta+2\lambda) $ 

0 0 $ -\delta+2\lambda $ ,

$\dfrac{\lambda^2-2\delta(5+2\lambda)+4(6+5\lambda+\lambda^2)}{\delta-2(4+\lambda)}$ ,

$ \delta-2\lambda-3 $ ,

$ \delta-2\lambda+\sigma $ 

1 $ {\dfrac{\delta-2\lambda}{3}} $ 

$ 2\lambda>\delta+\sigma $ and

$ \sigma>-3 $ 

D 1 0 0 0 −4,1, $ \dfrac{1}{2}(4-\delta+2\lambda) $ ,

$ 4+\sigma $ 

1 $ {\dfrac{4}{3}} $ 

unstable E 0 $ \dfrac{1}{3} $ 

0 0 −6,3, $ \delta-6-2\lambda $ ,

$ 6+\sigma $ 

1 1 unstable Table 2. Fixed points for k-essence with non-zero potential.
If the condition
$ 2\lambda<\lambda+\sigma $ with$ \sigma>-3 $ is satisfied, A is a stable fixed point. We show the evolutions flowing to the fixed point A in Fig. 5. Here we have fixed$ \sigma = 0 $ , which corresponds to the case of$ \omega_\phi = -1 $ ②. Regardless of whether it is the LQC or the standard FRW universe, the systems flow to the same fixed point A. We note that as the time evolves, the linear and quadratic kinetic energy terms x and y reduce to zero, but the potential term b increases and tends to the maximum value of$ b = 1 $ . This suggests that as in the quintessence dark energy model, the potential plays the dominant role in driving the cosmic acceleration in the later epoch of the universe. It is different from that for the pure k-essence, for which the kinetic energy terms play the role of driving the cosmic acceleration. As in the case of pure k-essence studied above, only in the early stage of the universe do the LQG effects play an important role. In most of the evolution time of the universe, the evolution of the system in LQC is basically consistent with that in the standard FRW cosmology [17, 18, 22, 23].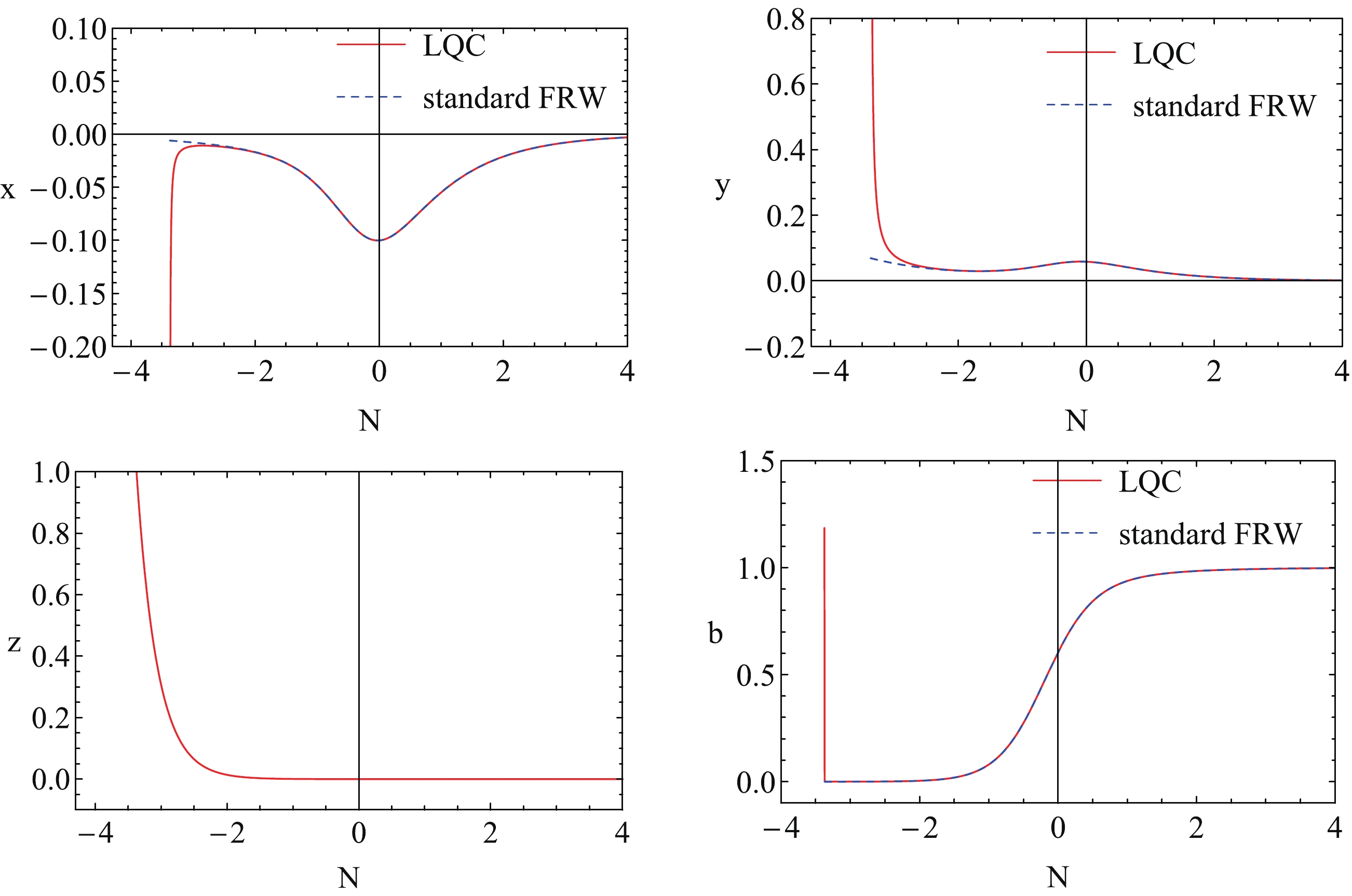
Figure 5. (color online) The evolutions flowing to fixed point A for k-essence with non-zero potential. The red curves are for LQC and the blue dashed curves for the standard FRW cosmology. Here we have chosen λ = 1 and δ = 3 and σ = 0.
The corresponding q and
$ \gamma_\phi $ /$ \Omega_\phi $ are also shown in Fig. 6 and Fig. 7, respectively. From the two figures, we can see that the LQG effect plays an important role in the early epoch of the universe, such that the universe undergoes a super-inflation stage. After that, the LQG effect is diluted and the evolution of the universe is almost the same as in the standard FRW universe. Finally, the universe flows to one dominated by the scalar field.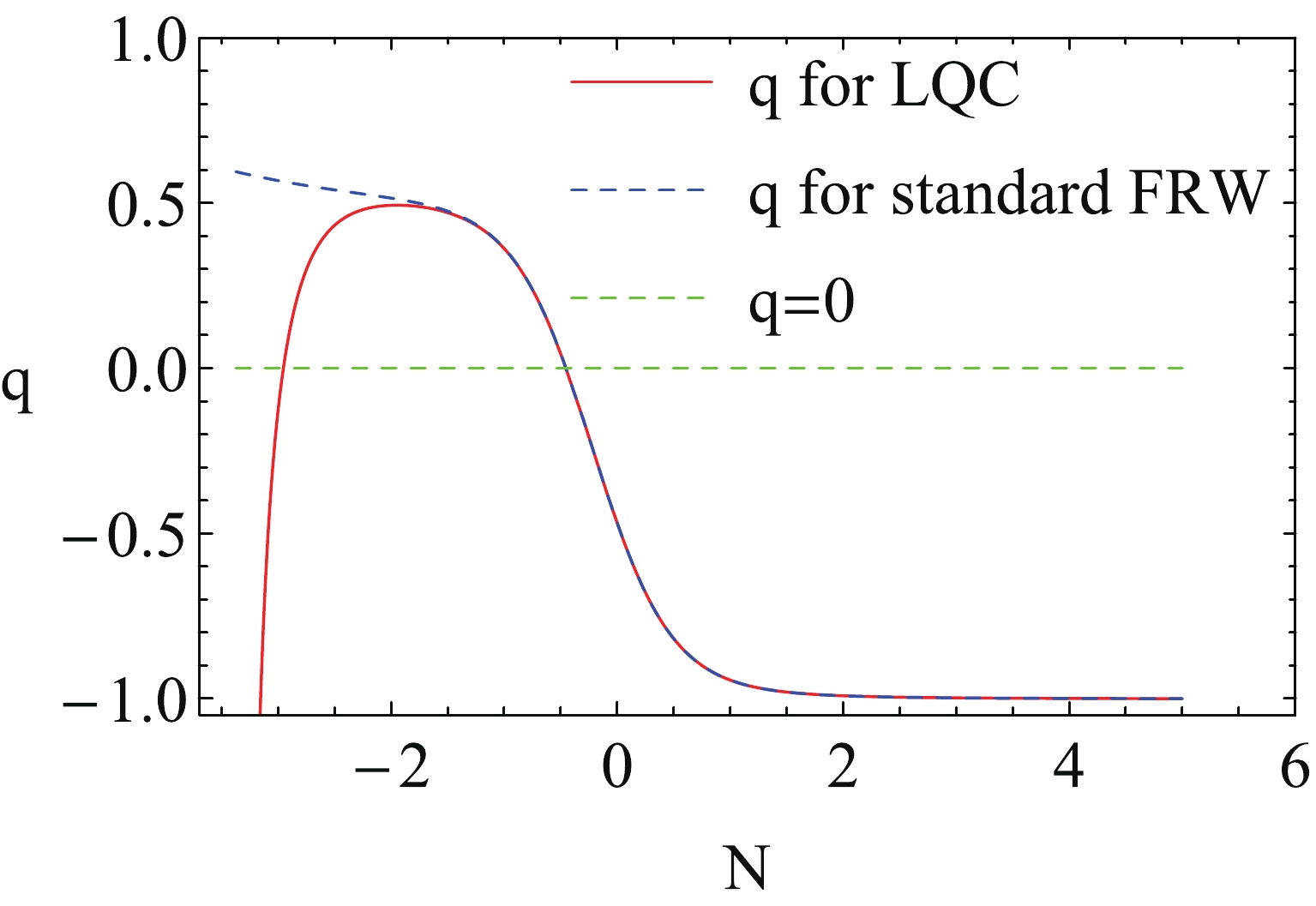
Figure 6. (color online) Evolutions of the deceleration parameter q with N for k-essence with non-zero potential. The red curve is for LQC and the blue dashed curve for the standard FRW cosmology. Here we have chosen
$\lambda=1$ and$\delta=3$ and$\sigma=0$ .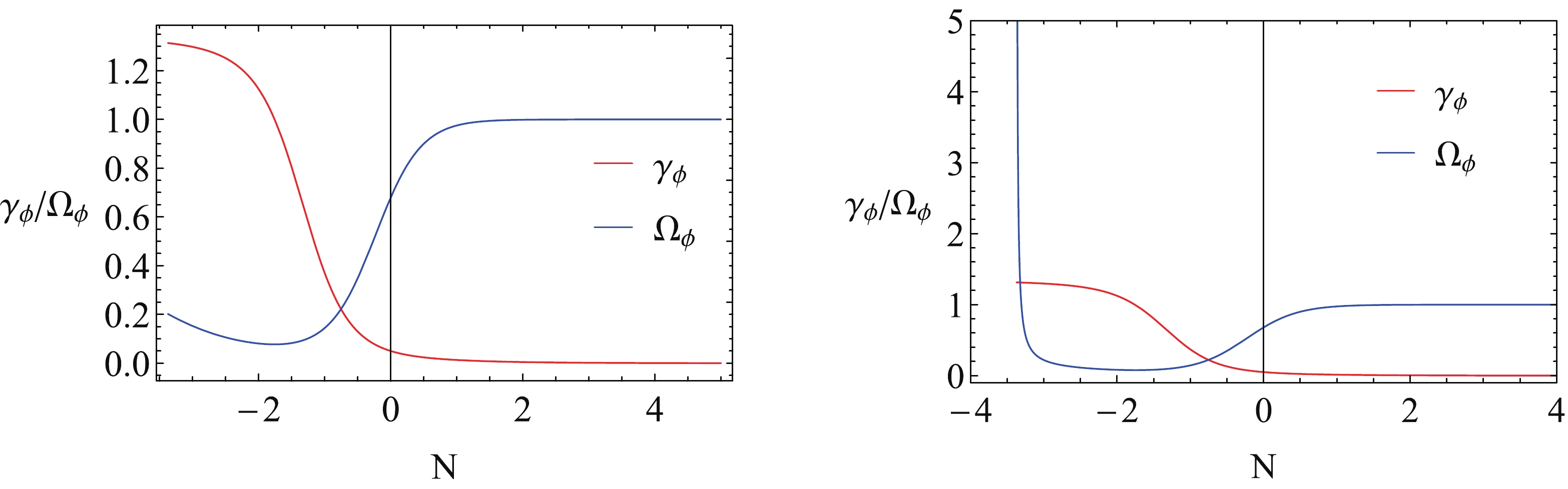
Figure 7. (color online) Evolutions of
$\gamma_\phi$ and$\Omega_\phi$ with N for k-essence with non-zero potential, for (left) standard FRW cosmology and (right) for LQC. Here we have chosen$\lambda=1$ and$\delta=3$ and$\sigma=0$ .When
$ 2\lambda>\delta+\sigma $ with$ \sigma>-3 $ , the universe can flow to different fixed points B and C depending on the initial conditions. When the initial condition$ x_0 $ belongs to the region$ x_0>0 $ , the universe flows to the fixed point B, which is a potential energy dominant case (see Fig. 8). If$ x_0<0 $ , then the universe evolves into the fixed point C, which is a kinetic energy dominant case (see Fig. 9). We plot the evolutions of the deceleration parameter q with N for the initial conditions$ x_0>0 $ and$ x_0<0 $ in Fig. 10. We find that for the different initial conditions, the evolutions of the deceleration parameter q are qualitatively consistent. That is to say, due to the LQG effect, the universe firstly undergoes a super-inflation stage. Soon afterwards, the universe enters a decelerated phase and finally, under the driving of scalar field, it enters the accelerated expansion stage.
Figure 8. (color online) Evolutions of x, y, z and b with N for k-essence with non-zero potential. The red curves are for LQC and the blue dashed curves for the standard FRW cosmology. Here we have chosen
$\lambda=1$ and$\delta=1$ and$\sigma=0$ . The initial condition is that$x_0>0$ .
Figure 9. (color online) Evolutions of x, y, z and b with N for k-essence with non-zero potential. The red curves are for LQC and the blue dashed curves for the standard FRW cosmology. Here we have chosen
$\lambda=1$ and$\delta=1$ and$\sigma=0$ . The initial condition is that$x_0<0$ .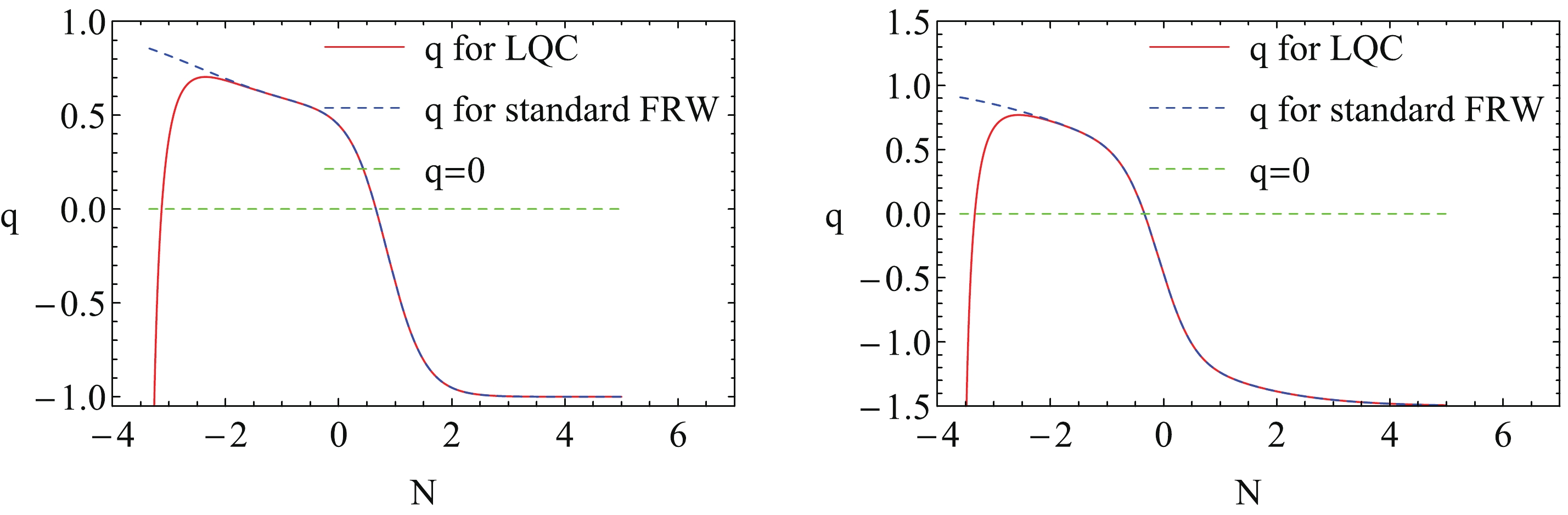
Figure 10. (color online) Evolutions of the deceleration parameter q with N for k-essence with non-zero potential. The red curve is for LQC and the blue dashed curve for the standard FRW cosmology. Here we have chosen
$\lambda=1$ and$\delta=1$ and$\sigma=0$ . The initial conditions are (left)$x_0>0$ and (right)$x_0<0$ . -
In the previous section,
$ \lambda $ and$ \delta $ are constant. Next, we study the evolution of the system with dynamically changing$ \lambda $ and$ \delta $ . We shall mainly study the case of pure k-essence. For the k-essence with nonzero potential, we only present a brief discussion.The system of pure k-essence with dynamically changing
$ \lambda $ and$ \delta $ is a$ 5 $ -dimensional. Following the same procedure as above, we can work out the fixed points and the corresponding eigenvalues, the parameters$ \Omega_\phi $ and$ \gamma_\phi $ , as shown in Table 3. The stability conditions are also summarized in this table.Point x y z $ \lambda $ 

$ \delta $ 

$ \Omega_{\phi} $ 

$ \gamma_{\phi} $ 

Eigenvalues Stability Condition A 0 $ \dfrac{1}{3} $ 

0 0 0 1 $ \dfrac{4}{3} $ 

$ {-4,2,1,1,1} $ 

Unstable B 0 $ \dfrac{1}{3} $ 

0 0 $ \dfrac{4}{5-4\tau} $ 

1 $ \dfrac{4}{3} $ 

$ \dfrac{4(-1+\tau)}{-5+4\tau} $ ,

$ \dfrac{8(-1+\tau)}{-5+4\tau} $ ,−4,−1,1

Unstable C 0 $ \dfrac{1}{3} $ 

0 $ \dfrac{1}{1-\Gamma} $ 

0 1 $ \dfrac{4}{3} $ 

−4,−1,1,1, $ \dfrac{-3+2\Gamma}{-1+\Gamma} $ 

Unstable D 0 $ \dfrac{1}{3} $ 

0 $ \dfrac{4(-1+\tau)}{(-1+\Gamma)(-5+4\tau)} $ 

$ \dfrac{4}{5-4\tau} $ 

1 $ \dfrac{4}{3} $ 

$ -\dfrac{4(-1+\tau)}{-5+4\tau} $ ,

$ \dfrac{4(-3+2\Gamma)(-1+\tau)}{(-1+\Gamma)(-5+4\tau)} $ ,−4,−1,1

Unstable E −2 1 0 0 0 1 0 −3,−3,0,0,0 Saddle point F 1 0 0 0 0 1 2 −6,−6,3,0,0 Unstable Table 3. Fixed points for pure k-essence with dynamically changing
$ \lambda $ and$ \delta $ Except for the fixed point E, all the fixed points are unstable because there is at least one positive eigenvalue for these fixed points. Since there are two negative eigenvalues and three zero eigenvalues for the fixed point E, it is a saddle point. These results for LQC are similar to those for the standard FRW universe [23, 24, 54].
We want to know the properties of the saddle point E. To this end, we show the evolutions of the system, the parameters
$ \Omega_\phi $ ,$ \gamma_\phi $ and q with N for different$ \Gamma $ and$ \tau $ , in Figs. 11, 12 and 13. The properties are summarized as follows.
Figure 11. (color online) Evolutions of the system with N for pure k-essence with dynamically changing
$\lambda$ and$\delta$ . From left to right,$\Gamma=\tau=0.5,1.4,1.6$ .
Figure 12. (color online) Evolutions of
$\gamma_\phi$ and$\Omega_\phi$ with N for pure k-essence with dynamically changing$\lambda$ and$\delta$ . From left to right,$\Gamma=\tau=0.5,1.4,1.6$ .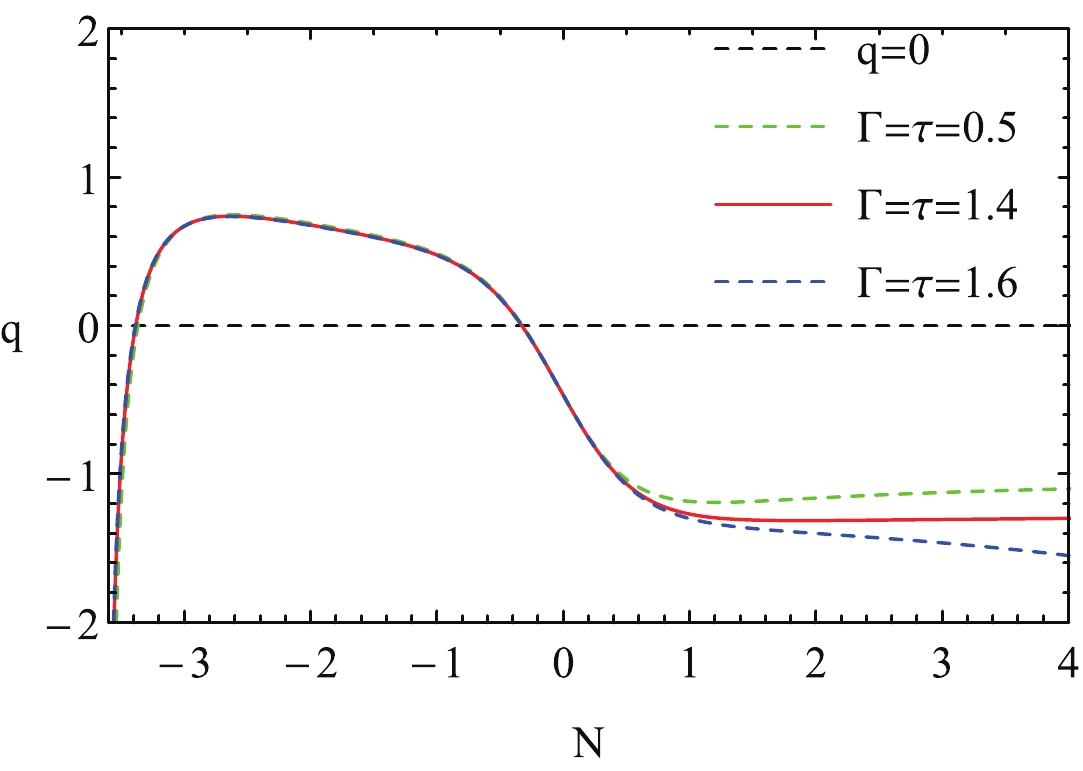
Figure 13. (color online) Evolutions of q with N for pure k-essence with dynamically changing
$\lambda$ and$\delta$ .● When
$ \Gamma $ and$ \tau $ are small, the system flows to the fixed point E at a later stage (the first plot in Fig. 11). Correspondingly,$ \Omega_\phi\rightarrow 1 $ and$ \gamma_\phi\rightarrow 0 $ , which are the corresponding values of the fixed point E (see Table 3).● As
$ \Gamma $ and$ \tau $ increase, some of the variables no longer flow to the fixed point E at the later stage (the second plot in Fig. 11). Some of the variables even become divergent at the later stage when$ \Gamma $ and$ \tau $ further increase (the third plot in Fig. 11). Correspondingly,$ \gamma_\phi $ begins to deviate from the value of$ \gamma_\phi = 0 $ for$ \Gamma = \tau = 1.4 $ (the second plot in Fig. 12) and even becomes divergent when$ \Gamma $ and$ \tau $ further increase to the value of$ \Gamma = \tau = 1.6 $ (the third plot in Fig. 12).● The deceleration parameter q is different for different
$ \Gamma $ and$ \tau $ in the later stage. In particular, when$ \Gamma = \tau = 1.6 $ , q tends to become divergent in the later stage (Fig. 13).● Again, the LQG effect plays a key role only in the early stage.
To sum up, the saddle point E is not an attractor. Whether or not the system flows to this fixed point depends on the values of
$ \Gamma $ and$ \tau $ .The most general case is the one with non-zero potential and dynamically changing
$ \lambda $ and$ \delta $ . In this case, the system is$ 6 $ -dimensional. The fixed points and the corresponding eigenvalues are worked out in Table 4. There are$ 9 $ fixed points for this system. However, there are only two stable fixed points (C and D) and two saddle points (E and J) when the parameters satisfy certain conditions. Compared with the case of the pure k-essence, the system possesses two stable fixed points under certain conditions such that we can model the evolution of the universe.Point x y z b $\lambda$ 

$\delta$ 

Eigenvalues Stability Condition A 0 $-\dfrac{\sigma}{12}$ 

0 $\dfrac{4+\sigma}{4}$ 

0 0 $-\dfrac{\sigma}{2}$ ,

$-\dfrac{\sigma}{4}$ ,

$\dfrac{\sigma}{4}$ ,

$\sigma$ ,

$-3-\sigma$ ,

$-4-\sigma$ ,

Unstable B 0 $-\dfrac{\sigma}{12}$ 

0 $\dfrac{4+\sigma}{4}$ 

$\dfrac{\sigma}{4(-1+\Gamma)}$ 

0 $-\dfrac{\sigma}{4}$ ,

$\dfrac{\sigma}{4}$ ,

$-\dfrac{(-3+2\Gamma)\sigma}{4(-1+\Gamma)}$ ,

$-3-\sigma$ ,

$-4-\sigma$ 

Unstable C 0 $-\dfrac{\sigma}{12}$ 

0 $\dfrac{4+\sigma}{4}$ 

0 $\dfrac{\sigma}{-5+4\tau}$ 

$-\dfrac{\sigma}{4}$ ,

$\dfrac{\sigma}{4}$ ,

$-3-\sigma$ ,

$-4-\sigma$ ,

$-\dfrac{2(-\sigma+\sigma\tau)}{-5+4\tau}$ ,

$-\dfrac{-\sigma+\sigma\tau}{-5+4\tau}$ 

$-3<\sigma<0$ ,

$1<\tau<5/4$ 

D 0 $-\dfrac{\sigma}{12}$ 

0 $\dfrac{4+\sigma}{4}$ 

$\dfrac{\sigma(-1+\tau)}{(-1+\Gamma)(-5+4\tau)}$ 

$\dfrac{\sigma}{-5+4\tau}$ 

$\dfrac{\sigma}{4}$ ,

$\sigma$ ,

$-3-\sigma$ ,

$-4-\sigma$ ,

$\dfrac{-\sigma+\sigma\tau}{-5+4\tau}$ ,

$-\dfrac{(2\Gamma-3)(\tau-1)\sigma}{(-1+\Gamma)(-5+4\tau)}$ 

$\tau>5/4$ or

$\tau<1$ 

$1<\Gamma<3/2$ 

$-3<\sigma<0$ 

E $-\dfrac{\sigma}{6}$ 

0 0 $\dfrac{6+\sigma}{6}$ 

0 0 0,0, $\sigma$ ,

$\sigma$ ,

$-3-\sigma$ ,

$-6-\sigma$ 

Saddle point for $-3\leq\sigma\leq 0$ 

F 0 $\dfrac{1}{3}$ 

0 0 0 0 −4,2,1,1,1, $4+\sigma$ 

Unstable G 0 $\dfrac{1}{3}$ 

0 0 0 $\dfrac{4}{5-4\tau}$ 

$\dfrac{4(-1+\tau)}{-5+4\tau}$ ,

$\dfrac{8(-1+\tau)}{-5+4\tau}$ ,-4,-1,1,

$4+\sigma$ 

Unstable H 0 $\dfrac{1}{3}$ 

0 0 $\dfrac{1}{1-\Gamma}$ 

0 −4,−1,1,1, $\dfrac{-3+2\Gamma}{-1+\Gamma}$ ,

$4+\sigma$ 

Unstable I 0 $\dfrac{1}{3}$ 

0 0 $-\dfrac{4(-1+\tau)}{(-1+\Gamma)(-5+4\tau)}$ 

$\dfrac{4}{5-4\tau}$ 

$-\dfrac{4(-1+\tau)}{-5+4\tau}$ ,

$\dfrac{4(-3+2\Gamma)(-1+\tau)}{(-1+\Gamma)(-5+4\tau)}$ ,−4,−1,1,

$4+\sigma$ 

Unstable J −2 1 0 0 0 0 −3,−3,0,0,0, $\sigma$ 

Saddle point for $\sigma\leq0$ 

K 1 0 0 0 0 0 ${-6,-6,3,0,0,6+\sigma}$ 

Unstable Table 4. Fixed points for k-essence with non-zero potential and dynamically changing
$\lambda$ and$\delta$ . -
In this paper, we have studied the dynamics of a k-essence in LQC. In particular, we have discussed the stability conditions of the fixed points. Compared with the standard FRW universe, we need an additional dimensionless variable
$ z\equiv\rho_t/\rho_c $ . Notice that non-zero z is related to the LQG effect. Our discussion is divided into two main parts. One is that$ \lambda $ and$ \delta $ are treated as constant coupling parameters. Another is that$ \lambda $ and$ \delta $ are dynamically changing variables. For every case, we explore the dynamics of the pure k-essence and k-essence with non-zero potential. We summarize the main properties of the dynamical system as follows:● z is zero for all fixed points. This means that the LQG effect is diluted in the later stage of the universe. The evolution of the system indicates that the LQG effect plays a key role only in the early epoch of the universe.
● The fixed points in LQC are basically consistent with those in standard FRW cosmology [66]. For most of the attractor solutions, the stability conditions are consistent with those for the standard FRW universe. For some special fixed points, however, for example the fixed point C in Table 1, tighter constraints are imposed thanks to the LQG effect.
In the LQC framework, there are several directions deserving further pursuit:
● The LQG effect is more evident in the early universe than the current universe. It would therefore be interesting to study the evolution of k-essence in the early universe in the LQC framework.
● We can explore the k-essence dynamical system in a spatially curved FRW universe [75].
● It would definitely be interesting to study the dynamical system when an interaction term between k-essence and the fluid is included.
● One of the important dark energy models, other than those driven by scalar fields, is the so-called Chaplygin gap model, which unifies dark energy and dark matter [76-78]. Its dynamical behavior has also been studied in Ref. [79]. It would be interesting to extend such studies to the LQC framework such that we can explore the effect of LQG.
● It would be especially interesting to study the dark energy evolution in the version of the modified Friedmann equation proposed in Refs. [59, 67]. The version of the modified Friedmann equation in Refs. [59, 67] reduces to the leading order effective one (Eq. (2)) if the higher correction terms are neglected. The higher correction terms may result in a qualitatively different scenario from that of the leading order effective theory (2).
Dynamics of k-essence in loop quantum cosmology
- Received Date: 2020-11-15
- Available Online: 2021-04-15
Abstract: In this paper, we study the dynamics of k-essence in loop quantum cosmology (LQC). The study indicates that the loop quantum gravity (LQG) effect plays a key role only in the early epoch of the universe and is diluted in the later stages. The fixed points in LQC are basically consistent with those in standard Friedmann-Robertson-Walker (FRW) cosmology. For most of the attractor solutions, the stability conditions in LQC are in agreement with those for the standard FRW universe. For some special fixed points, however, tighter constraints are imposed thanks to the LQG effect.





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF













 DownLoad:
DownLoad: