-
In classical physics, the three-body problem in gravitation systems can be traced back to Galileo Galilei. Its nonlinearity led to the research field of dynamical systems, founded by Henri Poincaré's works. Except for some special and stable solutions [1, 2], a generic dynamical system is usually too complicated to solve without supercomputers. Ineluctably this situation passed on to its descendants when married with quantum mechanics. Nevertheless, there are also supposed to be some special solutions in quantum systems, which are usually closely related to low energy or long range properties of the system [3]. The Efimov effect, which is found in the quantum spectrum of a three-heavy-particle system, is one of these special solutions. Intuitively, the three-body states are also referred to as Borromean-ring states in which any pairs of these three are bound infinitely loosely. The geometric series of three-body bound states (Efimov series) was first found in nuclear systems by Efimov in the 1970s [4, 5]. Theoretically, the Efimov effect can easily be seen in the hyperspherical formalism [6] where a scale-invariant
$ -r^{-2} $ potential emerges at long distances, with r being the hyper radius. From the renormalization group (RG) point of view, it corresponds to a limit cycle behavior of the RG flow [7]. The Efimov effect has been observed in hypernuclei [8], halo nuclei [9], and helium-4 atoms [10, 11]. In the past two decades, it has attracted renewed interest due to the fast development of experimental techniques of ultracold atomic physics, which offers an ideal platform for the study of such an effect. Measurement of the loss rate of ultracold Bose gases [12-14], which directly reflects the effect of underlying Efimov trimers, is in good agreement with theoretical predictions [7]. These few-body studies further provide valuable input for the understanding of more sophisticated quantum many-body problems.Although the Efimov effect, or Borromean states in general, is identified as a low-energy/long-range correlation effect, the original non-relativistic (NR) model does not apply to particles that do not have a proper non-relativistic limit, such as the massless case. It is thus appealing to ask whether such exotic few-body states exist in relativistic cases. Moreover, this question has much realistic meaning in high energy nuclear physics, for the following two reasons. First, in relativistic heavy ion collisions, the extremely hot quark-gluon plasma (QGP) generated contains a huge number of particles and anti-particles. In such a many-body system, a remarkable number of novel states, which are too rare to be detected in
$ p+p $ collisions, may be generated. For example, the population of the very rare heavy state$ \Xi^+_{cc} $ could be 4 orders of magnitude larger than in$ p+p $ collisions [15]. The light particles, such as the$ \pi $ meson, which serves as the Goldstone boson corresponding to chiral symmetry breaking, and light quarks, which can be treated as chiral fermions in QGP, may form different kinds of novel few-body states, and hence be observed. Second, the long-range two-body color confinement potential would be screened because of the finite temperature effect in the QGP [16, 17], which enhances the probability of Borromean state formation, such as more ordinary baryonic states of light quarks. We hope the study can provide some clues to the nuclear hadronization mechanism and the underlying quark confinement problem. Obviously these processes can only be studied in relativistic models. In this work we will focus on 3-body Borromean states because they are more model-independent and more nontrivial than bound states of a 2-body molecule and one particle, which is essentially more like a 2-body problem. Its existence mainly depends on the qualitative or even asymptotic behaviors of the interaction.There are a few works concerning the Efimov-like effect or Borromean states in relativistic bosonic systems [18-21] by straightforward Mandelstam variable replacement and the Bethe-Salpeter equation. On the other hand, fermions, which are believed to be trivial because of the Pauli exclusion principle, have attracted much less interest in the relativistic limit. Nevertheless, the potential novel states and quark confinement problem motivate us to reconsider the relativistic 3-body problem, especially the fermionic systems, more seriously. In order to study 2-body and 3-body interactions simultaneously, we will start from particle–di-particle models with only the 2-body fundamental interaction, whose scattering amplitude is supposed to be much larger than the 3-body one. The di-particle state, in particular the diquark [22-26], which can be viewed approximately as a 2-body bosonic bound state, is not only a useful effective degree of freedom in the model but also has important and realistic applications in the modelling of hadronization and phase diagram studies of baryon-rich matter. In the fermionic case we will more focus on a momentum-dependent 3-body interaction which is motivated by heavy baryon studies [27] with a similar model.
For the relativistic and fermionic case the Bethe-Salpeter equation and Dirac equation approaches are either too tedious in both analytical and numerical computation [28] or have difficulties in constructing a self-consistent relativistic spin-dependent 2-body potential [15, 29]. In this report we adopt an intuitive and self-consistent approach, the Wilsonian renormalization group [30], to study both the bosonic and fermionic systems in the relativistic limit. We start with an effective theory with an initial ultraviolet (UV) 3-momentum cutoff
$ \Lambda_0 $ , i.e. a theory defined at length scales$ \Lambda_0^{-1} $ . During the RG process, the cutoff is lowered by integrating out “fast modes” whose 3-momenta lie in a momentum shell between$ \Lambda (< \Lambda_0) $ and$ \Lambda_0 $ , yielding an effective theory at momentum scale$ \Lambda $ . In real space, this realizes a coarse-graining procedure from length scale$ \Lambda_0^{-1} $ to$ \Lambda^{-1} $ . To identify possible three-body bound states, we focus on the running particle-di-particle coupling, whose divergence signals the emergence of a bound state at the corresponding energy scale. We will firstly confirm the Efimov effect in the linear bosonic model, as in Refs. [31, 32], with the simplest coupling in both NR and relativistic limits. For the fermionic case, the fermion – di-fermion model will be introduced. It will be shown that there is an indicator of a single Borromean state in the relativistic limit, while the system becomes trivial in the non-relativitic limit, as expected. -
We adopt a boson-di–boson model to study the three-body problem. It is much easier to deal with than a fermionic model because there is no Dirac structure in the vertices. The Lagrangian density reads
$ \begin{aligned}[b] {\cal{L}} =& \partial^\mu\phi^\dagger\partial_\mu\phi +m^2\phi^2+\partial^\mu\Delta^\dagger\partial_\mu\Delta +M^2\Delta^2\\ & +h (\Delta^\dagger \phi^2+\Delta \phi^{\dagger 2})+g \Delta^2\phi^2, \end{aligned} $

(1) where
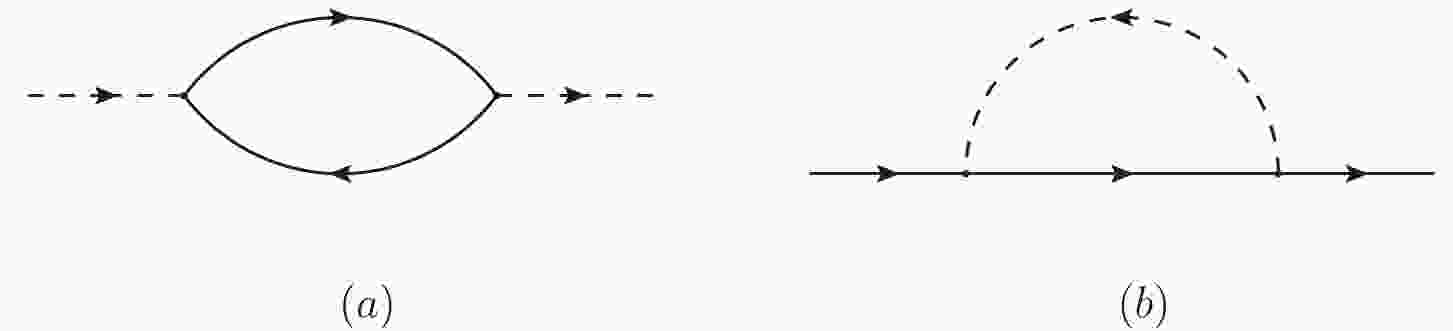
$ \Delta $ and$ \phi $ are both bosonic fields. Obviously the$ \Delta $ field can be viewed as a two-$ \phi $ composite field because of the field equation$ \Delta = h \phi^2 $ in the static limit. We will focus on poles of the 4-point vertex which represents potential bound states in the$ 3\phi\rightarrow 3\phi $ scattering process. In order to obtain the flow equation of g we follow the procedure in Refs. [33, 34] by computing the perturbative corrections to the 2, 3 and 4-point vertices with the 3-momentum shell renormalization, rather than the usual 4-momentum integration used in high energy physics. In this work we will treat field masses as free parameters and tune them to achieve two energy-scale limits and thus neglect the tadpole diagrams. Because of charge conservation there is no one-loop correction to the 3-point vertex. Hence the flow equation of h is given by the wave function renormalization of$ \Delta $ and$ \phi $ fields in Fig. 1 at leading order, i.e.$ \partial_s h = h \partial_s Z_{\phi}+\dfrac{1}{2}h\partial_s Z_\Delta $ . The arrows of the propagators represent the charge direction. In non-relativistic models there is no diagram (b) because of the absence of anti-particles. Here we will see that in the NR limit the contribution of diagram (b) is suppressed by mass.The flow equations of wave function renormalization,
$ Z_\Delta $ and$ Z_{\phi} $ , and vertices in the NR limit, i.e.$ \Lambda \ll m $ and$ E_k\simeq m+k^2/(2m) $ , are calculated as follows:$ \partial_s Z_\Delta = -\frac{2}{32\pi^2}\frac{h^2}{m\Lambda},\;\;\;\;\;\ \partial_s Z_{\phi} = -\frac{2}{32\pi^2}\frac{h^2}{\Lambda^2}, $

(2) $ \partial_s g = \frac{13}{48\pi^2}\frac{g h^2}{m\Lambda}-\frac{1}{3\pi^2}\frac{h^4}{m\Lambda^3}-\frac{1}{12\pi^2}\frac{g^2\Lambda}{m}, $

(3) where
$ \Lambda = \Lambda_0 {\rm e}^{-s} $ is the running 3-momentum cutoff. We consider 1-loop corrections to the 4-point vertex coupling g as presented in Fig. 2. In the NR case, diagram (e) is negligible at leading order. In the computation, the mass of the two-body field$ \Delta $ is chosen as$ M = 2m $ . This is justified by the fact that$ h^2 = 16\pi^2 m\Lambda $ approaches zero in the infrared limit$ \Lambda\rightarrow 0 $ (large s), which means that in this limit the two-body state is quite loosely bound. Making use of the result of h in this limit, the flow equation of coupling g gives the following solution,$ g = \frac{4\pi^2m}{\Lambda}\left[-\sqrt{39}{\rm Tan}\left(\frac{\sqrt{39}}{3}s+c_0\right)+5\right], $

(4) whose poles correspond to the spectra of potential 3-body states. Obviously the ratio between binding energies of two neighboring 3-body Borromean states is given by
$ {\rm e}^{2\delta s} $ , with the step of singularities$ \delta s \approx 0.48 \pi $ for this simple model. Besides the expected Efimov-like behavior, we find that the dimensionless 4-vertex coupling g behaves as a dimensionful quantity scaling with$ \Lambda^{-1} $ as the unit of mass. The same results can be obtained in an explicit NR model by replacing the propagators with$ (k_0-{\vec{k}}^2/(2m)+{\rm i} \eta)^{-1} $ .In the relativistic limit, the diagrammatic representations of 1-loop corrections are the same as those in Fig. 1 and Fig. 2. The difference is that in the limit
$ \Lambda\gg m $ , diagram (b) in Fig. 1 and diagram (e) in Fig. 2, due to anti-particles, will be at the same order as the others, and hence contribute equally to the corrections of vertices. Taking this anti-particle contribution and the relativistic dispersion relation$ E_k\simeq k+m^2/(2k) $ into account, the flow equations are:$ \partial_s Z_{\phi} = -\frac{4}{32\pi^2}\frac{h^2}{\Lambda^2},\;\;\;\;\;\ \partial_s Z_\Delta = -\frac{2}{32\pi^2}\frac{h^2}{\Lambda^2}, $

(5) $ \partial_s g = \frac{9}{16\pi^2}\frac{g h^2}{\Lambda^2}-\frac{5}{4\pi^2}\frac{h^4}{\Lambda^4}-\frac{g^2}{4\pi^2}. $

(6) Again we take
$ M = 2m $ in the computation because$ h^2 = \dfrac{32}{5}\pi^2\Lambda^2 $ tends to vanish in the IR limit. Since there is no mass dependence in these equations, their solution would not be changed even in the zero mass limit. As expected, the wave function renormalization$ Z_{\phi} $ is at the same order as$ Z_\Delta $ . This antiparticle contribution also appears in the$ g^2 $ term of Eq. (6). In the infrared limit, namely small$ \Lambda $ and large s, solutions read$ g = -\frac{4\sqrt{239}}{5}\pi^2{\rm Tan}\left(\frac{\sqrt{239}}{5}s+c_0\right)+\frac{36}{5}\pi^2. $

(7) Although the
$ \Lambda $ dependence of h and g has changed because of the relativistic dispersion relation, the structure of solution is qualitatively the same. We get the Efimov-like series of poles with the energy step reduced to$ \delta s\simeq 0.323\pi $ . -
As a reducible 4-dimensional representation, the Dirac spinor can be studied more straightforwardly and self-consistently in relativistic quantum field theory. Although it is well-known that the simplest 3-body Borromean states do not exist in the NR fermionic system because of the Pauli exclusion principle, we will still examine its Dirac structure, i.e. spin-spin interaction, in detail to find whether there is any non-trivial, such as Borromean, 3-body state. Similar to the bosonic case, we introduce a fermion–di-fermion model to study this problem,
$ \begin{aligned}[b] {\cal{L}} =\;& \bar{\psi}({\rm i} {\not\!\!{\partial}}-m)\psi+\partial^\mu\Delta^\dagger\partial_\mu\Delta +M^2\Delta^2\\ & -{\rm i} h (\Delta^\dagger {\bar\psi}_c\gamma^5\psi+\Delta \bar\psi \gamma^5 \psi_c)\\ & +g_1 (\Delta^2\bar\psi \psi+\Delta^{\dagger 2}\bar\psi_c \psi_c)\\ &+g_2 (\Delta^2\bar\psi {{\rm i} {\not\!\!{\partial}}}\psi+\Delta^{\dagger 2}\bar\psi_c {{\rm i} {\not\!\!{\partial}}}\psi_c), \end{aligned} $

(8) where
$ \psi_c = C\bar\psi^T = {\rm i}\gamma^2\gamma^0\bar\psi^T $ . This model is motivated by the so-call quark-diquark model for studies of quark matter in high energy nuclear physics. Here we choose the one-flavor and one-color quark field for simplicity, since the static isospin and color charge will not change the momentum dependence of the coupling constants which play crucial roles in the structure of the 4-point vertex flow equation. Effectively,$ \psi+\psi_c\rightarrow \Delta $ will generate two kinds of 4-point interaction, the s-wave$ g_1 \Delta^2\bar\psi \psi $ and the p-wave$ g_2 \Delta^2\bar\psi {i {\not{\partial}}}\psi $ , because of the Dirac structure. This can easily be checked by straightforward perturbative computation. Although in principle the s-wave part is supposed to vanish in the one-flavor and one-color scenario because of the Pauli exclusion principle, we still keep it for the following two reasons. First, the Pauli exclusion principle could be detoured by introducing more static color or flavor numbers which will bring no changes to the momentum dependence of the coupling constants, up to some symmetric factors. Second, the di-fermion is treated as a fundamental field in this model. As a result this will not technically forbid the s-wave 3-body interaction. It therefore gives us a chance to study its flow equation qualitatively in this simple model. For simplicity we will neglect mixing processes, i.e.$ g_1g_2 $ terms, and calculate corrections to the flow of the two 4-point vertices separately.The contributing diagrams are the same as those in Figs. 1 and 2 if we replace the solid propagators with fermionic ones. In the NR case for the s-wave coupling we get the flow equations as:
$ \partial_s Z_\Delta = -\frac{m h^2}{4\pi^2\Lambda},\;\;\;\;\;\ \partial_s Z_\psi = \frac{h^2 \Lambda^3}{18\pi^2 m^3}, $

(9) $ \partial_s g_1 = -\frac{5m h^2 g_1}{12\pi^2 \Lambda}-\frac{m^2 h^4}{12\pi^2\Lambda^3}-\frac{g_1^2 \Lambda}{12\pi^2}. $

(10) Similar to the bosonic case, the
$ Z_\psi $ term, due to the anti-fermion, is suppressed by the mass as$ m^{-3} $ . By safely neglecting the anti-fermion contribution and taking the small$ \Lambda $ and large m limit, we obtain solutions as$ g_1 = \frac{2\sqrt{21}\pi^2}{\Lambda}\left[{\rm Tanh}\left(\frac{\sqrt{21}s}{6}+c_0\right)-\frac{5}{\sqrt{21}}\right], $

(11) where M has been set as
$ 2m $ , since the two-body coupling$ h^{2} = 4\pi^2\dfrac{\Lambda}{m} $ approaches zero in the small$ \Lambda $ limit. When the system contains only s-wave coupling, there is no singularity along s for the hyperbolic tangent function, which means no 3-body state appears. This is a well-known result in the NR fermionic system. As a byproduct we also find that the 3-point vertex h is suppressed by m as well, which agrees with the vanishing of the$ \Delta \psi \psi $ term in the NR model because of the fermionic anti-exchange property. In contrast the bosonic result is enhanced by the mass.Although the p-wave vertex has a different momentum dependence, it does not give us any surprises either. The flow equation of
$ g_2 $ reads$ \partial_s g_2 = -\frac{7m h^2 g_2}{12\pi^2\Lambda}-\frac{m h^4}{12\pi^2\Lambda^3}-\frac{m g_2^2 \Lambda}{3\pi^2}. $

(12) Only the
$ g_2 h^2 $ and$ g_2^2 $ terms are modified. We get a similar hyperbolic tangent solution,$ g_2 = -\frac{\pi^2}{m \Lambda}\left[\sqrt{21}{\rm Tanh}\left(\frac{\sqrt{21}}{3}s+c_0\right)-5\right]. $

(13) In the relativistic case, i.e.
$ m\ll\Lambda $ , the s-wave case is trivial. The$ g_1^2 $ and$ h^4 $ terms are proportional to m, therefore the flow of$ g_1 $ should be governed by the$ g_1 h^2 $ term and results in a trivial solution$ g_1\sim s^{-1} $ . In the following we focus on the p-wave interaction, whose flow equations are:$ \partial_s Z_\Delta = -\frac{h^2}{4\pi^2},\;\;\;\;\;\ \partial_s Z_\psi = -\frac{h^2}{4\pi^2}, $

(14) $ \partial_s g_2 = -\frac{7h^2 g_2}{8\pi^2}-\frac{5h^4}{32\pi^2\Lambda^2}+\frac{3 g_2^2 \Lambda^2}{2\pi^2}. $

(15) There are no mass dependences, so the solution will not be altered even in the chiral limit
$ m = 0 $ . In the small$ \Lambda $ limit we find that the two-body coupling goes to zero as$ h^2 = 4\pi^2/(3s) $ . Furthermore,$ g_2 $ should satisfy$ \partial_s G = -2G -\frac{5\pi^2}{18s^2}-\frac{7}{6s}G+\frac{3}{2\pi^2}G^2, $

(16) where
$ G = \Lambda^2 g_2 $ . The solution goes to$ -{\rm e}^{-2s} $ at large s and converges to$ \pi^2(\sqrt{61}+1)s^{-1}/18 $ at small s. As a typical Riccati equation, it is usually linearized with an auxiliary function$ u(s) $ as$ G(s) = -\dfrac{2\pi^2}{3}\dfrac{\partial_s u}{u} $ . The corresponding solution is$ u(s) = c_1{\rm e}^{2s}s^{\beta-\alpha}[c_0 U_{\alpha}^{\beta}(2s)+ L_{-\alpha}^{\beta-1}(2s)], $

(17) where
$ \alpha = (13+\sqrt{61})/12 $ ,$ \beta = \sqrt{61}/6+1 $ ,$ U_\alpha^\beta $ is the Tricomi confluent hypergeometric function, and$ L_\alpha^\beta $ is the generalized Laguerre polynomial. Obviously the zeros of$ u(s) $ will generate singularities of$ G(s) $ . When the integral constant$ c_0>0 $ , there is an isolated zero of$ u(s) $ which generates a 1st order pole of$ G(s) $ at finite s, and the corresponding pole increases with c0. When$ c_0<0 $ , the pole approaches zero smoothly. The flow of G with different$ c_0 $ is presented in Fig. 3.In the UV range (small s) all of the lines converge to the same value
$ \pi^2\beta/(3s) $ , while in the IR range (large s), different$ c_0 $ correspond to different values at the low energy-scale. However, it is not easy to tune the coupling in the deep IR range to get the 3-body Borromean state, since the value differences are quite small in this range. -
We have checked the existence of Efimov-like states in bosonic systems with the linear bosonic model. In the NR limit we confirmed, firstly, that the contribution from antiparticles is negligible, as expected. Secondly, a series of Efimov-like singularities is found in the flow of the 4-point vertex. Although more detailed computations are needed to reduce the deviation from the standard value of
$ \delta s \approx \pi $ , qualitatively the NR approximation is promising. In the relativistic limit we find that the Efimov-like effect still exists but with a smaller energy ratio. Furthermore, the mass dependence disappears in the flow equations, which means the conclusion would hold even in the massless limit. For the fermionic case the fermion–di-fermion model, motivated by the quark-diquark model in the quark matter phase diagram and heavy baryon studies, is adopted. Because of the Dirac structure of fermions there are two kinds of 4-point vertices that should be taken into account, the s-wave and p-wave vertices. In the NR limit both vertices are trivial. The 3-vertex is suppressed by$ \Lambda/m $ and thus vanishes in the large mass limit. This agrees with straightforward computations of NR models.In the relativistic limit the result is more non-trivial. Depending on the IR value of the p-wave 4-vertex coupling, there may be one isolated pole at finite s. In quark matter the quark-diquark coupling originates from the fundamental strong interaction between color charge, so this singularity may indicate a special baryonic state of quarks. As in the bosonic case, this singularity has no mass dependence, which means it would persist even for chiral fermions. For both bosonic and fermionic systems, all of the singularities appear in the IR range where the 3-vertex approaches zero. They can therefore be identified as Borromean states. Although it is an exciting clue that there may be a single Borromean state in the chiral fermion case, we should admit that detection is actually difficult by considering the full interaction of different kinds of charges, such as color and isospin. The gauge fields may easily destroy the bound state due to the large amplitudes of processes involving soft gauge bosons. In order to determine the existence of the state, more work is required, such as fitting the IR value of the model and estimating the scattering amplitude of different processes from a more realistic model. We also believe that a more definite answer could be obtained by solving the 3-body Dirac equation with a suitable spin-dependent 2-body potential, such as that in Ref. [15].
Relativistic Borromean states
- Received Date: 2020-12-24
- Available Online: 2021-04-15
Abstract: In this work, the existence of Borromean states is discussed for bosonic and fermionic cases in both the relativistic and non-relativistic limits from the 3-momentum shell renormalization. With the linear bosonic model, we check the existence of Efimov-like states in the bosonic system. In both limits a geometric series of singularities is found in the 3-boson interaction vertex, while the energy ratio is reduced by around 70% in the relativistic limit because of the anti-particle contribution. Motivated by the quark-diquark model in heavy baryon studies, we have carefully examined the p-wave quark-diquark interaction and found an isolated Borromean pole at finite energy scale. This may indicate a special baryonic state of light quarks in high energy quark matter. In other cases, trivial results are obtained as expected. In the relativistic limit, for both bosonic and fermionic cases, potential Borromean states are independent of the mass, which means the results would also be valid even in the zero-mass limit.






 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF

















 DownLoad:
DownLoad: