Entropic force between two horizons of dilaton black holes with a power-Maxwell field

In the early cosmic inflation period, our universe is thought to have been a quasi-asymptotic de Sitter (dS) space-time, where the introduced cosmological constant term can be seen as the vacuum energy. If the cosmological constant corresponds to dark energy, our universe will evolve into a new de Sitter phase. In order to construct the whole evolutionary history for our universe and also find the reason for the accelerated expansion, the classical, quantum and thermodynamic properties of dS space-time should be studied. In addition, the success of the correspondence between anti-de Sitter space and conformal field theory (AdS/CFT) has prompted people to find a similar dual relationship for de Sitter space-time.

In recent years, the thermodynamic properties and possible phase transitions of dS black holes have been studied extensively [1-22]. For a dS black hole there is a black hole horizon and a cosmological horizon, and, in general, the radiation temperatures of the two horizons are different. Considering the two horizons as two thermodynamic systems, they each satisfy the first law of black hole thermodynamics, but their thermodynamic quantities are interrelated because of their common quantities, mass, electric charge, and cosmological constant. In most previous works on the thermodynamic properties of dS black holes, the whole entropy of the dS black hole is seen as the sum of the entropies of the black hole horizon and cosmological horizon. Considering the correlation of the two horizons, a correction term for the whole entropy is required. This is derived and analyzed in this work.

In 2011, Verlinde [23] thought of linking gravity to an entropic force. Gravity emerges as a consequence of information regarding the positions of material bodies, combining a thermal gravitation treatment with 't Hooft's holographic principle. The ensuing conjecture was later proved [24-31] in a classical scenario. Accordingly, gravitation ought to be viewed as an emergent phenomenon. This exciting idea of Verlinde's received a lot of attention [32-37]. The entropic force is therefore an important force in the universe and it is probably one of the participants in driving the accelerated cosmic expansion.

As an explanation for the accelerated cosmic expansion, the early theory of dark energy was proposed by Riess [38-41]. In this theory, the accelerated cosmic expansion is caused by an exotic component called dark energy, which accounts for about 73% of the universe's capacity according to astronomical observations. Astronomers assume that dark energy exists in the first second after the Big Bang. The Big Bang pushes all matter into the whole space, and then the initial expansion begins. Shortly after the Big Bang, dark energy bumps several times, which causes the present accelerated expansion. Some models for dark energy evolution have been proposed. For example, if the equation of state of dark energy is $ P = \omega \rho $, where $ \omega $ is the parameter of the equation of state, the evolution of dark energy is exponential with the power $ 3(1 + \omega ) $ when $ \omega > - 1 $ [42-46]. The effect of dark energy is to cause the accelerated expansion [32], which means it has some kind of repulsion. But what is the nature of dark energy? How does it evolve with the cosmic expansion? This is still unknown.

In addition, another possible reason for the accelerated cosmic expansion is dark matter, which interacts more strongly with normal matter and radiation than previously assumed. The existence of dark matter in the universe is commonly assumed in modern cosmology. Dark matter accounts for about 23% of the total cosmic components. Dark matter does not participate in electromagnetic interaction, nor interact with photons. The latest research shows [47-49] that dark matter appeared earlier than normal matter during the expansion of the universe, although normal matter is produced during the Big Bang. A kind of non-spin scalar particle is produced during the rapid cosmic expansion. To date, only one type of scalar particle has been found, the famous Higgs boson. According to Tenkanen, it could be a candidate for dark matter. But how do the dark energy, the dark matter and the total energy of the universe evolve in the expanding universe? The real reason for the accelerated expansion is still not clear.

The fact that the expansion of the universe is accelerating, along with the scheme of the standard Friedmann model [40], has created much interest in alternative theories of gravity in recent years. One such theory is dilaton gravity. Dilaton gravity can be thought as the low energy limit of string theory, and one recovers Einstein gravity along with a scalar dilaton field, which is non-minimally coupled to the gravity and other fields such as gauge fields. We are interested in studying the properties of dilaton black holes when the gauge field is in the form of a power-Maxwell field [50]. Being different from a linear electromagnetic field, nonlinear electrodynamics was introduced to remove the central singularity of the point-like charges and obtained finite energy solutions for particles by extending Maxwell's theory. In cosmology, one can call upon nonlinear electrodynamics to explain the inflationary epoch and the late-time accelerated expansion of the universe [51, 52]. A variety of nonlinear electrodynamics models [53-58] have been proposed and studied extensively, in which the power-Maxwell field [54] is conformally invariant in $ (n+1) $-dimensional space-time for $ p = (n+1)/4 $, where p is the power parameter of the power-Maxwell Lagrangian, while the Maxwell Lagrangian is only conformally invariant in four dimensions.

The effect of the dilaton field [15, 59, 60] and the power-law Maxwell field [61-64] on the thermodynamics of anti-de Sitter (AdS) black holes has been studied in extended phase space. However, as far as we know, the effective thermodynamic quantities with the effects of the power-law Maxwell field and the dilaton field have not been discussed for de Sitter space-time. In this paper, we study the entropy and entropic force of dilaton black holes coupled to a nonlinear power-Maxwell field in de Sitter space-time. We investigate the effects of the exponent p, the dilaton coupling constant $ \alpha $ and the space-time dimension n on the entropy and the entropic force of the black holes in dS space-time, and explore their connection to the expansion of the universe.

This paper is organized as follows. The solutions of a charged dilaton black hole with a power-Maxwell field in dS space-time are introduced in Section II. The thermodynamic quantities corresponding to the black hole event horizon and the cosmological event horizon in dS space-time are given in Section III. Considering the correlation of the two horizons, the effective thermodynamic quantities and the modified entropy are derived in Section IV. In Section V, based on the relationship between entropy and entropic force, the entropic force between the two horizons is obtained and analyzed. Discussion and conclusions are given in the last section. The units $ {G_{n + 1}} = \hbar = {k_B} = c = 1 $ will be used throughout this work.

In this section, we introduce the action of Einstein power-Maxwell-dilaton (EPMD) gravity, the solutions of the EPMD field equations, and the mass, electric charge, and cosmological constant of EPMD black holes in dS space-time.

The action of $ (n+1) $-dimensional $ (n\geqslant 3) $ EPMD gravity can be written as [50, 59, 65-67]

which can yield the following field equations by taking the action as varying with respect to the gravitational field $ g_{\mu,\nu} $, dilaton field $ \phi $ and the gauge field $ F_{\mu,\nu} :$

where R is the Ricci scalar, $ V(\Phi ) $ is a potential for $ \Phi $, and p and $ \alpha $ are two constants determining the nonlinearity of the electromagnetic field and the strength of coupling of the scalar and electromagnetic fields, respectively. $ {F_{\mu \nu }} = {\partial _\mu }{A_\nu } - {\partial _\nu }{A_\mu } $ is the electromagnetic field tensor and $ {A_\mu } $ is the electromagnetic potential.

The topological black hole solutions take the form [50, 59, 65-67]

where

and

in which b is an arbitrary nonzero positive constant, $ \gamma = {\alpha ^2}/({\alpha ^2} + 1) $, and $ \Pi = {\alpha ^2} + (n - 1 - {\alpha ^2})p $.

Note that $ \Lambda $ remains a free parameter and $ {\Lambda}>0 $ in dS space-time. It plays the role of the cosmological constant,

where l denotes the AdS length scale. In Eq. (5), m appears as an integration constant and is related to the ADM (Arnowitt-Deser-Misner) mass of the black hole. According to the definition of mass given by Abbott and Deser [68-72], the mass of the solution in Eq. (5) is [73]

The electric charge Q and potential U are expressed as [50]

The fact that the electric potential U should have a finite value at infinity and the term including m in the solution $ f(r) $ in spatial infinity should vanish lead to restrictions on p and $ \alpha $ [61]:

dS black holes have two horizons, the black hole event horizon (BEH) and the cosmological event horizon (CEH). The BEH is located at $ r = {r_ + } $ and the CEH is located at $ r = {r_c} $. Their positions can be determined by $ f({r_ + }) = 0 $ and $ f({r_c}) = 0 $ respectively. The thermodynamic quantities of the BEH and CEH each satisfy the first law of thermodynamics [3, 8, 13]. In this section, we introduce the thermodynamic quantities corresponding to the BEH and CEH respectively. Replacing r in Eq. (8) with $ r_+ $ or $ r_c $, one can get the electric potentials of the BEH or CEH.

The surface gravities of the BEH and CEH are respectively given by:

from which the radiation temperatures of the two horizons can be obtained from $ T_{+,c} = {\kappa _{+,c}}/{4\pi} $.

When $ f({r_{ + /c}}) = 0 $, we have:

$ m({r_ + }) = m({r_ c }) = m $, and taking $ x = {r_+ }/{r_c} $ as the ratio of the positions of BEH and CEH, which satisfies $ 0 < x \leqslant 1 $, then:

The thermodynamic volumes corresponding to the two horizons are respectively given by:

where $ {\omega _{n - 1}} $ represents the volume of constant curvature hypersurface described by $ {\rm d}\Omega _{k,n - 1}^2 $.

The entropies of BEH and CEH in dS space are expressed respectively as:

In general, the radiation temperatures of the BEH and CEH are different. So, If one investigates the black hole in dS space-time including BEH and CEH as a whole thermodynamic system, it is usually thermodynamically unstable or in non-equilibrium. We find that the radiation temperatures are equal if the charge of the system satisfies some condition. Under that condition, considering the correlation of the two horizons, we derive the effective thermodynamic quantities and the modified entropies of EPMD black holes in dS space-time.

When the radiation temperatures of BEH and CEH are equivalent, $ {\kappa _ + } = {\kappa _c} $, then Eq. (11) and Eq. (12) with Eq. (14) give the condition for the charge for the same radiation temperature of BEH and CEH,

where

Substituting Eq. (14) and Eq. (18) into Eq. (12), the temperature T for the same radiation temperature of BEH and CEH can be obtained as

Substituting Eq. (18) into Eq. (15) and Eq. (7) gives the energy (mass) of EPMD black holes in dS space-time as

where

Taking the EPMD dS space-time as a thermodynamic system, in Refs. [1, 3, 12, 16, 50, 67], the thermodynamic volume of the EPMD dS space-time is given by

Considering the correlation of BEH and CEH, we assume that the entropy of the EPMD dS space-time is expressed as

where $ {f_{AB}}(x) $ is an arbitrary function of x.

Using the effective thermodynamic quantities, the state parameters of the thermodynamic system satisfy the formula of the first law of thermodynamics, i.e.,

where the effective temperature $ {T_{\rm eff}} $, the effective pressure $ {P_{\rm eff}} $ and the effective potential $ {\Phi _{\rm eff}} $ of the EPMD dS black hole system are respectively defined as:

with

When $ T = {T_ + } = {T_c} $, which means the dS black hole thermodynamic system including BEH and CEH are in thermodynamic equilibrium, the effective temperature of the space-time should be equal to the radiation temperatures of the BEH and CEH. So, when the charge of the space-time $ {q^{2p}} $ is expressed by Eq. (18), $ {T_{\rm eff}} = {\tilde T_{\rm eff}}{\rm{ = }}{T_ + } = {T_c} $. Substituting Eq. (18) into Eq. (26) gives

where

Comparing Eq. (29) with Eq. (20), one can get

From Eq. (32) and Eq. (28), a differential equation for $ {F_n}(x) $ can be obtained. Taking the initial condition as $ {F_n}(0) = 1 $, i.e. $ {f_{AB}}(0) = 0 $, indicates that the interaction between the two horizons is zero when $ x = 0 $, and the solutions of the differential equation are

Substituting Eq. (33) into Eq. (26), the effective temperature of the EPMD dS space-time can be expressed as

The definition of the entropic force in the thermodynamic system is [24-37]

where T is the system temperature and r is the system radius. From Eq. (24), the entropy created by the interaction between the BEH and CEH is

According to Eq. (35), the corresponding entropic force between the two horizons can be given as

where $ {T_{\rm eff}} $ is the effective temperature of the system and $ r = {r_c} - {r_ + } = {r_c}(1 - x) $. Then

In order to describe the behaviors of the entropic force created by the interaction between the BEH and CEH and the effect of the parameters of the MPMD dS space-time on the entropic force, the solutions for the entropic force $ F(x) $ with different parameters, n, $ \alpha $, p and $ \kappa $ are depicted in the following figures, where we have taken

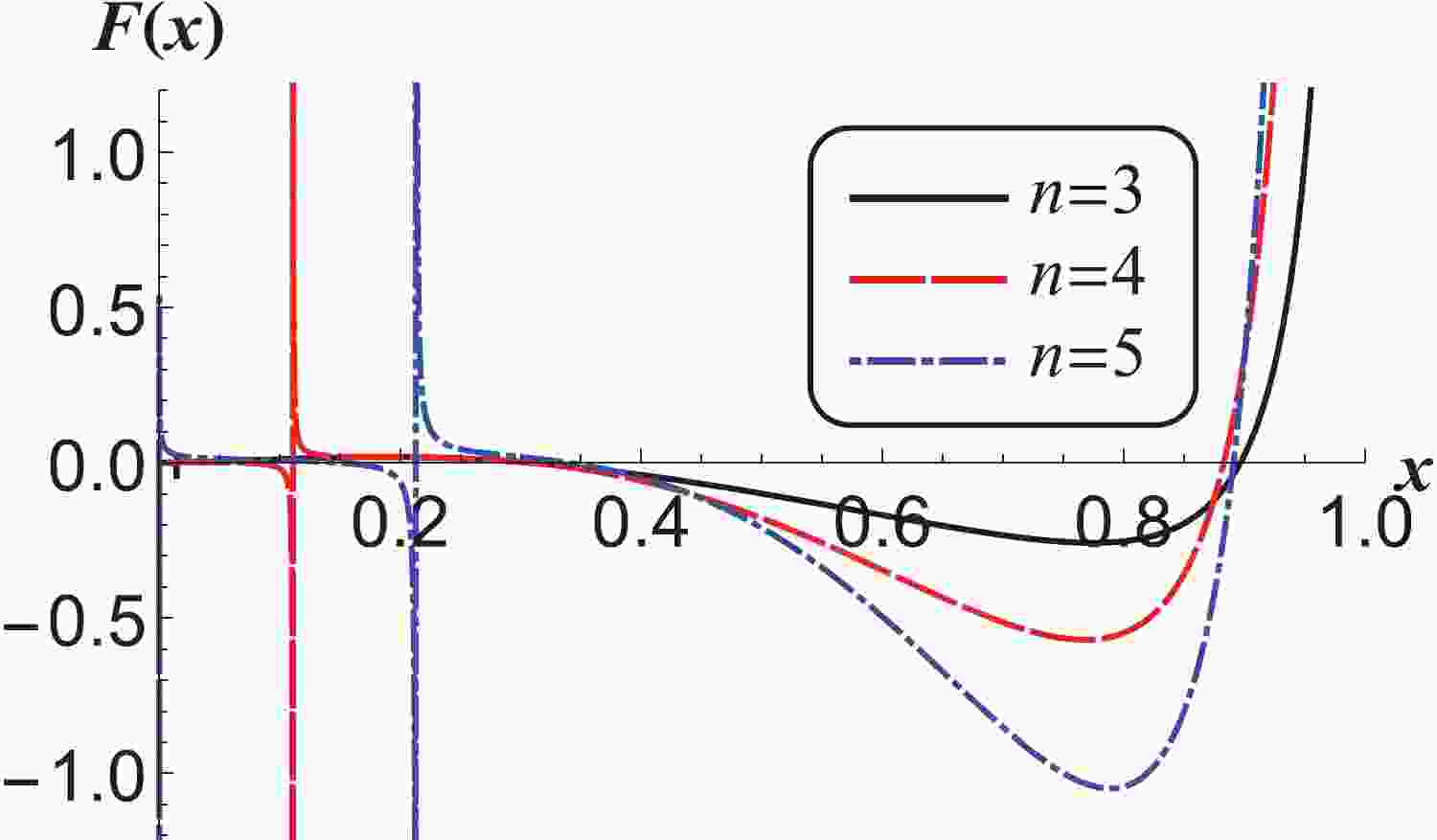
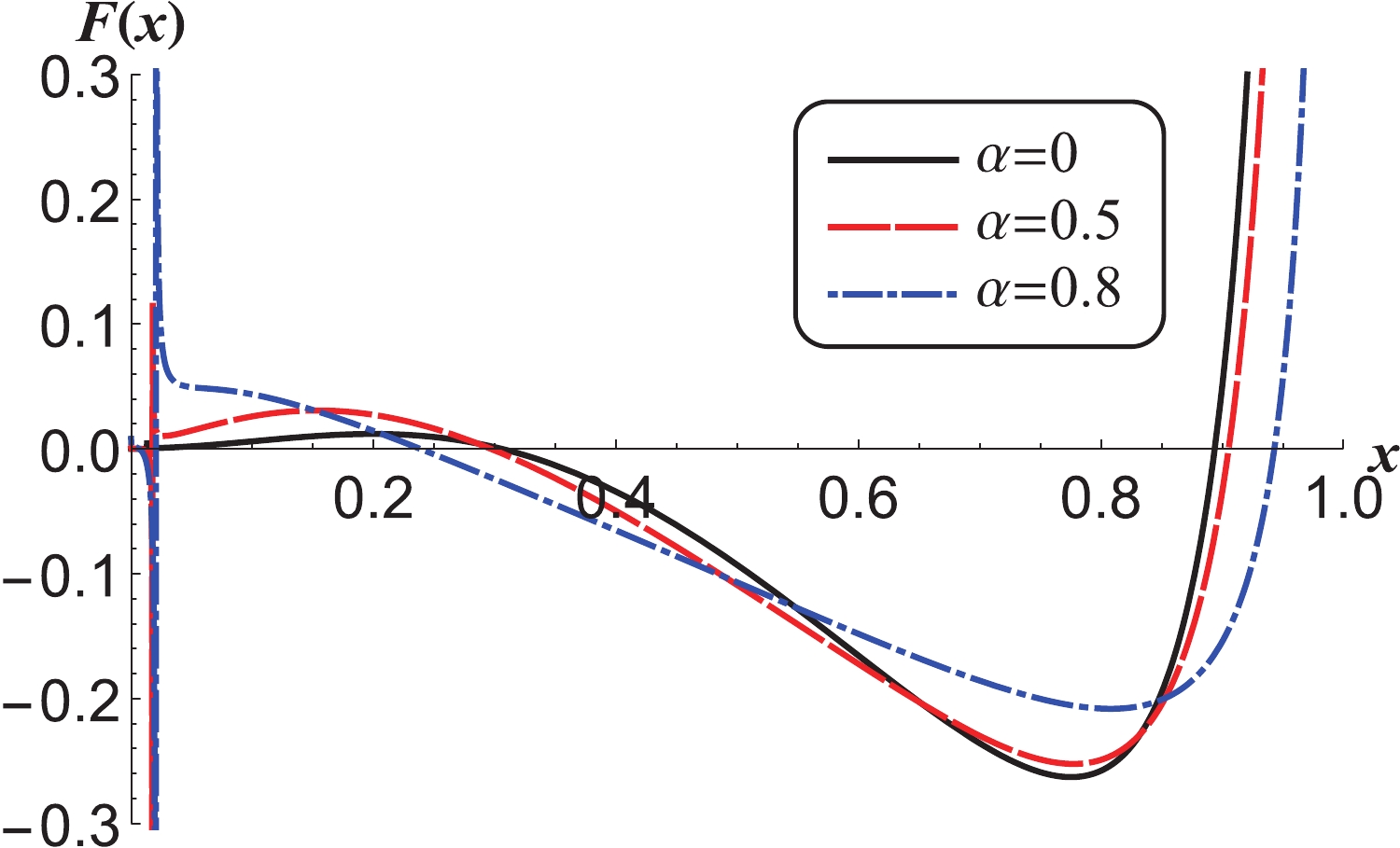
Figures 1-4 show the change of entropic force with x as each spacetime parameter takes different values. If the effect of entropic force is same as that of normal forces, from the four $ F(x)-x $ figures, it is clear that the entropic force tends to infinity with $ x \to 1 $, which means that when the BEH is close to the CEH in the dS space-time, the two horizons will separate from each other due to the entropic force with a corresponding large acceleration provided the other forces are absent. This agrees with the present viewpoint on early cosmic inflation. When the value of x reduces from 1, the entropic force between the two horizons decreases until it reaches a minimum, and at $ x = {x_1} $ in the interval, the entropic force is zero, which can be interpreted as the interaction between the two horizons being absent at $ x = {x_1} $. However, the two horizons may remain separate. When the value of x reduces gradually, the value of the entropic force temporarily remains negative, which means that the separation of the two horizons is decelerated and can be interpreted as decelerated cosmic expansion. If the expansion speed decelerates to zero before x reaches a minimum at $ x = {x_2} $, the two horizons will be in a relative oscillatory motion with the equilibrium position $ x = {x_1} $ under the circumstance that no other forces exist. In the four $ F(x)-x $ figures, when x reduces from $ x = {x_2} $, the value of the entropic force tends to zero in the negative territory before it turns positive (indicating repulsive force) at $ x = {x_3} $, except for the blue dot-dashed curve in Fig. 4. In the region of smaller x, the behaviors of the entropic force are complicated. Most of curves in the four $ F(x)-x $ figures go through their singularities and from positive to negative with decreasing x. However, the singularity disappears on the black solid curves in Fig. 2, which corresponds to the situations of smaller n with $ n = 3 $, smaller $ \alpha $ with $ \alpha = 0 $, smaller p with $ p = 1.3 $, and smaller $ \kappa $ with $ \kappa = 0.001 $. Besides that, when $ \kappa $ is bigger the behavior of the entropic force is different, which can be seen from the blue dot-dashed curve in Fig. 4. These $ F(x)-x $ curves indicate that the behavior of entropic force is affected by the parameters n, $ \alpha $, p and $ \kappa $. That is, it is influenced by the dimension of the space-time, the nonlinearity of the electromagnetic field, the strength of coupling of the dilaton scalar and electromagnetic field, the position of the cosmological horizon, and the electric charge of the black hole. In all these cases of the four figures, the behaviors of the entropic force near $ x = {x_1} $, or in the region of $ 1>x>x_3 $, are similar to that of the Lennard-Jones force between two particles [74-76]. They are similar but obtained in completely different ways. This indicates that the entropic force between the two horizons has a certain internal relationship with the Lennard-Jones force between two particles. More investigations and evidence are needed to consider the fate of the accelerated expanding universe, whether the entropic force between the BEH and CEH is one of the participant forces which drive the evolution of the universe, and whether the entropic force has the same effect as the Lennard-Jones force.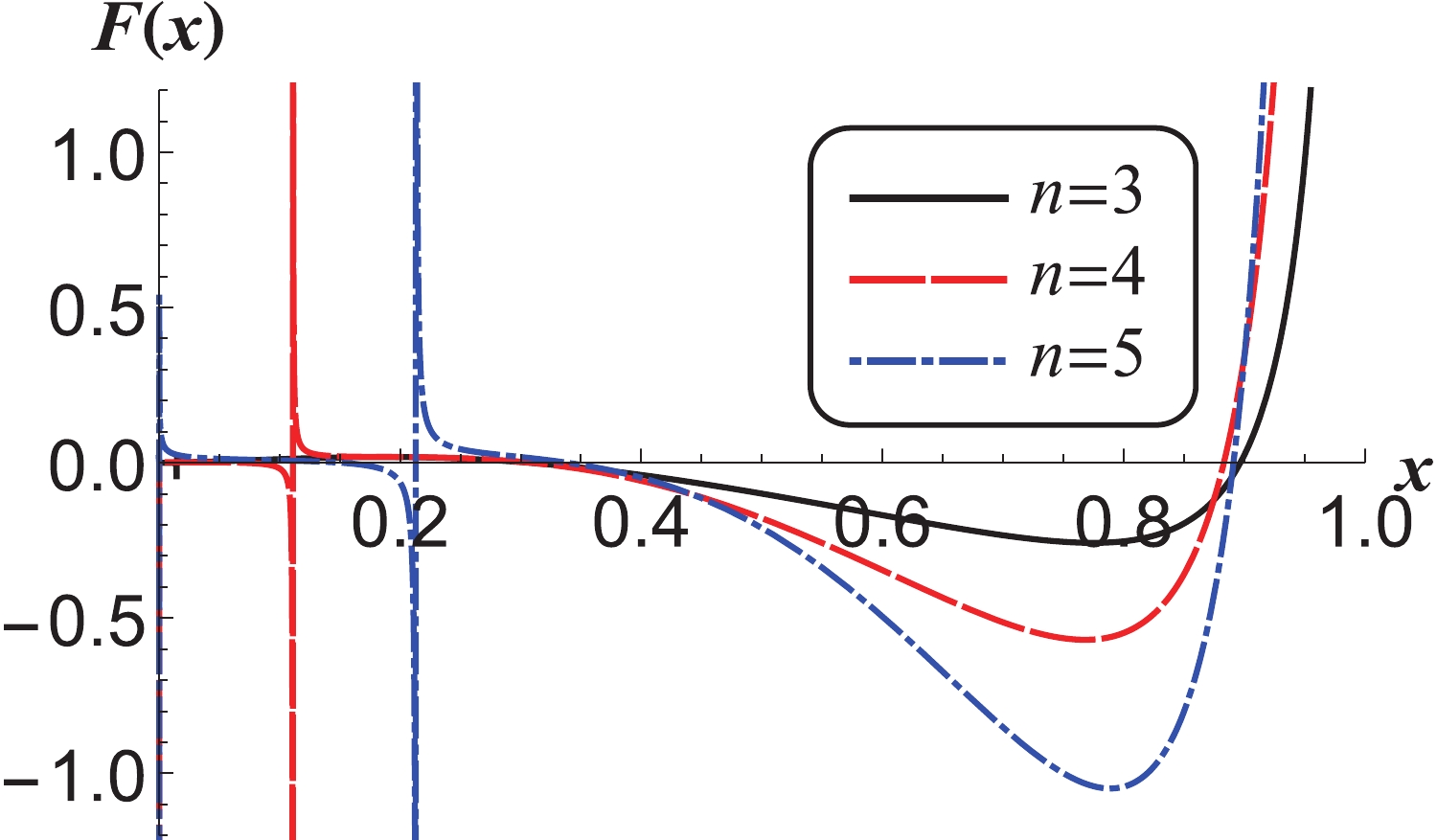

Figure 1.  (color online) $ F(x)-x $ curve with different values of n for $ \alpha=0.3 $, $ p=1.3 $ and $ \kappa=0.001 $.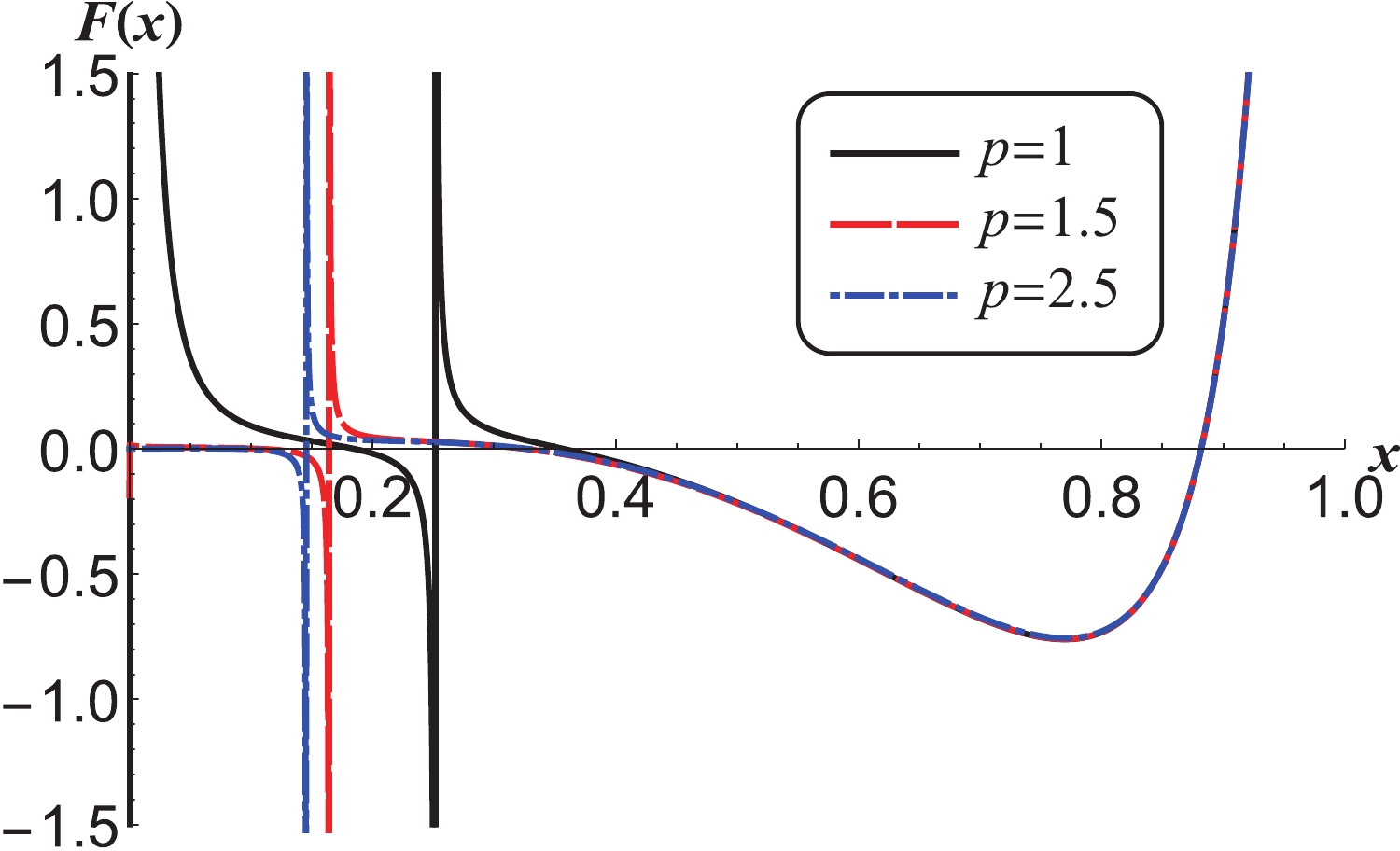

Figure 3.  (color online) $ F(x)-x $ curve with different values of p for $ n = 5 $, $ \alpha = 0.5 $ and $ \kappa = 0.001 $.

Figure 4.  (color online) $ F(x)-x $ curve with different values of the parameter $ \kappa $ for $ n = 3 $, $ \alpha = 0.3 $ and $ p = 1.3 $.

Figure 2.  (color online) $ F(x)-x $ curve with different values of $ \alpha $ for $ n=3 $, $ p=1.3 $ and $ \kappa=0.001 $.

The entropy of charged dilaton black holes with an Einstein power-Maxwell field in dS space-time has been derived and discussed, considering the correlation between the BEH and CEH, especially the correction term caused by the interaction between the BEH and CEH. The entropic force $ F(x) $ between the BEH and CEH has been deduced according to the definition of the entropic force in a thermodynamic system. We have discussed the changes in entropic force $ F(x) $ with x, the position ratio of BEH and CEH, in EPMD dS space-time when the parameters n, $ \alpha $, p, and $ \kappa $ take certain values. It is found that the behavior of the entropic force $ F(x) $ at a larger interval of x is similar to that of the Lennard-Jones force between two particles. At smaller intervals of x the behavior of the entropic force $ F(x) $ is complicated, and is related to the parameters of the space-time.

Comparing the $ F(x) -x $ curves in a large interval of x with the curve of the Lennard-Jones force versus the distance of two particles given in Refs. [74-76], we find that the two curves are very similar although they are obtained in different ways. The entropic force between the two horizons is completely derived from general relativity, but the Lennard-Jones force between two particles is concluded from simulations based on experiments. This indicates that there may be a relationship between the entropic force and the Lennard-Jones force.

According to modern cosmology, the fate of our universe is dominated by matter and energy. If there is enough matter and energy, the gravitational effect will stop the cosmic expansion at a certain time, and then our universe will start to contract. Otherwise, if the density of cosmic matter and energy is too low, the universe will expand forever. Different kinds of cosmic matter and energy play different roles in the cosmic expansion. In this work, we find that the entropic force probably plays a certain role in the cosmic expansion and contraction, as well as cosmic matter and energy. In EPMD dS space-time, the influence of different parameters on the entropic force between the BEH and CEH is shown in the $ F(x) - x $ curves. This indicates that different parameters in the EPMD dS space-time play different roles in the cosmic expansion.

The space-time and the thermodynamic effects are related to general relativity and quantum mechanics respectively, and all physical quantities satisfy the first law of thermodynamics. If the effect of entropic force is proved similar to that of normal forces, it indicates that there is a relationship among general relativity, quantum mechanics and thermodynamics. It will provide a new way to study the interaction between particles in black holes, the microstates of particles in black holes, the Lennard-Jones potential between particles, and the microstates of particles in ordinary thermodynamic systems.

We thank Prof. Z. H. Zhu for useful discussions.