-
Given the strong quantitative dependence of the breakup cross section on the projectile breakup threshold, as exemplified by Refs. [1-7], one may naively assume that as
$ \varepsilon_0\to 0 $ ,$ \sigma(\varepsilon_0)\to\infty $ , where$ \varepsilon_0 $ is the breakup threshold (ground-state binding energy) and$ \sigma $ the breakup cross section. Not only has this assumption not been given attention, but the breakup behavior for ground-state binding energies below the breakup threshold is just not known, let alone in the$ \varepsilon_0\to 0 $ limit, where the binding is dominated by correlations instead of the mean field. For a neutron-rich nucleus in this binding energy limit, a loosely-bound neutron is expected to move far away from the core nucleus, owing to the absence of the Coulomb barrier between the core nucleus and the valence neutron, to couple to unbound continuum states, thus leading to an “open” quantum system [8-13]. For a proton-rich nucleus, on the other hand, the Coulomb barrier eventually prevents a loosely-bound proton from moving away from the core nucleus, in which case an “open” proton-rich quantum system may also be prevented. The existence of bound states for$ \varepsilon_0 = 0 $ is well outlined in the literature, such as in Ref. [14]. In these references, a bound state for zero binding energy is justified by the fact that a potential that contains a Coulomb term, which falls asymptotically to zero from above, in which case the wave function must tunnel to infinity to reach the other free region, which takes forever, and hence the state is bound. Therefore, for a proton halo, one would then expect a bound state as$ \varepsilon_0\to 0 $ .In this paper, I study the elastic scattering, breakup, and reaction cross section behavior in the
$ ^8{\rm{B}}+{}^{58}{\rm{Ni}} $ reaction around the Coulomb barrier, in the event where the$ ^8{\rm{B}} $ breakup threshold becomes exceptionally small, i.e in the$ \varepsilon_0\to 0 $ limit. For practical purposes, apart from the experimental ground-state binding energy$ \varepsilon_0 = 137 $ keV [15], three more values are arbitrarily selected,$ \varepsilon_0 = 1.0 $ , 0.1, 0.01 keV, where$ 0.01 $ keV can be regarded as approaching zero compared to 137 keV. The main questions this work intends to elucidate are: How does the proton breakup process behave as$ \varepsilon_0\to 0 $ ? Does the breakup cross section converge in this limit? What is the role of the continuum-continuum couplings in this binding energy limit? While reactions induced by loosely-bound systems are known to be characterized by strong continuum-continuum couplings, as verified for example by Refs. [16-19] and references therein, the dependence of these couplings on the ground-state binding energy is not clear.The choice of this reaction is motivated, on one hand, by the availability of differential breakup cross section experimental data as a function of the centre-of-mass (c.m.) angle, around the Coulomb barrier [20], which is the incident energy of interest in the present work. On the other hand, the
$ ^8{\rm{B}} $ nucleus is the lightest established proton-halo system, and this reaction has been widely investigated in various studies, such as Refs. [21-28], making comparison easier. The importance of this study also stems from the fact that loosely-bound systems with very weak binding energies below 0.1 MeV, such as$ ^{19}{\rm{B}} $ , are being identified [29], making the investigation of the breakup process in such a low binding energy regime an interesting study. To obtain the breakup cross sections, the coupled differential equations obtained through the continuum-discretized coupled-channel (CDCC) formalism [30, 31] are solved numerically. This formalism has been found to be the most adequate theoretical tool to handle breakup reactions induced by weakly-bound projectiles. Its popularity in this field comes from the fact that it accurately includes the continuum-continuum couplings in the coupling matrix elements. Starting from the truncation and discretization of the projectile continuum, it leads to a set of finite coupled differential equations, which are numerically tractable.The paper is organized as follows: in Section II, the results are presented and discussed, and the conclusions are reported in Section III.
-
The fundamentals of the CDCC formalism can be found in Refs. [30, 31], and the details are not repeated in this work. This section starts with a description of the different input parameters for the numerical solutions of the CDCC coupled differential equations. The projectile is modeled as
$ ^8{\rm{B}}\to {}^7{\rm{Be}}+p $ , where the valence proton is loosely bound to the$ ^7{\rm{Be}} $ core nucleus, with a binding energy$ \varepsilon_0 = 137 $ keV [15]. The ground state is obtained by coupling the proton in the$ 0p_{\frac{3}{2}} $ orbit to the$ \dfrac{3}{2}^- $ ground state of the$ ^7{\rm{Be}} $ nucleus. However, for the sake of simplicity and in order to reduce the computational burden in this work, I consider an inert core, meaning that the$ ^7{\rm{Be}} $ spin was not taken into account. Consequently, the adopted model cannot describe the$ 1^+ $ and$ 3^+ $ resonances of the$ ^8{\rm{B}} $ nucleus, although the effect of the$ 1^+ $ resonance is reported in Ref. [32] as negligible. Also, the assumption of an inert core is not expected to dramatically affect the result due to the fact that in some cases, core excitations are reported to account for minor effects, as for example shown in Refs. [33, 34]. The parameters of the nuclear component of the$ ^7{\rm{Be}}+p $ Woods-Saxon potential, used to calculate ground-state bound and continuum wave functions, are$ V_0 = 44.65 $ MeV,$ V_{\rm{SO}} = 19.59\;{ {\rm{MeV}}\cdot {\rm{fm}}^2} $ ,$ R_0 = R_{\rm{SO}} $ = 2.391 fm, and$ a_0 = a_{\rm{SO}} = 0.52 $ fm, taken from Ref. [35], to which a Coulomb term is added. The parameters of the core-target and proton-target optical potentials are the same as those given in Tables 1 and 2 of Ref. [16], adopted from Ref. [21]. The parameters of the optical potential in the projectile-target centre-of-mass were also taken from Ref. [21]. For the numerical integration of the CDCC coupled differential equations, the maximum angular momentum between$ ^7{\rm{Be}} $ and the proton was truncated by$ \ell_{\rm{max}} = 5 $ , the maximum matching radius for bin integration by$ r_{\rm{max}} = 100 $ fm, the maximum projectile excitation energy by$ \varepsilon_{\rm{max}} = 8 $ MeV, the maximum order of the potential multipole expansion by$ \lambda_{\rm{max}} = 5 $ , the maximum matching radius of the integration of the coupled differential equations by$ R_{\rm{max}} = 1000 $ fm, and the maximum angular momentum of the relative center-of-mass motion by$ L_{\rm{max}} = 5000 $ . The interval$ [0,\varepsilon_{\rm{max}}] $ was further sliced into energy bins of width$ \Delta\varepsilon = 0.5\,{\rm{MeV}} $ for s- and p-states,$ \Delta\varepsilon = 1.0\,{\rm{MeV}} $ for f- and d-states, and$ \Delta\varepsilon = 1.5\,{\rm{MeV}} $ for higher partial waves. The computer code Fresco [36] was used for numerical calculations.Binding energy/keV $ \sqrt{\langle r^2\rangle} $ /fm

$B(E1)/({ {\rm{e} }^{\rm{2} } }{\rm{f} }{ {\rm{m} }^{\rm{2} } })$ 

137 2.39 0.53 1.0 2.55 0.60 0.10 2.57 0.61 0.01 2.57 0.61 Table 1. Root-mean-square radii and dipole electric response functions for the different ground-state binding energies. The value
$ \sqrt{\langle r^2\rangle} = 2.38\pm 0.04\;{\rm{fm}} $ was taken from Ref. [37].$ \varepsilon_0 $ /keV

$ \sigma_{\rm tot} $ /mb

$ \sigma_{\rm tot}^{\rm nccc} $ /mb

$ \sigma_{\rm Coul} $ /mb

$ \sigma_{\rm nucl} $ /mb

137 177 565 165 28 1.00 348 963 351 45 0.10 370 981 371 71 0.01 375 984 380 73 Table 2. Integrated total (
$ \sigma_{\rm tot} $ ), Coulomb ($ \sigma_{\rm Coul} $ ) and nuclear ($ \sigma_{\rm nucl} $ ) breakup cross sections (in millibarns) for the different ground-state binding energies. -
In Fig. 1, the ground-state wave functions corresponding to ground-state binding energies
$ \varepsilon_0 = 137 $ , 1.0, 0.10, 0.010 keV are shown in panel (a). One observes in this figure that for$ \varepsilon_0\leqslant 1.0 $ keV, the ground-state wave function becomes negligibly dependent on the ground-state binding energy, since the curves of all three wave functions can hardly be distinguished, and has an extended tail, compared to that corresponding to$ \varepsilon_0 = 137 $ keV. This indicates that the ground-state wave function is not sensitive to the binding energy as$ \varepsilon_0\to 0 $ (converges to a finite function). It is also noticed that in the asymptotic region, the wave function tends to zero even in the$ \varepsilon_0\to 0 $ limit. The result in this figure appears to suggest that the$ ^7{\rm{Be}}+p $ system might have a square-integrable solution at$ \varepsilon_0 = 0 $ . However, given the complexity of proving the existence of such a solution, the present work refrains from drawing such a forceful conclusion. Therefore, as expected, one can infer that the Coulomb barrier prevents the$ ^7{\rm{Be}}+p $ system reaching the state of an open quantum system, which would require the wave function to extend to infinity as$ \varepsilon_0\to 0 $ .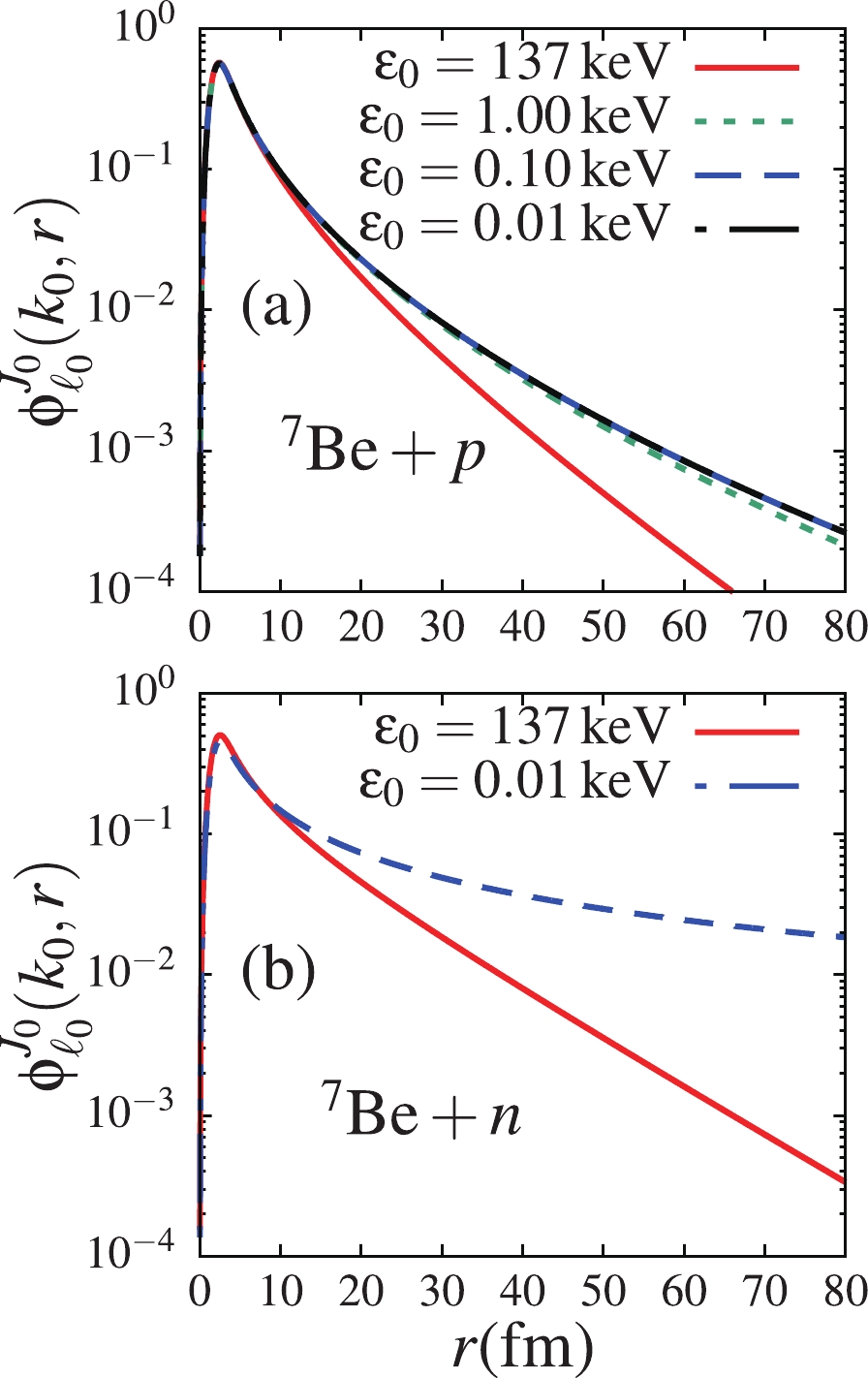
Figure 1. (color online) Ground-state wave functions for
$\varepsilon_0 = $ $ 137$ , 1.0, 0.10, 0.010 keV, for (a) the$ ^7{\rm{Be}}+p $ system and (b)$ ^7{\rm{Be}}+n $ (where only$ \varepsilon_0 = 137 $ keV and 0.01 keV results are shown).To show that the lack of extension of the
$ ^7{\rm{Be}}+p $ ground-state wave function to infinity as$ \varepsilon_0\to 0 $ is in fact due to the Coulomb barrier between the$ ^7{\rm{Be}} $ nucleus and the proton, I replaced the proton of the$ ^7{\rm{Be}}+p $ system with a neutron to give the$ ^7{\rm{Be}}+n $ system, such that only the centrifugal barrier due to the ground-state p-wave remains. Indeed, as shown in panel (b) of this figure, the wave function is largely extended (to infinity) for$ \varepsilon_0 = 0.01 $ keV, compared to panel (a).An extended ground-state wave function to infinity may be associated with a neutron already moving almost independently from the core nucleus, coupling to unbound continuum states. In conclusion, the Coulomb barrier between the
$ ^7{\rm{Be}} $ core nucleus and the valence proton prevents the$ ^7{\rm{Be}}+p $ system from reaching the limit of an “open” quantum system. Notice that the ground-state wave function plays an important role in the breakup process. In fact, breakup reactions induced by loosely-bound systems are known to be peripheral [38], thanks to an extended matter density in the peripheral region. Therefore, the convergence of the ground-state wave function to a definite function as$ \varepsilon_0\to 0 $ may also signal the convergence of the breakup observables. Also, the extended tail of the ground-state wave function for$ \varepsilon_0\leqslant 1 $ keV, compared to that for$ \varepsilon_0 = 137 $ keV, indicates that larger breakup cross sections are expected in the former case than in the latter.To further check the effect of the ground-state binding energy on the projectile's internal structure, the electric dipole response functions for the transitions from the p-wave ground-state to continuum s and d-waves for all four binding energies are shown in Fig. 2 as functions of the projectile excitation energy
$ \varepsilon $ (in MeV). As in Fig. 1 (a), one also observes in this figure a significant increase of the response function (at$ \varepsilon \leqslant 3.0 $ MeV) as the binding energy decreases from$ \varepsilon_0 = 137 $ to 1.0 keV, while a convergence is observed for$ \varepsilon_0\leqslant 1.0 $ keV. This convergence as$ \varepsilon_0\to 0 $ is also displayed in Table 1, where the root-mean-square radii [$ \sqrt{\langle r^2\rangle} $ ] and the reduced transition probabilities$ B(E1) $ (obtained after the integration of the dipole electric response functions up to$ \varepsilon_{\rm{max}} = $ 8.0 MeV) are shown for each binding energy. This table shows the convergence of the root-mean-square radius and the reduced probability as$ \varepsilon_0\to 0 $ .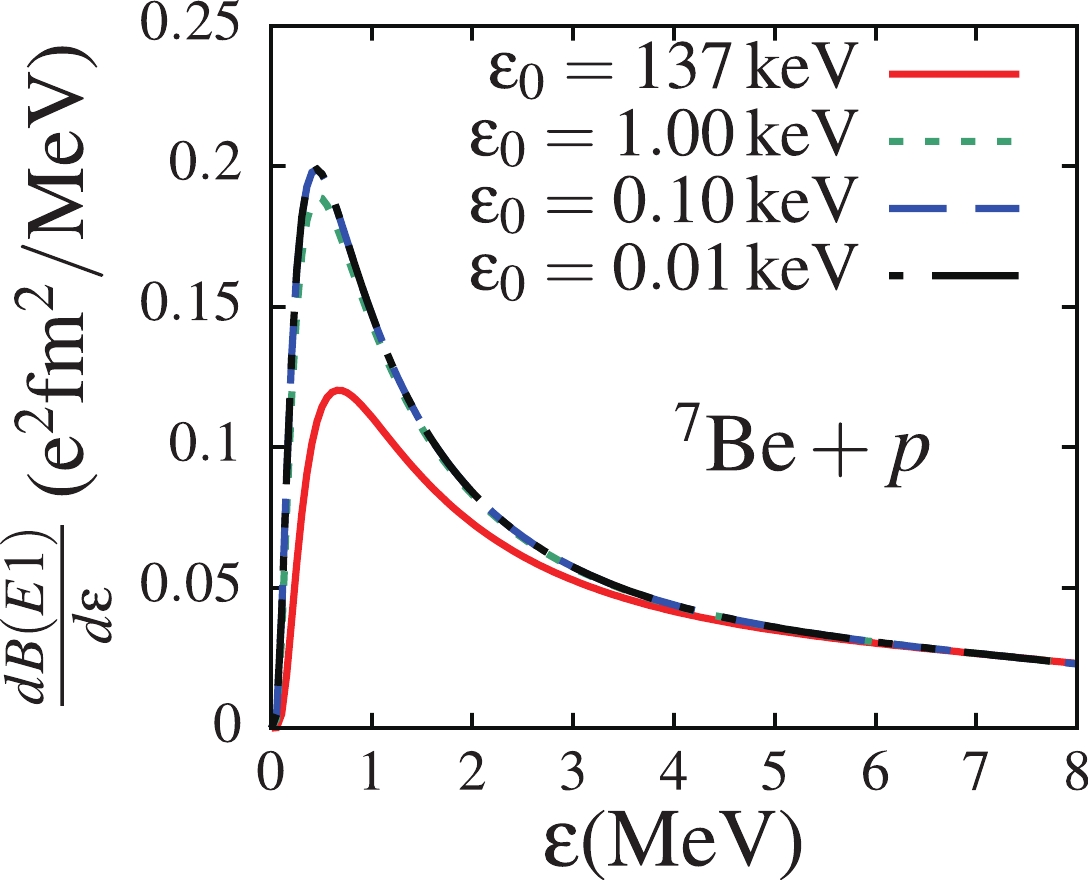
Figure 2. (color online) Dipole electric response functions for the transitions from the ground-state to continuum s and d-waves, for ground-state binding energies
$ \varepsilon_0 = 137 $ , 1.0, 0.10, 0.010 keV.In order to show how the different reaction observables depend on the breakup threshold in the
$ \varepsilon_0\to 0 $ limit, I start with the elastic scattering. The elastic scattering cross section depends on the square of the ground-state wave function through its scattering matrix elements, meaning that it has a strong dependence on the projectile ground-state density. The elastic scattering cross sections obtained for all four binding energies at an incident energy$ E_{\rm lab} = 26 $ MeV are shown in Fig. 3. This figure shows that the elastic scattering cross section has a negligible dependence on the ground-state binding energy, even in the$ \varepsilon_0\to 0 $ limit, similar to the ground-state wave function. These results single out the importance of the ground-state wave function in elastic scattering. Therefore, one can conclude that as$ \varepsilon_0\to 0 $ , the ground-state binding energy has a negligible effect on the elastic scattering cross section, due to its negligible effect on the ground-state wave function in this binding energy limit. Notice that although the centrifugal barrier does not appear to prevent the extension of the ground-state wave function to infinity in the asymptotic region, its effect on the elastic scattering cross section is reported to be important (see Ref. [39] for details).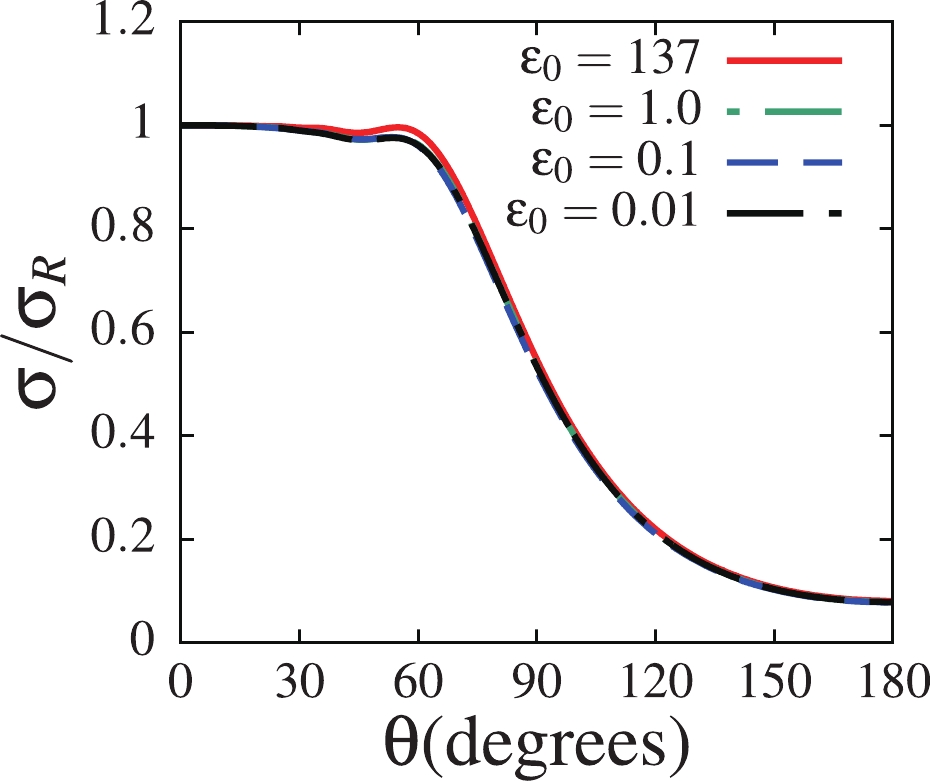
Figure 3. (color online) Elastic scattering cross sections obtained for ground-state binding energy
$ \varepsilon_0 = 137 $ , 1.0, 0.10, 0.010 keV, at an incident energy$ E_{\rm lab} = 26 $ MeV.Unlike elastic scattering, the breakup process does not depend on the square of the ground-state wave function. For transitions to and from the ground-state, the radial part of the coupling matrix elements contains the product of the ground-state wave function and the continuum bin wave functions. On the other hand, transitions between continuum states, which are known to be important in the breakup of loosely-bound systems, do not contain the ground-state wave function. These couplings might, to some extent, slow the convergence of the breakup cross section as
$ \varepsilon_0\to 0 $ . Before diving into the details, I first compare in Fig. 4 the differential breakup cross section as a function of the c.m. angle with the experimental data, taken from Ref. [20]. The theoretical calculations correspond to$ \varepsilon_0 = 137 $ keV, at an incident energy$ E_{\rm lab} = 26 $ MeV. This figure displays a nice agreement between the theoretical calculations and the data.
Figure 4. (color online) Differential breakup cross section as a function of the c.m. angle, corresponding to binding energy
$ \varepsilon_0 = 137 $ keV. The experimental data were taken from Ref. [20].As the binding energy decreases, the convergence of the breakup cross section can be expected to become tricky, owing to changes in the reaction dynamics. To this end, in Figs. 5, and 6, I discuss the convergence of the differential breakup cross section as a function of the c.m. angle in terms of the maximum orbital angular momentum
$ \ell_{\rm{max}} $ , and the maximum projectile excitation energy$ \varepsilon_{\rm{max}} $ , for all four ground-state binding energies. An inspection of Fig. 5 shows that regardless of the binding energy, convergence is achieved with$ \ell_{\rm{max}} = 3 $ , since the contribution from higher-order partial-waves appears to be negligible. Figure 6 shows that the convergence is achieved with$ \varepsilon_{\rm{max}} = 4 $ MeV. This figure also indicates that for$ \varepsilon_0<137 $ keV, the contribution from$ \varepsilon_{\rm{max}}>2 $ MeV is rather negligible. This suggests that in the$ \varepsilon_0\to 0 $ limit, higher projectile excitation energies are in fact less relevant.
Figure 5. (color online) Convergence of the differential breakup cross section as a function of the c.m. angle in terms of the maximum core-proton orbital angular momentum
$ \ell_{\rm{max}} $ , for all four binding energies.
Figure 6. (color online) Convergence of the differential breakup cross section as a function of the c.m. angle in terms of the maximum core-proton excitation energy
$ \varepsilon_{\rm{max}} $ , for all four binding energies.Quantitatively, it is noticed in Figs. 5 and 6 that the breakup cross section increases greatly from
$ \varepsilon_0 = 137 $ to$ 1.0 $ keV (see panels (a) and (b)), whereas for$ \varepsilon_0\leqslant 1.0 $ keV, the breakup cross sections appear to become more similar, building at smaller angles (around$ 10^\circ $ ). In the light of these results, one concludes that in the$ \varepsilon_0\to 0 $ limit, there is convergence of the breakup cross section, which can be attributed to the fact that the ground-state wave function converges to a definite function as the ground-state binding energy tends to zero, as observed in Fig. 1. Given the peripheral nature of the breakup process, the large increase of the breakup cross section when the binding energy decreases from$ \varepsilon_0 = 137 $ to$ 1.0 $ keV can be mainly attributed to the longer tail of the ground-state wave function for$ \varepsilon_0\leqslant 1.0 $ keV, compared to that for$ \varepsilon_0 = 137 $ keV, as observed in Fig. 1. Also, as the ground-state binding energy decreases, the breakup becomes more peripheral, leading to significant contributions of higher-order partial-waves to the L-distribution partial breakup cross sections, as will be shown in Fig. 9. This can further explain the large importance of the breakup cross sections for$ \varepsilon_0\leqslant 1.0 $ keV.To study the dependence of the continuum-continuum couplings (ccc) on the ground-state binding energy, Fig. 7 shows the differential breakup cross sections as a function of the c.m. angle, when these couplings are included ("All coupl.") and excluded ("No ccc") in the coupling matrix elements. As one would expect, the breakup cross section is largely suppressed when the ccc are taken into account compared to when they are excluded. This figure suggests that the effect of the ccc appears to lead to convergence as
$ \varepsilon_0\to 0 $ .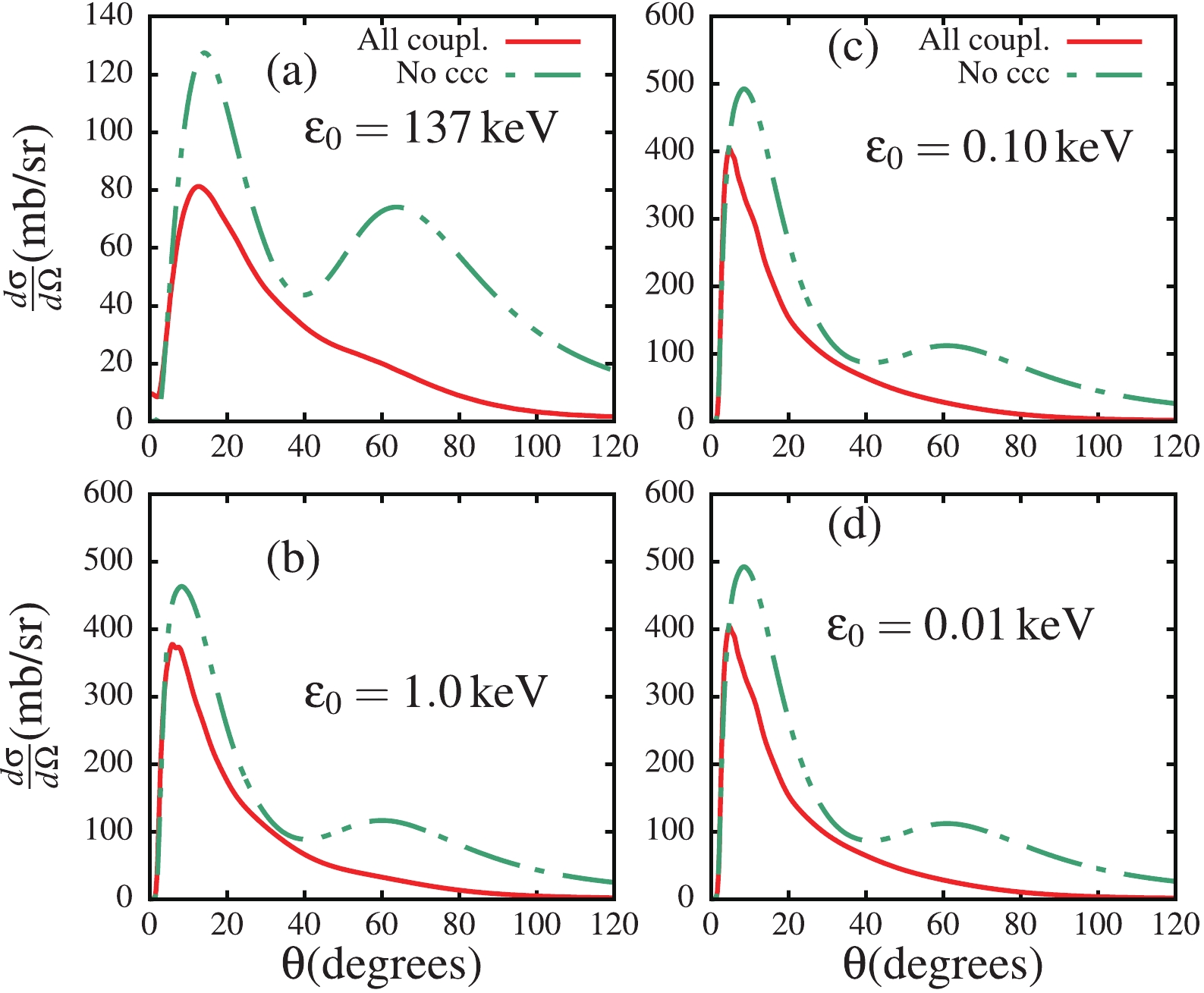
Figure 7. (color online) Differential breakup cross section as a function of the c.m. angle in the presence of all different couplings (“All coupl.”) and when the continuum-continuum couplings are excluded (“No ccc”), for all four binding energies.
In order to further analyze the breakup dynamics in the
$ \varepsilon_0\to 0 $ limit, I show in Fig. 8 shows the Coulomb and nuclear breakup cross sections. The Coulomb breakup cross section was approximately obtained by removing the off-diagonal projectile-target nuclear interactions ($ ^7{\rm{Be}} $ -target and proton-target nuclear interactions) in the coupling matrix elements, keeping only its diagonal monopole component, i.e., the nuclear interaction in the projectile-target centre-of-mass, to account for nuclear absorption in the centre-of-mass. The nuclear breakup cross section, on the other hand, was obtained by removing the off-diagonal projectile-target Coulomb interactions ($ ^7{\rm{Be}} $ -target and proton-target Coulomb interactions), retaining only its diagonal monopole part (i.e., the Coulomb interaction in the projectile-target centre-of-mass). The diagonal nuclear monopole component was also included. The total breakup cross section refers to that obtained when both Coulomb and nuclear interactions are simultaneously included in the coupling matrix elements. This is the case for the results discussed above. Since the early studies [18], this procedure, although approximative, has been widely used to study the Coulomb and nuclear breakup separately, and has produced the expected effects. This figure shows that the nuclear breakup cross section is much smaller than its Coulomb counterpart, which is approximately comparable to the total breakup cross section. Panels (b), (c) and (d) indicates that the nuclear and Coulomb breakup cross sections are also negligibly dependent on the ground-state binding energy in the$ \varepsilon_0\to 0 $ limit.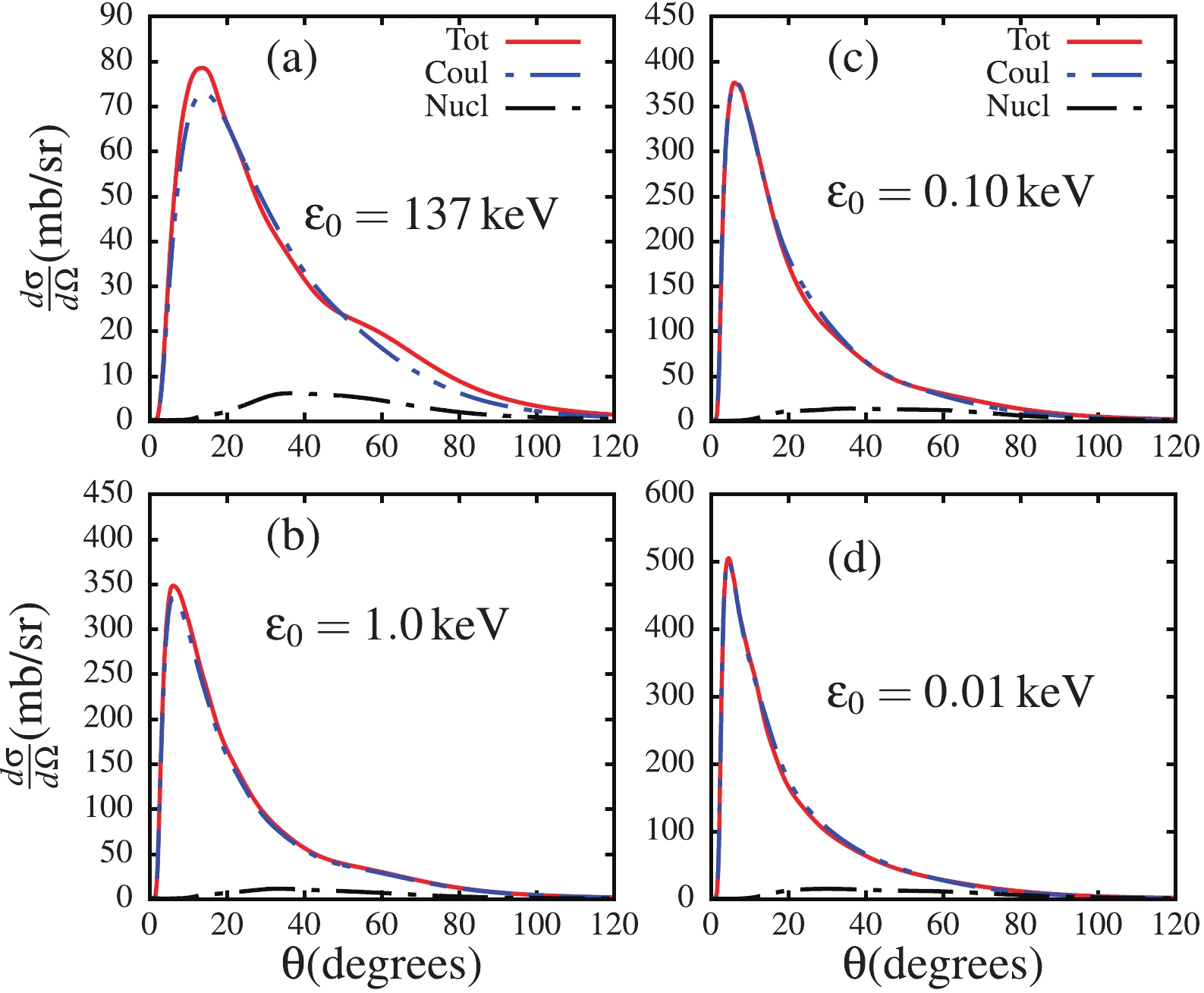
Figure 8. (color online) Differential breakup cross section as a function of the c.m. angle for total, Coulomb and nuclear breakups, for all four binding energies.
To better picture the negligible dependence of the total, Coulomb and nuclear breakup cross sections on the binding energy at short and long distances, their angular momentum distributions (L-distributions) are plotted in Fig. 9. It is noticed in the upper panels of this figure that the behaviour of all three breakup cross sections at lower and higher angular momenta is independent of the ground-state binding energy as
$ \varepsilon_0\to 0.01 $ keV. As expected, due to the long-range nature of Coulomb forces, the Coulomb and total breakup cross sections are significantly extended to larger angular momenta compared to the nuclear breakup cross section.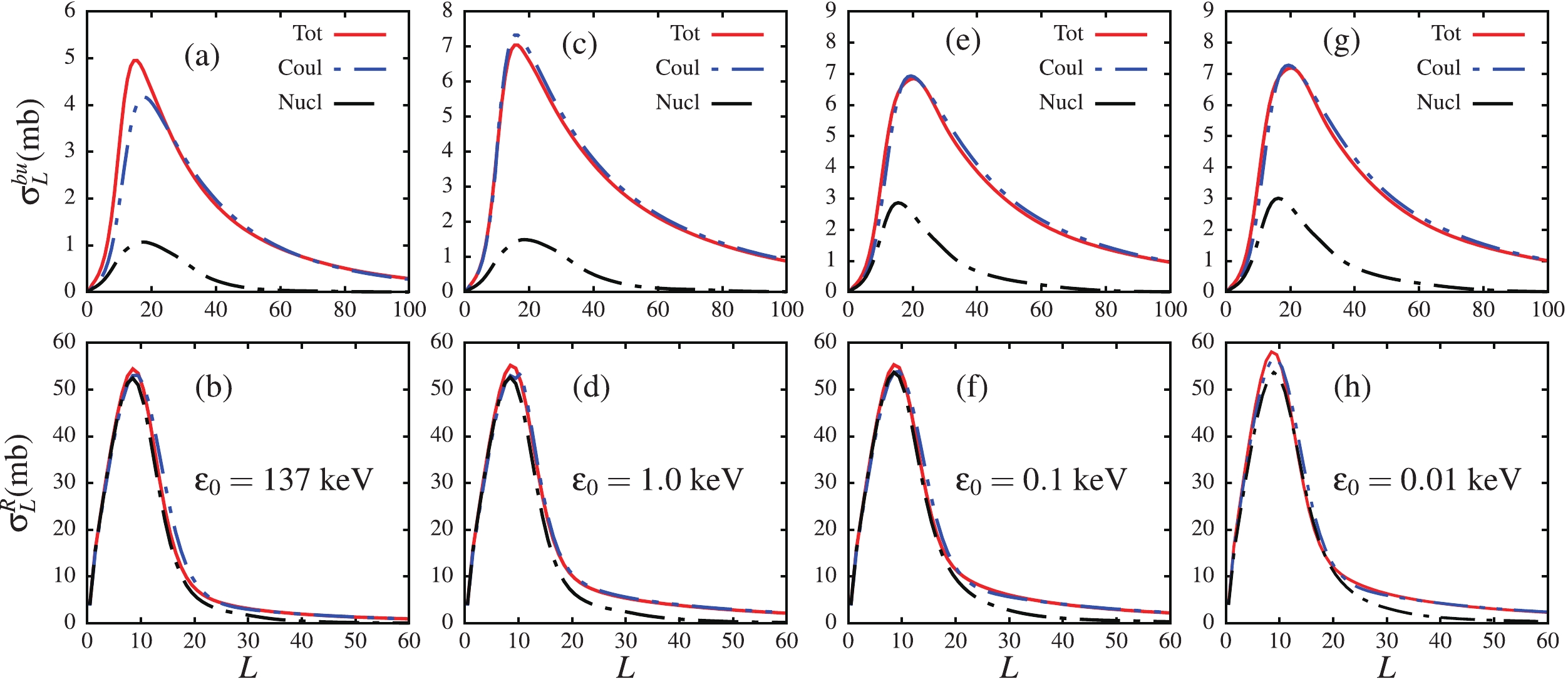
Figure 9. (color online) Angular momentum distribution breakup cross sections (
$ \sigma_L^{bu} $ ) (panels (a), (c), (e) and (g)), and reaction cross sections ($ \sigma_L^R $ ) (panels (b), (d), (f) and (h)), for total, Coulomb and nuclear breakups, and for all four binding energies.Another important reaction observable in the breakup process is the reaction cross section. This may contain information about the structure of the colliding partners. To test the dependence of this quantity on the ground-state binding energy, the lower panels of Fig. 9 display the partial reaction cross sections for total, Coulomb and nuclear breakups. The reaction cross section, in a similar way to the breakup cross section, has a negligible dependence on the ground-state binding energy as
$ \varepsilon_0\to 0.01 $ keV. It would have been assumed that as$ \varepsilon_0\to 0 $ , the nuclear effect would vanish due to the short-range nature of nuclear forces, where the breakup becomes exclusively asymptotic. However, looking at the behavior of the reaction cross section at lower angular momenta, it appears that the nuclear effect also converges as$ \varepsilon_0\to 0 $ . Another remarkable observation in this figure is the approximate similarity of all three different reaction cross sections at lower angular momenta ($ L\leqslant 20 $ ). If the Coulomb breakup were calculated without the diagonal nuclear component, then the resulting reaction cross section would have been lower than its total and nuclear counterparts. This result indicates that the diagonal nuclear potential has an important effect on the Coulomb breakup calculations. A further study of this effect may reveal other important breakup dynamics.To further show the convergence of the different breakup cross sections as
$ \varepsilon_0\to 0 $ , Table 2 summarizes the integrated total ($ \sigma_{\rm tot} $ ), Coulomb ($ \sigma_{\rm Coul} $ ) and nuclear ($ \sigma_{\rm nucl} $ ) breakup cross sections, as well as the total breakup cross section obtained in the absence of the continuum-continuum couplings ($ \sigma_{\rm tot}^{\rm nccc} $ ). This table exhibits the convergence that is already displayed in the different figures. In Table 3, the convergence rate is shown, where one sees that as$ \varepsilon_0\to 0.01 $ keV,$ \sigma_{\rm tot} $ only grows by about 1.3%,$ \sigma_{\rm tot}^{\rm nccc} $ by about 0.3%,$ \sigma_{\rm Coul} $ by about 2.4%, and$ \sigma_{\rm nul} $ by about 2.7%. Comparing the$ \sigma_{\rm tot}^{\rm nccc} $ and$ \sigma_{\rm tot} $ convergence rates, it can be deduced that the effect of the continuum-continuum couplings is to slightly slow down the convergence of the breakup cross section as$ \varepsilon_0\to 0 $ .$ \varepsilon_0 $ /keV

$ \sigma_{\rm tot} $ 

$ \sigma_{\rm tot}^{\rm nccc} $ 

$ \sigma_{\rm Coul} $ 

$ \sigma_{\rm nucl} $ 

$ 137\to 1.0 $ 

49.1% 41.3% 53.0% 38.0% $ 1.0\to 0.1 $ 

6.0% 1.8% 5.4% 36.6% $ 0.1\to 0.01 $ 

1.3% 0.30% 2.4% 2.7% Table 3. Total, Coulomb and nuclear breakup convergence rates as
$ \varepsilon_0\to 0.01 $ keV. -
In this paper, I have investigated the behavior of the breakup process in the
$ \varepsilon_0\to 0 $ limit for the$ ^8{\rm{B}}+{}^{58}{\rm{Ni}} $ reaction around the Coulomb barrier. For practical purposes, apart from the$ ^8{\rm{B}} $ ground-state experimental binding energy of 137 keV, three other arbitrarily selected values (1.0, 0.1, 0.01 keV) were also considered.Analyzing the dependence of the ground-state wave function on the binding energy, it is concluded that the Coulomb barrier between the
$ ^7{\rm{Be}} $ core nucleus and the valence proton prevents the$ ^7{\rm{Be}}+p $ system from reaching the state of an open quantum system, which would require the ground-state wave function to extend to infinity in the asymptotic region. Consequently, the elastic scattering cross section, whose matrix element contains the density of the ground-state wave function, is also found to be negligibly dependent on the binding energy as$ \varepsilon_0\to 0 $ .On the other hand, the total, Coulomb and nuclear breakup cross sections are reported to significantly increase when the ground-state binding energy decreases from
$ \varepsilon_0 = 137 $ to 1.0 keV, and converge to their maximum values as$ \varepsilon_0\to 0 $ . This increase is mainly understood as coming from the longer tail of the ground-state wave function for$ \varepsilon_0\leqslant 1.0 $ keV, compared to that for$ \varepsilon_0 = 137 $ keV. It is also found that the effect of the continuum-continuum couplings is to slightly delay the convergence of the breakup cross section to its maximum value in the$ \varepsilon_0\to 0 $ limit. The analysis of the reaction cross section signals shows a convergence of all the breakup observables as$ \varepsilon_0\to 0 $ .In conclusion, due to the Coulomb barrier, the
$ ^7{\rm{Be}}+p $ system does not reach the state of an open quantum system in the$ \varepsilon_0\to 0 $ limit, while the corresponding breakup observables converge to their maximum values. These results may serve to clear the ground toward an elaborated theory on the breakup dynamics in the$ \varepsilon_0\to 0 $ limit. It would be interesting to perform a similar study for a neutron-halo system, where there is no Coulomb barrier between the core nucleus and the valence neutron.
Proton-halo breakup dynamics for the breakup threshold in the ε0 → 0 limit
- Received Date: 2020-12-07
- Available Online: 2021-05-15
Abstract: Proton-halo breakup behavior in the





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF





















 DownLoad:
DownLoad: