-
The existence of dark matter (DM) has been established by substantial cosmological and astronomical observations, but the particle nature of DM is still unknown. An appealing candidate for DM is the weakly interacting massive particles (WIMPs) arising from various extensions of the standard model (SM). The experimental searches for DM consist of categories such as direct detection (DD) of possible scattering between DM and SM target materials, indirect detection (ID) looking for signals of DM annihilation/decay products, and collider search hunting for signals from DM production in high energy accelerators.
Although confident WIMP signals are still absent from today's DDs of DM and the present DD experiments set strong constraints on WIMPs with masses
$ \gtrsim $ 10 GeV [1-7], anomalous signals from IDs may shed light on some characteristics of DM. The long-standing Galactic center GeV gamma-ray excess may be a signature of WIMP annihilations [8-14], and millisecond pulsar is another alternative candidate suggested by point sources [11, 12, 15-21]. Recent analysis results indicate that WIMP annihilations could significantly contribute to the gamma-ray excess after considering possible point sources [22-25]. However, this excess, regarded as WIMP annihilation, seems to conflict with recent joint constraints from observations of dwarf spheroidal galaxies [26], the Milky Way halo [27], the Galactic center [28], and galaxy groups/clusters [29-31]. Can WIMP annihilations still be available to explain the Galactic center gamma-ray excess after considering these joint limits? To relax these conflicts, some exotic mechanism may be presumable; e.g., annihilation of a pair of DM particles into a pair of on-shell light mediators, followed by decay of the light mediators into$ e^+ e^- $ or$ \mu^+ \mu^- $ [14, 32, 33], with the spectrum of photons arising from radiative processes. For the slightly better fit provided by the scenario of light mediator decay into$ e^+ e^- $ , the required effective annihilation cross section is$ \sim 0.4 \times 10^{-26} $ cm3/s [14], which is smaller than the canonical value ($ 3 \times 10^{-26} $ cm3/s) of the DM annihilation cross section.To interpret the Galactic gamma-ray excess with DM cascade annihilations, what the light mediator is and which new interaction it carries become crucial questions. The new particle and interaction may leave some traces in anomalous processes. A new mediator X with mass
$ m_X \approx $ 16.8 MeV is indicated by the recent 8Be [34] and 4He [35] anomalous transitions (X predominantly decays into$ e^+ e^- $ ). We consider the case wherein X is a vector boson with primary axial couplings to light quarks as discussed in Ref. [36] and interpret the Galactic center gamma-ray excess with the X boson being the light mediator. The light X boson could induce the Sommerfeld effect [37] in DM annihilation at low velocities and suffers from the constraints from dwarf galaxies and the cosmic microwave background. In the following discussion, we thus require a vanishing coupling between X and the GeV scale DM indicated by the Galactic gamma-ray excess. To account for the Galactic gamma-ray excess via DM cascade annihilation, we consider another new scalar$ \phi $ , which connects DM and the X boson. In this paper, the s-wave process of scalar DM S cascade annihilation is$ S S^\ast $ $ \to $ $ \phi $ $ \to $ $ X X $ followed by$ X \rightarrow e^+ e^- $ . The$ \phi $ couplings to SM particles could be very small, and thus, the DM of concern can evade present stringent DD bounds. Note that the DM candidate here may account for only a fraction ($ f_\mathrm{DM} $ ) of the total DM of the universe, referred to as the multi-component DM scenario [38, 39]. In this case, the small effective annihilation cross section required by the Galactic gamma-ray excess can be obtained if$ S S^\ast $ contributes a small fraction of the total DM.The paper is outlined as follows. In Sec. II, we give a brief description of the X boson with Be and He anomalies. We also describe the DM model in terms of mediators X and
$ \phi $ and derive the DM annihilation cross section. In Sec. III, we explain the Galactic center gamma-ray excess and discuss the astrophysical constraints on this model. Section IV shows our numerical results for the DD of the DM in this model. Our conclusions are presented in Sec. V. -
Recently, anomalies were observed in the electromagnetic transitions of both 8Be (the 18.15 MeV
$ 1^+ $ state) [34] and 4He (the 21.01 MeV$ 0^- $ state) [35]. These two anomalies may be caused by the same origin; i.e., a new mediator X predominantly decaying into$ e^+ e^- $ with mass$ m_X \approx $ 16.8 MeV. The nuclear transitions of 8Be were analyzed in Ref. [40] with an improved nuclear physics model, although this cannot explain the anomaly. To account for the 8Be anomaly, the spin-parity of the X boson could be$ J^P = 1^- $ ,$ 1^+ $ , or$ 0^- $ . The corresponding X couplings to SM particles of the vector/axial-vector [36, 41-45] and pseudoscalar [46] forms were analyzed in the literature (see Refs. [47-52] for more studies). In addition, the spin-parity of the X boson required by the 4He anomaly is$ J^P = 1^+ $ ,$ 0^- $ . Thus, if parity is conserved in the two anomalous nuclear transitions of 8Be and 4He, X's couplings to light quarks could be of axial-vector ($ 1^+ $ ) or pseudoscalar ($ 0^- $ ) forms. Further estimates of the decay widths indicate that a pseudoscalar X for the two anomalies is disfavored [44].The 4He anomaly was analyzed by the experimental group [35] with the
$ 0^- $ state in the electro-magnetically forbidden transition$ 0^- \to 0^+ + X $ . Note that, if the He anomaly is produced by the excited state 0+ in$ 0^+ \to 0^+ + X $ transition, the spin-parity of the X boson could be$ J^P $ =$ 1^- $ (a vector X) for both Be and He anomalies [44]. Here, we follow the experimental group and focus on the excited state$ 0^- $ , and thus, the spin-parity of the X boson is taken as$ J^P $ =$ 1^+ $ for both Be and He anomalies. To account for anomalous 8Be and 4He transitions, the forms of X couplings to quarks and charged leptons are taken as those in Ref. [36]$ \mathcal{L}_{X} \supset - X_\mu \sum_q g_q \bar{q} \gamma^\mu \gamma^5 q + X_\mu \sum_i \bar{l}_i ( g_i^V \gamma^\mu + g_i^A \gamma^\mu \gamma^5 ) l_i \; , $

(1) where we assume that the X particle predominantly decays into
$ e^+ e^- $ . The X couplings to u, d quarks are in the range of$ 10^{-5} \lesssim |g_{u,d}| \lesssim 10^{-4} $ [36] and the typical value of the coupling parameter$ \sqrt{(g_e^V)^2 + (g_e^A)^2}/e \sim 10^{-3} $ (or$ \sim 5\times10^{-5} $ ) is allowed by experiments [53-55]. The mean decay length L of the X boson should be$ L \lesssim $ 1 cm [41]. The current and near future experiments can probe the parameter space of interest for the X boson [36]. It can be tested in other large-energy nuclear transitions, such as the transitions of$^{10}{\rm B}$ and$^{10}{\rm Be}$ to their ground state [56, 57]. The search for dark photon$ A' $ through$ D^*(2007)^0 \to D^0 + A' $ with$ A'\to e^+ e^- $ at LHCb can probe the region of the X gauge boson explaining the anomalies. The Mu3e experiment will be sensitive to dark photon masses above 10 MeV. The possible dark photon can be produced via electron scattering off a gas hydrogen target in the DarkLight experiment [58]. The Heavy Photon Search experiment searches for$ X\to e^+ e^- $ through a high-luminosity electron beam incident on a tungsten target [59]. The X boson can be produced in the bremsstrahlung reaction of$ e^- Z \to e^- Z X $ at NA64 [55], and the TREK experiment at J-PARC is expected to look for$ K\to \mu\nu (X\to e^+ e^-) $ . The$ e^+e^- $ colliders can search for$ e^+ e^-\to X\gamma $ . The new X boson may couple to the dark sector and bridge the transition between the SM and the dark sector. The possible X portal DM was investigated in Refs. [60-65]. The masses of the X portal DM in these models are generally in the MeV scale [60, 65]. In this paper, we focus on interpreting the Galactic gamma-ray excess with new interactions mediated by X bosons in DM cascade annihilations.Next, we consider the framework in which a fraction (
$ f_\mathrm{DM} $ ) of DM particles consist of a gauge singlet complex scalar S and the main transitions between S and the SM particles occur via another scalar field$ \phi $ and a spin-1 mediator X. The X boson causes the anomalous transitions of 8Be and 4He, but it does not directly couple to S to avoid the possible Sommerfeld effect. The real dark field$ \phi $ couples to both S and X, which mediates the transition between$ S S^\ast $ and the SM particles. Besides the kinetic energy terms, the general Lagrangian is given by①$ \begin{aligned}[d]& -\mathcal{L}_{\rm scalar} \supset \mu^2 |H|^2 + \lambda |H|^4 + \mu_\phi |H|^2\phi- {1\over 2}\mu_\phi v^2\phi + \lambda_\phi |H|^2\phi^2\\&\quad+m_\phi^2\phi^2+\lambda_4\phi^4 +\mu_S S S^\ast \phi + \lambda_S S S^\ast \phi^2 +\mu_X X^\mu X_\mu \phi\\&\quad + \lambda_X X^\mu X_\mu \phi^2\; , \end{aligned} $

(2) where H is the SU
$ (2)_L $ Higgs doublet as$ H = (0,h/\sqrt{2})^T $ . We assume that S is invariant under a global U$ (1) $ symmetry in the dark sector, which eliminates all the terms with complex coefficients. We follow Refs. [32, 66] to neglect the Higgs portal terms$ SS^\ast |H|^2 $ and$ XX|H|^2 $ as the new sector could be sequestered. If the bosonic particles are written as superfields in a SUSY theory at a higher scale, the superpotential does not lead to these Higgs portal terms [32]. Also, the sectors can be sequestered if the theory arises from an extra dimension [32]. As a result, the Higgs field H does not directly couple to S or X, with the absent$ SS^\ast |H|^2 $ and$ XX|H|^2 $ terms. After the SM Higgs doublet develops a vacuum expectation value (vev, v), the electroweak symmetry is broken. The trilinear term$ \mu_\phi |H|^2\phi $ is introduced to mix$ \phi $ and H. We also choose the linear term of$ \phi $ as$ -\dfrac{1}{ 2}\mu_\phi v^2\phi $ to ensure that$ \phi $ does not obtain a vev [66, 67]. The$ \mu_\phi $ term is very small to introduce a tiny amount of mixing between H and$ \phi $ . The introduction of the trilinear term is equivalent to the case in which the singlet develops a vev spontaneously. The latter case, however, would suffer from a domain wall problem. The phenomenological results of the two cases are the same. By minimizing the above potential, one arrives at the condition$ \mu^2 = -\lambda v^2 $ . The mass spectrum is obtained as follows:$ \mathcal{M}^2 = \left( \begin{array}{cc} 2\lambda v^2 & \mu_\phi v \\ \mu_\phi v & 2m_\phi^2+\lambda_\phi v^2 \\ \end{array} \right) \,. $

(3) The mass eigenstates after diagonalizing the CP-even scalars are
$\left( \begin{array}{l} {h_1}\\ {h_2} \end{array} \right) = \left( {\begin{array}{*{20}{c}} {\cos \theta }&{\sin \theta }\\ { - \sin \theta }&{\cos \theta } \end{array}} \right)\left( \begin{array}{l} h\\ \phi \end{array} \right),$

(4) with the masses of
$ h_1 $ and$ h_2 $ being$ M_1 $ and$ M_2 $ , respectively. The mixing angle,$ \theta $ , is very tiny with$ \sin\theta\ll 1 $ . We should keep in mind that there may be more particles in the new sector, and the particles playing key roles in transitions between the SM and the dark sector are considered here.In terms of the mass eigenstates, our parameter inputs can be traded into the scalar masses and the mixing angle as
$ \lambda = \frac{1}{2 v^2} \Big( \cos^2\theta M_1^2 + \sin^2\theta M_2^2 \Big) \,, $

(5) $ \mu_\phi = \sin\theta\cos\theta(M_1^2-M_2^2)/v\;, $

(6) $ m_\phi^2 = {1\over 2}\Big(\sin^2\theta M_1^2 + \cos^2\theta M_2^2 -\lambda_\phi v^2\Big)\;. $

(7) Besides
$ M_1 = 125 $ GeV and$ v\approx 246 $ GeV, the free parameters in the physical basis are$ M_2, \theta, \lambda_\phi, \lambda_4, \mu_S, \lambda_S, \mu_X, \lambda_X\;. $

(8) The relevant cubic Higgs and quartic self-couplings in the physical basis are
$ \lambda_{111} = 3\left({c^3_\theta M_1^2\over v}+ 2s^2_\theta c_\theta \lambda_\phi v\right)\;, $

(9) $ \lambda_{1111} = 3\left({c^6_\theta M_1^2+c^4_\theta s^2_\theta M_2^2\over v^2}+ 4c^2_\theta s^2_\theta \lambda_\phi + 8s^4_\theta \lambda_4\right)\;, $

(10) $ \lambda_{211} = -{s_\theta\over v}\Big(2c^2_\theta M_1^2+c^2_\theta M_2^2-4\lambda_\phi c^2_\theta v^2+2\lambda_\phi s^2_\theta v^2\Big)\;, $

(11) $\begin{aligned}[b]& \lambda_{SS1} = s_\theta \mu_S\;, \lambda_{SS2} = c_\theta \mu_S\;, \lambda_{SS11} = 2s^2_\theta \lambda_S\;,\\&\lambda_{SS22} = 2c^2_\theta \lambda_S\;, \lambda_{SS12} = 2c_\theta s_\theta \lambda_S\;, \end{aligned} $

(12) $\begin{aligned}[b] & \lambda_{XX1} = 2s_\theta \mu_X\;,\lambda_{XX2} = 2c_\theta \mu_X\;,\lambda_{XX11} = 4s^2_\theta \lambda_X\;,\\&\lambda_{XX22} = 4c^2_\theta \lambda_X\;, \lambda_{XX12} = 4c_\theta s_\theta \lambda_X\;, \end{aligned} $

(13) with
$ s_\theta = \sin\theta $ and$ c_\theta = \cos\theta $ .To give an explanation of the Galactic gamma-ray excess via the scenario of DM cascade annihilations, here, we assume that
$ M_2/2 > M_1/4, m_S \gg m_X $ for simplicity. For scalar DM S, the annihilation process is$ S S^\ast \to h_1, h_2\to X X $ , followed by X decaying into$ e^+ e^- $ . The annihilation cross section is$ \begin{aligned}[b] \sigma =& \frac{s^4_\theta \mu_S^2 \mu_X^2}{8 \pi s} \sqrt{\frac{s-4m_X^2}{s-4m_S^2}} \frac{ s^2/(4m_X^4)-s/m_X^2+3}{(s - M_1^2)^2 + M_1^2 \Gamma_{h_1}^2} \\ &+ \frac{c^4_\theta \mu_S^2 \mu_X^2}{8 \pi s} \sqrt{\frac{s-4m_X^2}{s-4m_S^2}} \frac{ s^2/(4m_X^4)-s/m_X^2+3}{(s - M_2^2)^2 + M_2^2 \Gamma_{h_2}^2} \; , \\ \sigma v_r \simeq &{c^4_\theta \mu_S^2 \mu_X^2\over 16\pi m_S^3}\left(4{m_S^4\over m_X^4}-4{m_S^2\over m_X^2}+3\right){\sqrt{m_S^2-m_X^2}\over (M_2^2-4m_S^2)^2 }\; , \end{aligned} $

(14) where
$ v_r $ is the relative velocity, and s is the squared total invariant mass. Our concern is the case in which the annihilation of DM is away from the resonance. In addition, the decay of$ h_2 $ includes$ h_2\to SS^\ast, XX $ for$ M_1>M_2/2 $ or$ h_2\to SS^\ast, XX, h_1h_1 $ for$ M_2/2>M_1 $ , and their partial decay widths are$ \Gamma(h_2\to SS^\ast) = {c^2_\theta \mu_S^2\over 16\pi M_2}\sqrt{1-{4m_S^2\over M_2^2}} \;, $

(15) $ \Gamma(h_2\to XX) = {c^2_\theta \mu_X^2\over 8\pi M_2}\sqrt{1-{4m_X^2\over M_2^2}} \left({M_2^4\over 4m_X^4}-{M_2^2\over m_X^2}+3\right) \;, $

(16) $ \Gamma(h_2\to h_1h_1) = {\lambda_{211}^2\over 32\pi M_2}\sqrt{1-{4M_1^2\over M_2^2}}\;. $

(17) Besides the scalar DM S of our concern, a very similar scenario is the case of vector DM V. The corresponding Lagrangian is
$ \begin{aligned}[b]& -\mathcal{L}_{V} \supset \mu^2 |H|^2 + \lambda |H|^4 + \mu_\phi |H|^2\phi - {1\over 2}\mu_\phi v^2\phi + \lambda_\phi |H|^2\phi^2\\&\quad+m_\phi^2\phi^2+\lambda_4\phi^4 +\mu_V V V^\ast \phi + \lambda_V V V^\ast \phi^2 +\mu_X X^\mu X_\mu \phi \\&\quad+ \lambda_X X^\mu X_\mu \phi^2\; . \end{aligned} $

(18) The s-wave annihilation process
$ V V^\ast \to h_1, h_2\to X X $ followed by X decaying into$ e^+ e^- $ could also account for the Galactic center gamma-ray excess as that of scalar DM$ SS^\ast $ . The phenomenology is the same for our purpose. -
The particles
$ S S^\ast $ acquire their relic abundance through cascade annihilation processes. For single-component thermal freeze-out DM with DM annihilations in the s-wave, the annihilation cross section of DM is approximately$ 2.2 \times 10^{-26} $ cm3/s for DM mass$ \gtrsim $ 10 GeV [68]. In fact, one possible DM candidate may account for only a fraction$ f_\mathrm{DM} $ of the total DM in the universe. For non-self-conjugate DM S, the annihilation cross section must be$ 4.4 \times 10^{-26} / f_\mathrm{DM} $ cm3/s. The present cascade annihilation of$ S S^\ast $ may account for the long-standing Galactic center gamma-ray excess, and next, we will present an analysis of it. -
In the cascade annihilation
$ S S^\ast \to h_1, h_2 \to X X $ followed by X decaying into$ e^+ e^- $ , the electron and positron are boosted in the final state. In this paper, we have the mass relation$ m_S \gg m_X \gg m_e $ , and thus, the corresponding energy of$ e^+ $ and$ e^- $ can be as high as$ m_S $ . A possible gamma-ray signal could be produced via inverse Compton scattering (ICS) and bremsstrahlung in DM cascade annihilation. To account for the Galactic center gamma-ray excess peak at around 1-3 GeV, the contribution from ICS emission is crucial, and the contribution from bremsstrahlung emission is subdominant.For the annihilation of
$ S S^\ast $ with a small fraction$ f_\mathrm{DM} $ , we assume that the DM spatial distribution follows that of the main DM component. The first case is that the main DM component is the WIMP type particle with a generalized Navarro-Frenk-White density profile. In this case, the S component with the mass$ m_S = 45.7^{+3.4}_{-3.3} $ GeV and the revised annihilation cross section$ f_\mathrm{DM}^2 \langle \sigma v_r \rangle /2 = 0.384^{+0.052}_{-0.051} \times 10^{-26} $ cm3/s (the factor 1/2 is for the$ S S^\ast $ pair required in annihilation) can fit the GeV excess [14]. In the second case, the main DM component is self-interacting DM (SIDM), motivated by the small-scale problem. The density of SIDM at the Galactic center could be comparable to or larger than the cold DM predictions when SIDM tracks the baryonic potential [69]. In this case, the S component with the mass$ m_S \sim 50 $ GeV and the revised annihilation cross section$ f_\mathrm{DM}^2 \langle \sigma v_r \rangle \sim 6.3 \times 10^{-27} $ cm3/s could fit the GeV excess [33]. Thus, to explain the Galactic gamma-ray excess, we adopt two benchmark points for DM mass and the revised annihilation cross section with [$ m_S = 45.7 $ GeV,$ f_\mathrm{DM}^2 \langle \sigma v_r \rangle /2 = 0.384\times 10^{-26} $ cm3/s] for the WIMP dominant case and [$ m_S = 50 $ GeV,$ f_\mathrm{DM}^2 \langle \sigma v_r \rangle /2 = 0.315\times 10^{-26} $ cm3/s] for the SIDM dominant case. The corresponding fraction$ f_\mathrm{DM} $ can then be derived as$ f_\mathrm{DM} \simeq \bigg \{ \begin{array}{cc} 0.175 \, , & \rm for \; WIMP \; dominant \, \\ 0.143 \, , & \rm for \; SIDM \; dominant \, \end{array} \, . $

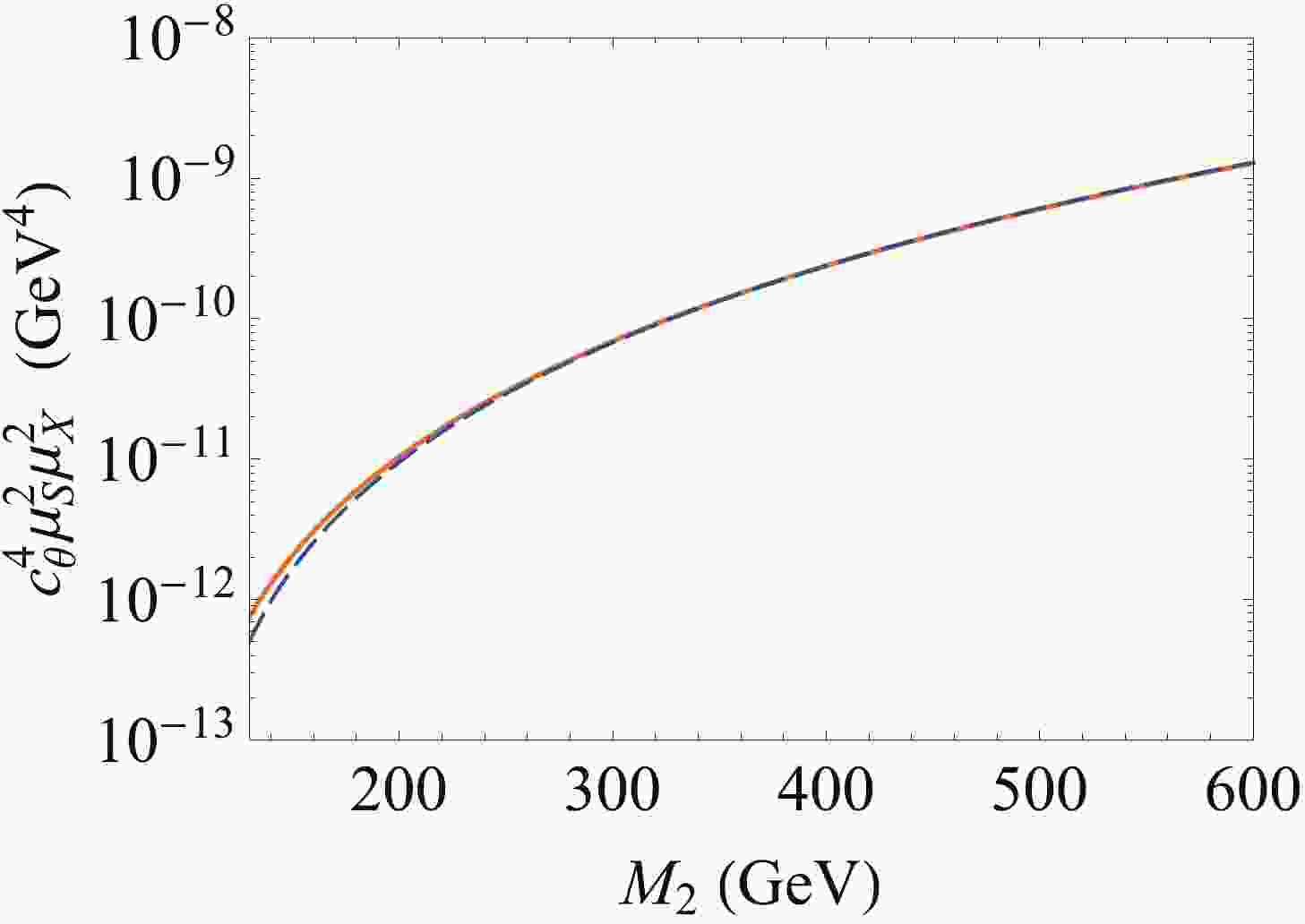
(19) We consider the case in which the DM annihilation is away from the resonance with
$ M_2 /2 m_S \gtrsim 1.3 $ (see e.g. Ref. [70]). Thus, today's annihilation cross section of$ S S^* $ is equal to that at the freeze-out epoch. We can obtain the coupling parameter saturating the annihilation cross section as a function of the mediator's mass$ M_2 $ , as shown in Fig. 1. -
As stated in the Introduction, the explanation of the Galactic center gamma-ray excess with DM annihilations needs to be compatible with the constraints from different scales of astrophysical observations, such as dwarf spheroidal galaxies, the Milky Way halo, and galaxy groups/clusters. Here, we will give a brief discussion about whether the cascade annihilation of concern is compatible with joint astrophysical limits.
To account for the 1-3 GeV gamma-ray excess at the Galactic center via DM cascade annihilation, the contribution from ICS emission is dominant and that from bremsstrahlung emission is subdominant. The ICS emission is closely related to the distribution of the ambient photon background, and the bremsstrahlung emission is related to the ambient gas densities. Hence, the constraints from dwarf spheroidal galaxies [26] and the Milky Way halo (regions away from the Galactic plane) [27] are relaxed owing to low starlight and gas densities. New likelihood analyses of the Galactic center region [28] set strong constraints on hadronic components produced by DM annihilations, whereas the constraints for light lepton components of
$ \mu^+ \mu^- $ ,$ e^+ e^- $ are relaxed. As the DM of concern here predominantly annihilates in the s-wave, the constraints from galaxy groups/clusters [29-31] with large relative velocity are alleviated.For DM cascade annihilations accounting for the gamma-ray excess with the contribution mainly from ICS emission, the most severe restriction is from the positron fraction observed by AMS-02. In the case of DM mass in tens of GeV, the effective cross section of DM cascade annihilations today indicated by AMS-02 [71] should be
$ \lesssim 1 \times 10^{-26} $ cm$^3/{\rm s}$ , and it can be achieved by a small fraction$ f_\mathrm{DM} $ of DM participating in the cascade process (the effective annihilation cross section today is proportional to$ f_\mathrm{DM}^2 $ ). For the WIMP dominant case, the upper limit of the revised annihilation cross section set by AMS-02 is approximately$ 0.8\times 10^{-26} $ cm3/s with$ m_S\simeq 45.7 $ GeV [71], and thus, the benchmark point [45.7 GeV,$ 0.384\times 10^{-26} $ cm3/s] is allowed by the AMS-02. For the SIDM dominant case, the fact that the SIDM tracks the baryonic potential can raise the density of SIDM at the Galactic center [69]. In this case, the benchmark point [50 GeV,$ 0.315\times 10^{-26} $ cm3/s] could fit the GeV excess and is allowed by the AMS-02 constraint [33]. Thus, the DM cascade annihilation of concern can give an interpretation on the Galactic gamma-ray excess and meanwhile is compatible with the joint astrophysical constraints mentioned above. -
Now, we turn to the DD via DM-target nucleus scattering. The quark-level effective Lagrangian for the evaluation of the DM-nucleon spin-independent (SI) scattering cross section is given by
$ \mathcal{L}_{\rm eff} = C_q m_q SS^\ast \bar{q}q\;, $

(20) with
$ C_q^{\rm tree} = {s_\theta c_\theta \mu_S\over v M_2^2}-{s_\theta c_\theta \mu_S\over v M_1^2} \;, \quad C_q^{\rm loop}\simeq {c^2_\theta \mu_S \mu_X g_q^2\over 8\pi^2 M_2^2 m_X^2}\;. $

(21) Besides contributions from
$ \phi $ -Higgs couplings, here, the contribution from X-quark coupling is considered. The diagrams for DM-quark scattering are given in Fig. 2. The DM-nucleon SI scattering cross section is given by$ \sigma_{\rm SI} = {1\over 4\pi} \left({m_N\over m_S+m_N}\right)^2 |C_N|^2 \;, $

(22) with the nucleon level coefficients being
$ C_N = m_N \sum_{q = u,d,s,c,b,t}C_q f_{q}^N \;. $

(23) Note that the heavy quark contribution for the loop diagram is through the two-loop diagram connecting to the scalar-type DM-gluon operator [72-74] and thus can be neglected.
If the tree-level contribution is dominant in DM-nucleon scattering, the following parameter values are adopted,
$ \sum_{q = u,d,s,c,b,t}C_q f_{q}^N = C_q^{\rm tree} f_N \;, \quad f_N = \sum_{q = u,d,s}f_{T_q}^N + {2\over 9}f_{TG}^N \;, $

(24) where
$ f_{T_q}^N $ and$ f_{TG}^N $ are light quark/gluon-nucleon form factors, with$ f_N \approx 0.308 $ [75-77]. In the case of the loop contribution from X-quark couplings being dominant in DM-nucleon scattering, the SI cross section induced by the loop level is$ \begin{aligned}[b] \sigma_{\rm SI}\simeq & 4.3\times 10^{-64}\; {\rm cm}^2 \left({g_s\over 10^{-3}}\right)^4 \left({c^4_\theta \mu_S^2 \mu_X^2\over 10^{-12}\; {\rm GeV}^4}\right) \\ &\times \left({100\; {\rm GeV}\over M_2}\right)^4 \left({17\; {\rm MeV}\over m_X}\right)^4 \left({45.7\; {\rm GeV}\over m_S}\right)^2 \; . \end{aligned} $

(25) For the cross section to be as large as possible, here, the s quark coupling parameter
$ g_s $ is considered to be$ \sim 10^{-3} $ . The typical value of this loop contribution is far below the neutrino floor. For the case in which the tree-level contribution dominates over the loop-level contribution in DM-nucleon scattering, the scattering cross section is shown in Fig. 3.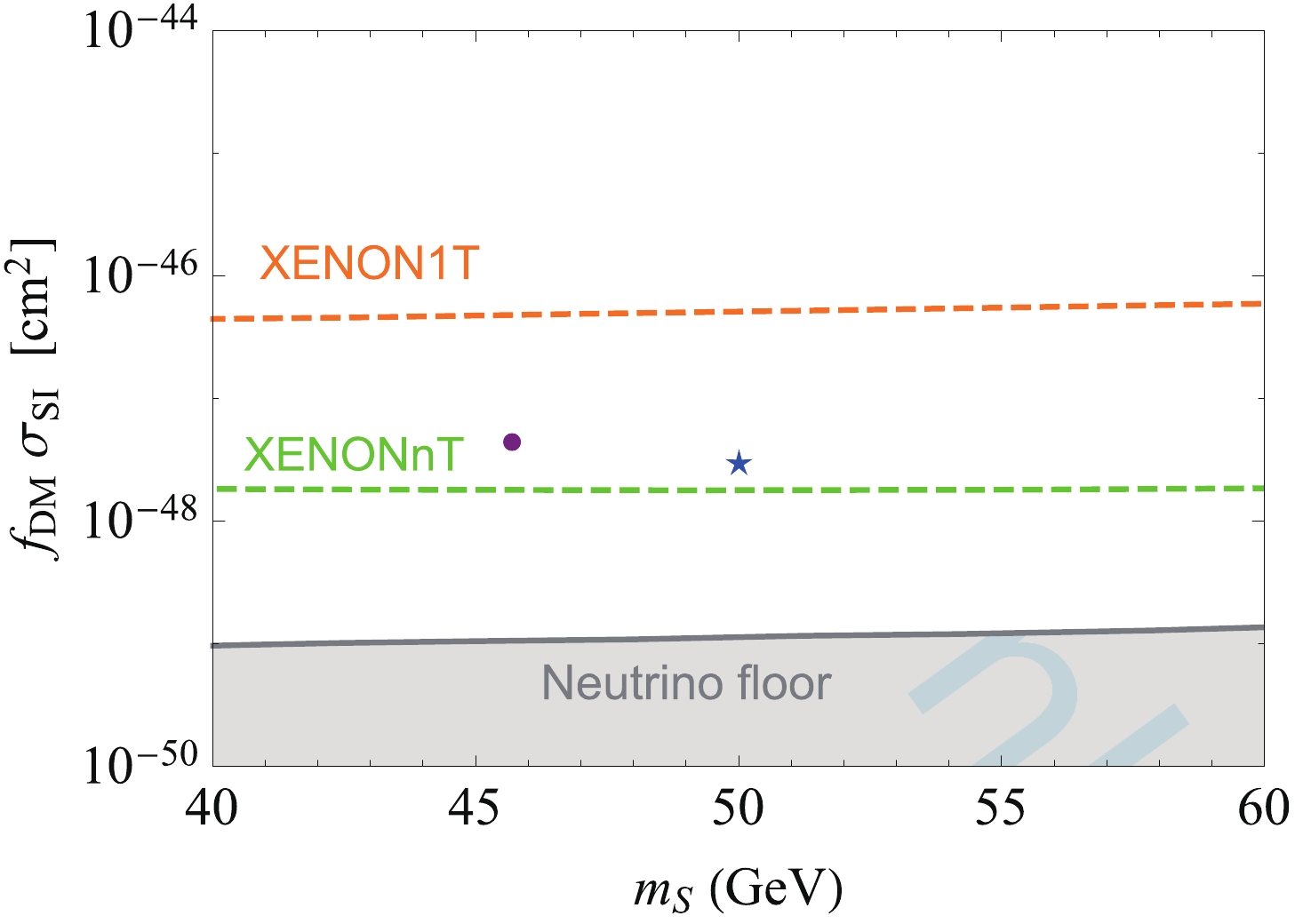
Figure 3. (color online) Rescaled DM-nucleon scattering cross section in the case of the tree-level contribution being dominant. Here, we adopt
$ M_2 = $ 200 GeV and$ s_\theta c_\theta \mu_S = 1 $ GeV. The dot (star) marker is for the WIMP (SIDM) dominant benchmark point. The upper and lower dashed curves correspond to the upper limits set by XENON1T [3] and the projection by XENONnT (20 t$ \cdot $ y) [78], respectively. The solid curve is the neutrino floor [79].The possible contribution from kinetic mixing between X and Z or X and
$ \gamma $ generated at one-loop level by virtual SM fermions is minor compared with the X couplings to light quarks and electron. Thus, the possible minor contributions from kinetic mixing are neglected for simplicity. -
We have investigated a small fraction of DM that mainly annihilates into a pair of on-shell vector boson X followed by
$ X \to e^+ e^- $ . The X boson is indicated by 8Be and 4He anomalous transitions. The long-standing Galactic center gamma-ray excess can be explained by a small fraction of scalar DM annihilation in the cascade process of$ S S^\ast \to h_1, h_2 \to X X $ followed by$ X \to e^+ e^- $ , with contributions from ICS emission being dominant. This DM cascade annihilation could be compatible with joint astrophysical limits from different scales of astronomical observations, such as dwarf spheroidal galaxies, the Milky Way halo, and galaxy groups/clusters, and meanwhile be allowed by the positron fraction observed by AMS-02. Hence, the scenario of DM annihilation is still available to explain the Galactic center gamma-ray excess after considering these joint astrophysical limits. The loop effect from X-quark couplings in DM-nucleon scattering is too small to be directly detected, and the tree-level contribution is analyzed. Moreover, we suppose that the coupling between$ S S^\ast $ and X is negligible. If there is a tiny amount of coupling between$ S S^\ast $ and X, the picture of DM-nucleus scattering with contact interactions fails in direct detection. A method to deal with this case is discussed in Ref. [80]. We look forward to the further investigation of DM in future joint detections. -
T. Li would like to thank Jia Liu for very useful discussion and communication.
Interpretation of the Galactic gamma-ray excess with the dark matter indicated by 8Be and 4He anomalous transitions
- Received Date: 2020-11-25
- Available Online: 2021-06-15
Abstract: The long-standing Galactic center gamma-ray excess could be explained by GeV dark matter (DM) annihilation, but the DM interpretation seems to conflict with recent joint limits from different astronomical scale observations such as dwarf spheroidal galaxies, the Milky Way halo, and galaxy groups/clusters. Motivated by 8Be and 4He anomalous transitions with possible new interactions mediated by a vector boson X, we consider a small fraction of DM mainly annihilating into a pair of on-shell vector bosons






 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF












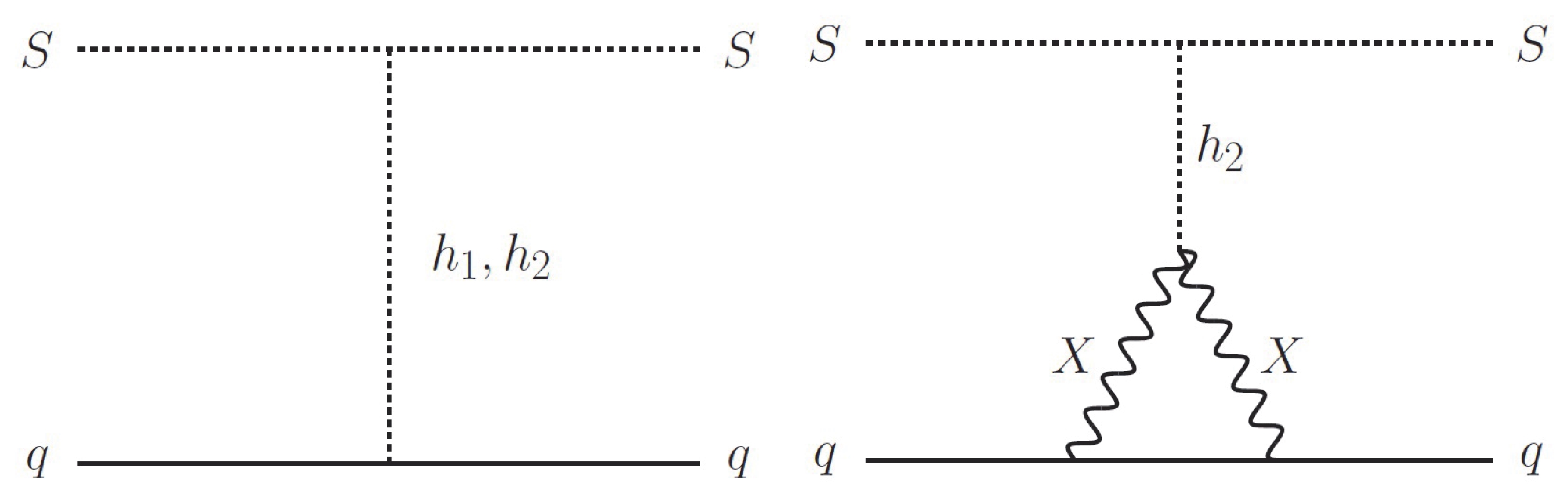



 DownLoad:
DownLoad: